Вероятность появления хотя бы одного события
Вероятность наступления события А, заключающийся в появлении хотя бы одного из n независимых в совокупности событий А1, А2,…, Аn определяется по формуле:
$P\left( A \right) = 1 — P\left( {\bar A} \right) = 1 — {q_1}\cdot{q_2}\cdot \ldots \cdot{q_n}$
$\overline {{A_1}} ,\overline {{A_2}} , \ldots ,\overline {{A_n}} $ — вероятности противоположных событий.
Вероятность наступления противоположного события $\overline {{A}}$ находится по формуле: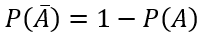
или
q=1–p
где q — вероятность наступления события, противоположного событию
Пример 1
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,02 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение
q1 — вероятность неисправности первого платёжного автомата;
q2 — вероятность неисправности второго платёжного автомата.
Искомая вероятность равна:
P=1–0.02·0.02=0.9996
Пример 2
Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый должен сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что стрелки получат приз.
Решение
А — «стрелки получат приз». Из условия задачи вероятность попадания равна р=0.3, следовательно вероятность их промаха
q=1–р=1–0,3=0,7
Отсюда искомая вероятность равна
P(A)=1–q4=1–0,74=
=1–0,2401=0,7599
Пример 3
Вероятность попадания при одном выстреле в мишень 0,7. Найдите вероятность хотя бы одного попадания при 4 выстрелах.
Решение
q=1–р=1–0,7=0,3
P(A)=1–q4=1–0,34=
=1–0,0081=0,9919
Пример 4
Устройство содержит два независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятности отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
Решение
А — «устройство не работает»
A1 — «отказал первый элемент»
A2 — «отказал второй элемент»
Найдём вероятности безотказной работы независимых элементов
q1=1-0,05=0,95,
q2=1-0,08=0,92
Следовательно, вероятность того, что устройство не работает равна
P(A)=1-q1·q2=1-0,95·0,92=
==1-0,874=0,126
Пример 5
Вероятность того что студент сдаст первый экзамен равна 0.7, второй — 0.5, третий — 0.6. Найти вероятность того, что студентом будет сдан хотя бы один экзамен.
Решение
Здесь событие A — студент сдаст все экзамены
Противоположное событие $\overline {{A}} $ студент не сдаст все экзамены
По теореме умножения имеем
P(A)=1-(1-p1)·(1-p2)·(1-p3)
P(A)=1-(1-0.7)·(1-0.5)·(1-0.6)=0.94
Пример 6
Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить четыре бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,5; 0,6
Решение
А — «мост разрушен»
$\overline {{A}}$— «ни одна авиационная бомба не попала в мост»
Здесь события:
A1=0.3, A2=0.4, A3=0.5, A4=0.6 из условия задачи.
Воспользуемся формулой: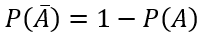
Находим соответствующие им вероятности
$\overline {{A_1}}$ — «первая авиационная бомба не попала в мост »
Р( $\overline {{A_1}}$ ) = 1-0,3 = 0,7
$\overline {{A_2}}$ — «вторая авиационная бомба не попала в мост »
Р($\overline {{A_2}}$) = 1 — 0,4 = 0,6
$\overline {{A_3}}$ — «третья авиационная бомба не попала в мост »
Р($\overline {{A_3}}$) = 1 — 0,5 = 0,5
$\overline {{A_4}}$ — «четвёртая авиационная бомба не попала в мост »
Р($\overline {{A_4}}$) = 1-0,6 = 0,4
Из условия задачи события A1, A2, A3 и A4 независимы, следовательно получаем
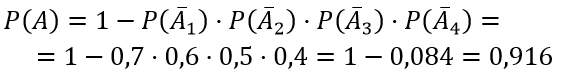
Пусть в результате испытания могут появиться п событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны.
Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.
Теорема. Вероятность появления хотя бы одного из событий А1,А2, Ап, независимых в совокупности, равна разности между единицей и произведением, вероятностей противоположных событий A1А2, Ап:
Р(А) = 1 – q1, qn
Частный случай. Если события A1А2, А„ имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий Р (Л) = 1 — qп(**)
Пример 1. Вероятности попадания в цель при стрельбе из трех орудий таковы: р1 = 0,8; р2 = 0,7;
р3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.
Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события A1(попадание первого орудия), А2(попадание второго орудия) и А3 (попадание третьего орудия) независимы в совокупности.
Вероятности событий, противоположных событиям А1 А2 и А3 (т.е. вероятности промахов), соответственно равны:
q1 = 1 – p1= 1-0,8 = 0,2; q2= 1 – p2 == 1-0,7 = 0,3; , q3= 1 – p3 = 1-0,9 = 0,1.
Искомая вероятность
Р (А) = 1 — q1q2q3 = 1 —0,2 * 0,3 * 0,1 = 0,994.
Пример 2. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).
Решение. События «машина работает» и «машина не работает» (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: p + q = 1
Отсюда вероятность того, что машина в данный момент не работает, равна q = 1-p = 1—0,9 = 0,1.
Искомая вероятность
Р (A) = 1 — q4 = 1 — 0,14 = 0,9999.
Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.
Пример 3. Вероятность того, что событие появится хотя бы один раз в трех независимых в совокупности испытаниях, равна 0,936. Найти вероятность появления события в одном испытании (предполагается, что во всех испытаниях вероятность появления события одна и та же).
Решение. Так как рассматриваемые события независимы в совокупности, то применима формула (**)
По условию, Р (А) = 0,936; п = 3. Следовательно,
0,936=1 — q3 или q3 = 1-0,936 = 0,064.
Отсюда q = 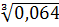 = 0,4.
= 0,4.
Искомая вероятность р = 1 — q = 1 — 0,4 = 0,6.
2.5. Вероятность появления хотя бы одного события
Теорема. Вероятность
появления хотя бы одного из событий А1,
А2,…,Аn, независимых
в совокупности, равна разности между
единицей и произведением вероятностей
противоположных событий 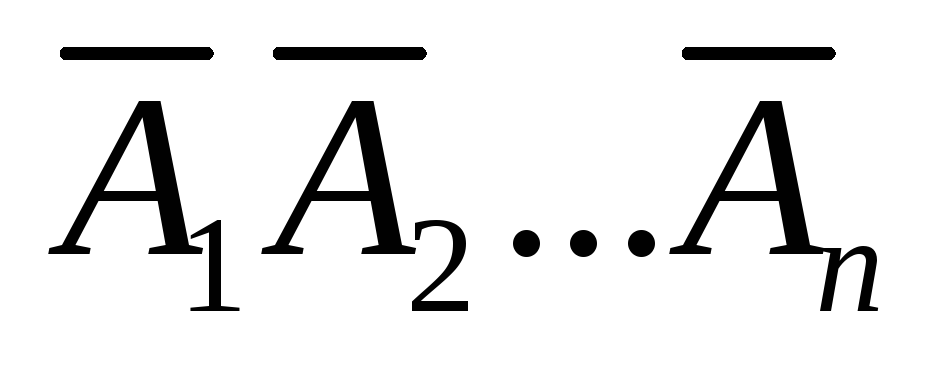 :
:
| (2.7) |
Пример 2.5. Три стрелка делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,7, второго – 0,8 и третьего – 0,9. Найти вероятность того, что хотя бы один стрелок попадет в мишень.
Решение. Рассмотрим следующие события: А – хотя бы один стрелок попадет в мишень А1 – первый стрелок попадет в мишень, А2 – второй стрелок, А3 – третий стрелок. Вероятность попадания в мишень каждым из стрелков не зависит от результатов стрельбы других стрелков, поэтому события А1, А2 и А3 независимы в совокупности.
Вероятности событий, противоположных событиям А1, А2 и А3 (т.е. вероятности промахов), соответственно равны:
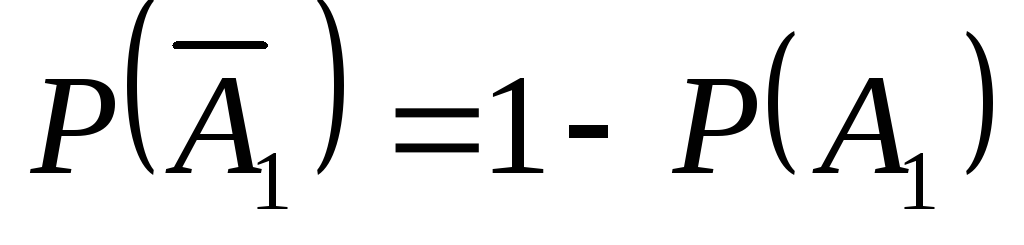
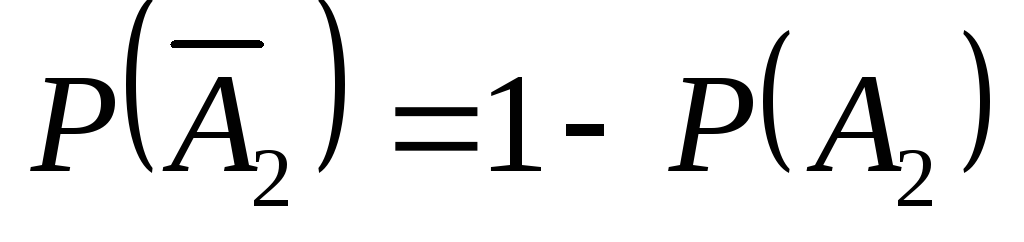 = 1 – 0,8 = 0,2;
= 1 – 0,8 = 0,2;
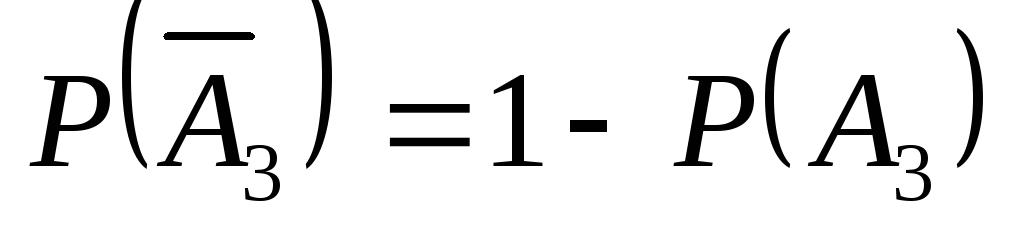 = 1 – 0,9 = 0,1.
= 1 – 0,9 = 0,1.
Искомая вероятность
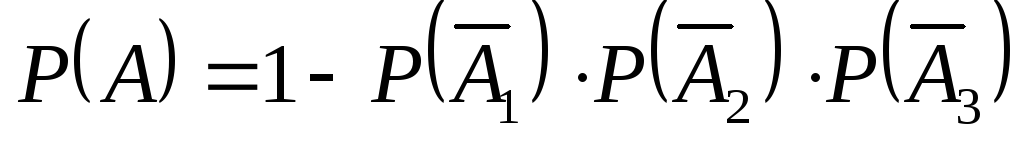 = 1 – 0,3·0,2·0,1
= 0,994. ◄
= 1 – 0,3·0,2·0,1
= 0,994. ◄
Частный случай. Если события А1, А2,…,Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
где q = 1 – p.
2.6. Условная вероятность
Пусть события А и В зависимые. Из определения зависимых событий следует, что вероятность одного из событий зависит от появления или непоявления другого события. Поэтому, если нас интересует вероятность события В, то важно знать, наступило событие А или нет.
Определение. Условной вероятностью РА(В) или Р(В|А) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Например, в урне находится пять шаров. Два из них белого цвета, остальные три – черного. Наудачу один за другим берут два шара, не возвращая их обратно в урну. Рассмотрим событие А – «первый вынутый шар оказался белого цвета» и событие В – «второй вынутый шар оказался белого цвета». Найдем условную вероятность события В, при условии, что событие А уже наступило. Если в первый раз был вынут шар белого цвета, то в урне осталось четыре шара, из которых один белого цвета. Следовательно, Р(В | А) = 1/4.
Если же вынутый шар возвращается назад в урну, то условия второго испытания остаются неизменными после проведения первого испытания. Тогда Р(В) = Р(В|А) = 2/5, т.е. в этом случае вероятность события В и его условная вероятность совпадают.
2.7. Теорема умножения вероятностей зависимых событий
Пусть события А и В зависимые, причем вероятности Р(А) и Р(В|А) известны. Как найти вероятность совмещения этих событий, т.е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.
Теорема. Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Р(АВ) = Р(А)·Р(В|А). | (2.9) |
Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
Р(А1А2…Аn) = Р(А1)·Р(А2| А1) …·Р(Аn| А1 А2… Аn-1). | (2.10) |
Пример 2.6. В урне находится пять шаров. Один из них красного цвета, два – зеленого и два – синего. Наудачу один за другим извлекают три шара, не возвращая их обратно в урну. Найти вероятность того, что последовательно будут извлечены красный, зеленый и синий шар.
Решение. Рассмотрим события: A – первым извлечен шар красного цвета, B – вторым извлечен шар зеленого цвета, C – третьим извлечен шар синего цвета. Вероятность события А: Р(А) = 1/5. Условная вероятность события В при условии, что событие А уже наступило: Р(В|А) = 2/4. Условная вероятность события С при условии, что события А и В уже наступили: Р(С|АВ) = 2/3. Вероятность совместного появления трех зависимых событий А, В и С:
Р(АВС)
= Р(А)·Р(В/А)·Р(С/АВ)
= 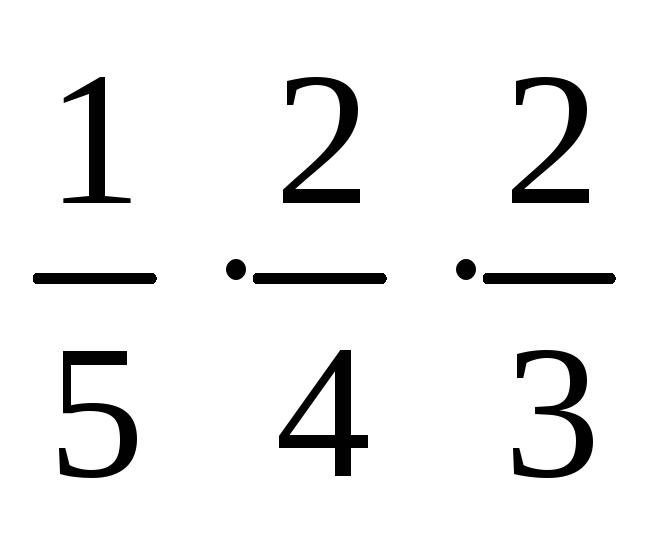 =
=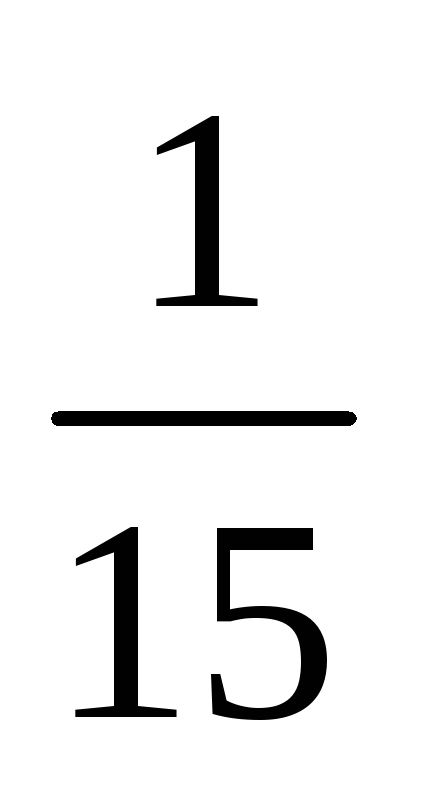 .
◄
.
◄
16 . Вероятность появления хотя бы одного события
Пусть имеется некоторый набор независимых в совокупности событий А1, А2, …, Аn, связанных с некоторым экспериментом. Допустим, что известны вероятности, с которыми каждое из этих событий может появиться: Р(А1) = р1, Р(А2) = р2 , …, Р(Аn) = рn. Выясним, с какой вероятностью появиться хотя бы одно из этих событий. Обозначим интересующее нас событие: А – появилось хотя бы одно из группы событий А1, А2, …, Аn. Здесь как раз тот случай, когда гораздо проще вычислить вероятность не самого события А, а противоположного ему события Ā – ни одно из событий А1, А2, …, Аn не произошло. Но если не произошло событие, к примеру, А1, то это означает, что произошло противоположное для него событие Ā1. Поэтому событие Ā происходит только в том случае, когда одновременно происходят все события А1, А2, …, Аn, т. е. Ā = Ā1·Ā2· … ·Ān. Из совокупной независимости событий А1, А2, …, Аn следует совокупная независимость системы противоположных событий Ā1, Ā2, …, Ān (см. замечание после теоремы с формулой (15.3)). Поэтому из формулы (15.3) получаем Р(Ā) = Р(Ā1·Ā2· … ·Ān) = Р(Ā1)·Р(Ā2)· … ·Р(Ān). Обозначим для краткости вероятности противоположных событий: q1 = Р(Ā1), q2 = Р(Ā2), …, qn = Р(Ān). Ясно, что q1 = 1 – p1 , …, qn =1– pn (так связаны вероятности противоположных событий). Таким образом, имеем формулу Р(Ā) = q1 q2 … qn, тогда Р(А)=1 – Р(Ā)=1 – q1 q2 … qn. Тем самым доказана следующая теорема.
Теорема. Вероятность появления хотя бы одного события из системы независимых в совокупности событий А1, А2, …, Аn равна единице минус произведение вероятностей событий, противоположных данным:
Р(А) = 1 – q1 q2 … qn, (16.1)
где qi = 1 – pi, pi = P(Ai), i = 1, 2, …, n. Рассмотрим некоторые задачи на применение этой формулы.
Задача 1. В продаже имеется 3 противоугонных устройства, которые в случае попытки угона срабатывют с вероятностями р1 = 0,75, р2 = 0,8 и р3 = 0,93 соответственно. Суммарная стоимость первых двух устройств равна стоимости третьего. Что выгоднее купить – два первых или одно третье?
Поскольку по стоимости обе покупки одинаковы, то предпочесть нужно ту, при использовании которой труднее угнать машину. Допустим, что на машину поставлены 2 два первых устройства. С какой вероятностью сработает хотя бы одно из них в случае попытки угона? Обозначим события: А1 – сработало первое, А2 – второе, А – сработало хотя бы одно из них. Поскольку устройства работают независимо одно от другого, то события А1 и А2 можно считать независимыми в совокупности (хотя легко видеть, что в случае двух событий независимость в совокупности равносильна обычной независимости двух событий). Поэтому по формуле (16.1) с параметрами р1 = =0,75 и р2 = 0,8 (а потому q1 = 0,25 и q2 = 0,2) Р(А) = 1 – 0,25 · 0,2 = 0,95. Если же на машину будет поставлено одно третье противоугонное устройство, то в случае попытки угона оно сработает с вероятностью р3 = 0,93. Вывод сделайте сами. Вот еще одна типичная задача на заданную тему.
Задача 2. Есть три стрелка, которые попадают в мишень с вероятностями р1 = 0,7, р2 = 0,8 и р3 = 0,9 соответственно. Какова вероятность поражения мишени при выстреле по ней всех стрелков залпом?
Обозначим события: А1 – попал первый, А2 – второй, А3 – третий стрелок, А – мишень поражена (т. е. попал хотя бы один из них). Поскольку результаты стрельбы одного из них не влияют на результаты стрельбы другого, то события А1, А2 и А3 можно считать независимыми в совокупности. Поэтому по формуле (16.1) с параметрами р1 = 0,7, р2 = 0,8 и р3 = 0,9 (а потому q1 = 0,3, q2 = 0,2 и q3 = 0,1) Р(А) = 1 – 0,3 · 0,2 · 0,1 = 0,994.
Посмотрим на эту задачу под другим углом зрения. У нас имелся один эксперимент (состоящий из трех выстрелов), и в рамках этого эксперимента мы рассматривали три независимых в совокупности события: А1 – попал первый, А2 – второй, А3 – третий стрелок. Часто подобную ситуацию удобно рассматривать как проведение трех независимых экспериментов (выстрел первого стрелка, выстрел второго и выстрел третьего), в каждом из которых мы интересуемся появлением некоторого события (попадание в мишень), которое в каждом эксперименте может произойти со своей вероятностью ( в нашем случае с вероятностями р1 = 0,7, р2 = 0,8 и р3 = 0,9). Нам нужно определить, с какой вероятностью интересующее нас событие (попадание в мишень) произойдет хотя бы один раз. Понятно, что это переформулировка одной и той же задачи, и решение будет использовать ту же формулу (16.1). Переформулируем аналогичным образом общую сформулированную теорему в виде следствия из нее (от одного испытания с n независимыми событиями перейдем к n независимым испытаниям, в которых будем интересоваться одним событием).
Следствие 1. Пусть производится n независимых опытов, в каждом из которых некоторое событие А может появиться с вероятностями р1, р2 , …, рn соответственно. Тогда вероятность того, что событие А в этих испытаниях появиться хотя бы один раз, равна
1 – q1 q2 … qn , (16.2)
где qi = 1 – pi, pi = P(Ai) , i = 1,2, … n.
Важным частным случаем является тот, при котором вероятность появления интересующего нас события одна и та же во всех независимых опытах , т. е. р1 = р2 = … = рn (например, если бы в задаче 2 стрелял бы один и тот же стрелок, но 3 раза).
Следствие 2. Пусть производится n независимых опытов, в каждом из которых некоторое событие А может появиться с одной и той же вероятностью р. Тогда вероятность того, что событие А в этих испытаниях наступит хотя бы один раз, равна
1 – qn , (16.3)
где q = 1 – p.
Изменим условие задачи 2, взяв вместо трех стрелков одного, но разрешив ему выстрелить 3 раза, причем вероятность попадания этого стрелка возьмем средней по стрелкам из задачи 2. Измениться ли вероятность поражения мишени?
Задача 3. Вероятность попадания стрелка в мишень в каждом выстреле р = 0,8. Какова вероятность поражения мишени при трех выстрелах?
Событие А – попадание в мишень после выстрела. Проводится 3 независимых испытания (производится 3 выстрела), в каждом из которых событие А (т. е. попадание в мишень) может произойти с одной и той же вероятностью р = 0,8. Нас интересует вероятность события В – событие А произошло хотя бы один раз (т. е. мишень поражена). Как мы видим, ситуация полностью совпадает с той, которая описана в следствии 2 при р = 0,8, q = 1 – 0,8 = 0,2. Поэтому по формуле (16.3) получаем Р(В) = 1 – 0,23 = 0,992. Быть может кто-то ждал того же результата, что в задаче 2? Уже теперь (после полученного результата) можно задуматься и понять, что этот результат логичен (попробуйте!). А вот вполне практическая “военная” задача.
Задача 4. Один самолет после бомбометания поражает некую цель с вероятностью р = 0,6. Сколько самолетов необходимо послать на задание, чтобы цель была уничтожена с вероятностью большей, чем 0,9?
Пусть на задание послано n самолетов (это число n нам и надо найти). Событие А – попадание в цель самолетом после бомбометания. Имеется n независимых испытаний (т. к. бомбометания производят n самолетов). По следствию 2 (при р = 0,6, а потому q = 0,4) вероятность поражения цели после всех бомбометаний равна 1 – 0,4n. По условию задачи нужно найти такое n, чтобы выполнялось неравенство 1 – 0,4n > 0,9, т. е. 0,4 n < 0,1. Можно подбором убедиться, что n = 2 еще мало, а n = 3 уже достаточно (для более продвинутых в математике предлагаем получить формулу n > ln 0,1 / ln 0,4). Аналогичная схема может работать и для вполне мирных практических задач, таких, как, например, следующая.
Задача 5. Вероятность выигрыша по лотерейному билету равна 0,1 (т. е. выигрывает в среднем 1 билет из 10). Сколько нужно купить билетов, чтобы выиграть хотя бы по одному из них с вероятностью большей, чем 0,95 (т. е. почти наверняка)?
Пусть куплено n билетов (необходимое число n нам и предстоит определить). Проведем n “опытов” – проверим каждый билет по таблице выигрышей. В каждом из них интересующее нас событие (А – билет выиграл) может произойти с одной и той же вероятностью р = 0,1. Тогда по формуле (16.2) вероятность того, что это событие произойдет хотя бы раз (т. е. выиграет хотя бы один билет) равна 1 – 0,9n. Число n должно быть таким, чтобы выполнялось неравенство 1 – 0,9n > 0,95, т. е. 0,9n < 0,05. Такое неравенство выполняется для всех n > ln 0,05 / ln 0,9 = 28,43 …, т. е. (учитывая, что число n может быть только целым) начиная с n = 29. Остается сравнить стоимость выигрыша со стоимостью такого количества билетов.
Следующая задача уходит глубоко в историю.
Задача 6 (задача Шевалье Де Мере). В средние века одним из основных развлечений феодалов были азартные игры (кстати, появление теории вероятности во многом обязано именно им). Некий француз Шевалье Де Мере не только был азартным игроком, но имел свойство замечать некоторые закономерности в играх, но не всегда мог их объяснить. По счастью одним из его хороших знакомых был знаменитый ученый Блез Паскаль (1623 – 1662, один из основателей теории вероятности), к которому Шевалье приходил за разъяснениями. Вот один из подобных эпизодов. Шевалье предлагал сопернику такую игру. Он (Шевалье) бросает пару кубиков 24 раза и выигрывает в случае, если хотя бы раз выпадает пара (6, 6). Противник бросает 4 раза один кубик (или, что то же самое, четыре кубика один раз) и выигрывает, если хотя бы раз выпало 6 очков. При этом Шевалье был уверен, что у него шансов на выигрыш при таких условиях больше, чем у соперника. Но почему-то Шевалье чаще проигрывал, чем выигрывал. Объяснить это он попросил Паскаля. Давайте вслед за Паскалем проанализируем эту ситуацию.
Посчитаем вероятности выигрыша Шевалье и его соперника и сравним их. Для Шевалье. Обозначим события: А – при бросании пары кубиков выпало две шестерки, В – при 24 подбрасываний пары кубиков событие А появилось хотя бы один раз (т. е. Шевалье выиграл). Посчитаем вероятность события А. В § 2 мы определили пространство элементарных исходов при однократном бросании пары кубиков = 11 , 12 , … , 16 , 21 , 22 , … , 26 , … ,61 , 62 , … ,66 }, состоящее из 36 исходов, причем для события А благоприятен лишь один из них А = 66, поэтому Р(А) = 1/36. Понятно, что 24 бросания пары кубиков это 24 независимых опыта, в каждом из которых событие А может появиться с одной и той же вероятностью р = 1/36. Поэтому вероятность того, что оно появиться хотя бы один раз (т. е. вероятность события В) можно посчитать по формуле (16.2) при р = =1/36 (а потому q = 35/36): Р(В) = 1 – (35/36)24 ≈ 0,4914. Посчитаем вероятность выигрыша противника Шевалье. Обозначим события: А – при бросании одного кубика выпала шестерка, В – при 4 бросаниях кубика событие А появилось хотя бы один раз (т. е. соперник выиграл). Для читателя уже должно быть очевидно, что Р(А) = 1/6, а вероятность того, что это событие в 4 испытаниях появится хотя бы один раз Р(В) = 1 – (5/6)4 ≈ 0,5177. Теперь становится ясно, почему Шевалье выигрывал реже, чем его соперники.
События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти. В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).
Зачем нужна теория вероятности
Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.
Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.
В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.
Основные понятия теории вероятности
Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.

Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.
Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.
События А и В называется несовместными, если они не могут произойти одновременно.
Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом
.
Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом
.
Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.
- Вероятность принимает значения на отрезке от 0 до 1, т.е.
 .
. - Вероятность невозможного события равна 0, т.е.
 .
. - Вероятность достоверного события равна 1, т.e.
 .
. - Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е.
 .
.
Важным частным случаем является ситуация, когда имеется  равновероятных элементарных исходов, и произвольные
равновероятных элементарных исходов, и произвольные  из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле
из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле  . Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.
. Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.
Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов  , прямо в условии написано число всех исходов
, прямо в условии написано число всех исходов  .
.

Ответ получаем по формуле  .
.
Пример задачи из ЕГЭ по математике по определению вероятности
На столе лежат 20 пирожков — 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?
Решение.
Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть  , где А — это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:
, где А — это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:
![Rendered by QuickLaTeX.com \[ P(A)=\frac{k}{n}=\frac{8}{20}=0,4 \]](/800/600/https/repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-acc0fc43beb84bd5ae7fdd464101705e_l3.png)
Ответ: 0,4
Независимые, противоположные и произвольные события
Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.
События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.
Событие B состоит в том, что событие А не произошло, т.е. событие B является противоположным к событию А. Вероятность противоположного события равна единице минус вероятность прямого события,т.е.  .
.
Теоремы сложения и умножения вероятностей, формулы
Для произвольных событий А и В вероятность суммы этих событий равна сумме их вероятностей без вероятности их совместного события, т.е.
.
Для независимых событий А и В вероятность произведения этих событий равна произведению их вероятностей, т.е. в этом случае
.
Последние 2 утверждения называются теоремами сложения и умножения вероятностей.
Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.
Сколькими способами можно усадить 6 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Для третьего ученика остается 4 свободных места, для четвертого — 3, для пятого — 2, шестой займет единственное оставшееся место. Чтобы найти число всех вариантов, надо найти произведение  , которое обозначается символом 6! и читается «шесть факториал».
, которое обозначается символом 6! и читается «шесть факториал».
В общем случае ответ на этот вопрос дает формула для числа перестановок из п элементов  В нашем случае
В нашем случае  .
.
Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение  .
.
В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам
![Rendered by QuickLaTeX.com \[ A^{k}_{n}=n \cdot (n-1) \cdot (n-2) \dots \cdot(n-k+1)= \frac{n!}{(n-k)!} \]](/800/600/https/repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-89b8eada25275ae01e07de0c9286712c_l3.png)
В нашем случае  .
.
И последний случай из этой серии. Сколькими способами можно выбрать трех учеников из 6? Первого ученика можно выбрать 6 способами, второго — 5 способами, третьего — четырьмя. Но среди этих вариантов 6 раз встречается одна и та же тройка учеников. Чтобы найти число всех вариантов, надо вычислить величину:  . В общем случае ответ на этот вопрос дает формула для числа сочетаний из
. В общем случае ответ на этот вопрос дает формула для числа сочетаний из  элементов по
элементов по  элементам:
элементам:
![Rendered by QuickLaTeX.com \[ C^{k}_{n}=\frac{n \cdot (n-1) \cdot (n-2) \dots (n-k+1)}{1\cdot 2 \cdot 3 \dots \cdot k}=\frac{n!}{k! \cdot (n-k)!}. \]](/800/600/https/repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-a3f4bbf13755f16c6e57eecaf8df2d84_l3.png)
В нашем случае  .
.
Примеры решения задач из ЕГЭ по математике на определение вероятности
Задача 1. Из сборника под ред. Ященко.
На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Саша наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение:
 .
.
Ответ: 0,3.
Задача 2. Из сборника под ред. Ященко.
В каждой партии из 1000 лампочек в среднем 20 бракованных. Найдите вероятность того, что наугад взятая лампочка из партии будет исправной.
Решение: Количество исправных лампочек 1000-20=980. Тогда вероятность того, что взятая наугад лампочка из партии будет исправной:

Ответ: 0,98.
Задача 3.
Вероятность того, что на тестировании по математике учащийся У. верно решит больше 9 задач, равна 0,67. Вероятность того, что У. верно решит больше 8 задач, равна 0,73. Найдите вероятность того, что У. верно решит ровно 9 задач.
Решение:
Если мы вообразим числовую прямую и на ней отметим точки 8 и 9, то мы увидим, что условие «У. верно решит ровно 9 задач» входит в условие «У. верно решит больше 8 задач», но не относится к условию «У. верно решит больше 9 задач».
Однако, условие «У. верно решит больше 9 задач» содержится в условии «У. верно решит больше 8 задач». Таким образом, если мы обозначим события: «У. верно решит ровно 9 задач» — через А, «У. верно решит больше 8 задач» — через B, «У. верно решит больше 9 задач» через С. То решение будет выглядеть следующим образом:
 .
.
Ответ: 0,06.
Задача 4.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,2. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Давайте подумаем какие у нас даны события. Нам даны два несовместных события. То есть либо вопрос будет относиться к теме «Тригонометрия», либо к теме «Внешние углы». По теореме вероятности вероятность несовместных событий равна сумме вероятностей каждого события, мы должны найти сумму вероятностей этих событий, то есть:

Ответ: 0,35.
Задача 5.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания одной лампы в течение года равна 0,29. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Решение:
Рассмотрим возможные события. У нас есть три лампочки, каждая из которых может перегореть или не перегореть независимо от любой другой лампочки. Это независимые события.
Тогда укажем варианты таких событий. Примем обозначения:  — лампочка горит,
— лампочка горит,  — лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события «лампочка перегорела», «лампочка горит», «лампочка горит»:
— лампочка перегорела. И сразу рядом подсчитаем вероятность события. Например, вероятность события, в котором произошли три независимых события «лампочка перегорела», «лампочка горит», «лампочка горит»:  , где вероятность события «лампочка горит» подсчитывается как вероятность события, противоположного событию «лампочка не горит», а именно:
, где вероятность события «лампочка горит» подсчитывается как вероятность события, противоположного событию «лампочка не горит», а именно:  .
.
















Заметим, что благоприятных нам несовместных событий всего 7. Вероятность таких событий равна сумме вероятностей каждого из событий:  .
.
Ответ: 0,975608.
Еще одну задачку вы можете посмотреть на рисунке:

Таким образом, мы с вами поняли, что такое теория вероятности формулы и примеры решения задач по которой вам могут встретиться в варианте ЕГЭ.
5. Вероятность появления хотя бы одного события
Теорема.
Вероятность появления хотя бы одного
из событий 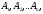 независимых в совокупности, равна
разности между единицей и произведением
вероятностей противоположных событий
независимых в совокупности, равна
разности между единицей и произведением
вероятностей противоположных событий 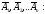
 ,
,
где 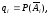
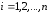 .
.
Доказательство. Обозначим через  событие, состоящее в появлении хотя бы
одного из событий
событие, состоящее в появлении хотя бы
одного из событий 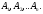 События
События 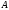 и
и 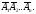 (ни одно из событий не наступило)
противоположны. Следовательно, сумма
их вероятностей равна единице:
(ни одно из событий не наступило)
противоположны. Следовательно, сумма
их вероятностей равна единице:
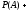
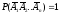 .
.
Отсюда, пользуясь теоремой умножения, получим


Или
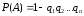 .
.
Если события  имеют одинаковую вероятность, равную
имеют одинаковую вероятность, равную 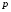 ,
то вероятность появления хотя бы одного
из этих событий равна
,
то вероятность появления хотя бы одного
из этих событий равна
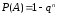 .
.
Пример. Вероятности попадания в цель при
стрельбе из трех орудий таковы: 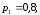
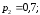
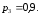 Найти вероятность хотя бы одного
попадания (события
Найти вероятность хотя бы одного
попадания (события 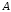 )
при одном залпе из трех орудий.
)
при одном залпе из трех орудий.
Решение. Вероятности не попаданий при залпе выстрелов:
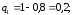
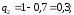
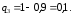
Искомая вероятность
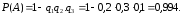
Глава 4. Следствия теорем сложения и умножения
1. Теорема сложения вероятностей совместных событий
Теорема. Вероятность появления хотя бы одного из двух событий равна сумме вероятностей этих событий без вероятности их совместного появления:
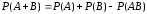 .
.
Пример. Вероятности попадания в цель при
стрельбе первого и второго орудий
соответственно равны: 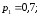
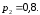 Найти вероятность попадания при одном
залпе хотя бы одним из орудий.
Найти вероятность попадания при одном
залпе хотя бы одним из орудий.
Решение.
Пусть событие  —
попадание первого орудия,
—
попадание первого орудия, 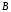 —
попадание второго орудия. Они независимы.
Тогда
—
попадание второго орудия. Они независимы.
Тогда

Искомая вероятность равна
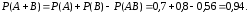
Задачу можно решить и пользуясь формулой
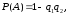
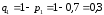 ,
, 

2. Формула полной вероятности
Пусть событие 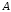 может
наступить при условии появления одного
из несовместных событий
может
наступить при условии появления одного
из несовместных событий 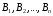 ,
которые образуют полную группу. Пусть
известны вероятности этих событий
,
которые образуют полную группу. Пусть
известны вероятности этих событий 
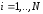 и условные вероятности
и условные вероятности 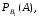
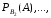 .
.
Теорема.
Вероятность события  ,
которое может наступить лишь при условии
появления одного из несовместных событий
,
которое может наступить лишь при условии
появления одного из несовместных событий 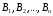 , образующих полную группу, равна сумме
произведений вероятностей каждого из
этих событий на соответствующую условную
вероятность события
, образующих полную группу, равна сумме
произведений вероятностей каждого из
этих событий на соответствующую условную
вероятность события  :
:
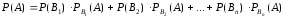 —
—
— формула полной вероятности.
Доказательство. По условию, событие  реализуется лишь при осуществлении
любого из несовместных событий
реализуется лишь при осуществлении
любого из несовместных событий 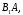
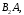 …,
…,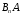 .
Тогда по теореме сложения
.
Тогда по теореме сложения
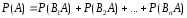 .
(*)
.
(*)
Каждое слагаемое в этой формуле по теореме умножения вероятностей зависимых событий:
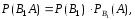
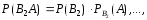

Подставляя эти формулы в (*) получим формулу полной вероятности.
Пример. Имеются три урны с шарами. В первой
находится 5 голубых и 3 красных шара, во
второй – 4голубых и 4 красных, в третьей
– 8 голубых. Наугад выбирается одна из
урн и из нее наугад извлекается шар.
Какова вероятность того, что он окажется
красным (событие 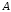 ).
).
Решение. Шар может быть извлечен из любых трех
урн. Обозначим через  —
выбор урн. Вероятности выбора урн
одинаковые:
—
выбор урн. Вероятности выбора урн
одинаковые: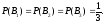 Из условия задачи
Из условия задачи 
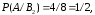

Тогда искомая вероятность
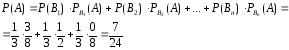
3. Вероятность гипотез. Формула Бейеса
Пусть событие 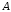 может
наступить при условии появления одного
из несовместных событий
может
наступить при условии появления одного
из несовместных событий 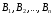 ,
образующих полную группу. Так как заранее
не известно, какое из этих событий
наступит, их называют гипотезами. Вероятность наступления события
,
образующих полную группу. Так как заранее
не известно, какое из этих событий
наступит, их называют гипотезами. Вероятность наступления события  определяется по формуле полной вероятности
определяется по формуле полной вероятности
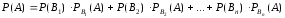 .
.
Допустим, что произведено испытание, в
результате которого появилось событие 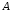 .
Поставим себе задачу, определить, как
изменились в связи с наступлением
события
.
Поставим себе задачу, определить, как
изменились в связи с наступлением
события 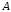 ,
вероятности гипотез
,
вероятности гипотез 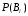 ,
т.е.,
,
т.е.,  ,
, 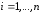 ?
?
Найдем
условные вероятности 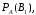

 по теореме умножения вероятностей
по теореме умножения вероятностей
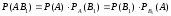 .
.
Отсюда

или
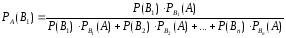 .
.
Аналогично выводятся условные вероятности остальных гипотез
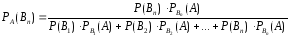 .
.
Это формулы
Бейеса, позволяющие переоценить
вероятности гипотез после того, как
становится известным результат испытания,
в итоге которого появилось событие 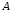 .
.
Пример. В
пяти ящиках находятся одинаковые по
весу и размерам ящиках шары. В двух
ящиках – 6 голубых и 4 красных шара (ящик
состава  ).
В двух других ящиках (состава
).
В двух других ящиках (состава  —
по 8 голубых и 2 красных шара. В одном
ящике (состава
—
по 8 голубых и 2 красных шара. В одном
ящике (состава  —
2 голубых и 8 красных шаров. Наудачу
выбирается ящик и из него извлекается
шар. Извлеченный шар оказался голубым.
Какова вероятность того, что голубой
шар извлечен из ящика первого состава?
—
2 голубых и 8 красных шаров. Наудачу
выбирается ящик и из него извлекается
шар. Извлеченный шар оказался голубым.
Какова вероятность того, что голубой
шар извлечен из ящика первого состава?
Решение. Обозначим через  событие, состоящее в том, что голубой
шар извлечен из ящика первого состава?
событие, состоящее в том, что голубой
шар извлечен из ящика первого состава?
Из условия задачи
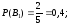

 .
.
Вероятности
вынуть голубой шар, если известно, что
взяты ящики состава 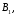

 соответственно:
соответственно:
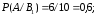
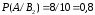 ;
;
В соответствии с формулой полной вероятности:
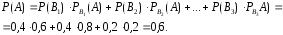
По формуле Бейеса найдем искомую вероятность
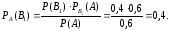
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Общая постановка задачи: известны вероятности некоторых событий, а вычислить нужно вероятности других событий, которые связаны с данными событиями. В этих задачах возникает необходимость в таких действиях над вероятностями, как сложение и умножение вероятностей.
Например, на охоте проиведены два выстрела. Событие A — попадание в утку с первого выстрела, событие B — попадание со второго выстрела. Тогда сумма событий A и B — попадание с первого или второго выстрела или с двух выстрелов.
Задачи другого типа. Даны несколько событий, например, монета подбрасывается три раза. Требуется найти вероятность того, что или все три раза выпадет герб, или того, что герб выпадет хотя бы один раз. Это задача на умножение вероятностей.
Сложение вероятностей используется тогда, когда нужно вычислить вероятность объединения или логической суммы случайных событий.
Сумму событий A и B обозначают A + B или A ∪ B. Суммой двух событий называется событие, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий. Это означает, что A + B – событие, которое наступает тогда и только тогда, когда при наблюдении произошло событие A или событие B, или одновременно A и B.
Если события A и B взаимно несовместны и их вероятности даны, то вероятность того, что в результате одного испытания произойдёт одно из этих событий, рассчитывают, используя сложение вероятностей.
Теорема сложения вероятностей. Вероятность того, что произойдёт одно из двух взаимно несовместных событий, равна сумме вероятностей этих событий:
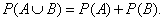 (3)
(3)
Например, на охоте произведены два выстрела. Событие А – попадание в утку с первого выстрела, событие В – попадание со второго выстрела, событие (А + В) – попадание с первого или второго выстрела или с двух выстрелов. Итак, если два события А и В – несовместные события, то А + В – наступление хотя бы одного из этих событий или двух событий.
Можно рассчитать как классические, так и статистические вероятности.
Пример 1. В ящике 30 мячиков одинаковых размеров: 10 красных, 5 синих и 15 белых. Вычислить вероятность того, что не глядя будет взят цветной (не белый) мячик.
Решение. Примем, что событие А – «взят красный мячик», а событие В – «взят синий мячик». Тогда событие 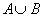 — «взят цветной (не белый) мячик». Найдём вероятность события А:
— «взят цветной (не белый) мячик». Найдём вероятность события А:
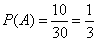
и события В:

События А и В – взаимно несовместные, так как если взят один мячик, то нельзя взять мячики разных цветов. Поэтому используем сложение вероятностей:

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей — на странице «Различные задачи на сложение и умножение вероятностей».
Теорема сложения вероятностей для нескольких несовместных событий. Если события 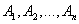 составляют полное множество событий, то сумма их вероятностей равна 1:
составляют полное множество событий, то сумма их вероятностей равна 1:
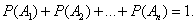
Сумма вероятностей противоположных событий также равна 1:

Противоположные события образуют полное множество событий, а вероятность полного множества событий равна 1.
Вероятности противоположных событий обычно обозначают малыми буквами p и q. В частности,
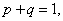
из чего следуют следующие формулы вероятности противоположных событий:
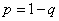 и
и 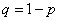 .
.
Пример 2. Цель в тире разделена на 3 зоны. Вероятность того что некий стрелок выстрелит в цель в первой зоне равна 0,15, во второй зоне – 0,23, в третьей зоне – 0,17. Найти вероятность того, что стрелок попадет в цель и вероятность того, что стрелок попадёт мимо цели.
Решение: Найдём вероятность того, что стрелок попадёт в цель:
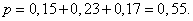
Найдём вероятность того, что стрелок попадёт мимо цели:
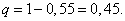
Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей — на странице «Различные задачи на сложение и умножение вероятностей».
Два случайных события называются совместными, если наступление одного события не исключает наступления второго события в том же самом наблюдении. Например, при бросании игральной кости событием А считается выпадение числа 4, а событием В – выпадение чётного числа. Поскольку число 4 является чётным числом, эти два события совместимы. В практике встречаются задачи по расчёту вероятностей наступления одного из взаимно совместных событий.
Теорема сложения вероятностей для совместных событий. Вероятность того, что наступит одно из совместных событий, равна сумме вероятностей этих событий, из которой вычтена вероятность общего наступления обоих событий, то есть произведение вероятностей. Формула вероятностей совместных событий имеет следующий вид:
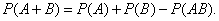
Поскольку события А и В совместимы, событие А + В наступает, если наступает одно из трёх возможных событий:  или АВ. Согласно теореме сложения несовместных событий,
вычисляем так:
или АВ. Согласно теореме сложения несовместных событий,
вычисляем так:
 (5)
(5)
Событие А наступит, если наступит одно из двух несовместных событий: 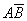 или АВ. Однако вероятность наступления одного события из нескольких несовместных событий равна сумме вероятностей всех этих событий:
или АВ. Однако вероятность наступления одного события из нескольких несовместных событий равна сумме вероятностей всех этих событий:
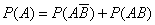
Поэтому
 (6)
(6)
Аналогично:
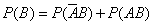
Поэтому
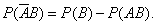 (7)
(7)
Подставляя выражения (6) и (7) в выражение (5), получаем формулу вероятности для совместных событий:
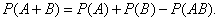 (8)
(8)
При использовании формулы (8) следует учитывать, что события А и В могут быть:
- взаимно независимыми;
- взаимно зависимыми.
Формула вероятности для взаимно независимых событий:
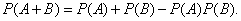
Формула вероятности для взаимно зависимых событий:
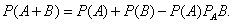
Если события А и В несовместны, то их совпадение является невозможным случаем и, таким образом, P(AB) = 0. Четвёртая формула вероятности для несовместных событий такова:

Пример 3. На автогонках при заезде на первой автомашине вероятность победить 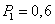 , при заезде на второй автомашине
, при заезде на второй автомашине 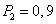 . Найти:
. Найти:
- вероятность того, что победят обе автомашины;
- вероятность того, что победит хотя бы одна автомашина;
Решение.
1) Вероятность того, что победит первая автомашина, не зависит от результата второй автомашины, поэтому события А (победит первая автомашина) и В (победит вторая автомашина) – независимые события. Найдём вероятность того, что победят обе машины:
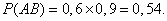
2) Найдём вероятность того, что победит одна из двух автомашин:
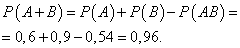
Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей — на странице «Различные задачи на сложение и умножение вероятностей».
Решить задачу на сложение вероятностей самостоятельно, а затем посмотреть решение
Пример 4. Бросаются две монеты. Событие A — выпадение герба на первой монете. Событие B — выпадение герба на второй монете. Найти вероятность события C = A + B.
Посмотреть правильное решение и ответ.
Умножение вероятностей используют, когда следует вычислить вероятность логического произведения событий.
При этом случайные события должны быть независимыми. Два события называются взаимно независимыми, если наступление одного события не влияет на вероятность наступления второго события.
Логическим произведением двух событий А и В, обозначаемым А ∩ В, называют событие, которое понимают как одновременное наступление событий А и В. Больше о сути логического произведения можно узнать в соответствующем месте статьи «Булева алгебра (алгебра логики)».
Теорема умножения вероятностей для независимых событий. Вероятность одновременного наступления двух независимых событий А и В  равна произведению вероятностей этих событий и вычисляется по формуле:
равна произведению вероятностей этих событий и вычисляется по формуле:
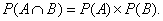 (4)
(4)
Пример 5. Монету бросают три раза подряд. Найти вероятность того, что все три раза выпадет герб.
Решение. Вероятность того, что при первом бросании монеты выпадет герб 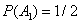 , во второй раз
, во второй раз 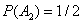 , в третий раз
, в третий раз 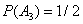 . Найдём вероятность того, что все три раза выпадет герб:
. Найдём вероятность того, что все три раза выпадет герб:

Решить задачи на умножение вероятностей самостоятельно, а затем посмотреть решение
Пример 6. Имеется коробка с девятью новыми теннисными мячами. Для игры берут три мяча, после игры их кладут обратно. При выборе мячей игранные от неигранных не отличают. Какова вероятность того, что после трёх игр в коробке не останется неигранных мячей?
Посмотреть правильное решение и ответ.
Пример 7. 32 буквы русского алфавита написаны на карточках разрезной азбуки. Пять карточек вынимаются наугад одна за другой и укладываются на стол в порядке появления. Найти вероятность того, что из букв получится слово «конец».
Посмотреть правильное решение и ответ.
Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей, а также вычислять произведение нескольких событий — на странице «Различные задачи на сложение и умножение вероятностей».
Вероятность того, что произойдёт хотя бы одно из взаимно независимых событий 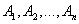 , можно вычислить путём вычитания из 1 произведения вероятностей противоположных событий
, можно вычислить путём вычитания из 1 произведения вероятностей противоположных событий 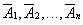 , то есть по формуле:
, то есть по формуле:
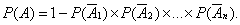
Пример 10. Грузы доставляют тремя видами транспорта: речным, железнодорожным и автотранспортом. Вероятность того, что груз будет доставлен речным транспортом, составляет 0,82, железнодорожным транспортом 0,87, автотранспортом 0,90. Найти вероятность того, что груз будет доставлен хотя бы одним из трёх видов транспорта.
Решение. Найдём вероятности противоположных событий – того, что груз не будет доставлен одним из видов транспорта:
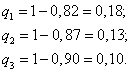
Теперь у нас есть всё, чтобы найти требуемую в условии задачи вероятность того, что груз будет доставлен хотя бы одним из трёх видов транспорта:
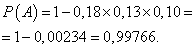
Решить задачу на умножение вероятностей самостоятельно, а затем посмотреть решение
Пример 11. Из полной колоды карт (52 карты) вынимают одновременно четыре карты. Событие А — среди вынутых карт будет хотя бы одна бубновая. Событие B — среди вынутых карт будет хотя бы одна червонная. Найти вероятность события C = A + B.
Посмотреть правильное решение и ответ.
Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей, а также вычислять произведение нескольких событий — на странице «Различные задачи на сложение и умножение вероятностей».
Если наступление одного события влияет на вероятность наступления второго события, то события называют взаимно зависимыми.
Если события А и В взаимно зависимы, то условной вероятностью 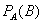 называют вероятность события В, принимая, что событие А уже наступило.
называют вероятность события В, принимая, что событие А уже наступило.
Теорема умножения вероятностей взаимно зависимых событий. Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого, то есть вычисляется по формуле:
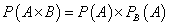
или
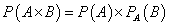
Пример 12. В ящике 26 лотерейных билетов, из которых 3 с выигрышем. Найти вероятности того, что первый билет будет с выигрышем, вероятность того, что второй билет будет с выигрышем при условии, что первого билета уже нет в ящике и вероятность того, что два взятые подряд билета будут с выигрышем.
Решение. Найдём вероятность того, что первый взятый билет будет с выигрышем:
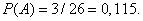
Найдём вероятность того, что второй взятый билет будет с выигрышем при условии, что первого билета уже нет в ящике:

Найдём теперь вероятность того, что оба взятые подряд билеты будут с выигрышем, т.е. вероятность общего наступления двух зависимых событий, которая является произведением вероятности первого события и условной вероятности второго события:
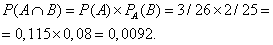
Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей, а также вычислять произведение нескольких событий — на странице «Различные задачи на сложение и умножение вероятностей».
 90000 probability theory | Definition, Examples, & Facts 90001 90002 Applications of simple probability experiments 90003
90004 The fundamental ingredient of probability theory is an experiment that can be repeated, at least hypothetically, under essentially identical conditions and that may lead to different outcomes on different trials. The set of all possible outcomes of an experiment is called a «sample space.» The experiment of tossing a coin once results in a sample space with two possible outcomes, «heads» and «tails.»Tossing two dice has a sample space with 36 possible outcomes, each of which can be identified with an ordered pair (90005 i 90006, 90005 j 90006), where 90005 i 90006 and 90005 j 90006 assume one of the values 1, 2, 3, 4, 5, 6 and denote the faces showing on the individual dice. It is important to think of the dice as identifiable (say by a difference in colour), so that the outcome (1, 2) is different from (2, 1). An «event» is a well-defined subset of the sample space. For example, the event «the sum of the faces showing on the two dice equals six» consists of the five outcomes (1, 5), (2, 4), (3, 3), (4, 2), and ( 5, 1).90013
Get exclusive access to content from our тисяча сімсот шістьдесят вісім First Edition with your subscription.
Subscribe today 90004 A third example is to draw 90005 n 90006 balls from an urn containing balls of various colours. A generic outcome to this experiment is an 90005 n 90006 -tuple, where the 90005 i 90006 th entry specifies the colour of the ball obtained on the 90005 i 90006 th draw (90005 i 90006 = 1, 2, …, 90005 n 90006) . In spite of the simplicity of this experiment, a thorough understanding gives the theoretical basis for opinion polls and sample surveys.For example, individuals in a population favouring a particular candidate in an election may be identified with balls of a particular colour, those favouring a different candidate may be identified with a different colour, and so on. Probability theory provides the basis for learning about the contents of the urn from the sample of balls drawn from the urn; an application is to learn about the electoral preferences of a population on the basis of a sample drawn from that population. 90013
90004 Another application of simple urn models is to use clinical trials designed to determine whether a new treatment for a disease, a new drug, or a new surgical procedure is better than a standard treatment.In the simple case in which treatment can be regarded as either success or failure, the goal of the clinical trial is to discover whether the new treatment more frequently leads to success than does the standard treatment. Patients with the disease can be identified with balls in an urn. The red balls are those patients who are cured by the new treatment, and the black balls are those not cured. Usually there is a control group, who receive the standard treatment. They are represented by a second urn with a possibly different fraction of red balls.The goal of the experiment of drawing some number of balls from each urn is to discover on the basis of the sample which urn has the larger fraction of red balls. A variation of this idea can be used to test the efficacy of a new vaccine. Perhaps the largest and most famous example was the test of the Salk vaccine for poliomyelitis conducted in 1954. It was organized by the U.S. Public Health Service and involved almost two million children. Its success has led to the almost complete elimination of polio as a health problem in the industrialized parts of the world.Strictly speaking, these applications are problems of statistics, for which the foundations are provided by probability theory. 90013
90004 In contrast to the experiments described above, many experiments have infinitely many possible outcomes. For example, one can toss a coin until «heads» appears for the first time. The number of possible tosses is 90005 n 90006 = 1, 2, …. Another example is to twirl a spinner. For an idealized spinner made from a straight line segment having no width and pivoted at its centre, the set of possible outcomes is the set of all angles that the final position of the spinner makes with some fixed direction, equivalently all real numbers in [0 , 2π).Many measurements in the natural and social sciences, such as volume, voltage, temperature, reaction time, marginal income, and so on, are made on continuous scales and at least in theory involve infinitely many possible values. If the repeated measurements on different subjects or at different times on the same subject can lead to different outcomes, probability theory is a possible tool to study this variability. 90013
90004 Because of their comparative simplicity, experiments with finite sample spaces are discussed first.In the early development of probability theory, mathematicians considered only those experiments for which it seemed reasonable, based on considerations of symmetry, to suppose that all outcomes of the experiment were «equally likely.» Then in a large number of trials all outcomes should occur with approximately the same frequency. The probability of an event is defined to be the ratio of the number of cases favourable to the event-i.e., The number of outcomes in the subset of the sample space defining the event-to the total number of cases.Thus, the 36 possible outcomes in the throw of two dice are assumed equally likely, and the probability of obtaining «six» is the number of favourable cases, 5, divided by 36, or 5/36. 90013
90004 Now suppose that a coin is tossed 90005 n 90006 times, and consider the probability of the event «heads does not occur» in the 90005 n 90006 tosses. An outcome of the experiment is an 90005 n 90006 -tuple, the 90005 k 90006 th entry of which identifies the result of the 90005 k 90006 th toss. Since there are two possible outcomes for each toss, the number of elements in the sample space is 2 90047 90005 n 90006 90050.Of these, only one outcome corresponds to having no heads, so the required probability is 1/2 90047 90005 n 90006 90050. 90013
90004 It is only slightly more difficult to determine the probability of «at most one head.» In addition to the single case in which no head occurs, there are 90005 n 90006 cases in which exactly one head occurs, because it can occur on the first, second, …, or 90005 n 90006 th toss. Hence, there are 90005 n 90006 + 1 cases favourable to obtaining at most one head, and the desired probability is (90005 n 90006 + 1) / 2 90047 90005 n 90006 90050.90013.90000 Probability | Theory, solved examples and practice questions 90001 90002 When MS and MBA applicants ask us — ‘90003 What are my chances of getting into Harvard? 90004 ‘or’ 90003 What’s my probability of getting scholarships from Oxford? 90004 ‘we get tongue-tied. There are so many variables at play, it’s difficult to give an accurate answer. 90007
90002 But when you get probability questions in your GRE and GMAT exam syllabus, you do not have to get flummoxed. Understanding the basic rules and formulas of probability will help you score high in the entrance exams.90009 90007
90011 Meaning and definition of Probability 90012
90002 As the Oxford dictionary states it, Probability means ‘The extent to which something is probable; the likelihood of something happening or being the case ‘. 90007
90002 In mathematics too, probability indicates the same — the likelihood of the occurrence of an event. 90007
90002 Examples of events can be: 90007
90019
90020 Tossing a coin with the head up 90021
90020 Drawing a red pen from a pack of different coloured pens 90021
90020 Drawing a card from a deck of 52 cards etc.90021
90026
90002 Either an event will occur for sure, or not occur at all. Or there are possibilities to different degrees the event may occur. 90007
90002 An event that occurs for sure is called a Certain event and its probability is 1. 90007
90002 An event that does not occur at all is called an impossible event and its probability is 0. 90007
90002 This means that all other possibilities of an event occurrence lie between 0 and 1. 90007
90002 This is depicted as follows: 90007
90002 90038 0 <= P (A) <= 1 90039 90007
90002 where A is an event and P (A) is the probability of the occurrence of the event.90007
90002 This also means that a probability value can never be negative. 90007
90002 Every event will have a set of possible outcomes. It is called the 'sample space'. 90007
90002 Consider the example of tossing a coin. 90007
90002 When a coin is tossed, the possible outcomes are Head and Tail. So, the sample space is represented as {H, T}. 90007
90002 Similarly when two coins are tossed, the sample space is {(H, H), (H, T), (T, H), (T, T)}. 90007
90002 The probability of head each time you toss the coin is 1/2.So is the probability of tail. 90009 90007
90056 Basic formula of probability 90057
90002 As you might know from the list of GMAT maths formulas, the Probability of the occurrence of an event A is defined as: 90007
90038 P (A) = (No. of ways A can occur) / (Total no. Of possible outcomes) 90039
90002 90007
90002 Another example is the rolling of dice. When a single die is rolled, the sample space is {1,2,3,4,5,6}. 90007
90002 What is the probability of rolling a 5 when a die is rolled? 90007
90002 No.of ways it can occur = 1 90007
90002 Total no. of possible outcomes = 6 90007
90002 So the probability of rolling a particular number when a die is rolled = 1/6. 90007 90011 Compound probability 90012
90002 Compound probability is when the problem statement asks for the likelihood of the occurrence of more than one outcome. 90009 90007
90056 Formula for compound probability 90057
90019
90020 P (A or B) = P (A) + P (B) - P (A and B) 90021
90026
90002 where A and B are any two events.90007
90002 P (A or B) is the probability of the occurrence of atleast one of the events. 90007
90002 P (A and B) is the probability of the occurrence of both A and B at the same time. 90007
90002 90007
90093 Mutually exclusive events: 90094
90002 Mutually exclusive events are those where the occurrence of one indicates the non-occurrence of the other 90007
90002 OR 90007
90002 When two events can not occur at the same time, they are considered mutually exclusive. 90007
90002 90102 Note: 90103 For a mutually exclusive event, P (A and B) = 0.90007
90002 90007
90002 90038 Example 1: 90039 What is the probability of getting a 2 90102 or 90103 a 5 when a die is rolled? 90007
90002 90102 Solution: 90103 90007
90002 Taking the individual probabilities of each number, getting a 2 is 1/6 and so is getting a 5. 90007
90002 Applying the formula of compound probability, 90007
90002 Probability of getting a 2 90038 or 90039 a 5, 90007
90002 P (2 or 5) = P (2) + P (5) - P (2 and 5) 90007
90002 ==> 1/6 + 1/6 — 0 90007
90002 ==> 2/6 = 1/3.90007
90002 90007
90002 90038 Example 2: 90039 Consider the example of finding the probability of selecting a black card or a 6 from a deck of 52 cards. 90007
90002 90102 Solution: 90103 90007
90002 We need to find out P (B or 6) 90007
90002 Probability of selecting a black card = 26/52 90007
90002 Probability of selecting a 6 = 4/52 90007
90002 Probability of selecting both a black card and a 6 = 2/52 90007
90002 P (B or 6) = P (B) + P (6) — P (B and 6) 90007
90002 = 26/52 + 4/52 — 2/52 90007
90002 = 28/52 90007
90002 = 7/13.90007
90002 90007
90093 Independent and Dependent Events 90094
90056 Independent Event 90057
90002 When multiple events occur, if the outcome of one event 90102 DOES NOT 90103 affect the outcome of the other events, they are called independent events. 90007
90002 Say, a die is rolled twice. The outcome of the first roll does not affect the second outcome. These two are independent events. 90007
90002 90007
90002 90038 Example 1: 90039 Say, a coin is tossed twice. What is the probability of getting two consecutive tails? 90007
90002 Probability of getting a tail in one toss = 1/2 90007
90002 The coin is tossed twice.So 1/2 * 1/2 = 1/4 is the answer. 90007
90002 Here’s the verification of the above answer with the help of sample space. 90007
90002 When a coin is tossed twice, the sample space is {(H, H), (H, T), (T, H), (T, T)}. 90007
90002 Our desired event is (T, T) whose occurrence is only once out of four possible outcomes and hence, our answer is 1/4. 90007
90002 90007
90002 90038 Example 2: 90039 Consider another example where a pack contains 4 blue, 2 red and 3 black pens. If a pen is drawn at random from the pack, replaced and the process repeated 2 more times, What is the probability of drawing 2 blue pens and 1 black pen? 90007
90002 90192 Solution 90193 90007
90002 Here, total number of pens = 9 90007
90002 Probability of drawing 1 blue pen = 4/9 90009 Probability of drawing another blue pen = 4/9 90009 Probability of drawing 1 black pen = 3/9 90009 Probability of drawing 2 blue pens and 1 black pen = 4/9 * 4 / 9 * 3/9 = 48/729 = 16/243 90007
90002 90007
90056 Dependent Events 90057
90002 When two events occur, if the outcome of one event affects the outcome of the other, they are called dependent events.90007
90002 Consider the aforementioned example of drawing a pen from a pack, with a slight difference. 90007
90002 90038 Example 1: 90039 A pack contains 4 blue, 2 red and 3 black pens. If 2 pens are drawn at random from the pack, 90102 NOT 90103 replaced and then another pen is drawn. What is the probability of drawing 2 blue pens and 1 black pen? 90007
90002 90192 Solution: 90193 90007
90002 Probability of drawing 1 blue pen = 4/9 90009 Probability of drawing another blue pen = 3/8 90009 Probability of drawing 1 black pen = 3/7 90009 Probability of drawing 2 blue pens and 1 black pen = 4/9 * 3 / 8 * 3/7 = 1/14 90007
90002 90007
90002 Let’s consider another example: 90007
90002 90038 Example 2: 90039 What is the probability of drawing a king and a queen consecutively from a deck of 52 cards, 90102 without 90103 replacement.90007
90002 Probability of drawing a king = 4/52 = 1/13 90007
90002 After drawing one card, the number of cards are 51. 90007
90002 Probability of drawing a queen = 4/51. 90007
90002 Now, the probability of drawing a king and queen consecutively is 1/13 * 4/51 = 4/663 90007
90002 90007
90011 Conditional probability 90012
90002 Conditional probability is calculating the probability of an event given that another event has already occured. 90007
90002 The formula for conditional probability P (A | B), read as P (A given B) is 90007
90038 P (A | B) = P (A and B) / P (B) 90039
90002 90007
90002 Consider the following example: 90007
90002 90038 Example: 90039 In a class, 40% of the students study math and science.60% of the students study math. What is the probability of a student studying science given he / she is already studying math? 90007
90002 90192 Solution 90193 90007
90002 P (M and S) = 0.40 90007
90002 P (M) = 0.60 90007
90002 P (S | M) = P (M and S) / P (S) = 0.40 / 0.60 = 2/3 = 0.67 90007
90002 90007
90093 Complement of an event 90094
90002 A complement of an event A can be stated as that which does NOT contain the occurrence of A. 90007
90002 A complement of an event is denoted as P (A 90278 c 90279) or P (A ‘).90007
90038 P (A 90278 c 90279) = 1 — P (A)
90002 or it can be stated, P (A) + P (A 90278 c 90279) = 1 90007 90039
90002 For example, 90007
90002 if A is the event of getting a head in coin toss, A 90278 c 90279 is not getting a head i.e., getting a tail. 90007
90002 if A is the event of getting an even number in a die roll, A 90278 c 90279 is the event of NOT getting an even number i.e., getting an odd number. 90007
90002 if A is the event of randomly choosing a number in the range of -3 to 3, A 90278 c 90279 is the event of choosing every number that is NOT negative i.e., 0,1,2 & 3 (0 is neither positive or negative). 90007
90002 90007
90002 Consider the following example: 90007
90002 90038 Example: 90039 A single coin is tossed 5 times. What is the probability of getting at least one head? 90007
90002 90102 Solution: 90103 90007
90002 Consider solving this using complement. 90007
90002 Probability of getting no head = P (all tails) = 1/32 90007
90002 P (at least one head) = 1 — P (all tails) = 1 — 1/32 = 31/32. 90007
90002 90007
90011 Sample Probability questions with solutions 90012 90056 Probability Example 1 90057
90002 What is the probability of the occurrence of a number that is odd or less than 5 when a fair die is rolled.90007
90002 90192 Solution 90193 90007
90002 Let the event of the occurrence of a number that is odd be ‘A’ and the event of the occurrence of a number that is less than 5 be ‘B’. We need to find P (A or B). 90007
90002 P (A) = 3/6 (odd numbers = 1,3 and 5) 90007
90002 P (B) = 4/6 (numbers less than 5 = 1,2,3 and 4) 90007
90002 P (A and B) = 2/6 (numbers that are both odd and less than 5 = 1 and 3) 90007
90002 Now, P (A or B) = P (A) + P (B) — P (A or B) 90007
90002 = 3/6 + 4/6 — 2/6 90007
90002 P (A or B) = 5/6.90007
90002 90007
90056 Probability Example 2 90057
90002 A box contains 4 chocobars and 4 ice creams. Tom eats 3 of them one after another. What is the probability of sequentially choosing 2 chocobars and 1 icecream? 90007
90002 90192 Solution 90193 90007
90002 Probability of choosing 1 chocobar = 4/8 = 1/2 90007
90002 After taking out 1 chocobar, the total number is 7. 90007
90002 Probability of choosing 2nd chocobar = 3/7 90007
90002 Probability of choosing 1 icecream out of a total of 6 = 4/6 = 2/3 90007
90002 So the final probability of choosing 2 chocobars and 1 icecream = 1/2 * 3/7 * 2/3 = 1/7 90007
90002 90007
90056 Probability Example 3 90057
90002 When two dice are rolled, find the probability of getting a greater number on the first die than the one on the second, given that the sum should equal 8.90007
90002 90192 Solution 90193 90007
90002 Let the event of getting a greater number on the first die be G. 90007
90002 There are 5 ways to get a sum of 8 when two dice are rolled = {(2,6), (3,5), (4,4), (5,3), (6,2)}. 90007
90002 And there are two ways where the number on the first die is greater than the one on the second given that the sum should equal 8, G = {(5,3), (6,2)}. 90007
90002 Therefore, P (Sum equals 8) = 5/36 and P (G) = 2/36. 90007
90002 Now, P (G | sum equals 8) = P (G and sum equals 8) / P (sum equals 8) 90007
90002 = (2/36) / (5/36) 90007
90002 = 2/5 90007
90002 90007
90011 Probability Quiz: Sample probability questions for practice 90012 90002 90396 90396 Probability Problem 1
90007 90002 A bag contains blue and red balls.Two balls are drawn randomly without replacement. The probability of selecting a blue and then a red ball is 0.2. The probability of selecting a blue ball in the first draw is 0.5. What is the probability of drawing a red ball, given that the first ball drawn was blue? 90009 a) 0.4 90009 b) 0.2 90009 c) 0.1 90009 d) 0.5
90007 90002 90396 90396 Problem 2
90007 90002 A die is rolled thrice. What is the probability that the sum of the rolls is atleast 5. 90009 a) 1/216 90009 b) 1/6 90009 c) 3/216 90009 d) 212/216
90007 90002 90009 Learn how to solve: 90009 — Simple and compound interest problems 90009 — Speed, distance and time problems 90009 — Ratio and proportion 90009 — List of Maths Formulas 90007
Take this highly affordable online course on probability and test your knowledge with 600+ practice questions.Over 18,000 students enrolled, with average rating of 4.6 stars. Click below.
90192 Become a Probability & Statistics Master 90193 .90000 Rules of Probability and Independent Events 90001
90002
The study of
probability mostly deals with combining different events and studying these
events alongside each other. How these different events relate to each other determines
the methods and rules to follow when we’re studying their probabilities. 90003
90002
Events can be pided into two major categories dependent or Independent events.90003
90006
Independent Events 90007
90002
When two events are said to be independent of each other, what this means is that
the probability that one event occurs in no way affects the probability of the other
event occurring. An example of two independent events is as follows; say you rolled
a die and flipped a coin. The probability of getting any number face on the die
in no way influences the probability of getting a head or a tail on the coin.90003
90006
Dependent Events 90007
90002
When two events are said to be dependent, the probability of one event occurring
influences the likelihood of the other event. 90003
90002
For example, if you were to draw a two cards from a deck of 52 cards. If on your
first draw you had an ace and you put that aside, the probability of drawing an
ace on the second draw is greatly changed because you drew an ace the first time.Let’s calculate these different probabilities to see what’s going on. 90003
90002
There are 4 Aces in a deck of 52 cards 90003
90018
90019 90003
90002
On your first draw, the probability of getting an ace is given by: 90003
90018
90024 90003
90002
If we do not return this card into the deck, the probability of drawing an ace on
the second pick is given by 90003
90018
90029 90003
90018
90032 90003
90018
90035 90003
90002
As you can clearly see, the above two probabilities are different, so we say that
the two events are dependent.The likelihood of the second event depends on what
happens in the first event. 90003
90039
Conditional Probability 90040
90002
We have already defined dependent and independent events and seen how probability
of one event relates to the probability of the other event. 90003
90002
Having those concepts in mind, we can now look at conditional probability. 90003
90002
Conditional probability deals with further defining dependence of events by looking
at probability of an event given that some other event first occurs.90003
90002
Conditional probability is denoted by the following: 90003
90018
90050 90003
90002
The above is read as 90053 the probability that B occurs given that A has already occurred 90054. 90003
90002
The above is mathematically defined as: 90003
90018
90059 90003
90039
Set Theory in Probability 90040
90002
A sample space is defined as a universal set of all possible outcomes from a given
experiment.90003
90002
Given two events 90053 A 90054 and 90053 B 90054 and given that these events are part of a
sample space 90053 S 90054. This sample space is represented as a set as in the diagram
below. 90003
90018
90074 90003
90002
The entire sample space of 90053 S 90054 is given by: 90003
90018
90081 90003
90002
Remember the following from set theory: 90003
90018
90086 90003
90018
90089 90003
90002
The different regions of the set 90053 S 90054 can be explained as using the rules of
probability.90003
90039
Rules of Probability 90040
90002
When dealing with more than one event, there are certain rules that we must follow
when studying probability of these events. These rules depend greatly on whether
the events we are looking at are Independent or dependent on each other. 90003
90002
First acknowledge that 90003
90018
90102 90003
90006
Multiplication Rule (A∩B) 90007
90002
This region is referred to as ‘A intersection B’ and in probability; this region
refers to the event that both 90053 A 90054 and 90053 B 90054 happen.When we use the word
90053 and 90054 we are referring to multiplication, thus 90053 A and B 90054 can be thought
of as 90053 AxB 90054 or (using dot notation which is more popular in probability) 90053 A 90054 • 90053 B 90054 90003
90002
If 90053 A 90054 and 90053 B 90054 are dependent events, the probability of this event happening
can be calculated as shown below: 90003
90018
90129 90003
90002
If 90053 A 90054 and 90053 B 90054 are independent events, the probability of this event happening
can be calculated as shown below: 90003
90018
90138 90003
90002
Conditional probability for two independent events can be redefined using the relationship
above to become: 90003
90018
90143 90003
90018
90146 90003
90018
90149 90003
90002
The above is consistent with the definition of independent events, the occurrence
of event 90053 A 90054 in no way influences the occurrence of event 90053 B 90054, and so
the probability that event 90053 B 90054 occurs given that event 90053 A 90054 has occurred
is the same as the probability of event 90053 B 90054.90003
90006
Additive Rule (A∪B) 90007
90002
In probability we refer to the addition operator (90053 + 90054) as 90053 or 90054. Thus when
we want to we want to define some event such that the event can be A or B, to find
the probability of that event: 90003
90018
90172 90003
90018
90175 90003
90002
Thus it follows that: 90003
90018
90180 90003
90002
But remember from set theory that and from the way we defined our sample space above: 90003
90018
90185 90003
90002
and that: 90003
90018
90190 90003
So we can now redefine out event as
90018
90193 90003
90018
90196 90003
90002
The above is sometimes referred to as the subtraction rule.90003
90039
Mutual Exclusivity 90040
90002
Certain special pairs of events have a unique relationship referred to as mutual
exclusivity. 90003
90002
Two events are said to be mutually exclusive if they can not occur at the same time.
For a given sample space, its either one or the other but not both. As a consequence,
mutually exclusive events have their probability defined as follows: 90003
90018
90207 90003
90002
An example of mutually exclusive events are the outcomes of a fair coin flip.When
you flip a fair coin, you either get a head or a tail but not both, we can prove
that these events are mutually exclusive by adding their probabilities: 90003
90018
90212 90003
90002
For any given pair of events, if the sum of their probabilities is equal to one,
then those two events are mutually exclusive.
90003
90006
Rules of Probability for Mutually Exclusive Events 90007
90218
90219
90002
Multiplication Rule 90003
90002
From the definition of mutually exclusive events, we should quickly conclude the
following: 90003
90018
90225 90003
90227
90219
90002
Addition Rule 90003
90002
As we defined above, the addition rule applies to mutually exclusive events as follows: 90003
90018
90234 90003
90227
90219
90002
Subtraction Rule
90003
90002
From the addition rule above, we can conclude that the subtraction rule for mutually
exclusive events takes the form; 90003
90018
90243 90003
90227
90246
90006
Conditional Probability for Mutually Exclusive Events 90007
90002
We have defined conditional probability with the following equation: 90003
90018
90252 90003
90002
We can redefine the above using the multiplication rule 90003
90018
90257 90003
90002
hence 90003
90018
90262 90003
90002
Below is a venn diagram of a set containing two mutually exclusive events 90053 A 90054
and 90053 B 90054.90003
90018
90271 90003
.90000 Conditional Probability and Independent Events 90001
90002 Conditional Probability 90003
90004 Suppose a fair die has been rolled and you are asked to give the probability that it was a five. There are six equally likely outcomes, so your answer is 1/6. But suppose that before you give your answer you are given the extra information that the number rolled was odd. Since there are only three odd numbers that are possible, one of which is five, you would certainly revise your estimate of the likelihood that a five was rolled from 1/6 to 1/3.In general, the 90005 revised 90006 probability that an event 90005 A 90006 has occurred, taking into account the additional information that another event 90005 B 90006 has definitely occurred on this trial of the experiment, is called the 90005 conditional probability of 90006 90005 A 90006 90005 given 90006 90005 B 90006 and is denoted by P (A | B). The reasoning employed in this example can be generalized to yield the computational formula in the following definition. 90019
90020 Definition 90021
90004 90005 The 90006 conditional probabilityThe probability of the event 90005 A 90006 taking into account the fact that event 90005 B 90006 is known to have occurred.90029 of 90030 90005 A 90006 90029 given 90030 90005 B 90006, 90005 denoted 90006 P (A | B), 90005 is the probability that event 90006 90005 A 90006 90005 has occurred in a trial of a random experiment for which it is known that event 90006 90005 B 90006 90005 has definitely occurred. It may be computed by means of the following formula: 90006 90019
90004 Rule for Conditional Probability 90019
P (A | B) = P (A∩B) P (B)
90020 Example 20 90021
90004 A fair die is rolled.90019
90056
90057 Find the probability that the number rolled is a five, given that it is odd. 90058
90057 Find the probability that the number rolled is odd, given that it is a five. 90058
90061
90004 Solution: 90019
90004 The sample space for this experiment is the set S = {1,2,3,4,5,6} consisting of six equally likely outcomes. Let 90005 F 90006 denote the event «a five is rolled» and let 90005 O 90006 denote the event «an odd number is rolled,» so that 90019
F = {5} and O = {1,3,5}
90056
90057
90004 This is the introductory example, so we already know that the answer is 1/3.To use the formula in the definition to confirm this we must replace 90005 A 90006 in the formula (the event whose likelihood we seek to estimate) by 90005 F 90006 and replace 90005 B 90006 (the event we know for certain has occurred) by 90005 O 90006: 90019
P (F | O) = P (F∩O) P (O)
90004 Since F∩O = {5} ∩ {1,3,5} = {5}, P (F∩O) = 1/6. 90019
90004 Since O = {1,3,5}, P (O) = 3/6. 90019
90004 Thus 90019
P (F | O) = P (F∩O) P (O) = 1/63/6 = 13
90058
90057
90004 This is the same problem, but with the roles of 90005 F 90006 and 90005 O 90006 reversed.Since we are given that the number that was rolled is five, which is odd, the probability in question must be 1. To apply the formula to this case we must now replace 90005 A 90006 (the event whose likelihood we seek to estimate) by 90005 O 90006 and 90005 B 90006 (the event we know for certain has occurred) by 90005 F 90006: 90019
P (O | F) = P (O∩F) P (F)
90004 Obviously P (F) = 1/6. In part (a) we found that P (F∩O) = 1/6. Thus 90019
P (O | F) = P (O∩F) P (F) = 1/61/6 = 1
90058
90061
90004 Just as we did not need the computational formula in this example, we do not need it when the information is presented in a two-way classification table, as in the next example.90019
90020 Example 21 90021
90004 In a sample of 902 individuals under 40 who were or had previously been married, each person was classified according to gender and age at first marriage. The results are summarized in the following two-way classification table, where the meaning of the labels is: 90019
90114
90057
90005 M 90006: male 90058
90057
90005 F 90006: female 90058
90057
90005 E 90006: a teenager when first married 90058
90057
90005 W 90006: in one’s twenties when first married 90058
90057
90005 H 90006: in one’s thirties when first married 90058
90135
90136
90137
90138
90139
90140 90005 E 90006 90143
90140 90005 W 90006 90143
90140 90005 H 90006 90143
90140 Total 90143
90154
90155
90156
90138
90158 90005 M 90006 90161
90158 43 90161
90158 293 90161
90158 114 90161
90158 450 90161
90154
90138
90158 90005 F 90006 90161
90158 82 90161
90158 299 90161
90158 71 90161
90158 452 90161
90154
90138
90158 Total 90161
90158 125 90161
90158 592 90161
90158 185 90161
90158 902 90161
90154
90197
90198
90004 The numbers in the first row mean that 43 people in the sample were men who were first married in their teens, 293 were men who were first married in their twenties, 114 men who were first married in their thirties, and a total of 450 people in the sample were men.Similarly for the numbers in the second row. The numbers in the last row mean that, irrespective of gender, 125 people in the sample were married in their teens, 592 in their twenties, 185 in their thirties, and that there were 902 people in the sample in all. Suppose that the proportions in the sample accurately reflect those in the population of all individuals in the population who are under 40 and who are or have previously been married. Suppose such a person is selected at random. 90019
90056
90057 Find the probability that the individual selected was a teenager at first marriage.90058
90057 Find the probability that the individual selected was a teenager at first marriage, given that the person is male. 90058
90061
90004 Solution: 90019
90004 It is natural to let 90005 E 90006 also denote the event that the person selected was a teenager at first marriage and to let 90005 M 90006 denote the event that the person selected is male. 90019
90056
90057 According to the table the proportion of individuals in the sample who were in their teens at their first marriage is 125/902.This is the relative frequency of such people in the population, hence P (E) = 125 / 902≈0.139 or about 14%. 90058
90057
90004 Since it is known that the person selected is male, all the females may be removed from consideration, so that only the row in the table corresponding to men in the sample applies: 90019
90136
90137
90138
90139
90140 90005 E 90006 90143
90140 90005 W 90006 90143
90140 90005 H 90006 90143
90140 Total 90143
90154
90155
90156
90138
90158 90005 M 90006 90161
90158 43 90161
90158 293 90161
90158 114 90161
90158 450 90161
90154
90197
90198
90058 90061.
90000 probability theory | Definition, Examples, & Facts 90001 90002 Applications of simple probability experiments 90003
90004 The fundamental ingredient of probability theory is an experiment that can be repeated, at least hypothetically, under essentially identical conditions and that may lead to different outcomes on different trials. The set of all possible outcomes of an experiment is called a «sample space.» The experiment of tossing a coin once results in a sample space with two possible outcomes, «heads» and «tails.»Tossing two dice has a sample space with 36 possible outcomes, each of which can be identified with an ordered pair (90005 i 90006, 90005 j 90006), where 90005 i 90006 and 90005 j 90006 assume one of the values 1, 2, 3, 4, 5, 6 and denote the faces showing on the individual dice. It is important to think of the dice as identifiable (say by a difference in colour), so that the outcome (1, 2) is different from (2, 1). An «event» is a well-defined subset of the sample space. For example, the event «the sum of the faces showing on the two dice equals six» consists of the five outcomes (1, 5), (2, 4), (3, 3), (4, 2), and ( 5, 1).90013
Get exclusive access to content from our тисяча сімсот шістьдесят вісім First Edition with your subscription.
Subscribe today 90004 A third example is to draw 90005 n 90006 balls from an urn containing balls of various colours. A generic outcome to this experiment is an 90005 n 90006 -tuple, where the 90005 i 90006 th entry specifies the colour of the ball obtained on the 90005 i 90006 th draw (90005 i 90006 = 1, 2, …, 90005 n 90006) . In spite of the simplicity of this experiment, a thorough understanding gives the theoretical basis for opinion polls and sample surveys.For example, individuals in a population favouring a particular candidate in an election may be identified with balls of a particular colour, those favouring a different candidate may be identified with a different colour, and so on. Probability theory provides the basis for learning about the contents of the urn from the sample of balls drawn from the urn; an application is to learn about the electoral preferences of a population on the basis of a sample drawn from that population. 90013
90004 Another application of simple urn models is to use clinical trials designed to determine whether a new treatment for a disease, a new drug, or a new surgical procedure is better than a standard treatment.In the simple case in which treatment can be regarded as either success or failure, the goal of the clinical trial is to discover whether the new treatment more frequently leads to success than does the standard treatment. Patients with the disease can be identified with balls in an urn. The red balls are those patients who are cured by the new treatment, and the black balls are those not cured. Usually there is a control group, who receive the standard treatment. They are represented by a second urn with a possibly different fraction of red balls.The goal of the experiment of drawing some number of balls from each urn is to discover on the basis of the sample which urn has the larger fraction of red balls. A variation of this idea can be used to test the efficacy of a new vaccine. Perhaps the largest and most famous example was the test of the Salk vaccine for poliomyelitis conducted in 1954. It was organized by the U.S. Public Health Service and involved almost two million children. Its success has led to the almost complete elimination of polio as a health problem in the industrialized parts of the world.Strictly speaking, these applications are problems of statistics, for which the foundations are provided by probability theory. 90013
90004 In contrast to the experiments described above, many experiments have infinitely many possible outcomes. For example, one can toss a coin until «heads» appears for the first time. The number of possible tosses is 90005 n 90006 = 1, 2, …. Another example is to twirl a spinner. For an idealized spinner made from a straight line segment having no width and pivoted at its centre, the set of possible outcomes is the set of all angles that the final position of the spinner makes with some fixed direction, equivalently all real numbers in [0 , 2π).Many measurements in the natural and social sciences, such as volume, voltage, temperature, reaction time, marginal income, and so on, are made on continuous scales and at least in theory involve infinitely many possible values. If the repeated measurements on different subjects or at different times on the same subject can lead to different outcomes, probability theory is a possible tool to study this variability. 90013
90004 Because of their comparative simplicity, experiments with finite sample spaces are discussed first.In the early development of probability theory, mathematicians considered only those experiments for which it seemed reasonable, based on considerations of symmetry, to suppose that all outcomes of the experiment were «equally likely.» Then in a large number of trials all outcomes should occur with approximately the same frequency. The probability of an event is defined to be the ratio of the number of cases favourable to the event-i.e., The number of outcomes in the subset of the sample space defining the event-to the total number of cases.Thus, the 36 possible outcomes in the throw of two dice are assumed equally likely, and the probability of obtaining «six» is the number of favourable cases, 5, divided by 36, or 5/36. 90013
90004 Now suppose that a coin is tossed 90005 n 90006 times, and consider the probability of the event «heads does not occur» in the 90005 n 90006 tosses. An outcome of the experiment is an 90005 n 90006 -tuple, the 90005 k 90006 th entry of which identifies the result of the 90005 k 90006 th toss. Since there are two possible outcomes for each toss, the number of elements in the sample space is 2 90047 90005 n 90006 90050.Of these, only one outcome corresponds to having no heads, so the required probability is 1/2 90047 90005 n 90006 90050. 90013
90004 It is only slightly more difficult to determine the probability of «at most one head.» In addition to the single case in which no head occurs, there are 90005 n 90006 cases in which exactly one head occurs, because it can occur on the first, second, …, or 90005 n 90006 th toss. Hence, there are 90005 n 90006 + 1 cases favourable to obtaining at most one head, and the desired probability is (90005 n 90006 + 1) / 2 90047 90005 n 90006 90050.90013.90000 Probability | Theory, solved examples and practice questions 90001 90002 When MS and MBA applicants ask us — ‘90003 What are my chances of getting into Harvard? 90004 ‘or’ 90003 What’s my probability of getting scholarships from Oxford? 90004 ‘we get tongue-tied. There are so many variables at play, it’s difficult to give an accurate answer. 90007
90002 But when you get probability questions in your GRE and GMAT exam syllabus, you do not have to get flummoxed. Understanding the basic rules and formulas of probability will help you score high in the entrance exams.90009 90007
90011 Meaning and definition of Probability 90012
90002 As the Oxford dictionary states it, Probability means ‘The extent to which something is probable; the likelihood of something happening or being the case ‘. 90007
90002 In mathematics too, probability indicates the same — the likelihood of the occurrence of an event. 90007
90002 Examples of events can be: 90007
90019
90020 Tossing a coin with the head up 90021
90020 Drawing a red pen from a pack of different coloured pens 90021
90020 Drawing a card from a deck of 52 cards etc.90021
90026
90002 Either an event will occur for sure, or not occur at all. Or there are possibilities to different degrees the event may occur. 90007
90002 An event that occurs for sure is called a Certain event and its probability is 1. 90007
90002 An event that does not occur at all is called an impossible event and its probability is 0. 90007
90002 This means that all other possibilities of an event occurrence lie between 0 and 1. 90007
90002 This is depicted as follows: 90007
90002 90038 0 <= P (A) <= 1 90039 90007
90002 where A is an event and P (A) is the probability of the occurrence of the event.90007
90002 This also means that a probability value can never be negative. 90007
90002 Every event will have a set of possible outcomes. It is called the 'sample space'. 90007
90002 Consider the example of tossing a coin. 90007
90002 When a coin is tossed, the possible outcomes are Head and Tail. So, the sample space is represented as {H, T}. 90007
90002 Similarly when two coins are tossed, the sample space is {(H, H), (H, T), (T, H), (T, T)}. 90007
90002 The probability of head each time you toss the coin is 1/2.So is the probability of tail. 90009 90007
90056 Basic formula of probability 90057
90002 As you might know from the list of GMAT maths formulas, the Probability of the occurrence of an event A is defined as: 90007
90038 P (A) = (No. of ways A can occur) / (Total no. Of possible outcomes) 90039
90002 90007
90002 Another example is the rolling of dice. When a single die is rolled, the sample space is {1,2,3,4,5,6}. 90007
90002 What is the probability of rolling a 5 when a die is rolled? 90007
90002 No.of ways it can occur = 1 90007
90002 Total no. of possible outcomes = 6 90007
90002 So the probability of rolling a particular number when a die is rolled = 1/6. 90007 90011 Compound probability 90012
90002 Compound probability is when the problem statement asks for the likelihood of the occurrence of more than one outcome. 90009 90007
90056 Formula for compound probability 90057
90019
90020 P (A or B) = P (A) + P (B) - P (A and B) 90021
90026
90002 where A and B are any two events.90007
90002 P (A or B) is the probability of the occurrence of atleast one of the events. 90007
90002 P (A and B) is the probability of the occurrence of both A and B at the same time. 90007
90002 90007
90093 Mutually exclusive events: 90094
90002 Mutually exclusive events are those where the occurrence of one indicates the non-occurrence of the other 90007
90002 OR 90007
90002 When two events can not occur at the same time, they are considered mutually exclusive. 90007
90002 90102 Note: 90103 For a mutually exclusive event, P (A and B) = 0.90007
90002 90007
90002 90038 Example 1: 90039 What is the probability of getting a 2 90102 or 90103 a 5 when a die is rolled? 90007
90002 90102 Solution: 90103 90007
90002 Taking the individual probabilities of each number, getting a 2 is 1/6 and so is getting a 5. 90007
90002 Applying the formula of compound probability, 90007
90002 Probability of getting a 2 90038 or 90039 a 5, 90007
90002 P (2 or 5) = P (2) + P (5) - P (2 and 5) 90007
90002 ==> 1/6 + 1/6 — 0 90007
90002 ==> 2/6 = 1/3.90007
90002 90007
90002 90038 Example 2: 90039 Consider the example of finding the probability of selecting a black card or a 6 from a deck of 52 cards. 90007
90002 90102 Solution: 90103 90007
90002 We need to find out P (B or 6) 90007
90002 Probability of selecting a black card = 26/52 90007
90002 Probability of selecting a 6 = 4/52 90007
90002 Probability of selecting both a black card and a 6 = 2/52 90007
90002 P (B or 6) = P (B) + P (6) — P (B and 6) 90007
90002 = 26/52 + 4/52 — 2/52 90007
90002 = 28/52 90007
90002 = 7/13.90007
90002 90007
90093 Independent and Dependent Events 90094
90056 Independent Event 90057
90002 When multiple events occur, if the outcome of one event 90102 DOES NOT 90103 affect the outcome of the other events, they are called independent events. 90007
90002 Say, a die is rolled twice. The outcome of the first roll does not affect the second outcome. These two are independent events. 90007
90002 90007
90002 90038 Example 1: 90039 Say, a coin is tossed twice. What is the probability of getting two consecutive tails? 90007
90002 Probability of getting a tail in one toss = 1/2 90007
90002 The coin is tossed twice.So 1/2 * 1/2 = 1/4 is the answer. 90007
90002 Here’s the verification of the above answer with the help of sample space. 90007
90002 When a coin is tossed twice, the sample space is {(H, H), (H, T), (T, H), (T, T)}. 90007
90002 Our desired event is (T, T) whose occurrence is only once out of four possible outcomes and hence, our answer is 1/4. 90007
90002 90007
90002 90038 Example 2: 90039 Consider another example where a pack contains 4 blue, 2 red and 3 black pens. If a pen is drawn at random from the pack, replaced and the process repeated 2 more times, What is the probability of drawing 2 blue pens and 1 black pen? 90007
90002 90192 Solution 90193 90007
90002 Here, total number of pens = 9 90007
90002 Probability of drawing 1 blue pen = 4/9 90009 Probability of drawing another blue pen = 4/9 90009 Probability of drawing 1 black pen = 3/9 90009 Probability of drawing 2 blue pens and 1 black pen = 4/9 * 4 / 9 * 3/9 = 48/729 = 16/243 90007
90002 90007
90056 Dependent Events 90057
90002 When two events occur, if the outcome of one event affects the outcome of the other, they are called dependent events.90007
90002 Consider the aforementioned example of drawing a pen from a pack, with a slight difference. 90007
90002 90038 Example 1: 90039 A pack contains 4 blue, 2 red and 3 black pens. If 2 pens are drawn at random from the pack, 90102 NOT 90103 replaced and then another pen is drawn. What is the probability of drawing 2 blue pens and 1 black pen? 90007
90002 90192 Solution: 90193 90007
90002 Probability of drawing 1 blue pen = 4/9 90009 Probability of drawing another blue pen = 3/8 90009 Probability of drawing 1 black pen = 3/7 90009 Probability of drawing 2 blue pens and 1 black pen = 4/9 * 3 / 8 * 3/7 = 1/14 90007
90002 90007
90002 Let’s consider another example: 90007
90002 90038 Example 2: 90039 What is the probability of drawing a king and a queen consecutively from a deck of 52 cards, 90102 without 90103 replacement.90007
90002 Probability of drawing a king = 4/52 = 1/13 90007
90002 After drawing one card, the number of cards are 51. 90007
90002 Probability of drawing a queen = 4/51. 90007
90002 Now, the probability of drawing a king and queen consecutively is 1/13 * 4/51 = 4/663 90007
90002 90007
90011 Conditional probability 90012
90002 Conditional probability is calculating the probability of an event given that another event has already occured. 90007
90002 The formula for conditional probability P (A | B), read as P (A given B) is 90007
90038 P (A | B) = P (A and B) / P (B) 90039
90002 90007
90002 Consider the following example: 90007
90002 90038 Example: 90039 In a class, 40% of the students study math and science.60% of the students study math. What is the probability of a student studying science given he / she is already studying math? 90007
90002 90192 Solution 90193 90007
90002 P (M and S) = 0.40 90007
90002 P (M) = 0.60 90007
90002 P (S | M) = P (M and S) / P (S) = 0.40 / 0.60 = 2/3 = 0.67 90007
90002 90007
90093 Complement of an event 90094
90002 A complement of an event A can be stated as that which does NOT contain the occurrence of A. 90007
90002 A complement of an event is denoted as P (A 90278 c 90279) or P (A ‘).90007
90038 P (A 90278 c 90279) = 1 — P (A)
90002 or it can be stated, P (A) + P (A 90278 c 90279) = 1 90007 90039
90002 For example, 90007
90002 if A is the event of getting a head in coin toss, A 90278 c 90279 is not getting a head i.e., getting a tail. 90007
90002 if A is the event of getting an even number in a die roll, A 90278 c 90279 is the event of NOT getting an even number i.e., getting an odd number. 90007
90002 if A is the event of randomly choosing a number in the range of -3 to 3, A 90278 c 90279 is the event of choosing every number that is NOT negative i.e., 0,1,2 & 3 (0 is neither positive or negative). 90007
90002 90007
90002 Consider the following example: 90007
90002 90038 Example: 90039 A single coin is tossed 5 times. What is the probability of getting at least one head? 90007
90002 90102 Solution: 90103 90007
90002 Consider solving this using complement. 90007
90002 Probability of getting no head = P (all tails) = 1/32 90007
90002 P (at least one head) = 1 — P (all tails) = 1 — 1/32 = 31/32. 90007
90002 90007
90011 Sample Probability questions with solutions 90012 90056 Probability Example 1 90057
90002 What is the probability of the occurrence of a number that is odd or less than 5 when a fair die is rolled.90007
90002 90192 Solution 90193 90007
90002 Let the event of the occurrence of a number that is odd be ‘A’ and the event of the occurrence of a number that is less than 5 be ‘B’. We need to find P (A or B). 90007
90002 P (A) = 3/6 (odd numbers = 1,3 and 5) 90007
90002 P (B) = 4/6 (numbers less than 5 = 1,2,3 and 4) 90007
90002 P (A and B) = 2/6 (numbers that are both odd and less than 5 = 1 and 3) 90007
90002 Now, P (A or B) = P (A) + P (B) — P (A or B) 90007
90002 = 3/6 + 4/6 — 2/6 90007
90002 P (A or B) = 5/6.90007
90002 90007
90056 Probability Example 2 90057
90002 A box contains 4 chocobars and 4 ice creams. Tom eats 3 of them one after another. What is the probability of sequentially choosing 2 chocobars and 1 icecream? 90007
90002 90192 Solution 90193 90007
90002 Probability of choosing 1 chocobar = 4/8 = 1/2 90007
90002 After taking out 1 chocobar, the total number is 7. 90007
90002 Probability of choosing 2nd chocobar = 3/7 90007
90002 Probability of choosing 1 icecream out of a total of 6 = 4/6 = 2/3 90007
90002 So the final probability of choosing 2 chocobars and 1 icecream = 1/2 * 3/7 * 2/3 = 1/7 90007
90002 90007
90056 Probability Example 3 90057
90002 When two dice are rolled, find the probability of getting a greater number on the first die than the one on the second, given that the sum should equal 8.90007
90002 90192 Solution 90193 90007
90002 Let the event of getting a greater number on the first die be G. 90007
90002 There are 5 ways to get a sum of 8 when two dice are rolled = {(2,6), (3,5), (4,4), (5,3), (6,2)}. 90007
90002 And there are two ways where the number on the first die is greater than the one on the second given that the sum should equal 8, G = {(5,3), (6,2)}. 90007
90002 Therefore, P (Sum equals 8) = 5/36 and P (G) = 2/36. 90007
90002 Now, P (G | sum equals 8) = P (G and sum equals 8) / P (sum equals 8) 90007
90002 = (2/36) / (5/36) 90007
90002 = 2/5 90007
90002 90007
90011 Probability Quiz: Sample probability questions for practice 90012 90002 90396 90396 Probability Problem 1
90007 90002 A bag contains blue and red balls.Two balls are drawn randomly without replacement. The probability of selecting a blue and then a red ball is 0.2. The probability of selecting a blue ball in the first draw is 0.5. What is the probability of drawing a red ball, given that the first ball drawn was blue? 90009 a) 0.4 90009 b) 0.2 90009 c) 0.1 90009 d) 0.5
90007 90002 90396 90396 Problem 2
90007 90002 A die is rolled thrice. What is the probability that the sum of the rolls is atleast 5. 90009 a) 1/216 90009 b) 1/6 90009 c) 3/216 90009 d) 212/216
90007 90002 90009 Learn how to solve: 90009 — Simple and compound interest problems 90009 — Speed, distance and time problems 90009 — Ratio and proportion 90009 — List of Maths Formulas 90007
Take this highly affordable online course on probability and test your knowledge with 600+ practice questions.Over 18,000 students enrolled, with average rating of 4.6 stars. Click below.
90192 Become a Probability & Statistics Master 90193 .90000 Rules of Probability and Independent Events 90001
90002
The study of
probability mostly deals with combining different events and studying these
events alongside each other. How these different events relate to each other determines
the methods and rules to follow when we’re studying their probabilities. 90003
90002
Events can be pided into two major categories dependent or Independent events.90003
90006
Independent Events 90007
90002
When two events are said to be independent of each other, what this means is that
the probability that one event occurs in no way affects the probability of the other
event occurring. An example of two independent events is as follows; say you rolled
a die and flipped a coin. The probability of getting any number face on the die
in no way influences the probability of getting a head or a tail on the coin.90003
90006
Dependent Events 90007
90002
When two events are said to be dependent, the probability of one event occurring
influences the likelihood of the other event. 90003
90002
For example, if you were to draw a two cards from a deck of 52 cards. If on your
first draw you had an ace and you put that aside, the probability of drawing an
ace on the second draw is greatly changed because you drew an ace the first time.Let’s calculate these different probabilities to see what’s going on. 90003
90002
There are 4 Aces in a deck of 52 cards 90003
90018
90019 90003
90002
On your first draw, the probability of getting an ace is given by: 90003
90018
90024 90003
90002
If we do not return this card into the deck, the probability of drawing an ace on
the second pick is given by 90003
90018
90029 90003
90018
90032 90003
90018
90035 90003
90002
As you can clearly see, the above two probabilities are different, so we say that
the two events are dependent.The likelihood of the second event depends on what
happens in the first event. 90003
90039
Conditional Probability 90040
90002
We have already defined dependent and independent events and seen how probability
of one event relates to the probability of the other event. 90003
90002
Having those concepts in mind, we can now look at conditional probability. 90003
90002
Conditional probability deals with further defining dependence of events by looking
at probability of an event given that some other event first occurs.90003
90002
Conditional probability is denoted by the following: 90003
90018
90050 90003
90002
The above is read as 90053 the probability that B occurs given that A has already occurred 90054. 90003
90002
The above is mathematically defined as: 90003
90018
90059 90003
90039
Set Theory in Probability 90040
90002
A sample space is defined as a universal set of all possible outcomes from a given
experiment.90003
90002
Given two events 90053 A 90054 and 90053 B 90054 and given that these events are part of a
sample space 90053 S 90054. This sample space is represented as a set as in the diagram
below. 90003
90018
90074 90003
90002
The entire sample space of 90053 S 90054 is given by: 90003
90018
90081 90003
90002
Remember the following from set theory: 90003
90018
90086 90003
90018
90089 90003
90002
The different regions of the set 90053 S 90054 can be explained as using the rules of
probability.90003
90039
Rules of Probability 90040
90002
When dealing with more than one event, there are certain rules that we must follow
when studying probability of these events. These rules depend greatly on whether
the events we are looking at are Independent or dependent on each other. 90003
90002
First acknowledge that 90003
90018
90102 90003
90006
Multiplication Rule (A∩B) 90007
90002
This region is referred to as ‘A intersection B’ and in probability; this region
refers to the event that both 90053 A 90054 and 90053 B 90054 happen.When we use the word
90053 and 90054 we are referring to multiplication, thus 90053 A and B 90054 can be thought
of as 90053 AxB 90054 or (using dot notation which is more popular in probability) 90053 A 90054 • 90053 B 90054 90003
90002
If 90053 A 90054 and 90053 B 90054 are dependent events, the probability of this event happening
can be calculated as shown below: 90003
90018
90129 90003
90002
If 90053 A 90054 and 90053 B 90054 are independent events, the probability of this event happening
can be calculated as shown below: 90003
90018
90138 90003
90002
Conditional probability for two independent events can be redefined using the relationship
above to become: 90003
90018
90143 90003
90018
90146 90003
90018
90149 90003
90002
The above is consistent with the definition of independent events, the occurrence
of event 90053 A 90054 in no way influences the occurrence of event 90053 B 90054, and so
the probability that event 90053 B 90054 occurs given that event 90053 A 90054 has occurred
is the same as the probability of event 90053 B 90054.90003
90006
Additive Rule (A∪B) 90007
90002
In probability we refer to the addition operator (90053 + 90054) as 90053 or 90054. Thus when
we want to we want to define some event such that the event can be A or B, to find
the probability of that event: 90003
90018
90172 90003
90018
90175 90003
90002
Thus it follows that: 90003
90018
90180 90003
90002
But remember from set theory that and from the way we defined our sample space above: 90003
90018
90185 90003
90002
and that: 90003
90018
90190 90003
So we can now redefine out event as
90018
90193 90003
90018
90196 90003
90002
The above is sometimes referred to as the subtraction rule.90003
90039
Mutual Exclusivity 90040
90002
Certain special pairs of events have a unique relationship referred to as mutual
exclusivity. 90003
90002
Two events are said to be mutually exclusive if they can not occur at the same time.
For a given sample space, its either one or the other but not both. As a consequence,
mutually exclusive events have their probability defined as follows: 90003
90018
90207 90003
90002
An example of mutually exclusive events are the outcomes of a fair coin flip.When
you flip a fair coin, you either get a head or a tail but not both, we can prove
that these events are mutually exclusive by adding their probabilities: 90003
90018
90212 90003
90002
For any given pair of events, if the sum of their probabilities is equal to one,
then those two events are mutually exclusive.
90003
90006
Rules of Probability for Mutually Exclusive Events 90007
90218
90219
90002
Multiplication Rule 90003
90002
From the definition of mutually exclusive events, we should quickly conclude the
following: 90003
90018
90225 90003
90227
90219
90002
Addition Rule 90003
90002
As we defined above, the addition rule applies to mutually exclusive events as follows: 90003
90018
90234 90003
90227
90219
90002
Subtraction Rule
90003
90002
From the addition rule above, we can conclude that the subtraction rule for mutually
exclusive events takes the form; 90003
90018
90243 90003
90227
90246
90006
Conditional Probability for Mutually Exclusive Events 90007
90002
We have defined conditional probability with the following equation: 90003
90018
90252 90003
90002
We can redefine the above using the multiplication rule 90003
90018
90257 90003
90002
hence 90003
90018
90262 90003
90002
Below is a venn diagram of a set containing two mutually exclusive events 90053 A 90054
and 90053 B 90054.90003
90018
90271 90003
.90000 Conditional Probability and Independent Events 90001
90002 Conditional Probability 90003
90004 Suppose a fair die has been rolled and you are asked to give the probability that it was a five. There are six equally likely outcomes, so your answer is 1/6. But suppose that before you give your answer you are given the extra information that the number rolled was odd. Since there are only three odd numbers that are possible, one of which is five, you would certainly revise your estimate of the likelihood that a five was rolled from 1/6 to 1/3.In general, the 90005 revised 90006 probability that an event 90005 A 90006 has occurred, taking into account the additional information that another event 90005 B 90006 has definitely occurred on this trial of the experiment, is called the 90005 conditional probability of 90006 90005 A 90006 90005 given 90006 90005 B 90006 and is denoted by P (A | B). The reasoning employed in this example can be generalized to yield the computational formula in the following definition. 90019
90020 Definition 90021
90004 90005 The 90006 conditional probabilityThe probability of the event 90005 A 90006 taking into account the fact that event 90005 B 90006 is known to have occurred.90029 of 90030 90005 A 90006 90029 given 90030 90005 B 90006, 90005 denoted 90006 P (A | B), 90005 is the probability that event 90006 90005 A 90006 90005 has occurred in a trial of a random experiment for which it is known that event 90006 90005 B 90006 90005 has definitely occurred. It may be computed by means of the following formula: 90006 90019
90004 Rule for Conditional Probability 90019
P (A | B) = P (A∩B) P (B)
90020 Example 20 90021
90004 A fair die is rolled.90019
90056
90057 Find the probability that the number rolled is a five, given that it is odd. 90058
90057 Find the probability that the number rolled is odd, given that it is a five. 90058
90061
90004 Solution: 90019
90004 The sample space for this experiment is the set S = {1,2,3,4,5,6} consisting of six equally likely outcomes. Let 90005 F 90006 denote the event «a five is rolled» and let 90005 O 90006 denote the event «an odd number is rolled,» so that 90019
F = {5} and O = {1,3,5}
90056
90057
90004 This is the introductory example, so we already know that the answer is 1/3.To use the formula in the definition to confirm this we must replace 90005 A 90006 in the formula (the event whose likelihood we seek to estimate) by 90005 F 90006 and replace 90005 B 90006 (the event we know for certain has occurred) by 90005 O 90006: 90019
P (F | O) = P (F∩O) P (O)
90004 Since F∩O = {5} ∩ {1,3,5} = {5}, P (F∩O) = 1/6. 90019
90004 Since O = {1,3,5}, P (O) = 3/6. 90019
90004 Thus 90019
P (F | O) = P (F∩O) P (O) = 1/63/6 = 13
90058
90057
90004 This is the same problem, but with the roles of 90005 F 90006 and 90005 O 90006 reversed.Since we are given that the number that was rolled is five, which is odd, the probability in question must be 1. To apply the formula to this case we must now replace 90005 A 90006 (the event whose likelihood we seek to estimate) by 90005 O 90006 and 90005 B 90006 (the event we know for certain has occurred) by 90005 F 90006: 90019
P (O | F) = P (O∩F) P (F)
90004 Obviously P (F) = 1/6. In part (a) we found that P (F∩O) = 1/6. Thus 90019
P (O | F) = P (O∩F) P (F) = 1/61/6 = 1
90058
90061
90004 Just as we did not need the computational formula in this example, we do not need it when the information is presented in a two-way classification table, as in the next example.90019
90020 Example 21 90021
90004 In a sample of 902 individuals under 40 who were or had previously been married, each person was classified according to gender and age at first marriage. The results are summarized in the following two-way classification table, where the meaning of the labels is: 90019
90114
90057
90005 M 90006: male 90058
90057
90005 F 90006: female 90058
90057
90005 E 90006: a teenager when first married 90058
90057
90005 W 90006: in one’s twenties when first married 90058
90057
90005 H 90006: in one’s thirties when first married 90058
90135
90136
90137
90138
90139
90140 90005 E 90006 90143
90140 90005 W 90006 90143
90140 90005 H 90006 90143
90140 Total 90143
90154
90155
90156
90138
90158 90005 M 90006 90161
90158 43 90161
90158 293 90161
90158 114 90161
90158 450 90161
90154
90138
90158 90005 F 90006 90161
90158 82 90161
90158 299 90161
90158 71 90161
90158 452 90161
90154
90138
90158 Total 90161
90158 125 90161
90158 592 90161
90158 185 90161
90158 902 90161
90154
90197
90198
90004 The numbers in the first row mean that 43 people in the sample were men who were first married in their teens, 293 were men who were first married in their twenties, 114 men who were first married in their thirties, and a total of 450 people in the sample were men.Similarly for the numbers in the second row. The numbers in the last row mean that, irrespective of gender, 125 people in the sample were married in their teens, 592 in their twenties, 185 in their thirties, and that there were 902 people in the sample in all. Suppose that the proportions in the sample accurately reflect those in the population of all individuals in the population who are under 40 and who are or have previously been married. Suppose such a person is selected at random. 90019
90056
90057 Find the probability that the individual selected was a teenager at first marriage.90058
90057 Find the probability that the individual selected was a teenager at first marriage, given that the person is male. 90058
90061
90004 Solution: 90019
90004 It is natural to let 90005 E 90006 also denote the event that the person selected was a teenager at first marriage and to let 90005 M 90006 denote the event that the person selected is male. 90019
90056
90057 According to the table the proportion of individuals in the sample who were in their teens at their first marriage is 125/902.This is the relative frequency of such people in the population, hence P (E) = 125 / 902≈0.139 or about 14%. 90058
90057
90004 Since it is known that the person selected is male, all the females may be removed from consideration, so that only the row in the table corresponding to men in the sample applies: 90019
90136
90137
90138
90139
90140 90005 E 90006 90143
90140 90005 W 90006 90143
90140 90005 H 90006 90143
90140 Total 90143
90154
90155
90156
90138
90158 90005 M 90006 90161
90158 43 90161
90158 293 90161
90158 114 90161
90158 450 90161
90154
90197
90198
90058 90061.
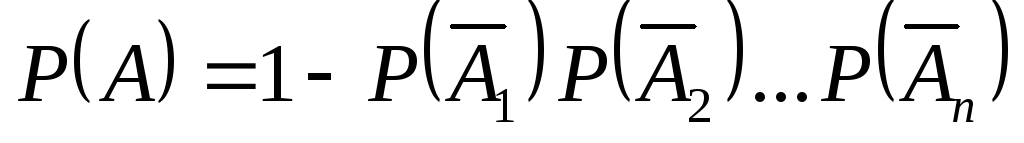
 .
. .
. .
. .
. .
. .
. .
. .
.