Контрольный тест по теме «Четырехугольники»
Контрольный тест по теме «Четырехугольники»| 12+ Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058 | Пользовательское соглашение Контактная и правовая информация |
Педагогическое сообщество | Бесплатные всероссийские конкурсы | Бесплатные сертификаты | Нужна помощь? Инструкции для новых участников | Бесплатная онлайн-школа для 1-4 классов |
Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости
Библиотека
▪Учебно-дидактические материалы
▪Тесты (специальный формат)
Материал опубликовал
10
#8 класс #Геометрия #ФГОС #Учебно-дидактические материалы #Тест (специальный формат) #Учитель-предметник #Школьное образование #УМК Л. С. Атанасяна
С. Атанасяна
Конкурсная работа Всероссийский дистанционный конкурс для учителей математики «Контрольная работа в формате теста» |
Тема: Контрольный тест по теме «Четырехугольники»
Предмет: геометрия
Класс: 8
Учебник: «Геометрия 7-9 класс» автор Атанасян Л.С., Бутузов В.Ф. и др.
Инструкция к тесту
Тест состоит из 14 заданий, включающих теоретические вопросы, а так же практические задачи. Для ответа на вопрос надо выбрать правильный ответ из четырех предложенных вариантов. Вопрос предполагает только один вариант ответа. В №6 и №11 следует записать ответ.
Критерии оценивания:
Каждый правильный ответ- 1балл.
За 13-14 баллов выставляется отметка «5»
За 9-12 баллов отметка «4»
За 6-8 баллов отметка «3»
В остальных случаях ставится отметка «2»
Ключ к тесту:
Вариант 1:
№ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
ответ | 4 | 3 | 2 | 3 | 2 | ромб | 2 | 3 | 4 | 4 | 8 | 2 | 3 | 2 |
Вариант 2:
№ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
ответ | 3 | 1 | 3 | 2 | 4 | квадрат | 3 | 2 | 1 | 1 | 16 | 4 | 2 | 1 |
Контрольная работа по теме «Четырехугольники»
Вариант 1
- Сумма углов равна 360º:
- В прямоугольнике
- В параллелограмме
- В ромбе
- Во всех перечисленных выше фигурах
- Фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков называется:
- Трапеция
- Прямоугольник
- Четырехугольник
- Квадрат
- Четырехугольник, у которого противоположные стороны параллельны называется:
- Квадрат
- Параллелограмм
- Трапеция
- прямоугольник
- По второму свойству параллелограмма:
- Диагонали делятся пополам
- Диагонали равны
- Диагонали в точке пересечения делятся пополам
- Диагонали делят параллелограмм пополам
- Если боковые стороны трапеции равны, то она называется:
- Правильной
- Равнобедренной
- Равносторонней
- Равнобокой
- Параллелограмм, у которого все стороны равны, называется ____________.

- Выберите верное утверждение:
- если в четырехугольнике диагонали равны, а один из углов прямой, то этот четырехугольник – квадрат
- если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм
- если в четырехугольнике две стороны равны, а два угла прямые, то этот четырехугольник – прямоугольник
- если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник — ромб
- Один из углов параллелограмма равен 50º. Найдите углы, соседние с ним:
- 50º и 130º
- 70º и 110º
- 130º и 130º
- 80º и 100º
- Периметр параллелограмма равен 40 см, а две из его сторон относятся как 3 : 1. Чему равна наибольшая из его сторон?
- 6
- 4
- 10
- 15
- Диагонали ромба ABCD пересекаются в точке О. Угол ОАВ равен 25º. Найти угол АВО:
- 165 º
- 75 º
- 85 º
- 65 º
- Найти диагональ ВD прямоугольника ABCD, если угол CAD равен 30 º, а CD = 4 см.

Ответ: __________
- В трапеции ABCD основания равны 10 см и 12 см. Чему равна ее средняя линия?
- 10
- 11
- 8
- 12
- В параллелограмме ABCD, сторона АВ=7, диагонали АС и ВD равны 6 и 10 см, т.О – пересечение диагоналей. Чему равен периметр треугольника АОВ:
- 11,5
- 17
- 15
- 12
- В равнобедренной трапеции высота образует с боковой стороной угол 30°, а ее основания равны 10 см и 6 см. Чему равен периметр трапеции?
- 28
- 24
- 26
- 32
Вариант 2
- Многоугольник, который лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины, называется:
- Правильным
- Неправильным
- Выпуклым
- Невыпуклым
- Сумма углов равна 360º:
- Во всех ниже перечисленных
- В параллелограмме
- В квадрате
- В трапеции
- Четырехугольник, у которого две противолежащие стороны параллельны, называется:
- Ромб
- Трапеция
- Параллелограмм
- прямоугольник
- По первому признаку параллелограмма:
- Противоположные стороны равны
- Противоположные углы и стороны равны
- Противоположные углы равны
- Диагонали равны
- Если в трапеции один из углов равен 90º, то она называется:
- Правильной
- Равнобокой
- Равнобедренной
- Прямоугольной
- Прямоугольник, у которого все стороны равны называется __________
- Выберите верное утверждение:
- если в четырехугольнике диагонали равны и точкой пересечения делятся пополам, то этот четырехугольник – ромб
- если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник – ромб
- если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник
- если в четырехугольнике диагонали равны, а один из углов прямой, то этот четырехугольник – квадрат
- Один из углов параллелограмма равен 70º.

- 70º и 110º
- 110º и 110º
- 80º и 100º
- 60º и 120º
- Периметр параллелограмма равен 24 см, а одна из сторон в два раза больше другой. Чему равна наименьшая из его сторон:
- 4
- 12
- 9
- 6
- Диагонали ромба MNEK пересекаются в точке О. Угол ОNE равен 35º. Найти угол NEO?
- 55º
- 45º
- 35º
- 65º
- Найти диагональ NK прямоугольника MNEK, если угол EMK равен 30 º, а EK = 8 см.
Ответ: ________
- В трапеции MNEK основания равны 12 см и 16 см. Чему равна ее средняя линия?
- 28
- 16
- 8
- 14
- В параллелограмме MNEK, сторона MN = 9, диагонали ME и NK равны 8 и 12 см, т.О – пересечение диагоналей. Чему равен периметр треугольника MNO:
- 39
- 19
- 29
- 25
- В равнобедренной трапеции высота образует с боковой стороной угол 30°, а ее основания равны 11 см и 5 см.
 Чему равен периметр трапеции:
Чему равен периметр трапеции:
- 28
- 26
- 24
- 32
Опубликовано в группе «Математика — наука великая»
Чтобы написать комментарий необходимо авторизоваться.
Закрыть
Тест №2 по геометрии. 8 класс. Тема «Четырехугольники»
Тест по геометрии по теме «Четырехугольники»
(к учебнику «Геометрия» Погорелова А. В., 8 класс)
Инструкция к тесту
Тест состоит из 14 заданий, включающих теоретические вопросы и вопросы с пробелами, а так же практические задачи. Для ответа на вопрос надо выбрать правильный ответ из четырех предложенных вариантов.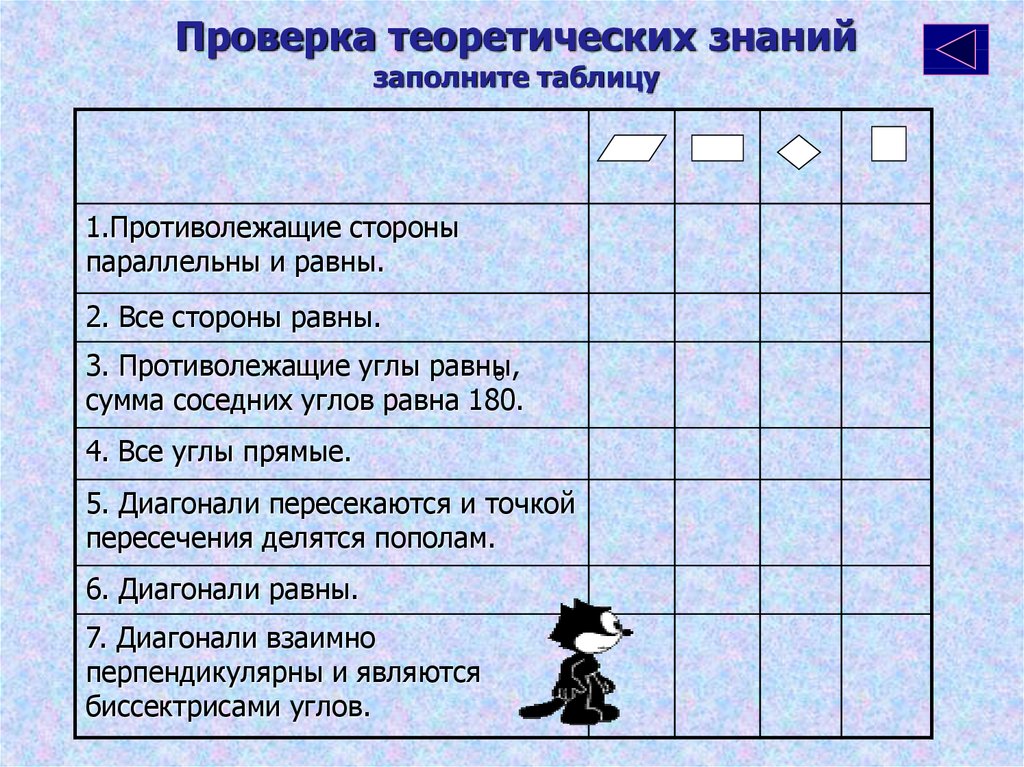 Вопрос предполагает только один вариант ответа.
Вопрос предполагает только один вариант ответа.
Вариант №1
1. Параллелограмм, у которого все углы прямые.
а) трапеция
б) четырехугольник
в) ромб
г) прямоугольник
2. Четырехугольник, у которого противолежащие стороны параллельны.
а) трапеция
б) параллелограмм
в) ромб
г) прямоугольник
3. Найдите на рисунке трапецию.
а) б) в) г)
4. Любой ромб является:
а) квадратом
б) ромбом
в) параллелограммом
г) трапецией
5. Один из углов равнобедренной трапеции равен 57º. Найдите остальные углы трапеции.
а) 103º, 103º, 57º
б) 113º, 113º, 57º
в) 123º, 123º, 57º
г) 133º, 133º, 57º
6. Трапеция, у которой один из углов равен 90º,называется:
а) равнобокой
б) прямоугольной
в) остроугольной
г) тупоугольной
7. Периметр параллелограмма равен 80 см, одна из сторон равна 15 см. Найдите остальные стороны параллелограмма.
Периметр параллелограмма равен 80 см, одна из сторон равна 15 см. Найдите остальные стороны параллелограмма.
а) 15 см, 20 см, 20 см
б) 25 см, 20 см, 20 см
в) 15 см, 35 см, 35 см
г) 15 см, 25 см, 25 см
8. Найдите периметр квадрата, если его сторона равна 16 см.
а) 64 см
б) 62 см
в) 68 см
г) 72 см
9. Диагонали ….. равны.
а) четырехугольника
б) ромба
в) прямоугольника
г) трапеции
10. Назовите боковые стороны трапеции КМNЕ.
а ) КЕ и МN
б) МN и ЕN
в) КМ и NЕ
г) МN и МК
11. Квадратом является:
а) параллелограмм, у которого все углы прямые
б) ромб, у которого диагонали равны
в) параллелограмм, у которого диагонали равны
г) прямоугольник, у которого все углы прямые
12. Выберите верное утверждение:
а) если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм
б) если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник — ромб
в) если в четырехугольнике две стороны равны, а два угла прямые, то этот четырехугольник — прямоугольник
г) если в четырехугольнике диагонали равны, а один из углов прямой, то этот четырехугольник — квадрат
13. Средняя линия трапеции ….. и равна их полусумме.
Средняя линия трапеции ….. и равна их полусумме.
а) перпендикулярна основаниям
б) делит боковые стороны пополам
в) параллельна основаниям
г) пересекает боковые стороны
14. В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большое основание на отрезки 20см и 40см. Найдите основания трапеции.
а) 20 см и 60 см
б) 30 см и 60 см
в) 40 см и 20 см
г) 50 см и 10 см
Вариант №2.
1. Параллелограмм, у которого все стороны равны.
а) четырехугольник
б) трапеция
в) ромб
г) прямоугольник
2. Четырехугольник, у которого только две противолежащие стороны параллельны.
а) трапеция
б) параллелограмм
в) ромб
г) прямоугольник
3. Найдите на рисунке параллелограмм
а) б) в) г)
4. Всякий прямоугольник является:
а) квадратом
б) ромбом
в) трапецией
г) параллелограммом
5. Один из углов параллелограмма 64º. Найдите остальные углы параллелограмма.
Один из углов параллелограмма 64º. Найдите остальные углы параллелограмма.
а) 64º, 106º, 106º
б) 64º, 116º, 116º
в) 64º, 126º, 126º
г) 64º, 96º, 96º
6. Трапеция, у которой боковые стороны равны, называется:
а) равнобокой
б) прямоугольной
в) остроугольной
г) тупоугольной
7. Периметр параллелограмма равен 100 см, одна из сторон равна 35 см. Найдите остальные стороны параллелограмма.
а) 35 см, 20 см, 20 см
б) 25 см, 20 см, 20 см
в) 35 см, 15 см, 15 см
г) 15 см, 25 см, 25 см
8. Найдите периметр ромба, если его сторона равна 12 см.
а) 40 см
б) 48 см
в) 46см
г) 52 см
9. Диагонали ….. пересекаются под прямым углом.
а) четырехугольника
б) ромба
в) прямоугольника
г) трапеции
10. Назовите основания трапеции КМNЕ.
а ) КЕ и МN
б) МN и ЕN
в) КМ и NЕ
г) МN и МК
11. Прямоугольником называется:
Прямоугольником называется:
а) параллелограмм, у которого все стороны равны
б) параллелограмм, у которого все углы прямые
в) четырехугольник, у которого диагонали равны
г) четырехугольник, у которого противолежащие стороны равны
12. Выберите верное утверждение:
а) если в четырехугольнике диагонали равны и точкой пересечения делятся пополам, то этот четырехугольник — ромб
б) если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник — ромб
в) если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник
г) если в четырехугольнике диагонали равны, а один из углов прямой, то этот четырехугольник — квадрат
13. Средняя линия трапеции параллельна основаниям и равна их …..
а) полуразности
б) полусумме
в) полупроизведению
г) сумме
14. В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большое основание на отрезки 10см и 30см. Найдите основания трапеции.
В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большое основание на отрезки 10см и 30см. Найдите основания трапеции.
а) 50 см и 20 см
б) 30 см и 20 см
в) 40 см и 10 см
г) 40 см и 20 см
Ответы к тесту
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
I вариант | г | б | в | в | в | б | г | а | в | в | г | а | в | а |
II вариант | в | б | б | г | б | а | в | б | б | а | б | в | б | г |
Тест по теме Четырёхугольники — Тур-инфо
Тест на четырёхугольники
Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.
Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.
Теоретический тест по теме «Четырёхугольники» содержит 10 вопросов. На выполнение теста отводится 10 минут.
Список вопросов теста
Вопрос 1
Какой из четырехугольников не является параллелограммом?
Варианты ответов
- ромб квадрат трапеция прямоугольник
Вопрос 2
Диагонали какого из четырехугольников равны?
Варианты ответов
- равнобедренная трапеция параллелограмм ромб прямоугольник
Вопрос 3
У какого из четырехугольников все углы прямые и противоположные стороны равны?
Варианты ответов
- квадрат ромб прямоугольник прямоугольная трапеция
Вопрос 4
Диагонали какого из четырехугольников взаимно перпендикулярны?
Варианты ответов
- параллелограмм квадрат ромб прямоугольник
Вопрос 5
У какого из четырехугольников противоположные стороны и углы не равны?
Варианты ответов
- ромб параллелограмм трапеция прямоугольник
Вопрос 6
Диагонали какого из четырехугольников не являются биссектрисами углов?
Варианты ответов
- параллелограмм трапеция ромб квадрат
Вопрос 7
Диагонали какого из четырехугольников делятся точкой пересечения пополам?
Список вопросов теста.
Videouroki. net
08.03.2018 16:12:44
2018-03-08 16:12:44
Источники:
Https://videouroki. net/tests/tiest-po-tiemie-chietyriokhughol-niki. html
Тест с ответами: “Четырёхугольники” | Образовательные тесты с ответами » /> » /> .keyword { color: red; }
Тест на четырёхугольники
5. Выберите верное утверждение:
А) если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник – ромб
Б) если в четырехугольнике две стороны равны, а два угла прямые, то этот четырехугольник – прямоугольник
В) если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм +
6. Существует ли четырехугольник с 3 тупыми углами:
А) нет
Б) да +
В) зависит от задачи
7. Квадратом является:
А) параллелограмм, у которого диагонали равны
Б) параллелограмм, у которого все углы прямые
В) прямоугольник, у которого все углы прямые +
8. Существует ли такой параллелограмм, который диагональю разбивается на два равносторонних треугольника:
Существует ли такой параллелограмм, который диагональю разбивается на два равносторонних треугольника:
А) да +
Б) нет
В) зависит от задачи
9. Диагонали … равны:
А) трапеции
Б) четырехугольника
В) прямоугольника +
10. Существует ли трапеция с тремя равными сторонами:
А) нет
Б) да +
В) зависит от задачи
11. Найдите периметр квадрата, если его сторона равна 16 см:
А) 64 см +
Б) 72 см
В) 68 см
12. Диагонали пересекаются под прямым углом в следующем четырехугольнике:
А) трапеция
Б) квадрат +
В) параллелограмм
13. Периметр параллелограмма равен 80 см, одна из сторон равна 15 см. Найдите остальные стороны параллелограмма:
А) 15 см, 25 см, 25 см +
Б) 15 см, 20 см, 20 см
В) 15 см, 35 см, 35 см
14. Диагонали пересекаются под прямым углом в следующем четырехугольнике:
А) трапеция
Б) прямоугольник
В) ромб +
15. Трапеция, у которой один из углов равен 90º, называется:
А) прямоугольной +
Б) равнобокой
В) тупоугольной
16. У какого четырехугольника диагонали пересекаются и точкой пересечения делятся пополам:
У какого четырехугольника диагонали пересекаются и точкой пересечения делятся пополам:
А) равносторонний треугольник
Б) параллелограмм +
В) пятиугольник
17. Один из углов равнобедренной трапеции равен 57º. Найдите остальные углы трапеции:
А) 113º, 113º, 57º
Б) 103º, 103º, 57º
В) 123º, 123º, 57º +
18. У какого четырехугольника диагонали пересекаются и точкой пересечения делятся пополам:
А) трапеция
Б) квадрат +
В) нонагон
19. Любой ромб является:
А) квадратом
Б) трапецией
В) параллелограммом +
20. У какого четырехугольника диагонали пересекаются и точкой пересечения делятся пополам:
А) пятиугольник
Б) прямоугольник +
В) равносторонний треугольник
21. Найдите периметр параллелограмма, площадь которого равна 144, а высоты 8 и 12:
А) 60 +
Б) 48
В) 34
22. У какого четырехугольника диагонали пересекаются и точкой пересечения делятся пополам:
А) трапеция
Б) ромб +
В) нонагон
23. Сопоставьте фигуру и формулу для нахождения её площади:
Сопоставьте фигуру и формулу для нахождения её площади:
S=ab:
А) параллелограмм
Б) трапеция
В) прямоугольник +
24. Выпуклый многоугольник, у которого каждый угол равен 120 гр., имеет:
А) 4 стороны
Б) 6 сторон +
В) 8 сторон
25. Сопоставьте фигуру и формулу для нахождения её площади:
S=a2:
А) трапеция
Б) ромб
В) квадрат +
26. Даны 3 точки, не лежащие на одной прямой. Сколько параллелограммов с вершинами в данных точках можно построить:
А) 5
Б) 3 +
В) 4
27. Сопоставьте фигуру и формулу для нахождения её площади:
S=ah:
А) параллелограмм +
Б) квадрат
В) ромб
28. В выпуклом многоугольнике провели все его диагонали. Их оказалось 5. Сколько сторон имеет этот многоугольник:
А) 8
Б) 6
В) 5 +
29. Сопоставьте фигуру и формулу для нахождения её площади:
S=1/2d1d2:
А) ромб +
Б) квадрат
В) прямоугольник
30. Сопоставьте фигуру и формулу для нахождения её площади:
S=(a+b)h/2:
А) ромб
Б) трапеция +
В) параллелограмм
Найдите остальные углы трапеции а 113º, 113º, 57º б 103º, 103º, 57º в 123º, 123º, 57º.
Liketest. ru
15.12.2018 3:09:57
2018-12-15 03:09:57
Источники:
Https://liketest. ru/geometriya/test-s-otvetami-chetyryoxugolniki. html
Тест на треугольники, четырёхугольники, многоугольники и их элементы по математике для ОГЭ — тестирование от Skills4U » /> » /> .keyword { color: red; }
Тест на четырёхугольники
Первичное тестирование для определения вашего уровня знаний — бесплатно.
Платформа определит, какие навыки у вас сформированы слабо, и предложит «прокачать» их до 100%.
Не забудьте, что для формирования стойкого навыка нужно выполнить 5 коротких повторений по несколько минут в течение ближайших 4 дней. Платформа пришлет своевременное напоминание. Содержание каждого из последующих вопросов будет подстраиваться под ваши индивидуальные особенности с учетом уже выполненных заданий.
Тест Треугольники, четырёхугольники, многоугольники и их элементы по математике для ОГЭ.
Skills4u. ru
ru
08.09.2017 21:16:57
2017-09-08 21:16:57
Источники:
Https://skills4u. ru/school/test_1759.html
Четырехугольники MCQ
Класс 9 Математика Глава 8 MCQ по четырехугольникам доступны здесь с ответами, онлайн. Вопросы здесь подготовлены в соответствии с учебным планом CBSE и учебным планом NCERT. Студенты могут подготовиться к своим экзаменам с помощью этих объективных вопросов, чтобы получить хорошие оценки. Ответы здесь доступны с подробными пояснениями.
Получите все MCQ по главам в Vedantu, а также проверьте важные вопросы по математике для 9 класса. В этой статье мы собираемся пройти MCQ по четырехугольникам. Этот MCQ по четырехугольникам поможет учащимся получить краткое представление о теме.
Определение четырехугольника (MCQ по четырехугольникам)
Четырехугольником называется плоская фигура, имеющая четыре стороны или ребра, а также четыре угла или вершины. Четырехугольники обычно имеют стандартные формы с четырьмя сторонами, такие как прямоугольник, квадрат, трапеция и воздушный змей или неправильные. В статье далее мы собираемся обсудить MCQ на Четырехугольниках. Всего на Четырехугольниках 10 MCQ.
Четырехугольники обычно имеют стандартные формы с четырьмя сторонами, такие как прямоугольник, квадрат, трапеция и воздушный змей или неправильные. В статье далее мы собираемся обсудить MCQ на Четырехугольниках. Всего на Четырехугольниках 10 MCQ.
Типы четырехугольников
Четырехугольники бывают разных типов. Слово «квадрат» означает четыре, и все эти типы четырехугольников имеют четыре стороны, сумма углов этих фигур составляет 360 градусов.
ТРАПЕЗИЙ
Параллелограмм
Квадраты
Прямоугольник
Rhombus
2019
2.
 Whatsleshal Why Farall Aralles Arallest 9002. Allest Arallest 9002. Allesles Arallest 9002. Allesles Arallest
Whatsleshal Why Farall Aralles Arallest 9002. Allest Arallest 9002. Allesles Arallest 9002. Allesles Arallest. Why Allesles Arally
Прямоугольник — это параллелограмм, у которого все углы равны 90 градусам.
Ромб – это параллелограмм, у которого все четыре стороны равны.
Квадрат — это прямоугольник, у которого все четыре стороны равны.
Трапеция — это параллелограмм, у которого одна пара противоположных сторон параллельна друг другу
Воздушный змей — это параллелограмм, у которого две пары смежных сторон равны
Allesles Arallest
. Why Why Allasles Arallest
.
Другой способ классификации типов четырехугольников приведен ниже:
Выпуклые четырехугольники: Обе диагонали четырехугольника полностью расположены внутри фигуры.

Вогнутые четырехугольники: По крайней мере, одна из диагоналей находится частично/полностью за пределами фигуры.
Пересекающиеся четырехугольники: Пересекающиеся четырехугольники не являются простыми четырехугольниками, в которых пересекаются пары несмежных сторон. Эти виды четырехугольников также известны как самопересекающиеся или скрещенные четырехугольники.
В этой статье мы также обсудим MCQ на четырехугольниках.
Area Formulas of Quadrilaterals
Quadrilateral Area Formulas | |
Area of the Square | (side)2 |
Area of the Kite | (1 ⁄ 2) × Произведение диагоналей |
Площадь параллелограмма | Основание × высота |
Площадь прямоугольника | Длина × Beartth |
 один из них. Ниже приведены MCQ на Четырехугольниках. Всего на Четырехугольниках 10 MCQ.
один из них. Ниже приведены MCQ на Четырехугольниках. Всего на Четырехугольниках 10 MCQ.1. Четырехугольник, все стороны которого равны, а углы равны 90 градусов, это называется:
а. Прямоугольник
б. Площадь
гр. Воздушный змей
d. Параллелограмм
Ответ: b
2. Сумма всех углов четырехугольника равна:
а. 180°
б. 270°
в. 360°
д. 90°
Ответ: с
3. Трапеция имеет:
а. Одна пара противоположных сторон параллельна
b. Две пары противоположных сторон, которые параллельны друг другу
c. Все его стороны равны
д. Все углы равны
Ответ: a
Объяснение: У трапеции одна пара противоположных сторон параллельна друг другу, а две другие стороны не параллельны.
4. Ромб может быть:
а. Параллелограмм
б. Трапеция
в. Воздушный змей
d. Квадрат
Ответ: d
5. Диагональ параллелограмма делит его на две равные части:
a. Квадрат
б. Параллелограмм
в. Треугольники
d. Прямоугольник
Ответ: c
6. Противоположные углы параллелограмма:
a. Равно
б. Неравные
c. Невозможно определить
d. Ничего из вышеперечисленного
Ответ: a
7. Диагонали параллелограмма:
a. Равно
б. Неравные
c. Делят друг друга пополам
d. Не имеют отношения
Ответ: c
8. Каждый угол прямоугольника:
а. Более 90°
Более 90°
б. Менее 90°
c. Равен 90°
d. Равно 45°
Ответ: c
Объяснение: ABCD — прямоугольник, а ∠A равно 90°
AD || BC и AB являются секущими
∠ A + ∠ B равны 180° (внутренние углы лежат по одну сторону от секущей)
∠ A = 90°
Итак, ∠ B равно 180° – ∠ A равно 180° – 90° равно 90°
Теперь ∠ C = ∠ A и ∠ D = ∠ B (Противоположные углы параллелограмма)
Итак, ∠ C равно 90° и ∠ D равно 90°
Следовательно, все стороны равны 90°.
9. Углы четырехугольника относятся как 4:5:10:11. Углы даны ниже:
a. 36°, 60°, 108°, 156°
б. 48°, 60°, 120°, 132°
в. 52°, 60°, 122°, 126°
d. 60°, 60°, 120°, 120°
Ответ: b
Объяснение: x — общий угол между всеми четырьмя углами четырехугольника.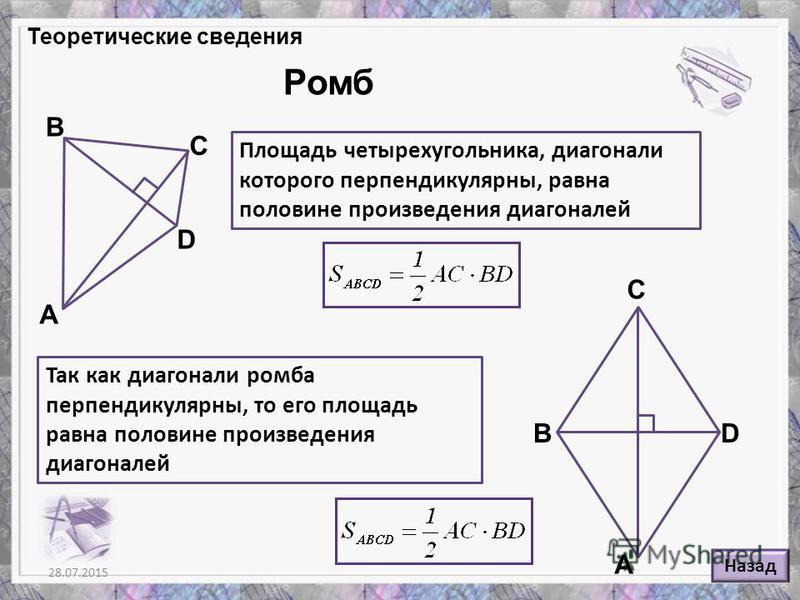
Из свойства суммы углов мы знаем, что:
4x+5x+10x+11x = 360°
30x = 360°
x = 12°
Следовательно, углы равны
4x = 4 (12) = 48°
1×9005 60°10x = 10 (12) = 120°
11x = 11 (12) = 132°
10. Если ABCD — трапеция, в которой AB || CD и AD = BC, тогда:
а. ∠А = ∠В
б. ∠A > ∠B
в. ∠A < ∠B
d. Ничего из вышеперечисленного
Ответ: a
Объяснение: Проведите прямую через C, параллельную DA и пересекающую AB, которая была произведена в точке E.
CE = AD (Противоположные стороны)
AD = BC (Дано)
BC = CE
⇒ ∠CBE = ∠CEB
также,
∠(при равных углах s0A + ∠18CBE
∠B + ∠CBE равно 180° (как линейная пара)
⇒ ∠A = ∠B
задал вопросы.
Типы четырехугольников
В геометрии четырехугольник — это любая четырехсторонняя замкнутая фигура или многоугольник, имеющий четыре ребра и четыре угла. Ниже приведены некоторые общепринятые определения четырехугольников:
Quick Supply
Кваровного-это полигон с закрытой формой
Кваровно-наборы образуются при соединении 4 нецелинейных точках
Кваровной на четырех сторон 9003
20192020202020202020202020202020202020202.20202020202020202. Четырехугольник имеет четыре угла и четыре ребраСумма всех внутренних углов четырехугольника равна 360°.
Длина всех четырех сторон четырехугольника может быть одинаковой или разной.

Обзор четырехугольников и их свойств
Ниже приведена таблица, в которой перечислены все свойства четырех четырехугольников, квадрата, прямоугольника, ромба и параллелограмма. Подробное сравнение всех четырех четырехугольников приведено ниже.
Property | Square | Rectangle | Parallelogram | Rhombus |
Angles | Each angle is equal to 90o | Each angle is equal to 90o | Opposite angles are equal | Two pairs of opposite angles are equal |
Стороны | Все четыре стороны равны и две пары противоположных сторон параллельны друг другу | две пары противоположных сторон параллельны друг другу | Стороны равны и параллельны каждому другу | Все четыре стороны равны, а две пара противоположных сторон параллельны каждую оставшуюся |
Engruence 9000 9000 | 3 Да. Да | Нет | Нет | |
Делят ли диагонали пополам? | Да | Да | Да | Да |
Диагонали перпендикулярны друг другу? | Да, | NO | NO | Да 9003 |
Полиметр | 4. где l — длина, b — ширина прямоугольника | A+b+c+d, где a, b, c, d — длины сторон параллелограмма | 4L (L = длина стороны) | |
Область | L2, где L — длина боковой стороны | L x B, где L & B — длина, а панель. | b x h, где b и h — основание и высота параллелограмма | ½ d1 x d2, где d1 и d2 — длины диагоналей ромба Для получения дополнительной информации воспользуйтесь бесплатными ресурсами, доступными на веб-сайте Vedantu, полезными для совета штата, CBSE, ICSE и конкурсных экзаменов. 30+ тестовых вопросов по четырехугольникам — Математика MCQMCQ по пониманию четырехугольников: Вопросы. Диагонали не обязательно делят пополам внутренние углы в вершинах Связанный: Проблемы со временем и работой Вопросы. Три угла четырехугольника равны 54°, 80° и 116°. Найдите величину четвертого угла. Сумма углов четырехугольника _____ прямых углов Вопрос. Можно ли иметь правильный многоугольник с мерой каждого внешнего угла 22º. Связанный: Тест по аналогии Вопросы. Вопрос. Сколько сторон имеет правильный многоугольник, каждый угол которого равен 108º? (a) 6 сторон Вопрос. Диагонали не обязательно пересекаются под прямым углом в Связанные: Вопросы о перестановке Вопрос. Какой максимальный внешний угол может быть у правильного многоугольника? Вопрос. Определить количество сторон многоугольника, внешние и внутренние углы которого относятся как 1 : 5. Вопрос. Связано с: Вероятностные вопросы Вопросы. Три угла четырехугольника равны 30º, 150º и 100º. Найдите четвертый угол. Вопрос. Стороны пятиугольника изготавливаются по порядку, и полученные таким образом внешние углы имеют размеры х °, (2 х °), (3 х + 10)°, (4 х + 5)° и (5 х °) соответственно. Найдите значение x Вопрос. Два смежных угла параллелограмма равны. Найдите величину каждого угла параллелограмма. Связанный: Кол. Вопросы. Четырехугольник имеет все четыре угла одинаковой величины. Какова мера каждого? Вопрос. Найдите количество сторон правильного многоугольника, если каждый из его углов имеет меру 150°? Вопрос. Если каждый внутренний угол правильного многоугольника равен 150°, сколько сторон у этого многоугольника? Связанный: вопрос, основанный на формуле процентов Ques. Найдите длину диагонали прямоугольника, стороны которого равны 5 см и 12 см. Вопрос. Два угла четырехугольника равны 80º каждый. Два других угла также равны. Чему равен каждый из этих двух углов? Вопрос. Количество градусов в каждом внешнем углу правильного пятиугольника равно Связанный: вопросы по силлогизму Ques. RENT — это прямоугольник. Его диагонали пересекаются в точке O . Найдите х , если ИЛИ = 3 х + 5 и ОТ = 2 х + 7. Вопрос. Какова мера каждого угла правильного шестиугольника? Вопрос. Если диагонали четырехугольника перпендикулярны друг другу, то это всегда квадрат. Правда или ложь? Связанные: Синонимы для общеупотребительных слов Вопрос. Вопрос. Тождество всех четырехугольников, имеющих четыре прямых угла Вопрос. Отношение внешнего угла к внутреннему углу правильного многоугольника равно 2 : 7. Найдите количество сторон многоугольника. Связанные: вопросы числового ряда Вопросы. Две диагонали не обязательно равны в Вопрос. Сколько сторон у правильного многоугольника, если градусная мера внешнего угла равна 36°. Вам также может понравитьсяОб автореЯш БансалЯш является соучредителем Examsegg. Яш любит решать вопросы по логике и математике. Он сам научился сочетать различные методы, чтобы получить точное решение за меньшее время. геометрия. Можем ли мы вычислить площадь четырехугольника с одним прямым углом, зная только длины любых трех сторон?Спросил Изменено 3 года, 6 месяцев назад Просмотрено 4k раз 22 Новинка! Сохраняйте вопросы или ответы и организуйте свой любимый контент. $\begingroup$ Недавно я прошел тест на IQ для развлечения, но не согласен с ответом на один из вопросов. Вот вопрос: Моя проблема в том, что объяснение предполагает, что угол DC является прямым углом. Таким образом, даже зная A, B, C и D, площадь невозможно рассчитать. Итак, мой вопрос состоит из двух частей:
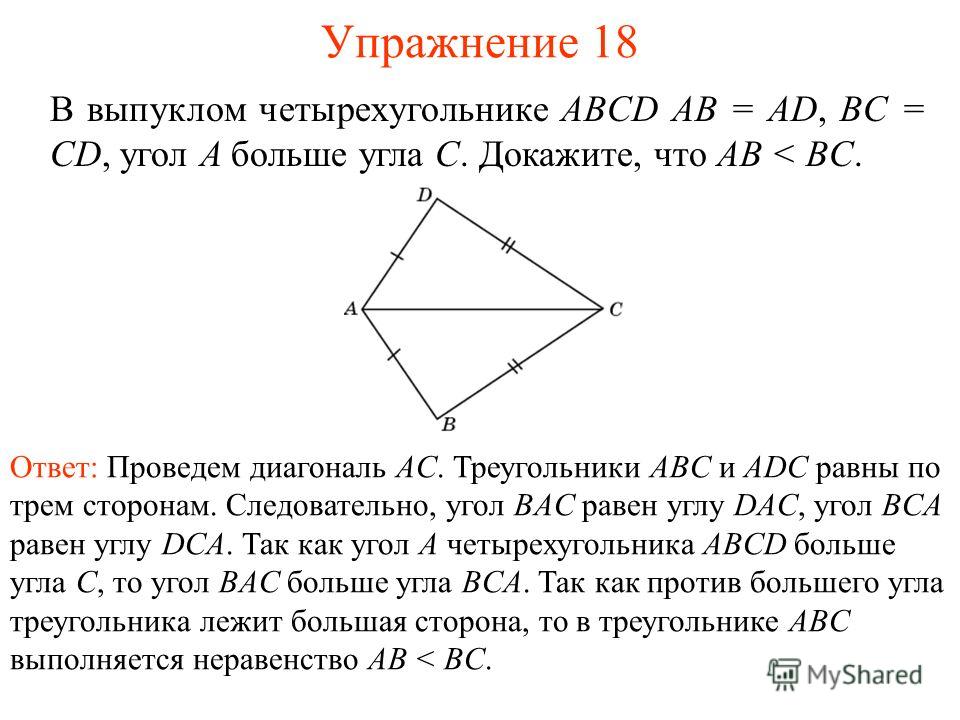
$\endgroup$ 5 $\begingroup$ Вы правы. Однако, если вы не сделаете этого предположения и возьмете $BC$ как единственный заданный прямой угол, правильный ответ будет «Должны быть известны все четыре стороны». Четырехугольник можно разложить на два непересекающихся треугольника. Первый представляет собой прямоугольный треугольник, образованный сторонами $B$, $C$ и гипотенузой, и его площадь легко определить. Вы можете использовать теорему Пифагора, чтобы найти гипотенузу этого прямоугольного треугольника, образованного сторонами $B$ и $C$. Эта гипотенуза вместе со сторонами $A$ и $D$ образует другой треугольник. Его площадь можно вычислить по формуле Герона. Просто суммируйте площади. Обратите внимание, что я все еще делаю молчаливое предположение, что это выпуклый четырехугольник. Возможен вогнутый четырехугольник с углом $AD$, являющимся отражением, что, по-видимому, не является репрезентативным для данной диаграммы, но возможно, когда имеется информация только об одном прямом угле и четырех заданных сторонах. $\endgroup$ 8 $\begingroup$ Вы правы, данное решение неверно. Что еще хуже, даже если вы знаете, что оба угла между BC и CD прямые, предполагаемый ответ все равно неверен ! Это потому, что если вам даны длины A, B, C, это все равно не определяет D однозначно, потому что нам не говорят, что угол между AB меньше 90°$. В общем, этого недостаточно, даже если у вас есть все четыре длины сторон. Например, рассмотрим выпуклый четырехугольник $PQRS$ такой, что $PQ = 6$ и $QR = 9$ и $RS = 7$ и $SP = 8$. Возможно, что $P,R$ разнесены друг от друга чуть меньше чем на $15$, что делает $PQRS$ очень тонким четырехугольником, площадь которого может быть сколь угодно близкой к нулю. В качестве альтернативы, перемещение $P,R$ на расстояние $10$ делает $PQRS$ скорее квадратным, а его площадь явно превышает $48$. |



 Чему равен периметр трапеции:
Чему равен периметр трапеции: Whatsleshal Why Farall Aralles Arallest 9002. Allest Arallest 9002. Allesles Arallest 9002. Allesles Arallest
Whatsleshal Why Farall Aralles Arallest 9002. Allest Arallest 9002. Allesles Arallest 9002. Allesles Arallest
 9000.013
9000.013 Все решения NCERT по всем предметам доступны на веб-сайте Vedantu.
Все решения NCERT по всем предметам доступны на веб-сайте Vedantu. №. пар противоположных углов четырехугольника _____.
№. пар противоположных углов четырехугольника _____.  Все воздушные змеи ромбы. Правда или ложь?
Все воздушные змеи ромбы. Правда или ложь?  примеры способностей
примеры способностей (d)
(d)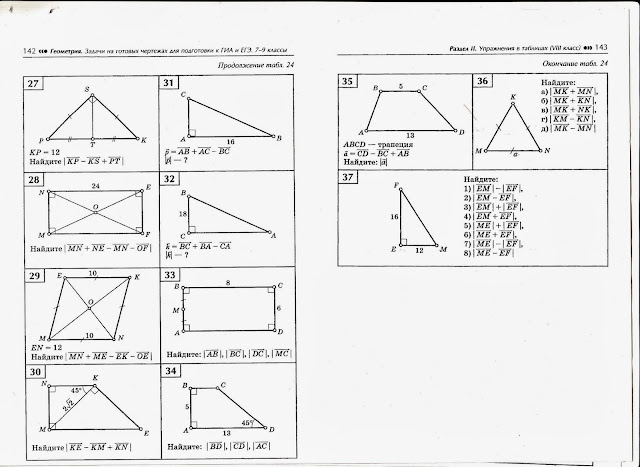 Внутренний угол правильного многоугольника равен 156º. Количество сторон многоугольника
Внутренний угол правильного многоугольника равен 156º. Количество сторон многоугольника 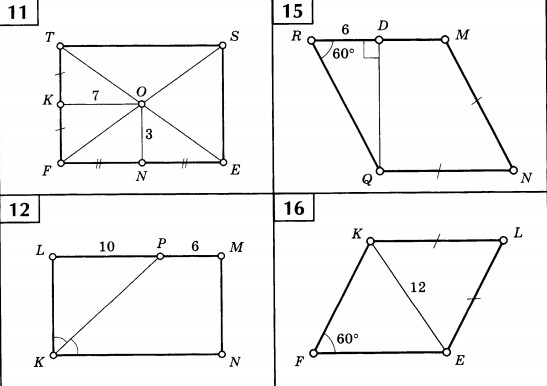 (г)
(г)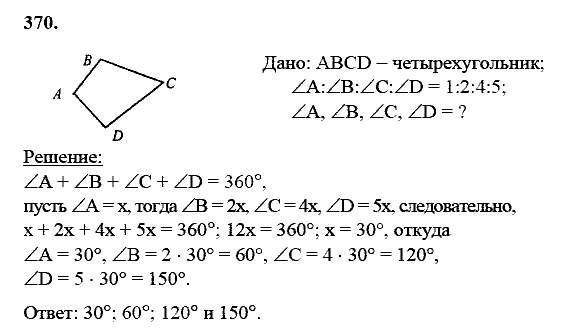 Учитывая это предположение, я вижу, что четырехугольник действительно является прямоугольником и прямоугольным треугольником, и могу следовать их объяснению. Однако (из того, что я помню, мой учитель геометрии в средней школе говорил мне), даже если угол выглядит как прямой угол, его не следует предполагать, если это явно не указано или вы не можете это доказать. Чтобы объяснить, что я имею в виду, если DC не является прямым углом, и мы усугубили эту разницу, это будет выглядеть следующим образом:
Учитывая это предположение, я вижу, что четырехугольник действительно является прямоугольником и прямоугольным треугольником, и могу следовать их объяснению. Однако (из того, что я помню, мой учитель геометрии в средней школе говорил мне), даже если угол выглядит как прямой угол, его не следует предполагать, если это явно не указано или вы не можете это доказать. Чтобы объяснить, что я имею в виду, если DC не является прямым углом, и мы усугубили эту разницу, это будет выглядеть следующим образом: Предоставленное объяснение бессмысленно. Угол $DC$ нельзя считать прямым.
Предоставленное объяснение бессмысленно. Угол $DC$ нельзя считать прямым.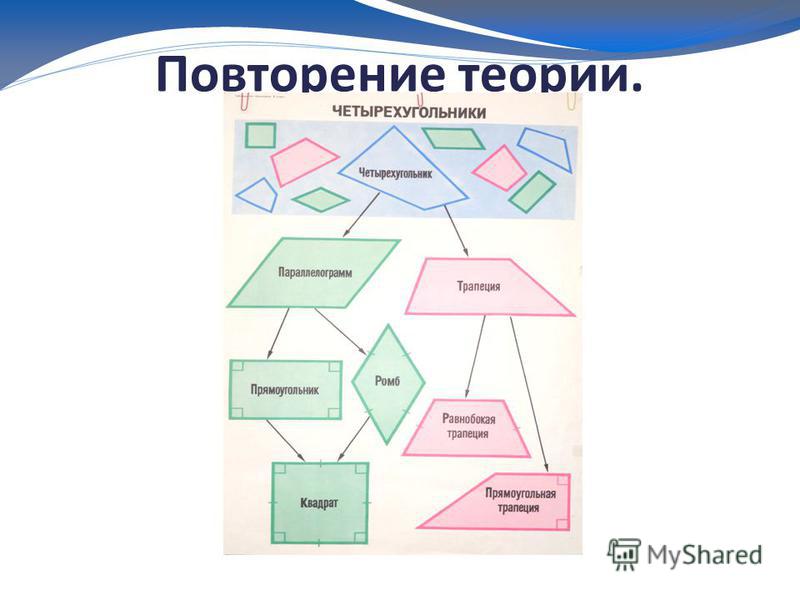 В случае вогнутого четырехугольника вычисление площади, которое я описал выше, будет неверным.
В случае вогнутого четырехугольника вычисление площади, которое я описал выше, будет неверным.