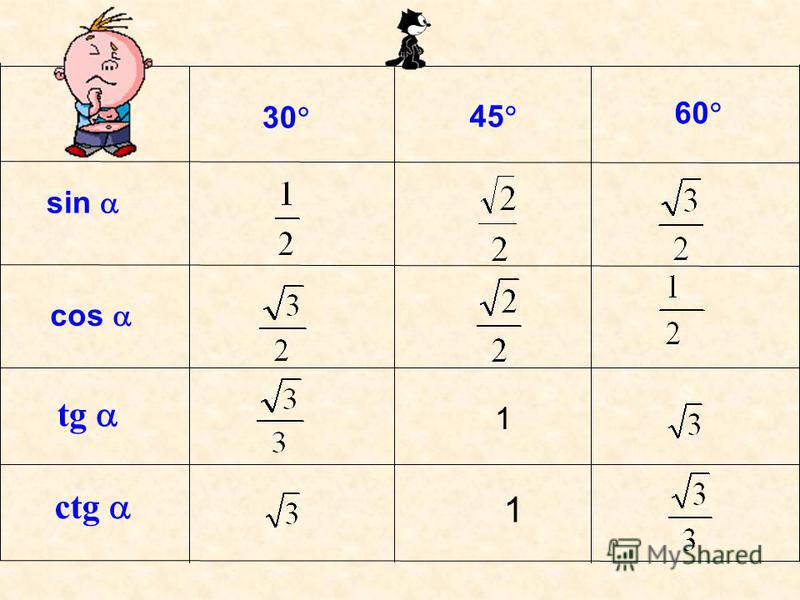
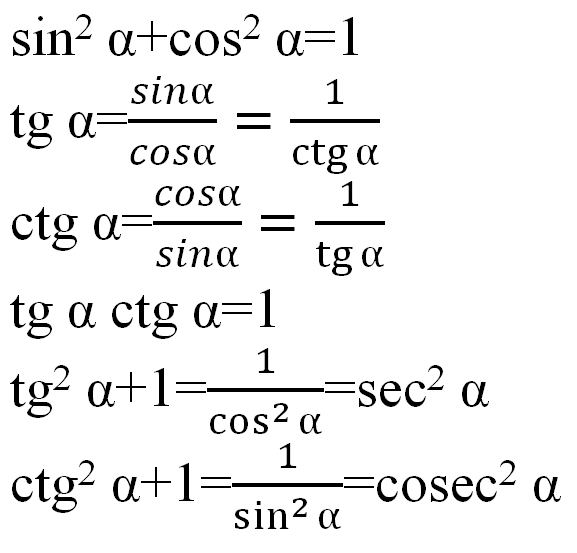Синус, косинус и тангенс угла
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
y
Положительное
направление поворота:
против часовой стрелки.
47 0
497 0
O
+
x
–
3230
Отрицательное
направление поворота:
по часовой стрелке.
Поворот
В т. М можем попасть,
выполнив множество
разных поворотов.
y
37 0
900
3230
M
1800
397 0
00
3600
O
2700
x
y
r=1
MD
sin
OМ
у
sin
1
M(x;y)
sin у
y
O
x
x
D
*
OD
cos
OМ
x
cos
1
cos х
*
Единичная окружность
y
O
x
r=1
MD
tg
OD
у
tg
x
M(x;y)
sin
tg
cos
y
x ctg OD
DМ
D
x
ctg
y
cos
ctg
sin
*
*
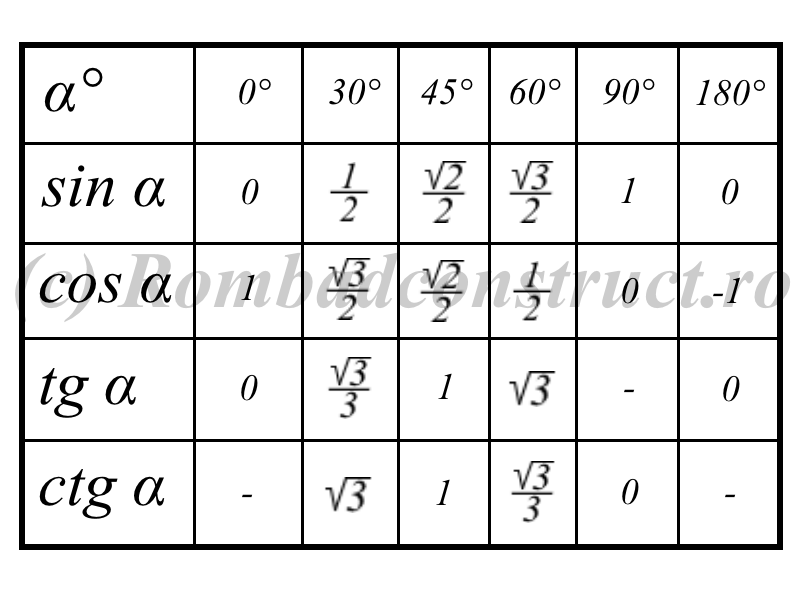
Cинусом угла
косинусом угла
называется ордината
y точки М, а
– абсцисса x точки М.
sin a = y; cos a = x
sin
tg
cos
cos
ctg
sin
sin cos
1
tg ctg
cos sin
sin a = y
cos a = x
y
0
sin 00 0,
0
cos 00 1,
M1(0;1)
90
sin 900 1,
0
cos 900 0,
180
M2(-1;0)
2700
3600
1800
0
sin 1800 0,
cos1800 1.
900
M(1;0)
x
O
270
0
sin 2700 1,
cos 2700 0.
360
M3(0;-1)
0
sin 3600 0,
cos 3600 1.
Единичная окружность
r=1
y
x2 + y2 = 1
sin у
M(x;y)
cos х
y
O
x
x
D
cos sin a 1
2
2
Основное тригонометрическое тождество
Если угол
острый, то
y
sin 0 и cos 0
tg 0; ctg 0
I
O
x
Если угол
y
тупой, то
sin 0 и cos 0
tg 0; ctg 0
I
I
O
x
180 270
0
Если угол
y
O
III
0
, то
sin 0 и cos 0
tg 0; ctg 0
x
Если угол
270 360
0
y
0
, то
sin 0 и cos 0
tg 0; ctg 0
x
O
IV
ЗНАКИ тригонометрических функций
cos a
sin a
+
+
–
+
–
–
–
+
tg a
ctg a
–
+
–
+
+
–
+
–
y
sin( ) sin
sin
O
sin( )
x
f ( x)
f (x)
Функция нечетная
y
cos( )
cos
f (x)
cos
O
x
cos( )
f ( x)
Функция четная
sin
tg
cos
sin ( ) sin
tg( )
tg
cos
cos
cos( )
f ( x)
f (x)
Функция нечетная
Докажи самостоятельно
tg( ) tg
ctg( ) ctg
f ( x)
f (x)
Функция четная
cos( )
cos
f ( x)
f (x)
Функция нечетная
sin( ) sin
tg( ) tg
ctg( ) ctg
y
Может ли абсцисса точки единичной
полуокружности иметь значения
0,3
[ 1;1]
– 2,8 [ 1;1]
-1
O
1 cos 1
1
x
1
[ 1;1]
3
1 [ 1;1]
3
2 [ 1;1]
1
3
y
Может ли ордината точки единичной
полуокружности иметь значения
1
0,6
[ 1;1]
– 0,3 [ 1;1]
1 sin 1
x
O
7 [ 1;1]
1
7
-1
[ 1;1]
1,002 [ 1;1]
Вычислите значение выражения:
2
cos
3
cos( 150 )
7
tg
6
sin 135
sin 610
5
ctg
3
sin 60 tg 210
tg 45 sin 60 ctg30
Найдите знак произведения,
используя правило знаков по четвертям:
tg 220 cos130
sin 205 cos 305
tg130 cos 320 ctg125
tg1,4 sin( 2,1) ctg ( 1,2)
English Русский Правила
Math Tutor — Функции — Теория
Math Tutor — Функции — Теория — Элементарные функции Zde budeme předpokládat, že znáte úhly a jak se meří, mimo jiné že znáte радиана .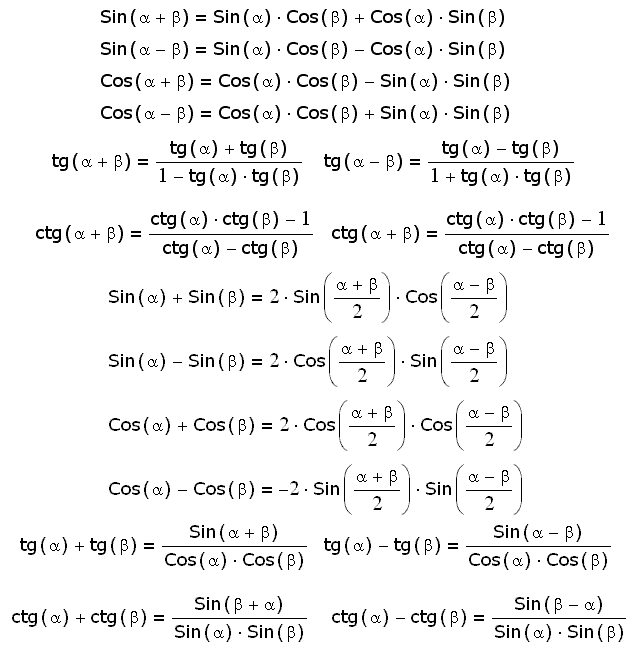
Pokud si nejste jisti, podívejte se na
туто познамку.
Existuje několik způsobů, как определенная гониометрическая функция. Припоменеме stručně dva z nich, založené naгеометрический představě. Pak se podíváme na vlastnosti goniometrických funkcí, připomeneme nějaké гониометрическая идентичность, zkusíme zavést inverzní funkce a vše zakončíme stručnou poznámkou o sekansu a косекансу.
Геометрическое определение
Едноткова кружница. Нехть α je libovolný úhel. Uvažujme jednotkovou kružnici v rovině a paprsek, který jde z počátku pod Улем α . Nechť (
Některé z definic samozřejmě nemají smysl, pokud x = 0, попр. г = 0,
Zřejmě pak máme
Функция сек( α )
(secans) a csc( α )
(kosecans) покупают популярные за старые добрые часы, kdy ještě lidé
museli počítat all the sami, protože docela zjednodušovaly výpočty s
Гониометрические функции.
Dnes jsou převážně zapomenuty a zahrnujeme je zde,
abychom to měli completní. Vrátíme se k ним на konci této sekce.
Všimněte si, že když tyto funkce definujeme takovýmto způsobem, pak jsou всечный 2π-периодический, первый ближайший pohledu jsou tangens a kotangens π-периодический.
Правосторонний троюхельник.
Нехть α je nějaký úhel z интервалu (0,π/2). Uvažujme libovolný pravoúhlý trojuhelník s dalším úhlem rovným α . Пак маме následující определить:Tyto funkce jsou navzájem propojeny stejnými vzorci jak předtím. Джек Тито definice rozšíříme na libovolný úhel α ? Nejprve definujeme sin(0) = 0, cos(0) = 1,sin(π/2) = 1, cos(π/2) = 0,
Pro α г 〈π/2,π〉 определение грех( α ) = sin(π − α ) а cos( α ) = -cos(π — α ).
Pro α г
〈π, 2π〉
определение
sin( α ) = -sin( α — π)
а
cos( α ) = -cos(2π — α ).
Достанем так синус и косинус на 〈0,2π〉, pak je rozšíříme na všechny полностью закрытым тето закладным периодом. Ostatní funkce se pak definují pomocí sinu, kosinu a oněch vzorců uvedených výše.
Вот что нужно упомянуть о том, что можно не ходить, а косить на популярные темы:
Existuje jednoduchý způsob, jak si je памать помочь леве руки.
Další praktická poznámka, namísto zápisu [sin( x )] n обвикле пишем sin n ( x ), соответствующий остаточной гониометрической функции.
Vlastnosti goniometrických funkcí
Синус. Определенный забор:
D (sin) = ℜ.
Граф:
Funkce je spojitá na svém definičním oboru, 2π-периодическая, омезенная симметричная, мужская личность, протоже плати sin(- x ) = -sin( x ). Мама возьми
sin( x + π) = −sin( x ), sin( x + π/2) = cos( x ), sin( x — π/2) = −cos( x ).
Z периодичность больше
sin( x + 2 k π) = sin( x ), sin( x + (2 k + 1)π) = −sin( x ).
Nulové body sinu jsou body ve tvaru k π, kde k свободно Целе Число; toto jsou принять тело inflexe. Местные экстремумы jsou v bodech π/2 + k π.
Co se týče limit v koncových bodech definičního oboru, limita sinu v nekonečnu ani minus nekonečnu neexistuje.
Деривация:
[sin( x )]′ = cos( x ).
Косинус. Определенный забор:
D (cos) = &реал;.
Граф:
Funkce je spojitá na svém definičním oboru, 2π-периодическая, омезенная асимметричная, юменовите суда, protože platí cos(− x ) = cos( x ). Мама возьми
cos( x + π) = −cos( x ), cos( x + π/2) = −sin(
Z периодичность достанеме
потому что( x + 2 k π) = cos( x ), cos( x + (2 k + 1)π) = −cos( x ).
Nulové body kosinu jsou body ve tvaru π/2 + к π, kde k je libovolné celé číslo; jsou принять тело inflexe. Местные экстремумы jsou v bodech к π.
Co se týče limit v koncových bodech definičního oboru, limita kosinu v nekonečnu ani minus nekonečnu neexistuje.
Деривация:
[потому что x )]′ = −sin( x ).
Тангенс. Определенный забор:
Граф:
Funkce je spojitá na svém definičním oboru, π-периодический, не повторяющийся a je symetrická, jmenovitě lichá, protože platí tg(− x ) = −tg( x ). Мама возьми
tg( x + π) = tg( x ), tg(π — x ) = -tg( x ).
Nulové body tangensu jsou body ve tvaru к π, кде к je libovolné celé číslo; jsou to i body inflexe. Lokální extrémy neexistují.
Co se týče limit tangensu v koncových bodech definičního oboru, limita tangensu v nekonečnu a minus neconečnu nemá smysl, protože definicní obor необсахуй жаднэ околи неконечна ани минус неконечна. Ограничения в конечном счете koncových bodech definičního oboru neexistují, ale mame tam jednostranné лимит:
Деривация:
[tg( x )]’ = 1/cos 2 ( х ).
Котангенс. Определенный забор:
Funkce je spojitá na svém definičním oboru, π-периодический, не повторяющийся a je symetrická, jmenovitě lichá, protože platí cog(- x ) = -cog( x ). Мама возьми
cog( x + π) = cog( x ), котг(π — х ) = -котг( х ).
Nulové body kotangensu jsou body ve tvaru π/2 + к π, kde k свободно Целе Число; jsou to i body inflexe. Nejsou местные крайности.
Co se týče limit v koncových bodech definičního oboru, limity kotangensu v неконечно а минус неконечно немай смысл, протоже дефиничні обор необсахуйе žádné okolí nekonečna či minus nekonečna. Limity v конечный конечный продукт neexistují, ale máme tam jednostranné limity:
Деривация:
[котг( x )]’ = -1/sin 2 ( х ).
Гониометрическая идентичность
Nejprve pár populárních identit pro sinus a kosinus.
Následující идентичность jsou méně populární, але občas velice užitečné.
Sinus a kosinus lze dostat (nebo přímo definovat) pomocí exponenciály a комплексный инструмент.
Nakonec tento trik, který je také užitečný.
Очевидные проблемы с мамой, když C 2 = 0. Пак мужского брата φ = π/2 кдыж C 2 > 0 а φ = −π/2 кдыж C 2 < 0,
Teď pár populárních identit pro tangens a kotangens.
Protože sinus a kosinus jdou vyjádřit pomocí complexních exponenciál, je totéž pravda i pro tangens a kotangens.
A nakonec pár vzorců, které spojují sinus/kosinus tangens.
Инверсионная гониометрическая функция (циклометрическая функция)
Když se podíváme na grafy nahoře, hned vidíme, že žádná ze základních
гониометрические функции не просты, а также имеют непостоянные функции. На друхоу
stranu, z praktického hlediska by se nějaká inverze velmi hodila, a lide také
skutečně přiřazovali úhly k velikostem stran trojúhelníku dlouho před tím,
než matematici vymysleli pojem inverzní funkce.
Абыхом ту уделали справне,
použijeme obvyklý trik, omezíme goniometrické funkce na intervaly, na kterých
jsou уж просте. Выберем интервалы так, абы были недавно можно (также
pokryjí celý obor hodnot) a také aby dávaly «rozumné» úhly, tedy kolem 0.
Je totiž mnohem praktičtější dozvědět se, že nějaký úhel je 30 stupňů, než
750 ступеней
si představit a hlavně je napsat na Web, tak jsme teď udělali výjimku).
Инверсионная гониометрическая функция (циклометрическая функция). Jsou определено такто. Нейтральные омезиме четыржи гониометрические функции на интервалы времени образ.
Pak uvažujeme inverzní funkce k těmto restrikcím. Jmenují se arkus sinus (значено arcsin), arkus косинус (значено arccos), arkus tangens (значено arctg) и arkus kotangens (значено arctg).
Grafy těchto funkcí jsou zde:
Teď vypíšeme základní vlastnosti těchto cyklometrických funkcí. Jsou všechny
смешайте, монотонно и омезене.
Познание: Mnoho autoroů (a většina výrobců kalkulaček) používá jiné značení, jmenovitě sin −1 ( x ), cos −1 ( x ) atd. Toto značení je silně matoucí a mnoho studentů cítí (přiznejme si oprávněně) silnou podobnost mezi sin −1 ( x ) и řekněme грех 2 ( x ) про друху мохнину сину; логический пакет Чекай, же sin −1 ( x ) моя власть 1/sin( x ). Samozřejmě inverzní funkce k sinu a 1/sin( x ) jsou dvě zcela rozdílné funkce. Ačkoliv pro toto značení je docela dobré odůvodnění (а именно uvedení инверторные функции в части Teorie — Real funkce), je to kvůli těm nedorozuměním velmi nešťastné. Protože máme Naprosto Správnou Alternativu, Která je Také široce Známá — jmenovitě ty arkus věci — budeme je tady důsledně používat.
Познание: Vraťme se k původní otázce, je dáno číslo y a my
chceme najít x splňující řekněme
sin( x ) = y .
Pokud je toto x z rozmezí, na které jsme před chvílí omezili sinus,
pak máme řešení x = arcsin( y ). Ко кдыж эль
z nějakého důvodu potřebujeme x z jiné části části realné osy? З Джинехо
úhlu pohledu, kdybychom omezili sinus na jiný rozumný interval, jaký by pak
был взорец про инвестиции функции к такто omezenému sinu? (A samozřejmě i kosinu
атд). Platí následující vzorce:
Nechť sin( x ) = y .
Покуд 2 k π − π/2 ≤ x ≤ 2 k π + π/2 pro nějaké celé číslo k , pakx = arcsin( y ) + 2 k π.
Покуд (2 k + 1)π − π/2 ≤ x ≤ (2 k + 1)π + π/2 pro nějaké celé číslo k , pak
x = (2 k + 1)π − arcsin( y ).
Nechť cos( x ) = y .
Покуд 2 k π ≤ x ≤ 2 k π + π pro nějaké celé číslo к , упак.
x = arccos( y ) + 2 k π.
Покуд (2 k + 1)π ≤ x ≤ (2 k + 1)π + π pro nějaké celé číslo k , pak
x = (2 k + 2)π − arccos( y ).
Nechť tg( x ) = y .
Покуд k π − π/2 < x < k π + π/2 pro nějaké celé číslo k , pakx = arctg( y ) + k π.
Nechť cog( x ) = y .
Покуд k π < x < k π + π pro nějaké celé číslo k , pakx = arccotg( y ) + k π.
Existují velice zajímavé vzorce spojující goniometrické funkce a jejich инверсия. Nejsou moc často používané, ale jsou tak pěkné, že se neudržíme a dáme je tu.
Sekans и косекан
Jen si stručně projdeme jejich vlastnosti.
Графи:
Деривация:
Гиперболическая функция
Zpět na Teorie — Elementární
функция
Tosamoci trygonometryczne
Tosamoci trygonometryczneСледующий: Rozwizywanie trjktw dowolnych Up: Funkcje trygonometryczne kta skierowanego Предыдущий: Wykresy funkcji trygonometrycznych
W tym ustpie podajemy okoo 30 tosamoci trygonometrycznych, ktrych biege opanowanie pamiciowe, wraz z dowodami, uwaamy za niezbdne. Tosamoci te dziel si na kilka grup. Пощегльне тосамоци май nazwy, ktrych brzmienie jest niekiedy подобне, нп. «синус сумы» и «сума синус». Uczc si ich, naley zwraca uwag na kolejno dziaa, gdy takie wyraenia jak грех (+) я sin + sin s na og nierwne.
Funkcje сумы кв.
Twierdzenie: Funkcje trygonometryczne sumy dwch ktw wyraaj si nastpujcymi wzorami:
- синус Сумы: sin ( + ) = sin cos + cos sin
- косинус сумы: cos ( + ) = cos cos — sin sin 905:00
- тангенс сумы: тг (+) =
Pierwsze dwa wzory s prawdziwe dla wszelkich i .
Wzr na tangens sumy jest prawdziwy dla wszystkich
,
опрч тыч, дла ктрыч тг , тг луб тг ( + ) шутка неокрелоны.
Dowd: Rozwaymy nastpujce przypadki:
Przypadek, gdy jeden z ktw , шутка нулевая лаб просты. Wwczas prawdziwoc wzorw jest oczywista albo wynika bezporednio ze wzorw redukcyjnych.
Przypadek, gdy i nale do i wiartki. Ввчас + нет, я луб II виартки:
W ukadzie OXY krelimy kt w pooeniu standardowym, a кт krelimy tak, aby pprosta a bdca kocowym ramieniem kta , bya jednoczenie pocztkowym ramieniem kta . Wwczas pprosta b bdca kocowym ramieniem kta , jest jednoczenie kocowym ramieniem kta + я кт десять ma pooenie стандартное. Przyjmujemy nastpujce oznaczenia:- на ппростей б обиерами пункт М рный од О ,
- rzut pointtu M na o OX oznaczamy A ,
- рзут пунту М на ппрост а означамы Д ,
- рзут пункту D на о OX означамы G ,
- рзут пункта Д на одинк
знак H .
| грех (+) | = | = = | |
| = | = + = | ||
| = | . + . |
Понева = грех , = , потому что , ШМД = БОГ = , СКД = , потому что и крещение = грех , wic .
+ . = sin cos + cos sin ,
co dowodzi prawdziwoci wzoru na sinus sumy. W dowodzie wzoru na cosinus sumy korzystamy z tego, e
= + = — .
Виктория
,
s skierowane zgodnie z osi OX , wic Миара = ОГ — ОГ
| cos (+) | = | = = | |
| = | — = — = | ||
| = | . + . |
Dziki zwizkom wymieniononym powyej, otrzymane wyraenie rwna si cos cos — sin грех ,
co dowodzi prawdziwoci wzoru na cosinus sumy.
Przypadek, gdy lub nie nale do I wiartki. Przypadek taki sprowadza si делать попрзедниего за помощь wzorw redukcyjnych.
Wzr na tangens sumy wynika bezporednio ze wzorw na sinus i cosinus sumy:
тг ( + ) = = .
W otrzymanym uamku dzielimy licznik i mianownik przez cos cos i otrzymujemy:=
Ко Кози Дауд.Funkcje rnicy ktw.
Zastpujc we wzorach na funkcje sumy ktw kt ktem — i stosujc wzory redukcyjne, otrzymujemy:
- носовой пазухи: sin (-) = sin cos — cos sin
- cosinus rnicy: cos (-) = cos cos + sin sin
- тангенсы rnicy: тг (-) =
Funkcje kta podwjnego.
Zastpujc we wzorach na funkcje sumy ktw kt ktem otrzymujemy:
- подвздошный синус: sin 2 = 2 sin cos
- cosinus kta podwjnego: cos 2 = cos 2 — sin 2
- tangens kta podwjnego: тг 2 =
Korzystajc z «jedynki trygonometrycznej» mona cosinus kta podwjnego wyrazi w postaciach:
- cos 2 = 1 — 2 sin 2
- cos 2 = 2 cos 2 — 1
Funkcje poowy kta.
Jeli we wzorach na funkcje kta podwjnego zastpimy kt ktem , чтобы отрываемы взоры:
sin = 2 sin cos
cos = cos 2 — sin 2
тг =
cos = 1 — 2 sin 2
cos = 2 cos 2 — 1
Z ostatnich dwch rwnoci otrzymujemy:- cosinus poowy kta: потому что =
- синусовая полость: грех =
- tangens poowy kta: тг =
- тг =
Wad powyszych wzorw jest dwoisto znaku i posta niewymierna (pierwiastek).
Wolne od tych wad s wzory:
- тг =
- тг =
Dowd: Удоводнимы пирвши зе взорв — другие доводзи си аналогичны:
тг = = = = .
Сумы и рнице тригонометрические функции.
Twierdzenie: Sumy i rnice funkcji trygonometrycznych wyraaj si wzorami:
- Сума синус sin + sin = 2 sin cos
- Сума косинус cos + cos = 2 cos cos
- сума tangensw тг + тг =
- rnica sinusw sin — sin = 2 cos sin
- rnica cosinusw cos + cos = — 2 sin sin
- рница tangensw тг — тг =
Dowd: Udowodnimy tylko pierwszy zw wzorw — pozostae dowodzi si Analogicznie. Do dwch danych liczb , mona zawsze dobra takie dwie liczby x , y , e
= х + х , = х — х .
х = , у = .
Korzystajc ze wzorw na funkcj sumy i rnicy ktw mamy:| грех + грех | = | sin ( x + y ) + sin ( x — y ) = | |
| = | sinxcosy + cosxsiny + sinxcosy — cosxsiny = | ||
| = | 2 sinxcosy = 2 sin cos . |
Pozostae tosamoci.
Korzystajc z podstawowych tosamoci wypowadzonych powyej (oraz — w czterech ostatnich przypadkach — взять z zasady indukcji matematycznej) z atwoci dowodzi si nastpujcych, poytecznych wzorw:
- sin 4 y — cos 4 у = 2 sin 2 у — 1
- tgxsin 2 x = 2 sin 2 x
- + =
- = тг 4 х
- тг (45 o — ) + тгx =
- тг (45 o + ) — тгx =
- =
- тг (45 о + х ) тг (45 или — х ) = 1
- cosx + sinx = sin (45 или + x )
- cosx — sinx = cos (45 или + x )
- тгх + тгх =
- ctgx — tgx = 2 ctg 2 x
- = тг (45 или + x )
- = ctg (45 o — x )
- 1 + cosx + cos 2 x +.
