Треугольник бинома: Бином Ньютона и треугольник Паскаля

Свойства биноминальных коэффициентов. Бином Ньютона

Похожие презентации:

Бином Ньютона и треугольник Паскаля

Бином Ньютона

Бином Ньютона. Полиномиальная формула. (Лекция 11)

Формула бинома Ньютона. Свойства биномиальных коэффициентов

Бином Ньютона

Бином Ньютона

Бином Ньютона. Треугольник Паскаля

Комбинаторика. Свойства сочетаний. (Лекция 11)

Бином Ньютона

Бином Ньютона

Свойства биномиальных
коэффициентов
Цель: познакомиться со свойствами
биноминальных коэффициентов;
научить применять формулу бинома Ньютона
при возведении в степень двучлена;
Бином Ньютона
Основные свойства
биномиальных коэффициентов:

4. Бином Ньютона.

Бином (лaт. bis − два, nomen — имя)
или двучлен — частный случай
многочлена (полинома), который
состоит из двух слагаемых
одночленов (мономов).
Например:
a + b,
a − b,
a2 + b2,
3b −4b3
Степени суммы двух чисел:
а b 1
1
а b 1 а 1 b
2
2
2
а b 1 а 2 аb 1 b
3
3
2
2
3
а b 1 а 3 а b 3 аb 1 b
4
а b 1 а 4 4 а 3b 6 а 2b 2 4 аb3 1 b 4
0
а b
5
1 а 5 5 а 4b1 10 а 3b 2 10 а 2b 3 5 а1b 4 1 b 5
Составим таблицу из коэффициентов в
записанных суммах
Составленная таблица
получила название
Треугольник
Паскаля
n = 0;
1
n = 1;
1
1
n = 2;
1
2
1
n = 3;
1 3
3
1
n = 4;
1 4
6
4 1
n = 5;
1 5
10
10 5 1
n = 6; 1 6 15
20
15 6 1
n = 7; 1 7 21 35
35
21 7 1
5-я строка (n = 4) получается так:
1, 4 = 1 + 3, 6 = 3 + 3, 4 = 3 + 1, 1

7.

Разложение бинома с помощью треугольника Паскаля.Коэффициенты 7 строки:
1; 7; 21; 35; 35; 21; 7; 1
Пример 1
(a b) 1 a 7 a b 21 a b 35 a b
7
7
6
1
5
2
4
3
35 a 3 b 4 21 a 2 b5 7 a1 b 6 1 b 7
a 7 7a 6b 21a 5b 2 35a 4b3 35a 3b 4 21a 2b5 7ab 6 b 7
Пример 2
Коэффициенты 7 строки:
1; 7; 21; 35; 35; 21; 7; 1
(1 x) 7 1 17 7 16 x1 21 15 x 2 35 14 x 3
35 13 x 4 21 12 x 5 7 11 x 6 1 x 7
1 7 x 21x 2 35 x 3 35 x 4 21x 5 7 x 6 x 7
Коэффициенты 4 строки:
Пример 3
1; 4; 6; 4; 1
(2 x 3) 4 1 (2 x) 4 4 (2 x)3 31 6 (2 x) 2 32
4 (2 x)1 33 1 34
16 x 96 x 216 x 216 x 81
4
3
2

9. Биномиальные коэффициенты

В основе построения треугольника Паскаля
лежит свойство сочетаний
C
n 1
m 1
C C
n
m
n 1
m
.
Поэтому коэффициенты разложения степени
бинома можно записать с помощью числа
сочетаний
Степени суммы двух чисел:
а b
1
1 а 1 b
С 1; С 1
0
1
1
1
а b
1
а b
и
a 1; b 1, тогда
0
0
С а b С а b
0 1 0
1
1 0 1
1
С 1; С 2; С 1
0
2
Аналогично:
2
Заметим, что
1
2
2
2
С а b С а b С а b
0
2
2 0
1 1 1
2
2
2
0 2
С 1; С 3; С 3; С 1
0
3
1
3
а b
3
2
3
3
3
С а b С а b С а b С а b и т. д.
0 3 0
3
1 2 1
3
2 1 2
3
3 0 3
3

11. Правило Паскаля:

С
C
n
m 1
n 1
m
C
n
m
Биноминальные коэффициенты:
m!
С
n!(m n)!
n
m
C C 1;
0
m
С
n
m 1
C C
m
m
C
n 1
m
1
m
C ;
n
m
С C … C
0
m
1
m
С
m 1
m
n
m 1
m 1
m
m;
C
n 1
m 1
C ;
C 2
m
m
n
m
m

12. Бином Ньютона:

а b
т
С а b C a
0
m
m 0
1
m
m 1 1
b … C
m 1 1 m 1
m
ab
C a b
m
m
0 m
Бином Ньютона – формула, выражающая целую
положительную степень суммы двух слагаемых
(двучлена, бинома) через степени этих слагаемых.
Частными случаями бинома Ньютона являются
формулы квадрата и куба суммы
двух слагаемых a и b
Применение формулы бинома Ньютона
Пример 4
1
1 2
1 5
1
4
2
3
5
(2a ) (2a ) C5 (2a) ( ) C5 (2a) ( )
2
2
2
1 3
1 4
1 5
4
1
C ( 2 a ) ( ) C5 ( 2 a ) ( ) ( )
2
2
2
5
1
5
4
3
2
32a 40a 20a 5a a
8
32
3
5
2

14.

Самостоятельная работа Задание 1. Найти разложение бинома

15. Задание 2.

У многочлена P(x) найдите коэффициент
при:
Задание 3.
4Р3+3А210-С25
Критерии оценки выполнения работы
Оценка
Число заданий,
необходимое для
получения оценки
«3» (удовлетворительно)
3
«4» (хорошо)
4
«5» (отлично)
5

English     Русский Правила

Бином Ньютона

Урок 24. Алгебра 11 класс ФГОС

В этом видеоуроке мы напомним, какие соединения называют сочетаниями. Вспомним формулу для подсчёта числа сочетаний, а также свойства сочетаний. Познакомимся с формулой бинома Ньютона. Скажем, что называют треугольником Паскаля. Познакомимся со свойством элементов строки треугольника Паскаля.

Конспект урока «Бином Ньютона»

Сегодня на уроке мы напомним, какие соединения называют сочетаниями. Вспомним формулу для подсчёта числа сочетаний, а также свойства сочетаний. Познакомимся с формулой бинома Ньютона. Скажем, что называют треугольником Паскаля. Познакомимся со свойством элементов строки треугольника Паскаля.

Прежде чем приступить к рассмотрению новой темы, давайте вспомним, что сочетаниями из  элементов по  элементов в каждом () называются соединения, каждое из которых содержит  элементов, взятых из данных  разных элементов, и которые отличаются одно от другого по крайней мере одним элементом.

Формула для подсчёта числа сочетаний из  различных элементов по  элементов в каждом имеет вид .

Также данную формулу можно представить в виде .

Напомним два свойства сочетаний, которые в ряде случаев упрощают вычисления при решении задач.

Свойство первое: .

Свойство второе: .

С сочетаниями тесно связана формула бинома Ньютона, с которой мы сегодня познакомимся.

Биномами в теории многочленов часто называют двучлены. Давайте с вами рассмотрим целые неотрицательные степени бинома  при условии, что .

Мы можем продолжить возводить бином  в шестую, седьмую и так далее степени. Но давайте обратим внимание, что эти формулы мы можем записать следующим образом:

Эту формулу часто называют просто

Биномом Ньютона. Она справедлива для каждого натурального значения . Числа  называют биномиальными коэффициентами, которые могут быть найдены по формуле .

Давайте, пользуясь этой формулой возведём бином  в шестую степень.

Вообще, биномиальные коэффициенты легко находить с помощью так называемого треугольника Паскаля.

Треугольник Паскаля – таблица значений , которая составлена на основе рекуррентного свойства числа сочетаний  с учётом того, что .

Сейчас вы видите фрагмент треугольника Паскаля, в котором показан процесс получения определённых членов таблицы на основании рекуррентного свойства сочетаний.

Отметим, что треугольник Паскаля можно продолжать как угодно далеко.

Данная таблица наглядно иллюстрирует известное нам первое свойство сочетаний. Его можно сформулировать так: числа, одинаково удалённые от концов строки треугольника Паскаля, равны.

Теперь запишем разложение бинома .

Обратите внимание, что показатель степени данного бинома равен пяти. А число членов полученного многочлена равно шести, то есть на единицу больше.

Показатели степени первого слагаемого, то есть , последовательно убывают на единицу от  до , а показатели степени второго слагаемого, то есть , возрастают на единицу от  до .

Кроме этого заметим, что биномиальные коэффициенты, которые одинаково удалены от начала и от конца разложения, равны между собой.

Таким образом, при записи разложения степени бинома полезно контролировать следующие моменты:

1) число членов получаемого многочлена на единицу больше показателя ЭМ степени бинома, то есть равно ;

2) показатели степени первого слагаемого бинома последовательно убывают на единицу от  до , а показатели второго последовательно возрастают на единицу от  до ;

3) биномиальные коэффициенты, равноудалённые от начала и конца разложения по формуле бинома Ньютона, равны между собой.

Сейчас вы видите свойство элементов строки треугольника Паскаля:

.

Это равенство получается из формулы бинома Ньютона при .

Действительно, подставим в формулу 1 вместо  и . Выполним преобразование и получим данное свойство.

А теперь выполним несколько заданий.

Задание первое. Запишите разложение бинома .

Решение.

Задание второе. С помощью свойства элементов строки треугольника Паскаля найдите суммы:

а) ; б) .

Решение.

Предыдущий урок 23 Сочетания и их свойства

Следующий урок 25 События

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 11 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Объяснение урока: Треугольник Паскаля и биномиальная теорема

В этом объяснении мы узнаем, как использовать треугольник Паскаля для нахождения коэффициентов алгебраического разложения любого бинома выражение вида (𝑎+𝑏).

Начнем с рассмотрения разложения (𝑎+𝑏) для последовательных степеней из 𝑛, начиная с 𝑛=0. Поскольку любое число, возведенное в степень нуля равна 1 (обратите внимание, что мы используем соглашение о том, что 0=1), (𝑎+𝑏)=1.

Аналогично, когда 𝑛=1, мы имеем несколько тривиальный случай: (𝑎+𝑏)=𝑎+𝑏.

Однако для 𝑛≥2 все становится немного интереснее. Использование знакомых алгебре, мы знаем (𝑎+𝑏)=𝑎+2𝑎𝑏+𝑏.

Теперь рассмотрим 𝑛=3 для этого случая. Мы будем использовать наш ответ от 𝑛=2, чтобы записать расширения следующим образом: (𝑎+𝑏)=(𝑎+𝑏)(𝑎+𝑏)=(𝑎+𝑏)𝑎+2𝑎𝑏+𝑏.

Раскрывая скобки, Аналогично имеем (𝑎+𝑏)=𝑎+2𝑎𝑏+𝑎𝑏+𝑎𝑏+2𝑎𝑏+𝑏=𝑎+3𝑎𝑏+3𝑎𝑏+𝑏. 𝑎+𝑏) с помощью разложения (𝑎+𝑏) следующим образом: (𝑎+𝑏)=(𝑎+𝑏)(𝑎+𝑏)=(𝑎+𝑏)𝑎+3𝑎𝑏+3𝑎𝑏+𝑏.

Теперь мы можем расширить скобки, чтобы получить (𝑎+𝑏) = 𝑎+3𝑎𝑏+3𝑎𝑏+𝑎𝑏+𝑎𝑏+3𝑎𝑏+3𝑎𝑏+𝑏 = 𝑎+4𝑎𝑏+6𝑎𝑏+4𝑎𝑏+𝑏. 

Как видите, если бы мы попытались найти расширение (𝑎+𝑏) этого Кстати, это может занять серьезное количество времени и усилий.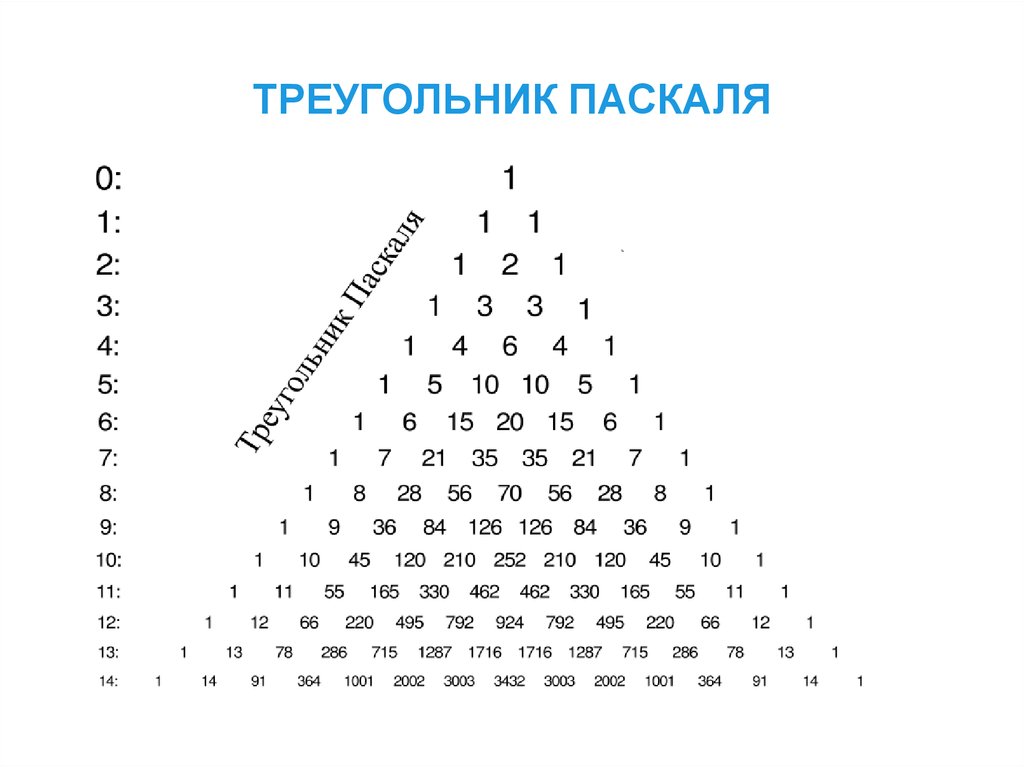 Нам нужен лучший метод, который обобщается на высшие степени. Чтобы найти такой метод, мы сначала будем искать шаблоны, которые может помочь нам. Начнем с организации расширения (𝑎+𝑏) одного над другим, чтобы увидеть, можем ли мы увидеть какие-либо закономерности.

Некоторые из наиболее очевидных закономерностей, которые мы замечаем, связаны с диагоналями: коэффициенты члены на первой диагонали содержат только единицы, тогда как коэффициенты на второй диагональ содержит последовательные целые числа.

Кроме того, мы можем видеть отражательную симметрию относительно центра.

Кроме того, мы замечаем, что в любой данной строке сумма индексов равна 𝑛. Например, в строке, представляющей 𝑛=4, второй термин 4𝑎𝑏. Индекс 𝑎 равен 3, а индекс 𝑏 равно 1. Следовательно, их сумма равна 4.

Наконец, мы видим связь между коэффициентами в последовательных строках: если мы добавим два последовательных коэффициента в строке выше, мы получим коэффициент ниже в следующей строке.

Треугольник, из которого состоят биномиальные коэффициенты, обычно называют Треугольник Паскаля.

Определение: Треугольник Паскаля

Треугольник Паскаля представляет собой треугольный массив биномиальных коэффициентов. Ряды пронумерованы сверху так, что первая строка имеет номер 𝑛=0. Точно так же элементы каждой строки пронумерованы от 𝑘=0 до 𝑛. Первые восемь рядов треугольника Паскаля показаны ниже.

Хотя в большей части западного мира треугольник назван в честь французского математика Блеза Паскаля, она была хорошо известна математикам за столетия до в таких местах, как Китай, Персия и Индия.

Треугольник Паскаля легко воспроизвести для малых 𝑛 и поэтому чрезвычайно полезно при расширении биномов со средними степенями. Позже мы увидим, как это свойства дают нам метод расширения общих биномов.

Мы должны быть осторожны, чтобы различать ссылки на строки с использованием порядковых номеров, таких как первую строку и вторую строку и ссылаясь на них, используя номер строки 𝑛: когда мы говорим вторая строка, мы имеем в виду строку, для которой 𝑛=1.

Пример 1. Использование треугольника Паскаля для нахождения биномиальных коэффициентов

Фейди изучал взаимосвязь между треугольником Паскаля и биномиальное расширение. Он заметил, что каждую строку треугольника Паскаля можно используется для определения коэффициентов биномиального разложения (𝑥+𝑦), как показано на рисунке. Например, пятая строка Треугольник Паскаля можно использовать для определения коэффициентов разложения (𝑥+𝑦).

1. Вычислив следующую строку треугольника Паскаля, найдите коэффициенты разложения (𝑥+𝑦).
2. Теперь Фейди хочет рассчитать коэффициенты для каждого из условий расширение (2𝑥+𝑦). Подставив 2𝑥 в выражение выше, или иначе, вычислить все коэффициенты расширение.

Ответ

Часть 1

Чтобы вычислить седьмую строку треугольника Паскаля, начнем с записи шестой ряд. Затем, поскольку все строки начинаются с цифры 1, мы можем записать это. Мы можем затем складываем каждую последующую пару элементов шестой строки и записываем их сумму в пропуск под ними. Мы продемонстрируем этот процесс ниже.

Начиная с первой пары слагаемых, 1 и 5, мы складываем их вместе, чтобы получить 6 и разместить в космическую щель под ними.

Переходя к следующей паре членов, мы имеем 5+10=15, что мы аналогично добавить в ряд.

Теперь рассмотрим средние члены 10+10=20.

Наконец, мы можем использовать симметрию треугольника Паскаля, чтобы записать остальную часть строка.

Поскольку элементами треугольника Паскаля являются биномиальные коэффициенты, мы можем утверждают, что коэффициенты членов разложения (𝑥+𝑦) будет 1, 6, 15, 20, 15, 6 и 1 соответственно.

Часть 2

Так как (𝑥+𝑦)=𝑥+4𝑥𝑦+6𝑥𝑦+4𝑥𝑦+𝑦,  мы можем заменить 2𝑥 и вместо 𝑥 запишем (2𝑥+𝑦)=(2𝑥)+4(2𝑥)𝑦+6(2𝑥)𝑦+4(2𝑥)𝑦+𝑦. 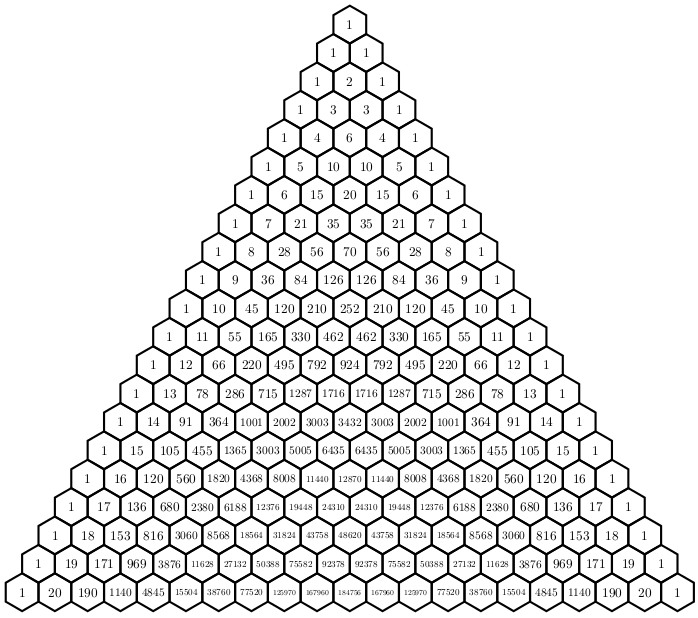

Упрощая, имеем (2𝑥+𝑦)= 2𝑥+4 × 2𝑥𝑦+6 × 2𝑥𝑦+4 × 2𝑥𝑦+𝑦 = 16𝑥+32𝑥𝑦+24𝑥𝑦+8𝑥𝑦+𝑦.

Следовательно, коэффициенты для каждого условий расширения (2𝑥+𝑦) равно 16, 32, 24, 8 и 1.

Пример 2. Использование треугольника Паскаля для нахождения биномиальных коэффициентов

Амер знает, что он может использовать 6-ю строку треугольника Паскаля для вычислить коэффициенты разложения (𝑎+𝑏).

1. Вычислите числа в 6-й строке треугольника Паскаля и, следовательно, выпишите коэффициенты разложения (𝑎+𝑏).
2. Теперь, учитывая разные степени 𝑎 и 𝑏 и с помощью треугольника Паскаля вычислить коэффициенты разложения (2𝑎−2𝑏).

Ответ

Часть 1

Напомним, что мы можем выписать строки треугольника Паскаля, попарно складывая термины в предыдущих строках. Поэтому, начиная с первого и второго рядов, которые только содержать единицы, мы можем создать третьи строки, добавляя последовательные термины, как показано на рисунок ниже.

Точно так же мы можем написать другие строки, используя тот же метод, пока не дойдем до шестой строка.

Поскольку элементами треугольника Паскаля являются биномиальные коэффициенты, мы можем утверждают, что коэффициенты членов разложения (𝑎+𝑏) будет 1, 5, 10, 10, 5 и 1 соответственно.

Часть 2

Чтобы найти коэффициенты при членах разложения (2𝑎−2𝑏), мы можем сначала разложить 2 в скобках следующим образом: (2𝑎−2𝑏)=2(𝑎−𝑏).

Теперь мы можем заменить −𝑏 на 𝑏 в расширении, Чтобы получить (−𝑏)+5𝑎(−𝑏)+(−𝑏).

Мы можем упростить это выражение следующим образом: (𝑎−𝑏)=𝑎−5𝑎𝑏+(−1)10𝑎𝑏 +(−1)10𝑎𝑏+(−1)5𝑎𝑏+(−1)𝑏=𝑎−5𝑎𝑏+10𝑎𝑏−10𝑎𝑏+5𝑎𝑏−𝑏. 

Следовательно, (2𝑎 — 2𝑏) = 2𝑎 — 5𝑎𝑏+10𝑎𝑏 — 10𝑎𝑏+5𝑎𝑏 — 𝑏 = 32𝑎 — 160𝑎𝑏+320𝑎𝑏 — 320𝑎𝑏+160𝑎𝑏 — 32𝑏. 

Следовательно, коэффициенты при каждом из членов разложения (2𝑎−2𝑏) равно 32, −160, 320, −320, 160 и −32.

При работе с биномиальными разложениями нас могут интересовать только определенные термины или даже коэффициенты определенных терминов.

Отдельные термины часто можно идентифицировать путем поиска степени определенной переменной. Рассмотрим степени переменной 𝑎 в простом разложении, таком как (𝑎+𝑏). Члены разложения будут включать все целые степени 𝑎 от 𝑎 до 𝑎. 𝑎,𝑎,𝑎,…,𝑎

Если, однако, оба члена бинома содержат одну и ту же переменную, может быть неясно, какие степени определенной переменной появятся. Одним из таких примеров может быть 𝑎+1𝑎. Выражая 1𝑎=𝑎, мы можем заметить, что такое разложение будет содержать только четные или нечетные степени переменной 𝑎 от 𝑎 до 𝑎. 100003

Давайте рассмотрим пример.

Пример 3. Использование треугольника Паскаля для нахождения коэффициента в произведении биномиальных разложений

Найдите коэффициент при 𝑎 в разложении 𝑎+1𝑎𝑎+1𝑎.

Ответ

Учитывая, что у нас есть произведение двух двучленов, возведенных в степень, обычно полезно раскрывать каждый набор скобок отдельно; тогда мы можем рассмотреть их произведение.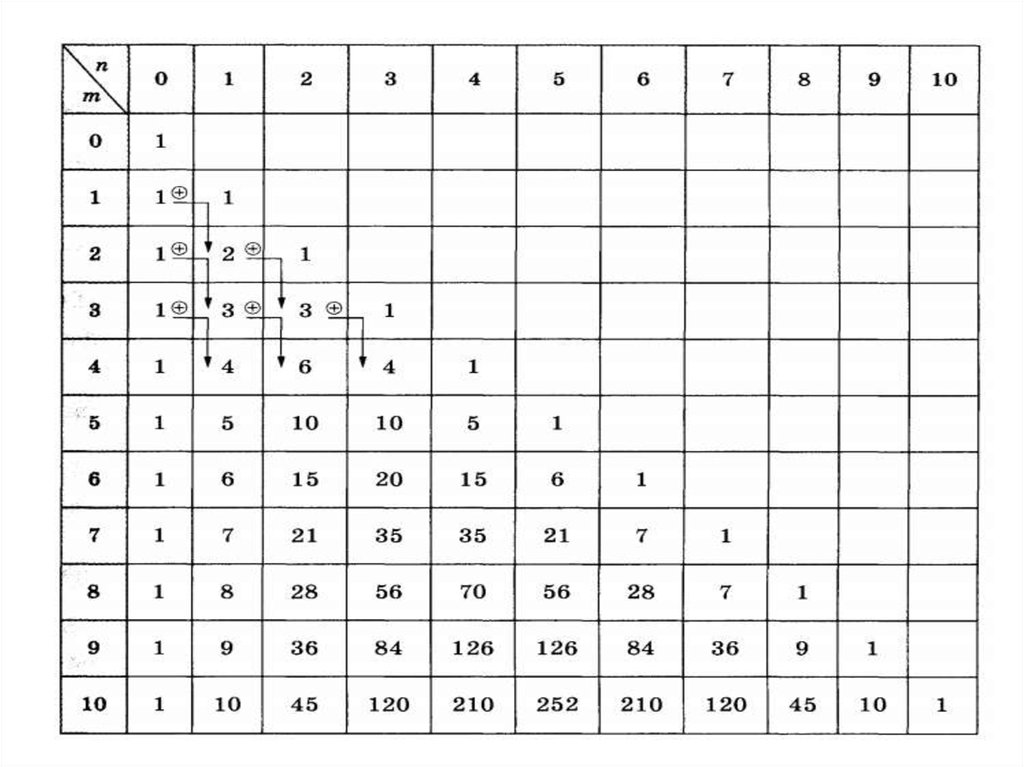 Поскольку оба бинома возведены в третью степень, мы можем найти коэффициенты для наших терминов, используя третью строку треугольника Паскаля.

Обратите внимание, что единственная запись в верхней части треугольника обычно называется 0-й строкой. Чтобы избежать двусмысленности, мы используем строку, составленную как 𝑛=3.

Начиная с первого набора скобок, 𝑎+1𝑎 мы можем применить метод разложения общего двучлена степени 3, который утверждает, что (𝑥+𝑦)=𝑥+3𝑥𝑦+3𝑥𝑦+𝑦.

Установка 𝑥=𝑎 и 𝑦=1𝑎, имеем 𝑎+1𝑎=𝑎+3𝑎1𝑎+3𝑎1𝑎+1𝑎=𝑎+3𝑎+3𝑎+1𝑎. 

Точно так же мы можем рассмотреть второй набор скобок, подставив 𝑥=𝑎 и 𝑦=1𝑎 в уравнение, которое у нас есть: 𝑎+1𝑎=𝑎+3𝑎1𝑎+3𝑎1𝑎+1𝑎=𝑎+3𝑎+3𝑎+1𝑎.

Следовательно, у нас есть 𝑎+1𝑎𝑎+1𝑎 = 𝑎+3𝑎+3𝑎+1𝑎𝑎+3𝑎+3𝑎+1𝑎.

Мы можем Теперь рассмотрим, какие пары термов имеют произведение, содержащее 𝑎. На самом деле таких терминов всего две пары: 𝑎 и 3𝑎, 3𝑎 и 𝑎:

Следовательно, так как оба эти термина будут содержать 𝑎, они оба будут вносить вклад в коэффициент этого члена в нашем окончательном разложении. Следовательно окончательный коэффициент 𝑎 будет суммой их двух соответствующих коэффициенты. Поскольку каждый имеет коэффициент 3, окончательный коэффициент 𝑎 будет 3+3=6.

Для больших значений 𝑛 требуется все больший объем работы для нахождения отдельных терминов, если наш метод включает запись всего расширения.

В оставшейся части этого объяснения мы попытаемся предоставить некоторые приемы, которые уменьшат количество вычислений, необходимых для таких вопросов.

Пример 4. Использование треугольника Паскаля для нахождения коэффициента определенного члена в биномиальном разложении

Найдите коэффициент при 𝑥 в разложении (2−5𝑥).

Ответ

Вспомним, что элементы треугольника Паскаля дают нам коэффициенты для членов биномиального разложения. Поскольку мы расширяем двучлен степени 8, мы будем использовать 8-ю строку треугольника (𝑛=8).

Нахождение коэффициентов треугольника Паскаля само по себе недостаточно для ответа на вопрос.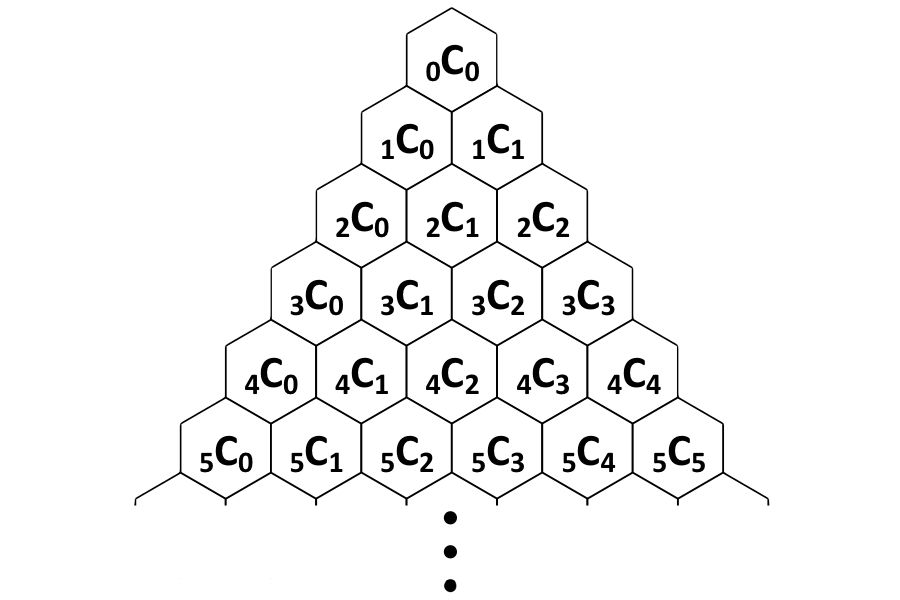 Поскольку мы пытаемся найти коэффициент при 𝑥 в окончательном разложении, мы также должны учитывать коэффициенты членов внутри самого бинома.

На этом этапе мы могли бы упростить, заменив 𝑎=2 и 𝑏=−5𝑥. Это позволило бы нам привести к более прямому расширению (𝑎+𝑏).

Мы также можем напрямую использовать члены исходного бинома и включить коэффициенты, найденные с помощью треугольника Паскаля. (2−5𝑥)=1⋅(2)+8⋅(2)(−5𝑥)+28⋅(2)(−5𝑥)+56⋅(2)(−5𝑥)+70⋅(2)(−5𝑥 )+56⋅(2)(−5𝑥)+28⋅(2)(−5𝑥)+8⋅(2)(−5𝑥)+1⋅(−5𝑥) 

На этом этапе мы могли бы упростить наши термины и получить ответ, однако для биномов с большими степенями заметьте, что запись такого расширения может быть довольно трудоемкой! Стоит пойти на некоторые хитрости, которые можно использовать для экономии времени.

Давайте посмотрим, какой термин (или термины) будет содержать 𝑥. В нашем случае нам нужно обратить внимание только на степени (−5𝑥). Как показано в разложении, каждый член содержит последовательно большие степени (−5𝑥).

Подобно соответствующей строке в треугольнике Паскаля, мы можем пометить эти термины с помощью 𝑘, где 𝑘=0 соответствует первому члену. Значение 𝑘 увеличивается до 𝑛, где 𝑛 — номер строки треугольника Паскаля.

Для этого биномиального разложения 𝑘=5 — единственный член, относящийся к нахождению коэффициента 𝑥. Если степень (−5𝑥) больше или меньше 5, мощность самого 𝑥 также будет больше или меньше 5. 𝑘∶×(2)(−5𝑥)𝑘=0∶×(2)(−5𝑥 )⋮𝑘=5∶×(2)(−5𝑥)КоэффициентКоэффициентКоэффициент

𝑘-й элемент треугольника Паскаля дает нам указанные выше коэффициенты.

Вместо того, чтобы записывать все расширение, этот метод дает нам возможность находить отдельные термины. 𝑘=5∶56⋅(2)⋅(−5𝑥)=56⋅8⋅(−3125)𝑥=−1400000𝑥

Следовательно, коэффициент при 𝑥 равен 1‎ ‎400‎ ‎000.

И последнее замечание: если бы порядок слагаемых в нашем предыдущем биноме был обратным, вместо этого появилось бы (−5𝑥), когда 𝑛−𝑘=5. Поскольку 𝑛=8, это означает, что мы бы оценили член, где 𝑘=3.

К счастью, это не изменило бы наш ответ. Самый простой способ понять почему — признать, что 𝑘-й элемент и (𝑛−𝑘)-й элемент в треугольнике Паскаля имеют одинаковую симметрию. Это означает, что коэффициент (и, следовательно, наш ответ на предыдущий пример) останется неизменным.

Метод, показанный для нахождения отдельных терминов, полезен и может быть обобщен для двучленов с большими степенями. Один оставшийся недостаток заключается в том, что для нахождения 𝑘-го элемента 𝑛-й строки в треугольнике Паскаля нам еще нужно построить 𝑛 строк треугольника!

Хотя использование треугольника Паскаля может серьезно упростить нахождение биномиальных разложений для степеней 𝑛 примерно до 10, намного дальше этой точки становится непрактично. Поэтому было бы полезно выяснить, существует ли связь между последовательные элементы в строках треугольника Паскаля.

В качестве примера рассмотрим девятую строку треугольника Паскаля (т. е. строку помечен 𝑛=8). Мы рассматриваем множители, переводящие нас от одного элемента к следующий.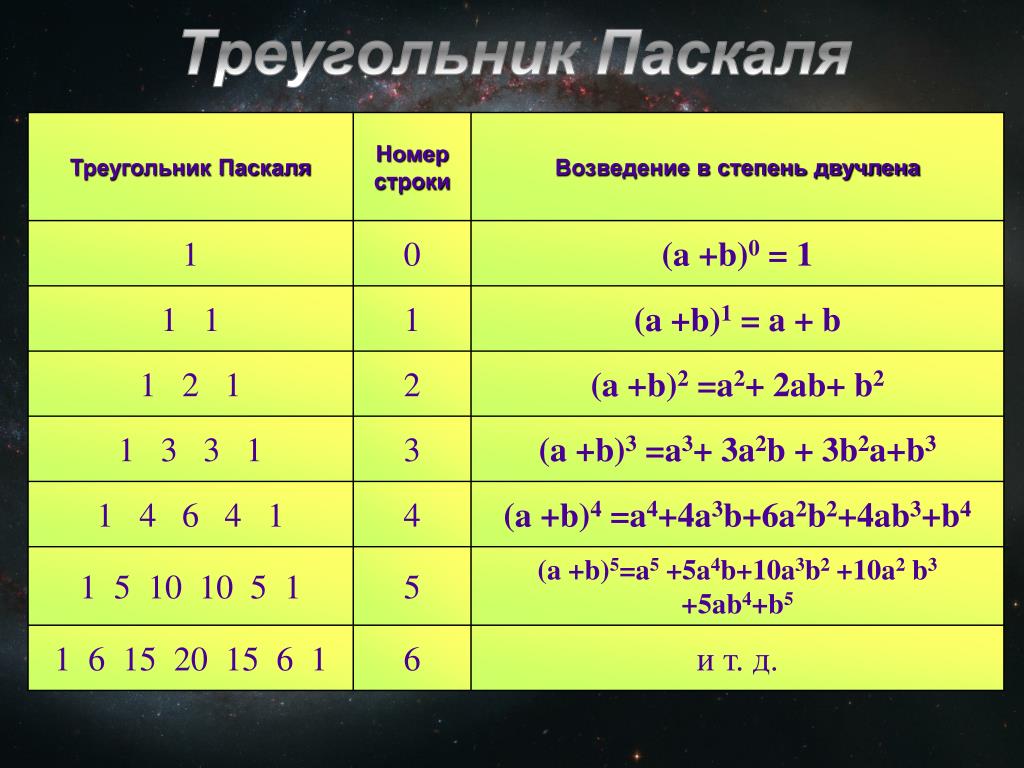 Фигура представляет это.

Мы можем ясно видеть, что существует шаблон, связывающий один элемент с другим. На самом деле, мы можем выразить это в общем виде следующим образом: перейти от (𝑘−1)-го элемента до 𝑘, умножаем на 𝑛−𝑘+1 и делим на 𝑘. Это правило применимо не только к девятой строке, но и обобщается на любая строка треугольника Паскаля. Используя этот факт, мы можем расширять биномы произвольно большие показатели.

Свойство: связь между последовательными терминами в одной строке Паскаля Треугольник

Соединение между последовательными элементами в (𝑛+1)-й строке (которое по соглашение, которое мы перечисляем 𝑛) в треугольнике Паскаля, следующее: чтобы перейти от (𝑘−1)-го элемента к 𝑘-му, мы умножаем на 𝑛−𝑘+1𝑘.

Следующие несколько примеров продемонстрируют этот факт.

Пример 5. Использование треугольника Паскаля для нахождения биномиальных разложений

Запишите первые 5 членов разложения (2+𝑥) по возрастанию полномочия 𝑥.

Ответ

Мы начнем с рассмотрения коэффициентов первых пяти членов этого разложения. Коэффициенты даны девятнадцатой строкой треугольника Паскаля, т. е. ряд мы помечаем 𝑛=18. Первый элемент в любой строке Паскаля треугольник равен 1. Вспомните связь между последовательными элементами в строке в Треугольник Паскаля: перейти от (𝑘−1)-го элемента к 𝑘, мы умножаем на 𝑛−𝑘+1𝑘. Применяя это правило, мы можем вычислить 1-й элемент, умножив 0-й элемент на 181. Затем, чтобы найти второй элемент, умножаем на 172. Продолжая таким образом, мы можем найти первые пять членов в строку, как показано на рисунке ниже.

Таким образом, первые пять слагаемых равны 2+18×2𝑥+153×2𝑥+816×2𝑥+3060×2𝑥.

Пример 6. Использование треугольника Паскаля для нахождения биномиальных разложений

Ответ

Начнем с нахождения биномиального коэффициента. Коэффициенты даны одиннадцатая строка треугольника Паскаля, которую мы обозначаем 𝑛=10. Первый элемент в любой строке треугольника Паскаля равен 1. Затем вспомните связь между последовательными элементами в строке в треугольнике Паскаля. треугольник: перейти от (𝑘−1)-го элемента к 𝑘-му, умножаем на 𝑛−𝑘+1𝑘. Применяя это правило, мы можем вычислить 1-й элемент путем умножения 0-го элемента (равного 1) на 101. Затем, чтобы найти второй элемент, умножаем на 92. Продолжая таким образом, мы можем найти первые пять слагаемых в строку, как показано на рисунке ниже.

Обратите внимание, что как только мы подошли к среднему члену, мы можем просто обратиться к симметрии треугольник Паскаля и заполните остальные записи.

Следовательно, (𝑎+𝑏) = 𝑎+10𝑎𝑏+45𝑎𝑏+120𝑎𝑏+210𝑎𝑏+252𝑎𝑏+210𝑎𝑏+120𝑎𝑏+45𝑎𝑏+10𝑎𝑏+𝑏. 

При установке 𝑎=2 и 𝑏=3𝑥 имеем (2+3𝑥)=2+10×2(3𝑥)+45×2(3𝑥)+120×2(3𝑥)+210×2(3𝑥)+252×2(3𝑥)+210×2(3𝑥)+

Наконец, мы можем упростить числовые термины следующим образом: (2+3𝑥) = 1024+15360𝑥+103680𝑥+414720𝑥+1088640𝑥+1959552𝑥+24494440𝑥+2099520𝑥+1180980𝑥+393660𝑥+59049𝑥. 99𝑥..59049𝑥. 

Возможно, вы знаете, что треугольник Паскаля тесно связан с областью комбинаторики. Хотя комбинаторика выходит за рамки этого урока, она предоставляет более мощный набор инструментов для понимания биномиальных расширений и управления ими. Вам предлагается продолжить изучение биномиальной теоремы, однако навыки, полученные в этом уроке, должны дать вам прочную основу.

Key Points

• Мы можем быстро воспроизвести треугольник Паскаля для маленького 𝑛 легко раскройте биномы вида (𝑎+𝑏).
• Для биномиального разложения формы (𝑎+𝑏) отдельные члены можно найти, рассматривая коэффициенты из треугольника Паскаля в сочетании с последовательными степенями 𝑎 и 𝑏: 𝑘∶×(𝑎)(𝑏)Коэффициент где 𝑛 — номер строки треугольника Паскаля, а 𝑘 принимает целые значения от 0 до 𝑛.
• Для большего 𝑛 мы можем использовать отношение между последовательными терминами расширить биномы: перейти от (𝑘−1)-го элемента к 𝑘, мы умножаем на 𝑛−𝑘+1𝑘.

12.5: Биномиальная теорема — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5198

• OpenStax
• ОпенСтакс

Цели обучения

К концу этого раздела вы сможете:

• Использовать треугольник Паскаля для расширения двучлена
• Вычислить биномиальный коэффициент
• Использование биномиальной теоремы для расширения бинома

Прежде чем начать, пройдите этот тест на готовность.

1. Упрощение: \(\frac{7 \cdot 6 \cdot 5 \cdot 4}{4 \cdot 3 \cdot 2 \cdot 1}\).
   Если вы пропустили эту проблему, просмотрите пример 1. 25. 9{н}\).

   Чтобы найти коэффициенты членов, мы снова напишем наши разложения, ориентируясь на коэффициенты. Перепишем коэффициенты вправо, образуя массив коэффициентов.

   Рисунок 12.4.3

   Массив справа называется треугольником Паскаля . Обратите внимание, что каждое число в массиве является суммой двух ближайших чисел в строке выше. Мы можем найти следующую строку, начиная и заканчивая единицей, а затем добавляя два соседних числа.

   Рисунок 12.4.4

   Этот треугольник дает коэффициенты членов, когда мы расширяем двучлены. 9{2}-12 х+1}\конец{массив}\)

   Вычисление биномиального коэффициента

   Хотя треугольник Паскаля — это один из методов расширения бинома, мы также рассмотрим еще один метод. Прежде чем мы доберемся до этого, нам нужно ввести еще несколько факториальных обозначений . Это обозначение используется не только для расширения биномов, но также при изучении и использовании вероятности.

   Чтобы найти коэффициенты членов расширенных биномов, нам нужно будет уметь вычислять обозначение \(\left( \begin{array}{l}{n} \\ {r}\end{array}\ справа)\), который называется биномиальный коэффициент . Мы читаем \(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\) как «\(n\) выбрать \(r\)» или «\ (n\) взятые \(r\) за один раз».

   Определение \(\PageIndex{1}\)

   Биномиальный коэффициент \(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)\), где \(r\) и \(b\) — целые числа с \(0 \leq r \leq n\), определяется как

   \(\left( \begin{array}{l}{n} \\ { r}\end{array}\right)=\frac{n !}{r !(n-r) !}\)

   Читаем \(\left( \begin{array}{l}{n} \\ { r}\end{array}\right)\) как «\(n\) выбрать \(r\)» или «\(n\) взять \(r\) за раз».

   Пример \(\PageIndex{4}\)

   Оценка:

   1. \(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)
   2. \(\left(\begin{array}{l}{7} \\ {7}\end{array}\right)\)
   3. \(\left(\begin{array}{l}{4} \\ {0}\end{array}\right)\)
   4. \(\left(\begin{array}{l}{8} \\ {5}\end{array}\right)\)

   Раствор :

   а. Мы будем использовать определение биномиального коэффициента:

   \(\left( \begin{array}{l}{n} \\ {r}\end{array}\right)=\frac{n !}{r !(н-р) !}\)

   \(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)\)

   Используйте определение, \(\left( \stackrel{5}{ 1}\right)=\frac{n !}{r !(n-r) !}\), где \(n=5, r=1\).

   \(\frac{5 !}{1 !(5-1) !}\)

   Упростить.

   \(\frac{5 !}{1 !(4) !}\)

   Переписать \(5!\) как \(5\cdot 4!\)

   \(\frac{5 \cdot 4 !}{1 ! \cdot 4 !}\)

   Упростить, удалив общие множители.

   \(\frac{5\cdot \cancel{4 !}}{1 ! \cdot \cancel{4 !}}\)

   Упростить.

   \(5\)

   \(\left( \begin{array}{l}{5} \\ {1}\end{array}\right)=5\)

   b. \(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)\)

   Используйте определение, \(\left( \stackrel{5}{1} \right)=\frac{n !}{r !(n-r) !}\), где \(n=7, r=7\).

   \(\frac{7 !}{7 !(7-7) !}\)

   Упростить.

   \(\frac{7 !}{7 !(0) !}\)

   Упростить. Помните \(0!=1\).

   \(1\)

   \(\left( \begin{array}{l}{7} \\ {7}\end{array}\right)=1\)

   в. \(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)\)

   Используйте определение, \(\left( \stackrel{5}{1} \right)=\frac{n !}{r !(n-r) !}\), где \(n=4, r=0\).

   \(\frac{4 !}{0 !(4-0) !}\)

   Упростить.

   \(\frac{4 !}{0 !(4) !}\)

   Упростить.

   \(1\)

   \(\left( \begin{array}{l}{4} \\ {0}\end{array}\right)=1\)

   d. \(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)\)

   Используйте определение \(\left( \stackrel{5}{1} \right)=\frac{n !}{r !(n-r) !}\), где \(n=8, r=5\).

   \(\frac{8 !}{5 !(8-5) !}\)

   Упростить.

   \(\frac{8 !}{5 !(3) !}\)

   Перепишите \(8!\) как \(8\cdot 7\cdot 6\cdot 5!\) и удалите общие множители.

   \(\frac{8\cdot7\cdot\cancel{6}\cdot\cancel{5!}}{\cancel{5!}\cdot\cancel{3}\cdot\cancel{2}\cdot1} \)

   Упрощение.

   \(56\)

   \(\left( \begin{array}{l}{8} \\ {5}\end{array}\right)=56\)

   Упражнение \(\PageIndex{ 7}\)

   Оценить каждый биномиальный коэффициент:

   1. \(\left(\begin{array}{l}{6} \\ {1}\end{array}\right)\)
   2. \(\left(\begin{array}{l}{8} \\ {8}\end{array}\right)\)
   3. \(\left(\begin{array}{l}{5} \\ {0}\end{array}\right)\)
   4. \(\left(\begin{array}{l}{7} \\ {3}\end{array}\right)\)

   Ответить

   1. \(6\)
   2. \(1\)
   3. \(1\)
   4. \(35\)

   Упражнение \(\PageIndex{8}\)

   Вычислить каждый биномиальный коэффициент:

   1. \(\left( \begin{array}{l}{2} \\ {1}\end{array}\right )\)
   2. \(\left(\begin{array}{l}{11} \\ {11}\end{array}\right)\)
   3. \(\left(\begin{array}{l}{9} \\ {0}\end{array}\right)\)
   4. \(\left(\begin{array}{l}{6} \\ {5}\end{array}\right)\)

   Ответить

   1. \(2\)
   2. \(1\)
   3. \(1\)
   4. \(6\)

   В предыдущем примере \((a)\), \((b)\), \((c)\) демонстрируют некоторые особые свойства биномиальных коэффициентов.

   Определение \(\PageIndex{2}\)

   Свойства биномиальных коэффициентов

   \(\left( \begin{array}{l}{n} \\ {1}\end{array}\right)= n \quad \left( \begin{array}{l}{n} \\ {n}\end{array}\right)=1 \quad \left( \begin{array}{l}{n} \\ {0}\конец{массив}\справа)=1\)

   9029{7}\).

   Решение :

   В нашем шаблоне \(n=7, a=x\) и \(b=y\).
   Ищем четвертый член. Так как \(r+1=4\), то \(r=3\).
   Напишите формулу
   Подставьте значения \(n=7, r=3, a=x\) и \(b=y\). 9{6}\), мы знаем \(r=3\).
   Напишите формулу.	Рисунок 12. 4.24
   Подставьте значения \(n=9, 4=3, a=x\) и \(b=3\).	Рисунок 12.4.25
   Рисунок 12.4.26	Рисунок 12.4.27
   Упрощение.	Рисунок 12.4.28 9{н}\). Показатели степени \(a\) уменьшаются на единицу при каждом члене слева направо. Показатели степени \(b\) увеличиваются на единицу при каждом члене слева направо. Сумма показателей любого члена равна \(n\). Треугольник Паскаля Рисунок 12.4.31 Биномиальный коэффициент \(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\ ) : Биномиальный коэффициент \(\left( \begin{array}{l}{\mathbf{n}} \\ {\mathbf{r}}\end{array}\right)\), где \(r \) и \(n\) — целые числа, где \(0≤r≤n\), определяется как . No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт