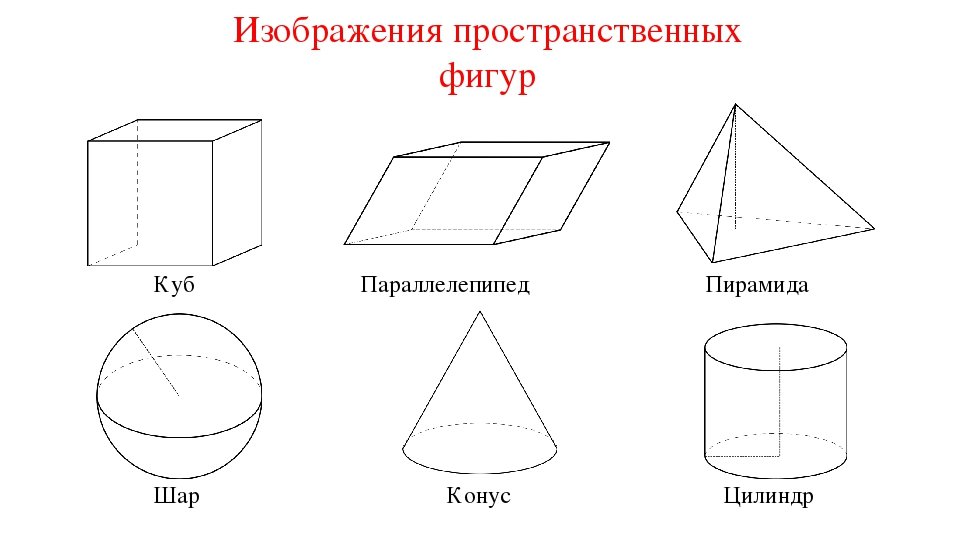
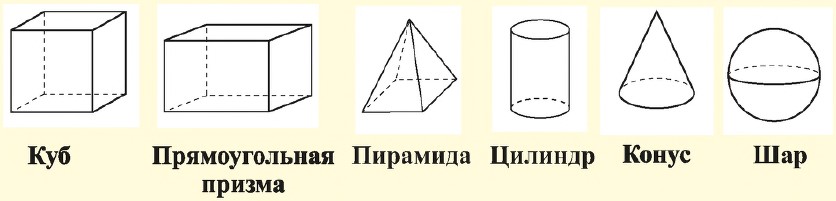
Тема: Математика вокруг нас. Пирамида. Цилиндр. Конус. | Тип: изучение нового материала. | |||
Задачи:
| ||||
Планируемые результаты | ||||
Предметные:
| Метапредметные:
| Личностные:
| ||
Ресурсы урока: Минаева С.С. Математика: 1 класс: часть 1; Минаева С.С. Математика: 1 класс: рабочая тетрадь №1, рабочая программа, электронное приложение | ||||
Ход урока | ||||
Содержание деятельности учителя: | Содержание деятельности обучающихся: | |||
Актуализация необходимых знаний | ||||
|
Выполняют задание: делят фигуры на 2 группы плоские и объёмные.
| |||
Мотивация познавательной деятельности | ||||
1. Учащимся 1 ряда: раскрасить на предложенной карточке все кубы; посчитать, сколько кубов на рисунке. 2. Учащимся 2 ряда: раскрасить на предложенной карточке все шары; посчитать, сколько шаров на рисунке. 3. Учащимся 3 ряда: раскрасить на предложенной карточке все параллелепипеды; посчитать, сколько параллелепипедов на рисунке. 4. Трём учащимся индивидуальные задания: построить из кубиков башню по рисунку.
|
Тема: «Пирамида. Цилиндр. Конус» Задача: познакомиться с геометрическими фигурами: пирамидой, цилиндром, конусом. | |||
Организация познавательной деятельности | ||||
|
Один ученик выполняет задание у доски.
| |||
Подведение итогов | ||||
|
| |||
Дополнительный материал: вылепить из пластилина конус и цилиндр (учебник задание на с. | ||||
Формулы объема цилиндра, шара, конуса — площадь поверхности и основания
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.
Например, такой важный факт:
Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз.
(ведь , ).
Вот такая задача.
1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.
Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу.
 Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться! Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.
Мы тоже расскажем о ней.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объема и площади поверхности. Цилиндр, конус и шар» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Цилиндр, конус и шар» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 08.04.2023
Формулы объема и поверхности
Объем выражает количество чего-то (например, воды), которое нам нужно, чтобы заполнить форму.
Космические фигуры имеют только объем. Плоские фигуры (треугольники, квадраты) не имеют объема.
Прямоугольный параллелепипед
Прямоугольный параллелепипед имеет 6 граней, которые являются прямоугольниками.
Если стороны прямоугольника внизу равны а и
b, а высота параллелепипеда c
(третье ребро прямоугольного параллелепипеда).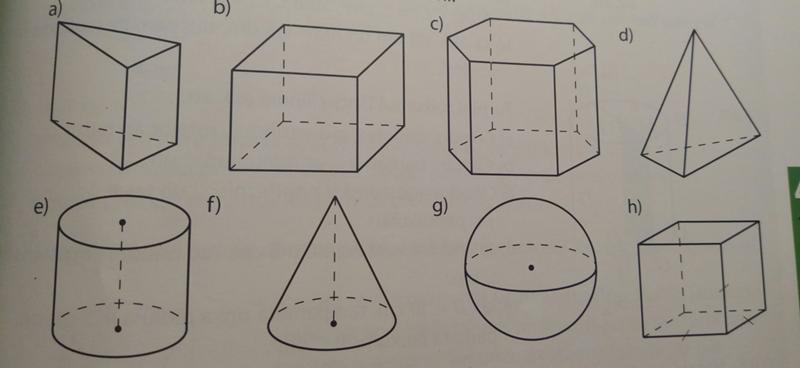 92$
92$
Параллелепипед
Параллелепипед образован 6 параллелограммами.
Если площадь дна равна А, а высота
параллелепипед h.
Формула объема:
$V = A \cdot h$
Пирамида
Пирамида — это фигура с многоугольным основанием (треугольник, квадрат, прямоугольник), соединенным с одной точкой, называемой вершиной.
Пусть высота (расстояние между вершиной и основанием) пирамиды равна h
а площадь основания равна A.92\cdot ч$
Площадь боковой поверхности = $\pi\cdot r \cdot l$
Полная площадь поверхности прямого круглого конуса равна площади боковой поверхности + площади основания.Общая площадь поверхности = $\pi\cdot r(r + l)$
Сфера
Сфера — это поверхность полностью круглого шара.
Каждая сфера имеет центральную точку, называемую «центром» сферы.
Радиус — это длина от центра до любой точки на поверхности сферы.
Объем сферы радиусом r:
92 \cdot ч$
Площадь криволинейной поверхности цилиндра:
Площадь изогнутой (боковой) поверхности = $2\cdot\pi\cdot r \cdot h$
Общая площадь поверхности = площадь изогнутой (боковой) поверхности + площадь двух круглых концов:
Общая площадь поверхности = $2\cdot\pi\cdot r(h + r)$
Викторина: Объем и площадь поверхности
Твердые формы — определение, типы, свойства, примеры, часто задаваемые вопросы
Твердые фигуры — это не что иное, как тела, состоящие из трех измерений, а именно длины, ширины и высоты.
| 1. | Что такое твердые формы? |
| 2. | Твердые формы и их свойства |
| 3. | Грани, ребра и вершины твердых фигур |
| 4. | Часто задаваемые вопросы о твердых формах |
Что такое твердые формы?
В математике мы изучаем формы и их различные типы и пытаемся применить их в реальной жизни. Теперь мы подробно узнаем о каждой твердой форме. Твердые формы подразделяются на несколько категорий. Некоторые из них имеют криволинейные поверхности; некоторые имеют форму пирамид или призм.
Твердые фигуры Определение: Твердые фигуры — это трехмерные фигуры, которые имеют длину, ширину и высоту в качестве трех измерений.
Давайте сначала узнаем о твердых формах с изогнутыми поверхностями на примерах.
Твердые формы и их свойства
Твердые фигуры соответствуют трехмерным объектам. Осмотреться! Любой другой трехмерный объект, будь то ноутбук, мобильный телефон, рожок мороженого, шарики и т. д., являются примерами твердотельных форм. Они занимают некоторое пространство, имеют длину, ширину и высоту. Давайте изучим типы твердых форм-
- Сфера
- Цилиндр
- Конус
- Пирамида
- Призма
Сфера
Сфера представляет собой твердое тело абсолютно круглой формы, определенное в трехмерном пространстве. Каждая точка поверхности равноудалена от центра.
В таблице ниже показаны свойства сферы:
| Свойства | Площадь поверхности | Том |
|---|---|---|
| 4πr 2 | (4/3)πr 3 |
Цилиндр
Цилиндр — это твердое тело, заданное на трехмерной плоскости. Он удерживает два параллельных основания круглой формы, соединенных изогнутой поверхностью (например, трубкой) на фиксированном расстоянии.
В таблице ниже показаны свойства цилиндра:
| Свойства | Площадь поверхности | Том |
|---|---|---|
| 2πr (р+ч) | πr 2 ч |
Конус
Конус представляет собой характерную твердую форму, заданную в трехмерном пространстве. Он имеет плоскую поверхность и изогнутую поверхность, направленную вверх. Он образован набором отрезков, соединенных от круглого основания с общей точкой, известной как вершина или вершина. В зависимости от того, как вершина совмещена с центром основания, формируется прямой конус или косой конус.
Он имеет плоскую поверхность и изогнутую поверхность, направленную вверх. Он образован набором отрезков, соединенных от круглого основания с общей точкой, известной как вершина или вершина. В зависимости от того, как вершина совмещена с центром основания, формируется прямой конус или косой конус.
В таблице ниже показаны свойства конуса, где r обозначает радиус, h обозначает высоту, а s обозначает наклонную высоту конуса:
| Свойства | Площадь поверхности | Том |
|---|---|---|
| π г (г + с) | 1/3 πr 2 ч |
Пирамида
Пирамида представляет собой объемную фигуру или многогранник с многоугольным основанием, а все боковые грани — треугольниками. Пирамиды обычно описываются формой их оснований. Пирамида с:
Пирамиды обычно описываются формой их оснований. Пирамида с:
- Треугольным основанием называется Тетраэдром.
- Четырехугольное основание называется квадратной пирамидой.
- Основание Пентагона называется пятиугольной пирамидой.
- Правильное шестиугольное основание называется шестиугольной пирамидой.
В таблице ниже показаны свойства пирамиды: (BA = площадь основания, P = периметр, A = высота и SH = высота наклона)
| Свойства | Площадь поверхности | Том |
|---|---|---|
| БА + 1/2 × П × (Ш) | 1/3 ВА 2 |
Призмы
Призма представляет собой твердое тело, определенное на трехмерной плоскости с двумя одинаковыми фигурами, обращенными друг к другу. Различные типы призм: треугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д. Призмы также широко классифицируются на правильные призмы и наклонные призмы.
Различные типы призм: треугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. д. Призмы также широко классифицируются на правильные призмы и наклонные призмы.
В таблице ниже показаны свойства призмы: (BA = площадь основания, P = периметр, H = высота)
| Свойства | Площадь поверхности | Том |
|---|---|---|
| 2 × (ВА) + П × В | БА × Н |
Многогранники/Платоновые тела
Платоновы тела имеют грани, идентичные правильным многоугольникам. Есть пять многогранников.
- Тетраэдр с четырьмя равносторонне-треугольными гранями
- Октаэдр с восемью равносторонне-треугольными гранями
- Додекаэдр с двенадцатью пятиугольными гранями
- Икосаэдр с двадцатью равносторонними треугольными гранями
- Шестигранник или куб с шестью квадратными гранями.

В таблице ниже показаны свойства платоновых форм: (EL = длина ребра)
| Свойства куба | Площадь поверхности | Том |
|---|---|---|
| 6 × (EL) 2 | (EL) 3 |
Грани, ребра и вершины твердых фигур
Как упоминалось ранее, объемные формы и объекты отличаются от двумерных форм и объектов наличием трех измерений — длины, ширины и высоты. Благодаря этим трем измерениям эти объекты имеют грани, ребра и вершины. Давайте разберемся с этими тремя подробно.
Грани твердых тел
- Гранью называется любая отдельная плоская поверхность твердого объекта.

- Твердые фигуры могут иметь более одной грани.
Ребра объемных фигур
- Ребро — это отрезок линии на границе, соединяющий одну вершину (угловую точку) с другой.
- Они служат стыком двух граней.
Вершины объемных фигур
- Точка, в которой встречаются две или более прямых, называется вершиной.
- Это угол.
- Точка пересечения ребер обозначает вершины.
Например:
Советы и рекомендации
- Рифма для запоминания объемных форм:
«Твердые фигуры толстые, а не плоские.
Найди шишку в праздничной шапке!
Вы видите сферу в баскетбольном мяче,
И прямоугольный параллелепипед в таком высоком здании!
Вы видите куб в кости, которую вы бросаете,
И цилиндр в блестящем флагштоке!»
- Движение пальцев по геометрическим фигурам поможет вам понять концепцию граней, ребер и вершин.

Важные моменты
- Твердые или трехмерные объекты имеют 3 измерения: длину, ширину и высоту.
- Твердые фигуры имеют грани, ребра и вершины.
- Изучение твердых форм поможет нам в нашей повседневной жизни, поскольку большая часть нашей деятельности вращается вокруг них и зависит от них.
Похожие темы
- Площадь прямоугольника
- Площадь квадрата
- Является ли квадрат прямоугольником
- Типы треугольников
- Форма многоугольника
Часто задаваемые вопросы о твердых формах
Что такое твердая форма?
Трехмерные объекты с определенной длиной, шириной и высотой называются объемными формами.
Как еще можно назвать твердую форму?
В геометрии объемную форму также можно назвать трехмерной.
Сколько твердых фигур существует?
В список твердых фигур входят куб, прямоугольный параллелепипед, сфера, конус, полусфера, призма, цилиндр, пирамида и т. д.
д.
Что такое объем твердой формы?
Объем сплошных фигур относится к объему кубического пространства, заполненного фигурами. Чтобы найти объем, нам нужны измерения трех измерений.
Шар твердый или плоский?
Сфера представляет собой твердое тело без краев и вершин (углов).
Каковы свойства твердых фигур?
Твердые фигуры — это трехмерные объекты. Они имеют три измерения — длину, ширину и высоту. Будучи трехмерными, они занимают место во Вселенной. Твердые формы идентифицируются в соответствии с особенностями — ребрами, вершинами, гранями и т. д.
Что такое плоские и твердые формы?
Плоские формы также известны как плоские формы, которые представляют собой 2D-формы, состоящие из прямых, изогнутых линий или того и другого. В то время как твердые формы представляют собой трехмерные формы, состоящие из длины, ширины и высоты. Разница между плоскими и сплошными формами заключается в размерах. Например, квадрат представляет собой плоскую форму, а его противоположная твердая форма представляет собой куб, который представляет собой трехмерную форму.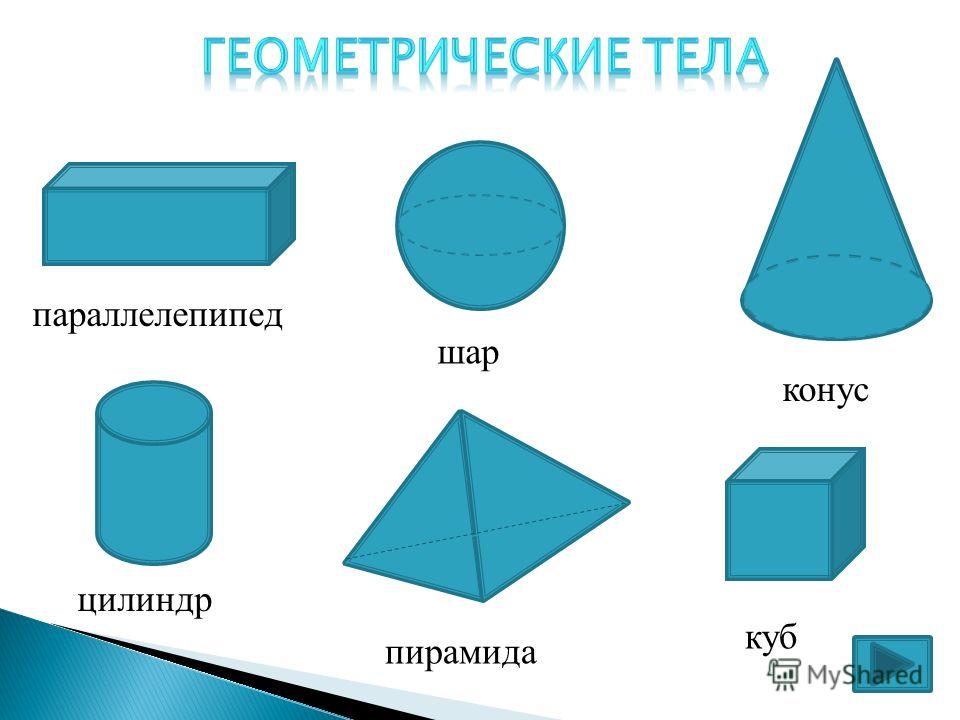



 34 в учебнике.
34 в учебнике.
 34)
34)