У 2х в квадрате график: Ответы: Постройте график функции:у=2х в квадрате…

Проходит ли график функции через точку? Работа № 7. Вариант 1. № 5. ГДЗ Алгебра 9 класс Кузнецова. – Рамблер/класс

Проходит ли график функции через точку? Работа № 7. Вариант 1. № 5. ГДЗ Алгебра 9 класс Кузнецова. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

а) Постройте график функции у = 2х — 5.

б) Проходит ли график через точку A(-35; -65)?
 

ответы

а) у = 2х — 5.
График прямая.
 
 
 
б) А(-35;-65)
y = 2(-35)-5;
y = -75,
-65 ≠ -75, равенство неверное, т. о. точка А не принадлежит графику функции у = 2х — 5.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

10 класс

11 класс

Химия

похожие вопросы 5

Напишите гдз по алгебре Мордкович 7 класс! Надо решить №32.20!

Решите уравнение:
●32.20.    а) х2 — 3x + 2 = 0;          в) х2 — 6x + 8 = 0;
б) x2 + 8х + 15 = 0;                      г) x2 (Подробнее…)

ГДЗАлгебраМордкович А.Г.7 класс

Будет ли введено устное собеседование по русскому языку на ГИА?

Подскажите, будет ли введено устное собеседование по русскому языку на ГИА? Как это будет проходить? (Подробнее. ..)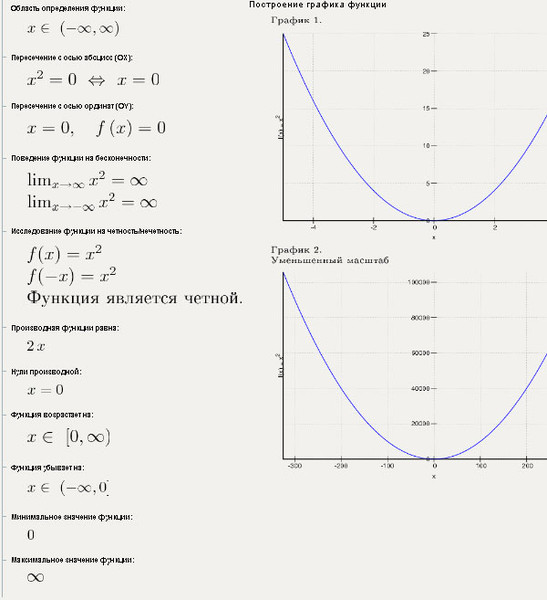

НовостиГИАЭкзамены9 классРусский язык

3. Вычислите… 6 класс А.П. Ершова Математика. К 2. Вариант А 1

3.
Вычислите: (Подробнее…)

ГДЗМатематика6 классЕршова А.П.

Радиус основания цилиндра равен 2. В этот цилиндр наклонно к оси вписан квадрат со стороной 4 так, что все вершины его находятся на окружностях осн

Радиус основания цилиндра равен 2. В этот цилиндр наклонно к оси вписан квадрат со стороной 4 так, что все вершины его находятся на (Подробнее…)

ВыпускнойЕГЭГДЗ

Помогите упростить № 443 ГДЗ Математика 6 класс Никольский С.М.

Упростите запись по образцу (Подробнее…)

ГДЗМатематика6 классНикольский С.М.

Урок алгебры в 9-м классе «Квадратичная функция. Ее свойства и график»

Цели – обобщить и систематизировать знания учащихся о квадратичной функции: повторить изученные приемы исследования свойств функции, методы построения графиков; закрепить и упрочить умения и навыки учащихся по данной теме, показать ее прикладной характер, ориентировать на использование полученных знаний при дальнейшем изучении математики.
 
План урока:

1. Разминка.
2. Фронтальная работа по построению графика квадратичной функции и исследованию ее свойств.
3. Работа в группах по построению графика квадратичной функции с модулем.
4. Решение задачи, носящей прикладной характер, с применением свойств квадратичной функции.
5. Тест, контролирующий знания учащихся по теме.

Ход урока

Учитель: Ребята, сегодня мы с вами продолжаем вести разговор об одном из важных разделов математики – функциональной зависимости. Прежде всего вспомним определение функции.

Ученик: Функция – это такая зависимость переменной у от переменной х, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Учитель: Какую функцию называют квадратичной? Что является ее графиком?

Ученик: Квадратичной функцией называется функция. которую можнозадать формулой вида y = ax² + bx + c, где x – независимая переменная, a, b и с – некоторые числа, причем а 0. График – парабола.

Учитель: С какими способами построения графиков квадратичной функции мы познакомились?

Ученик:

1. способ выделения полного квадрата и дальнейшего построения с использованием искусственных преобразований;
2. построение графика на основании специального исследования квадратного трехчлена.

Учитель: Повторим некоторые этапы построения графиков квадратичной функции при выполнении теста – разминки.

I. Разминка (ученики устно отвечают на вопросы теста, подготовленного на карточки или слайды). В это время предложить трем ученикам самостоятельно решить на доске задачи.

Тест:

1. Какому графику соответствует функция, заданная формулой y = x² – 2? (Рисунок 1)

Рисунок 1

2. На каком из рисунков изображен график функции  (Рисунок 2)

Рисунок 2

3. Функция задана формулой . На каком из рисунков изображен ее график? (Рисунок 3)

Рисунок 3

4. Функция задана формулой . Каковы координаты вершины параболы?
   a (2; – 7).
   b (– 2; 24).
   c (2; 25).
5. Каково наибольшее значение функции, заданной формулой ?
   a 5.
   b 7.
   c –7.

Ответы: 1b; 2c; 3b; 4a; 5b.

Индивидуальные задания на доске:

1. Параболу у = 2х² сдвинули влево на 3 единицы и вниз на 5 единиц. Задайте формулой функцию, график которой получился в результате таких преобразований.

Решение: у = 2(х + 3)² – 5.

2. Найдите область значений функции у = х² – 2х.

Решение:Функция ограничена снизу, у₀ ===1, E(f) = (2; +)

3. Постройте график функции у = (3 – x)(х+ 1).

Решение: у = — х² + 2х +3. Нули функции: х₁ = – 1 ; х₂ = 3.  =

(3 – 1)(1 + 1) = 4. (1; 4) – вершина параболы, ветви вниз.

II. Фронтальная работа.

Задание классу (ученик у доски):

Постройте график функции у = — х²+ 6х – 5.

По графику проведите исследование свойств функции.

Индивидуальные задания на карточках:

1. Определите, при каких значениях с наименьшее значение функции у = 2х² + 16х + с равно 2.

Решение:

; ; .

2. Определите, при каких значениях b и c вершиной параболы у = х² + bx + c является точка А(–2; –1).

Решение: ; –2 = ; b = 4. ; ; ; .

III. Работа в группах.

Задание группам:

Построить график функции y = |x² – 4x + 3|. Какие виды преобразований необходимо выполнить, чтобы получить данный график из графика функции y = x².

Решение:

Виды преобразований:

• смещение вправо на 2 единицы;
• смещение вниз на 1 единицу;
• симметрия относительно оси Ох отрицательной части графика.

Дополнительно: Построить график функции у = 3х² + 6|х| + 6.

Индивидуальные задания на карточках (ученики выполняют на доске, объясняют решение классу после работы по группам):

1. Найти наибольшее значение функции у = — 1,5(х – 1)²на отрезке [0; 2]

Решение: х₀ = 1 [0; 2], функция ограничена сверху, у_наиб = у(1) = 0.

2. Найти наименьшее значение функции у = 2(х +3)² на отрезке [– 4; 1]

Решение:

х₀ = -3  [– 4; 1], Функция ограничена снизу, у_наим = у(-3) = 0.

3. По графику у = ах² + bx + c определите знаки чисел a, b, c. (рисунок 4)

Решение:

• ветви вниз  a < 0
•  > 0, a < 0 b > 0
• при x = 0 y = c > 0

Рисунок 4

IV. Решение задачи с практическим содержанием на применение свойств квадратичной функции. (Ученик у доски)

Требуется оградить прямоугольную площадку, примыкающую к стене. Забор должен иметь длину 60 м. Какой должна быть длина и ширина площадки, чтобы площадь ее была бы наибольшей?

Решение:

Пусть х м – ширина площадки, тогда длина ее будет равна (60 – 2

х) м, а площадь составит у = х(60 – 2х) м² . Выделим полный квадрат:

у = -2(х² – 30х) = -2(х² – 30х + 225 – 225)= -2(х – 15)² + 450.

При х = 15 у_наиб = 450. Ширина – 15 м, длина – 30 м.

V. Тест.

Вариант I

1. Какая линия является графиком функции у = – (х – 3)² + 2?
   А. Прямая, проходящая через начало координат.
   Б. Прямая, не проходящая через начало координат.
   В. Парабола.
   Г. Гипербола.
2. График функции у = 2(х + 2)²получается из графика функции у =2х²сдвигом на две единицы:
   А. Вправо.
   Б. Влево.
   В. Вверх.
   Г. Вниз.
3. Найдите наименьшее значение функции у = 3(х – 2)²на отрезке [–2; 5].
   А. 0.
   Б. –12.
   В. 12.
   Г. 27.
4. Какая из перечисленных функций является ограниченной сверху?
   А. у = 2х² – 5х + 3.
   Б. у = 3х² – 1.
   В. у = -3х² + х + 1.
   Г. у = .
5. Уравнение оси симметрии параболы у = –3х² + 5х + 1 имеет вид:
   А. .
   Б. .
   В. .
   Г. .

Вариант II

1. Какая линия является графиком функции у = – (х + 2)² — 4?
   А. Прямая, проходящая через начало координат.
   Б. Прямая, не проходящая через начало координат.
   В. Парабола.
   Г. Гипербола.
2. График функции у = 3х² – 2 получается из графика функции у =3х²сдвигом на две единицы:
   А. Вправо.
   Б. Влево.
   В. Вверх.
   Г. Вниз.
3. Найдите наименьшее значение функции у = 3(х + 2)²на отрезке [–2; 1].
   А. 0.
   Б. –12.
   В. 12.
   Г. 27.
4. Какая из перечисленных функций является ограниченной снизу?
   А. у = –2х² – 5х + 3.
   Б. у = 3х² – 1.
   В. у = -3х² + х + 1.
   Г. у = .
5. Уравнение оси симметрии параболы у = 2х² – 7х + 1 имеет вид:
   А. .
   Б. .
   В. .
   Г. .

Ответы:

• Вариант I: Г Б Г Б В
• Вариант II: Б А А В В

VI. Итоги урока.

VII. Домашнее задание.

Домашняя контрольная работа

Вариант I

1. Разложите на множители квадратные трехчлены:
   а) х² – 12х + 35;
   б) 7у²+ 19у — 6
2. Постройте график функции у = х² – 6х + 5. Найдите с помощью графика:
   а) нули функции;
   б) промежутки знакопостоянства;
   в) промежуток, в котором функция возрастает.
3. Найдите наименьшее значение квадратного трехчлена х² – 8х + 7
4. Сократите дробь:
5. Найдите промежутки монотонности функции y = x² – 5|x| +4.

Вариант II

1. Разложите на множители квадратные трехчлены:
   а) х² – 18х + 45;
   б) 9у²+ 25у — 6
2. Постройте график функции у = х² – 8х + 13. Найдите с помощью графика:
   а) нули функции;
   б) промежутки знакопостоянства;
   в) промежуток, в котором функция убывает.
3. Найдите наименьшее значение квадратного трехчлена –х² + 6х — 4
4. Сократите дробь:
5. Найдите промежутки монотонности функции y = x² – 6|x| +5.

2-4*x-(-3)=0

Пошаговое решение :

Шаг 1 :

Уравнение в конце шага 1 :

 (2x  2  - 4x) - -3 = 0
 Шаг 2 
 Средний член равен -4x, его коэффициент равен -4. 
 Последний термин, "константа", равен  +3  
 
 Шаг-1 : Умножьте коэффициент первого члена на константу   2 • 3 = 6  
 
 Шаг-2 : Найдите два множителя  6 , сумма которых равна коэффициенту среднего члена, который равен   -4 . 
  
  
  
  
  
       
  
 -6 
  
    +    
  
 -1 
  
    =    
  
 -7 
  
  
  
  
       
  
 -3 
  
    +    
  
 -2 
  
    =    
  
 -5 
  
  
 
 
       
  
 -2 
  
    +    
  
 -3 
  
    =    
  
 -5 
  
  
  
  
       
  
 -1 
  
    +    
  
 -6 
  
    =    
  
 -7 
  
  
  
  
       
  
 1 
 
    +    
  
 6 
  
    =    
  
 7 
  
  
  
  
       
  
 2 
  
    +    
  
 3 
  
    =    
  
 5 
  
  
  
  
       
  
 3 
  
    +    
  
 2 
  
    =    
  
 5 
  
  
  
  
       
  
 6 
  
    +    
  
 1 
  
    =    
  
 7 
  
  
  
  
  
  
 Observation : No two such factors can быть найденным !! 
 Заключение: Трехчлен нельзя разложить на множители 
  
 Уравнение в конце шага 2 : 
  
 2x  2  - 4x + 3 = 0
 
 Шаг 3 : 
 Парабола, нахождение вершины : 
  3. 1      Найдите вершину   y = 2x  2  -4x+3
 Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили "у", потому что коэффициент первого члена, 2 , положителен (больше нуля).
  Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
  Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую ​​информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
  Для любой параболы, Ax  2  +Bx+C, x-координата вершины определяется как -B/(2A) .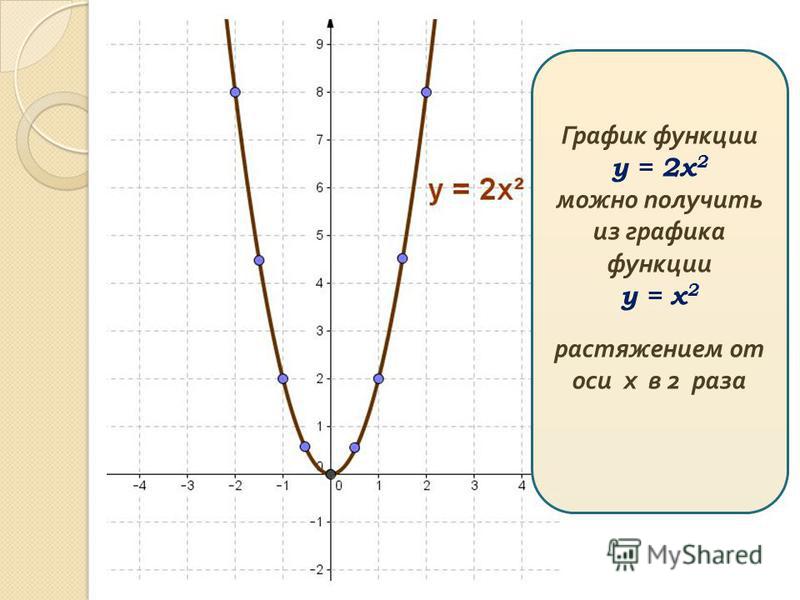 В нашем случае координата x равна   1,0000  
 Подключение к формуле Parabola 1.0000 для x Мы можем рассчитать y-координату: 
 y = 2,0 * 1,00 * 1,00-4,0 * 1,00 + 3,0 
 или Y = 1.000
 Парабола, график вертекс и x-intercepts: 
 Корневой график для:  y = 2x  2  -4x+3 
 Ось симметрии (штриховая)  {x}={ 1,00}  
 Вершина в  {x,y} = {1,00, 1,00}  
 Функция не имеет действительных корней
 Решите квадратное уравнение, заполнив квадрат 
  3.2     Решение   2x  2  -4x+3 = 0 при завершении Квадрата .
  Поделите обе части уравнения на 2, чтобы получить 1 в качестве коэффициента при первом члене: 
    x  2  -2x+(3/2) = 0
 Вычтите  3/2 из обеих частей уравнения: 
    x  2  -2x = -3/2
 Теперь хитрость: возьмите коэффициент x, равный 2, разделите на два, получите 1, и, наконец, возведите его в квадрат, получив 1
 Добавьте 1 к обеим частям уравнения : 
   В правой части у нас есть : 
    -3/2  +  1    или, (-3/2)+(1/1)  
   Общий знаменатель двух дробей равен 2   Сложение  (-3/2)+(2/2) дает -1/2  
 Итак, прибавив к обеим сторонам, мы окончательно получим : 
    x  2  -2x+1 = -1/2
 Добавление 1 дополнит левую часть до полного квадрата: 
    x  2  -2x+1 = 
    ( x-1) • (x-1)  = 
   (x-1)  2  
 Вещи, равные одной и той же вещи, также равны друг другу. Поскольку 
    x  2  -2x+1 = -1/2 и 
    x  2  -2x+1 = (x-1)  2  
 тогда по закону транзитивности 
    (x-1)  2  = -1/2
 Будем ссылаться на это Уравнение как уравнение #3.2.1  
 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
 Обратите внимание, что квадратный корень из 
    (x-1)  2   равен 
    (x-1)  2/2   = 
   (x-1)  1   = 
    Принцип квадратного корня в уравнении #3.2.1  получаем: 
    x-1 = √ -1/2
 Добавьте  1 к обеим частям, чтобы получить: 
    x = 1 + √ -1/2 
 В математике i называется мнимой единицей. Он удовлетворяет   i  2    =-1. И  i  , и   -i   являются квадратными корнями из   -1 
 Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное 
    x  2  - 2x + (3/2) = 0 
    имеет два решения: 
   x = 1 + √ 1/2 •  i  
    или 
   x = 1 - √ 1/2 •  i 
 Обратите внимание, что √ 1/2 можно записать как 
   √ 1 / √ 2   что равно 1/√ 2 
 Принято упрощать до тех пор, пока знаменатель не станет свободным от радикалов.
 Здесь этого можно добиться, умножив числитель и знаменатель на √ 2 
 После этого умножения числовое значение   1 /√ 2 остается неизменным, поскольку оно умножается на √ 2  / √ 2 , что равно   1 
 Хорошо, давайте:
 1 • √ 2  1 • √ 2  
 —————————————— = ————————————— 
 √ 2  • √ 2  2 
 
 Решение квадратного уравнения с помощью квадратной формулы 
  3.3     Решение    2x  2  -4x+3 = 0 с помощью квадратной формулы .
 Согласно квадратичной формуле, x, решение для AX  2  +BX +C = 0, где A, B и C цифры, часто называемые коэффициентами, определяются как: 
   
-B ± √ B  2  -4AC 
   x =   ———————— 
                      2A
 В нашем случае A = 2 
 B = -4 
 C = 3
 Соответственно, B  2  -4AC = 
 16 -24 = 
 -8
 Применение квадратичной формулы:
 4 ± √ - 8 
    x  =    ————— 
                     4
 В множестве действительных чисел отрицательные числа не имеют квадратных корней. Был изобретен новый набор чисел, называемый комплексным, чтобы отрицательные числа имели квадратный корень. Эти числа записываются  (a+b*i) 
 И I, и -i являются квадратными корнями минус 1
 Соответственно, √ -8 = 
 √ 8 • (-1) = 
 √ 8 • √ -1 = 
 ± √ 8 • I
 может √ 8 быть упрощенным?
 Да! Разложение числа 8 на простые множители – это 
    2•2•2 
. Чтобы можно было удалить что-то из-под радикала, должно быть  2 этих экземпляра (потому что мы берем квадрат, т.е. второй корень).
 √ 8   =  √ 2•2•2   = 
 ± 2 • √ 2
 √ 2, округленная до 4 десятичных цифр, составляет 1,4142 
, так что теперь мы рассмотрим: 
 x = (4 ± 2 • 1,414 I)/4
 =(4+√-8)/4=1+i/2√ 2 = 1,0000+0,7071i
или: 
 х = (4-√-8)/4=1-i/2√ 2 = 1,0000-0,7071i 
 

Было найдено два решения:

1.  x = (4-√-8)/4=1-i/2√ 2 = 1,0000-0,7071i
2.  x = (4+√-8)/4=1 +i/2√ 2 = 1,0000+0,7071i

92-8x-10, определите точку, в которой находится вершина, и является ли точка минимальной или максимальной точкой. 2+2,null,0,0,,,black,1,none»/>

См. eNotes Ad-Free

Начните 48-часовую бесплатную пробную версию , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь.

Утверждено редакцией eNotes

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 Ответы педагога

Математика

Последний ответ опубликован 09 октября 2017 г. в 00:54:39

Добавьте 1 плюс 2 плюс 3 плюс 4.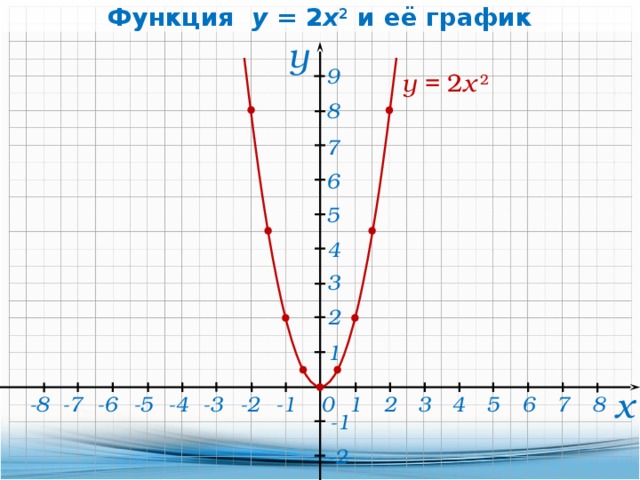 . . вплоть до 100.

3 Ответа учителя

Математика

Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.

Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?

1 Ответ учителя

Математика

Последний ответ опубликован 3 октября 2011 г. в 14:12:01.

Этот предел представляет собой производную некоторой функции f при некотором числе a. укажите это f и a. lim h->0  [(4-й корень из)(16+h)-2]/h    a=? ф=?

1 Ответ учителя

Математика

Последний ответ опубликован 23 мая 2012 г. в 2:05:32.

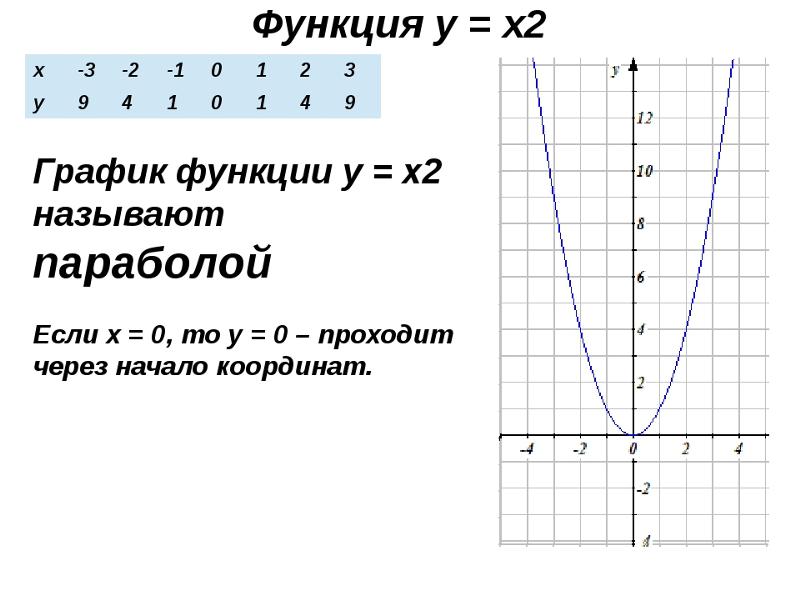
Определите, является ли это ростом или спадом. Затем найдите процент увеличения или уменьшения. 1.у=16(0,25)^х 2.