У х 4 2 график: Mathway | Популярные задачи

2

Тема

Тема

Тема: « Функция  у = ах² + bx + с, ее свойства и график».

ПРАКТИКУМ

 

Задание 1.Значения независимой переменной для функции у = х² указаны в таблице.

Х	-4	-3	-2	-1	-0,5	0	0,5	1	2	3	4
у

 

а) Найдите значения зависимой переменной, отметьте на рисунке точки графика функции у = х², постройте график, запишите, как он называется.

б) Укажите координаты вершины параболы.

в) Укажите, что является осью симметрии графика функции у = х

2. Запишите координаты точки, симметричной точке, абсцисса которой равна -8, и точке, абсцисса которой равна 5.

 

Решение:

 а) Функция у = х² называется квадратичной. Переменная х называется независимой переменной или аргументом, переменная у  —  зависимой переменной или значением функции.

График функции у = х² называется параболой.

Вычислим значения функции при заданном значении переменной.

При х = -4    у= (-4)² =16;                         при х = 4    у = 4² = 16

 при х = -3  у = (-3)² = 9;                           при х = 3    у = 3² = 9

 при х = -2  у = (-2)² = 4;                           при х = 2    у = 2²

= 4

при х = -1  у = (-1)²  = 1;                           при х = 1    у = 1² = 1

при х = -0,5   у = (-0,5)² = 0,25;                при х = 0,5   у = 0,25

при х = 0    у= 0² = 0
Внесем данные в таблицу

Х	-4	-3	-2	-1	-0,5	0	0,5	1	2	3	4
У	16	9	4	1	0,25	0	0,25	1	4	9	16

 

Построим график этой функции.

 

 

б) Координаты

 вершины параболы у = х²:    (0;0)

 

в) Осью симметрии параболы является ось ординат. Точке с абсциссой -8 симметрична точка с координатами (8; 64). Точке с абсциссой 5 симметрична точка  с координатами     (-5; 25).

 

Задание 2. Воспользуйтесь параболой, построенной при выполнении задания 1, чтобы найти наибольшее и наименьшее значение функции у = х² на промежутке:

а)[ -2;3]

б) (-2; 3]

Решение:

Воспользуемся построенным графиком

 

Отметим по оси х отрезок [-2; 3] и восстановим перпендикуляр до пересечения с графиком у = х². Получим, что наименьшего значения на этом промежутке функция достигает при х = 0; значение функции равно 0.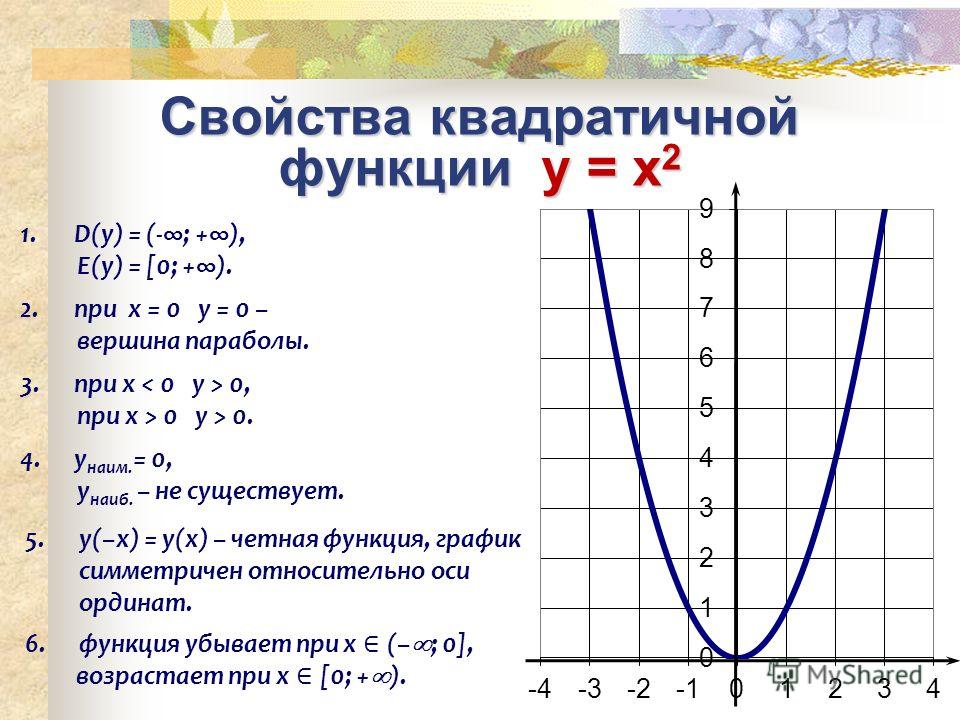

Наибольшее значение функции равно 9 при х = 3.

Ответ: наименьшее значение равно 0, наибольшее значение равно 9.

 

 

Задание для самостоятельного решения:

Воспользуйтесь параболой, построенной  при выполнении задания 1, чтобы найти наибольшее и наименьшее значения функции у = х² на промежутке: [-1;2].

 

 

 

Задание 3. Запишите, как построить, и постройте график функции:

 а) у = ( х + 7)²;

б) у = ( х – 4 )².

Решение:

 а) Если функция у = х²  при х = m принимает значение f(m)=g, то функция у = (х + 7)² принимает такое же значение g при х на 7 меньшем, чем m: f(m-7+7)=f(m)=g.

Это означает, что каждая точка графика у= х² смещается параллельно оси абсцисс на 7 единиц влево. Построим график.

 

 

б) Если функция у=х²  при х =m принимает значение f(m) =g то функция у= (х –4)²  принимает такое же значение g при х на 4 большем, чем m.

f(m+4 – 4) = f(m) = g . Это означает, что каждая точка графика у = х² смещается параллельно оси абсцисс на 4 единицы вправо. Построим график.

 

 

 

Задание 4. Запишите как построить и постройте график функции:

а) у = х² + 1;

б) у=х² – 2.

Решение:

а) Если функция у = х² при х = m принимает значениеf(m)=g то функция у = х²+1 принимает при том же значении х значение на 1 больше, чем g , т. е. g+1.  Это означает, что каждая точка графика у=х² смещается параллельно оси ординат на 1 единицу вверх. Построим график функции у = х²+1, сдвигая точки построенного графика у = х².

 

б) Если функция у=х²  при х =m принимает значение f(m)=g, то функция у =х²  — 2 принимает при том же значении х на 2 единицы меньше, чем g, т.е. g – 2. Это означает, что каждая точка графика у=х² смещается параллельно оси ординат на 2 единицы вниз. Построим график у=х

2, сдвигая точки построенного  графика  у=х².

 

 

 

 

Задание для самостоятельного решения.

Запишите, как построить графики функций:

а) у = х² +2;  б) у =( х – 2 )².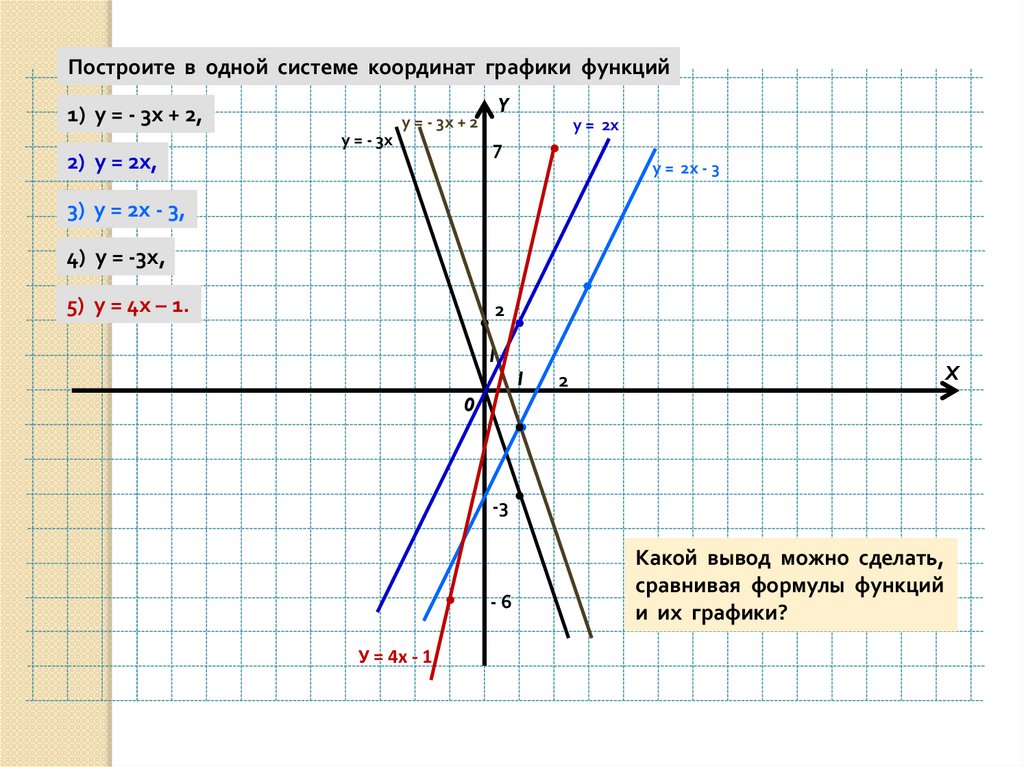 Постройте графики. 

 

Подсказкаа) График получен из графика у = х2 смещением параллельно оси ординат на 2 единицы вверх; б) График получен путем смещения графика у = х2 параллельно оси абсцисс на 2 единицы вправо

 

 

Задание 5. На рисунке построен график функции у = х². Запишите, как построить график функции: у = (х – 4)

2 – 2. Постройте график.

 

Решение:

Надо установить, вправо или влево, вверх или вниз надо сдвигать график функции  у= х².

Чтобы построить график функции у = f(х+l)+m, надо  график функции у = х² сдвинуть на l единиц влево, если l>0  или  на l единиц вправо, если l<0; затем сдвинуть график на m единиц вверх, если m>0  или на m единиц вниз, если m<0.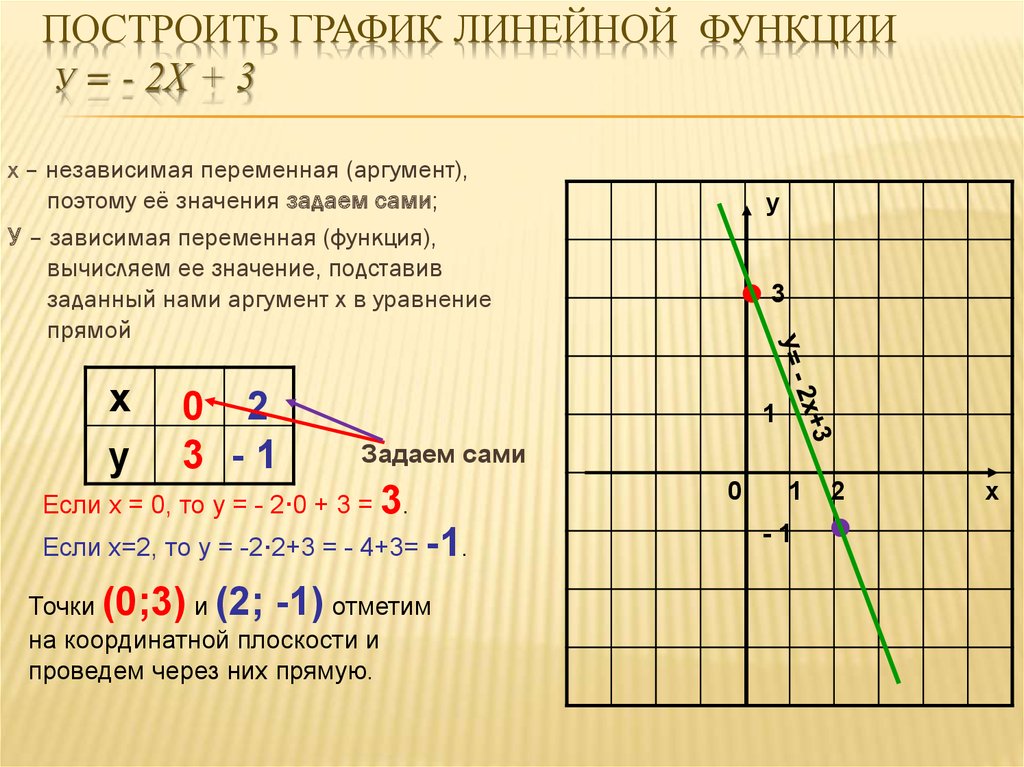 В данном случае l= — 4 (l<0), значит, сдвигаем вправо на 4 единицы график функции у = х².

m= — 2;(m<0), значит, сдвигаем вниз на 2 единицы.

Следовательно, в общем чтобы построить график функции у = ( х – 4)

2 – 2, если известен график функции у = х², надо сдвинуть график у = х²  параллельно оси абсцисс на 4 единицы вправо и параллельно оси ординат на 2 единицы вниз. Построим график.

 

 

 

Задание 6. Используя график функции у = (х – 4 )² – 2, ответьте на вопросы:

1.          какова область определения функции; множество значений функции.

2.          чему равны наибольшее и наименьшее значения функции;

3.          является ли функция непрерывной?

4.          При каких значениях аргумента значение функции равно нулю; больше нуля; меньше нуля;

5.           Где функция возрастает, где – убывает?

Решение:

1) область определения функции – это все значения, которые может принимать независимая переменная. Областью определения данной функции есть множество действительных чисел.

2)Функция ограничена только снизу. Поэтому наибольшего значения функции нет. Наименьшее значение, которое может принимать функция равно -2.

3) функция непрерывна. Точек разрыва нет.

4)Значение функции равно нулю в тех точках, в которых  график пересекает ось х.

х₁=2,5; х₂ = 5,5.

Функция положительна, если ее график находится выше оси  абсцисс. Функция положительна на промежутках х<2,5 и  х >5,5

Функция отрицательна, если ее график находится ниже оси абсцисс. Функция отрицательна на промежутке (2,5;  5,5)

5) функция возрастает на промежутке  Х>4

функция убывает на промежутке  х<4.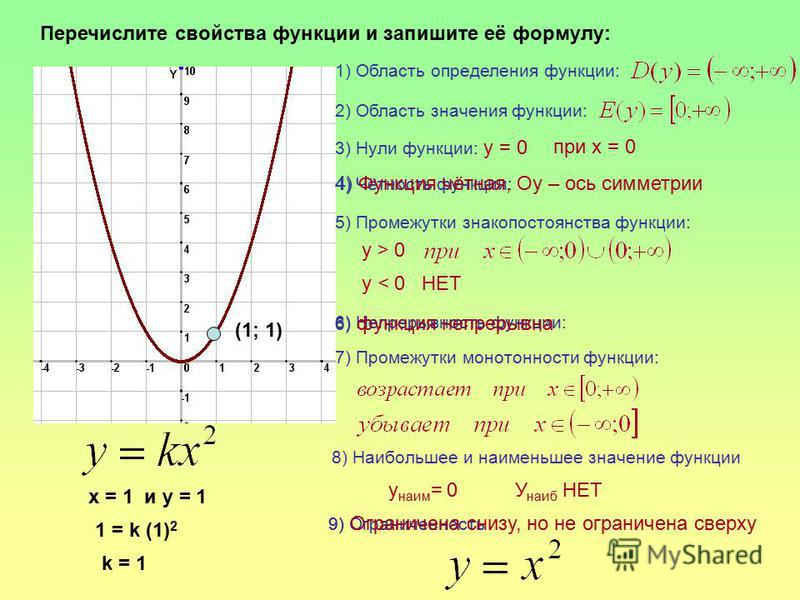

 

Задание для самостоятельного решения.

Запишите, как построить график функции у = (х +2)² + 1. Постройте этот график. Ответьте на вопросы:

1)какова область определения функции; множество значений функции;

2)чему равны наибольшее и наименьшее значения функции;

3)когда значение функции равно нулю; больше нуля; меньше нуля?

4) где функция возрастает; убывает? 

 

 

Задание 6. Найти уравнение оси симметрии и вычислить координаты вершины параболы  у = х² – 4х + 3. Построить график функции. Найти промежутки знакопостоянства функции; область определения и множество значений функции.

 

Решение.

у = х² – 4 х + 3 это уравнение общего вида у = ах² + bх +c

Найдем коэффициенты a,b,c

a= 1, b= -4, с = 3.