Построение графиков функций, содержащих знак модуля
Цель урока: получение более широких знаний о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины.
Задачи урока: использование различных методов исследования: теоретический и практический (решение задач), а так же исследовательский, расширение познавательного интереса к изучению алгебры, углубление знаний по теории модуля и решение задач, выходящих за пределы школьных учебников.
Оборудование: мультимедийное оборудование, компьютер, классная доска, планшет, творческие тетради, копировальная бумага.
1. Организационный момент.
2. Вступительное слово учителя.
Слово «модуль» произошло от
латинского слова «modulus», что в переводе
означает «мера». Это многозначное слово,
которое имеет множество значений и
применяется не только в математике, но и в
архитектуре, физике, технике,
программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и т.п.
Модуль объемного сжатия (в физике) — отношение нормального напряжения в материале к относительному удлинению.
3. Повторение
Чтобы глубоко изучать данную тему, нужно вспомнить простейшие определения, которые нам будут необходимы. Вопросы:
- Что называется уравнением? (Уравнение – это равенство, содержащее переменные.)
- Что называется уравнением с модулем? (Уравнение
с модулем – это уравнение, содержащее
переменную под знаком абсолютной
величины (под знаком модуля).
Привести
пример уравнения с модулем, используя
планшет.) - Что значит решить уравнение? (Решить уравнение – это значит, найти все его корни, или доказать, что корней нет. Привести пример уравнения, используя планшет).
- Используя планшет, изобразить график функции y=x, y=-x, y=x+2, y=2x.
Привести
пример уравнения с модулем, используя
планшет.)В математике модуль имеет несколько значений, но сегодня мы поработаем с одним из них.
Модуль — абсолютная величина числа, равная расстоянию от начала отсчета до точки на числовой прямой. Любое число можно изобразить точкой на координатной прямой. Расстояние этой точкой от начала отсчёта на этой прямой равно положительному числу или нулю, если точка совпадает с началом отсчёта числовой прямой. Вопросы:
1. Что называется модулем данного числа? (Расстояние
точки, изображающей данное число на
числовой прямой от начала этой прямой,
называется модулем данного числа.
)
2. Как обозначается модуль? (Модуль некоторого числа а обозначается |а| .)
Геометрический смысл модуля удобно использовать при решении некоторых уравнений.
Работа у доски.
Решим уравнение |х-6| = 9. Если число 6 мы изобразим точкой А (рисунок 1), то по определению модуля следует, что точка х стоит от точки А на 9 единиц. Но на числовой прямой таких точек две. Одна имеет координату х = 6 + 9 = 15, а вторая имеет координату
х = 6-9 = -3.
Следовательно, данное уравнение имеет два решения: х = 15 и х = -3.
Объяснение нового материала.
Теоремы, доказательства, следствия.
При решении уравнений, содержащих несколько выражений со знаком модуля, удобнее пользоваться алгебраическим определением модуля.
Определение. Модуль числа а или абсолютная величина числа а равна а, если а больше или равно нулю и равна -а, если а меньше нуля:
Из определения следует, что для любого
действительного числа а, |а|≥0.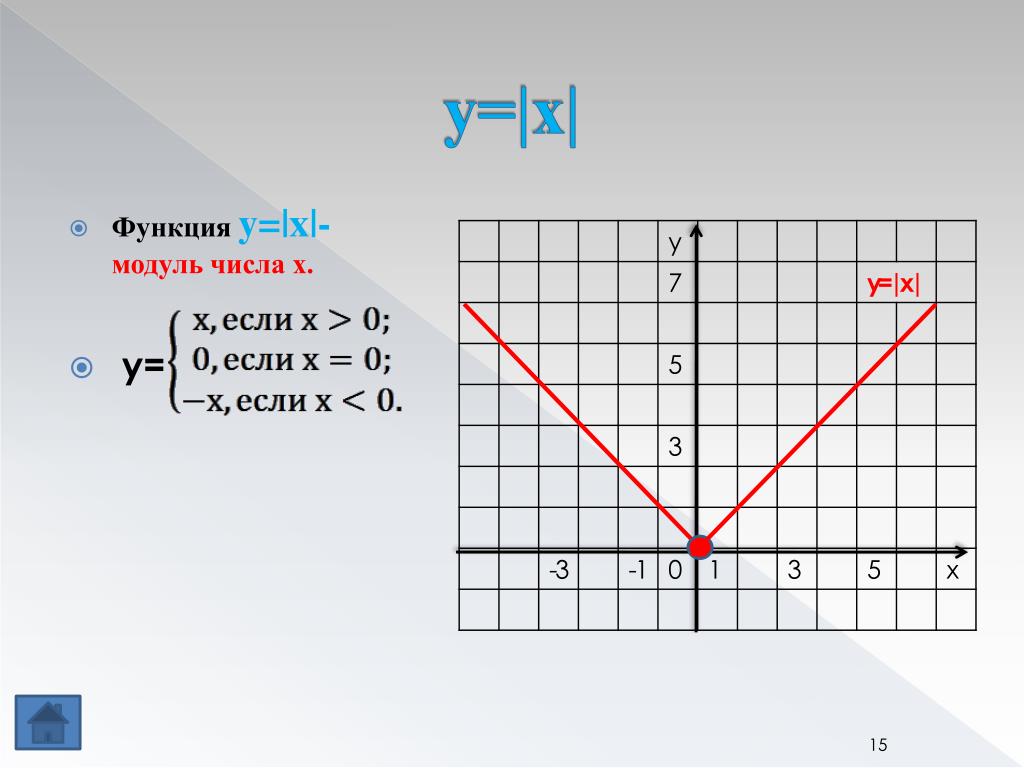
4. Объяснение нового материала
Теорема 1. Абсолютная величина действительного числа а≠0 равна большему из двух чисел а или -а.
Доказательство:
1. Если число а положительно, то -а отрицательно, т. е. -а < 0 < а. Отсюда следует, что -а < а. Например, число 7 положительно, тогда -7 — отрицательно и -7< 0 < 7 отсюда -7 < 7. В этом случае |а| = а, т. е. |а| совпадает с большим из двух чисел а и — а.
2. Если а отрицательно, тогда -а положительно и а < — а, т. е. большим числом является -а. По определению, в этом случае, |а| = -а — снова, равно большему из двух чисел -а и а.
Следствие 1. Из теоремы следует, что |-а| = |а|.
В самом деле, как |-а|, так и |а| равны большему из чисел -а и а, а значит, равны между собой
Следствие 2.
Для любого
действительного числа а справедливы
неравенства а≤|а|, -а≤|а|.
Умножая второе равенство -а≤|а|, на -1 (при этом знак неравенства изменится на противоположный), мы получим следующие неравенства: а≤|а|, а≥-|а|, справедливые для любого действительного числа а. Объединяя последние два неравенства в одно, получаем:
-|а|≤а≤|а|.
Работа у доски.
Решим уравнение |2х-12|+|6х+48|=160. Найдем корни (нули) каждого выражения, содержащего знак модуля: 2х-12=0, х=6; 6х+48=0, х= -8.
Найденные значения х разбивают
числовую прямую на три промежутка:
Решение этого уравнения рассматривается в каждом промежутке отдельно.
В промежутке х<-8 оба выражения,
стоящие под знаком модуля, отрицательны.
Поэтому в этом промежутке при записи
уравнения без знаков модуля знаки этих
выражений меняем на противоположные.
Получим уравнение –(2х-12) –(6х+48)=160.
откуда х=-24,5. Это значение принадлежит
рассматриваемому промежутку. Значит, оно
является решением данного уравнения.
Во втором промежутке —8≤х<6 первое выражение отрицательно, а второе положительно. Следовательно, в этом промежутке уравнение запишется так:
-(2х-12)-(6 х+48)=160. Откуда х=25 не принадлежит к промежутку.
В третьем промежутке х≥6 оба выражения положительны. Следовательно, в этом промежутке уравнение запишется так:
(2х-12)+(6х+48)=160. Откуда х=15.8. Значит, решением данного уравнения будут значения х =-24,5 и х=15,8
Для построения графиков функций,
содержащих выражения под знаком модуля, как
и при решении уравнений, сначала находят
корни выражений, стоящих под знаком модуля.
Эти корни разбивают числовую прямую на
промежутки. График строят в каждом
промежутке отдельно.
В простейшем случае, когда только одно выражение стоит под знаком модуля и нет слагаемых без знака модуля, можно построить график функции, опустив знак модуля, и затем часть графика, расположенную в области отрицательных значений
Функция у= |х|.
Рассмотрим график функции у=|х|, где |х| означает абсолютную величину, или модуль, числа х.
Построим её график, пользуясь
определением абсолютной величины. При
положительных х имеем |х|=х, т. Е.
этот график совпадает с графиком у=х и
является лучом, проходящим через начало
координат под углом 45° к оси абсцисс. При х<0
имеем |х|=-х, значит, для
отрицательных х график у=|х| совпадает
с биссектрисой второго координатного угла.
Впрочем, вторую половину графика (для отрицательных значений х) легко получить из первой, если заметить, что функция у=|х| четная, так как |-a|=|a|. Значит, график этой функции симметричен относительно оси Оу, и вторую половину графика можно получит, отразив относительно оси ординат часть, начерченную для положительных значений (рисунок 3).
Рассмотрим функция у=-|х|.
График функции у=-|х| получается симметричным отображением графика
у= |х| относительно оси х (рисунок 4).
Функции у=|х|+2, у=|х|-2
Этот график легко построить непосредственно. Однако мы его получим из графика у=|х|. Составим таблицу значений функций у=|х|+2 и сравним её с такой же таблицей, составленной для у=|х|, выписав эти таблицы рядом. Ясно, что из каждой точки первого графика у=|х| можно получить точку второго графика у=|х|+2, увеличив
Значит, чтобы получить точки
второго графика, надо каждую точку первого
сдвинуть на 2 вверх, т.е. второй график
получается из первого сдвигом вверх на 2.Сравним этот график с графиком у=|х|. Если х=а, у=|а| — точка первого графика, то точка х=а, у=|а|-1 будет лежать на втором графике. Поэтому каждая точка (|а|, |а|-1) второго графика может быть получена точки (а, |а|) первого графика сдвигом вниз на 2 единицы, и весь график получается, если у=|х| сдвинуть вниз на 2 единицы (рисунок 5).
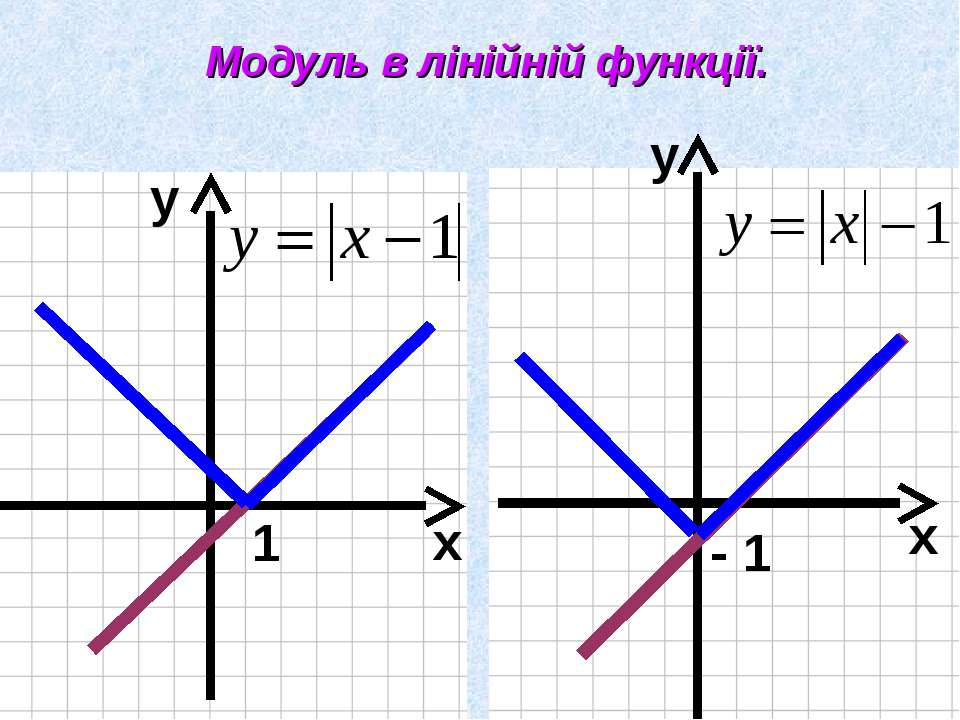
Функции у=|х+2|, у=|х+2|
График этой функции мы тоже можем
получить из графика у=|х|. Напишем опять
рядом две таблицы: для у=|х| и для у=|х+2|.
Если сравнивать значения этих функций при
одинаковых х, то окажется, что для
некоторых х ордината первого графика
больше, чем для второго, а для некоторых
наоборот.
Однако, если внимательно посмотреть на правые столбцы этих двух таблиц, связь между таблицами можно установить. Именно вторая функция принимает те же самые значения, что и первая, только принимает их на две единицы раньше, при меньших значениях. Значит, из каждой точки первого графика у=|х| получается точка второго графика у=|х|+2, сдвинутая на 2 влево; например из точки (-2, 2) получается точка с координатами (-3, 2). Поэтому и весь график у=|х|+2, получится, если сдвинуть график у=|х| на 2 влево вдоль оси абсцисс (рисунок 6).
Функция у=а|х|
График функции у=а|х| получается растяжением графика у=|х| вдоль оси у в а раз при а>1 и сжатием вдоль этой оси в 1/а раз при 0<а<1 (рисунок 7).
Функция у=||х-2|-3|
- Строим график функции у=|х|.
- Строим график функции у=|х-2|.
- Строим график функции у=|х-2|-3.
- Применяем к графику у=|х-2|-3 операцию «модуль» (рисунок 8).
Функции у=|2х-4|+|6+3х|. Находим корни каждого выражения, стоявшего под знаком модуля: 2х – 4 = 0; 6 + 3х = 0, х = -2. В результате ось Ох разбиваем на три промежутка. В каждом промежутке выражение, стоящее перед знаком модуля, имеет определенный знак. Опускаем знаки модуля, берём выражение в каждом промежутке с соответствующим знаком:
- х<-2, у = -(2х-4)-(6+3х)=-5х-2;
- –2≤ х < 2, у= —( 2х-4)+(6+3х)=х+10;
- х≥ 2, у = 2х-4+6+3х = 5х+2
Получим в каждом промежутке выражение
функции без знака модуля. Строим график
функции в промежутке. При правильном
построении в области определения график
должен представлять непрерывную линию (рисунок
9).
5. Итог урока.
Использую копировальную бумагу по вариантам построить график функции: у=|х-4|+2 (у=|х+4|-2).
6. Домашнее задание.
В творческой тетради составить функции, содержащие знак модуля, и построить их графики.
Литература.
- Детская энциклопедия. М., «Педагогика», 1990.
- Глейзер Г. И. История математики в школе. М. «Просвещение», 1982.
- Дынкин Е.Б., Молчанова С.А. Математические задачи. М., «Наука», 1993.
- Петраков И.С. Математические кружки в 8-10 классах. М., «Просвещение», 1987.
- Талочкин П.Б. Неравенства и уравнения. М., «Просвещение», 1989.
- Башмаков М.И. Уравнения и неравенства. Издательство Московского университета, 1974.
Приложение
16.9. Постройте график функции у = |x|. С помощью графика найдите.
.. Алгебра Мордкович 8 класс – Рамблер/класс 16.9. Постройте график функции у = |x|. С помощью графика найдите… Алгебра Мордкович 8 класс – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?16.9. Постройте график функции у = |x|. С помощью графика найдите:
а) значения у при х = 5; 0; -2,5;
б) значения х, если у = 7; 3; 1;
в) наименьшее и наибольшее значения функции на отрезке [-4; -1];
г) значения х, при которых функция убывает, возрастает.
ответы
решение тут такое
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ПсихологияЕГЭ10 класс9 класспохожие вопросы 5
Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее…)
ГДЗМордкович А.Г.Алгебра8 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1.
Практ. работа № 5.Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
3-8Функция модуля | Редакция
Функция модуля Редакция
youtube.com/embed/CJHYweZV-Pc» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/> Уровень AQAEdexcelOCR
Обозначение модуляСледующие обозначения относятся к модулю :
- Модуль числа, например. х записывается как |х|.
- Как правило, |x| = x для x \geq 0 и |x| = -x для x <0
- Функции также имеют модуль: напр. если f(x) = -2, то |f(x)| = 2
- |ф(х)| = f(x), когда f(x) \geq 0 и |f(x)| = -f(x), когда f(x)<0
- Если модуль находится внутри функции, т.е. f(|x|), то вы применяете модуль к значению x перед применением функции, то есть f(|-4|) = f(4)
УровеньAQAEdexcelOCR
Графики модульных функций – прямые линииСуществует 3 типа графиков модуля , которые вам могут предложить нарисовать:
- y = |f(x)| — все отрицательные значения f(x) становятся положительными на , отражающий отрицательный участок графика f(x) по оси x . Это ограничивает диапазон до |f(x)| \geq 0 (или подмножество внутри |f(x)| \geq 0, например, |f(x)| \geq 2.
- y = f(|x|) – отрицательные значения x дают тот же результат, что и соответствующие положительные значения x, поэтому график f(x) для x \geq 0 отражается на оси y , для отрицательных значений x.
- у = |f(-x)| — знак перестановки значений x (т.е. с положительного на отрицательное или с отрицательного на положительное), поэтому график f(x) отражается по оси y. Затем все отрицательные значения f(x) становятся положительными с помощью , отражающего отрицательный участок графика f(x) по оси x. Диапазон ограничен, как и в случае y = |f(x)|.
Это ограничивает диапазон до |f(x)| \geq 0 (или подмножество внутри |f(x)| \geq 0, например, |f(x)| \geq 2.Лучший и самый простой способ построить эти графики — сначала построить график y = f(x), а затем отразить его на соответствующей оси или осях.
Пример: Для f(x) = 2x-1 нарисуйте графики
\begin{aligned} y &= |f(x)| \\ y &= f(|x|) \\ y &= f|(-x)| \end{выровнено} 92-2x, нарисуйте графики
\begin{aligned} y &= |f(x)| \\ y &= f(|x|) \\ y &= |f(-x)| \end{выровнено}
A LevelEdexcel
Графическое решение уравнений модуляЧтобы решить уравнений модуля формы |f(x)| = n или |f(x)| = |g(x)|, вы можете решить их графически , используя следующий метод:
Шаг 1: Нарисуйте графики y = |f(x)| и y = n на той же паре осей.
Шаг 2: Определите диапазоны x, для которых f(x) \geq 0 и f(x) < 0 из графика.
напр. f(x) \geq 0 для x \leq \textcolor{red}{a} или x \geq \textcolor{blue}{b} и f(x) < 0 для \textcolor{red}{a} < x < \textcolor{blue}{b}
Шаг 3: Используйте шаг 2, чтобы написать 2 новых уравнения, по одному для каждого диапазона значений x:
f(x) = n для x \leq \textcolor{red} {a} или x \geq \textcolor{blue}{b}
— f(x) = n для \textcolor{red}{a} < x < \textcolor{blue}{b}
Шаг 4: Решите каждое уравнение по очереди и убедитесь, что решения верны, и удалите все, которые находятся за пределами диапазона x для этого уравнения.
Шаг 5: Проверьте правильность решения, взглянув на график.
Примечание: Используйте тот же метод для |f(x)| = |g(x)|, заменив n на g(x).
Уровень AQAEdexcelOCR
Алгебраическое решение уравнений модуля Для уравнений вида |f(x)| = n и |f(x)| = g(x) вы можете решить их алгебраически вместо графически — если вы чувствуете, что достаточно хорошо разбираетесь в теме.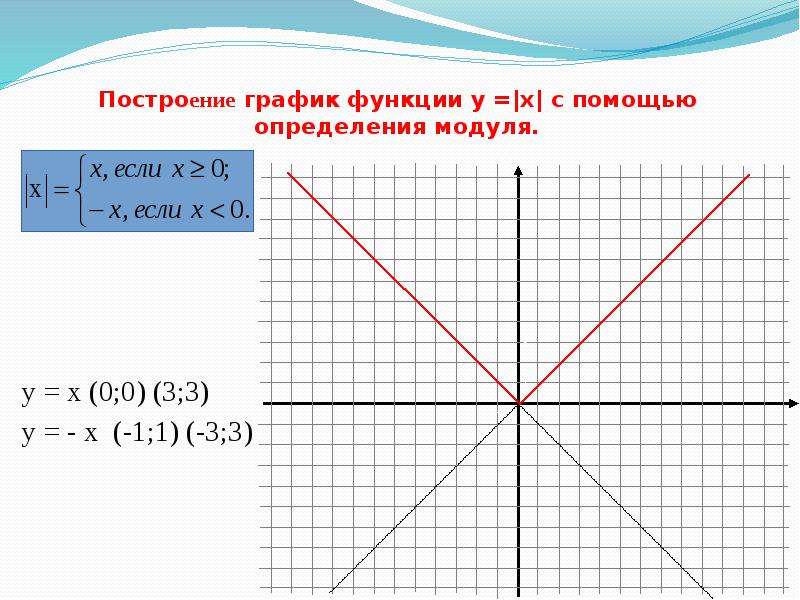
Пример: Решить |2x+2| = x+4
Шаг 1: Решите для положительных значений:
\begin{aligned} 2x + 2 &= x+4 \\ \textcolor{red}{x} &= \textcolor{red}{2 } \end{align}
Шаг 2: Решите для отрицательных значений:
\begin{aligned} -(2x + 2) &= x+4 \\ 3x &= -6 \\ \textcolor{red} {x} &= \textcolor{red}{-2} \end{aligned} 92 + 14x + 8 &= 0 \\ (3x+2)(x+4) &= 0 \end{aligned}
Шаг 3: Итак, решения:
\textcolor{red}{x = — \dfrac{2}{3}} и \textcolor{red}{x = -4}
A LevelAQAEdexcelOCR
Примечание:Вы также можете решить модульное неравенство , используя эти методы. Графический метод решения неравенств будет полезен, так как часто используется квадратное уравнение. Еще одно полезное правило:
|х-а| < b \, \ тогда и только тогда, когда \, a - b < x < a+b
ПродуктПрогнозные работы по математике уровня A 2023
11,99 фунтов стерлингов
Прогнозные работы по математике уровня A MME — это отличный способ попрактиковаться, используя аутентичные экзаменационные вопросы, которые уникальны для наших работ.
Наши экзаменаторы изучили прошлые работы по математике уровня A, чтобы разработать прогнозируемые вопросы экзамена по математике уровня A в аутентичном формате экзамена. Прибыль от каждого пакета реинвестируется в создание бесплатного контента на MME, что приносит пользу миллионам учащихся по всей стране.
Карточки повторения математики уровня A
16,99 фунтов стерлингов
Лучшие карточки повторения математики уровня A для AQA, Edexcel, OCR, MEI и WJEC. Maths Made Easy поможет вам эффективно подготовиться к экзаменам по математике A Level. Прибыль от каждого пакета реинвестируется в создание бесплатного контента на MME, что приносит пользу миллионам учащихся по всей стране.
Посмотреть продуктУровень AQAEdexcelOCR
Пример 1: графическое решение уравнений модуля – прямые линииРешить |2x+3| = x+2
[3 балла]
Шаг 1: Нарисуйте графики y = |2x+3| и y = x+2 на той же паре осей.
Шаг 2: Определите диапазоны значений x, для которых f(x) \geq 0 и f(x) < 0, из графика:
2x+3 \geq 0 для x \geq — \dfrac{3 {2} и 2x+3 < 0 для x < - \dfrac{3}{2}
Шаг 3: Используйте шаг 2, чтобы написать 2 новых уравнения, по одному для каждого диапазона x:
(1) 2x+3 = x+2 для x \geq — \dfrac{3}{2}
(2) — (2x+3) = x+2 для x < - \dfrac{3}{2}
Шаг 4: Решите каждое уравнение по очереди и проверьте правильность решения, а затем удалите все уравнения, выходящие за пределы диапазона х для этого уравнения.
Решение (1): x=-1 (это верно, поскольку -1 \geq — \dfrac{3}{2})
Решение (2): 3x = -5 \Rightarrow x = — \dfrac{5 }{3} (действительно, поскольку — \dfrac{5}{3} < - \dfrac{3}{2}) 92 + 4(2) - 9 = 11
г) — |f(2)| = — |11| = — 11
a)i) Отрицательное сечение должно быть отражено по оси x:
ii) Для отрицательных значений x необходимо отразить линию по оси y:
III ) Отразите f(x) по оси y, а затем отразите отрицательное сечение по оси x:
b)
Сначала нарисуйте графики y = |3x — 3| (используя часть a)i)) и y = \dfrac{3}{2} на той же паре осей:
3x — 3 \geq 0 при x \geq 1 и 3x — 3 < 0 при x < 1
Таким образом, мы можем составить два уравнения:
9 0911
(1) 3x — 3 = \dfrac{3}{2} для x \geq 1
(2) — (3x-3) = \dfrac{3}{2} для x < 1
Затем мы можем решить следующие задачи:
Решение (1): 3x = \dfrac{9}{2} \Rightarrow x = \dfrac{3}{2} для x \geq 1 (это верно, поскольку \dfrac{3}{2} \ экв 1)
Решение (2): 3x = \dfrac{3}{2} \Rightarrow x = \dfrac{1}{2} для x < 1 (это верно, поскольку \dfrac{1}{2} < 1 )
Судя по графику, оба решения кажутся правильными.