Функция y sin x ее свойства и график Математика
Функция y=sin x, ее свойства и график Математика 10 класс МБОУ СШ № 12 Учитель: Шудраков Николай Николаевич
Свойства функции y=sin x Свойство 1. Область определения D(f)=(-∞; + ∞) Найти: sin 35 sin 23 /3 sin -15 /4
Свойства функции y=sin x Свойство 2. Четность y=sin x — нечетная функция sin (-x)= — sin x Найти: sin (-24 ) sin (-17 /3)
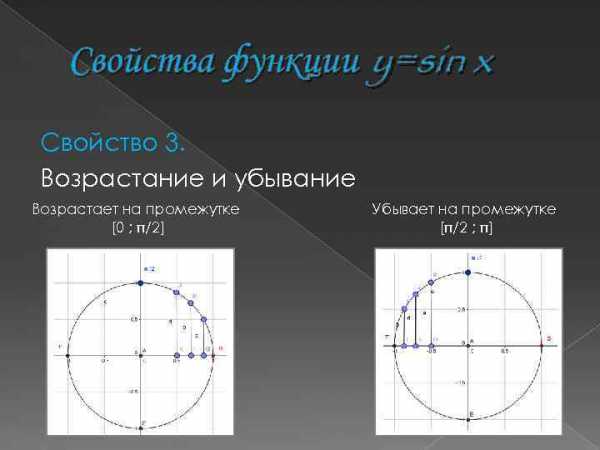Свойства функции y=sin x Свойство 3. Возрастание и убывание Возрастает на промежутке [0 ; /2] Убывает на промежутке [ /2 ; ]
Свойства функции y=sin x Свойство 4. Ограниченность Функция ограничена снизу и сверху -1 ≤ sin x ≤ 1
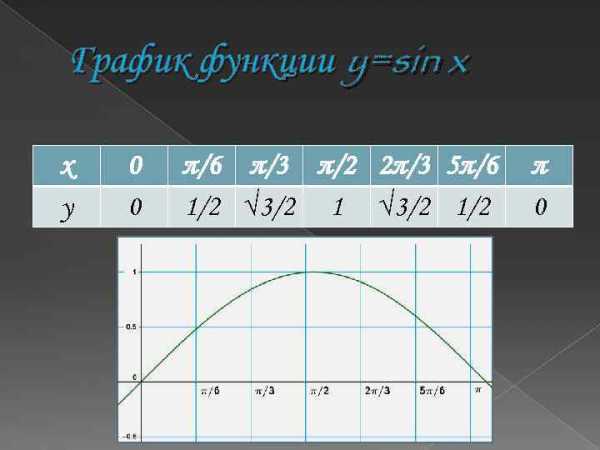График функции y=sin x x y 0 0 π/6 π/3 π/2 2π/3 5π/6 1/2 √ 3/2 1/2 π 0
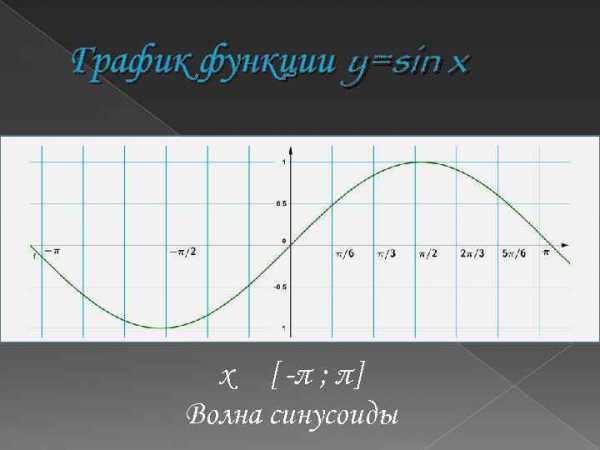График функции y=sin x x [ -π ; π] Волна синусоиды
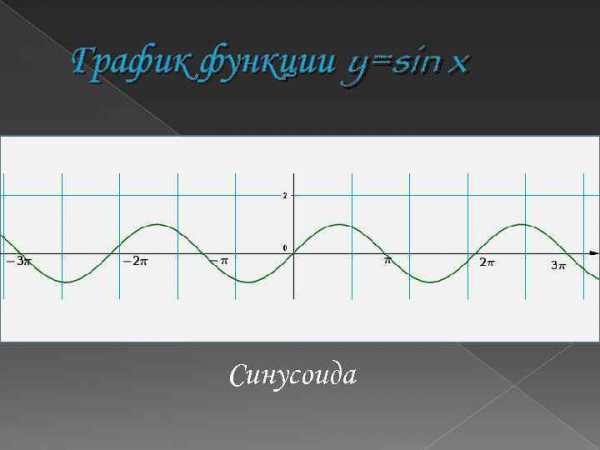График функции y=sin x Синусоида
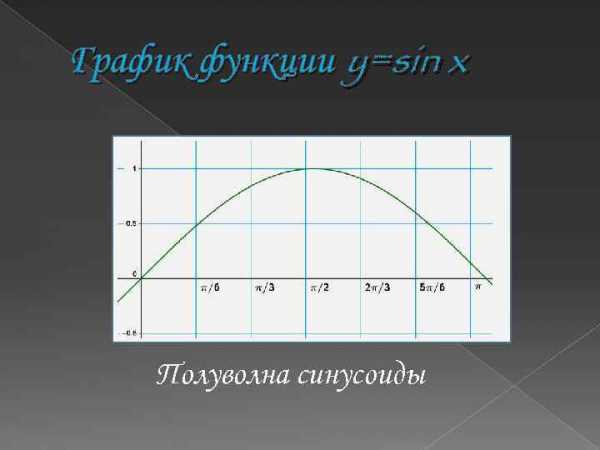График функции y=sin x Полуволна синусоиды
Свойства функции y=sin x Свойство 6. Функция y=sin x возрастает на любом отрезке вида [ — π/2 + 2πk ; π/2+2πk ] и убывает на любом отрезке вида [ π/2 + 2πk ; — π/2+2πk ]
Свойства функции y=sin x Свойство 7. Непрерывность Функция y=sin x непрерывна на всей области определения
Свойства функции y=sin x Свойство 8. Область значений функции Е(f)=[ -1 ; 1 ]
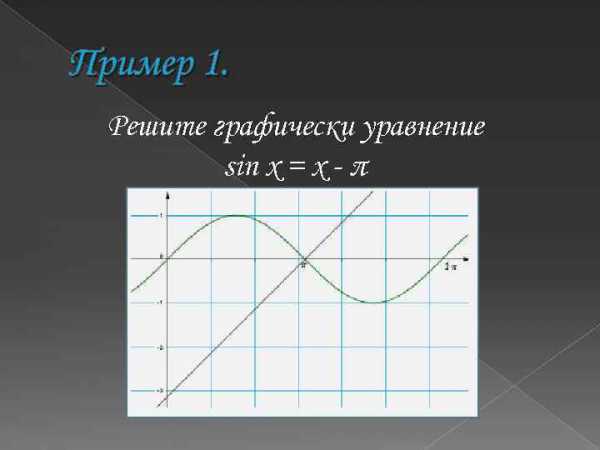Пример 1. Решите графически уравнение sin x = x — π
Пример 2. Постройте график функции y=sin (x — π /3)+2
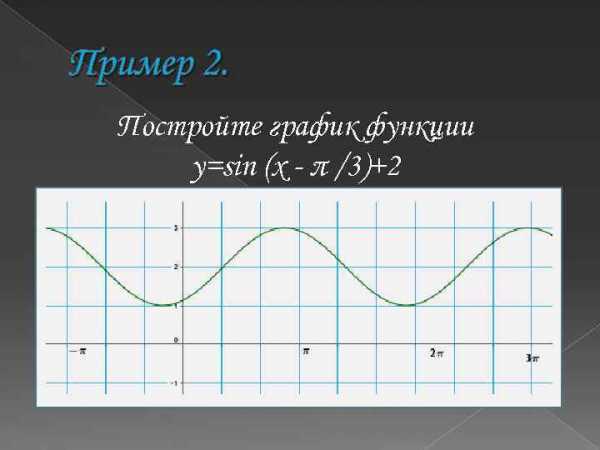Пример 2. Постройте график функции y=sin (x — π /3)+2
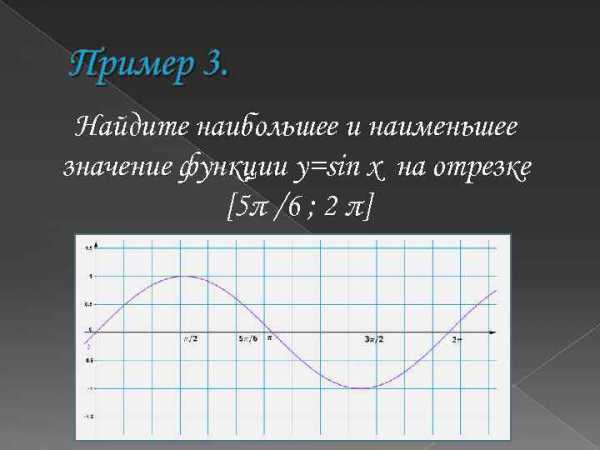Пример 3. Найдите наибольшее и наименьшее значение функции y=sin x на отрезке [5π /6 ; 2 π]
Домашнее задание 10. 7 а 10. 8 в 10. 11 а, б ______ 10. 9 б 10. 10 а
present5.com
«Функция y=sin x, ее свойства и график»
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Железо ржавеет, не находя себе применения,
стоячая вода гниет или на холоде замерзает,
а ум человека, не находя себе применения, чахнет.
Леонардо да Винчи
Используемые технологии: проблемного обучения, критического мышления, коммуникативного общения.
Цели:
- Развитие познавательного интереса к обучению.
- Изучение свойств функции у = sin x.
- Формирование практических навыков построения графика функции у = sin x на основе изученного теоретического материала.
Задачи:
1. Использовать имеющийся потенциал знаний о свойствах функции у = sin x в конкретных ситуациях.
2. Применять осознанное установление связей между аналитической и геометрической моделями функции у = sin x.
Развивать инициативу, определенную готовность и интерес к поиску решения; умение принимать решения, не останавливаться на достигнутом, отстаивать свою точку зрения.
Ход урока
1 этап. Актуализация опорных знаний, мотивация изучения нового материала
«Вход в урок».
На доске написаны 3 утверждения:
- Тригонометрическое уравнение sin t = a всегда имеет решения.
- График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
- График тригонометрической функции можно построить, используя одну главную полуволну.
Учащиеся обсуждают в парах: верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».
| Утверждение | До | После |
| 1 | ||
| 2 | ||
| 3 |
Учитель ставит цели и задачи урока.
2. Актуализация знаний (фронтально на модели тригонометрического круга).
Мы уже познакомились с функцией s = sin t.
1) Какие значения может принимать переменная t. Какова область определения этой функции?
2) В каком промежутке заключены значения выражения sin t. Найти наибольшее и наименьшее значения функции s = sin t.
3) Решите уравнение sin t = 0.
4) Что происходит с ординатой точки при ее движении по первой четверти? (ордината увеличивается). Что происходит с ординатой точки при ее движении по второй четверти? (ордината постепенно уменьшается). Как это связано с монотонностью функции? (функция s = sin t возрастает на отрезке и убывает на отрезке ).
5) Запишем функцию s = sin t в привычном для нас виде у = sin x (строить будем в привычной системе координат хОу) и составим таблицу значений этой функции.
2 этап. Восприятие, осмысление, первичное закрепление, непроизвольное запоминание
Изучение нового материала ( презентация, слайды 2- 5).
Построение графика функции у = sin x и запись свойств функции в тетради.
1) D(y) =
2) E (y) =
3) функция ограничена и сверху, и снизу
4) унаиб = 1, унаим = -1
5) непрерывная функция
6) нечетная функция
7) возрастает на ; убывает на
3 этап. Первичное обобщение, произвольное запоминание, применение знаний и способов деятельности в типичных ситуациях
4. Постройте график функции (самостоятельно с проверкой, слайды 8-11):
а) у = sin x + 2
б) у = sin x — 1
в) у = sin
г) у = sin
5. Решите графически уравнение sin x = (проверка слайд 12).
4 этап. Первичная систематизация знаний и
способов деятельности, их перенос и применение в
новых ситуациях
6. № 10.18 (б,в)
5 этап. Итоговый контроль, коррекция, оценка и самооценка
7. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрической функции у = sin x, и заполняем в таблице столбец «После».
8. Д/з: п.10, №№ 10.7(а), 10.8(б), 10.11(б), 10.16(а)
28.05.2012
Поделиться страницей:urok.1sept.ru
Напишите пожалуйста подробное решение производной sinx/x
Да легко! y ‘ =((sin x) ‘ *x-(x) ‘ *sin x)/x^2=(x*cosx-1*sinx)/x^2=(x*cosx-sinx)/x^2 Использованы формулы: производная частного: (u/v) ‘ =(u’ * v — v ‘ *u)/ v ^2 табличные производные: (sinx) ‘ =cosx (x) ‘ =1 Ну или вот так, после алгебраических преобразований, хотя они дела не меняют: y ‘ =(cosx)/х -(sinx)/x^2
Держи.. . sin(x)/x — это произведение двух функций, sin(x) и 1/x. Получаем: (sin(x))’ *(1/x) + sin(x)*(1/x)’= cos(x)/x-sin(x)(1/x^2)= (x*cos(x)-sin(x))/x^2
Уважаемый «спрашивател», функцию sin(x)/x можно представить в форме sin(x)*1/x и тогда мы имеем дело с произведением двух сложных функций. И «Да легко» здесь не проходит. Если мы имеем произведение двух сложных функций, мы используем формулу (uv)`=uv`+u`v. Согласно этой формулы ваш ответ -sin(x)/x^2 не верный (я не знаю где вы его взяли) . Верный ответ здесь будет : (cos(x)/x)-(sin(x)/x^2). Хотите-верьте, хотите-нет.
touch.otvet.mail.ru
План-конспект урока по алгебре (10 класс) по теме: Урок по теме «Функция у = sin x, её свойства и график
Алгебра и начала анализа (10 класс)
Урок по теме «Функция у = sin x, её свойства и график».
Певцова Ольга Евгеньевна, учитель математики.
Используемые технологии:
проблемного обучения, критического мышления, коммуникативного общения.
Цели:
Развитие познавательного интереса к обучению.
Изучение свойств функции у = sin x.
Формирование практических навыков построения графика функции у = sin x на основе изученного теоретического материала.
Задачи:
1. Использовать имеющийся потенциал знаний о свойствах функции у = sin x в конкретных ситуациях.
2. Применять осознанное установление связей между аналитической и геометрической моделями функции у = sin x.
Развивать инициативу, определенную готовность и интерес к поиску решения; умение принимать решения, не останавливаться на достигнутом, отстаивать свою точку зрения.
Воспитывать у учащихся познавательную активность, чувство ответственности, уважения друг к другу, взаимопонимания, взаимоподдержки, уверенности в себе; культуру общения.
Ход урока
1 этап. Актуализация опорных знаний, мотивация изучения нового материала
«Вход в урок».
На доске написаны 3 утверждения:
Тригонометрическое уравнение sin t = a всегда имеет решения.
График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
График тригонометрической функции можно построить, используя одну главную полуволну.
Учащиеся обсуждают в парах: верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».
Утверждение | До | После |
Учитель ставит цели и задачи урока.
Актуализация знаний (фронтально на модели тригонометрического круга).
Мы уже познакомились с функцией s = sin t.
1) Какие значения может принимать переменная t. Какова область определения
этой функции?
2) В каком промежутке заключены значения выражения sin t. Найти наибольшее и наименьшее значения функции s = sin t.
3) Решите уравнение sin t = 0.
4) Что происходит с ординатой точки при ее движении по первой четверти? (ордината увеличивается). Что происходит с ординатой точки при ее движении по второй четверти? (ордината постепенно уменьшается). Как это связано с монотонностью функции? (функция s = sin t возрастает на отрезке и убывает на отрезке ).
5) Запишем функцию s = sin t в привычном для нас виде у = sin x (строить будем в привычной системе координат хОу) и составим таблицу значений этой функции.
2 этап. Восприятие, осмысление, первичное закрепление, непроизвольное запоминание
Изучение нового материала (презентация, слайды 2- 5).
Построение графика функции у = sin x и запись свойств функции в тетради.
1) D(y) =
2) E (y) =
3) функция ограничена и сверху, и снизу
4) унаиб = 1, унаим = -1
5) непрерывная функция
6) нечетная функция
7) возрастает на ; убывает на
3 этап. Первичное обобщение, произвольное запоминание, применение знаний и способов деятельности в типичных ситуациях
4. Постройте график функции (самостоятельно с проверкой, слайды 6-9):
а) у = sin x + 2
б) у = sin x – 1
в) у = sin
г) у = sin
5. Решите графически уравнение sin x = (проверка слайд 10).
4 этап. Первичная систематизация знаний и способов деятельности, их перенос и применение в новых ситуациях
6. № 10.18 (б,в)
5 этап. Итоговый контроль, коррекция, оценка и самооценка
7. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрической функции у = sin x, и заполняем в таблице столбец «После».
8. Д/з: п.10, №№ 10.7(а), 10.8(б), 10.11(б), 10.16(а)
nsportal.ru