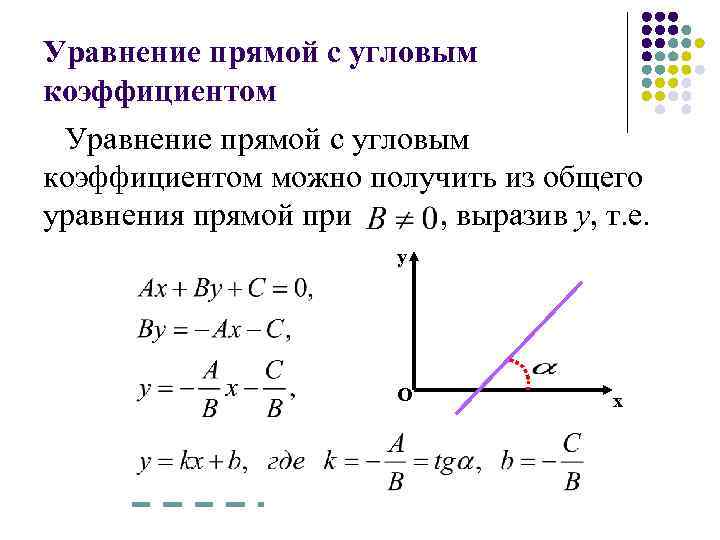
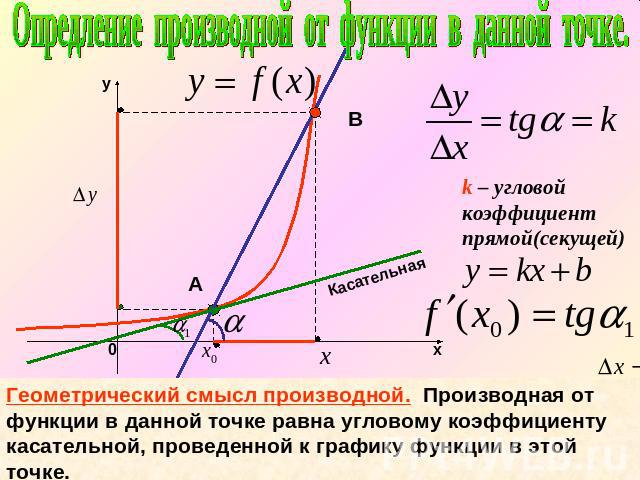
Угловой коэффициент прямой онлайн калькулятор: Калькулятор нахождения углового коэффициента прямой

alexxlab / / Разное

Угловой коэффициент прямой — формула вычисления, калькулятор, применение в геометрии и физике

Калькулятор углового коэффициента прямой может не только рассчитать коэффициент, но и найдет точки пересечения прямой с осями абсцисс и ординат (x и y), а также покажет решение и построит график прямой.

Содержание:
  1. калькулятор углового коэффициента прямой
  2. определение углового коэффициента прямой
  3. формула углового коэффициента прямой
  4. геометрический смысл углового коэффициента
    1. k>0
    2. k
    3. k=0
    4. k не определен (k=∞)
    5. угловой коэффициент параллельных прямых
    6. угловой коэффициент перпендикулярных прямых
  5. примеры расчета углового коэффициента прямой по заданным координатам точек

Определение углового коэффициента прямой

Угловой коэффициент прямой — это число, которое определяет наклон прямой относительно положительного направления оси OX. Численно он равен тангенсу угла (отсчитываемого против часовой стрелки) между положительным направлением оси OX и прямой.

Угловой коэффициент прямой обозначается буковой k.

Угловой коэффициент показывает, как быстро прямая меняет свое положение по оси OX при изменении координаты y и является ключевым понятием в геометрии и физике, используемым для описания многих физических явлений, например, движения тела в пространстве или распространение света.

В геометрии, угловой коэффициент прямой используется для определения угла наклона прямой относительно оси абсцисс и для вычисления ее точек пересечения с осями координат. Также угловой коэффициент прямой используется для записи уравнения прямой в общем виде. Знание углового коэффициента прямой является необходимым при решении многих задач геометрии, таких как построение перпендикуляров и параллельных линий, определение углов между прямыми и плоскостями, а также решение задач на поиск расстояний между прямыми и плоскостями.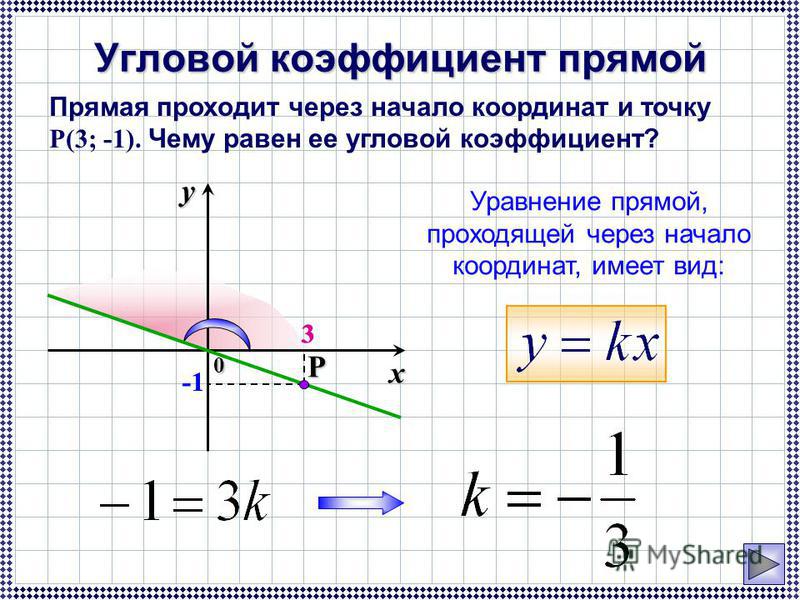

Формула углового коэффициента прямой

Формула вычисления углового коэффициента прямой определяется как отношение изменения координаты y к изменению координаты x между любыми двумя точками на прямой. Математически это можно записать следующим образом:

{k=\dfrac{y_b — y_a}{x_b — x_a} = \tg(\alpha)}

k — угловой коэффициент прямой,

xa, ya

— координаты точки A,

xb, yb — координаты точки B

α — угол между осью OX и прямой (против часовой стрелки).

Если прямая задана уравнением в общем виде y = kx + b, то угловой коэффициент прямой равен коэффициенту при x, то есть k.

Геометрический смысл углового коэффициента прямой

Рассмотрим возможные значения углового коэффициента и какой геометрический смысл он несет.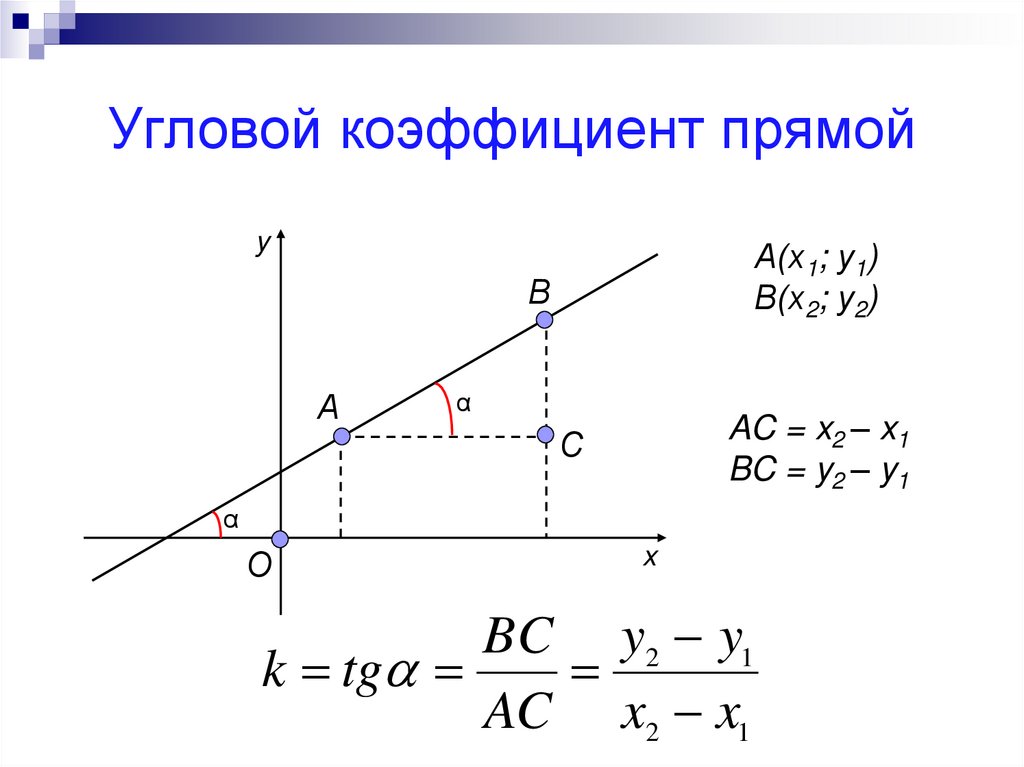

Угловой коэффициент прямой больше нуля

Если угловой коэффициент прямой больше нуля (k>0), то угол между осью OX и прямой является острым, а график прямой возрастающий. Обратное утверждение также справедливо — если график прямой возрастает, то ее угловой коэффициент больше нуля.

Угловой коэффициент прямой меньше нуля

Если угловой коэффициент прямой меньше нуля (k

Угловой коэффициент равен нулю

Если угловой коэффициент прямой равен нулю (k=0), то это значит, что прямая параллельна оси x.

Угловой коэффициент не определен (равен бесконечности)

Если угловой коэффициент прямой не определен (или можно сказать обращается в бесконечность) (k=∞), то это значит, что прямая параллельна оси y.

Угловой коэффициент параллельных прямых

Если прямые параллельны, то их угловые коэффициенты равны и наоборот — если у прямых равные угловые коэффициенты, то они параллельны друг другу.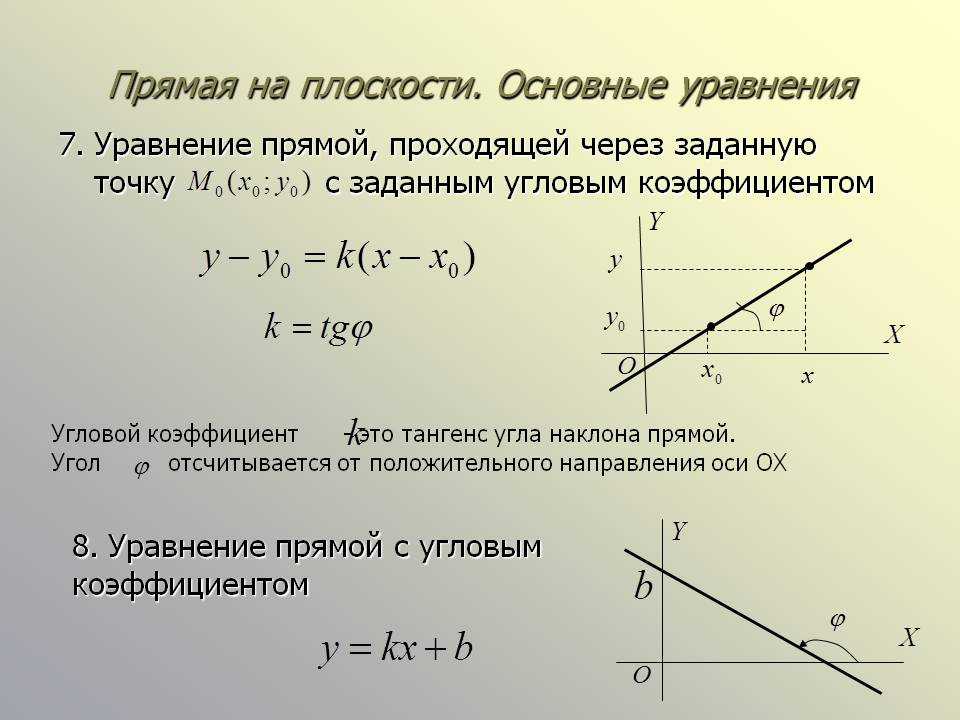

Угловой коэффициент перпендикулярных прямых

Если прямые перпендикулярны, то их угловые коэффициенты обратно пропорциональны и имеют противоположный знак.

Для примера рассмотрим две прямые, заданные угловыми коэффициентами:

y = k_{m} x + b_m

y = k_{n} x + b_n

Прямые будет перпендикулярны, если k_{m} = — \dfrac{1}{k_{n}}

Как рассчитать угловой коэффициент прямой по заданным координатам точек

Чтобы закрепить материал, рассмотрим решение задачи.

Задача 1

Найдите угловой коэффициент прямой, проходящей через точки A(5, -2) и B(-3, 1).

Решение

Воспользуемся формулой углового коэффициента прямой. Для начала найдем разницу между соответствующими координатами двух точек:

{\Delta x = x_b — x_a = -3 -5 -= -8}

{\Delta y = y_b — y_a = 1 — -(2) = 3}

Осталось применить формулу и поделить \Delta y на \Delta x:

k = \dfrac{\Delta y}{\Delta x} = \dfrac{3}{-8} = — \dfrac{3}{8} \approx -0.375

Это и есть угловой коэффициент прямой AB.

2

Наклон регрессии из калькулятора корреляции

Решатели Статистика

Инструкции: Этот расчет наклона регрессии будет вычислять коэффициент наклона из коэффициента корреляции и Стандартное отклонение. Пожалуйста, введите корреляцию (\(r\)) и типовые стандартные отклонения (\(s_x\) и \(s_y\)) для получения показаны пошаговые расчеты (\(s_x\) не может быть нулевым):

Корреляция выборки (\(r\))

Стандартное отклонение выборки X (\(s_x\))

Стандартное отклонение выборки Y (\(s_y\))

Обычно, когда мы думаем о расчете наклона линии регрессии, мы думаем о разновидности лонгана.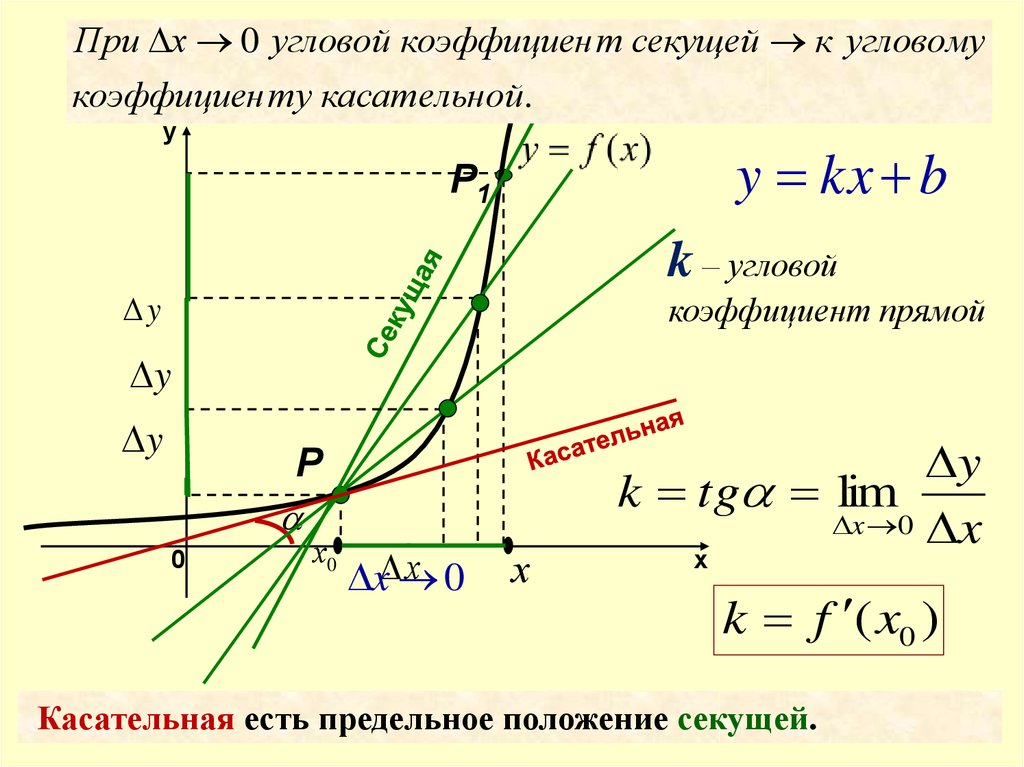 и громоздкая формула, обычно используемая для расчета. Но есть ярлык для расчета уклона.

Действительно, когда вы знаете коэффициент корреляции \(r\) и стандартные отклонения как \(X\) (\(s_x\)) и \(Y\) (\(s_y\)), есть очень простой способ найти наклон, который делается с использованием следующей формулы наклона из корреляции:

\[м = \displaystyle r \frac{s_y}{s_x}\]

где \(m\) — наклон линии регрессии \(y = mx + n\).

Какова связь между наклоном и корреляцией?

Интересно, что из приведенной выше формулы для наклона можно сделать прямой вывод: коэффициент корреляции и коэффициент наклона имеет тот же знак. То есть при отрицательной корреляции наклон также будет отрицательным, а если корреляция положительная, то и наклон будет положительным.

Это можно непосредственно увидеть по формуле, так как \(m = \displaystyle r \frac{s_y}{s_x}\), и когда известно, что оба стандарта отклонения \(s_x\) и \(s_y\) неотрицательны, поэтому \( \frac{s_y}{s_x} \ge 0\), что указывает на то, что \(m\) и \(r\) имеют в тот же знак.

Калькулятор наклона линии регрессии

Обратите внимание, что этот калькулятор вычисляет коэффициент наклона в предположении, что корреляция и стандартные отклонения известны. Если это не так, вам нужно использовать обычный калькулятор линии регрессии, который использует выборочные данные для X и Y.

Решатель статистики Коэффициент наклона от корреляции Калькулятор статистики

Корреляция

Корреляция

 Линейная корреляция и регрессия

Версия импорта данных

Для выборки N двумерных значений X и Y эта страница вычислит: T

  • r = коэффициент корреляции Пирсона произведение-момент; T
  • r 2 = коэффициент детерминации; T
  • наклон линии регрессии; Т
  • пересечение Y линии регрессии;
    T
  • стандартная ошибка оценки; T
  • значение t, связанное с вычисленным значением r, вместе с соответствующими односторонними и двусторонними вероятностями; T
  • остаток для каждого значения Y, рассчитанный как
    остаток = Y(отрезок+[наклон(X)]) T
  • нижняя и верхняя границы доверительных интервалов 0,95 и 0,99 для коэффициента корреляции (rho), который существует в двумерной совокупности, из которой взята выборка нарисован; и T
  • нижний и верхний пределы доверительных интервалов 0,95 и 0,99 для наклона регрессии.
Логические и вычислительные детали корреляции и регрессии
описаны в Главе 3 Концепций и приложений.
  • Импорт данных с помощью копирования и вставки: T
    При импорте данных из электронной таблицы парные значения X и Y должны быть представлены в виде двух соседних столбцов. В приложении для работы с электронными таблицами выберите и скопируйте два столбца данных. Затем вернитесь на эту страницу, щелкните курсором в поле ввода данных и выполните операцию «Вставить». T
  • Прямой ввод в поле данных: T
    Щелкните курсором в пустом поле ввода данных, введите первое значение X; затем нажмите пробел один (и только один) раз; затем введите значение Y; затем нажмите клавишу возврата каретки. Сделайте то же самое для последующих парных значений X и Y, за исключением того, что после последней записи , а не , должен следовать возврат каретки.
    T
  • Проверка данных: T
    Убедитесь, что последней строкой в ​​поле ввода данных является , а не , за которым следует возврат каретки. (Дополнительный возврат каретки в конце списка будет интерпретироваться как дополнительная запись данных, значение которой равно нулю. Импорт данных с помощью процедуры копирования и вставки почти всегда приводит к дополнительному возврату каретки в конце столбца.) После двумерный список был вставлен в поле ввода данных, щелкните курсором справа от последней записи в списке, затем нажмите клавишу со стрелкой вниз. Если присутствует дополнительная строка, курсор переместится вниз. Дополнительные строки можно удалить, нажимая клавишу со стрелкой вниз до тех пор, пока курсор не перестанет двигаться, а затем нажимая клавишу «Backspace» (на платформе Mac — «удалить»), пока курсор не станет сразу справа от последней записи. T
  • После
    проверки ввода данных нажмите кнопку «Рассчитать».
Ввод данных
Отчет о данных
Пожалуйста, не забудьте выполнить
процедуру проверки данных
.		 Столбец 1: X
Столбец 2: Y
Столбец 3: Остаток

   Сбросить            Рассчитать   

Сводка данных T

iX = iX 2 i =
iY = iY 2 i =
iXY =
х Д
Н 
Среднее
Разница 
Станд. Дев.
Стандартная ошибка.
р р 2 Склон Д
Перехват		 Станд. Ошиб. из
Оценка
  P   однохвостый
двусторонний

0,95 и 0,99 Доверительные интервалы для ро Q

Нижний предел Верхний предел
0,95
0,99

0,95 и 0,99 Доверительные интервалы для наклона регрессии Q

Нижний предел Верхний предел
0,95
0,99


Дом Нажмите на эту ссылку только , если вы пришли сюда не через главную страницу VassarStats.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

Карта сайта