Табличное умножение и деление — Мегаобучалка
Тема «Умножение и деление чисел в пределах 100» является одной из основных тем начального курса математики. Изучается она по программе 1-3 во 2-м классе, по программе 1-4 — во 2-м и 3-м классе. В изучении этой темы выделяются такие виды умножения и деления:
1. Табличное умножение и деление.
2. Внетабличное умножение и деление.
3. Деление с остатком.
К табличному умножению и делению относятся случаи умножения однозначных натуральных чисел на однозначное число и соответствующие случаи деления.
Примеры: 5 · 3 = 15; 15 : 3 = 5
7 · 4 = 28; 28 : 7 = 4 и т.п.
При изучении этого вида умножения и деления необходимо:
1) познакомить детей с новыми для них действиями умножения и деления;
2) изучить таблицу умножения и деления. Таким образом, табличное умножение и деление, в свою очередь, разбивается на два вопроса:
1) знакомство с действиями умножения и деления;
2) изучение таблицы умножения и деления.
а) Знакомство с действиями умножения и деления
Отметим, что познакомить детей с действиями умножения и деления, это значит:
— раскрыть смысл каждогоиз этих действий;
— ввести соответствующую терминологию;
— рассмотреть некоторые свойства действий, установить зависимости между ними.
Прежде всего, следует отметить, что работа по раскрытию смысла этих действий начинается еще в 1 классе. Здесь:
— ведется счет группами;
— вычисляются суммы нескольких одинаковых слагаемых;
— решаются простые задачи: на нахождение суммы нескольких одинаковых слагаемых, на деление по содержанию, и деление на равные части.
Задачи на деление решаются там только практически (устно). Во 2-м классе эта работа получает свое естественное продолжение. Сначала происходит знакомство с действием умножения. Смысл этого действия раскрывается через решение простых задач на нахождение суммы нескольких одинаковых слагаемых.
Задача. В одном пучке 3 морковки.
Сколько морковок в 4-х таких пучках?
Выполнив соответствующую демонстрацию, учитель с детьми выясняет, что для ответа на вопрос задачи нужно найти сумму 4-х слагаемы каждое из которых равно 3.
3 + 3 + 3 + 3 = 12 (морк.)
Обращается внимание на то, что все слагаемые полученной суммы одинаковые. Поэтому эту сумму можно прочитать по-другому: по 3 взять четыре раза и записать так
3 · 4=12. Т.е. сложение одинаковых слагаемых называют умножением. Точка обозначает знак действия умножения.
Дается образец чтения этой записи 3 · 4=12.
1) по 3 взять четыре раза.
2) 3 умножить на 4.
Обращается внимание на смысл каждого числа в этой записи: 3 — этослагаемое, 4 — показывает, сколько одинаковых слагаемых.
Смысл действия деления раскрывается в ходе решения простых задач двух видов:
— деление по содержанию;
— деление на равные части.
Задача. 6 морковок раздали кроликам по две каждому. Сколько кроликов получили морковки?
Для решения этой задачи необходимо выполнение практических действий с предметами, как учителем, так и учащимися.
Разговор может быть таким.
Учитель. У меня 6 морковок, а вы положите столько же треугольников. Будем раздавать их кроликам по 2, я у доски, а вы на партах. (Раздвигаются по 2 морковки и выставляются изображения кроликов). Сколько кроликов получили морковки?
Дети. 3.
Учитель. Давайте запишем решение этой задачи. Мы морковки раздавали, делили, и решение будем записывать новым действием — делением. Это записывается так:
6 : 2 = 3 (к.) Ответ: 3 кролика.
» : » — знак деления.
Аналогично рассматриваются задачи на деление на равные части. При этом также необходима демонстрация с использованием предметов наглядности.
Пример. 6 морковок раздали 3 кроликам поровну. Сколько морковок дали каждому кролику?
Здесь нужно показать и принцип деления на равные части. Выставив изображение 3-х кроликов, выясняем, сколько морковок надо взять, чтобы дать им по одной морковке? — 3. Берем и раздаем.
Операцию повторяем до тех пор, пока не кончатся все морковки. Эта задача решается также действием деления. 6 : 3 = 2 (морк.) Ответ: 2 морковки.
После знакомства с каждым из действий вводятся названия компонентов и результата каждого из этих действий (методика уже известна).
Изучается переместительное свойство умножения (методика изучения свойств действий нами рассмотрена отдельно).
Рассматривается зависимость между компонентами и результатом вначале для действия умножения, затем — деления (методику рассмотрения зависимости смотреть в теме №2).
При рассмотрении зависимости между компонентами и результатом действия умножения мы подводим детей к выводу:если произведение разделить на первый множитель, получим второй множитель и т.д.И как следствие этого, показываем, что для каждого примера на умножение, можно составить два примера на деление.
Пример. 5 • 3 = 15;
15 : 5 = 3;
15 : 3 = 5.
Здесь же рассматриваются и некоторые частные случаи умножения и деления с числами 1 и 10:
а) с числом I.
Сначала берется случай умножения 1 на число, большее 1.
1 • З = 1 + 1 + 1 = З;
1• 5 = 1 + 1 + 1 + 1 + 1 = 5.
После решения ряда примеров на основе смысла действия умножения подводим детей к выводу: 1 • = .
Случай • 1 постулируется. Детям сообщается правило и приводятся примеры.
. Деление на 1 вводится на основе зависимости между компонентами и результатом действия умножения.
Из решения соответствующих примеров 1• 5 = 5; => 5 : 1 = 5 подводим детей к выводу : 1 = .
Умножение 10 и деление на 10 рассматривается с использованием знания нумерации и связи между действиями умножения и деления:
10• 3 => 1д.• 3 = 3д. => 10• 3 = 30.
3•10 =10•3.
Случаи вида 30 : 10 рассматриваются на основе зависимости между компонентами и результатом действия деления.
Все перечисленные нами вопросы помогут нам при рассмотрении следующего вопроса, т.е. при изучении таблицы умножения.
Рассматривая их, мы вели подготовку детей к изучению таблицы умножения.
Урок математики во 2 классе по теме: «Табличное умножение и деление. Умножение и деление числа 3 и на 3» | План-конспект урока по математике (2 класс):
Тема урока: «Таблица умножения и деления. Умножение и деление числа 3 и на 3».
Класс: 2
Учебник: Математика, Моро М.И., Волкова С.И., Степанова С.В., Бантова М.А., Бельтюкова Г.В., Учебник, 2 класс, 2 часть.
Тип урока: урок изучения нового материала.
Цель: усвоение табличных случаев умножения на 3 и соответствующих случаев деления.
Задачи:
- образовательные:
повторить, уточнить и систематизировать знания таблицы умножения и деления с числом 2;
повторить компоненты действий умножения и деления;
активизировать познавательную деятельность учащихся при закреплении табличного умножения и деления;
систематизировать знания и умения находить неизвестный компоненты умножения и деления;
составить таблицу умножения числа 3 и на 3 и соответствующие случаи деления.
продолжить работу над формированием навыков счета;
- воспитательные:
воспитывать интерес к математике;
воспитывать умение работать в коллективе, умение слышать и слушать каждого;
- развивающие:
развивать внимание, мышление учащихся, математическую речь учащихся;
расширять словарный запас учащихся.
Оборудование: учебники, проектор, презентация, тренажёр «Таблица умножения в мультиках», солнце, лучи солнца.
Ход урока:
1.Организационный момент.
-Прозвенел уже звонок,
Сядьте тихо и неслышно,
И скорей начнём урок.
Будем мы писать, трудиться,
Ведь заданья нелегки.
Нам, друзья, нельзя лениться,
Так как мы ученики.
-Садитесь.
-Ребята, сегодня на уроке я вам желаю удачи, чтобы вы хорошо потрудились, хорошо усвоили новый материал.
2.Актуализация знаний.
— Ребята, я предлагаю вам игру «Крестики и нолики». Если вы согласны с прочитанным утверждением, то ставите КРЕСТИК, если же вы не согласны, то ставите НОЛИК.
(У каждого ребёнка на парте лист с таблицей)
- Если 18 разделить на 2, получится 9. (х)
- Произведение чисел 2 и 3 равно 8. (0)
- 14 разделить на 7 получится 3 (0)
- Число 16 больше 8 в 8 раз (0)
- Если число 6 увеличить в 2 раз, то получится 12. (х)
- Чтобы узнать во сколько раз одно число больше или меньше другого надо из большего вычесть меньшее (0)
- Число, в котором 8 сотен и 4 единицы — это 84. (х)
- Если число 10 уменьшить в 5 раз, получиться 5. (0)
- Площадь измеряется в квадратных см. (х)
-Теперь передаем листочки вперед на первую парту. Я их проверю после урока и скажу вам оценки завтра.
-Немного с вами поиграем. Сыграем игру «День-Ночь».
(Когда учитель произносит слово «Ночь», учащиеся кладут голову на парту и закрывают глаза. В это время учитель читает (записывает) выражение для устного счета на деление или умножение на 2. Следует небольшая пауза. Затем учитель говорит: «День».
Дети открывают глаза, садятся прямо, и те, кто сосчитал, поднимают руку и говорят ответ.)
-Что вы должны делать: когда я произношу слово «Ночь», вы кладете голову на парту и закрываете глаза. Когда я говорю: «День», вы открываете глаза, садитесь прямо, и те, кто сосчитал, поднимаете руку и говорите ответ.
3. Постановка учебной задачи.
− Посмотрите на доску. Найдите значения следующих выражений (Учитель открывает на доске задание)
3 х 1=
3 х 2=
3 х 7=
21+3=
− Прочитайте выражения. Что в них общего? (Во всех выражениях один их компонентов равен 3)
− Какое выражение лишнее? (Последнее, так как во всех выражениях действие умножение, а в этом выражении – действие сложения.)
− Подумайте, как изменить это выражение, чтобы его можно было отнести к этой группе? (Выслушиваются разные гипотезы детей. 3 х 7 + 3)
− Представьте 24 в виде произведения 2 множителей 3 х 8=24. (Учитель под выражением 21 + 3 подписывает выражение 3 х 7 + 3=)
− Сколько всего раз взяли по 3?
− Как это записать? (3+3+3+3+3+3+3+3)
− А как по-другому можно записать? (3 х 8) (Учитель под выражением 21+3 записывает выражение 3 х 8)
− Найдите значения данных выражений в порядке возрастания.
− Что помогло вам быстро выполнить это задание? (Мы эти случаи умножения уже выучили ранее)
− Почему последнее выражение вызвало затруднение? (Не изучали таблицу умножения на 3)
− Так какая будет тема нашего урока? (Таблица умножения и деления на 3)
− Какие цели мы поставим? Изучить таблицу умножения и деления на 3. Использовать ее при решении примеров и задач. Развивать мышление, память, внимание, речь.
4.Открытие нового знания.
−С какого случая вы начнете заполнять таблицу умножения на 3? (2 умножить на 3)
−Какую еще таблицу нужно составить? (умножение числа 3)
− Каким свойством умножения будем пользоваться? (переместительным).
− Какие еще таблицы можем составить? (деления на 3, деления с ответом 3)
− Какое правило при этом надо знать? (если произведение разделить на один из множителей, то получится другой)
− Составьте таблицу умножения на 3 и таблицу деления на 3.
− Проверьте правильность выполнения задания.
− А теперь ребята давайте поищем закономерности, ключики к лучшему запоминанию таблицы.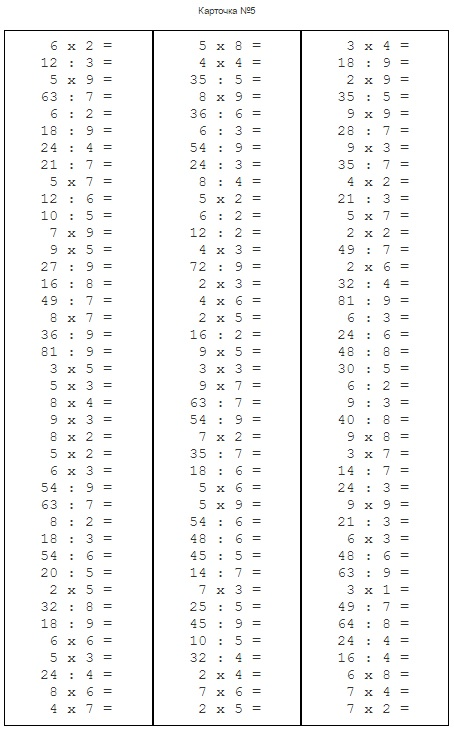
− Посмотрите внимательно и скажите, что интересного вы увидели?
Закономерности:
- первый множитель увеличивается на 1,
- второй множитель неизменный,
- произведение увеличивается на 3 (сверху вниз, а снизу вверх уменьшается на 3),
- все произведения двузначные числа.
5.Физкультминутка.
-А теперь немножко отдохнем. Выйдите из-за своих парт.
Раз, два – выше голова.
Три, четыре – руки шире.
Пять, шесть – тихо сесть.
Раз – подняться. Подтянуться.
Два – согнуться, разогнуться.
Три – в ладоши три хлопка,
Головою три кивка.
На четыре – руки шире,
Пять – руками помахать,
Шесть – за стол тихонько сесть.
6.Перичное закрепление.
Работа по учебнику.
-Открываем учебник на стр. 90 № 1. Какое перед нами задание? (Поставить знаки =).
-Выполняем это задание самостоятельно.
-Выполнили. Молодцы! Теперь решим задачу на этой же странице.
-Прочитайте задачу. Что известно в задаче? (Есть 3 аквариума, каждый аквариум поместили по 4 рыбки).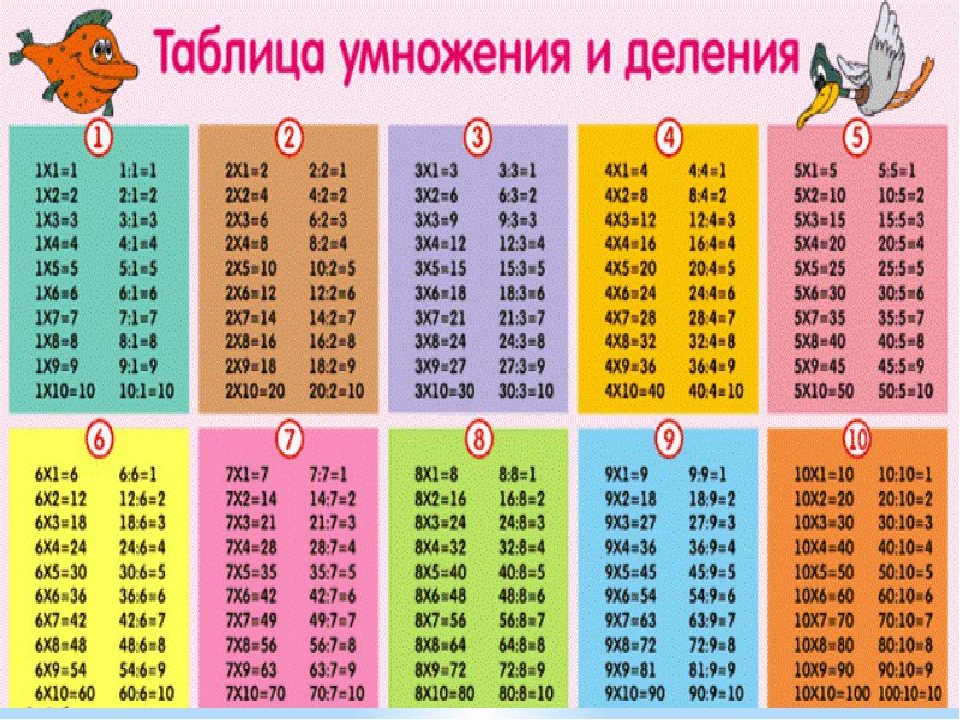
-Что неизвестно в задаче? (Сколько всего рыбок в этих аквариумах).
-Можем мы сразу ответить на главный вопрос задачи? (Да).
-Как мы узнаем? (Надо 4 умножить на 3).
-Сколько всего будет рыбок? (Всего будет 12 рыбок).
-Ответили на главный вопрос задачи? (Да).
-Можем записать ответ? (Да).
-Молодцы! Записываем решение задачи.
6. Оперирование знаниями и способами деятельности.
-У нас осталось с вами последнее задание.
-Переходим к самому интересному: игре-тренажеру «Таблица умножения в мультиках». Ваша задача — открыть полностью изображение из мультфильма, допустив при этом минимум ошибок. Правильные ответы отмечаются зеленым цветом, а их количество отображается на эквалайзере справа. Неправильные ответы отмечаются красным цветом, и их количество отображается на эквалайзере слева. Если вы все решите правильно, то перед вами откроется картинка из мультика.
-Кому непонятно, что надо делать, поднимите руки.
-Приступаем.
-Молодцы! А вот и какая картинка вышла у нас.
Это кадр из какого мультика? (Ответ детей)
7. Подведение итогов и формулирование выводов.
-Ребята, какая была тема сегодняшнего урока? (Таблицу умножения и деления с числом 3).
-Какую цель мы перед собой сегодня ставили? (Составить таблицу умножения числа3 и на 3 и соответствующие случаи деления).
-Достигли мы этой цели? (Да).
-Как вы понимаете значимость изучения таблицы умножения и деления? (Ответы детей).
-Без знания таблицы умножения и деления вы не сможете изучать все последующие темы.
-Вы сегодня поработали хорошо. Таблицу умножения и деления знаете хорошо.
-На доске у нас есть солнышко. На ваших партах лежат лучики голубого и желтого цветов. Лучики нужно прикрепить к солнышку: желтого цвета – мне очень понравилось занятие, получили новую информацию; голубого цвета – занятие не интересное, ничего нового не узнал.
-Посмотрите, какое красивое солнышко у нас получилось.
8. Домашнее задание. (3 мин.)
-Открываем дневники и записываем домашнее задание: выучить таблицу умножения и деления с числом 3.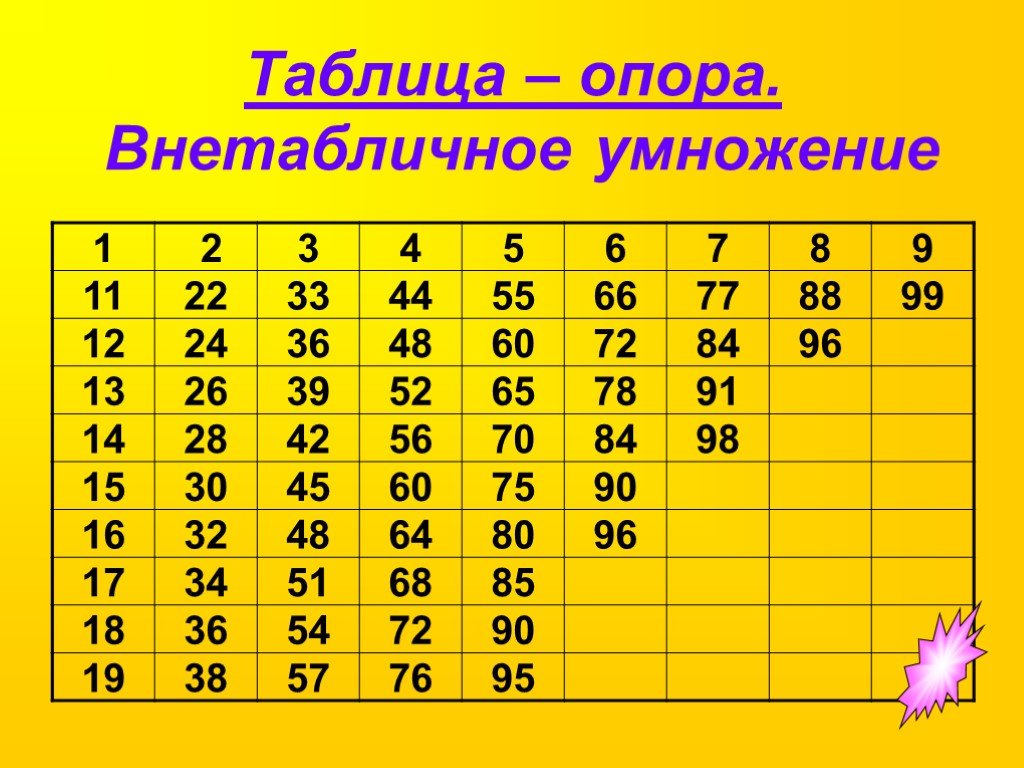
Завтра на уроке будет проверочная работа по данной теме.
-Урок окончен. Можете готовиться к следующему уроку.
(Оценки за выполнение первого задания сообщаются на следующий день).
бесплатных печатных листов по умножению и делению. Таблица 0
Бесплатные печатные листы по умножению и делению: таблицы 0-12
Бесплатные печатные рабочие листы по умножению и делению — Сборник простых в печати рабочих листов по умножению и делению. Начните с простых в печати таблиц умножения. Он включает в себя все числа, разделенные от 1 до 12, смешанные листы для просмотра и рабочий лист со всеми таблицами умножения на одном листе. Есть доска умножения и лист ответов для изучения. После этого вы найдете задачи на двузначное и трехзначное умножение с перегруппировкой, а также на смешанные числа и деление на две части. Представлять и решать задачи на умножение и деление. CCSS.Math.Content.3.OA.A.1 Интерпретировать произведения целых чисел, например, интерпретировать 5 × 7 как общее количество объектов в 5 группах по 7 объектов в каждой. CCSS.Math.Content.3.OA.A. 3 Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, используя рисунки и уравнения с символом неизвестного числа для представления задачи.1 CCSS. Math.Content.3.OA.A.4 Определение неизвестного целого числа в умножении или уравнении деления, связывающем три целых числа. 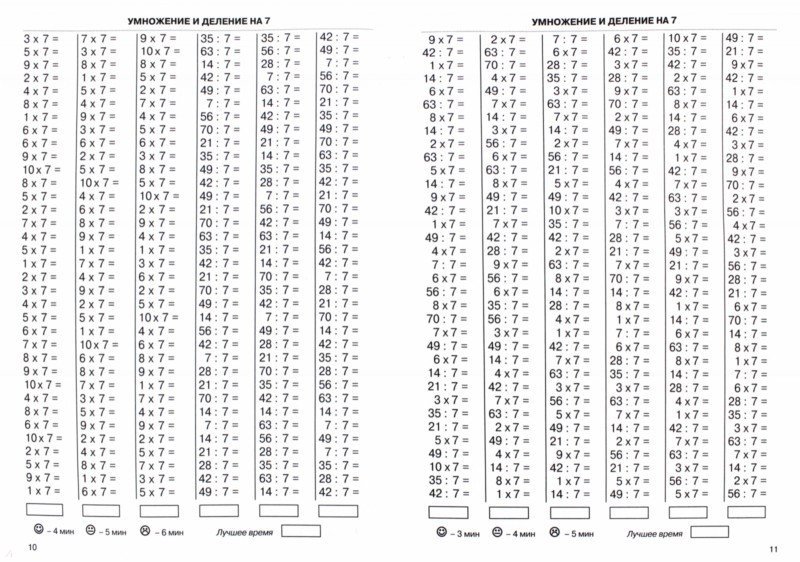 Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ? Понимать свойства умножения и связь между умножением и делением. CCSS.Math.Content.3.OA.B.5 Умножьте и разделите в пределах 100. CCSS. CCSS.Math.Content.3.NBT.A.3 Умножение однозначных целых чисел на кратные 10 в диапазоне от 10 до 90 (например, 9 × 80, 5 × 60) с использованием стратегий, основанных на разрядное значение и свойства операций. Познакомьтесь с множителями и множителями. CCSS.Math.Content.4.OA.B.4 Найти все пары множителей для целого числа в диапазоне от 1 до 100. Признать, что целое число является кратным каждого из его делителей. Определить, является ли заданное целое число в диапазоне от 1 до 100 кратным заданному однозначному числу. Определите, является ли заданное целое число в диапазоне от 1 до 100 простым или составным. CCSS.Math.Content.4.NBT.B.5 Умножение целого числа, состоящего из максимум четырех цифр, на однозначное целое число и умножение двух двузначных чисел с использованием стратегий, основанных на разрядности и свойства операций. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей. Выполнять операции с целыми многозначными числами и с десятичными дробями до сотых. CCSS.Math.Content.5.NBT.B.5 Свободно умножайте многозначные целые числа, используя стандартный алгоритм. [lwptoc] 1-12 Учебные таблицы умноженияСкачать/распечатать вопросы Индивидуальные упражнения с таблицами умножения (1-12)Тройки Семерки Восьмерки Одиннадцать Двенадцать Упражнения на умножение двузначных и однозначных чисел (плюс листы с ответами)Частичное умножение коробки продуктаУпражнение на умножение частичной коробки продукта (двузначное число X двузначное)Упражнение на умножение частичной коробки продукта (трехзначное число X двузначное)Упражнения на умножение двузначных чисел X двузначных десятков (плюс листы ответов)Упражнения на умножение двузначного числа на двузначное число (плюс листы ответов)Упражнения на умножение трехзначных и однозначных чисел (плюс листы ответов)Упражнения на умножение трехзначного числа X двузначного числа 10 (плюс листы ответов)Упражнения на умножение трехзначных и двузначных чисел (плюс листы ответов)Упражнения на умножение трехзначного числа на трехзначное число (плюс листы ответов)Таблицы отдельных дивизионов (1-12)Небольшая дивизия с остаткамиДлинное деление без остаткаДлинное деление с остатками
Инструкции по печати
Бесплатные печатные рабочие листы по умножению и делению — Коллекция простых в печати рабочих листов по умножению и делению. Начните с простых в печати таблиц умножения. Он включает в себя все числа, разделенные от 1 до 12, смешанные листы для просмотра и рабочий лист со всеми таблицами умножения на одном листе. Есть доска умножения и лист ответов для изучения. После этого вы найдете задачи на двузначное и трехзначное умножение с перегруппировкой, а также на смешанные числа и деление на две части. Представлять и решать задачи на умножение и деление. CCSS.Math.Content.3.OA.A.1 Интерпретировать произведения целых чисел, например, интерпретировать 5 × 7 как общее количество объектов в 5 группах по 7 объектов в каждой. Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7. Понимать свойства умножения и связь между умножением и делением. CCSS.Math.Content.3.OA.B.5 Применение свойств операций как стратегий умножения и деления.2 Примеры: если известно 6 × 4 = 24, то 4 × 6 = 24 также известен. (Перестановочное свойство умножения.) 3 × 5 × 2 можно найти, если 3 × 5 = 15, тогда 15 × 2 = 30, или 5 × 2 = 10, тогда 3 × 10 = 30. (Ассоциативное свойство умножения. ) Зная, что 8 × 5 = 40 и 8 × 2 = 16, можно найти 8 × 7 как 8 × (5 + 2) = (8 × 5) + (8 × 2) = 40 + 16 = 56. (Дистрибутивное свойство.) Умножьте и разделите в пределах 100. CCSS.Math.Content.3.OA.C.7 Свободно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. CCSS.Math.Content.3.NBT.A.3 Умножение однозначных целых чисел на кратные 10 в диапазоне от 10 до 90 (например, 9 × 80, 5 × 60) с использованием стратегий, основанных на разрядное значение и свойства операций. Познакомьтесь с множителями и множителями. CCSS.Math.Content.4.OA.B.4 Найти все пары множителей для целого числа в диапазоне от 1 до 100. Признать, что целое число является кратным каждого из его делителей. Определить, является ли заданное целое число в диапазоне от 1 до 100 кратным заданному однозначному числу. Определите, является ли заданное целое число в диапазоне от 1 до 100 простым или составным. CCSS.Math.Content.4.NBT.B.5 Умножение целого числа, состоящего из максимум четырех цифр, на однозначное целое число и умножение двух двузначных чисел с использованием стратегий, основанных на разрядности и свойства операций. Выполнять операции с целыми многозначными числами и с десятичными дробями до сотых. CCSS.Math.Content.5.NBT.B.5 Свободно умножайте многозначные целые числа, используя стандартный алгоритм. |
Страницы 
Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7. 
Math.Content.3.OA.C.7 Свободно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел. 
Или нажмите «Файл», затем «Печать». Страницы 
К концу 3 класса знать наизусть все произведения двух однозначных чисел. 
Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей. 
Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей. Умножение и деление: Введение в умножение
Урок 1: Введение в умножение
Что такое умножение?
Когда вы умножаете , вы фактически добавляете определенное число более одного раза. Например, если вы съели 4 конфеты, затем съели еще 4, затем еще 4, вы можете сказать, что вы умножили на количество съеденных конфет.
В реальной жизни умножение происходит постоянно.
Например, рассмотрим ситуацию ниже.
Представьте, что вы покупаете 6 банок газировки. У вас есть 1 набор из 9 штук0014 6 банок.
В терминах умножения мы бы сказали, что у вас есть 1 x 6 банок. Вы можете прочитать это как один раз шесть .
Что делать, если вы покупаете 2 упаковки по 6 штук?
Теперь у вас есть 2 комплекта по 6 банок или 2 x 6 банок. Это 2 умножить на столько банок, сколько было раньше!
Это может продолжаться вечно. Как насчет 3 x 6 банок или в 3 раза больше банок?
Теперь у вас есть 8 x 6 банок. это 8 раз столько банок, сколько было в начале.
Важно знать, что числа в выражении умножения можно записывать в любом порядке.
Таким образом, 8 x 6 также можно записать как 6 x 8.
Другими словами, 6 x 8 = 8 x 6.
Итак, если вы купили 6 наборов по 8 банок в каждом..
Итак, если вы купили 6 комплектов по 8 банок в каждом… это будет тот же , что и 8 комплектов по 6 банок в каждом. У вас будет точно такое же количество банок.
Запись выражения умножения
Как вы только что видели, выражение умножения записывается так:
2 x 6
два раза Символ умножения (x) также можно назвать символом умножения
на . Помните, вы всегда ставите между числами, которые хотите умножить.Многие жизненные ситуации можно выразить с помощью умножения. Например, представьте, что вы хотите испечь три торта. В рецепте сказано, что на каждую лепешку понадобится два яйца. Другими словами, вам нужно 3 х 2 яйца.
Попробуйте!
Запишите следующие ситуации в виде выражений умножения. Пока не пытайтесь их решить.
У вас есть шесть пар по два носков в каждой.
Вам необходимо принимать по две таблетки по четыре раза в день.
Каждый пакет содержит девять пончиков. Вы покупаете три пакета .
Решение задач на умножение
Счет и сложение можно использовать для решения небольших простых задач на умножение. Например, на последней странице мы пытались вычислить, сколько яиц нам понадобится, чтобы испечь три торта. Для каждого торта требовалось два яйца, поэтому мы записали задачу так:
3 x 2
Как вы уже знаете, это выражение означает три раза по два , или 3 лепешки с 2 яйцами в каждой. Это простая проблема. Чтобы решить эту проблему, вы можете либо подсчитать яиц, либо добавить их : 2 + 2 + 2. В любом случае ответ равен 6. Мы знаем, что 3 x 2 = 6.
Хотя это работает для небольших задач, подсчет больших чисел может занять много времени, к тому же это довольно скучно.
По этой причине большинство людей запоминают общих задач на умножение, чтобы быстро их решать. Если это звучит сложно, не волнуйтесь. Чем больше ты потренируйтесь , тем легче будет запомнить ответы на задачи.
До тех пор вы можете решать задачи на умножение с помощью таблицы умножения . Ее также называют таблицей умножения на . Таблица умножения — это таблица с ответами на все задачи на умножение, в которых используются числа от 1 до 12. Она проста в использовании. Нажмите на слайд-шоу ниже, чтобы узнать, как это сделать.
Это таблица умножения на .
В верхней части таблицы умножения вы можете найти числа от 1 до 12. Они идут по порядку от слева направо.
Каждое из чисел сверху находится в начале столбца . Например, это столбец, который идет с 5. Все числа в этом столбце кратны из 5.
Это означает, что все эти числа можно получить, умножив 5.Вы также можете найти числа от 1 до 12 в левой части таблицы умножения. Здесь числа идут по порядку от сверху вниз .
Каждое из этих чисел является началом строки . Эта строка содержит числа, кратные 4.
Попробуем решить задачу с таблицей умножения. Начнем с 7 x 3.
В 7 x 3 найдите первое число, на которое мы умножаем, слева от знака времени. Это 7.
Найдите 7 вверху таблицы.
Далее, посмотрите на второе число, на которое мы умножаем, справа от знака времени. В 7 х 3 это 3,
Найдите цифру 3 сбоку от таблицы.
Ответ будет в квадрате, где столбец 7 и ряд 3 встречаются и перекрываются.
Это квадрат, 21. Таким образом, 7 x 3 равно 21.
Попробуем еще раз. На этот раз мы решим 5 x 9.
Сначала, для 5 x 9, мы находим столбец 5.
Это означает, что все эти числа можно получить, умножив 5.