404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Другие возможные причиныВы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или ваша учетная запись должна быть создана заново. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлыКогда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен использовать попытка запроса.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в папке public_html/example/Example/
Обратите внимание, что CaSe важен в этом примере. На платформах с учетом регистра e xample и E xample не совпадают.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.
Разбитое изображение Если на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным цветом X , где изображение отсутствует. Щелкните правой кнопкой мыши X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера. Если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотреть информацию о странице» и перейдите на вкладку «Мультимедиа».
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/
Обратите внимание, что в этом примере важен CaSe . На платформах с учетом регистра символов PNG и png не совпадают.
404 Ошибки после перехода по ссылкам WordPress
При работе с WordPress часто могут возникать ошибки 404 Page Not Found, когда была активирована новая тема или когда были изменены правила перезаписи в файле .htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
- Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете пользовательскую структуру, скопируйте или сохраните ее где-нибудь.)
- Выберите По умолчанию .
- Нажмите Сохранить настройки .
- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.
- Нажмите Сохранить настройки .
Во многих случаях это сбросит постоянные ссылки и устранит проблему. Если это не сработает, вам может потребоваться отредактировать файл .htaccess напрямую.
Вариант 2. Измените файл .htaccess Добавьте следующий фрагмент кода 9index.php$ — [L]
RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule .
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и перезапись URL-адресов — это две очень распространенные директивы, которые можно найти в файле .htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассматривается, как редактировать файл в cPanel, но не то, что может потребоваться изменить. статьи и ресурсы для этой информации. )
)
- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Используйте SSH и текстовый редактор
- Используйте файловый менеджер в cPanel
Самый простой способ отредактировать файл .htaccess для большинства людей — через диспетчер файлов в cPanel.
Как редактировать файлы .htaccess в файловом менеджере cPanelПрежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджер- Войдите в cPanel.
- В разделе «Файлы» щелкните значок «Диспетчер файлов ».
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.

- Убедитесь, что установлен флажок Показать скрытые файлы (точечные файлы) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
- Щелкните правой кнопкой мыши файл .htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы.
- Может появиться диалоговое окно с вопросом о кодировании. Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.
- При необходимости отредактируйте файл.
- Нажмите Сохранить изменения в правом верхнем углу, когда закончите. Изменения будут сохранены.
- Протестируйте свой веб-сайт, чтобы убедиться, что ваши изменения были успешно сохранены.
 Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает. - После завершения нажмите Закрыть , чтобы закрыть окно диспетчера файлов.
Матричный калькулятор | Умножение, транспонирование, инверсия, определитель
О калькуляторе матриц
С помощью этого онлайн-калькулятора матриц вы легко найдете решение своих задач с матрицами. Он поддерживает почти все операции. Вы можете складывать, вычитать или умножать матрицы, находить их обратные, вычислять определители и так далее. Короче говоря, можно сказать, что это универсальное место для всех операций. Кроме того, он сочетает в себе все различные калькуляторы, такие как калькулятор умножения матриц, калькулятор обратной матрицы, калькулятор определителя и многое другое.
Что такое Матрица?
Матрица может быть просто определена как набор чисел, которые расположены в строках и столбцах, образуя прямоугольный массив. Чтобы сформировать матрицу, должен быть хотя бы один столбец или строка. Кроме того, существуют различные виды матриц, и они широко используются в математических расчетах, статистических реализациях, физике, экономике, информатике и экономике.
Кроме того, существуют различные виды матриц, и они широко используются в математических расчетах, статистических реализациях, физике, экономике, информатике и экономике.
Размеры
Размеры матрицы говорят о количестве строк и столбцов матрицы. Он обозначается как m x n, где m — количество строк, а n — количество столбцов.
Представление
Рассмотрим матрицу A 2 × 3. Таким образом, ее можно представить как A 2 x 3 . Он включает 2 строки и 3 столбца.
The elements of the matrix can be represented in an array form as follows:
| A= |
|
Каждый элемент в вышеуказанных матрицах, представленных как:
A 1, 1 = 4
A 1, 2 = 2
A 1, 3 = 3
A 2726 2726 272626 272626 2 2 2 2 2 2 2 2 2
2
2
2
2
2
. = 5
= 5
A 2 , 2 = 6
A 2 , 3 = 1
Это способ представления матрицы как отдельных объектов. Первый нижний индекс обозначает строку, а второй — столбец. Используя это значение, вы можете легко определить положение элемента.
Операции
Это основной контекст, о котором мы будем говорить в этой статье. Матричные операции — это набор операций, которые мы можем применить для получения некоторых результатов. Матричный калькулятор делает вашу задачу легкой и быстрой. Кроме того, вы можете выполнять эти операции всего несколькими нажатиями клавиш. Наиболее распространенными матричными операциями являются сложение, вычитание, умножение, возведение в степень, транспонирование, обращение и вычисление определителя. Давайте изучим их все один за другим.
Дополнение к матрице
Добавление матриц выполняется, только если обе матрицы имеют одинаковый размер. Другими словами, добавляемые матрицы должны иметь одинаковое количество строк и столбцов.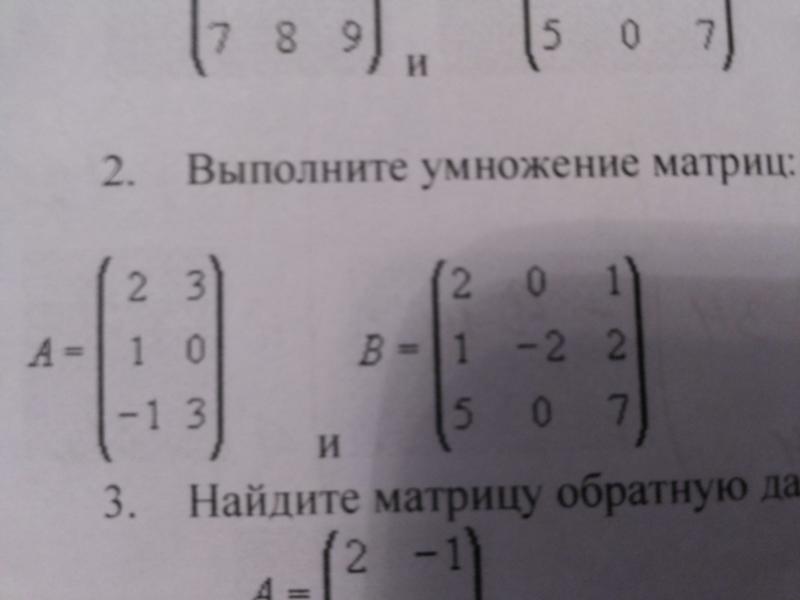 Это означает, что они должны иметь одинаковые размеры.
Это означает, что они должны иметь одинаковые размеры.
Процесс сложения: Если размер/размеры матриц одинаковы, то для нахождения суммы необходимо сложить соответствующие элементы матриц.
Формула: C i , j = A i , j + B i , j
Здесь A и B — элементы добавляемых матриц, а C — результирующая матрица.
Пример:
| A = | B = |
| C = |
|
Вычитание матриц
Вычитание матриц очень похоже на сложение. Это также выполняется, если обе матрицы имеют одинаковый размер. Другими словами, обе матрицы должны иметь одинаковое количество строк и столбцов.
Процесс вычитания: Вам необходимо вычесть соответствующие элементы матриц.
Формула: C i , j = A i , j — B i , j
Давайте разберемся на простом примере.
Пример:
| A = |
| B = |
|
| C = |
|
| C = |
|
Matrix Multiplication
There are two types of matrix multiplication we can perform.
- Скалярное умножение
- Умножение матрицы на другую матрицу
1. Скалярное умножение
При скалярном умножении каждый элемент отдельной матрицы умножается на скалярное значение. Давайте возьмем пример, чтобы понять это.
Пример:
| A = | B = 3 |
| 3 × | = |
|
2. Умножение матрицы на другую матрицу
Для умножения двух матриц количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Например, вы можете умножить 3 × 4 на 4 × 2. Но вы не можете умножить 3 × 4 на 2 × 4.
Примечание. . Это означает, что нет необходимости, чтобы A × B всегда было равно B × A.
Процесс умножения: Две матрицы перемножаются путем нахождения скалярного произведения между соответствующими элементами строки первой матрицы и столбца второй матрицы.
Formula:
C 1 , 1 = (A 1 , 1 , A 1 , 2 ) × (B 1 , 1 , B 2 , 2 )
Or
C 1 , 1 = A 1 , 1 × B 1 , 1 + A 1 , 2 × B 2 , 2
Здесь A и B — элементы перемножаемых матриц, а c результирующая матрица.
Пример:
| A = | B = |
| C = |
Power of Matrix Power of смысл матрицы в том, чтобы возвести матрицу в заданную степень. Например, задана матрица A. Теперь вычислите матрицу A со степенью двойки: A 2 = A × A . Самое главное, степень можно повышать только до квадратных матриц. Потому что неквадратную матрицу нельзя умножить на саму себя. Пример:
Транспонирование матрицыТранспонирование матрицы переворачивает ее элементы по диагонали. Элементы строки становятся элементами столбца, тогда как элементы столбца становятся элементами строки. Самое главное, матрица не должна быть пустой. Процесс транспонирования: Чтобы транспонировать матрицу, просто поменяйте местами элементы строк и столбцов. Формула: T m, n = T n, m = T’ Здесь T — матрица, содержащая m строк и n столбцов, которые после транспонирования станут n строками и m столбцами. Пример:
| .
| |A|= |
|
| = |
|
= a(ei-fh) — b(di-fg) + c(dh-eg)
Example:
| |A|= |
|
| = |
|
= 3(1×4 — 5×3) – 5(7×4 – 5×3) + 2(7×3 – 3×1)
= 3(-11) – 5 (13) + 2(18)
= -62
Заключение
Это все об очень полезном матричном калькуляторе, который быстро и точно решает все задачи, связанные с матрицами.


 Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
 Если матрица содержит 2 строки и 3 столбца, матрица теперь будет состоять из 3 строк и 2 столбцов.
Если матрица содержит 2 строки и 3 столбца, матрица теперь будет состоять из 3 строк и 2 столбцов. Давайте поймем процесс с помощью этой формулы и примера:
Давайте поймем процесс с помощью этой формулы и примера: