Минимизация скнф сднф
Часть 11. Минимизация СКНФ, СДНФ.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ, является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:
Аналогично для КНФ:
Возможность поглощения следует из очевидных равенств
Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей.
Карты Карно.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ, могут иметь в своём составе 2
 Все эти члены составляют
некоторую структуру, топологически
эквивалентную N–мерному
кубу, причём любые два терма, соединённые
ребром, пригодны для склейки и поглощения.
Все эти члены составляют
некоторую структуру, топологически
эквивалентную N–мерному
кубу, причём любые два терма, соединённые
ребром, пригодны для склейки и поглощения.На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
Часть 12. Полином Жегалкина.
Метод неопределенных коэффициентов
Построение полинома Жегалкина
Существует несколько способов построения полинома Жегалкина.
[править]
По таблице истинности
Пусть для функции задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что , а . За каждую подстановку находим только один коэффициент.
Пример: Дана функция и её таблица истинности:
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 0 |
0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 1 | 0 |
0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 1 |
1 | 0 | 0 | 1 | 0 |
1 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 0 |
Построим для неё полином Жегалкина:
Так
как
,
то
.
Таким образом, полином Жегалкина выглядит так:
Преобразование дизъюнктивной нормальной формы
Этот способ основан на том, что . Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило Де-Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю (так как ), а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу:
.
Если
функция задана в СДНФ, то так как при
любых значениях входных переменных в
единицу обращается не более одного
члена выражения, то достаточно просто
заменить все дизъюнкции исключающим
ИЛИ.
Пример: Дана функция в ДНФ , построим полином Жегалкина.
Запишем функцию так:
;
Сгруппируем слагаемые и воспользуемся преобразованием (1):
Воспользуемся свойствами конъюнкции и , а также тем, что , и упростим выражение:
Ещё раз воспользуемся преобразованием (1):
Раскроем скобку по алгебраическим правилам:
Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:
Заменим отрицание на прибавление :
Раскроем скобки:
Выкинем парные слагаемые и получим окончательную формулу:
Построение СКНФ и СДНФ по таблице истинности
- СКНФ
- СДНФ
Нормальной форме логической формулы не свойственна эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Выделяют такие виды формы нормального типа:
- КНФ (конъюнктивная нормальная форма), где подразумевается конъюнкция того или иного количества дизъюнкций, как пример, ;
- ДНФ (дизъюнктивная нормальная форма), где осуществляется дизъюнкция конъюнкций, как пример, .

СКНФ
Совершенная КНФ является разновидностью конъюнктивной нормальной формы, удовлетворяющей такие условия:
- отсутствие одинаковых элементарных дизъюнкций;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную НФ такого типа.
Построение СКНФ согласно таблице истинности
Если функция равна нулю, то в случае каждого набора записывают сумму, причем с отрицанием берутся те переменные, которые равны единице.
СДНФ
Совершенная ДНФ является разновидностью дизъюнктивной нормальной формы, удовлетворяющей следующие условия:
- отсутствие одинаковых элементарных конъюнкций;
- конъюнкции не свойственно обладать одинаковыми переменными;
в случае любой конъюнкции элементарного типа имеет место быть переменная, входящая в такую нормальную дизъюнктивную форму. При этом в одинаковом порядке.
Все формулы булевого типа, которые не относятся к тождественно ложным, могут быть представлены в совершенной разновидности ДНФ, при этом в единственном возможном варианте.
Построение СДНФ согласно таблице истинности
Если функция соответствует единице, то в случае каждого набора записывается произведение, причем с отрицанием берутся те переменные, которые равны нулю.
Нахождение СКНФ и СДНФ: примеры
Пример
Согласно таблице истинности записать логическую функцию:
Рисунок 1.
Решение:
Прибегнем к правилу построения совершенной ДНФ
Рисунок 2.
Получаем такую СДНФ
Задействовав правило её построения:
Рисунок 3.
Получаем СКНФ:
Пример
Представить функцию как СДНФ и СКНФ, при том, что она задаётся таблицей истинности.
Рисунок 4.
РешениеДля начала нужно записать логическую функцию в СДНФ. Чтобы упростить решение, добавляем к таблице столбец. Прибегнув к правилу составления СДНФ, вводим знак отрицания для переменных с нулевым значением. Инвертирование нулевых значений переменных имеет большое значение, поскольку без этого значения конъюнкций будут преобразованы в нули ключевой функции.
Рисунок 5.
Вычисленные конъюнкции из вспомогательного столбца необходимо объединить знаком дизъюнкции и получим необходимую логическую функцию, имеющую вид совершенной конъюнктивной формы нормального типа:
Запишем логическую функцию в СКНФ.
Прибегнув к правилу, по которому составляется СКНФ, нужно помнить о введения знака отрицания для переменных с единицей. Инвертирование единичных значений имеет большое значение, поскольку без этого значения дизъюнкций будут преобразованы в единицы ключевой функции.
Рисунок 6.
Вычисленные дизъюнкции из вспомогательного столбца необходимо объединить знаком конъюнкции, так как таким образом и можно получить необходимую логическую функцию, имеющую вид совершенной нормальной формы конъюнктивного типа.
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Устройства хранения информации Алфавитный подход к оценке количества информации. Формула Хартли Информационные процессы и информация Прикладное программное обеспечение Архитектура персонального компьютера
Формула Хартли Информационные процессы и информация Прикладное программное обеспечение Архитектура персонального компьютера
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Презентация: Упрощение булевых функций
Булевы функции
План:
- Упрощение булевых функций
Способы задания булевых функций
- табличный;
- графический;
- аналитический.

- Элементарными конъюнкциями называются….
- Дизъюнктивной нормальной формой (ДНФ) называется формула, имеющая …..
- Элементарными дизъюнкциями называются …..
- Конъюнктивной нормальной формой (КНФ) называется формула, имеющая вид …..
ДНФ (КНФ) представляет формулу неоднозначно. Частным случаем ДНФ является совершенная ДНФ (СДНФ) – однозначное представление формул логики высказываний.
Совершенная ДНФ (СДНФ) – ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно с отрицанием).
Пример записи формулы с СДНФ: (А&B&С) ∨(A&B& ┐C).
Совершенная КНФ (СКНФ) – КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно с отрицанием).
Пример записи формулы с СКНФ: (A ∨B∨ ┐C) &(A ∨C∨B)
Методика представления булевой функции в нормальной форме и совершенной нормальной форме.
- Если булева функция задана таблицей истинности, то она может быть представлена в аналитической форме с использованием операций конъюнкции, дизъюнкции и инверсии с помощью следующих правил:
Алгоритм получения СДНФ по таблице истинности:
Шаг 1: Отметить те строки таблицы истинности, в которых формула принимает значение «истина» (λ(F) = 1).
Шаг 2: Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно «истине», то в конъюнкцию включают саму эту переменную, иначе – ее отрицание.
Шаг 3: Все полученные конъюнкции связать в дизъюнкцию.
– каждой единице в таблице истинности сопоставляется конъюнкция ранга n , где n – число аргументов функции; рангом конъюнкции называют число аргументов, входящих в конъюнкцию, причем в эту конъюнкцию аргумент входит без инверсии, если в соответствующем наборе он принимает значение 1, и с инверсией, если принимает значение 0;
– все полученные конъюнкции объединяются знаками дизъюнкции.
Такое аналитическое выражение функции называют совершенной дизъюнктивной нормальной формой (СДНФ) функции, при этом под нормальной формой понимают выражение, в котором инверсии применяются только к отдельным аргументам, под совершенной формой понимают аналитическое выражение функции, когда во все конъюнкции входят все аргументы, т. е. все конъюнкции имеют ранг n .
Если в таблице истинности число нулей существенно меньше числа единиц, используют аналитическую запись в виде совершенной конъюнктивной нормальной формы (СКНФ).
Алгоритм получения СКНФ по таблице истинности:
Шаг 1: Отметить те строки таблицы истинности, в которых формула принимает значение «ложь» (λ(F) = 0).
Шаг 2: Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно «ложь», то в дизъюнкцию включают саму эту переменную, иначе – ее отрицание.
Шаг 3: Все полученные дизъюнкции связать в конъюнкцию.
Она строится по следующим правилам:
– каждому нулю в таблице истинности сопоставляется дизъюнкция ранга n , где n –число аргументов функции; рангом дизъюнкции называют число аргументов, входящих в дизъюнкцию, причем в эту дизъюнкцию аргумент входит без инверсии, если в соответствующем наборе он принимает значение 0, и с инверсией, если принимает значение 1;
– все полученные дизъюнкции объединяются знаками конъюнкции.
Построить СДНФ (СКНФ)
X1
X1
X2
0
0
X2
0
0
X3
0
0
X3
0
F
0
0
F
0
0
0
1
1
1
1
0
1
1
0
0
0
0
0
1
1
1
1
1
1
0
0
1
1
1
1
1
0
0
1
1
0
0
1
1
1
0
0
1
1
1
1
1
0
1
1
0
1
1
1
1
1
1
1
Минимизация булевых функций – представление булевых функций в самом экономичном коротком виде.
Дизъюнктивная нормальная форма называется минимальной, если она содержит наименьшее число вхождений переменных по сравнению со всеми равносильными ей ДНФ.
2. Упрощение булевых функций
Cвойства булевых функций
Идемпотентность
(Повторение)
Коммутативность (Переместительный закон)
Ассоциативность
(Сочетательный закон)
Законы поглощения
Дистрибутивность (Распределительный закон)
Свойства константы 1
Свойства константы 0
Двойное отрицание
Закон де Моргана
Правило исключения третьего
(Закон непротиворечия)
Булевы функции n элементов
- Мажоритарная функция
1. Универсальные :
Универсальные :
xV1 = 1;
xV 0 = х ;
х 1 = х ;
х 0 = 0.
Ассоциативность конъюнкции и дизъюнкции:
x ( yz ) = ( xy ) z ; xV ( y V z ) = ( x V y )V z .
Это свойство означает, что в конъюнкции или дизъюнкции нескольких переменных можно как угодно расставлять скобки (а значит, можно вообще их не ставить).
Поглощение (“целое поглощает часть”)
х V ху = х (1V у ) = х
Два распределительных закона
х ( yV z ) = x y V x z ;
хV ( y z) = ( xV y )( xV z )
оба свойства могут быть доказаны простым рассуждением (например, если х = 0, тогда по свойству 1 справа выражение равно 0 и слева тоже 0, если х = 1, то справа стоит y Ú z и слева будет то же самое)
Правила де Моргана
оба эти правила обобщаются на любое число переменных:
Правило Блейка
Пусть К 1 и К 2 – какие-то логические функции, тогда:
что легко доказывается справа налево :
Всякую формулу можно преобразовать так, что в ней не будет отрицаний сложных высказываний — все отрицания будут применяться только к простым высказываниям.
Замена эквиваленции и импликации на конъюнкцию, дизъюнкцию и отрицание.
Имеют место следующие равносильности:
(1)
(2)
Основные теоремы
Правильные элементарные конъюнкции
Преобразовать до ДНФ
Задания
Докажите тождество
Преобразовать
Найти СДНФ
Найти СКНФ
Упрощение логических выражений — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Упрощение логических выражений
Шаг 1. Заменить операции на их выражения
через И, ИЛИ и НЕ:
A B A B A B
A B A B
A B A B A B
Шаг 2. Раскрыть инверсию сложных выражений по
формулам де Моргана:
A B A B,
A B A B
Шаг 3. Используя законы логики, упрощать выражение,
стараясь применять закон исключения третьего.
1
Упрощение логических выражений
Q M X H M X H (M M ) X H X H
X (B A) (A B) (A C)
( B A) (A B) (A C)
формула де Моргана
( B A) A B (A C)
( B A A A ) B (A C)
B A B (A C)
B A (A C)
B A
раскрыли
распределительный
исключения третьего
повторения
поглощения
2
3
Логические уравнения
A B A B C 1
A B 1
A=1, B=0, C=1
или
A=0, B=1, C – любое
2 решения: (0, 1, 0), (0, 1, 1)
A B C 1
!
Всего 3 решения!
K L M L N K L M 1
K=1, L=1,
M и N – любые
4 решения
M=1, L=1, N=1,
K – любое
2 решения
L (K M N) 1
K=1, L=1, M=0,
N – любое
2 решения
!
Всего 5 решений!
4.
 Как построить логическую формулу4
Как построить логическую формулу4Как построить
логическую
формулу
Синтез логических выражений
Совершенная Дизъюнктивная
Нормальная форма (СДНФ)
Формулу называют элементарной конъюнкцией, если
она является конъюнкцией переменных или их
отрицаний без повторения
Формула называется дизъюнктивной нормальной
формой (ДНФ), если она является дизъюнкцией
неповторяющихся элементарных конъюнкций.
Формула называется совершенной дизъюнктивной
нормальной формой (СДНФ), если:
1) она является ДНФ
2) В каждую элементарную конъюнкцию входят все
переменные (или их отрицания), от которых зависит
функция
6. Алгоритм построения СДНФ по таблице истинности
1. В таблице истинности отмечаем наборы переменных, накоторых значение функции F равно 1.
2. Записываем для каждого отмеченного набора
конъюнкцию всех переменных следующим образом: если
значение некоторой переменной в этом наборе равно 1,
то в конъюнкцию включаем саму переменную, в
противном случае — ее отрицание.

3. Все полученные конъюнкции связываем операциями
дизъюнкции.
Синтез логических выражений (СДНФ)
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
A B
A B
Шаг 1. Отметить строки в
таблице, где X = 1.
Шаг 2. Для каждой из них
записать логическое
выражение, которое истинно
только для этой строки.
Шаг 3. Сложить эти выражения и
упростить результат.
распределительный
X A B A B A B A (B B) A B
A A B ( A A) ( A B) A B
исключения
третьего
распределительный
исключения
третьего
7
Синтез логических выражений (СДНФ)
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
X A B C A B C
A B C
A B C
A B C
A B C
A B C
A B C
A B C A B C
A B C A B C
A B ( C C)
A B ( C C)
A C ( B B)
A B A B A C
A (B B) A C
A A C
(A A) (A C) A C
8
Совершенная Конъюнктивная
Нормальная форма (СКНФ)
Формулу называют элементарной дизъюнкцией, если
она является дизъюнкцией переменных или их
отрицаний без повторения
Формула называется конъюнктивной нормальной
формой (КНФ), если она является конъюнкцией
неповторяющихся элементарных дизъюнкций.

Формула называется совершенной конъюнктивной
нормальной формой (СКНФ), если:
1) она является КНФ
2) В каждую элементарную дизъюнкцию входят все
переменные (или их отрицания), от которых зависит
функция
10. Алгоритм построения СКНФ по таблице истинности
1. В таблице истинности отмечаем наборы переменных,на которых значение функции F равно 0.
2. Записываем для каждого отмеченного набора
дизъюнкцию всех переменных следующим образом:
если значение некоторой переменной в этом наборе
равно 0, то в конъюнкцию включаем саму
переменную, в противном случае — ее отрицание.
3. Все полученные дизъюнкции связываем операциями
конъюнкции.
Синтез логических выражений (СКНФ)
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
Шаг 1. Отметить строки в
таблице, где X = 0.
Шаг 2. Для каждой из них
записать логическое
выражение, которое истинно
только для этой строки.
Шаг 3.
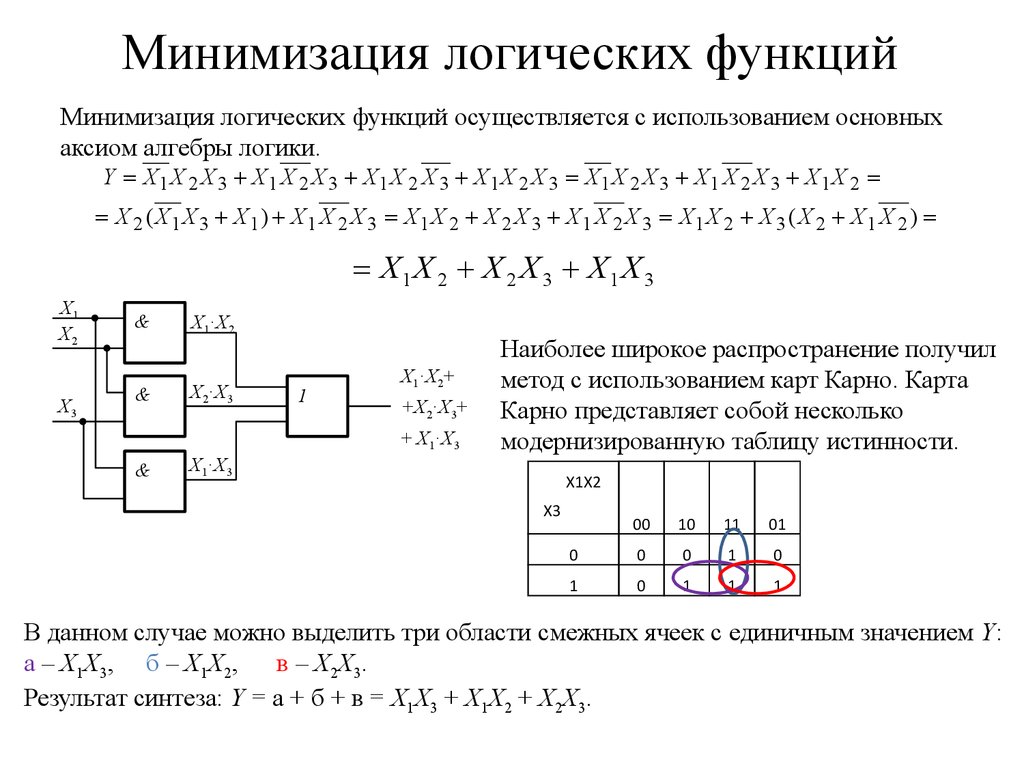 Сложить эти выражения и
Сложить эти выражения иупростить результат, который
равен X .
Шаг 4. Сделать инверсию.
X A B X A B A B
11
Синтез логических выражений (СКНФ)
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
X A B C A B C
A C ( B B)
A C
X A C A C
A B C
A B C
12
13. Задание №1.
Найти логическую функцию F,зависящую от логических
переменных A, B, C, по
заданной таблице истинности.
Упрощенный вид функции должен
содержать не более трех
логических операций. В
упрощенном виде функции
допустимо использовать только
операции ИНВЕРСИЯ,
КОНЪЮНКЦИЯ и ДИЗЪЮНКЦИЯ.
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
F
0
1
0
1
1
1
0
1
14.
 Способ 1а. Решение через СДНФСпособ 1а.
Способ 1а. Решение через СДНФСпособ 1а.A B C F
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 0
1 1 1 1
Решение через СДНФ
Способ 1б.
A B C F
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 0
1 1 1 1
Решение через СДНФ
16. Способ 2. Решение через СКНФ
A B C F0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 1
1 1 0 0
1 1 1 1
Задание №2.
Дан фрагмент таблицы истинности логической функции
трех переменных, содержащий только те строки, которые
содержит ложные значения функции. Все остальные строки
таблицы истинности дают в результате истинное значение
функции.
Запишите логическую функцию
А
В
С
F(A,B,C)
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
0
и упростите ее.
Результат упрощения может
содержать только операции
инверсии, конъюнкции и
дизъюнкции.

Решения
Решение
А
0
0
1
1
В
0
1
0
1
С
1
1
1
1
F
0
0
0
0
19. Задание для самостоятельного решения
Постройте и упростите логические выражения, соответствующиеприведённым таблицам истинности. В каждом случае выбирайте
наиболее простой способ синтеза. В вашем решении опишите все
шаги алгоритма.
19
English Русский Правила
1
Первый слайд презентации
Учебная дисциплина Схемотехника дискретных устройств Тема: Арифметические и логические основы ЭВМ Московский Государственный Технический Университет имени Н.Э. Баумана 1830
Изображение слайда
2
Слайд 2: Тема: Арифметические и логические основы ЭВМ
Логика- наука о формах и законах мышления (в общем понимании)
Математическая логика- наука о применении математических методов для решения различного рода логических задач.
Изображение слайда
3
Слайд 3: Высказывание
Основное понятие алгебры логики-высказывание. Простое Высказывание — некоторое предложение, о котором можно утверждать, что оно истинно или ложно.
Изображение слайда
4
Слайд 4: Высказывание
Сложным высказыванием является предложение, состоящее из нескольких простых предложений (т.е. простых высказываний), связанных между собой какими либо логическими связями.
Изображение слайда
5
Слайд 5: Высказывание
Под логическими связями понимаются грамматические союзы типа «НЕ», «И», «ИЛИ», «ЕСЛИ.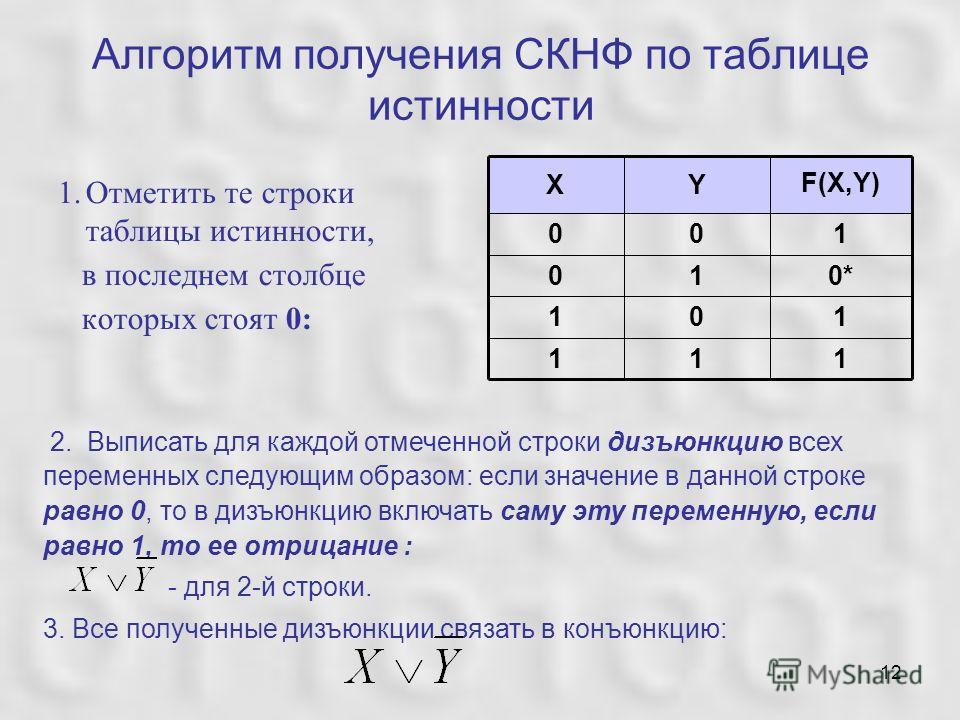 ., ТО..».
., ТО..».
Изображение слайда
6
Слайд 6: Высказывание
Любое высказывание можно обозначить символом х и считать, что х=1, если высказывание истинно, а х=0, если высказывание ложно. Логическая (булева) переменная – такая величина х, которая может принимать только два значения: х= {0,1}.
Изображение слайда
7
Слайд 7: Высказывание
Высказывание абсолютно истинно, если соответствующая ему логическая величина принимает значение х=1 при любых условиях. Высказывание абсолютно ложно, если соответствующая ему логическая величина принимает значение х=0 при любых условиях.
Изображение слайда
8
Слайд 8: Определение булевой функции
Под булевой функцией (БФ) понимают сложное высказывание. Эта функция принимает лишь два значения : 0 или 1. Булева функция всегда конечна.
Эта функция принимает лишь два значения : 0 или 1. Булева функция всегда конечна.
Изображение слайда
9
Слайд 9: Определение булевой функции
Простые высказывания, входящие в булеву функцию, называют переменными (или булевыми переменными). Булева (двоичная) функция – это двоичная переменная Y, значение которой зависит от её двоичных переменных (аргументов функции).
Изображение слайда
10
Слайд 10: Определение булевой функции
Чтобы задать булеву функцию надо каждому из возможных сочетаний аргументов x1,x2,…,xn поставить в соответствие 0 или 1 (т.е. значение функции).
Изображение слайда
11
Слайд 11: Определение булевой функции
Количество возможных булевых функций N при количестве переменных p, определяется по формуле:
Изображение слайда
12
Слайд 12: Симвилярная БФ
БФ одной переменной называется симвилярной функцией.
Изображение слайда
13
Слайд 13: Симвилярная БФ
X=0 x=1 обозначе-ние название Y1 0 0 0 Константа нуль Y2 0 1 x Повторение Y3 1 0 !x Отрицание (инверсия) Y4 1 1 1 Константа единица
Изображение слайда
14
Слайд 14: Бинарная булева функция
Булева функция от двух переменных называется бинарной.
Изображение слайда
15
Слайд 15: Бинарные булевы функции
x1 x2 Y0 Y1 Y2 Y3 Y4 Y5 Y6 Y7 0 0 0 1 0 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 1 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0
Изображение слайда
16
Слайд 16: Бинарные булевы функции
x1 x2 Y8 Y9 Y10 Y11 Y12 Y13 Y14 Y15 0 0 0 1 0 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Изображение слайда
17
Слайд 17: Наименования бинарных булевых функций
Y0- константа 0 Y0=0
Y1 – функция Пирса Y1=!(x1+x2)
Y2 – запрет по x1 Y2=!x1*x2
Y3 – переменная ! x1 Y3=!x1
Y4 – запрет по x2 Y4=x1*!x2
Y5 – переменная ! x2 Y5=!x2
Y6 – искл. ИЛИ ( сложение по модулю 2)
ИЛИ ( сложение по модулю 2)
Изображение слайда
18
Слайд 18: Наименования бинарных булевых функций
Y7 – функция Шеффера Y7=!(x1*x2) Y8 – конъюнкция Y8=x1*x2 Y9 – равнозначность Y9=x1=x2 Y10- перемен. x2 Y10=x2 Y11- импликация x1 x2 Y11=!x1+x2
Изображение слайда
19
Слайд 19: Наименования бинарных булевых функций
Y12 – переменная x1 Y12=x1 Y13 – импликация x2 к x1 Y13=x1+!x2 Y14 – дизъюнкция Y14=x1+x2 Y15 – константа единицы Y15=1
Изображение слайда
20
Слайд 20: Определение логической функции
Логическая функция алгебры логики – функция f(x1, x2, …. , xn), принимающая значение, равное 0 или 1 на наборе логических переменных х1, х2, …..х n.
, xn), принимающая значение, равное 0 или 1 на наборе логических переменных х1, х2, …..х n.
Изображение слайда
21
Слайд 21: Применимость алгебры логики
Возможность применения алгебры логики к задачам проектирования вычислительных устройств обусловлена аналогией понятий и категорий алгебры логики и двоичной системы счисления.
Изображение слайда
22
Слайд 22: Технический аналог булевой функции
Техническим аналогом булевой функции является комбинационная схема, выполняющая соответствующее этой функции преобразование информации.
Постоянные уровни напряжения, соответствующие принятому в схеме представлению 0 и 1, могут рассматриваться как технические аналоги функции «ложь» и «истина».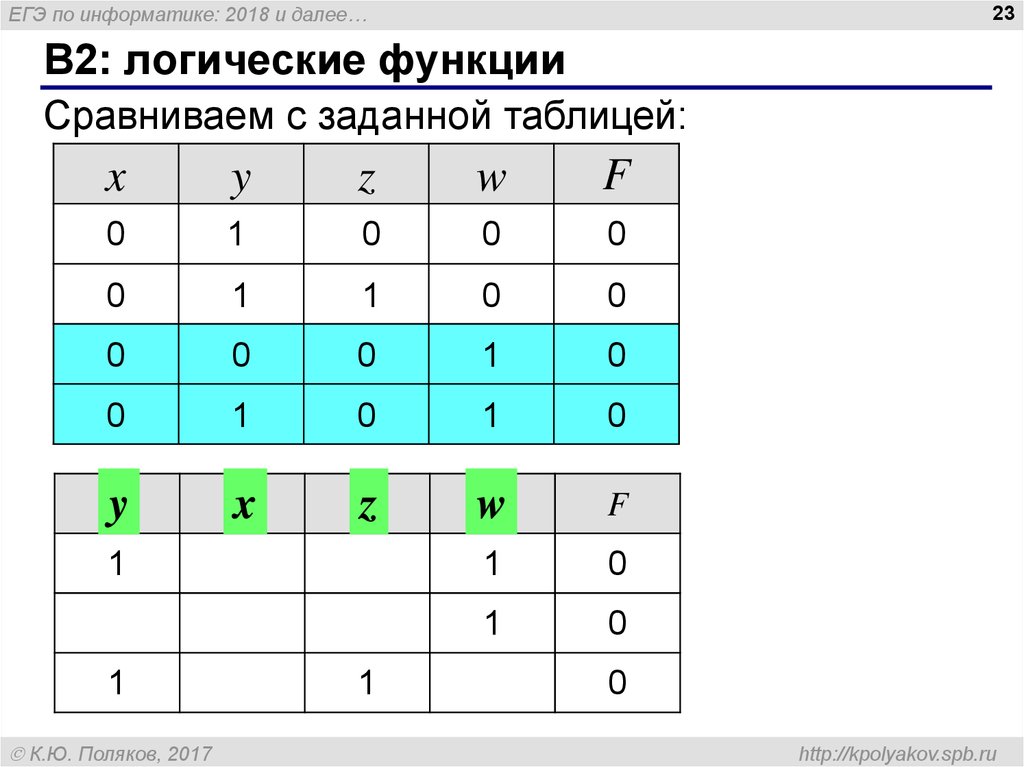
Изображение слайда
23
Слайд 23: Понятие логического элемента
Логические операции над двоичными переменными реализуются схемами, которые называются логическими элементами. Число входов логического элемента соответствует числу аргументов воспроизводимой им булевой функции.
Изображение слайда
24
Слайд 24: Законы и аксиомы алгебры логики
Закон одинарных элементов: Х+1=1 Х*1=Х Х+0=Х Х*0=0 Законы отрицания: — закон двойного отрицания — закон дополнительности
Изображение слайда
25
Слайд 25: Законы и аксиомы алгебры логики
Закон двойственности Де Моргана
Изображение слайда
26
Слайд 26: Законы и аксиомы алгебры логики
Из этих выражений следует следствие:
Изображение слайда
27
Слайд 27: Комбинационные законы
Закон тавтологии:
Х+Х+Х+……. +Х=Х
Х*Х*Х*……*Х=Х
Переместительный (коммутативный) закон:
Х1+Х2=Х2+Х1 Х1*Х2=Х2*Х1
+Х=Х
Х*Х*Х*……*Х=Х
Переместительный (коммутативный) закон:
Х1+Х2=Х2+Х1 Х1*Х2=Х2*Х1
Изображение слайда
28
Слайд 28: Комбинационные законы
Сочетательный (ассоциативный) закон: ( Х1+Х2)+Х3=Х1+(Х2+Х3) (Х1*Х2)*Х3=Х1*(Х2*Х3)
Изображение слайда
29
Слайд 29: Комбинационные законы
Распределительный закон: X1*(X2+X3)=(X1*X2)+(X1*X3) X1+(X2*X3)=(X1+X2)*(X1+X3)
Изображение слайда
30
Слайд 30: Комбинационные законы
Сочетательный закон: X1*(X2*X3)=(X1*X3)*X2 X1+(X2+X3)=(X1+X2)+X3
Изображение слайда
31
Слайд 31: Комбинационные законы
Переместительный закон (закон коммутативности): X1*X2*X3=X3*X2*X1 X1+X2+X3=X3+X1+X2
Изображение слайда
32
Слайд 32: Комбинационные законы
Закон поглощения (абсорбции): X1+X1*X2=X1 X1*(X1+X2)=X1
Изображение слайда
33
Слайд 33: Комбинационные законы
Закон склеивания:
Изображение слайда
34
Слайд 34: Теорема Шеннона
Операция инвертирования произвольной комбинации двоичных переменных, связанных знаками дизъюнкции и конъюнкции эквивалентна замене в этой комбинации
Изображение слайда
35
Слайд 35: Теорема Шеннона (продолжение)
исходных значений двоичных переменных их инверсными значениями при одновременной замене знаков дизъюнкции и конъюнкции.
Изображение слайда
36
Слайд 36: Пример применения теоремы Шеннона
Изображение слайда
37
Слайд 37: Определение Основного Функционально полного набора
Набор функций дизъюнкции, конъюнкции и инверсии, который соответствует трём операциям булевой алгебры-логики, получил название Основного функционально-полного набора.
Изображение слайда
38
Слайд 38: Другие функционально полные наборы
Двумя другими функционально полными наборами являются функции Пирса и Шеффера.
Изображение слайда
39
Слайд 39: Функционально полная система логических элементов
Систему логических элементов называют функционально полной, если есть возможность создать любые заданные переключательные выходные функции.
Изображение слайда
40
Слайд 40: Понятие « базис»
Система переключательных функций, образующую функционально полную систему, логических функций называется базисом.
Изображение слайда
41
Слайд 41: Переключательная функция
Переключательной функцией называется математическое выражение, связывающее между собой элементарные двоичные логические переменные, принимающие значения «0» и «1».
Изображение слайда
42
Слайд 42: Дизъюнктивно-нормальная форма (ДНФ)
Если логическая функция выражена посредством логической суммы элементарных конъюнкций, то считается, что она задана своей ДНФ. (CvD)
(CvD)
Изображение слайда
46
Слайд 46: Элементарная дизъюнкция
Элементарной дизъюнкцией n- го ранга называется логическая сумма двоичных переменных и их отрицаний, причём, каждая переменная в сумме должна встречаться только один раз. Например: X1vX2v!X3vX4v!X5
Изображение слайда
47
Слайд 47: Ранг дизъюнкции
Рангом дизъюнкции называется число двоичных переменных, составляющих элементарную дизъюнкцию. Например : X1vX2v!X3vX4v!X5 ; — это дизъюнкция 5-го ранга, так как составлена из логической суммы пяти переменных и их отрицаний.
Изображение слайда
48
Слайд 48: Эквивалентность представления
Одна и та же логическая функция может быть представлена как своей ДНФ так и КНФ, путём эквивалентных преобразований. Из множества этих нормальных форм функций выделяют одну совершенную дизъюнктивную (СДНФ) и одну совершенную конъюнктивную (СКНФ) формы.
Из множества этих нормальных форм функций выделяют одну совершенную дизъюнктивную (СДНФ) и одну совершенную конъюнктивную (СКНФ) формы.
Изображение слайда
49
Слайд 49: СДНФ
Совершенная дизъюнктивно-нормальная форма логической функции от n двоичных переменных называется такая ДНФ логической функции в которой: — все конъюнкции имеют один и тот же ранг;
Изображение слайда
50
Слайд 50: СДНФ
— нет двух одинаковых конъюнкций; — каждая конъюнкция содержит либо прямое, либо инверсное значение двоичной переменной; — ни одна конъюнкция не содержит двух одинаковых двоичных переменных.
Изображение слайда
51
Слайд 51: Определение минтерма
Конъюнкции n -го ранга, составляющие СДНФ функции и обращающие функцию в 1 при определённом наборе переменных получили название минтермы.
Изображение слайда
52
Слайд 52: СКНФ
Совершенная конъюнктивно-нормальная форма логической функции от n двоичных переменных называется такая КНФ логической функции в которой: — все дизъюнкции имеют один и тот же ранг;
Изображение слайда
53
Слайд 53: СКНФ
— нет двух одинаковых дизъюнкций; — каждая дизъюнкция содержит либо прямое, либо инверсное значение двоичной переменной; — ни одна дизъюнкция не содержит двух одинаковых двоичных переменных.
Изображение слайда
54
Слайд 54: Определение минтерма
Дизъюнкции n -го ранга, составляющие СКНФ функции и обращающие функцию в 0 при определённом наборе переменных получили название минтермы.
Изображение слайда
55
Слайд 55: Примеры СКНФ и СДНФ
СДНФ: СКНФ:
Изображение слайда
56
Слайд 56: Табличное задание булевой функции
X3 X2 X1 Y 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1
Изображение слайда
57
Слайд 57: Составление СДНФ по табличному заданию булевой функции
Правило:
Соответствующие минтермам элементарные конъюнкции объединить знаками дизъюнкций,
в элементарных конъюнкциях переменная=1 записывается прямым значением, а переменная=0, своим инверсным значением (с черточкой над именем переменной).
Изображение слайда
58
Слайд 58: Итоговая запись СДНФ
Изображение слайда
59
Слайд 59: Составление СКНФ по табличному заданию булевой функции
Правило: Соответствующие минтермам элементарные дизъюнкции объединить знаками конъюнкций, в элементарных дизъюнкциях переменная=0 записывается прямым значением, а переменная=1, своим инверсным значением (с черточкой над именем переменной).
Изображение слайда
60
Слайд 60: Итоговая запись СКНФ
Изображение слайда
61
Слайд 61: Технический аналог булевой функции
Техническим аналогом булевой функции является комбинационная схема, выполняющая соответствующее этой функции преобразование информации. Постоянные уровни напряжения, соответствующие принятому в схеме представлению 0 и 1, могут рассматриваться как технические аналоги функции «ложь» и «истина».
Постоянные уровни напряжения, соответствующие принятому в схеме представлению 0 и 1, могут рассматриваться как технические аналоги функции «ложь» и «истина».
Изображение слайда
62
Слайд 62: Типовой порядок проектирования комбинационных устройств
Этапы: 1. Определение табличных значений поведения булевой функции. 2. Составление СДНФ по минтермам табличной записи булевой функции. 3. Упрощение СДНФ и получение его минимальной ДНФ. 4. Переход от минимальной ДНФ к минимизированной форме в каком-либо базисе ФПН.
Изображение слайда
63
Слайд 63: Типовой порядок проектирования комбинационных устройств
5. Составление комбинационной схемы из логических элементов, входящих в указанный базис.
Изображение слайда
64
Слайд 64: Минимизация логических функций
Упрощение и преобразование логических функций имеет целью получение такого вида функции, при котором построенная в соответствии с ней цифровая комбинационная схема отличалась бы минимальным расходом логических элементов на её изготовление.
Изображение слайда
65
Слайд 65: Минимизация логических функций
Различают эвристические и формализованные методы преобразования логических функций. При эвристических методах преобразования логических функций используют законы, аксиомы и тождества алгебры логики.
Изображение слайда
66
Слайд 66: Принципы минимизации
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке.
Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке.
Изображение слайда
67
Слайд 67: Принципы минимизации
главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2 N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N –мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения. На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
Изображение слайда
68
Слайд 68: Метод Карт Карно
При формализованных методах, при ограничении числа переменных до пяти-шести используется «метод Карт Карно». Карта Карно́ — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями.
Изображение слайда
69
Слайд 69: Карты Карно
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
Изображение слайда
70
Слайд 70: Правило составления карты Карно
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.
Изображение слайда
71
Слайд 71: Пример карты Карно для 4-х переменных
Изображение слайда
72
Слайд 72: Метод скручивания карты Карно
Крайние квадраты карты являются соседними при ее скручивании. Это значит, что они тоже подлежат минимизации. На плоскости можно изобразить карту Карно для 4-х переменных. Для 5 и более переменных необходимы объемные фигуры.
На плоскости можно изобразить карту Карно для 4-х переменных. Для 5 и более переменных необходимы объемные фигуры.
Изображение слайда
73
Слайд 73: Метод скручивания карты Карно
Изображение слайда
74
Слайд 74: Карта Карно для двух переменных
Изображение слайда
75
Последний слайд презентации: Учебная дисциплина Схемотехника дискретных устройств Тема: Арифметические и: Карта Карно для 3-х переменных
Изображение слайда
СДНФ. Теорема о представлении в виде СДНФ.
 Построение СДНФ по таблице / Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] / 3dstroyproekt.ru
Построение СДНФ по таблице / Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] / 3dstroyproekt.ruДНФ
Простой конъюнкцией или конъюнктом называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
Простая конъюнкция
- полная, если в неё каждая переменная { или её отрицание } входит ровно 1 раз;
- монотонная, если она не содержит отрицаний переменных.
ДНФ { Дизъюнктивная Нормальная Форма } — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.
Пример ДНФ: $f(x,y,z) = (x \land y) \lor (y \land \neg { z } )$
СДНФ
СДНФ { Совершенная Дизъюнктивная Нормальная Форма } — это такая ДНФ, которая удовлетворяет условиям:
- в ней нет одинаковых простых конъюнкций
- каждая простая конъюнкция полная
Пример СДНФ: $f(x,y,z) = (x \land \neg { y } \land z) \lor (x \land y \land \neg { z } )$
Теорема: Для любой булевой функции $f(\vec { x } )$, не равной тождественному нулю (), существует СДНФ, ее задающая.
Доказательство:
Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона.
$f(\vec { x } ) = \neg x_i \wedge f(x_1, \dots ,x_ { i-1 } ,0,x_ { i+1 } , \dots ,x_n) \vee x_i \wedge f(x_1, \dots ,x_ { i-1 } ,1,x_ { i+1 } , \dots ,x_n)$
Данное соотношение легко проверить подстановкой всевозможных значений $x_i$ { $0$ и $1$ } . Эта формула позволяет выносить $x_i$ за знак функции. Последовательно вынося $x_1$, $x_2$,.., $x_n$ за знак $f(\vec { x } )$, получаем следующую формулу :
$ f(\vec { x } ) = \neg x_1 \wedge \neg x_2 \wedge …\wedge \neg x_ { n-1 } \wedge \neg x_n \wedge f(0,0,…,0,0)~\vee~$
$\neg x_1 \wedge \neg x_2 \wedge … \wedge \neg x_ { n-1 } \wedge x_n \wedge f(0,0,…,0,1) ~\vee~ $ $\dots $ $~\vee~ x_1 \wedge x_2 \wedge … \wedge x_ { n-1 } \wedge \neg x_n \wedge f(1,1,…,1,0) ~\vee~ $ $x_1 \wedge x_2 \wedge … \wedge x_ { n-1 } \wedge x_n \wedge f(1,1,…,1) $
Так как применение данного соотношения к каждой из переменных увеличивает количество конъюнктов в два раза, то для функции от $n$ переменных мы имеем { { { $2^ { n } $ } } } конъюнктов. { n } $ } } } возможных наборов значений $n$ переменных. Если на некотором наборе $f(\vec { x } )=0$, то весь соответствующий конъюнкт также равен нулю и из представления данной функции его можно исключить. Если же $ f(\vec { x } )=1$, то в соответствующем конъюнкте само значение функции можно опустить. В результате для произвольной функции была построена СДНФ.
{ n } $ } } } возможных наборов значений $n$ переменных. Если на некотором наборе $f(\vec { x } )=0$, то весь соответствующий конъюнкт также равен нулю и из представления данной функции его можно исключить. Если же $ f(\vec { x } )=1$, то в соответствующем конъюнкте само значение функции можно опустить. В результате для произвольной функции была построена СДНФ.
Алгоритм построения СДНФ по таблице истинности
- В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
- Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Пример построения СДНФ для медианы
В таблице истинности отмечаем те наборы переменных, на которых значение функции равно 1.
x y z $\langle x,y,z \rangle$ 0 0 0 0 0 0 1 0 0 1 1 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1 Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть 1, то в конъюнкцию включаем саму переменную, иначе ее отрицание.

x y z $ \langle x,y,z \rangle $ 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 $(\neg { x } \land y \land z)$ 1 0 0 0 1 0 1 1 $(x \land \neg { y } \land z)$ 1 1 0 1 $(x \land y \land \neg { z } )$ 1 1 1 1 $(x \land y \land z)$ Все полученные конъюнкции связываем операциями дизъюнкции. $ \langle x,y,z \rangle = (x \land y \land z) \lor (\neg { x } \land y \land z) \lor (x \land \neg { y } \land z) \lor (x \land y \land \neg { z } )$
Примеры СДНФ для некоторых функций
Стрелка Пирса: $x \downarrow y = (\neg { x } \land \neg { y } )$
Исключающее или: $x \oplus y \oplus z = (\overline { x } \land \overline { y } \land z) \lor (\overline { x } \land y \land \overline { z } ) \lor (x \land \overline { y } \land \overline { z } ) \lor (x \land y \land z)$
Совершенной дизъюнктивной нормальной формой формулы $A(x_1,x_2,…,x_n)$ называется ДНФ, обладающая следующими свойствами:
а } в ней нет одинаковых дизъюнктивных элементов;
б } ни одна элементарная конъюнкция не содержит двух одинаковых высказываний;
в } ни какая элементарная конъюнкция не содержит высказывание вместе с ее отрицанием;
г } в каждой элементарной конъюнкции содержится либо $X_i$, либо $\overline { X } _i$, где $i = 1, n$.
Условие а } – г } являются необходимыми и достаточными для того, чтобы ДНФ стала СДНФ. В свою очередь эти условия дают возможность составить алгоритм получения СДНФ из ДНФ:
1) если какая-нибудь элементарная конъюнкция не содержит высказывание $X_i$, то заменим выражением $B\wedge (X_i\vee \overline { X } _i) \equiv (B\wedge X_i)\vee (B\wedge \overline { X } _i)$;
2) если в полученном выражении окажутся одинаковые элементарные конъюнкции, то лишние опускаются;
3) если в некоторых элементарных конъюнкциях окажутся одинаковые высказывания, то лишние опускаются;
4) удаляем элементарные конъюнкции, в которых содержатся высказывания вместе с их отрицанием.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Если все элементарные конъюнкции окажутся таковыми, т.е. вся формула будет ложной, то она не будет иметь СДНФ.
Формула называется дизъюнктивной нормальной формой { ДНФ } , если она является дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ записываются в виде: $A_1\vee A_2\vee …\vee A_n$ , где каждое $A_n$ — элементарная конъюнкция.
ДНФ записываются в виде: $A_1\vee A_2\vee …\vee A_n$ , где каждое $A_n$ — элементарная конъюнкция.
Формула $A$ от $k$ переменных называется совершенной дизъюнктивной нормальной формой { СДНФ } , если:
$A$ является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция $k$ переменных $x_1,x_2,…,x_k$, причем на $i$-м месте этой конъюнкции стоит либо переменная $x_i$ либо ее отрицание;
Все элементарные конъюнкции в такой ДНФ попарно различны.
Например: $A = x_1 \wedge$ НЕ $x_2 \vee x_1 \wedge x_2$
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций { дизъюнктивных членов } в ней.
Она является примером однозначного представления булевой функции в виде формульной { алгебраической } записи.
Теорема о СДНФ: Пусть $f(x_1 x_2, …, x_n)$ – булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию $f$.
Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию $f$.
Алгоритм построения СДНФ по таблице истинности:
- В таблице истинности отмечаем наборы переменных, на которых значение функции $f = 1$.
- Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае – ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Далее:
Формула Грина
Логические операции над высказываниями
Решение задач с помощью алгебры высказываний
Вычисление площади поверхности
Вычисление объёмов
Критерий полноты {формулировка}. Лемма о немонотонной функции
Выражение площади плоской области через криволинейный интеграл
Криволинейный интеграл первого рода
Вычисление криволинейного интеграла первого рода. Примеры
Примеры
Теорема о полныx системаx в Pk
Равносильные формулы алгебры высказываний
Упрощение логических функций
Вычисление двойного интеграла
Примеры применения цилиндрических и сферических координат
Теорема об аналоге СДНФ в Pk
Огравление $\Rightarrow $
04 сентября 2016, 19:46 проектирование км, кмд, кж Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв] 0 37020 0
СДНФ | Tekla User Assistance
Обзор
Нейтральный файл детализации стали (SDNF) изначально был определен Intergraph® для электронного обмена данными между системами анализа и проектирования инженеров-строителей и системами моделирования стальных конструкций. Версия 3.0 — это новейший формат, поддерживаемый индустрией программного обеспечения, и этот формат уже много лет используется для передачи даже сложных структур предприятия между такими системами, как Tekla Structures, и системами проектирования предприятий, такими как приложения Intergraph PDS или Aveva PDMS.
Формат SDNF
В качестве краткого обзора файлы SDNF разделены на пакеты и записи. Основные пакеты определяются следующим образом:
Пакет 00 — Пакет заголовков
Пакет 10 — Линейные элементы
Пакет 20 — Пластинчатые элементы
Пакет 22 — Элементы отверстий
Пакет 30 — Нагрузки на стержни (не поддерживаются Tekla Structures)
Пакет 40 — Сведения о соединении (не поддерживается Tekla Structures)
Пакет 50 — Сетки (не поддерживается Tekla Structures)
Пакет 60 — Изогнутые элементы
Если мы посмотрим на файл SDNF и сосредоточимся только на элементах пакета 10 (линейный член), то увидим, что в нем десять строк записей. После строки пакета 10, единиц и количества элементов краткий обзор записей будет следующим:
Запись 1 — идентификатор участника; Кардинальная точка; Статус; Учебный класс; Тип; Марка и редакция
Запись 2 – Размер; Оценка; Вращение и т. д.
Запись 3 – Векторы ориентации
Запись 4 – Информация о смещениях
Запись 5 – Информация о смещениях
Запись 6 – Информация о выпуске
Запись 7 – Информация о производстве
Запись 8 – Информация о соединении
Запись 9 – Информация об отделке
Запись 10 – Информация об атрибутах
Примечание – ссылки на конкретные системы см. в PDS и PDMS.
в PDS и PDMS.
Как импортировать файл SDNF в Tekla Structures
1. В дополнительных параметрах экспорта установите для XS_SDNF_CONVERT_PL_PROFILE_TO_PLATE значение FALSE .
2. Выберите Файл — Импорт — CAD
Изображение
3. Выберите Импорт модели и нажмите кнопку свойств.
Изображение
4. Для импорта SDNF необходимо заполнить только вкладки Преобразование, Параметры, SDNF и Отчет. При необходимости вкладку преобразования можно заполнить. Для получения дополнительной информации см. файл преобразования
Изображение
5. Выберите нужный файл SDNF и убедитесь, что для параметра Тип установлено значение SDNF.
Изображение
6. На вкладке SDNF выберите тип формата SDNF (2.0 или 3.0). Узнайте, как определить различные отраслевые файлы, чтобы получить дополнительную информацию.
Примечание . В большинстве случаев важно, чтобы для параметра Учитывать смещения было установлено значение Да, а для Типа номера позиции — Универсальный идентификатор.
Изображение
7. При необходимости можно запросить файл отчета об импорте.
Изображение
8. Затем можно настроить дополнительные действия. Все обычные значения установлены, и нет необходимости изменять эти настройки.
Изображение
9. Нажмите кнопки «Применить» и «ОК» , а затем «Импорт» 9.Кнопка 0034 в форме импорта модели.
Изображение
10. Затем выбирается диалоговое окно с информацией об импорте модели. В обычном случае можно выбрать кнопку «Принять все».
Изображение
11. Затем вам нужно подтвердить, что вы хотите сохранить импортированную модель для последующего импорта.
Изображение
12. После импорта модели рекомендуется щелкнуть правой кнопкой мыши вид модели и выбрать параметр « Подогнать рабочую область ко всей модели », чтобы убедиться, что импортированная модель полностью видна. Кроме того, если части отсутствуют, необходимо увеличить значения глубины просмотра вверх и вниз.
Как создать файл SDNF в Tekla Structures для PDMS
Во-первых, обычно важно в дополнительных параметрах экспорта установить XS_SDNF_CONVERT_PL_PROFILE_TO_PLATE на FALSE .
Изображение
Для создания файла SDNF необходимо заполнить только вкладки «Преобразование», «Параметры» и «SDNF».
Изображение
Необходимо заполнить имя выходного файла. Использование расширения *.dat или иногда *.sdnf для файлов SDNF является обычным преобразованием, но можно добавить любое расширение.
Изображение
Примечание . В большинстве случаев важно, чтобы для параметра Учитывать смещения было установлено значение Да, а для Типа номера позиции — Универсальный идентификатор.
После заполнения формы выберите «Применить и создать», и нужный файл будет создан в текущей рабочей папке.
Замечания по моделированию
Для переноса проемов разрезы должны быть созданы с помощью параметра «вырезать деталь с многоугольником». В этом случае все открытия будут переданы как элементы пакета 22 (открытие), а все остальные сокращения будут проигнорированы.
В этом случае все открытия будут переданы как элементы пакета 22 (открытие), а все остальные сокращения будут проигнорированы.
Криволинейные балки должны быть созданы с параметром криволинейной балки на вкладке «Свойства положения», поскольку кривизна криволинейных элементов, созданных как составные балки, будет игнорироваться.
Также следует отметить, что составные балки уникальны для Tekla Structures и обычно не передаются. Например, если составная балка создается с изменением направления, при создании файла SDNF в файл будет включена только исходная длина прямой, а другие элементы будут проигнорированы.
В некоторых случаях фитинги и соединения не включаются в файлы SDNF. В этом случае соединение необходимо расчленить, прежде чем части соединения будут включены в файл экспорта.
СДНФ | Программные решения для гражданского строительства
/ Graitec Group / 5 комментариев
GRAITEC BIM Connect — это программная надстройка для Autodesk REVIT, которая является частью решения GRAITEC BIM. С помощью GRAITEC BIM Connect пользователи Autodesk REVIT могут быстро подключить свои модели REVIT к пакету GRAITEC Advance, а затем оптимизировать проектирование своих конструкций в соответствии со стандартами США и ЕВРОКОДА, создавать эффективные и безошибочные чертежи общего вида, рабочие чертежи, Спецификации и файлы ЧПУ как для стальных, так и для бетонных конструкций.
В версии 2013 были добавлены важные функции:
- Автоматическая установка из ADVANCE Setup;
- Новый формат файла GTCX;
- Экспорт фальцованных плит и фальцевых балок;
- Добавлено 6000 линий отображения профиля, включая повороты профиля для Северной Америки и Великобритании;
- В Autodesk REVIT добавлена новая специальная вкладка ленты для включения всех команд («Экспорт», «Импорт», «Синхронизация», «Настройки» и «О программе»).

Внесено множество новых улучшений для повышения производительности и обеспечения большего отклика при работе с большими проектами:
- Сокращение времени импорта модели в Autodesk REVIT независимо от количества пластин;
- Правильный импорт и вращение для криволинейных балок и криволинейных фундаментов;
- Импорт гнутых или криволинейных стен вне зависимости от формата;
- Автоматическое распознавание конкретных разделов, независимо от формата файла и без необходимости сопоставления.
Используя GRAITEC BIM Connect 2013, вы также можете импортировать/экспортировать в другие форматы файлов BIM, такие как IFC, SDNF, CIS2 (уже сертифицирован), PSS и KISS.
Вы можете прочитать здесь полные документы о новых функциях и улучшениях для GRAITEC BIM Connect 2013. Не стесняйтесь оставлять нам свои отзывы, чтобы помочь нам улучшить другие функции программного обеспечения.
Для этого слайд-шоу требуется JavaScript.
Вот так:
Нравится Загрузка…
/ Graitec Group / Оставить комментарий
Инженеры-строители:
Вам нужно использовать Еврокоды и сократить время проекта?
в четверг, 15 мая th , 2012 с 09:00 до 09:30 CET или с 17:00 до 17:30 CET
| Зарегистрируйтесь на этот вебинар онлайн |
Advance Design® специально предназначен для инженеров-строителей, которым требуется профессиональное и простое в использовании решение для моделирования и оптимизации всех их проектов. Advance Design® включает в себя удобное средство моделирования конструкций, автоматические генераторы нагрузок и комбинированных генераторов, мощный механизм анализа методом конечных элементов (статический, динамический, временной анализ, нелинейный анализ, анализ потери устойчивости, анализ больших перемещений и т. д.), комплексные мастера для проектирования бетона и стали. участников, а также эффективную постобработку результатов и автоматические генераторы отчетов. Он автоматически обновляет все отчеты, включая графические результаты, когда в модель вносятся изменения.
д.), комплексные мастера для проектирования бетона и стали. участников, а также эффективную постобработку результатов и автоматические генераторы отчетов. Он автоматически обновляет все отчеты, включая графические результаты, когда в модель вносятся изменения.
Advance Design TOP 5 преимуществ:
1 – Мощная система моделирования, предназначенная для инженеров: реалистичная визуализация, управление этажами зданий, полная библиотека конструктивных элементов, определяемых пользователем, генератор нагрузки и т. д.
2 – Расширенный анализ функции: автоматическое создание сетки, временной анализ, статический, динамический, нелинейный анализ и т. д.
3 – Последние версии реализованных Еврокодов: Трехмерные кривые взаимодействия, проверка прогибов, проверка потери устойчивости и поперечной потери устойчивости, проектирование соединений и т. д.
4 – Технология «Память результатов»: избегайте повторяющихся задач, автоматически обновляя все документы постобработки (виды и отчеты) при изменении 3D-модели.
5 — BIM и совместная работа: Импорт DXF / DWG / Revit, многопользовательская технология, подход BIM для синхронизации данных, совместимость с отраслевыми стандартами (SDNF, CIS/2, IFC) и т. д.
Интернационализация — это основная тема версии 2012 Advance Design® с реализацией нескольких новых национальных приложений к Еврокоды 0, 1, 2, 3, 5 и 8.
Эта версия также позволяет пользователям пойти дальше в применении Еврокодов с ее многочисленными дополнительными функциями: управление зданиями, открытыми для ветра, проектирование деревянных конструкций для EC5 или расчет трещин в зависимости от примененной арматуры для EC2.
Advance Design® — незаменимый инструмент для разработки крупномасштабных проектов.
Нравится:
Нравится Загрузка…
/ Graitec Group / Оставить комментарий
Специалисты по обработке стали, инженеры-конструкторы:
Откройте для себя Advance Steel 2012: мощное и доступное программное обеспечение для обработки стали
, среда, 3 мая rd , 9:00 3:00 CET 9:00:00 CET :00–17:30 CET
| Зарегистрируйтесь на этот вебинар онлайн |
Advance Steel® специально разработана для профессионалов, которым требуется простое в использовании программное обеспечение для трехмерной детализации металлоконструкций, которое автоматизирует создание чертежей, спецификаций и файлов ЧПУ.
Advance Steel® является частью решения GRAITEC для структурной BIM, автоматизируя весь процесс проектирования конструкций, от инженерного проектирования до детализации и изготовления.
Преимущества Advance Steel TOP 5:
1 — Повышение производительности благодаря гибким и эффективным автоматическим инструментам 3D-моделирования: полных международных каталога, библиотека параметрических соединений, однопользовательский или многопользовательский режим и т. д.
2 – Короткая кривая обучения: сокращает время адаптации новых сотрудников.
3 – Специальные функции для различной стали и листового металла: автоматические функции для всех типов лестниц и перил, автоматические инструменты для создания листового металла, гнутые и скрученные пластины. и т. д.
4 – Точное и автоматическое создание и обновление конструкторской документации: спецификации, автоматически создаваемые из 3D-модели, контроль версий, облака редакций, шаблон презентации чертежа, автоматическое масштабирование чертежа, форматы бумаги и виды и т. д.
д.
5 – BIM и совместная работа: Импорт DXF/DWG/Revit, многопользовательская технология, совместимость с ведущими в отрасли пакетами для детализации/производства/инжиниринга/MRP (CIS/2, SDNF, DSTV, KISS и т. д.) и т. д.
Advance Steel® 2012, исторически основанная на платформе AutoCAD®, позволяет пользователям использовать свое программное обеспечение с AutoCAD® или без него. Фактически продукт включает в себя собственный графический движок, и пользователь может выбрать нужную платформу САПР. Независимо от выбранной платформы сохраняются все основные функции программного обеспечения, а также совместимость с DWG®.
Это крупное изменение также позволило GRAITEC упростить пользовательский интерфейс, сосредоточив внимание на отраслевых функциях программного обеспечения и организовав их.
Еще одно важное преимущество для пользователей: общая стоимость решения и простота установки и развертывания. Окупаемость инвестиций для текущей версии улучшена на 30 % .
Нравится:
Нравится Загрузка…
Домашняя страница — SAP2000 — Computers and Structures, Inc.
SAP2000 — это универсальное программное обеспечение для гражданского строительства, идеально подходящее для анализа и проектирования структурных систем любого типа. Базовые и расширенные системы, от 2D до 3D, от простой геометрии до сложной, можно моделировать, анализировать, проектировать и оптимизировать с помощью практичной и интуитивно понятной среды объектно-ориентированного моделирования, которая упрощает и оптимизирует процесс проектирования. SAPFire® Analysis Engine, встроенный в SAP2000, управляет сложной процедурой конечно-элементного анализа. Пользователям доступен дополнительный набор расширенных функций анализа, использующих самые современные методы анализа нелинейных и динамических характеристик. SAP2000, созданный инженерами для эффективного проектирования, является идеальным программным инструментом для пользователей любого уровня опыта при проектировании любой структурной системы.
Интегрированные шаблоны моделирования, назначения нагрузки на основе кода, расширенные параметры анализа, процедуры оптимизации конструкции и настраиваемые выходные отчеты — все это координируется на мощной платформе, что делает SAP2000 особенно полезным для практикующих профессионалов.
SAP2000 также является отличным средством обучения. Откройте SAP2000 и просмотрите серию видеороликов Watch & Learn, чтобы получить не только инструкции по использованию программного обеспечения, но и ознакомиться с философией и практикой проектирования конструкций.
На этой странице:
Встроенные шаблоны моделирования, универсальный и удобный интерфейс, интуитивно понятные элементы управления и функции — все это в совокупности упрощает и ускоряет сложный процесс объектно-ориентированного моделирования. Широкий спектр вариантов моделирования обеспечивает использование методов и технологий, находящихся на переднем крае проектирования строительных конструкций. Домен модели может быть компонентным, системным или глобальным по объему, охватывая при этом компоненты земляного полотна и взаимодействие между грунтом и конструкцией. Линия сетки, привязка и инструменты репликации — это лишь некоторые из множества практических функций, которые делают среду и процесс моделирования доступными для начинающих и сложными для опытных пользователей.
Линия сетки, привязка и инструменты репликации — это лишь некоторые из множества практических функций, которые делают среду и процесс моделирования доступными для начинающих и сложными для опытных пользователей.
Линейные или криволинейные элементы, тросы и предварительно натянутые арматуры, соединительные элементы с модельными пружинами, демпферы, изоляторы и связанные с ними нелинейные и гистерезисные характеристики, каркас, оболочка или многослойная оболочка, сплошные элементы с изопериметрической формулой и нелинейной реакцией все варианты моделирования сборки объектов в SAP2000. Если предпочтительные элементы конструкции не представлены в обширных библиотеках SAP2000, конструктор сечений доступен для пользовательского проектирования поперечных сечений. Пользователи задают геометрию и состав материала до того, как Section Designer автоматически рассчитает свойства стержня и создаст диаграммы двухосного взаимодействия и кривизны момента.
Назначение нелинейных волоконных шарниров — еще один доступный расширенный метод моделирования. SAP2000 реализует поведение шарниров на основе кода или эмпирически, моделируя геометрию и материалы как дискретные точки в поперечном сечении, а затем сопоставляя эти дискретные области с их нелинейным поведением. Соображения предельного состояния и гистерезиса также могут быть реализованы при нелинейно-статическом и динамическом анализе.
SAP2000 реализует поведение шарниров на основе кода или эмпирически, моделируя геометрию и материалы как дискретные точки в поперечном сечении, а затем сопоставляя эти дискретные области с их нелинейным поведением. Соображения предельного состояния и гистерезиса также могут быть реализованы при нелинейно-статическом и динамическом анализе.
После создания объектной модели SAPFire® Analysis Engine автоматически преобразует сборку в конечно-элементную модель, объединяя область материала с эффективной сетью четырехугольных подэлементов. Алгоритмы совместной интерполяции управляют технологией автоматического ограничения границ для соединения несоответствия сетки. После этого доступен инструмент Reshaper Tool для изменения формы и уточнения сетки.
SAP2000 — идеальный инструмент для моделирования структурных систем любой сложности и любого типа проекта. Здания, мосты, транспортная инфраструктура, такие специальные конструкции, как дамбы, спортивные сооружения и морские системы — вот лишь несколько примеров безграничных возможностей проектирования.
Мощные встроенные шаблоны также упрощают и ускоряют процесс загрузки приложений. Сейсмические, ветровые, транспортные, волновые и тепловые силы могут автоматически генерироваться и назначаться в соответствии с набором правил на основе кодов. Пользователи могут свободно определять и ограничивать неограниченное количество загружений и комбинаций.
Функции создания движущейся нагрузки и библиотека приложений для транспортных средств AASHTO обеспечивают оценку систем транспортной инфраструктуры. Для морских систем функции создания волновой нагрузки учитывают статическую и динамическую реакцию волн, течений, плавучести и ветра при учете инерционных эффектов.
Условия огибающей нагрузки могут сочетаться с некоторыми передовыми методами анализа и построения (эффект P-Delta, сегментное построение и т. д.) для дополнительного понимания реакции конструкции.
Ряд инновационных методов анализа интегрирован в возможности SAP2000. Пользователи могут свободно дополнять стандартный, но сложный процесс анализа, реализуя расширенные функции для нелинейного и динамического рассмотрения. Эта универсальность делает SAP2000 практичным и продуктивным инструментом для любого типа анализа, от простого статического, линейно-упругого до более сложного динамического, нелинейно-неупругого.
Эта универсальность делает SAP2000 практичным и продуктивным инструментом для любого типа анализа, от простого статического, линейно-упругого до более сложного динамического, нелинейно-неупругого.
Прежде всего SAPFire® Analysis Engine обеспечивает оптимизацию анализа с помощью нескольких 64-разрядных решателей. Варианты включают анализ Эйгена (с автоматическим сдвигом для плохо обусловленных отношений) и анализ Ритца (для ускоренной сходимости). Эффект P-дельта улавливает геометрическую нелинейность. Анализ потери устойчивости дает представление о структурной устойчивости с помощью методов, характеризующих линейную потерю устойчивости (при которой учитываются несколько режимов потери устойчивости в нелинейно-статическом или динамическом приложении), нелинейная потеря устойчивости (при которой учитывается P-дельта и эффекты большого отклонения), сквозная потеря устойчивости и прогрессирующее разрушение. . Нелинейность материала отражает неупругое поведение и поведение в предельном состоянии, а также такие зависящие от времени явления, как поведение ползучести и усадки в железобетонных системах. Пластмассовый шарнир может быть указан в изгибаемых элементах в соответствии со стандартами на основе норм или эмпирическими данными. Пружины растяжения и сжатия могут быть назначены с ограничениями и нелинейными атрибутами для имитации пластичности опоры.
Пластмассовый шарнир может быть указан в изгибаемых элементах в соответствии со стандартами на основе норм или эмпирическими данными. Пружины растяжения и сжатия могут быть назначены с ограничениями и нелинейными атрибутами для имитации пластичности опоры.
Для имитации землетрясений доступны статические и динамические методы. Анализы нелинейно-статического толкания могут учитывать модальные, равномерные или заданные пользователем схемы поперечной нагрузки, пластическое шарнирное поведение гибких элементов, неупругую реакцию сдвиговых стен, плит перекрытий и стальных пластин, а затем формулировать требуемую мощность, демпфирование, и расчеты производительности с настраиваемыми сводными отчетами.
Динамические методы включают спектр отклика (для вероятного максимального сейсмического отклика с учетом псевдоспектрального ускорения в зависимости от кривой структурного периода), спектрально-плотностную мощность и установившийся режим (для усталостного поведения с необязательными свойствами демпфирования и комплексного импеданса) и анализ истории времени. Временные истории могут следовать модальным методам или методам прямого интегрирования, и они могут быть объединены в цепочку и охвачены такими расширенными анализами, как P-дельта и процедуры поэтапного построения.
Временные истории могут следовать модальным методам или методам прямого интегрирования, и они могут быть объединены в цепочку и охвачены такими расширенными анализами, как P-дельта и процедуры поэтапного построения.
Особенности многоступенчатого строительства. Последовательность построения запланирована с вариантами диаграммы Ганта, окружена показателями производительности и сопряжена с процедурами анализа. На каждом этапе строительства оценка может учитывать статическую или динамическую реакцию конструкции, опорные реакции, геометрическую и материальную нелинейность (включая коробление, ползучесть и усадку), применение арматуры и тросов с целевым натяжением и т. д. Функция «Моделирование в реальном времени» доступна для небольших для проектов среднего размера для анализа реальных или возможных структурных модификаций.
Программа Design полностью интегрирована с процессом расчета, обрабатывая результаты перед автоматическим определением размеров стальных элементов и проектированием железобетонных профилей. Автоматическая проверка норм проектирования стальных, бетонных, алюминиевых и холодногнутых каркасов гарантирует, что конструкции соответствуют критериям американских, канадских и различных международных стандартов.
Автоматическая проверка норм проектирования стальных, бетонных, алюминиевых и холодногнутых каркасов гарантирует, что конструкции соответствуют критериям американских, канадских и различных международных стандартов.
Вывод и варианты отображения интуитивно понятны и практичны. Окончательная конструкция стержня, деформированная геометрия в соответствии с комбинацией нагрузок или формой режима, диаграммы момента, сдвига и осевой силы, отображение отклика сечения и анимация зависимых от времени смещений представляют собой некоторые из графиков, доступных по завершении анализа. SAP2000 автоматически генерирует отчеты для представления изображений и данных. Пользователям доступны встроенные и настраиваемые шаблоны для специализированного форматирования.
SAP2000 также предоставляет набор функций взаимодействия . Выходные отчеты могут передаваться на платформы Microsoft в формате файла RTF или на веб-сайты в формате HTML. Модели SAP2000 можно импортировать и экспортировать между STEP CIS/2, SDNF, AutoCAD, Frameworks Plus, IGES и Prosteel.
Открытый интерфейс прикладного программирования SAP2000 (OAPI) позволяет разработчикам создавать собственные программные приложения, связывающие соответствующие платформы проектирования с функциями SAP2000. Поддерживаются Visual Basic и большинство стандартных языков. Посетите страницу OAPI веб-сайта CSI, чтобы узнать больше о совместимости с SAP2000.
Для продукта SAP2000 предлагается несколько различных уровней возможностей. Каждый последующий уровень предоставляет дополнительный набор возможностей. Подробную информацию см. на странице «Уровни и функции» веб-сайта CSI.
См. страницу учебника по SAP2000.
См. страницу «Проблемы тестирования SAP2000».
Авирам, А., Маки, К., Стоядинович, Б. (2008). Руководство по нелинейному анализу мостовых конструкций в Калифорнии . Беркли, Калифорния: Тихоокеанский центр инженерных исследований землетрясений (PEER).
Подведены богатыми и несостоятельными бедными, глобальная схема вакцинации должна быть встряхнута – ресурсы SDNF
Отверженные богатыми странами и неспособные удовлетворить потребности самых бедных, программа, совместно возглавляемая Всемирной организацией здравоохранения (ВОЗ) для справедливого распределения вакцин против COVID-19 планирует встряску, как показывают внутренние документы, с которыми ознакомилось агентство Reuters.
Программа COVAX далека от своей цели по доставке 2 миллиардов доз к концу года, но ожидает значительного увеличения поставок к началу 2022 года и хочет убедиться, что, по крайней мере, они достигнут стран в крайней нужде.
Первоначальные высокие амбиции COVAX действовать в качестве информационного центра для мировых вакцин, собирая вакцины у производителей в наиболее развитых странах и быстро распределяя их среди наиболее нуждающихся, не оправдались.
На данный момент было распространено всего 90 миллионов вакцин. В то время как густонаселенные страны с низким уровнем дохода выступают в качестве инкубаторов для новых и более опасных штаммов коронавируса, некоторые из самых бедных стран вакцинировали менее 1% своего населения, согласно оценкам Gavi, глобального альянса по вакцинам, который управляет схемой с ВОЗ.
Капитальный ремонт призван снизить финансовые риски COVAX, сосредоточить внимание на наиболее нуждающихся странах и сократить участие более богатых стран в качестве доноров и получателей помощи, согласно документу, подготовленному Gavi.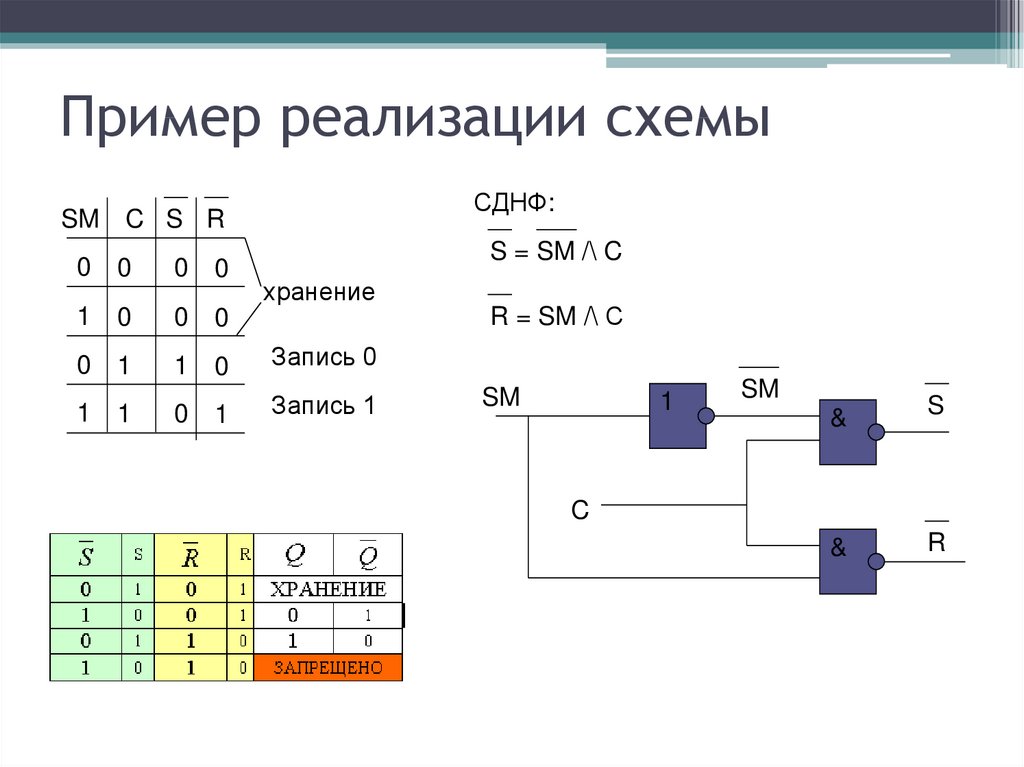
Ожидается, что документ будет принят на заседании правления Гави в среду и четверг.
«Предложение состоит в том, чтобы при условии утверждения Советом директоров сосредоточить усилия COVAX по закупкам на всех SFP (самофинансирующихся участниках), которые будут по-прежнему нуждаться в средстве, таким образом, чтобы упростить операции и снизить финансовые риски на основе уроки, извлеченные за последний год», — сказала пресс-секретарь Gavi.
ВОЗ не дает немедленных комментариев, но обычно позволяет Гави говорить о COVAX от своего имени.
БЛАГОТВОРИТЕЛЬНОСТЬ НАЧИНАЕТСЯ НА ДОМУ
Богатые страны обычно предпочитают использовать свое финансовое влияние, чтобы покупать собственные вакцины напрямую у производителей.
И, несмотря на просьбы ВОЗ поделиться любыми излишками вакцин через свою программу, Соединенные Штаты, Япония и Европейский Союз наметили планы по безвозмездной помощи странам, а также COVAX.
Ставя в приоритет свои собственные дипломатические и коммерческие интересы, богатые страны фактически разрушили стремление COVAX взять на себя полную ответственность за глобальную борьбу с пандемией.
«Тот факт, что правление Gavi в настоящее время пересматривает способ, которым более богатые страны могут продолжать участвовать в учреждении, частично является признанием того, что установка не работает», — сказала Кейт Элдер, старший советник по вопросам политики в медицинской помощи. группа «Врачи без границ».
Около 190 стран в настоящее время являются членами COVAX, но одна треть не использует его вакцины, и только около 40 начали свои кампании по вакцинации с прививками от COVAX, говорится в документе Gavi.
В отдельном внутреннем документе Гави оценивает, что количество членов может сократиться до 120-130 в следующем году.
Ожидается, что многие богатые страны добровольно уйдут в отставку, но запланированное изменение политики также сделает участие стран со средним уровнем дохода более дорогостоящим.
В то время как сейчас Gavi берет на себя значительные финансовые риски, заказывая вакцины от имени своих членов, в следующем году страны со средним уровнем дохода, которые все еще нуждаются в вакцинах COVAX, должны будут заплатить за них полностью заранее.
Это означает, что страны Латинской Америки и Ближнего Востока, а также страны, подобные Южной Африке, могут столкнуться с более высокими затратами и должны занимать деньги для получения доз.
НАИБОЛЕЕ БЕДНЫЕ В ПЕРВУЮ ОЧЕРЕДЬ
Тем не менее, самые бедные страны, в основном в Африке и Юго-Восточной Азии, сохранят те же условия с минимальными или нулевыми затратами на покупку вакцин.
«Модель будет переработана с менее гибкими условиями, направленными на упрощение и снижение финансовых рисков, чтобы удержать страны, которые нуждаются в средстве, при этом лишив другие страны возможности продолжать участие после конца 2021 года», — говорится в одном из документов.
И это должно иметь ощутимые преимущества для самых бедных стран.
Компания COVAX привлекла почти 10 миллиардов долларов сверх запланированного на этот год плана и начала получать избыточные дозы от богатых стран. Однако массовые закупки вакцин богатыми государствами и ограничение экспорта из Индии, основного поставщика вакцины, привели к тому, что более бедные страны столкнулись с нехваткой поставок.
Гави считает, что прогнозируемое увеличение поставок во второй половине года может увеличить долю вакцинированных в беднейших странах почти до 30% к началу 2022 года9.0005
Gavi планирует потратить 775 миллионов долларов, чтобы помочь странам распространять эти вакцины и избежать повторных случаев потерь, вызванных недостаточной подготовкой и недостаточной инфраструктурой.
Поскольку эти страны столкнулись с возможным пятикратным увеличением ежемесячного производства вакцин, риск таких потерь высок, говорится в одном документе.
Деньги будут использованы для укрепления системы доставки COVAX, предоставления более качественного холодильного оборудования и улучшения систем здравоохранения, говорит Гави.
Источник: https://www.thedailystar.net/coronavirus-deadly-new-threat/news/let-down-rich-and-failing-the-poor-global-vaccine-scheme-be-shaken- 2116709
Конъюнктивные формы представления логических функций. Нормальные формы логических функций Алгоритм построения нормальных форм
Простая конъюнкция вызываемая конъюнкция одна или несколько переменных , at this each variable meets not more one times ( or herself , or her negation ).
Например, простой союз,
дизъюнктивный нормальный форма (ДНФ) называется дизъюнктивный простой
3 союзы0494 .Например, выражение DNF.
Perfect disjunctive normal form (SDNF) called such disjunctive normal the form , at which in every conjunction включены все переменные данные список ( или Сами , или Им Отказ ), и в One и . и . и .
Например, выражение является DNF, но не SDNF. Выражение — SDNF.
Аналогичные определения (с заменой конъюнкции на дизъюнкт и наоборот) верны для КНФ и СКНФ. Приводим точные формулировки.
Простой disjunction called disjunction one or several variables , at this each variable included not more one times ( или сама , или ее отрицание ).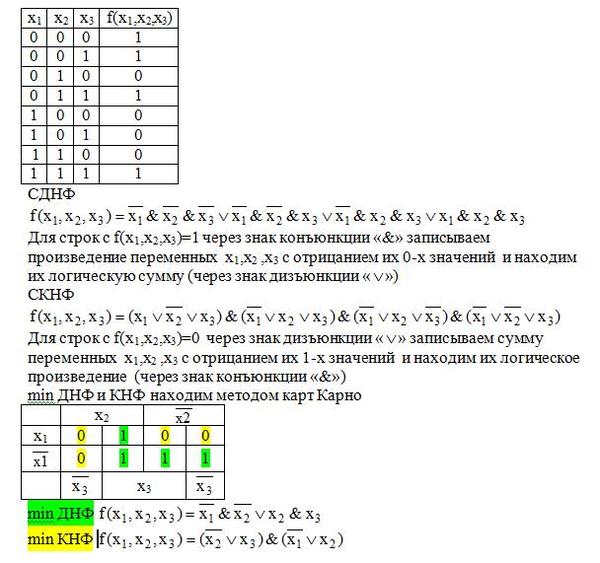 Например, выражение представляет собой простую дизъюнкцию,
Например, выражение представляет собой простую дизъюнкцию,
Конъюнктивальный нормальная форма (КНФ) вызываемая конъюнкция простая дизъюнкция (например, выражение — КНФ).
Совершенная конъюнктивная нормальная форма (ПКНФ) — это КНФ, в которой каждая простая дизъюнкция включает все переменные из этого списка (либо самих себя, либо их отрицания) и в том же порядке.
Например, выражение SKNF.
Представлены алгоритмы перехода из одной формы в другую. Естественно, в конкретных случаях (при определенном творческом подходе) использование алгоритмов может оказаться более трудоемким, чем простые преобразования, использующие конкретную форму заданной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: над ДНФ ставим два отрицания и по правилам де Моргана (не трогая верхнее отрицание) возвращаем отрицание ДНФ обратно в ДНФ. В этом случае вы должны раскрыть скобки, используя правило поглощения (или правило Блейка). (Верхнее) отрицание полученной ДНФ (опять же по правилу де Моргана) немедленно дает нам КНФ:
(Верхнее) отрицание полученной ДНФ (опять же по правилу де Моргана) немедленно дает нам КНФ:
Заметим, что КНФ также можно получить из исходного выражения, если вычесть и для кронштейнов;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (в этом случае снова используется правило поглощения)
Таким образом, мы получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с задачей минимизации ДНФ. Это будет обсуждаться более подробно в разд. 5, здесь мы показываем, как упростить DNF (или SDNF) по правилу Блейка. Такая ДНФ называется , сокращенно ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей: К 1 К 2. Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар термов, а затем применяем обычное поглощение;
Если добавленный терм уже содержался в ДНФ, то его можно вообще отбросить, например,
или
Конечно, сокращенная ДНФ определяется не однозначно, но все они содержат одни и те же числовые буквы (например, есть ДНФ , после применения к ней правила Блейка можно прийти к ДНФ, эквивалентной заданной 1):
в) переход из ДНФ в СДНФ
Если в какой-то простой конъюнкции отсутствует переменная, например, z , вставляем в нее выражение, после чего раскрываем скобки (повторяющиеся не пишем дизъюнктные термины). Например:
Например:
г) переход от КНФ к СКНФ
Этот переход осуществляется аналогично предыдущему: если в простой дизъюнкции отсутствует какая-либо переменная (например, z , то к ней прибавляется выражение ( это не меняет самой дизъюнкции), после чего раскрываем скобки по закону распределения):
Таким образом, СКНФ получается из КНФ.
Обратите внимание, что минимальная или сокращенная CNF обычно получается из соответствующей DNF.
Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к CNF. Для этого можно использовать: закон двойного отрицания, закон де Моргана, дистрибутивность.
Энциклопедический YouTube
1 / 5
Формулы в KNF :
¬ A ∧ (B ∨ C) , (\ displaystyle \ neg A \ клин (B \ vee C),) (A ∨ B) ∧ (¬ B ∨ C ∨ ¬ D) ∧ (D ∨ ¬ E) , (\ displaystyle (A \ vee B) \ клин (\ neg B \ vee C \ vee \ neg D) \ клин ( D\vee\neg E),) А ∧ Б . (\ Displaystyle А \ клин Б.)
(\ Displaystyle А \ клин Б.)Формулы не в KNF :
¬ (B ∨ C) , (\ displaystyle \ neg (B \ vee C),) (A ∧ B) ∨ C, (\ displaystyle (A \ клин B) \ vee C,) А ∧ (В ∨ (D ∧ Е)) . (\ displaystyle A \ клин (B \ vee (D \ клин E)).)Но эти 3 формулы не эквивалентны в CNF следующим формулам в CNF:
¬ B ∧ ¬ C , (\ Displaystyle \ отр. B \ клин \ отр. C,) (A ∨ C) ∧ (B ∨ C) , (\ Displaystyle (A \ vee C) \ клин (B \ vee C),) А ∧ (В ∨ D) ∧ (В ∨ Е) . (\ displaystyle A \ клин (B \ vee D) \ клин (B \ vee E).)Строительство УЯТ
Алгоритм построения УТС
1) Избавьтесь от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать с помощью эквивалентных формул:
A → B знак равно ¬ A ∨ B , (\ displaystyle A \ rightarrow B = \ neg A \ vee B,) А ↔ В знак равно (¬А ∨ В) ∧ (А ∨ ¬В) . (\ displaystyle A \ leftrightarrow B = (\ neg A \ vee B) \ клин (A \ vee \ neg B).)2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимся к отдельным переменным высказываниям, исходя из формул:
¬ (A ∨ B) = ¬ A ∧ ¬ B , (\ displaystyle \ neg (A \ vee B) = \ neg A \ клин \ neg B,) ¬ (А ∧ В) знак равно ¬ А ∨ ¬ В . (\ displaystyle \ neg (A \ клин B) = \ neg A \ vee \ neg B.)
(\ displaystyle \ neg (A \ клин B) = \ neg A \ vee \ neg B.)3) Избавьтесь от двойных отрицательных знаков.
4) Применить, если необходимо, к операциям конъюнкции и дизъюнкции свойства формул дистрибутивности и поглощения.
Пример построения УНВ
Приведем формулу к CNF
F = (X → Y) ∧ ((¬Y → Z) → ¬X) . (\ Displaystyle F = (X \ стрелка вправо Y) \ клин ((\ отрицательный Y \ стрелка вправо Z) \ стрелка вправо \ отрицательный X).)Преобразуем формулу F (\displaystyle F) в формулу, не содержащую → (\displaystyle\rightarrow ):
F = (¬X ∨ Y) ∧ (¬ (¬Y → Z) ∨ ¬X) = (¬X ∨ Y) ∧ (¬ (¬ ¬Y ∨ Z) ∨ ¬X) . (\ displaystyle F = (\ neg X \ vee Y) \ клин (\ neg (\ neg Y \ стрелка вправо Z) \ vee \ neg X) = (\ neg X \ vee Y) \ клин (\ neg (\ neg \ отрицательный Y\vee Z)\vee \neg X).)В полученной формуле переносим отрицание в переменные и уменьшаем двойные отрицания:
F = (¬X ∨ Y) ∧ ((¬Y ∧ ¬Z) ∨ ¬X) . (\ displaystyle F = (\ neg X \ vee Y) \ клин ((\ neg Y \ клин \ neg Z) \ vee \ neg X). )
)Например, следующая формула записана в 2-CNF:
(A ∨ B) ∧ (¬B ∨ C) ∧ (B ∨ ¬C) . (\displaystyle (A\lor B)\land (\neg B\lor C)\land (B\lor \neg C).)Определение 1. Конъюнктивным мономом (элементарной конъюнкцией) от переменных называется конъюнкция этих переменных или их отрицаний.
например , это элементарное соединение.
Определение 2. Дизъюнктивный одночлен (элементарная дизъюнкция) от переменных называется дизъюнкцией этих переменных или их отрицаний.
например , это элементарная дизъюнкция.
Определение 3. Формула, эквивалентная заданной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных конъюнктивных мономов, называется дизъюнктивной нормальной формой (ДНФ) этой формулы.
Например, — ДНФ.
Определение 4. Формула, эквивалентная заданной формуле алгебры высказываний и являющаяся конъюнкцией элементарных дизъюнктивных мономов, называется конъюнктивная нормальная форма (CNF) этой формулы.

например , — КНФ.
Для каждой формулы алгебры высказываний можно найти набор дизъюнктивных и конъюнктивных нормальных форм.
Алгоритм построения нормальных форм
Используя эквивалентности алгебры логики, заменить все операции в формуле на основные: конъюнкция, дизъюнкция, отрицание:
Избавьтесь от двойных отрицаний.
При необходимости применить к операциям конъюнкции и дизъюнкции свойства формул дистрибутивности и поглощения.
2.6. Совершенные дизъюнктивные и совершенные конъюнктивные нормальные формы
Любая булева функция может иметь множество представлений ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).
Определение 1. Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, в которой каждый конъюнктивный моном содержит каждую переменную из множества ровно один раз, причем входит либо она сама, либо ее отрицание.

Структурно СДНФ для каждой приведенной к ДНФ формулы алгебры высказываний можно определить следующим образом:
Определение 2. Совершенная дизъюнктивная нормальная форма (СДНФ) формулы алгебры высказываний называется ее ДНФ, которая обладает следующими свойствами:
Определение 3. Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, в которой каждый дизъюнктивный моном содержит каждую переменную из множества ровно один раз, причем входит либо она сама, либо ее отрицание.
Структурно СКНФ для каждой формулы алгебры высказываний, приведенной к КНФ, можно определить следующим образом.
Определение 4. Совершенная конъюнктивная нормальная форма (СКНФ) данной формулы алгебры высказываний является ее КНФ, которая удовлетворяет следующим свойствам.
Теорема 1. Любая булева функция переменных, не являющаяся тождественно ложной, может быть представлена в СДНФ, причем единственным образом.

Способы найти SDNF
1-й путь
2-й путь
выберите строки, где формула принимает значение 1;
делаем дизъюнкт союзов при условии, что если переменная входит в союз со значением 1, то пишем эту переменную, если со значением 0, то ее отрицание. Получаем СДНФ.
Теорема 2. Каждая булева функция переменных, не являющаяся тождественно истинной, может быть представлена в СКНФ, причем единственным образом.
Способы нахождения СКНФ
1-й способ – с помощью эквивалентных преобразований:
2-й способ – с помощью таблиц истинности:
выделить строки, где формула принимает значение 0;
составляем конъюнкции дизъюнкции при условии, что если переменная входит в дизъюнкт со значением 0, то пишем эту переменную, если со значением 1, то ее отрицание. Получаем СКНФ.
Пример 1 График функций CNF .
Решение
Устранить связь «» с помощью законов преобразования переменных:
= /законы де Моргана и двойное отрицание/ =
/дистрибутивные законы/ =
Пример 2 Преобразовать формулу в ДНФ.

Решение
Выразим логические операции в терминах и:
= /Связать отрицание с переменными и уменьшить двойное отрицание/ =
= /закон дистрибутивности/ .
Пример 3 Запишите формулу в DNF и SDNF.
Решение
Используя законы логики, приведем эту формулу к виду, содержащему только дизъюнкции элементарных конъюнкций. Полученная формула будет искомой ДНФ:
Для построения СДНФ составим таблицу истинности для этой формулы:
Отмечаем те строки таблицы, в которых формула (последний столбец) принимает значение 1. Для каждой такой строки выписываем формулу, истинную на множестве переменных ,этой строки:
строка 1: ;
строка 3: ;
строка 5: .
Дизъюнкция этих трех формул примет значение 1 только на наборах переменных в строках 1, 3, 5 и, следовательно, будет искомой совершенной дизъюнктивной нормальной формой (ПДНФ):
Пример 4 Приведите формулу к СКНФ двумя способами:
а) с помощью эквивалентных преобразований;
б) с использованием таблицы истинности.

Решение:
Преобразуем вторую элементарную дизъюнктию:
Формула имеет вид:
б) составим для этой формулы таблицу истинности:
Отмечаем те строки таблицы, в которых формула (последний столбец) принимает значение 0. Для каждой такой строки выписываем формулу, истинную на множестве переменных ,этой строки:
строка 2 : ;
строка 6: .
Конъюнкция этих двух формул будет принимать значение 0 только на наборах переменных в строках 2 и 6 и, следовательно, будет искомой совершенной конъюнктивной нормальной формой (СКНФ):
Вопросы и задания для самостоятельного решения
1. С помощью эквивалентных преобразований привести формулы к ДНФ:
2. С помощью эквивалентных преобразований привести формулы к КНФ:
3. С помощью второго закона дистрибутивы преобразовать ДНФ в КНФ :
а) ;
4. Преобразовать заданные ДНФ в ОДНФ:
5. Преобразовать заданную КНФ в СКНФ:
6.
 По заданным логическим формулам построить ОДНФ и СКНФ двумя способами: с помощью эквивалентных преобразований и с помощью таблицы истинности.
По заданным логическим формулам построить ОДНФ и СКНФ двумя способами: с помощью эквивалентных преобразований и с помощью таблицы истинности.б) ;
Дизъюнктивные и конъюнктивные нормальные формы алгебры высказываний. Для каждой функции логики высказываний может быть составлена таблица истинности. Обратная задача также всегда разрешима. Введем несколько определений.
Элементарными союзами (конъюнктами) называются союзы переменных или их отрицаний, в которых каждая переменная встречается не более
один раз.
Дизъюнктивная нормальная форма (ДНФ) — это формула, имеющая вид дизъюнкции элементарных союзов.
Элементарными дизъюнкциями (по клаузулам) называются дизъюнкции переменных с отрицанием или без него.
Конъюнктивная нормальная форма (КНФ) – это формула, имеющая вид конъюнкции элементарных дизъюнкций.
Для каждой функции алгебры высказываний можно найти набор дизъюнктивных и конъюнктивных нормальных форм.

Алгоритм построения ДНФ:
1. Перейти к булевым операциям с использованием эквивалентных формул преобразования.
2. Перейти к формулам с близкими отрицаниями, т. е. к формуле, в которой отрицания расположены не выше, чем над переменными — применить законы де Моргана.
3. Раскрыть скобки — применить законы дистрибутивности.
4. Повторяющиеся члены брать один раз — закон идемпотентности.
5. Применять законы поглощения и полупоглощения.
Пример 6 Найти формулы ДНФ: .
В алгебре Буля принцип двойственности . Это происходит следующим образом.
Функция вызывается двойная функция если . Те. чтобы найти функцию, двойственную данной, необходимо построить отрицание функции из отрицаний аргументов.
Пример 7 Найдите функцию, двойственную .
Среди элементарных функций алгебры логики 1 двойственна 0 и наоборот, х двойственна х, двойственна , двойственна и наоборот.

Если в формуле F 1 , представляющей функцию, заменить все союзы
по дизъюнкции, дизъюнкция по конъюнкции, 1 по 0, 0 по 1, то получим формулу F*, представляющую функцию *, двойственную.
Конъюнктивная нормальная форма (КСН) является двойственным понятием для ДНФ, поэтому ее легко построить по схеме:
Пример 8 Найти формулы КНФ: .
Используя результат примера 6, мы имеем
Совершенные дизъюнктивные и совершенные конъюнктивные нормальные формы. В каждом из типов нормальных форм (дизъюнктивных и конъюнктивных) можно выделить класс совершенных форм СДНФ и СКНФ.
Совершенная элементарная конъюнкция представляет собой логическое произведение всех переменных с отрицанием или без него, причем каждая переменная входит в произведение только один раз.
Любая ДНФ может быть сведена к СДНФ путем расщепления конъюнкций, не содержащих всех переменных, т.е. сложение по отсутствующей переменной x i умножается по закону дистрибутивности
Пример 9 Найти SDNF для примера 6 DNF
Совершенная элементарная дизъюнкция называется логическая сумма всех переменных с отрицаниями или без них, причем каждая переменная входит в сумму только один раз.

Любая КНФ может быть сведена к СКНФ путем добавления члена-конъюнкции, не содержащего какой-либо переменной X i, путем конъюнкции и применения дистрибутивного закона
Пример 10 . Преобразовать CNF в SKNF:
Для построения СКНФ можно использовать схему
Пример 11. Найти СКНФ для формулы примера 6.
Каждая функция имеет SDNF и притом единственная . Каждая функция имеет СКНФ и, кроме того, единственный .
Поскольку SDNF и SKNF однозначно определяются формулами, их можно построить в соответствии с таблицей истинности формулы.
Для построения СДНФ необходимо выбрать строки, в которых F принимает значение 1, и записать для них совершенные элементарные конъюнкции. Если значение переменной в искомой строке таблицы истинности равно единице, то в совершенном конъюнкте оно берется без отрицания, если ноль, то с отрицанием. Затем совершенные конъюнкции (их количество равно количеству единиц в таблице) соединяются знаками дизъюнкции.

Для построения СКНФ по таблице истинности необходимо выделить в ней строки, где F=0, и записать совершенные элементарные дизъюнкции, а затем соединить их знаками конъюнкции. Если в искомой строке таблицы истинности (F=0) значение переменной соответствует нулю, то в совершенном дизъюнкте оно берется без отрицания, если равно единице, то с отрицанием.
Пример 12. Найти SDNF и SKNF по таблице истинности формулы примера 6.
В таблице 14 показано только окончательное значение F=10101101. Справедливость этого утверждения следует проверить самостоятельно, построив расширенную таблицу истинности.
Таблица 14
Введем понятие элементарной дизъюнкции.
Элементарная дизъюнкция представляет собой выражение вида
Конъюнктивной нормальной формой (КНФ) логической функции называется конъюнкция любого конечного множества попарно различных элементарных дизъюнкций. Например, логические функции
— это конъюнкции элементарных дизъюнкций.
 Поэтому они записываются в конъюнктивной нормальной форме.
Поэтому они записываются в конъюнктивной нормальной форме.Произвольную логическую функцию, заданную аналитическим выражением, можно привести к КНФ, выполнив следующие операции:
Использование правила инверсии, если операция отрицания применяется к логическому выражению;
Использование аксиомы дистрибутивности по отношению к умножению:
Использование операции поглощения:
Исключения в дизъюнкциях повторяющихся переменных или их отрицаний;
Удаление всех одинаковых элементарных дизъюнкций, кроме одной;
Удаление всех дизъюнкций, включающих одновременно переменную и ее отрицание.
Справедливость перечисленных операций следует из основных аксиом и соотношений тождеств алгебры логики.
Конъюнктивная нормальная форма называется совершенной, если каждая входящая в нее элементарная дизъюнкция содержит в прямой или обратной форме все переменные, от которых зависит функция.
Преобразование УНВ в совершенные УНВ осуществляется путем выполнения следующих операций:
Дополнения к каждой элементарной дизъюнкции союзов переменных и их отрицаний, если они не входят в эту элементарную дизъюнктию;
Использование аксиомы дистрибутивности;
Удаление всех одинаковых элементарных дизъюнкций, кроме одной.

Любая логическая функция может быть представлена в совершенной КНФ, кроме
.тождественно равно единице (). Отличительным свойством совершенной КНФ является уникальность представления в ней логической функции.
Элементарные дизъюнкции, входящие в совершенную КНФ-функцию, называются нулевыми составляющими. Каждая нулевая компонента в совершенной КНФ обращается в нуль на единственном множестве значений переменных, которое является нулевым множеством функции. Следовательно, число нулевых множеств логической функции совпадает с числом нулевых составляющих, входящих в ее совершенную КНФ.
Константа нуля логической функции в совершенной КНФ представлена конъюнкцией 2n, составляющей ноль. Сформулируем правило составления СКНФ логической функции по таблице соответствий.
Для каждой строки таблицы соответствий, в которой функция равна нулю, составляется элементарная дизъюнкция всех переменных. В дизъюнктию входит сама переменная, если ее значение равно нулю, или отрицание, если ее значение равно единице.
 Полученные элементарные дизъюнкции объединяются знаком конъюнкции.
Полученные элементарные дизъюнкции объединяются знаком конъюнкции.Пример 3.4. Для логической функции z(x), заданной интерполяционной таблицей 2.2, мы определяем совершенную конъюнктивную форму.
Для первой строки таблицы, соответствующей нулевому набору функций 000, находим нулевую компоненту . Выполняя аналогичные операции для второй, третьей и пятой строк, определяем искомую совершенную функцию КНФ:
Следует отметить, что для функций, число единичных множеств которых превышает число нулевых множеств, компактнее записывать их в виде СКНФ и наоборот.
Постройте логические схемы для следующих функций. Логические схемы и логические выражения. Требования к знаниям и умениям
4) Ответ: l v 0 & l = 1.
Пример 2
Постройте логическую схему, соответствующую логическому выражению
F = X & Y v (Y v X).
Вычислите значения выражения для X = 1, Y = 0.
1) Имеются две переменные: X и Y;
2) Есть три логических операции: конъюнкция и две дизъюнкции: 14 3 2 X & Y v (Y v X).
3) Строим схему слева направо в соответствии с порядком логических операций:
3) Вычислите значение выражения: F = l & 0 v (0 v 1) = 0
Выполните упражнение
Постройте логическую схему, соответствующую логическому выражению, и найдите значение логического выражения выражение:
A) F = A v B & C, если A = 1, B = 1, C = 1.
B) F = (A v B & C), если A = 0, B = 1, C = 1.
B) F = A v B и C, если A = 1, B = 0, C = 1,
D) F = (A v B) & (C v B), если A = 0, B = 1, C = 0.
E) F = (A & B & C), если A = 0, B = 0, C = 1.
E) F = (A & B & C) v (B & C vA), если A = 1, B = 1, C = 0.
G) F = B & A v B & A, если A = 0, B = 0.
Законы логики
Если логическое выражение содержит большое количество операций, то составить для него таблицу истинности достаточно сложно, так как приходится перебирать большое количество вариантов. В таких случаях удобно сократить формулы до нормальная форма.
В таких случаях удобно сократить формулы до нормальная форма.
Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, а знаки отрицания встречаются только у логических переменных.
Для приведения формулы к нормальному виду используются законы логики и правила логических преобразований.
| А = А | Закон тождества | |
| A & A = 0 | Закон противоречия | |
| Av A = l | Исключающий третий закон | |
| А = А | Закон двойного отрицания | |
| A & 0 = 0 A v 0 = A | Постоянные законы исключения | |
| A & 1 = A A v 1 = 1 | Постоянные законы исключения | |
| А & А = А A v A = A | Правило идемпотентности | |
| AvA = l | ||
| (А → В) = А и В | ||
| А → В = А против В | ||
| A & (Av B) = A | Закон поглощения | |
| A v (A и B) = A | Закон поглощения | |
| А и (Ав В) = А и В | ||
| AvA и B = A v B | ||
| (AvB) vC = Av (BvC) (A&B) & C = A & (B&C) | Правило ассоциативности | |
| (A&B) v (A&C) = A & (BvC) (AvB) & (AvC) = Av (B&C) | Правило распределения | |
| AvB = BvA A&B = B&A | Правило взаимозаменяемости | |
| A—B = A и Bv (A и B) | ||
| (AvB) = A и B | Законы Моргана | |
| (A&B) = Av B | Законы Моргана | |
Пример
Упростить логическое выражение F = ( (A v B) → (B v WITH)) . .. Это логическое выражение необходимо привести к нормальной форме, так как оно содержит импликация и отрицание логической операции.
.. Это логическое выражение необходимо привести к нормальной форме, так как оно содержит импликация и отрицание логической операции.
1. Избавимся от импликации и отрицания. Мы будем использовать (8). Получается: ((AvB) → (BvC)) = (AvB) & (BvC).
2. Применяем закон двойного отрицания (4). Получаем: (AvB) & (BvC) = (AvB) & (BvC)
3. Применяем правило дистрибутивности (15). Получаем:
(AvB) & (BvC) = (AvB) & Bv (AvB) & C.
4. Применяем закон коммутативности (17) и дистрибутивности (15). Получаем: (AvB) & Bv (AvB) & C = A и BvB и BvA и CvB и C.
5. Применяем (16) и получаем: A&BvB&BvA&CvB&C=A&BvBvA&CvB&C
6. Применяем (15), то есть выносим B.
A& BvBv A & Cv B & C = B & (Av1) v A & Cv B & C
7. Применим (6). Получаем: B & (Avl) v A & Cv B & C = Bv A & Cv B & C.
8. Переставим члены, сгруппируем их и вынесем B за скобки. Получаем:
BvA & CvB & C = B & (1vC) vA & C.
9. Подать заявку (6) и получить ответ:
Ответ: F = ((A v B) → (B v C)) = B v A & C.
Упростить выражение:
1 ) F = (А и В) v (В v С).
2) F = (А → В) v (В → А).
3) F = A и C vA и C.
4) F = A vB vC v A v B v C.
5) F = (X & Y v (X & Y)).
6) F = X & (Y v X).
7) F = (X v Z) & (X v Z) & (Y v Z).
10) F = B & C & (AvA).
11) F = A и B и CvAvB
12) F = (AvB) и (BvA) и (CvB)
Упростите выражение:
1.F = A и C vA и C
2.F = A ↔ B v A&C
3. F = A & (B↔C)
4. F = (X v Y) & (Y ↔ X).
5. F = A vB vC v A v B v C.
6.F = (AvB) → (AvC)
7.F = A ↔ (B v C)
8.F = A и B → C и D.
9.F = (X и Y v (X и Y)).
10. F = (X v Y) и (Y v X).
11.F = A ↔ B и C
12. F = (A v B) & (B v A → B).
13. F = X & (Y v X).
14.F = A → B v A&C
15. F = X & Y v X.
F = X & Y v X.
16.F = ((X v Y) & (Z → X)) & (Z v Я).
17.F = (X v Z) & (X v Z) & (Y v Z).
18.F = A → (B v C)
19.F = A ↔ B v C
20. F = ((X v Y) & (Z v X)) & ( Z → Y).
21. F = (B & (A → C))
22. F = A → B v A&C
23. F = A ↔ (B v C) 2 5 F = ((X v Y) & (Z v X)) & (Z v Y).
25. F = (А → В) v (В → А).
26. F = A & B & C & D.
27. F = A ↔ (B v C)
28. F = A & (B → C).
29. F = A & (AvB)
30. F = A ↔ (B v C)
31. F = A → B v A & C 5 3 5 = (А v B) и (B v A v B).
33. F = B&C & (AvA).
34. F = A и B v A&C
35. F = X и Y ↔ X.
36. F = ((X v Y) & (Z → X)) & (Z ↔ Y).
37. F = A & B & CvAvB
38. F = (X → Y) & (Y v X).
39. F = A → B и C
40. F = (A ↔ B) & (B v A и B).
41. F = (AvB) & (BvA) & (CvB) .
42. F = A и B v A&C
43. F = A и (BvC)
44. F = (X → Y) & (Y ↔ X).
45. F = Av (A и B)
46. F = A и B ↔ C и D.
47. F = A ↔ (B 12 0 9 C) 900 F = (X и Y) v (Y и X).
Пример решения логических задач средствами логической алгебры
Логика
Логическая схема подается и снимается электрический сигнал.
Каждый переключатель имеет только два состояния: замкнут и разомкнут ... Переключателю X присвоена логическая переменная x, которая принимает значение 1 тогда и только тогда, когда переключатель X замкнут и цепь проводит ток; если переключатель разомкнут, то x равен нулю.
Обе схемы называются равносильно , если ток проходит через один из них тогда и только тогда, когда он проходит через другой (при том же входном сигнале).
Из двух эквивалентных схем более простой является схема, функция проводимости которой содержит меньше логических операций или переключателей.
При рассмотрении коммутационных схем возникают две основные проблемы: синтез и анализ схемы.
СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трем этапам:
- составление функции проводимости по таблице истинности, отражающей эти условия;
- упрощение этой функции;
- построение соответствующей схемы.
АНАЛИЗ СХЕМЫ сводится к:
- определению значений ее функции проводимости для всех возможных наборов переменных, входящих в эту функцию.
- получение упрощенной формулы.
Задача : Составьте таблицу истинности для данной формулы: (x ~ z) | ((х у) ~ (у z)).
Решение : полезно включить таблицы истинности промежуточных функций в таблицу истинности этой формулы:
| xyz | x ~ z | x y | y z | (x y) ~ (y z) | (x ~ z) | ((х у) ~ (у г) |
Методические указания к выполнению практического задания №2.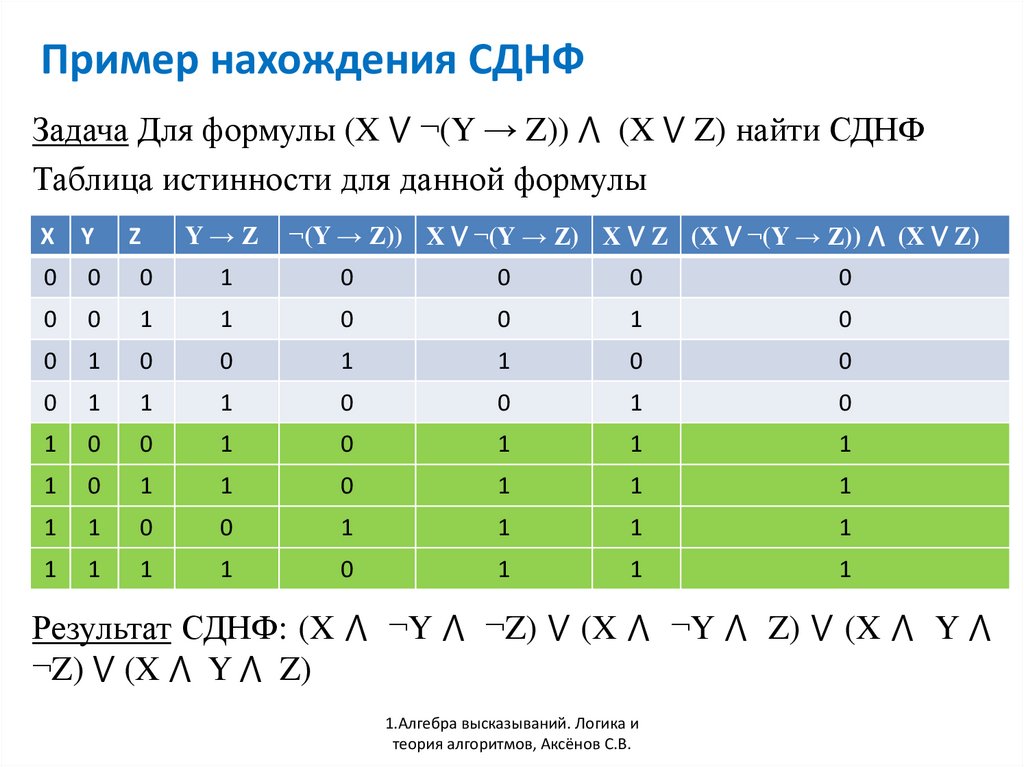 «Алгебра логики». Построение таблиц истинности.
«Алгебра логики». Построение таблиц истинности.
Цель работы : Ознакомиться с основными арифметическими действиями, основными логическими элементами (И, И-НЕ, ИЛИ, ИЛИ-НЕ, исключающее ИЛИ) и изучить методы построения таблиц истинности на их основе.
Упражнение:
1. В приложении 2 выбрать вариант задачи и составить таблицу истинности .
2. Выполнить задание на примере решения логических задач средствами логической алгебры.
Задача :
Построить логическую схему для заданного логического выражения:
F = `BA + B`A + C`B.
Решение:
Как правило, построение и расчет любой схемы осуществляется начиная с ее выпуска.
Первый шаг : выполняется логическое сложение, операция логического ИЛИ, учитывая входные переменные функции `BA, B`A и C`B:
Вторая фаза : логические элементы И подключаются ко входам элемента ИЛИ, входными переменными которых уже являются А, В, С и их инверсии:
Третья стадия : для получения инверсий `А и` B на соответствующие входы поставить инверторы:
Данная конструкция основана на следующей особенности - так как значения логических функций могут быть только нулями и единицами, то любые логические функции могут быть представлены как аргументы других более сложных функций. Таким образом, построение логической схемы осуществляется от выхода к входу.
Таким образом, построение логической схемы осуществляется от выхода к входу.
Методические указания к выполнению практического задания №3. «Алгебра логики». Построение логических схем
Цель работы : Ознакомиться с основными арифметическими действиями, основными логическими элементами (И, И-НЕ, ИЛИ, ИЛИ-НЕ, исключающее ИЛИ) и изучить способы построения простых логических схем на их основе .
Упражнение:
1. В приложении 2 выбрать вариант задачи и построить логическую схему .
2. Выполнить задание на примере построения логических схем.
3. Оформить работу в тетради для практической работы.
4. Представить результат работы учителю.
5. Защитить выполненную работу с преподавателем.
Приложение 2. Таблица вариантов задач
| Создать таблицу истинности и логическую схему для этих операций | |
| Опция | Операции |
4. Индивидуальное задание. Модуль 1. «Построение логических схем по заданным булевым выражениям»
Индивидуальное задание. Модуль 1. «Построение логических схем по заданным булевым выражениям»
Задания для ИДЗ:
- В Приложении 3 выберите вариант индивидуального задания.
- Выполните задание, используя теоретическую информацию
- Проверьте логику с репетитором.
- Выдать ИДЗ в формате А4, титульный лист по образцу Приложение 4.
- Результат работы представить преподавателю.
- Защитите выполненную работу вместе с учителем.
Приложение 3. Таблица вариантов индивидуального задания
| Варианты | Составление таблицы истинности и логической схемы с использованием формул |
Приложение 4. Титульный лист ИДЗ
Титульный лист ИДЗ
При построении отдельных узлов ЭВМ часто приходится решать задачу построения функциональных логических схем по заданным функциям. Для этого достаточно договориться, что верное утверждение соответствует тому, что цепь проводит ток, а ложное - цепь разомкнута.
Логические операции конъюнкции, дизъюнкции, инверсии реализуются в ЭВМ с помощью следующих элементарных схем.
Союз логический элемент "и":
Этот элемент выполняет операцию логического умножения (конъюнкции): f = x 1 х 2 х х 3 х… х n; и имеет n входов и один выход.
Дизъюнкция - логический элемент "или":
Этот элемент выполняет операцию логического сложения (дизъюнкции): f = x 1 Ú x 2 Úx 3 Ú… Úx n; и имеет n входов и один выход.
Инверсия - логический элемент "не":
Этот элемент выполняет операцию логического отрицания (инверсии): f =; и имеет один вход и один выход.
Сложные функциональные схемы могут быть построены из основных логических элементов с использованием основных законов булевой алгебры
Пример задачи управления
Упражнение:
Дана функция,
1. Составьте функционально-логическую схему для этой функции.
Составьте функционально-логическую схему для этой функции.
2. Упростить логическую функцию (используя законы булевой алгебры) и проверить преобразование по таблице истинности.
3. Составьте функционально-логическую схему для упрощенной функции.
Производительность:
1. Составим таблицу истинности для заданной функции:
2. Составим функционально-логическую схему для заданной функции:
3. Упростим заданную функцию, используя законы булевой алгебры:
а) по закону де Моргана - 9
б) по закону идемпотентности - 13
в) закон отрицания отрицания - 1
г) закон распределения - 6
д) свойства 1 и 0 - 19
е) свойства 1 и 0 - 16
Таким образом, упрощенный функция имеет вид:
4. Составим таблицу истинности для упрощенной функции:
Таким образом, сравнивая таблицы истинности исходной и упрощенной функций (их последние столбцы), делаем вывод о правильности выполненных преобразований.
5. Составим функционально-логическую схему для упрощенной функции:
Задание на выполнение контрольной работы
Дана функция f(x,y), номер функции в таблице соответствует порядковому номеру студента в списке.
4. Составьте функциональную логическую схему для этой функции.
5. Упростите логическую функцию (используя законы булевой алгебры) и проверьте преобразование по таблице истинности.
Знания из области математической логики могут быть использованы для проектирования электронных устройств. Мы знаем, что 0 и 1 в логике — это не просто числа, а обозначение состояний некоторого объекта нашего мира, условно называемых «ложными» и «истинными». Таким объектом, имеющим два фиксированных состояния, может быть электрический ток. Устройства, фиксирующие два устойчивых состояния, называются бистабильными (например, переключатель, реле). Если вы помните, первые компьютеры были релейными. Позднее были созданы новые электрические устройства управления — электронные схемы, состоящие из набора полупроводниковых элементов. Такие электронные схемы, преобразующие сигналы только двух фиксированных напряжений электрического тока (бистабильные), стали называть логических элемента .
Такие электронные схемы, преобразующие сигналы только двух фиксированных напряжений электрического тока (бистабильные), стали называть логических элемента .
На элементарном уровне конъюнкция может рассматриваться как последовательно соединенные переключатели, а дизъюнкция как параллельно соединенные переключатели:
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, условно обозначаемые 0, если есть нет электрического сигнала, и 1, если есть электрический сигнал. Простейшим логическим элементом является инвертор , выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот. Этот элемент имеет один вход и один выход. На функциональных схемах указывается:
Логический элемент, выполняющий логическое сложение, называется дизъюнктором ... Он имеет не менее двух входов. На функциональных схемах указывается:
Логический элемент, выполняющий логическое умножение, называется конъюнктором. Имеет как минимум два входа. На функциональных схемах указывается:
Имеет как минимум два входа. На функциональных схемах указывается:
Особых логических элементов импликации и эквивалентности нет, так как А => В можно заменить на А В В; AB можно заменить на (A и B) V (A и B).
Другие логические элементы строятся из этих трех простейших и выполняют более сложные логические преобразования информации. Сигнал, формируемый одним логическим элементом, может подаваться на вход другого элемента, это дает возможность формировать цепочки из отдельных логических элементов. Например:
Эта схема соответствует сложной логической функции F (A, B) = (AV B).
Попробуйте проследить изменения электрического сигнала в этой цепи. Например, какое значение электрического сигнала (0 или 1) будет на выходе, если на входе: А = 1 и В = 0,
Такие схемы логических элементов называются логическими устройствами ... Логические устройства при соединении в свою очередь образуют функциональные схемы (их также называют структурными или логическими схемами ). По заданной функциональной схеме можно определить логическую формулу, по которой работает эта схема, и наоборот.
По заданной функциональной схеме можно определить логическую формулу, по которой работает эта схема, и наоборот.
Пример 1. Логическая схема для функции будет выглядеть так:
Правила составления электронных логических схем по заданным таблицам истинности остаются такими же, как и для контактных схем.
Пример 2. Составьте логическую схему тайного голосования трех лиц А, В, С, условия которой определяются следующей таблицей истинности:
| А | ||||||||
| Б | ||||||||
| С | ||||||||
| Ф |
Решение
По таблице построим СДНФ логической функции и упростим ее:
Правильность полученной формулы можно проверить, составив для нее таблицу истинности:
Значение полученной функции совпадает с исходной, в чем можно убедиться, сравнив таблицы.
Логическая схема полученной функции выглядит следующим образом:
Рассмотрим еще два логических элемента, играющих роль базовых при создании более сложных элементов и схем.
Логический элемент И-НЕ состоит из конъюнктора и инвертора:
Логический элемент ИЛИ-НЕ состоит из дизъюнктора и инвертора:
Выходная функция выражается формулой.
Вопросы для самоконтроля
1. Основные логические операции: конъюнкция, дизъюнкция (оба вида), отрицание, импликация, эквивалентность. Примеры логических выражений.
2. Таблица истинности. Примеры. А, а не А; А или нет А
3. Основные законы математической логики: перестановки, сочетания и распределения
4. Законы де Моргана (закон отрицания).
5. (Совершенная) дизъюнктивная нормальная форма. Пример
Зачем нужно уметь строить логические схемы?
Дело в том, что более сложные схемы состоят из вентилей, позволяющих выполнять арифметические операции и хранить информацию. Причем схема, выполняющая определенные функции, может быть построена из вентилей разного сочетания и количества. Поэтому значение формального изложения логической схемы чрезвычайно велико. Это необходимо для того, чтобы разработчик мог выбрать наиболее подходящий вариант построения схемы из вентилей. Таким образом, процесс разработки общей логической схемы устройства (в том числе компьютера в целом) становится иерархическим, и на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.
Причем схема, выполняющая определенные функции, может быть построена из вентилей разного сочетания и количества. Поэтому значение формального изложения логической схемы чрезвычайно велико. Это необходимо для того, чтобы разработчик мог выбрать наиболее подходящий вариант построения схемы из вентилей. Таким образом, процесс разработки общей логической схемы устройства (в том числе компьютера в целом) становится иерархическим, и на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе.
Алгебра логики дала разработчикам мощный инструмент для разработки, анализа и улучшения логических схем. Действительно, гораздо проще, быстрее и дешевле изучить свойства и доказать правильность работы схемы по формуле, выражающей ее, чем создать реальное техническое устройство. Именно в этом смысл любого математического моделирования.
Логические схемы должны быть построены из минимально возможного количества элементов, что, в свою очередь, обеспечивает высокое быстродействие и повышает надежность устройства.
Алгоритм построения логических схем :
1) Определите количество логических переменных.
2) Определите количество основных логических операций и их порядок.
3) Нарисуйте соответствующий вентиль для каждой логической операции.
4) Соедините вентили в порядке логических операций.
Пример 10 Построить логическую схему для логического выражения: F = ¬ Х против Y и X. 1) Две переменные - X и Y. 2) Две логические операции:1 3 2 ¬ Xv Y и X. 3) Строим схему, соединяя гейты в порядке выполнения логических операций: Пример 11 Постройте логическую схему, соответствующую логическому выражению F = X & Y v ¬ (Y v X). Вычислить значения выражения для X = 1, Y = 0. 1) Есть две переменные: X и Y. 2)
Логических операций четыре: конъюнкция, две дизъюнкции и отрицание. |





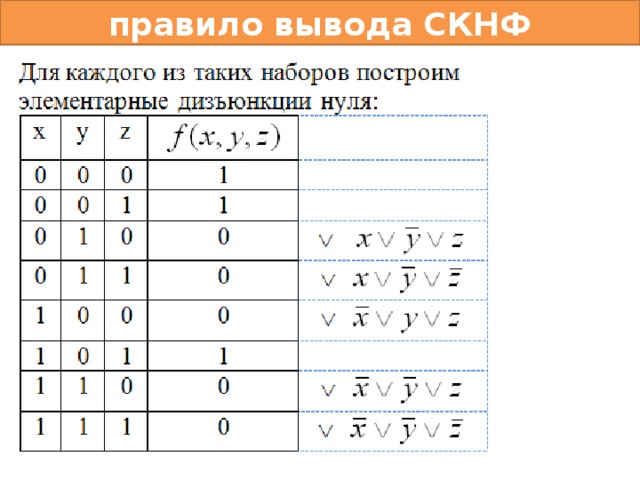 (\ Displaystyle А \ клин Б.)
(\ Displaystyle А \ клин Б.) (\ displaystyle \ neg (A \ клин B) = \ neg A \ vee \ neg B.)
(\ displaystyle \ neg (A \ клин B) = \ neg A \ vee \ neg B.) )
)




 По заданным логическим формулам построить ОДНФ и СКНФ двумя способами: с помощью эквивалентных преобразований и с помощью таблицы истинности.
По заданным логическим формулам построить ОДНФ и СКНФ двумя способами: с помощью эквивалентных преобразований и с помощью таблицы истинности.



 Поэтому они записываются в конъюнктивной нормальной форме.
Поэтому они записываются в конъюнктивной нормальной форме.
 Полученные элементарные дизъюнкции объединяются знаком конъюнкции.
Полученные элементарные дизъюнкции объединяются знаком конъюнкции.