Компьютерная дискретная математика. Нормальные формы
1. Нормальные формы
Компьютерная дискретная математикаНормальные формы
Лекция 6
Н.В. Белоус
Факультет компьютерных наук
Кафедра ПО ЭВМ, ХНУРЭ
ХНУРЭ, кафедра ПО ЭВМ, Тел. 7021-446, e-mail: [email protected]
2. Совершенная нормальная форма
Средимножества
эквивалентных
формул, представляющих выбранную
булеву функцию f, выделяется одна
формула,
которая
называется
совершенной
нормальной
формой
функции f, имеет регламентированную
логическую структуру и однозначно
определяется по функции f .
2
3. Обозначения
x,σ B={0,1}x , если 0
x
x , если 1
1, x
x
0 , x
x x x
3
4. Теорема о дизъюнктивном разложении функции f(x1,…,xn) по k переменным
Любую булеву функцию f(x1,x2,…,xn) можнопредставить в следующей форме:
f(x1,…,xk,xk+1,…,xn)=
x1 x2 … xk f( 1, 2,…, k,xk+1,…,xn)
1
2
k
( 1, 2,…, k)
4
5.
 Теорема о дизъюнктивном разложении функцииЗапись ( 1, 2,…, k )
Теорема о дизъюнктивном разложении функцииЗапись ( 1, 2,…, k )означает
многократную
дизъюнкцию, которая берется по всем возможным
наборам значений ( 1, 2,…, k) при любом k (1≤k≤n).
f( 1, 2,…, k,xk+1,…,xn) представляет значение
функции на интерпретации x1,x2,…,xn, когда вместо
значений переменных x1,x2,…,xk, по которым
ведется
разложение,
подставлены
значения
1, 2,…, k.
5
6. Пример
Получить дизъюнктивное разложение функцииf ( x, y, z, t ) ( x y z) t по переменным x, z.
f ( x, y, z, t ) x 1 z 2 f ( 1 , y, 2 , t ) x z f (0, y,0, t )
x z f (0, y,1, t ) x z f (1, y,0, t ) x z f (1, y,1, t )
f ( 0 , y ,0 , t ) (0 y 0) t 0 ,
f ( 0 , y ,1 , t ) ( 0 y 1 ) t t ,
f ( 1 , y ,0 , t ) ( 1 y 0 ) t 0 ,
f ( 1 , y ,1 , t ) ( 1 y 1 ) t y t .
Подставим f(0,y,0,t), f(0,y,1,t), f(1,y,0,t), f(1,y,1,t) в
формулу дизъюнктивного разложения
f ( x , y, z ,t ) x z 0 x z t x z 0 x z ( y t )
x z t x z y t
6
7.
 Дизъюнктивное разложение булевой функции f(x1,x2,…,xn) по одной переменнойЛюбую булеву функцию f(x1,x2,…,xn) можно
Дизъюнктивное разложение булевой функции f(x1,x2,…,xn) по одной переменнойЛюбую булеву функцию f(x1,x2,…,xn) можнопредставить в следующей форме:
f(x1, x2, …, xn)=
x
σi
i
f(x1, x2, …, xi-1, i, xi+1, …, xn)
i
7
8. Дизъюнктивное разложение булевой функции f(x1,x2,…,xn) по всем n переменным
Любую булеву функцию f(x1,x2,…,xn) 0 можнопредставить в следующей форме:
f(x1,x2,…,xn) =
x1 x2 … xn
1
2
n
( 1, 2,…, n)
f( 1, 2,…, n) = 1
8
9. Пример
Получить дизъюнктивное разложение функцииf ( x , y , z ) xy z по всем переменным.
Определим значение функции на каждой из
интерпретаций:
f ( 0 ,0 ,0 ) 0 0 0 0 1 1
f ( 1 ,0 ,0 ) 1 0 0 0 1 1
f ( 0 ,0 ,1 ) 0 0 1 0 0 0
f ( 1 ,0 ,1 ) 1 0 1 0 0 0
f ( 0 ,1 ,0 ) 0 1 0 0 1 1
f ( 1 ,1 ,0 ) 1 1 0 1 1 1
f ( 0 ,1 ,1 ) 0 1 1 0 0 0
f ( 1 ,1 ,1 ) 1 1 1 1 0 1
f ( x , y , z ) x0 y0 z0 x0 y1z0 x 1 y0 z0 x 1 y1 z0
x 1 y 1 z 1 x y z x y z x y z xy z xyz
9
10.
 Определения и понятияЭлементарной
Определения и понятияЭлементарнойконъюнкцией
называется
конъюнкция любого числа булевых переменных,
взятых с отрицанием или без него, в которой каждая
переменная встречается не более одного раза.
Примеры
Элементарными конъюнкциями для функции от
одной переменной могут быть y, z,
двух переменных x y, x z
трех переменных x y z , x y z , x y z .
10
11. Определения и понятия
Дизъюнктивной нормальной формой (ДНФ)называется формула, представленная в виде
дизъюнкции элементарных конъюнкций.
Примеры:
f(x, y,z)= x y x z x y z x ДНФ
f(x, y,z)= x y x y z
f(x, y,z)= x y z
ДНФ
–
11
12. Определения и понятия
Элементарная конъюнкцияx1 x2 … xn
называется конституентой единицы (минтермом)
функции f(x1,x2,…,xn), если f( 1, 2,…, n)=1, то есть
интерпретация, обращающая в единицу данную
элементарную конъюнкцию, обращает в единицу и
функцию f.
1
2
n
12
13.
 Свойства конституенты единицыКонституента единицы функции n переменных
Свойства конституенты единицыКонституента единицы функции n переменныхимеет вид x1 x2 … xn и соответствует
интерпретации ( 1, 2,…, n).
Конституента единицы обладает следующими
свойствами:
Конституента единицы равна единице только на
соответствующей ей интерпретации.
Конституента единицы однозначно определяется
номером соответствующей ей интерпретации.
Конъюнкция
любого
числа
различных
конституент единицы функции равна нулю.
1
2
n
13
14. Определение и понятия
Совершенной дизъюнктивной нормальнойформой (СДНФ) булевой функции называется
формула, представленная в виде дизъюнкции
конституент единицы данной функции.
Примеры:
f(x, y,z)= x y z x y z
f(x, y,z)= x y z
f(x, y,z)= x yz
СДНФ
ДНФ
СДНФ
14
15. Определения и понятия
Совершенной конъюнктивной нормальнойформой (СКНФ) функции называется формула,
представленная в виде конъюнкции конституент
нуля данной функции.

Примеры
f(x, y,z)= x y z
f(x, y,z)= ( x y ) ( y z ) z
f(x, y,z)= ( x y z ) ( x y z )
СКНФ
КНФ
СКНФ
15
16. Следствия из определений СДНФ и СКНФ булевых функций
Для каждой булевой функции f(x1,x2,…,xn), неявляющейся
константой
нуля,
существует
представление в виде СДНФ.
Для каждой булевой функции f(x1,x2,…,xn), не
являющейся константой единицы, существует
представление в виде СКНФ.
Две различные булевы функции не могут иметь
одинаковые СДНФ или СКНФ.
Для каждой булевой функции f(x1,x2,…,xn)
существует представление в виде формулы булевой
алгебры, содержащей только операции дизъюнкции,
конъюнкции и отрицания.
16
17. Пример конституент 1 и конституент 0
xy
z
17
18. Алгоритм перехода от таблицы истинности булевой функции к СДНФ
• Выделить все интерпретации ( 1, 2,…, n), накоторых значение функции равно единице.
• Записать
конституенты
единицы
вида
x1 x2 … xn , соответствующие отмеченным
интерпретациям.

• Получить
СДНФ
функции
посредством
соединения операцией дизъюнкции записанных
конституент единицы.
1
2
n
18
19. Алгоритм перехода от таблицы истинности булевой функции к СДНФ. Пример
Получить СДНФ для функций f13(x,y).Функция f13(x,y)
x
0
y
f13(x,y)
f8(x,y)
0
1
1
0
1
0
1
1
0
1
0
1
1
0
0
f 13 ( x , y ) x y x y x y x y xy xy
0 0
0 1
1 1
f8 ( x , y ) x y x y
0
0
19
20. Алгоритм перехода от таблицы истинности булевой функции к СКНФ
1. Выделить все интерпретации ( 1, 2,…, n), накоторых значение функции равно нулю
2. Записать конституенты нуля вида х х … х ,
соответствующие выделенным интерпретациям.
3. Записав конъюнкцию конституент нуля, получить
СКНФ функции.
1
2
n
1
2
n
20
21. Алгоритм перехода от таблицы истинности булевой функции к СКНФ
ПримерПолучить СКНФ для функций f7(x,y) и f9(x,y).

x
0
y
f7(x,y)
f9(x,y)
0
1
1
0
1
0
1
1
0
1
1
f7 ( x, y )
0
1
x1 y 1 x0 y 0 х y
0
1
f 9 ( x , y ) ( x0 y 1 ) ( x 1 y 0 )
( x1 y0 ) ( x0 y1 ) ( x y ) ( x y )
21
22. Алгоритм построения таблицы истинности функции, заданной СДНФ
1. Построить таблицу истинности, содержащую 2nинтерпретаций вида ( 1, 2,…, n).
2. Отметить в таблице истинности все интерпретации
( 1, 2,…, n),
соответствующие
конституентам
единицы вида х х … х из заданной СДНФ.
3. Напротив выделенных интерпретаций в столбец
значения функции записать единицы.
4. Напротив оставшихся интерпретаций в столбец
значения функции записать нули.
1
2
n
1
2
n
22
23. Алгоритм перехода от произвольной формулы алгебры логики к СДНФ
1. Исключить константы, используя законы действий сконстантами.
2. Опустить знаки отрицания непосредственно на
переменные, используя законы де Моргана.
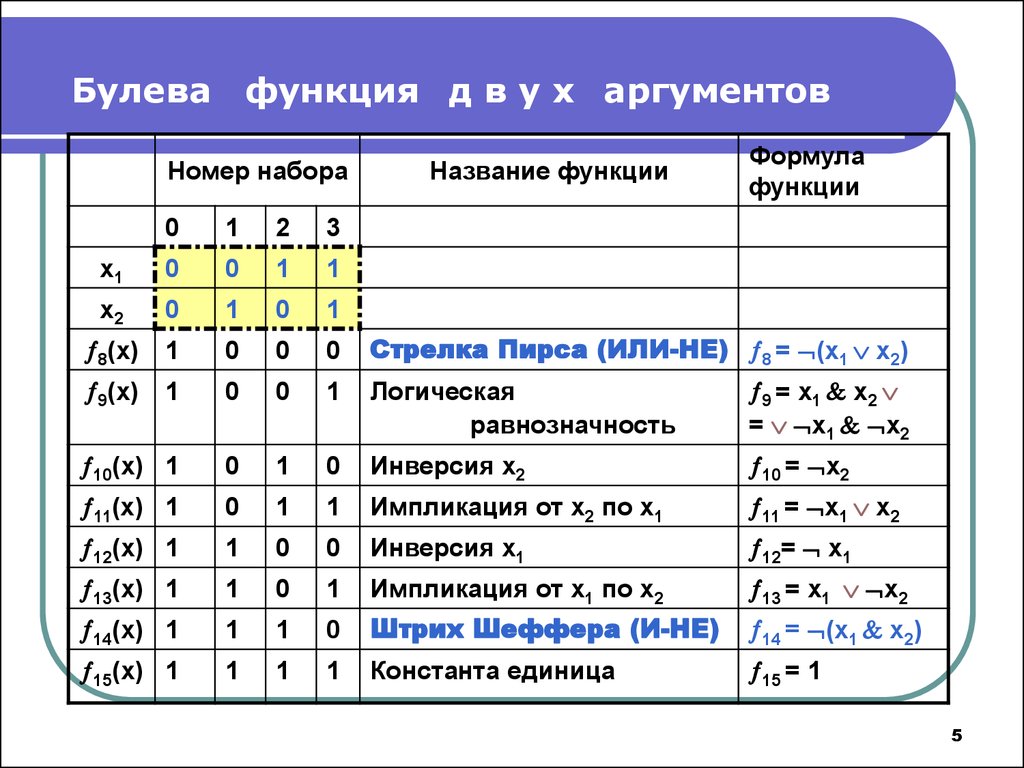
3. Используя дистрибутивный закон, раскрыть скобки.
К полученным элементарным конъюнкциям
применить
законы
идемпотентности
и
противоречия, упростить их и привести подобные.
Результатом выполнения указанных действий
является получение ДНФ булевой функции.
23
24. Алгоритм перехода от произвольной формулы алгебры логики к СДНФ. Продолжение
4. Построить конституенты единицы функции,введением в каждую элементарную конъюнкцию
недостающих переменных, используя закон
исключенного третьего.
5. С помощью дистрибутивного закона раскрыть
скобки и привести подобные, используя закон
идемпотентности
6. Полученная
формула
соответствует
СДНФ
функции.
24
25. Примеры
Пример 1. Переход от СДНФ к таблице истинностиПример 2. Переход от СКНФ к таблице истинности
25
Цифровые схемы — булева алгебра
Булева алгебра – это алгебра, которая имеет дело с двоичными числами и двоичными переменными. Следовательно, он также называется бинарной алгеброй или логической алгеброй. Математик по имени Джордж Буль разработал эту алгебру в 1854 году. Переменные, используемые в этой алгебре, также называются булевыми переменными.
Следовательно, он также называется бинарной алгеброй или логической алгеброй. Математик по имени Джордж Буль разработал эту алгебру в 1854 году. Переменные, используемые в этой алгебре, также называются булевыми переменными.
Диапазон напряжений, соответствующий логике «Высокий», обозначен «1», а диапазон напряжений, соответствующий логике «Низкий», представлен «0».
Постулаты и основные законы булевой алгебры
В этом разделе давайте поговорим о булевых постулатах и основных законах, которые используются в булевой алгебре. Они полезны при минимизации булевых функций.
Булевы Постулаты
Рассмотрим двоичные числа 0 и 1, булеву переменную (x) и ее дополнение (x ‘). Булева переменная или ее дополнение называется литералом . Четыре возможных логических операции ИЛИ среди этих литералов и двоичных чисел показаны ниже.
х + 0 = х
х + 1 = 1
х + х = х
х + х ‘= 1
Точно так же четыре возможные логические операции И среди этих литералов и двоичных чисел показаны ниже.
х.1 = х
х.0 = 0
хх = х
x.x ‘= 0
Это простые булевы постулаты. Мы можем легко проверить эти постулаты, заменив логическую переменную на «0» или «1».
Примечание . Дополнение к любой булевой переменной равно самой переменной. т.е. (x ‘)’ = x.
Основные законы булевой алгебры
Ниже приведены три основных закона булевой алгебры.
- Коммутативное право
- Ассоциативный закон
- Распределительное право
Коммутативное право
Если какая-либо логическая операция двух булевых переменных дает один и тот же результат независимо от порядка этих двух переменных, то эта логическая операция называется коммутативной . Логическое ИЛИ и логические И операции двух булевых переменных x & y показаны ниже
х + у = у + х
xy = yx
Символ «+» указывает на логическую операцию ИЛИ. Точно так же символ «.» указывает логическую операцию И, и это необязательно для представления. Коммутативное право подчиняется логическому ИЛИ, логическому И операциям.
Коммутативное право подчиняется логическому ИЛИ, логическому И операциям.
Ассоциативное право
Если сначала выполняется логическая операция любых двух логических переменных, а затем выполняется та же самая операция с оставшейся переменной, которая дает тот же результат, то эта логическая операция называется ассоциативной . Логические операции ИЛИ, логические И трех булевых переменных x, y & z показаны ниже.
x + (y + z) = (x + y) + z
x. (yz) = (xy) .z
Ассоциативный закон подчиняется логическому ИЛИ и логическому И операциям.
Распределительный закон
Если какая-либо логическая операция может быть распространена на все члены, присутствующие в булевой функции, то эта логическая операция называется распределительной . Распределение логических ИЛИ и логических И операций трех булевых переменных x, y & z показано ниже.
х. (у + г) = ху + хз
x + (yz) = (x + y). (x + z)
Распределительный закон подчиняется логическому ИЛИ и логическому И операциям.
Это основные законы булевой алгебры. Мы можем легко проверить эти законы, заменив логические переменные на «0» или «1».
Теоремы булевой алгебры
Следующие две теоремы используются в булевой алгебре.
- Теорема двойственности
- Теорема Деморгана
Теорема двойственности
Эта теорема утверждает, что двойственность булевой функции получается путем замены логического оператора AND на логический оператор OR и нулей на единицу. Для каждой булевой функции будет соответствующая двойная функция.
Давайте сделаем булевы уравнения (отношения), которые мы обсуждали в разделе булевых постулатов и основных законов, на две группы. В следующей таблице показаны эти две группы.
| Группа 1 | Group2 |
|---|---|
| х + 0 = х | х.1 = х |
| х + 1 = 1 | х.0 = 0 |
| х + х = х | хх = х |
| х + х ‘= 1 | x. x ‘= 0 x ‘= 0 |
| х + у = у + х | xy = yx |
| x + (y + z) = (x + y) + z | x. (yz) = (xy) .z |
| х. (у + г) = ху + хз | x + (yz) = (x + y). (x + z) |
В каждой строке есть два булевых уравнения, и они двойственны друг другу. Мы можем проверить все эти булевы уравнения группы 1 и группы 2, используя теорему двойственности.
Теорема Деморгана
Эта теорема полезна при поиске дополнения к булевой функции . В нем говорится, что дополнение логического ИЛИ по крайней мере двух логических переменных равно логическому И каждой дополненной переменной.
Теорема Деморгана с 2 булевыми переменными x и y может быть представлена в виде
(x + y) ‘= x’.y’
Двойственная из вышеупомянутых булевых функций
(xy) ‘= x’ + y ‘
Следовательно, дополнение логического И двух логических переменных равно логическому ИЛИ каждой дополненной переменной. Точно так же мы можем применить теорему Деморгана для более чем 2 булевых переменных.
Точно так же мы можем применить теорему Деморгана для более чем 2 булевых переменных.
Упрощение булевых функций
До сих пор мы обсуждали постулаты, основные законы и теоремы булевой алгебры. Теперь давайте упростим некоторые булевы функции.
Пример 1
Упростим булеву функцию: f = p’qr + pq’r + pqr ‘+ pqr
Мы можем упростить эту функцию двумя способами.
Способ 1
Для данной булевой функции f = p’qr + pq’r + pqr ‘+ pqr.
Шаг 1 – В первом и втором членах r является общим, а в третьем и четвертом членах pq является общим. Итак, примите общие термины, используя Распределительный закон .
⇒ f = (p’q + pq ‘) r + pq (r’ + r)
Шаг 2 – Термины, представленные в первых скобках, могут быть упрощены до операции Ex-OR. Термины, присутствующие во второй скобке, могут быть упрощены до «1» с использованием булева постулата
⇒ f = (p ⊕q) r + pq (1)
Шаг 3 – Первый термин не может быть упрощен в дальнейшем. Но второй член можно упростить до pq, используя булев постулат .
Но второй член можно упростить до pq, используя булев постулат .
⇒ f = (p ⊕q) r + pq
Следовательно, упрощенная булева функция имеет вид f = (p⊕q) r + pq
Способ 2
Для данной булевой функции f = p’qr + pq’r + pqr ‘+ pqr.
Шаг 1 – Используйте булев постулат , х + х = х. Это означает, что операция логического ИЛИ с любой логической переменной n раз будет равна той же самой переменной. Итак, мы можем написать последний член pqr еще два раза.
⇒ f = p’qr + pq’r + pqr ‘+ pqr + pqr + pqr
Шаг 2 – Используйте Распределительный закон для 1- го и 4- го терминов, 2- го и 5- го терминов, 3- го и 6- го терминов.
⇒ f = qr (p ‘+ p) + pr (q’ + q) + pq (r ‘+ r)
Шаг 3 – Используйте булев постулат , x + x ‘= 1 для упрощения терминов, присутствующих в каждой скобке.
⇒ f = qr (1) + pr (1) + pq (1)
Шаг 4 – Используйте булев постулат , x. 1 = x для упрощения трех указанных выше терминов.
1 = x для упрощения трех указанных выше терминов.
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
Следовательно, упрощенная булева функция имеет вид f = pq + qr + pr .
Итак, мы получили две разные булевы функции после упрощения данной булевой функции в каждом методе. Функционально эти две булевы функции одинаковы. Таким образом, исходя из требования, мы можем выбрать одну из этих двух булевых функций.
Пример 2
Найдем дополнение к булевой функции f = p’q + pq ‘.
Дополнением к булевой функции является f ‘= (p’q + pq’) ‘.
Шаг 1 – Используйте теорему Деморгана, (x + y) ‘= x’.y’.
⇒ f ‘= (p’q)’. (Pq ‘)’
Шаг 2 – Используйте теорему Деморгана, (xy) ‘= x’ + y ‘
⇒ f ‘= {(p’) ‘+ q’}. {P ‘+ (q’) ‘}
Шаг 3 – Используйте булев постулат, (x ‘)’ = x.
⇒ f ‘= {p + q’}. {P ‘+ q}
⇒ f ‘= pp’ + pq + p’q ‘+ qq’
Шаг 4 – Используйте булев постулат, хх ‘= 0.
⇒ f = 0 + pq + p’q ‘+ 0
⇒ f = pq + p’q ‘
Следовательно, дополнение к булевой функции p’q + pq ‘равно pq + p’q’ .
Упростить логическое выражение i.t.o вхождение переменной
Задать вопрос
спросил
Изменено 4 года, 7 месяцев назад
Просмотрено 1к раз
Как упростить заданное логическое выражение с большим количеством переменных (>
10), чтобы количество вхождений каждой переменной было минимальным? В моем сценарии значение переменной должно считаться эфемерным, т. е. должно пересчитываться для каждого доступа (оставаясь при этом, конечно, статическим). Поэтому мне нужно свести к минимуму количество раз, когда переменная должна быть оценена, прежде чем пытаться решить функцию.
Рассмотрим функцию
f(A,B,C,D,E,F) = (ABC)+(ABCD)+(ABEF)
Рекурсивно используя закон распределения и поглощения, получаем
f'(A,B,C,E,F) = AB(C+(EF))
Мне вот интересно, есть ли алгоритм или метод для решения этой задачи с минимальным временем выполнения.
Использование только Quine-McCluskey в приведенном выше примере дает
f'(A,B,C,E,F) = (ABEF) + (ABC)
что не оптимально для моего случая. Безопасно ли предположить, что оптимально сначала упростить с помощью QM, а затем использовать алгебру, как указано выше, для дальнейшего сокращения?
- логическое значение
- логическое значение
1
Для таких вещей я обычно использую Wolfram Alpha.
Попробуйте Logic Friday 1
Отличается многоуровневым дизайном логических схем.
В вашем примере ввод и вывод выглядят следующим образом:
6
Вы можете использовать онлайн-калькулятор логических выражений, такой как https://www.dcode.fr/boolean-expressions-calculator
Вы можете обратиться к любому хорошему упростителю логических выражений? это обязательно поможет.
2Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
логика — Упрощение логического выражения с 9 переменными
2.
 Упрощенное условие:
Упрощенное условие:Исходное выражение
a&b&c|d&e&f|g&h&i|a&d&g|b&e&h|c&f&i|a&e&i|g&e&c
можно упростить до следующего, зная, что & является более приоритетным, чем |
e&(d&f|b&h|a&i|g&c)|a&(b&c|d&g)|i&(g&h|c&f)
, который на 4 символа короче, работает в худшем случае 18 и и | оценок (в оригинале было 23)
Не существует более короткой логической формулы (см. пункт ниже). Если вы переключитесь на матрицы, возможно, вы найдете другое решение.
1. Убедиться, что мы получили наименьшую формулу
Обычно очень трудно найти наименьшую формулу. См. эту недавнюю статью, если вы более заинтересованы. Но в нашем случае есть простое доказательство.
Мы будем рассуждать о формуле, являющейся наименьшим по отношению к размеру формулы, где для переменной a , size(a)=1 , для логической операции size(A&B) = size(A |B) = размер(A) + 1 + размер(B) , а для отрицания size(!A) = size(A) (таким образом, мы можем предположить, что у нас есть нормальная форма отрицания бесплатно).
Доказательство того, что вы не можете сделать лучше, состоит в том, чтобы сначала заметить, что нужно проверить 8 строк и что всегда есть пара букв, различающих 2 разные строки. Поскольку мы можем перегруппировать эти 8 проверок не менее чем в 3 конъюнктах с оставшейся переменной, число переменных в итоговой формуле должно быть не менее 8*2+3 = 19 , из которого мы можем вывести минимальный размер дерева.
Подробное доказательство
Предположим, что данная формула F является наименьшим и имеет формат NNF.
Fне может содержать отрицательные переменные, такие как!a. Для этого заметим, чтоFдолжно быть монотонным , то есть если оно возвращает «истина» (есть выигрышная строка), то изменение одной из переменных сtrueне должно изменять этот результат. Согласно Википедии,
Согласно Википедии, Fможно писать без отрицания. Более того, мы можем доказать, что можем удалить отрицание. Следуя этому ответу, мы могли бы преобразовать обратно и из формата DNF, удалив инвертированные переменные в середине или заменив их наtrue.Fне может содержать поддерево, подобное дизъюнкции двух переменныхa|b. Чтобы эта формула была полезной и не заменялась ни наaилиb, это будет означать, что существуют противоречащие друг другу назначения, такие как, например,F[a|b] = trueиF[a] = false, поэтомуa = falseиb = trueиз-за монотонности. Кроме того, в этом случае преобразованиеbвfalseделает всю формулуfalse, потому чтоfalse = F[a] = F[a|false] >= F[a|b](b = false). Следовательно, есть ряд, проходящий черезb, который является причиной истины, и он не может пройти черезa, поэтому, например,e = trueиh = true. И проверка этой строки проходит по выражению
И проверка этой строки проходит по выражению a|bдля проверкиb. Однако это означает, что еслиa,e,hявляется истинным, а все остальные равны ложным,Fпо-прежнему остается истинным, что противоречит цели формулы.Каждое поддерево, похожее на
a&b, проверяет уникальную строку. Таким образом, последняя буква должна стоять чуть выше соответствующей дизъюнкции 9.0049 (a&b|…)&{c где-то здесь наверняка}cне встречается выше, и игра состоит в том, чтоa&b&cравноtrue, а все остальные переменные равныfalse. Тогда выражение, где c должно быть выше, возвращаетfalse, поэтомуa&bвсегда будет бесполезным. Таким образом, можно сократить выражение, удаливa&b.Имеется 8 независимых ветвей, поэтому существует как минимум 8 поддеревьев типа
a&b.

 Согласно Википедии,
Согласно Википедии, 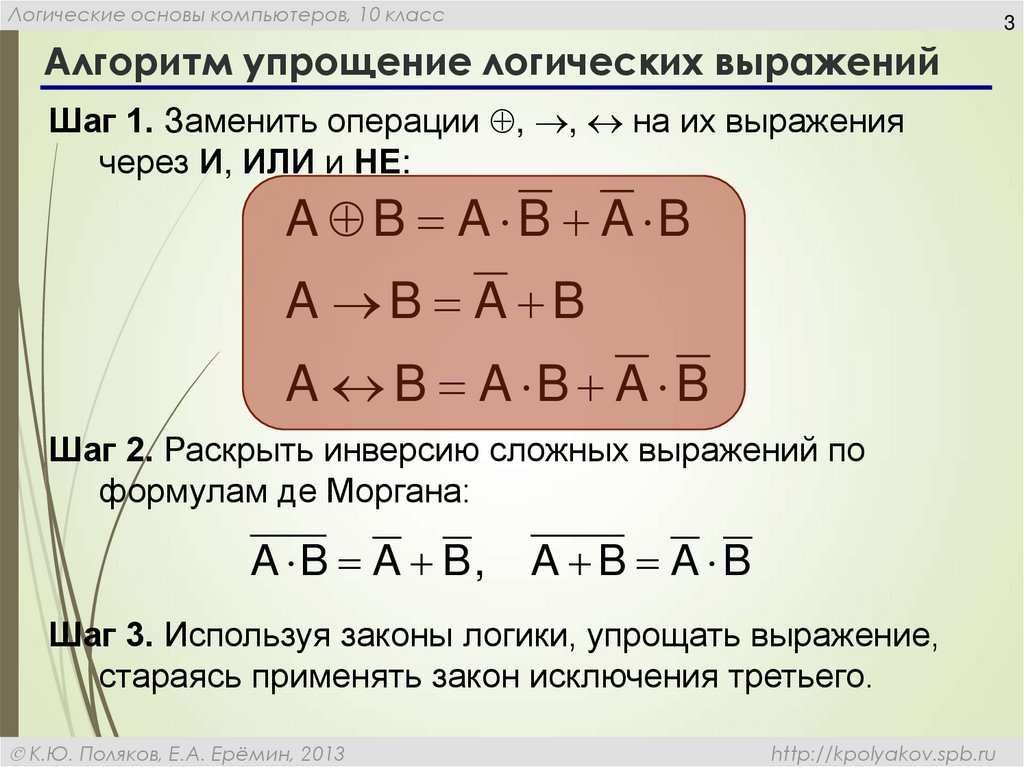 И проверка этой строки проходит по выражению
И проверка этой строки проходит по выражению 