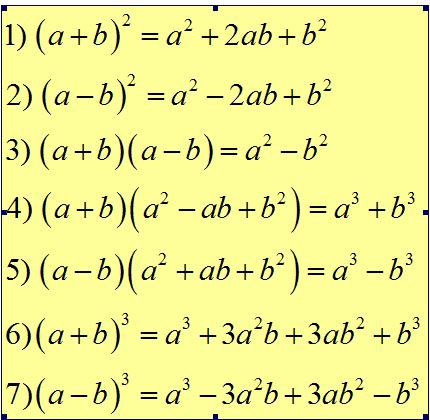Упрощение выражений – формулы и примеры алгоритма в таблице (5 класс, математика)
4.7
Средняя оценка: 4.7
Всего получено оценок: 179.
4.7
Средняя оценка: 4.7
Всего получено оценок: 179.
Упрощение выражений – это возможность быстро посчитать достаточно сложный пример или свернуть сложный многочлен, выведя за скобки некоторые его члены. Навыки упрощения помогают в решении уравнений, развитии умения быстрого счета и сокращении дробей. Поговорим подробнее о методах упрощения численных выражений и многочленов.
Распределительное свойство умножения
Распределительное свойство геометрии состоит в том, что при умножении суммы на число, можно умножить каждое из слагаемых на это число, а полученные результаты сложить. Благодаря этому свойству можно раскрывать скобки в некоторых выражениях.
Раскроем скобки в следующем примере: $31а(2+3с)=62а+93ас$
Сочетательное свойство умножения
Сочетательное свойства гласит: при умножении трех чисел умножать одно число на другое можно в любом порядке.
2}\over{(a+b)(b+d)}}= {(a+b)(b+d)\over{(a+b)(b+d)}}=1$$
Вот и все.
Очень часто при упрощении выражений получается небольшой многочлен, 1 или 0, но это не значит, что других результатов быть не может. Просто так легче сделать первые шаги в обучении данному навыку.
Если в результате решения получается что-либо «простое», то сразу возникает уверенность в собственных силах. Специальной формулы нет хотя есть таблицы формул сокращенного умножению, которые начинают учить примерно с математики 5 класса.
Что мы узнали?
Мы узнали, какие методы существуют для упрощения выражений и разобрали эти методы и алгоритмы на практике. Решили несколько примеров, подробно разобрав алгоритм размышлений при решении.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4.7
Средняя оценка: 4.
Всего получено оценок: 179.
А какая ваша оценка?
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | ||
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |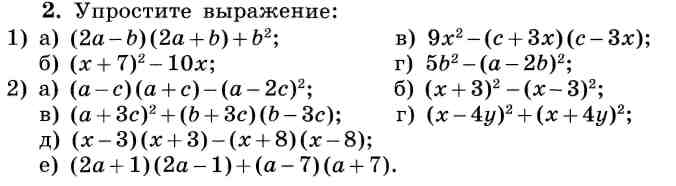
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | cos(45) | ||
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Как упростить выражения?
Чтобы понять алгебру, важно научиться упрощать выражения! Упрощая выражения, мы можем преобразовать сложное выражение в более компактную и простую форму. Прежде чем мы начнем, давайте посмотрим на определение алгебраического выражения.
4. 94 + 21x +38
Это все для упрощения алгебраических выражений! Просто запомните четыре основных правила и шага, и вы будете на пути к освоению алгебры!
- Автор
- Последние сообщения
Сидней Ле
Будучи старшеклассницей, Сидни проявляет глубокий интерес к медицине и любит находить способы помочь своему сообществу. Она амбициозная и целеустремленная личность, которая вовлекает себя в различные виды деятельности. Ей нравится знакомиться с новыми людьми, учиться и писать.
Последние сообщения Сидни Ле (посмотреть все)
Темы по алгебре: Упрощение выражений
Урок 7: Упрощение выражений
выражение — это просто другой способ сказать решение математической задачи . Когда вы упрощаете выражение, вы, по сути, пытаетесь записать его простейшим возможным способом. В конце концов, не нужно больше ничего складывать, вычитать, умножать или делить.
Например, возьмем это выражение:
4 + 6 + 5
Если вы упростите , объединив термины до тех пор, пока не останется ничего, выражение будет выглядеть так: написать 4 + 6 + 5. Оба варианта выражения равны одной и той же сумме; один просто намного короче.
Упрощение алгебраических выражений — это та же идея, за исключением того, что в вашем выражении есть переменные (или буквы). По сути, вы превращаете длинное выражение во что-то легко понятное. Итак, такое выражение…
(13x + -3x) / 2
…можно упростить так:
5x
Если это кажется большим скачком, не волнуйтесь! Все, что вам нужно для упрощения большинства выражений, — это базовая арифметика — сложение, вычитание, умножение и деление — и порядок операций.
Порядок операций
Как и в любой задаче, при упрощении алгебраического выражения вам нужно следовать порядку операций .
Порядок операций — это правило, которое подскажет вам правильный заказ на выполнение расчетов. Согласно порядку операций, вы должны решить задачу в следующем порядке:
- Скобки
- Показатель степени
- Умножение и деление
- Сложение и вычитание
Давайте рассмотрим задачу, чтобы увидеть, как это работает.
В этом уравнении вы должны начать с упрощения части выражения в скобках : 24 — 20.
2 ⋅ (24 — 20) 2 + 18 / 6 — 30
24 минус 20 равно 4. В соответствии с порядком операций далее мы упростим любые показателей . В этом уравнении есть один показатель степени: 4 2 , или четыре во второй степени .
2 ⋅ 4 2 + 18 / 6 — 30
4 2 равно 16. Далее нам нужно позаботиться о умножении и делении .
Сделаем слева направо: 2 ⋅ 16 и 18 / 6.
2 ⋅ 16 + 18 / 6 — 30
2 ⋅ 16 равно 32, а 18/6 равно 3. Остался последний шаг в порядке операций: сложение и вычитание .
32 + 3 — 30
32 + 3 равно 35, а 35 — 30 равно 5. Наше выражение упростилось — делать больше нечего.
5
Это все, что нужно! Помните, вы должны следовать порядку операций при выполнении вычислений, иначе вы можете не получить правильный ответ.
Все еще немного запутались или нужно больше практики? Мы написали целый урок о порядке действий. Вы можете проверить это здесь.
Добавление одинаковых переменных
Чтобы добавить одинаковые переменные, вы можете просто добавить коэффициенты . Таким образом, 3 x + 6 x равно 9 x . Вычитание работает точно так же, поэтому 5 y — 4 y = 1 y или просто y .
5 лет — 4 года = 1 год
Вы также можете умножить и разделить переменных с коэффициентами. Чтобы умножить переменные на коэффициенты, сначала умножьте коэффициенты, затем запишите переменные рядом друг с другом. Итак, 3 x ⋅ 4 y равно 12 xy .
3x ⋅ 4y = 12xy
Распределительное свойство
Иногда при упрощении выражений можно увидеть что-то вроде этого:3(x+7)-5
внутри сначала круглые скобки. Однако в этом случае x+7 нельзя упростить, поскольку мы не можем добавить переменную и число. Итак, каков наш первый шаг?
Как вы, возможно, помните, 3 снаружи скобок означает, что нам нужно умножить все внутри скобок на 3. В скобках два числа: x и 7 . Нам нужно умножить их и на 3.
3(x) + 3(7) — 5
3 · x равно 3x и 3 · 7 равно 21 .