Уравнение касательной к нормали к графику функции: Уравнение касательной и уравнение нормали к графику функции

Содержание

Уравнение касательной и уравнение нормали к графику функции

Как получить уравнение касательной и уравнение нормали
Решаем задачи вместе
Решить задачи самостоятельно, а затем посмотреть решение
Снова решаем задачи вместе

Касательная — это прямая, которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой.

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

Вспомним уравнение прямой с угловым коэффициентом:

y = kx

+ b.

В нём k — угловой коэффициент.

Отсюда получаем следующую запись:

y — y0 = k(x — x0).

Значение производной f ‘(x0) функции y = f(x) в точке x0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M0(x0, y0), где y0 = f(x0). В этом состоит геометрический смысл производной.

Таким образом, можем заменить k на f ‘(x0) и получить следующее уравнение касательной к графику функции:

y — y0 = f ‘(x0)(x — x0).

Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

Теперь об уравнении нормали. Нормаль — это прямая, проходящая через точку касания к графику функции перпендикулярно касательной. Уравнение нормали:

(x — x0) + f ‘(x0)(y — y0) = 0

Переходим к примерам. Для решений потребуется таблица производных (откроется в новом окне).

Для разминки первый же пример прелагается решить самостоятельно, а затем посмотреть решение. Есть все основания надеяться, что для наших читателей эта задача не будет «холодным душем».

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1).

Правильное решение и ответ.

Пример 1. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции (функция представляет собой многочлен и её производную можно найти по формулам 1, 2 и 3 в таблице производных):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Теперь у нас есть всё, что требуется подставить в приведённую в теоретической справке запись, чтобы получить уравнение касательной. Получаем

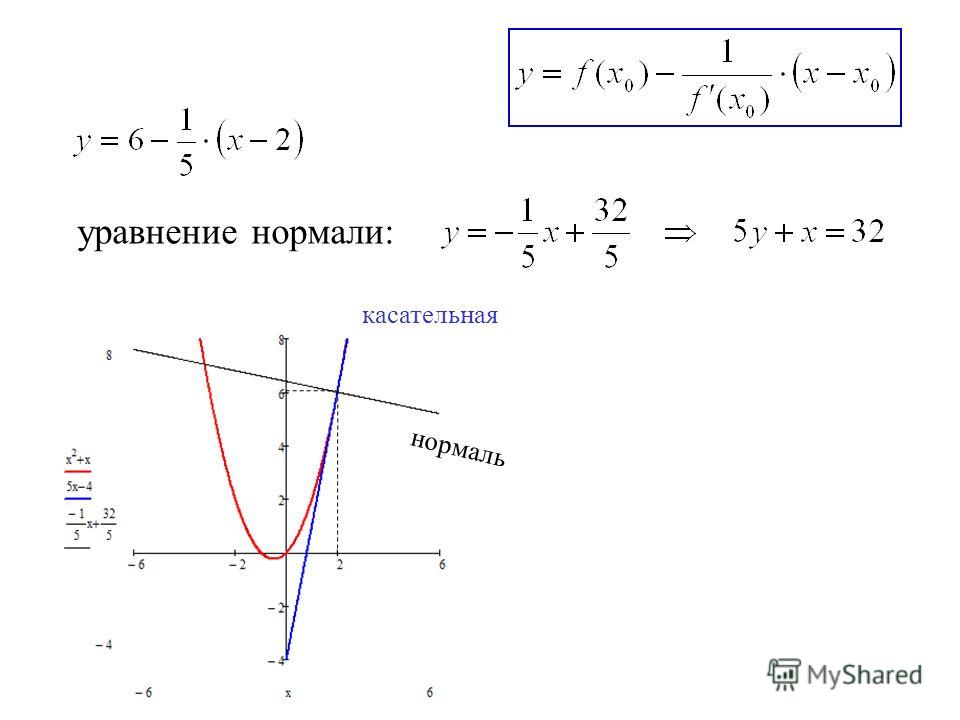
В этом примере нам повезло: угловой коэффициент оказался равным нулю, поэтому отдельно приводить уравнение к общему виду не понадобилось. Теперь можем составить и уравнение нормали:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Следующий пример — тоже не сложный: функция, как и в предыдущем, также представляет собой многочлен, но угловой коэффициен не будет равен нулю, поэтому добавится ещё один шаг — приведение уравнения к общему виду.

Пример 2. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Приводим уравнение к общему виду (все буквы и числа, отличные от нуля, собираем в левой части, а в правой оставляем ноль):

Составляем уравнение нормали:

Пример 3. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции (по формуле 5 в таблице производных):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Находим уравнение касательной:

Перед тем, как привести уравнение к общему виду, нужно его немного «причесать»: умножить почленно на 4. Делаем это и приводим уравнение к общему виду:

Составляем уравнение нормали:

Нет времени вникать в решение? Можно заказать работу!

Пример 4. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Правильное решение и ответ

Пример 5. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Правильное решение и ответ.

Пример 6. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Найдём производную функции (по формуле 14 в таблице производных):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).

Пример 7. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Внимание! Данная функция — сложная, так как аргумент тангенса (2x) сам является функцией. Поэтому найдём производную функции как производную сложной функции (потребуется формула 9 в таблице производных сложной функции):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Пример 8. Составить уравнение касательной и уравнение нормали к графику функции , если абсцисса точки касания .

Решение. Найдём ординату точки касания:

Как и в предыдущем примере, данная функция — сложная, так как степень () сама является функцией. Поэтому найдём производную функции как производную сложной функции (используя формулу 1 в таблице производных сложной функции):

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Производная, дифференциал и их применение

Поделиться с друзьями

Весь блок «Производная»

Что такое производная
Найти производную: алгоритмы и примеры решений
Производные произведения и частного функций
Производная суммы дробей со степенями и корнями
Производные простых тригонометрических функций
Производная сложной функции
Производная логарифмической функции
Дифференциал функции
Дифференциал сложной функции, инвариантность формы дифференциала
Правило Лопиталя
Частные производные

Что такое угловой коэффициент касательной.

Уравнение касательной и уравнение нормали к графику функции

Главная > Остекление > Что такое угловой коэффициент касательной. Уравнение касательной и уравнение нормали к графику функции

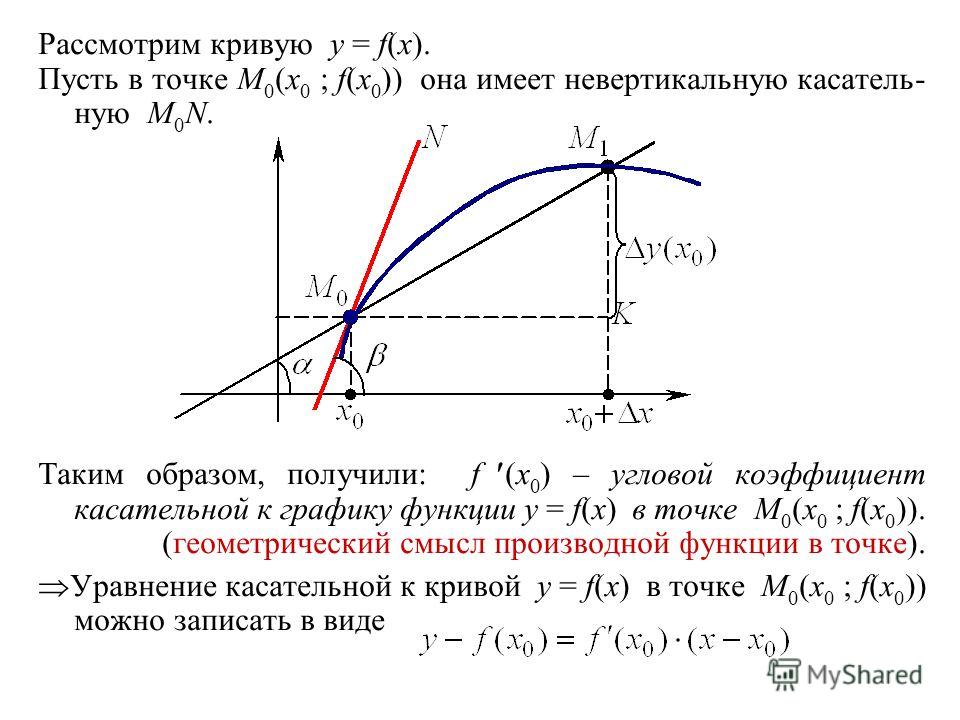
С понятием касательной к графику функции вы уже знакомы. График дифференцируемой в точке х 0 функции f вблизи х 0 практически не отличается от отрезка касательной, а значит, он близок к отрезку секущей l, проходящей через точки (х 0 ; f (х 0)) и (х 0 +Δx; f (x 0 + Δx)). Любая из таких секущих проходит через точку А (х 0 ; f (х 0)) графика (рис. 1). Для того чтобы однозначно задать прямую, проходящую через данную точку A, достаточно указать ее угловой коэффициент. Угловой коэффициент Δy/Δx секущей при Δх→0 стремится к числу f ‘(x 0) (его мы примем за угловой коэффициент касательной) Говорят, что касательная есть предельное положение секущей при Δх→0 .

Если же f’(х 0) не существует, то касательная либо не существует (как у функции у = |x| в точке (0; 0), см. рис.), либо вертикальна (как у графика функции в точке (0; 0), рис. 2).

Итак, существование производной функции f в точке хо эквивалентно существованию (невертикальной) касательной в точке (х 0 , f (х 0)) графика, при этом угловой коэффициент касательной равен f» (х 0). В этом состоитгеометрический смысл производной

Касательная к графику дифференцируемой в точке xо функции f — это прямая, проходящая через точку (x 0 ; f (x 0)) и имеющая угловой коэффициент f ‘(х 0).

Проведем касательные к графику функции f в точках x 1 , х 2 , х 3 (рис. 3) и отметим углы, которые они образуют с осью абсцисс. (Это угол, отсчитываемый в положительном направлении от положительного направления оси до прямой.) Мы видим, что угол α 1 острый, угол α 3 тупой, а угол α 2 равен нулю, так как прямая l параллельна оси Ох. Тангенс острого угла положителен, тупого — отрицателен, tg 0 = 0. Поэтому

F»(x 1)>0, f’(x 2)=0, f’(x 3)
Построение касательных в отдельных точках позволяет более точно строить эскизы графиков. Так, например, для построения эскиза графика функции синус предварительно находим, что в точках 0; π/2 и π производная синуса равна 1; 0 и -1 соответственно.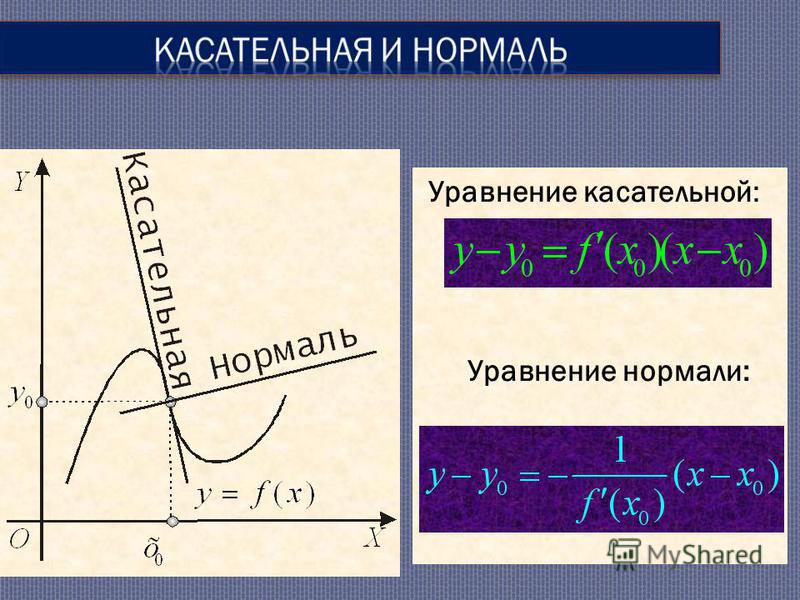 Построим прямые, проходящие через точки (0; 0), (π/2,1) и (π, 0) с угловыми коэффициентами 1, 0 и -1 соответственно (рис. 4) Остается вписать в полученную трапецию, образованную этими прямыми и прямой Ох, график синуса так, чтобы при х, равном 0, π/2 и π, он касался соответствующих прямых.

Отметим, что график синуса в окрестности нуля практически не отличим от прямой у = х. Пусть, например, масштабы по осям выбраны так, что единице соответствует отрезок в 1см. Имеем sin 0,5 ≈ 0,479425, т. е. |sin 0,5 — 0,5| ≈ 0,02, и в выбранном масштабе это соответствует отрезку длиной 0,2 мм. Поэтому график функции y = sin x в интервале (-0,5; 0,5) будет отклоняться (в вертикальном направлении) от прямой у = х не более чем на 0,2 мм, что примерно соответствует толщине проводимой линии.

Прямая y = f(x) будет являться касательной к графику, изображенному на рисунке в точке х0 при том условии, если она проходит через данную точку с координатами (х0; f(x0)) и имеет угловой коэффициент f»(x0). Найти этот коэффициент, учитывая особенности касательной, несложно.

Вам понадобится

— математический справочник;
— тетрадь;
— простой карандаш;
— ручка;
— транспортир;
— циркуль.

Инструкция

Примите к сведению, что график дифференцируемой функции f(x) в точке х0 не имеет различий с отрезком касательной. Поэтому он является достаточно близким к отрезку l, к проходящему через точки (х0; f(х0)) и (х0+Δx; f(x0 + Δx)). Чтобы задать прямую, проходящую через точку А с коэффициентами (х0; f(х0)), укажите ее угловой коэффициент. При этом он равен Δy/Δx секущей касательной (Δх→0) , а также стремится к числу f‘(x0).
Если значений f‘(x0) не существует, то, возможно, касательной нет, или же она проходит вертикально. Исходя из этого, присутствие производной функции в точке х0 объясняется существованием невертикальной касательной, которая соприкасается с графиком функции в точке (х0, f(х0)). В данном случае угловой коэффициент касательной равняется f»(х0). Становится понятен геометрический смысл производной, то есть расчет углового коэффициента касательной.
То есть для того чтобы найти угловой коэффициент касательной, нужно найти значение производной функции в точке касания. Пример: найти угловой коэффициент касательной к графику функции у = х³ в точке с абсциссой Х0 = 1. Решение: Найдите производную данной функции у΄(х) = 3х²; найдите значение производной в точке Х0 = 1. у΄(1) = 3 × 1² = 3. Угловой коэффициент касательной в точке Х0 = 1 равен 3.
Начертите на рисунке дополнительные касательные таким образом, чтобы они соприкасались с графиком функции в следующих точках: x1, х2 и х3. Отметьте углы, которые образуются данными касательными с осью абсцисс (угол отсчитывается в положительном направлении — от оси до касательной прямой). Например, первый угол α1 будет острым, второй же (α2) – тупой, ну а третий (α3) будет равняться нулю, так как проведенная касательная прямая является параллельной оси ОХ. В этом случае тангенс тупого угла есть отрицательное значение, а тангенс острого угла – положительное, при tg0 и результат равен нулю.

Вам понадобится

— математический справочник;
— тетрадь;
— простой карандаш;
— ручка;
— транспортир;
— циркуль.

Инструкция

Примите к сведению, что график дифференцируемой функции f(x) в точке х0 не имеет различий с отрезком касательной. Поэтому он достаточно близким к отрезку l, к проходящему через точки (х0; f(х0)) и (х0+Δx; f(x0 + Δx)). Чтобы задать прямую, проходящую через точку А с коэффициентами (х0; f(х0)), укажите ее угловой коэффициент. При этом он равен Δy/Δx секущей касательной (Δх→0) , а также стремится к числу f‘(x0).

Если значений f‘(x0) не существует, то, касательной нет, или же она проходит вертикально. Исходя из этого, производной функции в точке х0 объясняется существованием невертикальной касательной, которая соприкасается с графиком функции в точке (х0, f(х0)). В данном случае угловой коэффициент касательной равняется f»(х0). Становится понятен геометрический производной, то есть углового коэффициента касательной.

То есть для того чтобы найти угловой коэффициент касательной, нужно найти значение производной функции в точке касания. Пример: найти угловой коэффициент касательной к функции у = х³ в точке с абсциссой Х0 = 1. Решение: Найдите производную данной функции у΄(х) = 3х²; найдите значение производной в точке Х0 = 1. у΄(1) = 3 × 1² = 3. Угловой коэффициент касательной в точке Х0 = 3.

Начертите на рисунке дополнительные касательные таким образом, чтобы они соприкасались с графиком функции в точках: x1, х2 и х3. Отметьте углы, которые образуются данными касательными с осью абсцисс (угол отсчитывается в положительном направлении — от оси до касательной прямой). Например, угол α1 будет острым, же (α2) – тупой, ну а третий (α3) будет равняться нулю, так как проведенная касательная прямая является параллельной оси ОХ. В этом случае тангенс тупого угла есть отрицательное значение, а тангенс острого угла – положительное, при tg0 и результат равен нулю.

Касательной к заданной окружности называется прямая линяя, которая имеет только одну общую точку с этой окружностью. Касательная к окружности всегда перпендикулярна его радиусу, проведённому к точке касания. Если две касательные проведены из одной точки, не принадлежащей окружности, то расстояния от этой точки до точек касания всегда будет одинаковым. Касательные к окружностям строятся разными способами, в зависимости от их расположения относительно друг друга.

Инструкция

Построение касательной к одной окружности.
1. Строится окружность радиуса R и берётся A, которую будет проходить касательная.
2. Строится окружность с центром в середине отрезка OA и радиусам равным этого отрезка.
3. Пересечения двух точками касания касательных проведённых через точку A к заданной окружности.

Внешняя касательная к двум окружностям .

2. Проводится окружность радиусом R – r с центром в точке O.
3. К полученной окружности проводится касательная из O1, точка касания обозначена M.
4. Радиус R проходящий через точку M на точку T – точку касания окружности.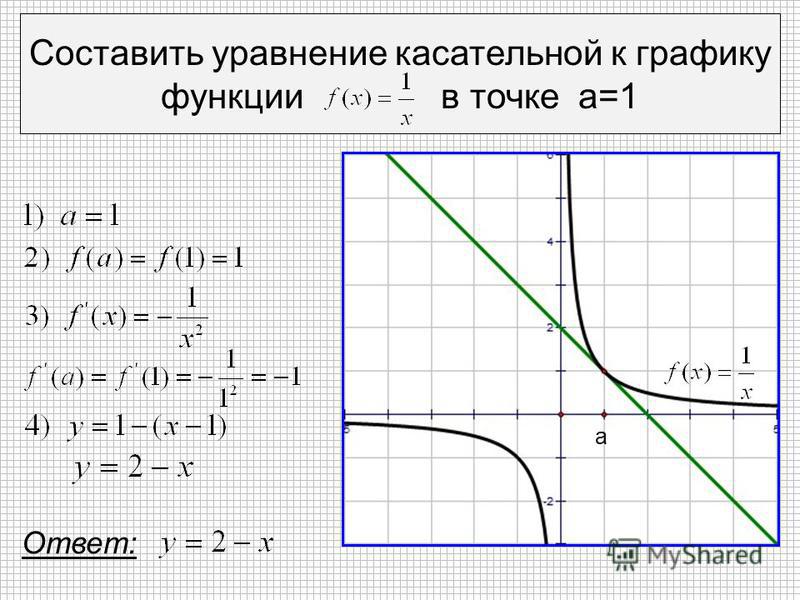
5. Через центр O1 малой окружности проводится радиус r параллельно R большой окружности. Радиус r указывает на точку T1 – точку касания малой окружности.
окружностям .

Внутренняя касательная к двум окружностям .
1. Строятся две окружности радиусом R и r.
2. Проводится окружность радиусом R + r с центром в точке O.
3. К полученной окружности проводится касательная из точки O1, точка касания обозначена буквой M.
4. Луч OM пересекает первую окружность в точке T – в точке касания большой окружности.
5. Через центр O1 малой окружности проводится радиус r параллельно лучу OM. Радиус r указывает на точку T1 – точку касания малой окружности.
6. Прямая TT1 – касательная к заданным окружностям .

Источники:

внутренняя касательная

Угловой шкаф – идеальный вариант для пустующих углов в квартире. Кроме того, конфигурация угловых шкаф ов придает интерьеру классическую атмосферу. В качестве отделки угловых шкаф ов может быть использован любой материал, который подходит для этой цели.

Вам понадобится

ДВП, МДФ, шурупы, гвозди, пильный диск, фриз.

Инструкция

Вырежьте из фанеры или ДВП шаблон шириной 125 мм, длиной 1065 мм. Кромки необходимо запилить под углом 45 градусов. По готовому шаблону определите размеры боковых стенок, а так же место, где будет расположен шкаф .

Крышку соедините с боковыми стенками и треугольными полками. Крепление крышки должно происходить к верхним кромкам боковых стенок при помощи шурупов. Для прочности конструкции дополнительно используют клей. Полки прикрепите к планкам.

Наклоните пильный диск под углом 45 градусов и скосите по направляющей планке переднюю кромку боковых стенок. Неподвижные полки прикрепите к планкам МДФ. Соедините боковые стенки при помощи шурупов. Следите за тем, чтобы не было щелей.

В стене сделайте отметки, между которыми поставьте каркас углового шкаф а. С помощью шурупов прикрепите шкаф к стене. Длина дюбеля должна быть 75 мм.

Из цельной плиты МДФ выпилите лицевую рамку. С помощью дисковой пилы вырежьте в ней проемы, используя линейку. Допилите углы.

Найдите значение абсциссы точки касания, которую обозначаются буквой «а». Если она совпадает с заданной точкой касательной, то «а» будет ее х-координате. Определите значение функции f(a), подставив в уравнение функции величину абсциссы.

Определите первую производную уравнения функции f’(x) и подставьте в него значение точки «а».

Возьмите общее уравнение касательной, которое определяется как y = f(a) = f (a)(x – a), и подставьте в него найденные значения a, f(a), f «(a). В результате будет найдено решение графика и касательной.

Решите задачу иным способом, если заданная точка касательной не совпала с точкой касания. В этом случае необходимо в уравнение касательной вместо цифр подставить «а». После этого вместо букв «х» и «у» подставьте значение координат заданной точки.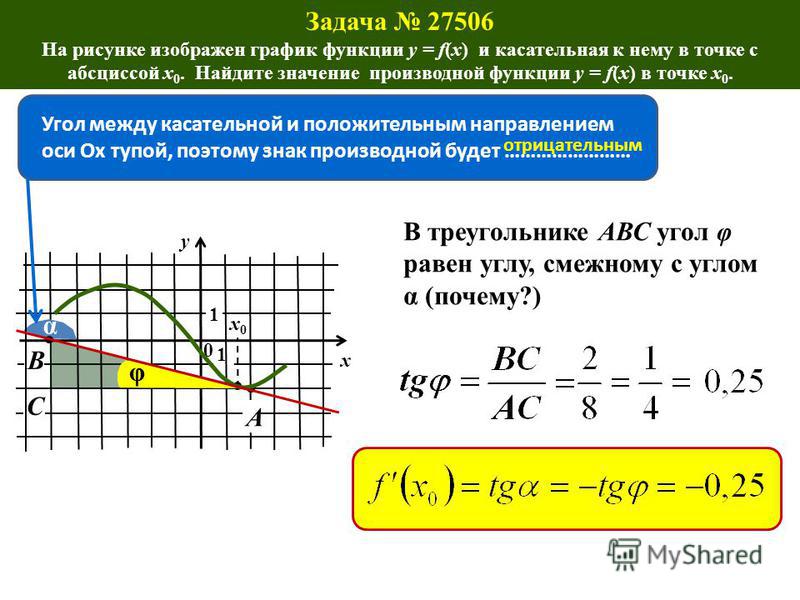 Решите получившееся уравнение, в котором «а» является неизвестной. Поставьте полученное значение в уравнение касательной.

Составьте уравнение касательной с буквой «а», если в условии задачи задано уравнение функции и уравнение параллельной линии относительно искомой касательной. После этого необходимо производную функции , чтобы координату у точки «а». Подставьте соответствующее значение в уравнение касательной и решите функцию.

При составлении уравнения касательной к графику функции используется понятие «абсцисса точки касания». Данная величина может задаваться изначально в условиях задачи или же ее необходимо определять самостоятельно.

Инструкция

Начертите на листе в клеточку оси координат х и у. Изучите заданное уравнение для графика функции. Если оно является , то достаточно два значения для параметра у при любых х, после чего построить найденные точки на оси координат и соединить их линией. Если же график нелинейный, то составьте таблицу зависимости у от х и подберите как минимум пять точек для построения графика.

Определите значение абсциссы точки касания для случая, когда заданная точка касательной не совпадает с графиком функции. Задаем третий параметр буквой «а».

Запишите уравнение функции f(a). Для этого в исходное уравнение вместо х подставьте а. Найдите производную функции f(x) и f(a). Подставьте необходимые данные в общее уравнение касательной, которое имеет вид: y = f(a) + f «(a)(x – a). В результате получить уравнение, которое из трех неизвестных параметров.

Подставьте в него вместо х и у координаты заданной точки, через которую проходит касательная. После этого найдите решение полученного уравнения для всех а. Если оно является квадратным, то будет два значения абсциссы точки касания. Это , что касательная проходит два раза возле графика функции.

Нарисуйте график заданной функции и , которые заданы по условию задачи. В этом случае необходимо также задать неизвестный параметр а и подставить его в уравнение f(a). Приравняйте производную f(a) к производной уравнения параллельной прямой.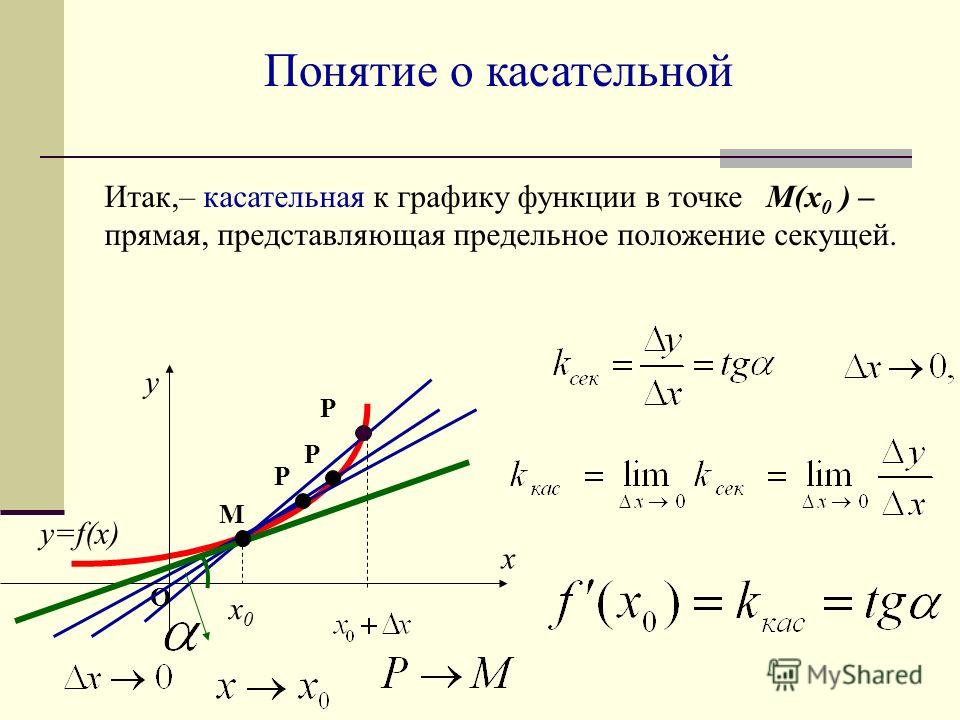 Данное выходит из условия параллельности двух . Найдите корни полученного уравнения, которые будут являться абсциссами точки касания.

Прямая y=f(x) будет касательной к изображенному на рисунке графику в точке х0 в том случае, если она проходит через точку с координатами (х0; f(x0)) и обладает угловым коэффициентом f»(x0). Найти такой коэффициент, зная особенности касательной, несложно.

Вам понадобится

— математический справочник;
— простой карандаш;
— тетрадь;
— транспортир;
— циркуль;
— ручка.

Инструкция

Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.

Определите общую . Подобного рода сведения можно получить, обратившись к данным переписи населения. Для определения общих коэффициентов рождаемости, смертности, брачности и разводимости вам понадобится найти произведение общей населения и расчетного периода. Получившееся число запишите в знаменатель.

Поставьте на числителя показатель, соответствующий искомому относительному. Например, если перед вами стоит определить общий коэффициент рождаемости, то на месте числителя должно находиться число, отражающее общее количество рожденных за интересующий вас период. Если вашей целью является уровня смертности или брачности, то на место числителя поставьте число умерших в расчетный период или число вступивших в брак, соответственно.

Умножьте получившееся число на 1000. Это и будет искомый вами общий коэффициент. Если же перед вами стоит задача найти общий коэффициент прироста, то вычтите из коэффициента рождаемости коэффициент смертности.

Видео по теме

Источники:

Общие коэффициенты естественного движения населения

Главным показателем эффективности экстракции является коэффициент распределения . Он считается по формуле: Со/Св, где Со – концентрация извлекаемого вещества в органическом растворителе (экстракторе), а Св – концентрация этого же вещества в воде, после наступления равновесия. Как можно опытным путем найти коэффициент распределения?

Инструкция

Определяем угловой коэффициент касательной к кривой в точке М.
Кривая, представляющая собой график функции y = f(x), непрерывна в некоторой окрестности точки М (включая саму точку М).

Определите первую производную уравнения функции f’(x) и подставьте в него значение точки «а».

Касательная — это прямая , которая касается графика функции в одной точке и все точки которой находятся на наименьшем расстоянии от графика функции. Поэтому касательная проходит касательно графика функции под определённым углом и не могут проходить через точку касания несколько касательных под разными углами. Уравнения касательной и уравнения нормали к графику функции составляются с помощью производной.

Уравнение касательной выводится из уравнения прямой .

Выведем уравнение касательной, а затем — уравнение нормали к графику функции.

y = kx + b .

В нём k — угловой коэффициент.

Отсюда получаем следующую запись:

y — y 0 = k (x — x 0 ) .

Значение производной f «(x 0 ) функции y = f (x ) в точке x 0 равно угловому коэффициенту k = tgφ касательной к графику функции, проведённой через точку M 0 (x 0 , y 0 ) , где y 0 = f (x 0 ) . В этом состоит геометрический смысл производной .

Таким образом, можем заменить k на f «(x 0 ) и получить следующее уравнение касательной к графику функции :

y — y 0 = f «(x 0 )(x — x 0 ) .

В задачах на составление уравнения касательной к графику функции (а мы уже скоро к ним перейдём) требуется привести получившееся по вышеприведённой формуле уравнение к уравнению прямой в общем виде . Для этого нужно все буквы и числа перенести в левую часть уравнения, а в правой части оставить ноль.

(x — x 0 ) + f «(x 0 )(y — y 0 ) = 0

Пример 0. Составить уравнение касательной и уравнение нормали к графику функции в точке M (1, 1) .

Найдём производную функции:

На рисунке ниже: график функции бордового цвета, касательная зелёного цвета, нормаль оранжевого цвета.

Пример 2.

Решение. Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Подставляем все полученные данные в «формулу-болванку» и получаем уравнение касательной:

Составляем уравнение нормали:

Решение. Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Находим уравнение касательной:

Составляем уравнение нормали:

Решение. Найдём ординату точки касания:

Найдём производную функции:

Найдём значение производной в точке касания, то есть угловой коэффициент касательной:

Получаем уравнение касательной:

Приводим уравнение к общему виду:

Составляем уравнение нормали:

Распространённая ошибка при составлении уравнений касательной и нормали — не заметить, что функция, данная в примере, — сложная и вычислять её производную как производную простой функции. Следующие примеры — уже со сложными функциями (соответствующий урок откроется в новом окне).

Решение. Найдём ординату точки касания:

Внимание! Данная функция — сложная, так как аргумент тангенса (2x ) сам является функцией. Поэтому найдём производную функции как производную сложной функции.

Производная функции в точке. Касательная к графику функции, геометрический смысл производной. Вывод уравнений касательной и нормали к графику функции.

Поделись

Опр. Пусть функция y=f(x) определена в точке х и некоторой её окрестности. Придадим значению аргумента х приращение Dх (положительное или отрицательное, но не выводящее за пределы этой окрестности) и найдем соответствующее приращение функции Dу=f(x+Dх)- f(x). Передел отношения приращение функции Dу к приращению аргумента Dх при Dх ®0 называется производной функции y=f(x) в точке х.

. Операция нахождения производной называется дифференцированием.

Геометрический смысл производной у’(x₀) — угловой коэффициент касательной к графику функции y=f(x) в точке (x₀,y₀=f(x₀)). Не любая функция имеет касательную в каждой точке, так, невозможно построить касательную к графику функции |x| в точке (0,0). Чтобы в точке (x₀,y₀=f(x₀)) существовала касательная, необходимо существование предела , т.е. существование производной. Функции, имеющие производную в каждой точке своей области определения (т.е. функции, графики которых имеют касательную в каждой точке), будем называть гладкими.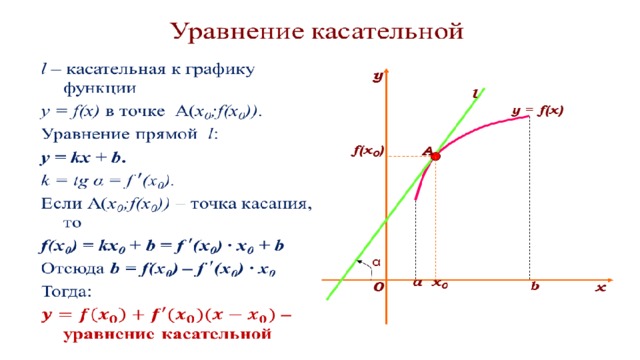

уравнение касательной в точке (x₀,y₀=f(x₀)): ;

уравнение нормали к графику функции в точке (x₀,y₀=f(x₀)): (при условии, что у’(x₀)¹0).

Дифференцируемость функции в точке. Теорема о связи Дифференцируемости с существованием конечной производной (с доказательством). Связь дифференцируемости и непрерывности функции (с доказательством).

Опр. Функция y = f(x) называется дифференцируемой в точке х, если её приращение Dу в этой точке можно представить в виде , где А — не зависящая от Dх величина, a(Dх) — БМ высшего порядка по сравнению с Dх: при Dх®0.

В более краткой записи для дифференцируемой в точке х функции .

Теор. Для того, чтобы функция y = f(x) имела в точке х конечную производную

y’ = f’(x), необходимо и достаточно, чтобы она была дифференцируемой в этой точке.

Док-во. Необходимость. Пусть в точке х существует конечная производная y’. По теор.6.2о приращении функции, имеющей производную, Dу= у’(x) Dх + a(Dх) Dх, где a(Dх) — бесконечно малая функция при Dх ®0. Сравнивая это выражение с определением 6.2, делаем вывод: А= у’(x), БМ a(Dх) Dх имеет более высокий порядок по сравнению с Dх, т. е. f(x) действительно дифференцируема в точке х.

Достаточность. Пусть f(x) дифференцируема в точке х, т.е. её приращение Dу можно представить в виде , где А — не зависящая от Dх величина, a(Dх) — БМ высшего порядка по сравнению с Dх: при Dх®0. Тогда . Следовательно, существует предел отношения приращения функции к приращению аргумента, т.е. $ у’(x), и у’(x)=А.

Как найти уравнения касательных и нормальных прямых

Краткий обзор

Чтобы найти уравнение прямой, вам нужны точка и наклон.
Наклон касательной представляет собой значение производной в точке касания.
Нормальная линия — это линия, перпендикулярная касательной и проходящая через точку касания.

Примеры

Пример 1 92) = 12 $$

Наклон касательной равен $$m = 12$$.

Шаг 3

Найдите точечно-наклонную форму прямой с наклоном $$m = 12$$, проходящей через точку $$(2,8)$$.

$$ \начать{выравнивать*} y — y_1 & = m(x-x_1)\\[6pt] у — 8 и = 12 (х-2) \конец{выравнивание*} $$ 92 — х$$. Найдите уравнение касательной с наклоном $$m = -3$$.

Шаг 1

Найдите производную.

$$ f'(x) = 2x -1 $$

Шаг 2

Найдите значение $$x$$, где $$f'(x)$$ равно наклону.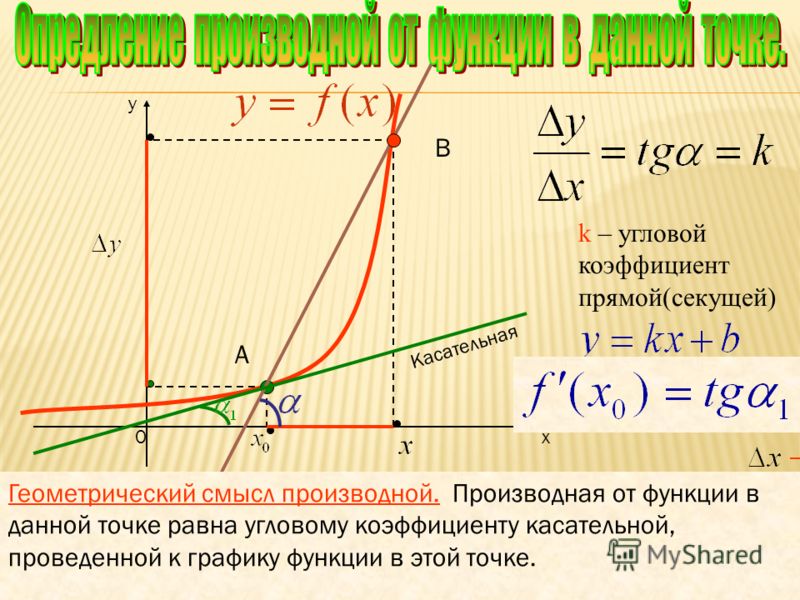

$$ \начать{выравнивать*} f'(x) & = 2x -1\\[6pt] -3 & = 2x -1\\[6pt] -2 & = 2x\\[6pt] х & = -1 \конец{выравнивание*} $$ 92 — (-1) = 1 + 1 = 2 $$

Точка $$(-1, 2)$$.

Шаг 4

Найдите уравнение прямой, проходящей через точку $$(-1,2)$$ с наклоном $$m=-3$$.

$$ \начать{выравнивать*} y -y_1 & = m(x-x_1)\\[6pt] у — 2 & = -3(х — (-1))\\[6pt] у — 2 и = -3 (х + 1) \конец{выравнивание*} $$

Отвечать

$$ у — 2 = -3(х+1) $$

Для справки, вот график функции и касательной, которую мы только что нашли. 2 = 16$$. Найдите уравнение касательной в точке $$x = 2$$ при $$y>0$$. 92 & = 12\\[6pt] y & = \pm\sqrt{12}\\[6pt] y & = \pm\sqrt{4\cdot 3}\\[6pt] у & = \pm2\sqrt 3 \конец{выравнивание*} $$

Поскольку в задаче указано, что нас интересует $$y>0$$, мы используем $$y = 2\sqrt 3$$.

Точка касания $$(2, 2\sqrt 3)$$.

Шаг 2

Найдите уравнение для $$\frac{dy}{dx}$$.

Поскольку уравнение определено неявно, мы используем неявное дифференцирование.

$$ \начать{выравнивать*} 2x + 2y\,\frac{dy}{dx} & = 0\\[6pt] 2y\,\frac{dy}{dx} & = -2x\\[6pt] \frac{dy}{dx} & = -\frac{2x}{2y}\\[6pt] \frac{dy}{dx} & = -\frac{dy} x y \конец{выравнивание*} $$

Шаг 3

Найдите наклон касательной в точке касания.

В точке $$(2,2\sqrt 3)$$ наклон касательной равен

$$ \начать{выравнивать*} \ frac {dy} {dx} \ bigg | _ {(\ blue {2}, \ red {2 \ sqrt 3})} & = — \ frac {\ blue 2} {\ red {2 \ sqrt 3}} \\[6pt] & = — \ frac 1 {\ sqrt 3} \\ [6pt] & = — \ frac 1 {\ sqrt 3} \ cdot \ blue {\ frac {\ sqrt 3} {\ sqrt 3}} \\ [6pt] & = -\frac{\sqrt 3} 3 \конец{выравнивание*} $$

Наклон касательной равен $$m = -\frac{\sqrt 3} 3$$.

Шаг 4

Найдите уравнение касательной через $$(2,2\sqrt 3)$$ с наклоном $$m=-\frac{\sqrt 3} 3$$.

В точке $$(2,2\sqrt 3)$$ наклон касательной равен

$$ \начать{выравнивать*} y — y_1 & = m(x-x_1)\\[6pt] y — 2 \ sqrt 3 & = — \ frac {\ sqrt 3} 3 (x-2) \конец{выравнивание*} $$

Отвечать

Уравнение касательной: $$y — 2\sqrt 3 = -\frac{\sqrt 3} 3(x-2)$$

Для справки график кривой и найденной нами касательной линии показан ниже.

Нормальные линии

Предположим, у нас есть касательная к функции. Функция и касательная пересекаются в точке касания. Линия, проходящая через эту же точку и перпендикулярная касательной, называется 9.0008 обычная строка .

Напомним, что когда две прямые перпендикулярны, их наклоны являются отрицательными обратными величинами. Поскольку наклон касательной равен $$m = f'(x)$$, наклон нормальной линии равен $$m = -\frac 1 {f'(x)}$$.

Пример 4

Предположим, что $$f(x) = \cos x$$. Найдите уравнение прямой, нормальной к функции в точке $$x = \frac \pi 6$$.

Шаг 1

Найдите точку на функции.

$$ f\left(\frac \pi 6\right) = \cos \frac \pi 6 = \frac{\sqrt 3} 2 $$

Точка $$\left(\frac\pi 6, \frac{\sqrt 3} 2\right)$$.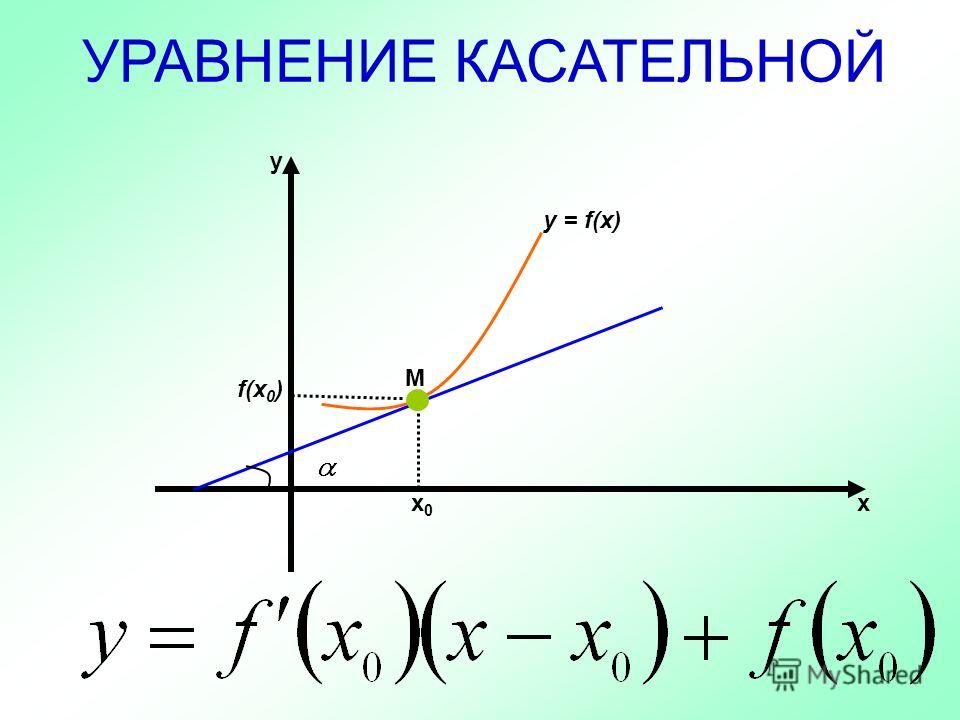

Шаг 2

Найдите значение производной при $$x = \frac \pi 6$$.

$$ f'(x) = -\sin x\longrightarrow f’\left(\frac \pi 6\right) = -\sin\frac\pi 6 = -\frac 1 2 $$

Наклон касательной равен $$m = -\frac 1 2$$. Поскольку мы ищем линию, перпендикулярную касательной, мы хотим использовать $$m = 2$$.

Шаг 3

Найдите уравнение прямой, проходящей через точку $$\left(\frac \pi 6, \frac{\sqrt 3} 2\right)$$ с наклоном $$m =2$$.

$$ \начать{выравнивать*} y -y_1 & = m(x-x_1)\\[6pt] y — \frac{\sqrt 3} 2 & = 2\left(x — \frac\pi 6\right) \конец{выравнивание*} $$

Отвечать

Прямая, нормаль к функции в точке $$x = \frac \pi 6$$, равна $$y — \frac{\sqrt 3} 2 = 2\left(x — \frac \pi 6\right)$$.

Для справки, вот график функции и найденная нами нормаль.

Проблемы с продолжением практики

Объяснение урока: уравнения касательной и нормали

В этом объяснении мы узнаем, как найти наклон и уравнение прямой касательная и нормаль к кривой в данной точке с использованием производных.

Производная кривой в точке говорит нам о наклоне касательной к кривой в этой точке, и существует множество различных методов нахождения производные различных функций. Мы можем использовать эти различия методы, которые помогут нам найти уравнение касательных линий к различным дифференцируемые функции.

Во-первых, давайте вспомним, что именно мы подразумеваем под касательной к кривой в точке.

Определение: касательная к кривой в точке

Для кривой 𝑦=𝑓(𝑥) и точки (𝑥,𝑦) на кривой, говорят, что прямая 𝑎𝑥+𝑏𝑦+𝑐=0 — касательная к кривой в точке точка (𝑥,𝑦) если

касательная проходит через точку (𝑥,𝑦);
кривая и касательная имеют одинаковый наклон в точке (𝑥,𝑦).

В приведенном выше определении мы утверждаем, что наша касательная и кривая будут иметь такой же наклон в точке (𝑥,𝑦). Это означает, что, вокруг точки (𝑥,𝑦) линия будет касаться только Кривая.

Уравнение прямой линии можно найти, используя значение ее наклона и координаты точки, лежащей на прямой. Из определения выше, мы знаем, что касательная и кривая проходят через точку (𝑥,𝑦). Следовательно, единственная недостающая часть информация наклон.

Затем мы можем использовать дифференцирование, чтобы найти наклон кривой, 𝑦=𝑓(𝑥), на данный момент. Для функции 𝑓 который дифференцируем в 𝑥, этот наклон определяется выражением 𝑓′(𝑥).

Давайте посмотрим на пример того, как мы можем использовать это, чтобы найти уравнение касательной к кривой в точке.

Пример 1. Нахождение уравнения касательной к кривой полиномиальной функции при заданном значении для 𝑥

Найдите уравнение касательной к кривой 𝑦=−2𝑥+8𝑥−19 в 𝑥=2.

Ответ

Чтобы найти уравнение касательной к кривой в точке, нам нужны два части информации: координаты точки и наклон кривая в этой точке.

Вопрос требует, чтобы мы нашли касательную, когда 𝑥=2, поэтому 𝑥-координата равна 2. Мы можем найти 𝑦-координата для этого значения 𝑥 подставив 𝑥=2 в уравнение нашей кривой: 𝑦=−2(2)+8(2)−19=−16+32−19=−3.

Это дает нам точку (2,−3) на нашей кривой через которую должна пройти наша касательная.

Далее нам нужен наклон кривой, когда 𝑥=2; найти это нам нужно различать: dddd𝑦𝑥=𝑥−2𝑥+8𝑥−19=−6𝑥+16𝑥.

Затем мы подставляем в 𝑥=2, чтобы найти наклон касательная в этой точке: dd𝑦𝑥|||=−6(2)+16(2)=−24+32=8.

Теперь, чтобы найти уравнение нашей касательной, вспомним, что уравнение линии наклона 𝑚, проходящей через (𝑥,𝑦) определяется выражением 𝑦−𝑦=𝑚(𝑥−𝑥). 

В нашем случае имеем 𝑦-(-3)=8(𝑥-2)𝑦+3=8𝑥-16𝑦-8𝑥+19=0.

Следовательно, уравнение касательной к нашей кривой в точке 𝑥=2 задается уравнением 𝑦−8𝑥+19=0.

Этот метод дает нам действительно полезный результат для нахождения уравнения касательной прямой к кривой в точке (при условии, что производная кривой существует на данный момент). Если у нас есть кривая 𝑦=𝑓(𝑥) и точку (𝑥,𝑦) на нашей кривой, то касательная к нашей кривой в этой точке должна иметь наклон 𝑓′(𝑥). Напомним, что точка-наклон Форма прямой линии сообщает нам уравнение прямой, проходящей через точка (𝑥,𝑦) с наклоном 𝑚, данный 𝑦−𝑦=𝑚(𝑥−𝑥).

Итак, если мы знаем наклон этой касательной и точку, через которую она проходит, это вся информация, которая нам нужна, чтобы найти его уравнение.

Определение: Уравнение касательной

Уравнение касательной к кривой 𝑦=𝑓(𝑥) в точке (𝑥,𝑦) определяется выражением 𝑦−𝑦=𝑓′(𝑥)⋅(𝑥−𝑥). 

Эта формула предполагает, что 𝑓 дифференцируемо в 𝑥. Если наша функция 𝑓 не дифференцируема в 𝑥, то мы не можем использовать эту формулу, чтобы найти уравнение касательная в точке 𝑥. Вместо этого нам нужно будет рассмотреть проблему графически. Попробуйте найти касательные линии к следующим двум кривые при 𝑥=0.

На нашем первом графике видно, что кривая не определена при 𝑥=0, что также означает, что он не дифференцируем при 𝑥=0. Если наша кривая не определена при 𝑥=0, то она не может иметь касательную в этой значение 𝑥.

На нашем втором графике мы видим, что касательная в точке 𝑥=0 должен быть вертикальным. Если бы мы должны были дифференцировать нашу функцию 𝑓(𝑥)=√𝑥,𝑓′(𝑥)=13𝑥.

Затем мы могли бы попытаться найти наклон нашей кривой при 𝑥=0: 𝑓′(0)=130=10.

Затем мы видим, что this не определено. Когда 𝑓 не дифференцируем в точка, набросок графика часто может помочь нам определить, имеет ли эта точка вертикальная касательная.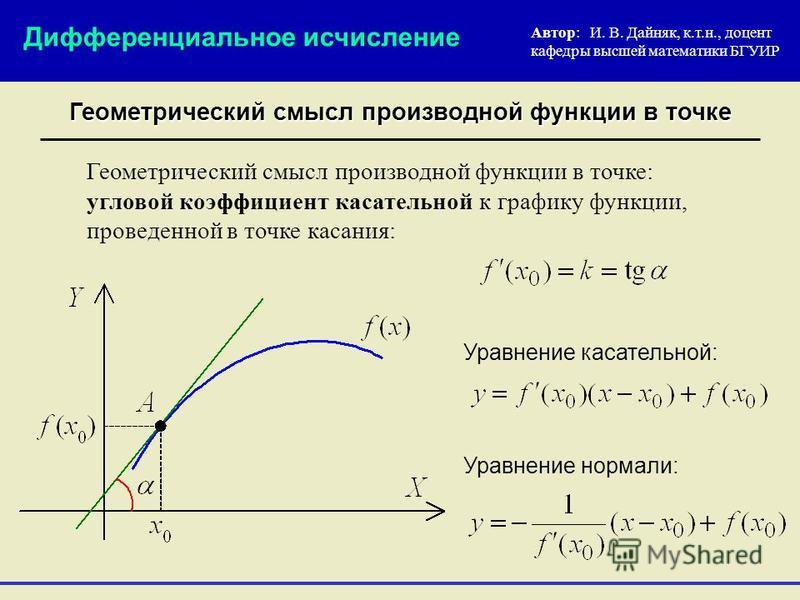

До сих пор мы были сосредоточены на касательных линиях. Однако есть еще один важный тип линии, который мы должны рассмотреть, называется нормальной линией. Нормальная линия чтобы кривая в точке была очень похожа на касательную; единственная разница что нормальная линия будет перпендикулярна касательной.

Определение: нормальная линия к кривой в точке

Для кривой 𝑦=𝑓(𝑥) и точки (𝑥,𝑦) на кривой, говорят, что прямая 𝑎𝑥+𝑏𝑦+𝑐=0 — нормаль к кривой в точке (𝑥,𝑦) если

точка (𝑥,𝑦) лежит на нашей прямой;
эта линия перпендикулярна касательной к нашей кривой в точке эта точка.

Стоит отметить, что мы можем определить нормальную линию на основе информации что он перпендикулярен кривой в этой точке; тем не менее, может быть проще представьте, что линия перпендикулярна касательной.

Нахождение уравнения нормальной линии потребует немного больше усилий поскольку производная функции дает нам только наклон касательной. Чтобы найти уравнение нормали к кривой в точке, нам нужна точка на линию и ее наклон, чтобы найти уравнение точка-наклон.

Поскольку мы уже знаем, что нормаль проходит через точку (𝑥,𝑦), нам нужно только найти наклон нормальной линии, чтобы найти ее уравнение точка-наклон.

Мы хотим найти выражение для наклона нашей нормальной линии в терминах наклона касательной. Для этого сначала заметим, что если касательная линия горизонтальна, то нормальная линия должна быть перпендикулярна, поэтому она должна быть вертикальная линия, и то же самое будет верно и в обратном направлении.

Это означает, что теперь мы можем предположить, что имеем дело с касательной, которая не горизонтальный или вертикальный. Итак, мы можем написать уравнение касательной прямой в точке точка (𝑥,𝑦) в виде 𝑦=𝑚𝑥+𝑐, где 𝑚 не равно нулю. Мы также скажем что уравнение нашей нормальной линии 𝑦=𝑛𝑥+𝑑.

Чтобы найти выражение для наклона нашей нормальной линии, 𝑛, мы начнем с эскиза.

Чтобы найти выражение для наклона 𝑛, мы добавим в строка 𝑥=𝑥+1.

Теперь мы видим, что у нас есть треугольник с прямым углом при (𝑥,𝑦). Мы можем найти координаты вершины. Мы уже знаем координаты вершины в (𝑥,𝑦); мы сравним две другие вершины до этой точки, чтобы найти их координаты.

Так как мы выбрали нашу вертикальную линию на одну единицу правее (𝑥,𝑦), наши другие две вершины будут одной единицей Направо. Мы можем найти 𝑦-координаты этих двух вершин вспомнив, что наклон линии говорит нам об изменении 𝑦 за каждую единицу изменения 𝑥. С момента изменения в 𝑥 составляет 1 единицу для обеих вершин, изменение 𝑦 для касательной будет 𝑚 и изменение в 𝑦 для нормальной линии будет 𝑛.

Следовательно, координаты вершин равны (𝑥,𝑦), (𝑥+1,𝑦+𝑚) и (𝑥+1,𝑦+𝑛).

Затем мы можем найти длины каждой стороны в этом треугольнике, используя расстояние Формула между двумя точками. Мы не будем проводить индивидуальный расчет шаги, но результаты показаны ниже.

Наконец, поскольку это прямоугольный треугольник, мы можем применить к нему теорему Пифагора. этого треугольника, где гипотенуза этого треугольника является стороной, противоположной прямой угол, в данном случае вертикальная линия. На самом деле, поскольку это вертикальной линии, длина этой линии равна разнице между ее 𝑦-координаты. В этом случае мы будем использовать |𝑚−𝑛|, так как мы не знаем знака из 𝑚−𝑛: √1+𝑚+√1+𝑛=|𝑚−𝑛|1+𝑚+1+𝑛=𝑚−2𝑚𝑛+𝑛2=−2𝑚𝑛𝑛=−1𝑚.0019

Это дает нам уравнение для определения наклона нашей нормальной линии; это отрицательное значение, обратное наклону касательной. Мы также знаем, как найдите наклон касательной, используя производную.

Это означает, что мы можем использовать тот факт, что 𝑚=𝑓′(𝑥) найти формулу уравнения нормальной прямой.

Определение: Уравнение нормальной линии к кривой

Если 𝑓′(𝑥)≠0, то уравнение нормали к 𝑦=𝑓(𝑥) в точке (𝑥,𝑦) определяется выражением 𝑦−𝑦=−1𝑓′(𝑥)(𝑥−𝑥). 

Если наклон нашей кривой в точке 𝑥 равен нулю, то нормальная линия в этой точке будет вертикальным, и его уравнение будет 𝑥=𝑥. Если наклон нашей кривой не определен в точке, есть две возможности.

Касательная к кривой в этой точке вертикальна; в таком случае, нормальная линия будет горизонтальной.
Касательная к кривой в этой точке не существует; в таком случае, нормальной линии не существует.

Рассмотрим несколько примеров применения этих формул к некоторым кривым.

Пример 2. Нахождение уравнения нормали к кривой многочлена Функция в точке с заданной 𝑥-координатой

Найти уравнение нормали к кривой 𝑦=−2𝑥−7𝑥+2 при 𝑥=−2.

Ответ

Мы хотим найти уравнение нормали к кривой в точке. Для этого нам нужно найти точку на линии и ее наклон. Мы можем найти точку на прямой, подставив 𝑥=−2 в уравнение нашей кривой: 𝑦=−2(−2)−7(−2)+2=−10,

Итак, нормаль проходит через точку (−2,−10).

Далее мы вспоминаем, что мы можем найти наклон нормальной линии по формуле используя наклон касательной.

Если положить 𝑓(𝑥)=−2𝑥−7𝑥−2, тогда касательная будет иметь наклон 𝑓′(−2): 𝑓′(𝑥)=−6𝑥−14𝑥,𝑓′(−2)=−6(−2)−14(−2)=4.

Мы показали, что касательная будет иметь наклон 4, но уклон нормальная линия — это отрицательная величина, обратная этому значению: наклон нормали = −1𝑓′(−2)=−14.

Мы знаем, что наклон нашей линии равен −14. и мы также знаем, что он проходит через (−2,−10). Это дает нам уравнение 𝑦-(-10)=-14(𝑥-(-2))𝑦+10=-14(𝑥+2)−4𝑦-40=𝑥+24𝑦+𝑥+42=0.

Следовательно, уравнение нормали к кривой при 𝑥=−2 дан кем-то 4𝑦+𝑥+42=0.

В нашем следующем примере мы рассмотрим, как найти точки на кривой, где его касательная в этой точке будет параллельна данной прямой.

Пример 3. Нахождение 𝑥-координаты точки на кривой Квадратичная функция, где касательная Параллельно 𝑥-оси

Какова 𝑥-координата точки, где касательная к 𝑦=𝑥+12𝑥+11 параллельна 𝑥-ось?

Ответ

Мы хотим найти 𝑥-координату, где проходит касательная к эта кривая будет параллельна оси 𝑥. Мы знаем, что 𝑥-ось горизонтальна, поэтому любая линия, параллельная ей, также должна быть горизонтальным; другими словами, наклон этой касательной должен быть равен нуль.

Мы также знаем, что для кривой 𝑦=𝑓(𝑥) наклон касательной к этой кривой в точке (𝑥,𝑦) будет его производной в этой точке, в этом случае 𝑓′(𝑥).

Следовательно, чтобы решить этот вопрос, мы должны найти значения 𝑥, для которого производная равна нулю.

Поскольку наша функция является многочленом, мы можем дифференцировать ее, используя степенное правило дифференцирования: dd𝑥𝑥+12𝑥+11=2𝑥+12.

Приравняв нашу производную к нулю, мы можем найти значения 𝑥 где касательная параллельна 𝑥-ось: 2𝑥+12=0𝑥=−6.

Следовательно, касательная к этой кривой параллельна 𝑥-ось, когда 𝑥=−6.

В нашем следующем примере мы найдем уравнение касательной к кривой, которая образует определенный угол с положительной 𝑥-осью.

Пример 4. Нахождение уравнения касательной к кривой кубической функции учитывая угол, который образует касательная с осью 𝑥

Найдите уравнение касательной к кривой 𝑦=𝑥+9𝑥+26𝑥, который составляет угол 135∘ с положительной 𝑥-осью.

Ответ

В этом вопросе мы хотим найти касательную к кривой, которая образует угол 135∘ с положительной 𝑥-осью. Это означает, что для ответа на этот вопрос, который нам понадобится, чтобы определить соответствующий наклон для линия, которая составляет этот угол с положительной 𝑥-осью.

Во-первых, если мы переместим линию, она не изменит угол, который она образует с положительной 𝑥-осью. Итак, мы можем начать с наброска наша линия, проходящая через начало координат (поскольку это самый простой случай), образуя угол 135∘ с положительной 𝑥-осью. Это будет иметь то же самое наклон в качестве нашей касательной.

Тогда мы увидим, что 135=90+45∘∘∘, что дает нам следующую диаграмму:

Тогда есть два способа найти наклон этой линии; мы можем использовать факт что наклон прямой есть тангенс угла, который она образует с положительная 𝑥-ось; в таком случае, тангенс135=-1∘; или мы могли бы использовать тригонометрию, чтобы найти наклон этой линии. В любом случае мы видим, что вопрос требует, чтобы мы нашли касательную линия с наклоном −1.

Наклон касательной в точке равен производной кривой в этой точке, поэтому мы хотим установить производную равной −1 и решить для 𝑥: dddd𝑦𝑥=𝑥𝑥+9𝑥+26𝑥=3𝑥+18𝑥+26.

Это означает, что мы хотим решить 3𝑥+18𝑥+26=−13𝑥+18𝑥+27=0𝑥+6𝑥+9=0(𝑥+3)=0,

Решение 𝑥=−3.

Чтобы найти уравнение касательной к кривой, когда 𝑥=−3, нам нужно найти координаты точки на линия. Мы можем найти это, подставив 𝑥=−3 в уравнение для нашей кривой: 𝑦=(−3)+9(−3)+26(−3)=−24. 

Искомая касательная проходит через (−3,−24) и имеет наклон −1.

Мы можем использовать это, чтобы найти уравнение прямой 𝑦-(-24)=-1(𝑥-(-3))𝑦+24=-(𝑥+3)𝑦+24=-𝑥-3𝑦+𝑥+27=0.

Следовательно, касательная к кривой, образующей угол 135∘ с положительной 𝑥-осью имеет уравнение 𝑦+𝑥+27=0.

Не всегда так просто, как дифференцировать многочлен, найти наклон касательная или нормаль к нашей кривой. Иногда нам нужно будет применять другие производные правила, которые помогут нам найти это значение. Давайте посмотрим на пример этого.

Пример 5. Нахождение уравнения нормали к кривой функции, включающей Тригонометрические функции по заданной 𝑥-координате

Найти все точки с 𝑥-координатами в [0,𝜋[ где кривая 𝑦=2𝑥sin имеет касательную, параллельную прямой 𝑦=−𝑥−18.

Ответ

Во-первых, чтобы прямая была параллельна прямой 𝑦=−𝑥−18, он должен иметь одинаковый наклон.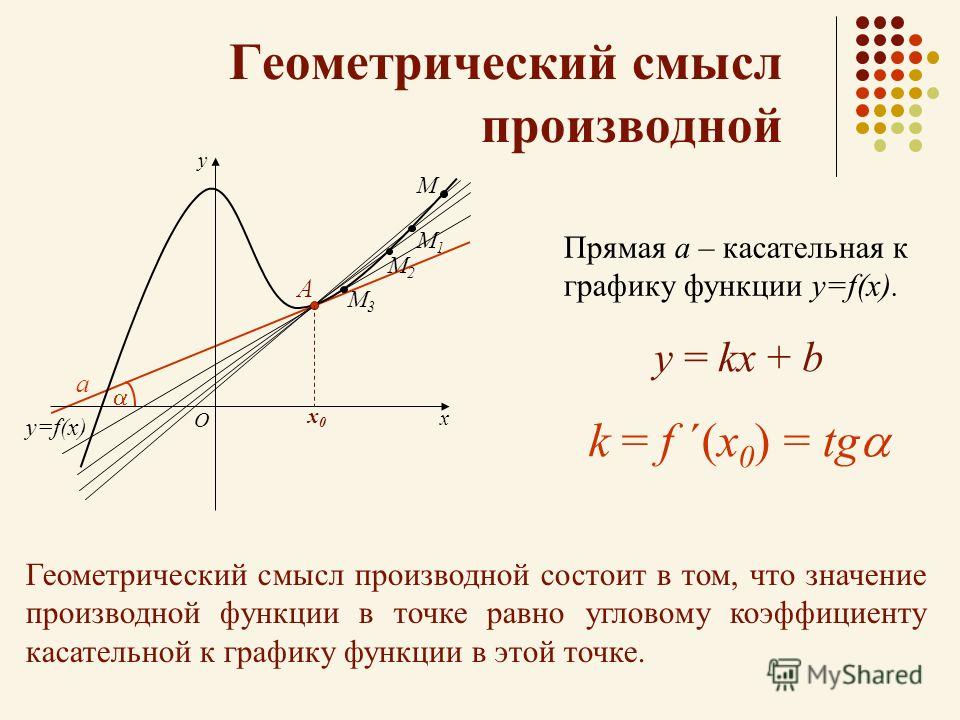 Следовательно, наша касательная должна иметь наклон из −1. Напомним, что наклон касательной к кривой 𝑦=𝑓(𝑥) в точке 𝑥 есть 𝑓′(𝑥). В нашем случае 𝑓(𝑥)=2𝑥грех. Мы можем дифференцировать это используя тот факт, что для любой константы 𝑛, где 𝑥 измеряется в радианы, ddsincos𝑥(𝑎𝑥)=𝑎𝑎𝑥.

Следовательно, 𝑓′(𝑥)=22𝑥.cos

Установка наклона нашей касательной равной −1 дает нам 22𝑥=−1.cos

Затем мы можем решить это для 𝑥 в интервале [0,𝜋[: cos2𝑥=−12.

Мы можем набросать это следующим образом.

У этого есть решения 𝑥=𝜋3 и 𝑥=2𝜋3. Наконец, нам нужно найти координаты этих точек, подставив эти 𝑥-значения в функцию sin2𝑥: sinandsin2𝜋3=√3222𝜋3=−√32, давая нам координаты 𝜋3,√32 и 2𝜋3,−√32.

Следовательно, координаты точек с 𝑥-координатами в [0,𝜋[ где кривая 𝑦=2𝑥sin имеет касательную, параллельную строка 𝑦=−𝑥−18, являются 𝜋3,√32 и 2𝜋3,−√32.

В нашем последнем примере мы определим точку пересечения двух кривых где пересечение ортогонально.

Пример 6. Нахождение точки пересечения двух квадратных кривых Ортогонально

Кривые 𝑦=2𝑥−3𝑥−2 и 𝑦=−3𝑥+5𝑥−5 пересекаются ортогонально в точке. Что это за точка?

Ответ

Мы говорим, что две кривые пересекаются ортогонально, если они пересекаются справа углы. Эквивалентно, касательные к обеим кривым в точке пересечения ортогональны (встречаются под прямым углом).

Напомним, что наклон кривой в точке определяется значением ее производная в этой точке. Начнем с поиска всех точек пересечение этих двух кривых, установив функции равными друг к другу и решение для 𝑥: 2𝑥−3𝑥−2=−3𝑥+5𝑥−52𝑥−3𝑥−2+3𝑥−5𝑥+5=05𝑥−8𝑥+3=0(5𝑥−3)(𝑥−1)=0,

Следовательно, кривые пересекаются при 𝑥=35 и когда 𝑥=1. Нам нужно найти наклоны обеих кривых в каждом из этих 𝑥-значений, чтобы определить, являются ли они ортогональный. Мы делаем это, дифференцируя каждую кривую, используя степень правило дифференцирования. Для первой кривой: dd𝑥2𝑥−3𝑥−2=4𝑥−3.

Мы можем использовать это, чтобы найти наклон при обоих 𝑥-значениях.

При 𝑥=35, dd𝑥2𝑥−3𝑥−2||=435−3=−35.

При 𝑥=1, дд𝑥2𝑥−3𝑥−2||=4(1)−3=1.

То же самое можно сделать со второй кривой: дд𝑥−3𝑥+5𝑥−5=−6𝑥+5.

При 𝑥=35, дд𝑥−3𝑥+5𝑥−5||=−635+5=725.

При 𝑥=1, dd𝑥−3𝑥+5𝑥−5||=−6(1)+5=−1.

ортогональны, их наклоны должны быть отрицательными обратными величинами. Взятие отрицательной обратной величины −35 дает нам −−35=−−53=53, который не равен наклону второй кривой в этой точке, так что касательные не ортогональны.

Возврат отрицательного числа к 1 дает нам −(1)=−1, что равно наклону второй кривой в этой точке. Следовательно, касательные ортогональны.

Мы можем найти координаты этой точки, подставив 𝑥=1 в уравнение любой кривой: 𝑦=2(1)−3(1)−2=2−3−2=−3.

Следовательно, кривые пересекаются ортогонально в точке (1,−3).

Давайте закончим, повторив некоторые вещи, которые мы рассмотрели при поиске уравнения касательных и нормалей к кривым.

Ключевые точки

Уравнение касательной к кривой 𝑦=𝑓(𝑥) в точке (𝑥,𝑦) определяется выражением 𝑦−𝑦=𝑓′(𝑥)(𝑥−𝑥).
Если 𝑓′(𝑥)≠0, тогда уравнение нормальной линии к 𝑦=𝑓(𝑥) в точке (𝑥,𝑦) определяется выражением 𝑦−𝑦=−1𝑓′(𝑥)(𝑥−𝑥).
Если 𝑓′(𝑥)=0, то касательная к 𝑦=𝑓(𝑥) в точке (𝑥,𝑦) горизонтальна и имеет уравнение 𝑦=𝑦.
Если 𝑓′(𝑥)=0, нормальная линия к 𝑦=𝑓(𝑥) в точке (𝑥,𝑦) вертикальна и имеет уравнение 𝑥=𝑥.
Две кривые пересекаются ортогонально в точке (𝑥,𝑦) если обе кривые пересекают эту точку и наклоны их касательных в этой точке точки ортогональны.
Если 𝑓′(𝑥) не определено, мы все равно можем быть в состоянии найти касательную и нормали в 𝑥. Однако это не всегда возможно.

Объяснение урока: Касательные и нормали к графику функции

В этом объяснении мы узнаем, как находить уравнения касательных и нормалей к тригонометрическим, параметрическим и неявно определенным кривые с использованием производных.

Мы знаем, что производная dd𝑦𝑥 в точке, если она существует, дает наклон касательной к кривой в данной точке. Используя координаты точки с наклоном, можно получить форму точка–наклон кривой. уравнение касательной к кривой в этой точке. Начнем с рассмотрения того, как найти уравнение касательной к кривой.

Практическое руководство. Нахождение уравнения касательной к кривой

Для кривой на плоскости 𝑥𝑦 определяется наклон касательной к кривой в точке (𝑥,𝑦) оценивая dd𝑦𝑥 в точке (𝑥,𝑦), если он существует в этой точке. Это обозначается dd𝑦𝑥|||().

Тогда уравнение касательной 𝑦=𝑦𝑥|||(𝑥−𝑥)+𝑦.dd()

Когда нам задана неявная кривая на 𝑥𝑦-плоскости, мы можем получить выражение для dd𝑦𝑥, применяя неявное дифференцирование. Вспомним цепное правило, т. основной компонент неявной дифференциации.

Правило: Цепное правило

Если переменная дифференцирования не совпадает с переменной дифференцируемой функции, необходимо заменить переменные применяя цепное правило. В частности, если производные 𝑓′ и dd𝑦𝑥 существуют, то имеем ддддддд𝑥𝑓(𝑦)=𝑦𝑓(𝑦)×𝑦𝑥=𝑓′(𝑦)𝑦𝑥.

В нашем первом примере мы найдем уравнение касательной к неявно заданной кривой, а также определим, где касательная пересекает кривую не в точке касания.

Пример 1: Теорема о неявной функции

Уравнение 𝑦−24𝑥+24𝑥=0 описывает кривую на плоскости.

Найдите координаты двух точек на этой кривой, где 𝑥=−12.
Определите уравнение касательной в точке, где 𝑥=−12 и 𝑦-координата положительна.
Найдите координаты другой точки, если она существует, в которой касательная пересекает кривую.

Ответ

Часть 1

Поскольку нам даны 𝑥-координаты, нам нужно определить все возможные 𝑦-координаты, когда 𝑥=−12. Замена данного 𝑥-координата в неявное уравнение, имеем 𝑦−24−12+24−12=0𝑦+3−12=0𝑦=9𝑦=±3.

Следовательно, возможные 𝑦-координаты равны 3 и −3. Координаты двух точек на этом кривая с 𝑥=−12 −12,3−12,−3.и

Часть 2

Чтобы определить уравнение касательной, нам нужно вычислить выражение dd𝑦𝑥 в точке касания. Начнем с неявного дифференцирования уравнения: dddddddddd𝑥𝑦−24𝑥+24𝑥=𝑥(0)𝑥𝑦−𝑥24𝑥+𝑥(24𝑥)=0.

Второе и третье слагаемые в приведенном выше уравнении являются правильными производными мы различаем функцию 𝑥 по отношению к 𝑥. Применяя степенное правило для дифференцирования, члены равны дддд𝑥24𝑥=24×3𝑥=72𝑥𝑥(24𝑥)=24. 

Для первого члена, дд𝑥𝑦, мы должны применить цепное правило, так как мы дифференцируют функцию 𝑦 по 𝑥: dddddddd𝑥𝑦=𝑦𝑦𝑦𝑥=2𝑦𝑦𝑥.

Подставляя эти выражения в наше дифференцированное уравнение, получаем 2𝑦𝑦𝑥−72𝑥+24=0.dd

Чтобы найти наклон касательной, нам нужно вычислить выражение dd𝑦𝑥 в точке точка касания. Поскольку мы хотим, чтобы 𝑦-координата была положительной, эта прямая касается кривой в точке −12,3. Следовательно, мы можем заменить 𝑥=−12 и 𝑦=3 в уравнение выше: 2𝑦𝑦𝑥−72𝑥+24=02(3)𝑦𝑥−72−12+24=06𝑦𝑥−18+24=06𝑦𝑥=−6𝑦𝑥=−1.dddddddddd

Это говорит нам о том, что наклон касательной в этой точке равен −1. Мы также знаем, что эта линия проходит через точка −12,3. Используя точечно-наклонную форму уравнения прямой, уравнение касательная 𝑦=−𝑥+12+3.

Упрощение дает 𝑦=−𝑥−12+3𝑦=52−𝑥.

Итак, уравнение касательной 𝑦=52−𝑥.

Часть 3

Мы хотим найти точку пересечения касательной, отличную от точки касания. Поскольку мы знаем уравнение касательной, 𝑦=52−𝑥, мы можем подставить это выражение в данное неявное уравнение кривой: 𝑦−24𝑥+24𝑥=052−𝑥−24𝑥+24𝑥=0254−5𝑥+𝑥−24𝑥+24𝑥=0254+19𝑥+𝑥−24𝑥=0.

Мы знаем, что одним из возможных решений этого уравнения является 𝑥=−12, так как это точка касание. Следовательно, по теореме об остатках имеем, что 𝑥+12 есть множитель кубического многочлен в левой части уравнения. Выполним длинное деление:

Это приводит к факторизованному выражению 𝑥+12−24𝑥+13𝑥+252.

Вынося из второго множителя 12, получаем 12𝑥+12−48𝑥+26𝑥+25.

Разложение квадратичного члена на (−24𝑥+25)(2𝑥+1) приводит к уравнению 12𝑥+12(−24𝑥+25)(2𝑥+1)=0.

Первый и третий множители дают корень 𝑥=−12, который является точкой касания. Середина фактор дает 𝑥 = 2524, что является новой точкой пересечения между касательной и кривой. Мы можем найдите 𝑦-координату этой точки, используя уравнение касательной: 𝑦=52−𝑥=52−2524=60−2524=3524.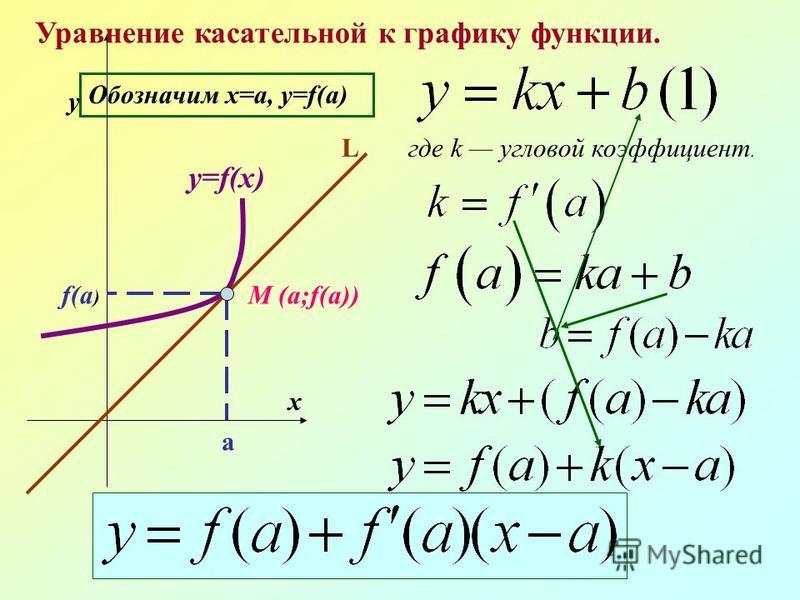

Следовательно, другой точкой пересечения касательной и кривой является 2524,3524.

До сих пор мы вычисляли уравнения касательных к различным кривым, описанным неявными уравнениями. В этих случаях, наклоны касательных обычно можно получить, вычислив dd𝑦𝑥. Давайте теперь рассмотрим примеры, где мы находим уравнения касательных к кривым, описываемым параметрическими уравнениями. Напомним параметрическое дифференцирование.

Теорема: параметрическое дифференцирование

Рассмотрим кривую на 𝑥𝑦-плоскости, описываемую параметрическими уравнениями 𝑥=𝑓(𝑡),𝑦=𝑔(𝑡).

Если производные 𝑓′ и 𝑔′ существуют и непрерывны, dd𝑦𝑥 получается дд𝑦𝑥==𝑔′(𝑡)𝑓′(𝑡),дддд где знаменатель не равен нулю.

Мы можем найти наклон касательной к параметрической кривой, оценив dd𝑦𝑥 в значение параметра, соответствующее точке касания. Рассмотрим пример, в котором мы найдем уравнение касательной к параметрической кривой.

Пример 2.

Нахождение уравнения касательной к заданной кривой

Найти уравнение касательной к кривой 𝑥=𝑡+1, 𝑦=𝑡+𝑡 в точке, соответствующей значению 𝑡=−1.

Ответ

Начнем с нахождения координат точки касания. Мы можем найти эти координаты, подставив 𝑡=−1 в параметрические уравнения 𝑥=(−1)+1=0,𝑦=(−1)+(−1)=0.

Это говорит нам о том, что касательная проходит через начало координат (0,0).

Далее найдем наклон касательной. Мы знаем, что наклон касательной получается вычислением выражения dd𝑦𝑥 в точке касания. Поскольку нам даны параметрические уравнения для кривой, нам нужно применить параметрическое дифференцирование, чтобы получить это выражение. Мы помним, что дд𝑦𝑥=.дддд

Мы можем вычислить dddddddd𝑥𝑡=𝑡𝑡+1=3𝑡,𝑦𝑡=𝑡𝑡+𝑡=4𝑡+1.

Следовательно, dd𝑦𝑥==4𝑡+13𝑡.dddd

Нам дано, что точка касания приходится на значение параметра 𝑡=−1. Оценка dd𝑦𝑥 в этот момент дает dd𝑦𝑥|||=4(−1)+13(−1)=−33=−1. 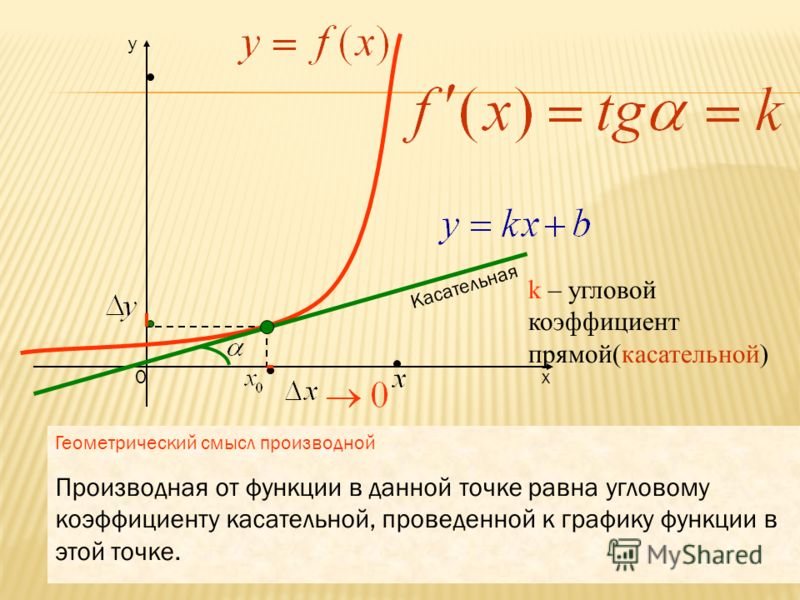

Это говорит нам о том, что наклон касательной к кривой при 𝑡=−1 равен − 1.

Используя форму точка-наклон с точкой (0,0) и наклоном −1, мы получаем 𝑦=−(𝑥−0)+0.

Следовательно, уравнение касательной имеет вид 𝑦=−𝑥.

В предыдущих примерах мы вычисляли наклон касательной к кривой, оценивая dd𝑦𝑥 в точке касания. Рассмотрим, как найти уравнение прямой, ортогональной кривой, которая называется нормально к кривой.

В нашем первом примере мы вспомнили, что две линии ортогональны друг другу, если их наклоны умножаются на -1. Исключением из этого правила являются случаи, когда одна из линий является вертикальной или горизонтальной, поскольку в этих случаях наклон линии либо нулевой или неопределенный. Однако эти случаи проще, поскольку линия, ортогональная горизонтальной линии, должна быть вертикальной, и наоборот. Следовательно, если мы знаем, что касательная горизонтальна или вертикальна, то мы можем сразу найти уравнение нормали.

Если касательная не является ни вертикальной, ни горизонтальной, то есть dd𝑦𝑥 оценивается в этой точке определен и не равен нулю, то наклон нормали к прямой есть отрицательная величина, обратная наклону касательной к Кривая. Мы резюмируем это следующим образом.

Как найти уравнение нормали к кривой

Дана кривая на 𝑥𝑦-плоскости, нормаль к кривой в точке (𝑥,𝑦) это прямая, проходящая через точку, ортогональную касательной в этой точке. Уравнение нормали приведено в следующие случаи:

Если dd𝑦𝑥|||=0(), то норма вертикальный. В этом случае уравнение нормали имеет вид 𝑥=𝑥.
Если dd𝑦𝑥|||() не определено, то либо касательная вертикальна, либо касательная не определена. Если касательная не определена, то нормаль не определена либо. Если касательная вертикальна, то нормаль горизонтальна. В этом случае уравнение нормали имеет вид 𝑦=𝑦.
Если dd𝑦𝑥|||≠0() и определено, то наклон нормали задается отрицательной величиной, обратной этому выражению, −1||dd(). Уравнение нормали к кривая в этом случае 𝑦=−1||(𝑥−𝑥)+𝑦.dd()

В следующем примере мы найдем нормаль к кривой, используя этот метод.

Пример 3. Нахождение уравнения нормали к кривой функции, включающей тригонометрические функции, в заданной 𝑥-координате

Найти уравнение нормали к кривой 𝑦=8𝑥−3𝑥cossec при 𝑥=𝜋3.

Ответ

Начнем с нахождения координат точки, в которой прямая перпендикулярна кривой. Мы знаем, что нормально проходит через точку 𝑥=𝜋3. Мы можем найти 𝑦-координату этой точки по формуле подставляя это значение в функцию: 𝑦=8𝜋3−3𝜋3=8×12−3×2=4−6=−2.cossec

Следовательно, координаты этой точки равны 𝜋3,−2.

Далее найдем наклон нормали. Мы знаем, что нормаль к кривой в точке — это прямая, проходящая через данной точке и ортогональна касательной в этой точке. Сначала вычислим наклон касательной к кривой в этой точке. точка, которая определяется производной в этой точке.

Напомним следующие производные тригонометрической и обратной тригонометрической функций: ddcossinddsecsectan𝑥𝑥=−𝑥,𝑥𝑥=𝑥𝑥.

Используя эти правила, мы имеем ddddcossecddcosddsecsinsectan𝑦𝑥=𝑥(8𝑥−3𝑥)=8𝑥𝑥−3𝑥𝑥=−8𝑥−3𝑥𝑥.

Оценка производной при 𝑥=𝜋3 дает ddsinsectan𝑦𝑥|||=−8𝜋3−3𝜋3𝜋3=−8×√32−3×2×√3=−4√3−6√3=−10√3.

Следовательно, наклон касательной в этот момент -10√3. Напомним, что если наклоны двух прямых умножить чтобы дать −1, то линии ортогональны. Поскольку наклон касательной не равен нулю, наклон нормали должен быть его отрицательной обратной величиной. Это приводит к наклону нормали: −1||=−1−10√3=√330.dd

Используя точку 𝜋3,−2 и наклон √330, точечно-наклонная форма уравнения нормали 𝑦=√330𝑥−𝜋3−2.

Запишем уравнение в общем виде. Упрощение дает 𝑦=√330𝑥−𝜋3−2𝑦=√330𝑥−𝜋√390−2𝑦−√330𝑥+𝜋√390+2=0.

Уравнение нормали 𝑦−√330𝑥+𝜋√390+2=0.

В предыдущем примере мы нашли наклон нормали к неявной кривой, сначала найдя dd𝑦𝑥 через неявное дифференцирование, а затем взяв отрицательную обратную величину этого выражение оценивается в данной точке. Мы можем найти нормаль к параметрической кривой, используя аналогичный метод, где только разница в том, что нам нужно использовать параметрическое дифференцирование, чтобы получить выражение dd𝑦𝑥.

В нашем следующем примере мы найдем уравнение нормали к параметрической кривой.

Пример 4. Нахождение уравнения нормали к кривой функции, определяемой параметрическими уравнениями, содержащими обратную Тригонометрические функции

Определить уравнение нормали к кривой 𝑥=−4𝜃+3cot, 𝑦=3𝜃+√2𝜃sinsec при 𝜃=𝜋4.

Ответ

Начнем с нахождения координат точки, в которой прямая перпендикулярна кривой. Нам дано, что норма проходит через точку при значении параметра 𝜃=𝜋4. Мы можем найти координаты этой точки по формуле подставляя это значение в параметрические уравнения 𝑥=−4𝜋4+3=−4×1+3=−1,𝑦=3𝜋4+√2𝜋4=3√22+√2×2√2=32+2=72.cotsinsec

Следовательно, координаты этой точки равны −1,72.

Далее найдем наклон нормали. Мы знаем, что нормаль к кривой в точке — это прямая, проходящая через данной точке и ортогональна касательной в этой точке. Сначала вычислим наклон касательной к кривой в этой точке, который мы можем получить, оценив dd𝑦𝑥 в этой точке, если он существует.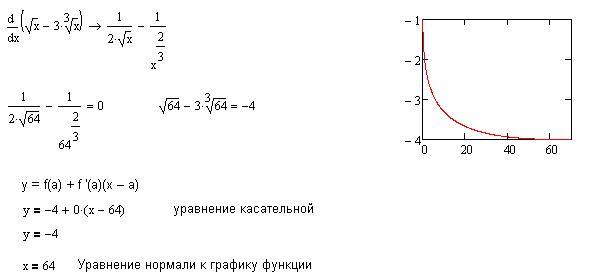 Чтобы найти выражение dd𝑦𝑥 применяем параметрическое дифференцирование: дд𝑦𝑥=.дддд

Напомним следующие производные тригонометрической и обратной тригонометрической функций: ddcotcscddsincosddsecsectan𝜃𝜃=−𝜃,𝜃𝜃=𝜃,𝜃𝜃=𝜃𝜃.

Дифференцируя параметрическое уравнение для 𝑥-переменной по 𝜃, получаем ddddcotddcotddcsccsc𝑥𝜃=𝜃(−4𝜃+3)=−4𝜃𝜃+𝜃(3)=−4−𝜃+0=4𝜃.

Дифференцируя 𝑦-уравнение, получаем ddddsinsecddsinddsec𝑦𝜃=𝜃3𝜃+√2𝜃=3𝜃𝜃+√2𝜃𝜃.

Нам нужно применить цепное правило для производной sin𝜃. Мы можем записать это выражение в виде композиции 𝑓∘𝑔, где 𝑓(𝜃)=𝜃 и 𝑔(𝜃)=𝜃sin. Тогда 𝑓′(𝜃)=2𝜃 и 𝑔′(𝜃)=𝜃cos, что приводит к ddsinsincos𝜃𝜃=𝑓′(𝑔(𝜃))𝑔′(𝜃)=2𝜃𝜃.

Подставляя это выражение, а также производную от sec𝜃 в наше выражение для дд𝑦𝜃, мы получаем ddsincossectan𝑦𝜃=6𝜃𝜃+√2𝜃𝜃.

Следовательно, путем параметрического дифференцирования имеем ddsincossectancsc𝑦𝑥==6𝜃𝜃+√2𝜃𝜃4𝜃.dddd

Поскольку линия нормальна при значении параметра 𝜃=𝜋4, нам нужно оценить выражение выше в этот момент: ddsincossectancsc𝑦𝑥|||=6+√24=6××+√2××14×=3+28=58. √√√ √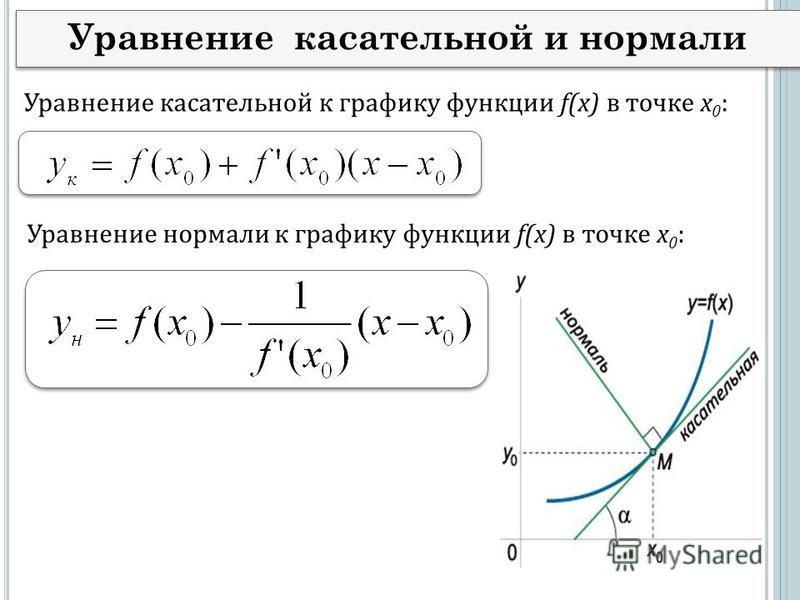

Следовательно, наклон касательной в этой точке равен 58. Напомним, что можно найти наклон нормали взяв отрицательную обратную величину этого значения: −1||=−1=−85.dd

Используя точку −1,72 и наклон −85, точка–наклон форма уравнения нормали 𝑦=−85(𝑥+1)+72.

Запишем это уравнение в общем виде. Упрощение дает 𝑦=-85(𝑥+1)+72𝑦=-85𝑥-85+72𝑦=-85𝑥-1610+3510𝑦=-85𝑥+191085𝑥+𝑦-1910=0.

Это одна из форм уравнения, которое мы ищем. В качестве альтернативы мы можем упростить это уравнение так, чтобы коэффициент 𝑥 равно 1. Умножая уравнение на 58, чтобы упростить коэффициент из 𝑥 дает 58×85𝑥+𝑦−1910=58×0𝑥+58×1910=0×+58×1916=0.

Следовательно, уравнение нормали к заданной параметрической кривой при 𝜃=𝜋4 имеет вид 𝑥+58𝑦−1916=0.

В предыдущих уравнениях мы вычисляли уравнения касательных и нормалей к кривой. Используя касательные, мы можем определить, когда две кривые пересекаются ортогонально.

Определение: кривые, пересекающиеся ортогонально

Предположим, что две кривые пересекаются в точке (𝑥,𝑦). Кривые пересекаются ортогонально, если касательные к обеим кривым в этой точке хорошо определены, и касательные ортогональны друг другу.

В нашем следующем примере мы найдем наклоны касательных к двум неявным кривым в точке пересечения, чтобы определить, они пересекаются ортогонально.

Пример 5. Определение того, являются ли две кривые, определенные неявно, ортогональными или нет пересекаются ортогонально в начале координат?

Ответ

Прежде чем мы начнем, мы можем убедиться, что кривые пересекаются в начале координат, проверив оба уравнения, оцененные в (0,0). Когда 𝑥=0 и 𝑦=0, мы видим, что оба уравнения становятся 0=0, что говорит нам о том, что обе кривые проходят через начало координат.

Помните, что две кривые пересекаются ортогонально в точке, если их касательные в этой точке четко определены и ортогональны каждой из них. Другой. Найдем наклоны касательных в начале каждой кривой путем неявного дифференцирования данных уравнений. За первая кривая, мы dddd𝑥9𝑦−8𝑦=𝑥(6𝑥).

Выражение в левой части уравнения выражено через переменную 𝑦, поэтому нам нужно применить цепочку правило: ддддддд𝑥9𝑦−8𝑦=𝑦9𝑦−8𝑦𝑦𝑥=36𝑦−8𝑦𝑥.

С другой стороны, правая часть dd𝑥(6𝑥)=6. Следовательно, у нас есть 36𝑦−8𝑦𝑥=6.dd

Мы знаем, что dd𝑦𝑥, вычисленное в начале координат, дает наклон касательной. Подстановка начала координат (0,0) в приведенное выше уравнение, чтобы найти это значение, дает нам 36×0−8𝑦𝑥|||=6−8𝑦𝑥|||=6𝑦𝑥|||=6−8=−34.()()()dddddd

Таким образом, наклон касательной к первой кривой в начале координат равен −34.

Далее найдем наклон касательной ко второй кривой. Неявное дифференцирование второго уравнения дает нам ддддд𝑥−5𝑥−𝑥(3𝑦)=𝑥(−4𝑥).

Первый член в левой части и член в правой части уравнения являются правильными производными, так как переменная этих выражений соответствует переменной дифференцирования 𝑥. На второй срок на слева, нам нужно использовать цепное правило.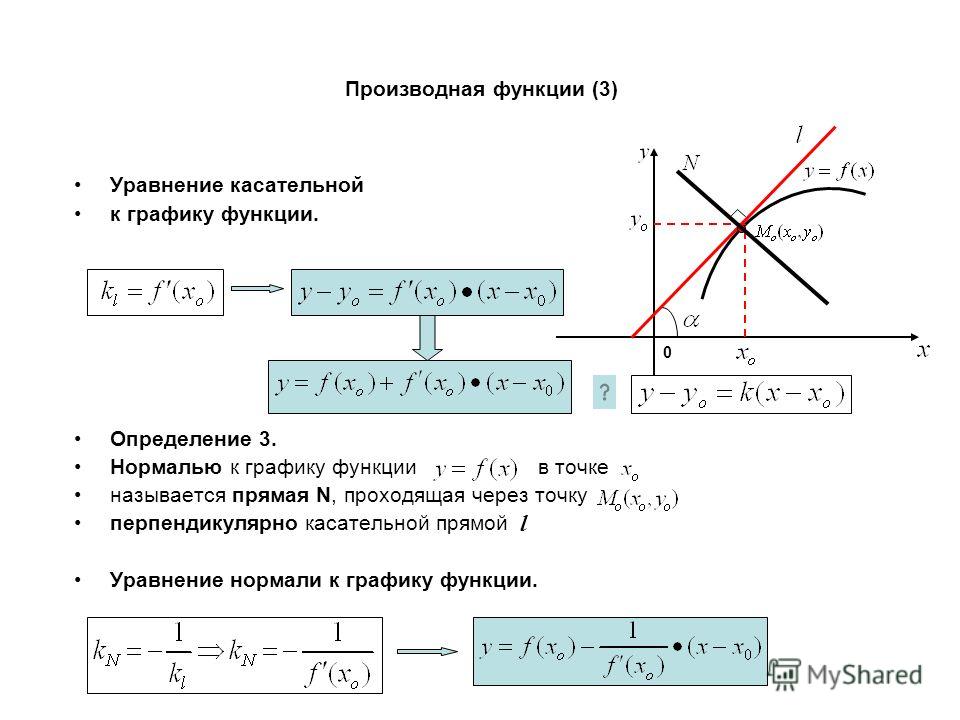 У нас есть dddddddddddd𝑥−5𝑥=−10𝑥𝑥(3𝑦)=𝑦(3𝑦)𝑦𝑥=3𝑦𝑥𝑥(−4𝑥)=−4.

Подставляя их в приведенное выше уравнение, мы получаем −10𝑥−3𝑦𝑥=−4.dd

Вычисляя это уравнение в начале координат (0,0) и упрощая, имеем −10×0−3𝑦𝑥|||=−4−3𝑦𝑥|||=−4𝑦𝑥|||=−4−3=43.dddddd()()()

Таким образом, наклон касательной ко второй кривой в начале координат равен 43.

Помните, что если наклоны двух прямых умножить на -1, то они ортогональны. Мы получили наклоны касательных для этих двух кривых, −34 и 43, и мы видим, что −34×43=−1.

Мы заключаем, что две кривые пересекаются ортогонально в начале координат.

В нашем последнем примере мы применим понятия касательных и нормалей к кривой, чтобы найти площадь треугольника.

Пример 6. Нахождение площади треугольника, образованного из оси 𝑥, касательной и нормали к кривой эллипса с помощью Дифференцирование

Найти площадь треугольника, ограниченного осью 𝑥, касательной и нормалью к кривой 𝑥+5𝑦=101 в точке (9,2) с точностью до тысячной.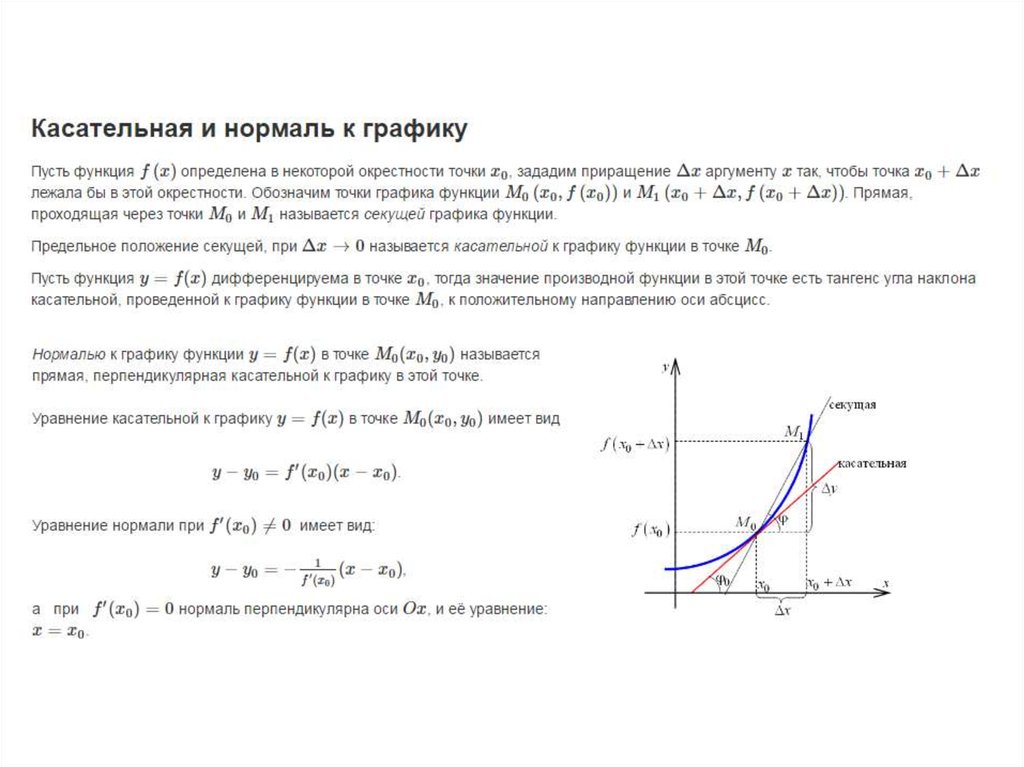

Ответ

Давайте начнем с визуализации этой проблемы. Мы знаем, что данное уравнение описывает эллипс с центром в начале координат. Подставив 𝑥=9и 𝑦=2 в уравнение, можно убедиться, что точка (9,2) лежит на этом эллипсе. Рисуем касательную (зеленый) и нормаль (красный) эллипса. в этот момент на диаграмме ниже.

Мы хотим найти площадь треугольника, образованного касательной, нормалью и осью 𝑥. Высота треугольник задается 𝑦-координатой точки (9,2), равной 2. Напомним, что площадь треугольника определяется как площадь основания треугольника = 12×.

Поскольку мы знаем, что высота равна 2 единицам длины, нам нужно найти основание треугольника. Основание этого треугольника равно положительная разница между 𝑥-пересечениями касательной и нормали, для чего нам понадобятся уравнения касательной и нормали к эллипсу в точке (9,2).

Начнем с нахождения уравнения касательной, которое приведет нас к 𝑥-перехвату касательной. Неявно дифференцируя данное уравнение по 𝑥, имеем dddddddd𝑥𝑥+5𝑦=𝑥(101)𝑥𝑥+5𝑥𝑦=0. 

Первый член в приведенном выше уравнении является правильной производной, поскольку мы дифференцируем функцию от 𝑥 по отношению к 𝑥. Применяя степенное правило дифференцирования, получаем dd𝑥𝑥=2𝑥.

Для второго члена, dd𝑥𝑦, мы должны применить цепное правило, поскольку мы дифференцируют функцию 𝑦 по 𝑥: ддддддд𝑥𝑦=𝑦𝑦𝑦𝑥=2𝑦𝑦𝑥.

Подставляя эти выражения в наше дифференцированное уравнение 2𝑥+10𝑦𝑦𝑥=0дд приводит к выражению дд𝑦𝑥=−2𝑥10𝑦=−𝑥5𝑦.

Помните, что наклон касательной к кривой в точке (𝑥,𝑦) определяется выражением дд𝑦𝑥|||(). Таким образом, мы можем найти наклон нашу касательную, подставив точку (9,2) в выражение дд𝑦𝑥: dd𝑦𝑥|||=−95×2=−910.()

Таким образом, уравнение касательной, проходящей через точку (9,2), имеет наклон −910. Точечно-наклонная форма уравнения линии дает 𝑦=−910(𝑥−9)+2𝑦=-910𝑥+8110+2𝑦=-910𝑥+8110+2010𝑦=-910𝑥+10110.

Мы можем найти 𝑥-пересечение касательной, подставив 𝑦=0 в это уравнение и решение для 𝑥-переменной: 0=-910𝑥+10110-10110=-910𝑥𝑥=-109×-10110=1019.

Далее найдем уравнение нормали к эллипсу в той же точке. Напомним, что нормалью кривой является линия которая ортогонально пересекается с касательной в точке касания. Мы знаем, что до тех пор, пока две линии не являются горизонтальными или вертикальны, а их наклоны умножаются на -1, тогда они пересекаются ортогонально. Другими словами, наклон нормали отрицателен. обратная величине наклона касательной. Поскольку мы знаем, что наклон касательной равен −910, получаем наклон нормали равен 109. Эта линия также проходит через точку (9,2). Точечно-наклонная форма уравнения нормали имеет вид 𝑦=109(𝑥−9)+2𝑦=109𝑥−10+2𝑦=109𝑥−8.

Установив 𝑦=0, мы можем получить 𝑥-перехват: 0=109𝑥−88=109𝑥𝑥=910×8=7210=365.

Мы можем вычислить основание треугольника, найдя положительную разницу между этими двумя 𝑥-перехватами: 1019−365=50545−32445=18145.

Следовательно, основание треугольника равно 18145 единицам длины. Мы также знаем, что высота треугольника равна 2 единицам длины. Площадь треугольника 12×18145×2=18145=4,0222….

Площадь треугольника, ограниченного осью 𝑥, касательной и нормалью к данному эллипсу в точке (9,2) равно 4,022 квадратных единиц, округленных до тысячных.

Давайте закончим повторением нескольких важных понятий из этого объяснения.

Ключевые точки

Учитывая неявную кривую на 𝑥𝑦-плоскости, мы можем найти dd𝑦𝑥 применяя неявное дифференцирование. Для параметрической кривой на 𝑥𝑦-плоскости мы можем найти dd𝑦𝑥, применяя параметрическое дифференцирование.
Для кривой на 𝑥𝑦-плоскости наклон касательной к кривой в точке (𝑥,𝑦) получается вычислением dd𝑦𝑥 в точке (𝑥,𝑦), если она существует. Это обозначается dd𝑦𝑥|||().
В этом случае уравнение касательной к кривой в точке (𝑥,𝑦) имеет вид 𝑦=𝑦𝑥|||(𝑥−𝑥)+𝑦.dd()
Дана кривая на 𝑥𝑦-плоскости, нормаль к кривой в точке (𝑥,𝑦) это прямая, проходящая через точку, ортогональную касательной в этой точке.
No related posts.

Уравнение касательной и уравнение нормали к графику функции

Что такое угловой коэффициент касательной.

Вам понадобится

Инструкция

Производная функции в точке. Касательная к графику функции, геометрический смысл производной. Вывод уравнений касательной и нормали к графику функции.

Как найти уравнения касательных и нормальных прямых

Краткий обзор

Примеры

Пример 1 92) = 12 $$

Нормальные линии

Пример 4

Объяснение урока: уравнения касательной и нормали

Определение: касательная к кривой в точке

Пример 1. Нахождение уравнения касательной к кривой полиномиальной функции при заданном значении для 𝑥

Ответ

Определение: Уравнение касательной

Определение: нормальная линия к кривой в точке

Определение: Уравнение нормальной линии к кривой

Пример 2. Нахождение уравнения нормали к кривой многочлена Функция в точке с заданной 𝑥-координатой

Ответ

Пример 3. Нахождение 𝑥-координаты точки на кривой Квадратичная функция, где касательная Параллельно 𝑥-оси

Ответ

Пример 4. Нахождение уравнения касательной к кривой кубической функции учитывая угол, который образует касательная с осью 𝑥

Ответ

Пример 5. Нахождение уравнения нормали к кривой функции, включающей Тригонометрические функции по заданной 𝑥-координате

Ответ

Пример 6. Нахождение точки пересечения двух квадратных кривых Ортогонально

Ответ

Ключевые точки

Объяснение урока: Касательные и нормали к графику функции

Практическое руководство. Нахождение уравнения касательной к кривой

Правило: Цепное правило

Пример 1: Теорема о неявной функции

Ответ

Теорема: параметрическое дифференцирование

Пример 2.

Ответ

Как найти уравнение нормали к кривой

Пример 3. Нахождение уравнения нормали к кривой функции, включающей тригонометрические функции, в заданной 𝑥-координате

Ответ

Пример 4. Нахождение уравнения нормали к кривой функции, определяемой параметрическими уравнениями, содержащими обратную Тригонометрические функции

Ответ

Определение: кривые, пересекающиеся ортогонально

Пример 5. Определение того, являются ли две кривые, определенные неявно, ортогональными или нет пересекаются ортогонально в начале координат?

Ответ

Пример 6. Нахождение площади треугольника, образованного из оси 𝑥, касательной и нормали к кривой эллипса с помощью Дифференцирование

Ответ

Ключевые точки

Добавить комментарий Отменить ответ