Уравнение окружности 9 класс онлайн-подготовка на Ростелеком Лицей
Определение окружности
Начнем с определения, что такое окружность. Вот одно из неверных определений.
Окружностью называется множество точек плоскости, равноудаленных от одной точки, от центра.
В чем ошибочность?
Давайте рассмотрим множество из четырех вершин квадрата. Все вершины квадрата равноудалены от одной точки, от центра квадрата. Но ведь это не окружность, а совсем небольшая часть окружности.
Дадим правильное определение окружности.
Окружностью называется множество ВСЕХ точек плоскости, равноудаленных от одной точки – от центра. Ключевое слово здесь «всех», это важно, так как мы хотим вывести уравнение окружности.
Формула расстояния между двумя точками (напоминание)
В определении окружности фигурирует расстояние между точкой окружности и центром.
Формула расстояния между двумя точками и
или
Рис.
1. Расстояние между двумя точками
Опираясь на формулу и определение окружности, можно вывести уравнение окружности с центром в точке радиуса .
Рис. 2. Уравнение окружности
Выбираем произвольную точку на этой окружности.
Если точка принадлежит окружности с центром и радиусом , то .
Тогда и координаты точки удовлетворяют уравнению окружности
.
Если же точка не лежит на окружности, то и координаты точки не удовлетворяют уравнению окружности.
Таким образом, уравнение окружности с центром в точке радиуса имеет вид:
.
Частный случай уравнения окружности с центром в точке :
.
Решение задач
Рассмотрим задачи на уравнение окружности.
Задача 1.
Начертить окружность, заданную уравнением , указать ее центр и радиус. Найти длину окружности и площадь круга, общие точки с осями координат.
Решение:
Центр этой окружности, исходя из уравнения, точка , радиус .
Рис. 3. Иллюстрация к задаче
Длина окружности и площадь круга вычисляются по формулам:
.
Общие точки с осью х:; с осью у: ;
Задача 2.
Дано уравнение окружности: .
Указать центр и радиус, найти длину окружности и площадь круга, общие точки с осями координат.
Решение:
Центр этой окружности точка , радиус .
Рис. 4. Иллюстрация к задаче
Если известен радиус, то по формулам можно вычислить длину окружности и площадь круга:
Точки пересечения с осями:
С осью х: точка это точка касания, ее координаты
Найдем точки пересечения с осью
Ось имеет уравнение , подставив в уравнение окружности, получим уравнение относительно :
Итак, точки пересечения с осью у: ; .
Задача 3.
Дано уравнение окружности: .
Указать центр и радиус, найти длину окружности и площадь круга, общие точки с осями координат.
Решение: центр этой окружности точка радиус
Рис.
5. Иллюстрация к задаче
; .
Точки пересечения с осями:
С осью у: точка касания .
С осью : ось имеет уравнение , подставляем в уравнение окружности :
Итак, точки пересечения с осью y: ; .
Задача 4.
Начертить окружность, заданную уравнением , указать ее центр, радиус. Найти точки пересечения с осями.
Решение:
Центр этой окружности точка адиус .
Рис. 6. Иллюстрация к задаче
Точки пересечения с осями:
С осью у: уравнение оси подставляем в уравнение окружности:
и
Точки пересечения с осью у:
С осью х: уравнение оси подставляем в уравнение окружности:
и
Точки пересечения с осью х:
Рис. 7. Иллюстрация к задаче
Найти длину хорды .
Решение (рис. 8):
Рис. 8. Иллюстрация к задаче
Зная координаты точек и , по формуле расстояния между точками находим длину хорды:
Найти координаты точки – середины отрезка .
Решение (рис. 9):
Рис. 9. Иллюстрация к задаче
Координаты концов отрезка известны, координаты середины отрезка определяем по формулам:
Найти площадь треугольника .
Решение (рис. 10):
Рис. 10. Иллюстрация к задаче
Треугольник равносторонний,
;
Задача 5.
Окружность задана уравнением .
Не пользуясь чертежом, укажите какие из точек лежат:
а) внутри круга, ограниченного данной окружностью;
б) на окружности;
в) вне круга, ограниченного данной окружностью.
Решение:
Центр окружности – точка радиус
Для того чтобы проверить, где расположена точка относительно окружности, будем вычислять расстояние от точки до центра окружности и сравнивать его с радиусом.
Точка :
т. лежит вне круга.
Точка :
т. лежит на окружности.
Точка
т. лежит внутри круга.
Точка :
т. лежит вне круга.
Задача 6.
Составить уравнение окружности с диаметром , если
Решение: найдем координаты центра окружности , это координаты середины отрезка
Найдем радиус, это половина диаметра:
– уравнение окружности.
Заключение
Итак, мы вывели уравнение окружности и использовали его для решения простейших задач. На следующем уроке мы продолжим изучать уравнение окружности и будем использовать его для решения более сложных задач.
Список литературы
- Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
- Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
- Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- E-science.ru (Источник).
- E-science.ru (Источник).
- Mathematics.ru (Источник).
Домашнее задание
- Атанасян Л.
1.11. Окружность
Определение. Окружностью называется множество всех точек плоскости, для которых расстояние от данной точки, называемой центром окружности, есть величина постоянная, называемая радиусом окружности.
Выведем уравнение окружности. Пусть точка произвольная точка окружности радиуса . Введем прямоугольную систему координат, у которой начало совпадает с центром окружности. В этом случае точкаимеет координаты. По определению окружности. Учитывая, что, получим, или
. (1.27)
Выражение (1.27) называется уравнением окружности с центром в точке и радиуса.
Покажем, что любая точка, координаты которой удовлетворяют уравнению (1.27), принадлежит окружности с центром в точке и радиуса.
Пусть
координаты точки
удовлетворяют уравнению (1.27). Тогда,
т.
е.является точкой окружности.
С учетом формулы преобразования прямоугольных координат точки при параллельном переносе осей получим уравнение окружности с центром в точке и радиуса:
. (1.28)
П р и м е р 13.Составить уравнение окружности, проходящей через начало координат, центр которой находится на одинаковом расстоянии от параллельных прямых и.
Решение. Для того чтобы составить уравнение
окружности вида
,
необходимо найти координатыее центраи радиус.
Искомая окружность касается прямыхи,
поэтому радиусравен половине расстояниямежду этими прямыми. Расстояние между
параллельными прямыми равно расстоянию
от произвольной точки одной прямой до
другой прямой. На прямой, задаваемой
уравнением,
возьмем произвольную точку,
тогда.
По формуле (1.15) имеем:.
Таким образом,.
Центр окружности равноудален от заданных
прямых, поэтому координатыее центрадолжны удовлетворять равенству,
т. е..
Известно, что окружность проходит через
начало координат, поэтому.
Определение. Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Выберем прямоугольную систему координат таким образом, чтобы ось абсцисс проходила через фокусы и, а начало координатсовпадало с серединой отрезка. Обозначим,,, где, фокальные радиусы (расстояния от точки до фокусов) точки эллипса. Тогда фокусы иимеют координаты,.
O
Пусть произвольная точка эллипса. Имеем: ,. Из определения эллипса
, (1.29)
или
искомое уравнение эллипса, которое
неудобно для использования.
Из последнего
равенства следует, что
.Так
как,
то можем обе части уравнения возвести
в квадрат и после эквивалентных
преобразований получим:.
Следовательно,.
Введем новую переменную.
Имеем:.
Из этого равенства следует, что
. (1.30)
Уравнение (1.30) называется каноническим (простейшим) уравнением эллипса. Это уравнение является уравнением второго порядка. Таким образом, любая точка эллипса, удовлетворяющая уравнению (1.29), удовлетворяет и уравнению (1.30). Докажем, что все точки плоскости, координаты которых удовлетворяют уравнению (1.30), являются точками эллипса, т. е. их координаты удовлетворяют уравнению (1.29).
Для фокального радиуса выполняется соотношение. Из уравнения (1.30) имеем:. Поэтому, или. Аналогично находим, что. Следовательно,.
Эллипс
симметричен относительно координатных
осей, так как содержит только четные
степени
и,
и относительно начала координат. Оси
симметрии эллипса называются его осями,
а центр симметрии
центром эллипса.
b
с
х
О
aЭллипс пересекает координатные оси в точках ,,,. Эти точки называются вершинами эллипса. Приэллипс вырождается в окружность радиусоми центром в начале координат. Вершины эллипса ограничивают на осях отрезки длинойи, причем(это следует из того, что).
Величины иназываются большой и малой полуосями эллипса, оси эллипса соответственно большой и малой осью.
Определение. Эксцентриситетом эллипса называется отношение, где половина расстояния между фокусами, большая полуось, т. е.
. (1.31)
Учитывая,
что
,
получим.
Так как,
то.
Если,
т. е. эллипс приближается к окружности,
то.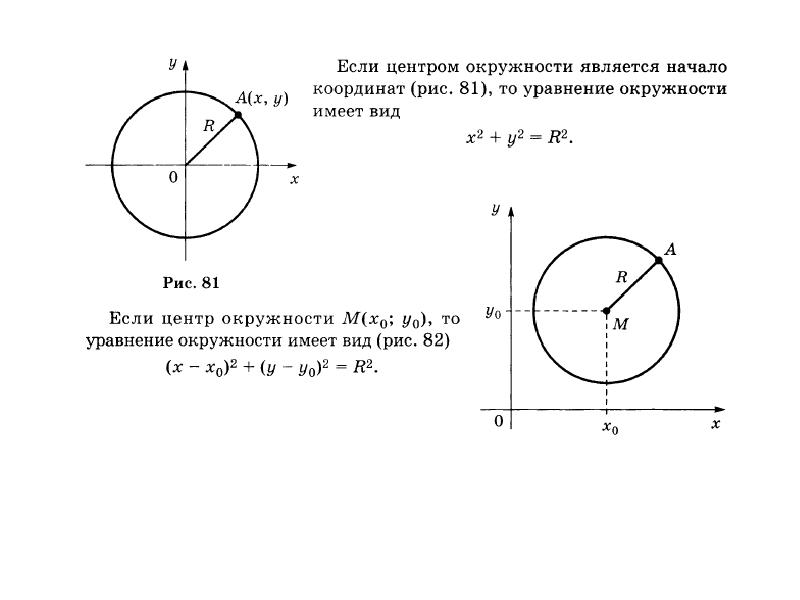
Если,
ак нулю не стремится, то эллипс вытянут
вдоль большой оси. Таким образом,
эксцентриситет эллипса характеризует
меру его вытянутости вдоль большой оси.
Если фокусы эллипса ирасположены на оси ординат, то в этом случаеи большой является полуось. Уравнение эллипса также имеет вид (1.30), но, а его эксцентриситет вычисляется по формуле.
П р и м е р 14. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, что расстояние между его фокусами и эксцентриситет.
Решение. Половина расстояния между фокусами . Фокусы эллипса расположены на оси абсцисс, поэтому большой полуосью является. Из (1.31) следует, что. Тогда. Таким образом, уравнение эллипса имеет вид.
П р и м е р 15. Дан эллипс . Найти его полуоси, фокусы, эксцентриситет.
Решение. Приведем
уравнение эллипса к каноническому виду.
Для этого обе части уравнения разделим
на 45, получим
.
Таким образом, его полуось,.
Большой полуосью является полуось,
поэтому фокусы эллипса расположены на
оси ординат и,
следовательно, фокусы находятся в точкахи.
Эксцентриситет эллипса равен отношению
половины расстояния между фокусами к
большой полуоси, т. е..
П р и м е р 16. Вычислить площадь четырехугольника , две вершиныикоторого лежат в фокусах эллипса, две другиеисовпадают с концами его малой оси.
Решение. Каноническое уравнение эллипса имеет вид , поэтому,. Следовательно, вершины четырехугольникаиимеют соответственно координатыи. Найдем координаты вершини. Так как, то,. Полученный четырехугольник симметричен относительно координатных осей и относительно начала координат, следовательно,.
Уравнение окружности (без центра в начале координат) (Ключевой этап 3)
Урок
Уравнение окружности, с центром в декартовых координатах (a,b) имеет вид:
В этом уравнении
- x и y — декартовы координаты точек на (границе) окружности.
- a и b — декартовы координаты центра окружности.
- r радиус окружности.
На изображении ниже показано, что мы подразумеваем под точкой на окружности с центром в (a, b) и ее радиусом:
Реальные примеры уравнений окружностей (без центра в начале координат)
Уравнение окружности проще понять на примерах.
- Окружность с центром в точке (2, 3) и радиусом 5 будет иметь уравнение:
- Окружность с центром в точке (−1, 1) и радиусом 3 будет иметь уравнение:
Слайды урока
Ползунок ниже объясняет, почему работает «Уравнение круга». Откройте слайдер в новой вкладкеЦентр окружности имеет отрицательные координаты
Уравнение окружности:
Центр (а, б) .
- Число, вычитаемое из x в скобках, является координатой x центра.
- Число, вычитаемое из и в скобках, является координатой y центра.
Что делать, если координата центра отрицательна? Представьте, что центр круга равен (−1, 2) . Уравнение начнется:
(х — -1) 2 + …
Помните, что вычитание отрицательного числа равносильно добавлению положительного числа:
(х — -1 ) 2 = (х + 1 ) 2
Перед отрицательной координатой будет стоять знак + . Перед положительной координатой будет стоять знак − .
Уравнения, которые выглядят не совсем правильно
(х — 1) 2 + (у — 3) 2 — 49 = 0
Это все еще уравнение окружности, как видно с небольшой перестановкой:
(х — 1) 2 + (у — 3) 2 = 49
Окружность с центром в начале координат
Окружность с центром в начале координат имеет центр в точке (0, 0) .
Если он имеет радиус r , уравнение выглядит так:
(x − 0) 2 + (y − 0) 2 = r 2 x 2 + y 2 = r 2
Это уравнение для окружности с центром в начале координат.
Рабочий лист
(для печати и отправки)
Параметрическое уравнение окружности
В другой нашей статье мы узнали о стандартной форме и общей форме уравнения окружности. Здесь, в этой статье, мы будем иметь дело с другой формой, параметрической формой уравнения окружности.
Параметрическое уравнение окружности с центром в начале координат (0, 0)
Известно уравнение окружности в декартовых координатах с центром в начале координат (0, 0) и точкой (x, y) на окружности. определяется как x 2 + y 2 = r 2
Подобно параметрическому уравнению прямой, параметрическое уравнение окружности поможет нам найти координаты любой точки на окружности с центром в точке начало (0, 0) с радиусом ‘r’.
См. нашу статью «Уравнение окружности» для справки.
Пусть P (x, y) — координаты любой точки на окружности. Если мы проведем перпендикулярную линию из точки P к оси x, пересекающейся в точке S, мы получим прямоугольный треугольник.
Таким образом, треугольник OPS является прямоугольным, где OS — основание треугольника, SP — перпендикуляр треугольника, а θ — угол, образуемый OP с осью x, называется параметром.
Из основ тригонометрии,
OS/OP = cos θ
=> OS = OP cos θ …… (1)
Аналогично,
SP/OP = sin θ
=> SP = OP sin θ …… (2)
Так как OS = x, SP = y, OP = r
Подставляя эти значения в уравнения (1) и (2 ), получаем
x = rcos θ, y = rsin θ
Таким образом, параметрическое уравнение окружности с центром в начале координат записывается в виде P (x, y) = P (r cos θ, r sin θ ), где 0 ≤ θ ≤ 2π. См. рис. 1 (а) на приведенной ниже диаграмме.
Параметрическое уравнение окружности Другими словами, для всех значений θ точка (rcosθ, rsinθ) лежит на окружности x 2 + у 2 = г 2 .
Или любая точка на окружности (rcosθ, rsinθ), где θ — параметр.
Давайте рассмотрим пример, чтобы лучше понять концепцию.
Если у нас есть окружность радиусом 10 единиц с центром в начале координат, окружность может быть описана парой уравнений Как обсуждалось выше, угол θ (тета) называется параметром, который представляет собой угол, образуемый линией, соединяющей точку (x, y) с центром, а также с осью x. Это просто переменная, появляющаяся в системе уравнений, которая может иметь любое значение (если не указано иное), но имеет одно и то же значение везде, где она используется. Таким образом, уравнение окружности, представленное в виде x = r cos θ, r sin θ, называется параметрическим уравнением окружности.
Теперь давайте выведем параметрическое уравнение окружности без центра в начале координат.
Параметрическое уравнение окружности – центр в точке (h,k)
Это просто. Нам просто нужно добавить или вычесть фиксированные суммы к координатам x и y.