Нахождение уравнений прямой, заданной пересечением двух плоскостей
УчебаМатематикаГеометрия
Этот онлайн калькулятор находит уравнения прямой, заданной пересечением двух плоскостей в пространстве. Калькулятор выводит канонические и параметрические уравнения прямой, а также координаты точки, принадлежащей прямой и направляющего вектора прямой.
Этот онлайн калькулятор предназначен для проверки решений задач, которые можно сформулировать следующим образом:
Записать канонические (или параметрические) уравнения прямой, заданной уравнениями двух плоскостей
.
Вы задаете коэффициенты уравнений плоскостей, А₁, B₁, C₁, D₁ и A₂, B₂, C₂, D₂, калькулятор выдает уравнения прямой в параметрической и канонической формах, а также найденную точку, принадлежащую прямой и направляющий вектор прямой.
Обратите внимание, в том случае если уравнения плоскостей заданы в виде
при вводе коэффициентов D₁ и D₂ надо поменять знак.
Немного теории, как обычно, можно почерпнуть под калькулятором
Нахождение уравнений прямой, заданной пересечением двух плоскостей
Общее уравнение первой плоскости
Общее уравнение второй плоскости
Точка, принадлежащая прямой
Направляющий вектор прямой
Канонические уравнения прямой
Параметрические уравнения прямой
Точность вычисления
Знаков после запятой: 2
Канонические уравнения прямой, заданной пересечением двух плоскостей
Если плоскости пересекаются, то система уравнений, приведенная в начале статьи, задает прямую в пространстве. Для записи уравнений этой прямой в каноническом виде, надо найти какую либо точку, принадлежащую этой прямой, и направляющий вектор.
Точка, принадлежащая прямой, также принадлежит и каждой из плоскостей, то есть является одним из решений системы уравнений выше.
Для нахождения точки, принадлежащей прямой, переходят от системы из двух уравнений с тремя неизвестными к системе из двух уравнений с двумя неизвестными, произвольно принимая какую-либо координату точки за ноль. Как правило, при решении задач, выбирают ту координату, при занулении которой решение системы из двух уравнений с двумя неизвестными дает в ответе целые числа. Калькулятор учитывает этот факт и также пытается найти целочисленное решение, зануляя все координаты по очереди.
Направляющий вектор прямой ортогонален нормальным векторам плоскостей, которые задаются коэффициентами A, B и С в общем уравнении плоскости . Таким образом его можно найти как результат векторного произведения нормальных векторов плоскостей .
Точка и вектор дают нам канонические уравнения прямой:
Существуют частные случаи, когда одна или две координаты направляющего вектора равны нулю.
В случае, если нулю равны две координаты, направляющий вектор коллинеарен одной из координатных осей.
Соответственно, точки прямой могут принимать любое значение по этой оси, при этом значения по двум другим осям будут постоянны. Например, если двумя нулевыми координатами будут y и z, канонические уравнения прямой будут выглядеть так:
В случае. если нулю равна одна координата, направляющий вектор лежит в одной из координатных плоскостей (плоскостей, образованных парами координатных осей), значение координаты по третьей оси, ортогональной этой плоскости (как раз той, для которой координата направляющего вектора равна нулю), опять будет постоянным. Например, если нулевой координатой будет x, то канонические уравнения прямой будут выглядеть так:
Эти случаи также учитываются калькулятором.
Параметрические уравнения прямой, заданной пересечением двух плоскостей
Зная точку, принадлежащую прямой и ее направляющий вектор, несложно записать и параметрические уравнения прямой.
Для точки , принадлежащей прямой, и направляющего вектора параметрические уравнения прямой выглядят так:
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Уравнения прямой, проходящей через две точки в трехмерном пространстве
- • Уравнение прямой по двум точкам
- • Условия параллельности и перпендикулярности прямых на плоскости
- • Уравнение плоскости по трём точкам
- • Развертка (выкройка) конуса
- • Раздел: Геометрия ( 95 калькуляторов )
#геометрия #Прямая Геометрия Математика плоскость прямая уравнения прямой
PLANETCALC, Нахождение уравнений прямой, заданной пересечением двух плоскостей
Timur2022-10-27 08:43:34
Кривые второго порядка на плоскости
1.
Курс высшей математикиЧасть 1УГТУ-УПИ
2004г.
Лекция 8.
Кривые второго порядка на плоскости
I. Основные понятия.
2. Исследование формы кривых второго
порядка по их каноническим уравнениям.
3. Приведение уравнений кривых второго
порядка к каноническому виду.
1. Основные понятия.
Алгебраической кривой второго порядка
называется кривая , уравнение которой в декартовой
системе координат имеет вид:
1
Ax 2 2Bxy Cy 2 Dx Ey F 0,
где не все коэффициенты А, В, С равны нулю.
Вырожденные кривые второго порядка :
1. пустое множество
x2 y 2 1 0
2. точка
x2 y 2 0
3. прямая
x 2 2x 1 0 x 1
4. пара прямых
x2 y 2 0 x y
O (0,0)
Т
Всякое уравнение (1), задающее невырожденную
кривую, путём преобразования координат можно
привести к каноническому виду (одному из трех):
2
2
2
2
x
y
2 1 эллипс
I.
2
a b
II .
x
y
2 1 гипербола
2
a b
III .
y 2 2 px парабола
2.
Исследование формы кривых второго порядка
по их каноническим уравнениям.
2.1. Эллипс.
Эллипсом называется кривая второго порядка
с каноническим уравнением
x2
y2
2 1
2
a
b
Если
( x0 , y 0 )
x 0,
( x0 , y 0 ), ( x0 , y 0 ), ( x0 , y 0 ) .
y 0 оси симметрии эллипса (буквой Г
обозначена кривая – эллипс)
Достаточно исследовать кривую и построить её
в области x 0, y 0 ,
достроив затем остальные части путём зеркального
отражения найденных фрагментов кривой
относительно координатных осей.
Так как если
( x0 , y 0 )
, то
( x0 , y0 ) ,
эллипс ,задаваемый каноническим уравнением (I),
имеет центр симметрии, совпадающий с началом
координат О(0,0).
Рассмотрим уравнение эллипса в первой четверти.
I.
y b 1
x2
a2
Y
a
x
b
R
1
F
1
x,y
M
a
x
R2
F
2
a X
Характеристики эллипса
1.
a – большая полуось; b – малая полуось.2. Точки (a,0), ( a,0), (0, b ), (0, b ) — вершины.
3. Точка O 0,0 — центр.
4. Точки
F1 ( c,0), F2 (c,0)
— фокусы, где
Y
a
x
c2 a2 b 2
b
R
1
F
1
x,y
M
a
x
R
2
F
2
a X
5. Числа
R1 , R 2 — фокальные расстояния точки М
6. Число
c
a
эллипса.
— эксцентриситет эллипса.
Чем больше значение , тем больше вытянут эллипс.
0 1
a
7. Прямые x — директрисы эллипса.
Замечание.
Если a b R уравнение I
x2 y 2 R 2
— уравнение окружности радиуса R с центром
в начале координат О(0,0).
Вычислим
R1 R2
x c
2
y
2
x c
2
y 2
R1 R 2 2a
Вывод.
Эллипс является геометрическим местом точек
M x , y , сумма расстояний от которых до двух
заданных точек плоскости F1 c ,0 и F2 c ,0
является постоянной величиной.
Замечание.
Последнее высказывание можно использовать как
определение эллипса.
Тогда, используя рисунок,можно получить каноническое уравнение эллипса.
2.2. Гипербола.
Гиперболой называется кривая второго порядка
с каноническим уравнением
2
2
x
y
2 1
2
a
b
x 0, y 0 — оси симметрии, O 0,0 — центр симметрии.
Рассмотрим уравнение гиперболы в первой четверти.
II .
y b
x2
a2
1
y b
x
2
a
2
1;
x2
b
x 2 1 y x
a
a
b
a
y x x
a
Y
a
x
b
b
y x
a
M x, y
R1
R2
F1
a
a
b
F2
X
b
y x
a
Характеристики гиперболы
1. a – действительная полуось; b – мнимая полуось.
2. Точки (a,0), ( a,0)
y
— вершины.
b
x
a
x
Y
x
b
3. Точка O 0,0 — центр.
4. Точки F1 ( c,0), F2 (c,0)
— фокусы, где c2 a 2 b 2
a
a
y
b
x
a
M x, y
R1
R2
F1
a
a
F2
X
b
5. Числа R1 , R 2 — фокальные расстояния точки М
гиперболы.
6. Число
c
a
— эксцентриситет гиперболы.
1
a
7. Прямые x — директрисы гиперболы.
8. Прямоугольник со сторонами
x a, y b
y
b
a
x x
a
— основной прямоугольник.
b
9. Прямые y a x
– асимптоты гиперболы
a
F
(диагонали основного
прямоугольника).
Вычислим
R1 R2 ( x c) 2 y 2 ( x c) 2 y 2
Y
b
R1 R 2 2a
a
y
b
x
a
M x, y
R1
R2
a
1
x
b
F2
X
Вывод.
Гипербола является геометрическим местом точек
M x , y , модуль разности расстояний от которых
до двух заданных точек плоскости F1 c ,0 и F2 c ,0
является постоянной величиной.
Замечание.
Последнее высказывание можно использовать как
определение гиперболы. Тогда, используя рисунок,
можно получить её каноническое уравнение.
Алгоритм построения чертежа гиперболы.
1. Построение основного прямоугольника.
2. Построение асимптот – диагоналей.
3.
Определение вершин гиперболы (выяснениевопроса о том, какую координатную ось гипербола
2
2
пересекает).
x
y
4. Построение гиперболы.
2
a
2
b
2
x
y
2 2 1
a
b
2
1
Y
b
a
a
b
X
2.3. Парабола.
Параболой называется кривая второго порядка с
каноническим уравнением
y 2 px
2
Прямая
y 0 — ось симметрии (единственная!).
Рассмотрим уравнение параболы в первой четверти.
III .
y 2px
x p /2
Y
d
M x, y
R
p /2
F p / 2 ,0
Характеристики параболы.
1. Точка O 0,0 — вершина.
2. OX — Ось симметрии.
X
p
3. Точка F ,0
2
— фокус.
x p /2
Y
d
4. Число R
— фокальный радиус
точки параболы.
M x , y
R
p/2
F p / 2 ,0
p
— директриса.
5. Прямая x
2
Пусть
d — расстояние от точки параболы до
директрисы.
Вычислим
d
d R
X
Вывод.
Парабола является геометрическим местом точек
p
M x , y , равноудаленных от заданной точки F
,
0
2
плоскости и прямой x= -p/2 .
Замечание.
Последнее высказывание можно использовать как
определение параболы. Тогда, используя рисунок,
можно получить её каноническое уравнение.
Канонические уравнения кривых второго порядка
со смещенным центром (вершиной).
I*.
II * .
x x0 2 y y 0 2 1
a2
x x0 2 y y 0 2 1
a2
III * .
b2
b2
y y 0 2 2p x x0
Выполним замену
x x x0
y y y 0
Тогда уравнения
I * . III * .
x , y .
относительно переменных
Геометрически:
OXY
I . III .
O X Y
O 0,0 O x0 , y 0
— параллельный перенос в точку
x0 , y 0 .
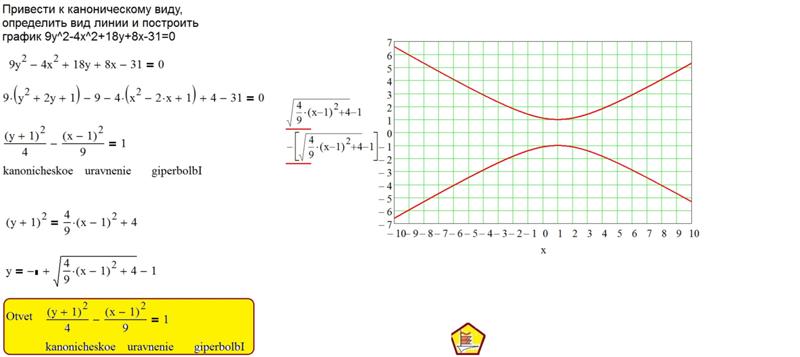
Пример.
y 1 2 x 1 2 1
4
9
Тип кривой – гипербола со смещенным в точку (-1,1)
центром. b=2 — действительная полуось, a=3 — мнимая
полуось.
3.
Приведение уравнений кривых второго
порядка к каноническому виду.
Ax 2 2Bxy Cy 2 Dx Ey F 0
Два признака неканоничности:
I . Наличие смешанного произведения xy.
II . Переменные присутствует в уравнении и
в первой, и во второй степени.
Устранение признаков неканоничности:
I.
x x cos y sin
y x sin y cos
Геометрически: OXY
— поворот на угол
O X Y
вокруг точки
O 0,0
II .
x x x 0
y y y 0
Геометрически: O X Y O X Y
O 0,0 O x 0 , y 0
— параллельный перенос в точку x 0 , y 0 .
Каноническая и стандартная форма — Geeksforgeeks
- Напишите опыт интервью
- Уровень сложности: Easy
- Последнее обновление: 23 фев, 2022
- Читать
- Обсудить
- минтерма для каждой комбинации переменных, которая дает 1 в функции, а затем выполнения операции ИЛИ всех этих термов.
- maxterm для каждой комбинации переменных, которая дает 0 в функции, а затем выполняет И всех этих условий.
- Пример – Выразите логическую функцию F = A + B’C в виде стандартной суммы minterms.
- Решение –
A = A(B + B’) = AB + AB’
В этой функции по-прежнему отсутствует одна переменная, поэтому
A = AB(C + C’) + AB'(C + C’) = ABC + ABC’+ AB’C + AB’C’
Во втором члене B’C отсутствует одна переменная; следовательно,
B’C = B’C(A + A’) = AB’C + A’B’C
Объединив все термины, мы получим
F = A + B’C = ABC + ABC’ + AB’C + AB’C’ + AB’C + A’B’C
Но AB’C встречается дважды, и
соответственно теореме 1 (x + x = x) можно удалить одно из этих вхождений. Переставляя minterms в порядке возрастания, окончательно получаем
F = A’B’C + AB’C’ + AB’C + ABC’ + ABC
= m1 + m4 + m5 + m6 + m7
SOP представлен как Sigma( 1, 4, 5, 6, 7) - Введение
- Формирование таблицы истинности
- Формирование таблицы истинности
- Сумма выражений произведения (СОП)
- Произведение суммы выражений (POS)
- Канонические выражения
- Minterms
- Макстермс
- Преобразование канонических форм
- Преобразование минимальной формы в каноническую
- Минимальная POS в каноническую POS
- От минимальной СОП до канонической СОП
- Пример алгебраического упрощения
- Неопределенный ввод и безразличие
- Попробуйте интерактивный генератор таблиц истинности
- Методы упрощения булевой функции
Напишите статью
Комбинационные схемы
последовательные схемы
.
Сохранить статью
Улучшить статью
Сохранить статью
Каноническая форма – В булевой алгебре логическая функция может быть выражена в виде канонической дизъюнктивной нормальной формы, известной как minterm , а некоторые выражаются в виде канонической конъюнктивной нормальной формы, известной как maxterm .
В Minterm мы ищем функции, результатом которых является «1», а в Maxterm мы ищем функцию, результатом которой является «0».
Мы выполняем Продукт Maxterm также известный как Продукт суммы (POS).
Булевы функции, выраженные в виде суммы minterms или произведения maxterms, называются каноническими.
Стандартная форма – Логическая переменная может быть выражена как в истинной, так и в дополненной форме. В стандартной форме булева функция будет содержать все переменные либо в истинной форме, либо в дополненной форме, тогда как в канонической форме количество переменных зависит от вывода SOP или POS.
Булева функция может быть выражена алгебраически из заданной таблицы истинности путем формирования :
Таблица истинности, представляющая minterm и maxterm –
Из приведенной выше таблицы видно, что minterm выражается в формате произведения, а maxterm выражается в формате суммы. 9н)). Иногда бывает удобно выразить булеву функцию в виде суммы minterm.
Переставляя minterms в порядке возрастания, окончательно получаем Статьи по теме
Что нового
Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство просмотра нашего веб-сайта. Используя наш сайт, вы подтверждаете, что вы прочитали и поняли наши Политика в отношении файлов cookie и Политика конфиденциальности
Канонические функции | CircuitVerse
Оглавление
Вступление
Логические функции состоят из двух компонентов: переменных и логических операций (И, ИЛИ, НЕ.
.. и т. д.). Любое уравнение со смесью этих двух компонентов образует булеву функцию. Значение переменных может быть или не быть заранее определенным. Сокращенное обозначение булевой функции состоит в том, что она представлена заглавной буквой F, за которой следует скобка, состоящая из всех переменных этого уравнения, разделенных запятой (‘,’). Вы можете представить любое логическое выражение в виде таблицы истинности. Подпишитесь, чтобы узнать Как?
Рассмотрим следующий пример:
Пример: Сокращенная запись, представляющая логическое выражение / F(A,B) = A + B //Это логическая функция, состоящая из переменных A и B F (А, В, С) = А (В + С (А + В)) \ Логическое выражение
Формирование таблицы истинности
Таблица истинности формируется путем оценки логического выражения для каждого значения истинности переменной. Теперь значения истинности переменной либо «истина», либо «ложь». Суть в том, чтобы оценить значение логического выражения для каждой комбинации истинностных значений
присутствуют переменные.
(количество переменных) комбинаций. Следуйте приведенным ниже примерам, чтобы узнать, как сопоставить эти значения.
Пример: F (А, В) = А + В
Таблица истинности::
| А | Б | Ф(А,Б) | |
|---|---|---|---|
| 0 | 0 | 0 | и |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
Здесь у вас есть 4 комбинации для 2 переменных, попробуйте понять следующий пример, где переменные 3, которые предполагает 8 комбинаций. Запишите, как истинные значения переменной записываются в каждом столбце для каждая переменная. Пример: F(A,B,C) = A + B.C
Формирование таблицы истинности
Таблица истинности показывает таблицу со всеми комбинациями входных данных и соответствующими им результатами.
Уравнение переключения также можно преобразовать в таблицу истинности. Например, рассмотрим уравнение переключения: F(A,B,C) = A + BC.
| А | Б | С | Ф |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Сумма выражений продукта (SOP)
Давайте рассмотрим более сложное выражение F(A, B, C, D) = AB'C + BD + CD + D . Составим таблицу истинности:
| F(AB’C+BD+CD+D) | А | Б | С | Д |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
В этом примере интересное наблюдение заключается в том, что вы выполняете оценку суммы продуктов, то есть AB'C + BD + CD + D — это сумма продуктов.
Значение суммы произведения заключается в том, что когда вы выполняете + , вы фактически вызываете оператор ИЛИ .
Более того, оператор ИЛИ возвращает true , пока любой из его аргументов возвращает истинному , то вы точно знаете, что конечное выражение верно .
Продукт выражений суммы (POS)
Давайте посмотрим на другое выражение F(A, B, C, D) = (A + B + C + D')(A + B' + C' + D)(A' + B' + C + Д') . Сгенерируем таблицу истинности:
| F(A,B,C,D) | А | Б | С | Д |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Судя по алгебраическому выражению, видно, что выражение представляет собой произведение сумм .
Такое выражение называется выражением Product of Sum или сокращенно POS .
Здесь условия суммы определяются с помощью операции ИЛИ , а условия произведения определяются с помощью операции И . Когда два или более членов суммы умножаются на логическое значение ИЛИ , результирующее выходное выражение будет в форме произведения сумм или в форме POS .
Форма произведения сумм также называется конъюнктивной нормальной формой , так как сумма членов составляет И вместе, а операция конъюнкции является логическим И. Форма произведения сумм также называется стандартной POS.
Канонические выражения
Прежде чем разбираться в канонических выражениях, давайте разберемся с Minterms и Maxterms первый.
Минтермс
Минтерм определяется как произведение n переменных, в котором каждая из n переменных встречается один раз либо в дополненной, либо в недополненной форме.
Минимальный член обозначается как mi, где i находится в диапазоне 0 ≤ i < 2 n .
Для булевой функции с двумя переменными (x и y) возможные minterms:
x’y’, x’y, xy’ и xy .
Для булевой функции с 3 переменными (x, y и z) возможные minterms:
x’y’z’, x’y’z, x’yz’, x’yz, xy’z’, xy’z, xyz’ и xyz.
1 – Minterms = minterms, для которых функция F = 1. 0 – Minterms = minterms, для которых функция F = 0. Любая булева функция может быть выражена в виде суммы (ИЛИ) ее 1-минутных членов. Представление уравнения будет
F(список переменных) = Σ(список индексов 1-минутного члена)
Пример: F(x, y, z) = Σ(3, 5, 6, 7)
Обратная функция может быть выражена как сумма (ИЛИ) ее нулевых членов. Представление уравнения будет
F(список переменных) = Σ(список нулевых индексов) Пример: F’(x, y, z) = Σ(0, 1, 2, 4)
Примеры канонической формы выражения суммы произведений (каноническая форма минимального члена):
Z = XY + XZ'F = XYZ' + X'YZ + X'YZ' + XY'Z + XYZ
В стандартной форме СОП максимально возможные термины произведения для n переменных задаются как 2 n .
Таким образом, для уравнений с двумя переменными условия произведения равны 2 2 = 4. Аналогично, для уравнений с 3 переменными условия произведения равны 2 3 = 8.
Макстермс
Максимальный термин определяется как произведение n переменных в диапазоне 0 ≤ i < 2 n . Максимальный член обозначается как Mi. В максимальном термине каждая переменная является дополненной , если ее значение присвоено 1, и каждая переменная не дополнена , если ее значение присвоено 0.
Для логической функции с 2 переменными (x и y) , возможные максимальные члены:
х + у, х + у’, х’ + у и х’ + у’
Для булевой функции с тремя переменными (x, y и z) возможные maxterms:
x + y + z, x + y + z', x + y' + z, x + y' + z ', x' + y + z, x' + y + z', x' + y' + z и x' + y' + z'
1 – Максимальное число членов = максимальное число членов, для которых функция F = 1.
0 – Максимальное число членов = максимальное число членов, для которых функция F = 0.
Любая логическая функция может быть выражена произведением (И) ее 0 – максимальные сроки. Представление уравнения будет
F(список переменных) = Π (список 0-максимальных индексов терминов)
Пример: F(x, y, z) = Π(0, 1, 2, 4)
Обратное функции может быть выражена как произведение (И) ее 1 — максимальное количество членов. Представление уравнения будет следующим:
F(список переменных) = Π(список индексов 1-max)
Пример: F'(x, y, z) = Π(3, 5, 6 , 7)
Примеры канонической формы произведения выражений сумм (каноническая форма максимального члена):
1. Z = (X + Y).(X + Y′) 2. F = (X′ + Y + Z′).(X′ + Y + Z).(X′ + Y′ + Z′)
В стандартной форме POS максимально возможные члены суммы для n переменных задаются как 2 n . Итак, для уравнений с 2 переменными сумма членов равна 2 2 = 4. Аналогично, для уравнений с 3 переменными сумма членов равна 2 3 = 8.
. положение для понимания канонических форм.
Говорят, что любая булева функция, которая выражается как сумма minterms или как произведение maxterms, находится в своем каноническая форма .
Когда форма SOP логического выражения находится в канонической форме, каждый из его терминов продукта называется minterm . Таким образом, каноническая форма функции суммы произведений также известна как каноническая форма minterm или Sum-of-minterms или стандартная каноническая форма SOP.
Аналогично, когда POS-форма логического выражения находится в канонической форме, каждый из его суммируемых членов называется maxterm . Итак, каноническая форма произведения сумм известна также как maxterm каноническая форма или произведение суммы или стандартная каноническая форма POS.
Преобразование канонических форм
Вы можете представить одно каноническое сформированное уравнение в другой канонической форме, т.
е. вы можете представить форму уравнения SOP в форме POS и уравнение формы POS в форме SOP. Чтобы преобразовать канонические уравнения, вы поменяете местами символы Σ и Π после перечисления порядковых номеров уравнений, которые исключены из исходной формы уравнения.
Важно помнить о логических функциях: формы SOP и POS дублируют друг друга . Чтобы преобразовать каноническую форму уравнений, необходимо выполнить 2 шага. Они:-
Замена рабочих символов Σ и Π в уравнении.
Используйте Принцип двойственности Де Моргана для индексов булевой функции или записывайте индексы членов, которые не представлены в данной форме уравнения.
Например:-
Функция SOP F(A, B, C) = ∑(0, 2, 3, 5, 7) = A'B'C' + AB'C' + AB'C + ABC' + ABC записывается в форме POS
изменение рабочего знака на Π
записывая недостающие индексы терминов 001, 100 и 110.
Теперь напишите форму суммы для этих отмеченных терминов.
Теперь напишите форму суммы для этих отмеченных терминов. 001 = (A + B + C'), 100 = (A' + B + C), 110 = (A' + B' + C)
Запись нового уравнения в виде формы POS ,
F(A, B, C) = Π(1, 4, 6) = (A + B + C') * (A' + B + C) * (A' + B' + C')
Функция POS F(A, B, C) = Π(2, 3, 5) = (A + B' + C)(A + B' + C')(A' + B + C') написан в форме СОП
изменение рабочего знака на Σ
напишите недостающие индексы терминов 000, 001, 100, 110 и 111. Теперь напишите форму произведения для этих отмеченных терминов.
000 = A’B’C’, 001 = A’B’C, 100 = AB’C’, 110 = ABC’, 111 = ABC
Запись нового уравнения в форме СОП,
F(A, B, C) = Σ(0, 1, 4, 6, 7) = (A'B'C') + (A 'В'С) + (АВ'С') + (АВС') + (АВС)
Преобразование из минимальных форм в канонические
От минимального POS до канонического POS
Вы можете включить все переменные в каждое условие продукта уравнения формы POS, которое не содержит всех переменных, путем преобразования в стандартную форму POS.
Обычная функция формы POS может быть преобразована в стандартную форму POS с помощью логического алгебраического закона 9.0037 (A * A’ = 0) и выполнив следующие шаги.
Путем добавления каждого нестандартного суммирующего члена к произведению его отсутствующей переменной и ее дополнения, что дает 2 суммирующих члена
Применяя закон булевой алгебры, A + BC = (A + B) * (A + C)
Повторяя шаг 1, пока все результирующие члены суммы не будут содержать все переменные
С помощью этих трех шагов вы можете преобразовать функцию POS в стандартную функцию POS.
Пример: F = (A' + B + C)*(B' + C + D') * (A + B' + C' + D)
В первом члене отсутствует переменная D или D’, поэтому добавьте к нему D*D’ = 1. Тогда
(A' + B + C + D*D') = (A' + B + C + D) * (A' + B + C + D')
Аналогично, во втором члене переменная A или A’ отсутствует, поэтому добавьте к ней A*A’ = 1.
Тогда
(B' + C + D' + A*A') = (A + B' + C + D') * (A' + B' + C + D')
Третий член равен уже в стандартной форме, так как имеет все переменные. Теперь стандартное уравнение формы POS функции равно
F = (A' + B + C + D) * (A' + B + C + D') * (A + B' + C + D') * (A' + B' + C + D ') * (А + В' + С' + Г)
От минимальной СОП к канонической СОП
Вы можете включить все переменные в каждое условие продукта уравнения формы СОП, которое не содержит всех переменных, путем преобразования в стандартную форму СОП. Функцию нормальной формы SOP можно преобразовать в стандартную форму SOP, используя закон булевой алгебры, (A + A’ = 1) , и выполнив следующие шаги.
Путем умножения каждого нестандартного термина продукта на сумму его отсутствующей переменной и его дополнения, что дает 2 термина продукта
Повторяя шаг 1 до тех пор, пока все результирующие условия продукта не будут содержать все переменные
С помощью этих двух шагов вы можете преобразовать функцию SOP в стандартную функцию SOP.
В этом процессе для каждой отсутствующей переменной в функции количество терминов продукта будет удваиваться.
Пример:
Преобразование нестандартной функции SOP F = x y + x z + y z
Sol:
F = x y + x z + y z = x y (z + z’) + x (y + y’) z + (x + x’) y z = x y z + x y z’ + x y z + x y’ z + x y z + x’ y z = x y z + x y z’ + x y’ z + x’ y z
Стандартная форма СОП: F = x y z + x y z’ + x y’ z + x’ y z
Пример алгебраического упрощения
Давайте упростим наше выражение из предыдущего примера с таблицей истинности. вы можете применить обычные алгебраические приемы, такие как факторинг. Помните, что 9Оператор 0332 + вызывает вентиль ИЛИ , и этот true или x всегда возвращает true независимо от x (как показано в нашей первой таблице истинности).
AB'C + BD + CD + D // Исходное выражение AB'C + BD + D // Применение закона поглощения к CD + D, что сводит его к D AB'C + D // Применение закона поглощения к BD + D, сводящее его к D => AB'C + D // Окончательное выражение
В качестве упражнения для читателя заполните таблицу истинности, чтобы показать, что они логически эквивалентны.
Неопределенный ввод и безразличие
Определение «безразлично» — это комбинация неизвестных входных значений, которая может быть либо 0 , либо 1 . В целях упрощения переменных мы бы выбрали жадный подход выбора между { 0 , 1 } таким образом, чтобы упрощенное выражение содержало меньше членов.
Рассмотрим следующую таблицу истинности:
| A | Б | Ф(А,Б) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | ? |
| 1 | 1 | 1 |
Замечаем, что у нас есть пофиг . Рассмотрим различия в случаях для F(1,0) :
Случай 1: F(1, 0) = 0 => F(AB) = A'B' + A'B + AB Случай 2: F(1, 0) = 1 => F(AB) = A'B' + A'B + AB' + AB Упрощение случаев... F(АВ) = А'В' + А'В + АВ = А'(В' + В) + АВ = А' + АВ F(АВ) = А'В' + А'В + АВ' + АВ = А'(В' + В) + А (В' + В) = А' + А = 1
Вы можете ясно видеть, что если вы установите F(1, 0) = 1 , вы получите истинное значение для любого ввода.