Уравнение сторон треугольника | Треугольники
Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Пример.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
Решение:
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
Уравнение стороны AC —
Уравнение прямой
Все формулы для треугольника
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
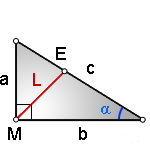
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
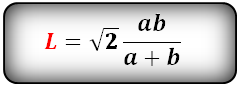
Формула длины биссектрисы через гипотенузу и угол, ( L):
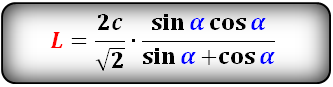
2. Найти по формулам длину биссектрисы из острого угла на катет:
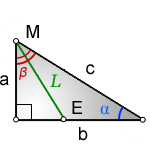
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
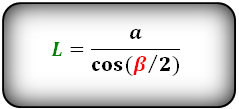
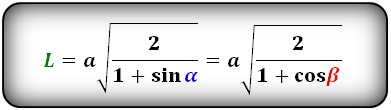
Формула длины биссектрисы через катет и гипотенузу, (L):
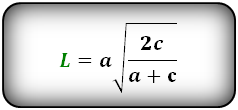
Треугольник. Формулы и свойства треугольников.
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
Остроугольный треугольник — все углы треугольника острые.
- Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
- Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
Остроугольный треугольник — все углы треугольника острые.
Тупоугольный треугольник — один из углов треугольника тупой (больше 90°).
Прямоугольный треугольник — один из углов треугольника прямой (равен 90°).
По числу равных сторон
- Разносторонний треугольник — все три стороны не равны.
- Равносторонним треугольник или правильный треугольник — все три стороны равны.
Равносторонним треугольник или правильный треугольник — все три стороны равны.
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
α + β + γ = 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β, тогда a > b
если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a2 = b2 + c2 — 2bc·cos α
b2 = a2 + c2 — 2ac·cos β
c2 = a2 + b2 — 2ab·cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианыa = 23√2(mb2 + mc2) — ma2
b = 23√2(ma2
c = 23√2(ma2 + mb2) — mc2
Медианы треугольника
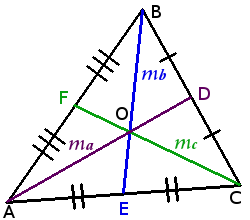
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
Медианы треугольника пересекаются в одной точке. (Точка пересечения медиан называется центроидом)
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
AOOD = BOOE = COOF = 21
Медиана треугольника делит треугольник на две равновеликие части
S∆ABD = S∆ACD
S∆BEA = S∆BEC
S∆CBF = S∆CAF
Треугольник делится тремя медианами на шесть равновеликих треугольников.
S∆AOF = S∆AOE = S∆BOF = S∆BOD = S∆COD = S∆COE
Из векторов, образующих медианы, можно составить треугольник.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 12√2b2+2c2-a2
mb = 12√2a2+2c2-b2
mc = 12√2a2+2b2-c2
Биссектрисы треугольника
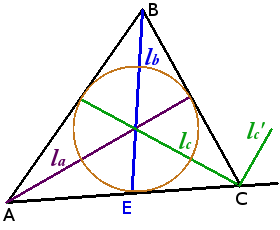
Определение. Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — центре вписанной окружности
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
AEAB = ECBC
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Угол между lc и lc‘ = 90°
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√bcp(p — a)b + c
lb = 2√acp(p — b)a + c
lc = 2√abp(p — c)a + b
где p = a + b + c2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2bc cos α2b + c
lb = 2ac cos β2a + c
lc = 2ab cos γ2a + b
Высоты треугольника
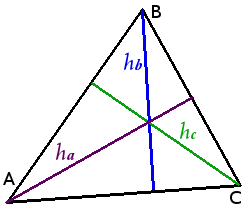
Определение. Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Если в треугольнике две высоты равны, то треугольник — равнобедренный.
ha:hb:hc = 1a:1b:1c = (bc):(ac):(ab)
Формулы высот треугольника
Формулы высот треугольника через сторону и угол:ha = b sin γ = c sin β
hb = c sin α = a sin γ
ha = 2Sa
hb = 2Sb
hc = 2Sc
Формулы высот треугольника через две стороны и радиус описанной окружности:ha = bc2R
hb = ac2R
hc = ab2R
Окружность вписанная в треугольник
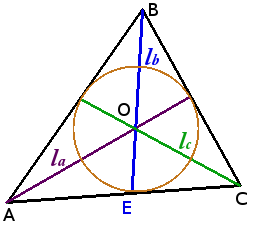
Определение. Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру: Радиус вписанной в треугольник окружности через три стороны:r = (a + b — c)(b + c — a)(c + a — b)4(a + b + c)
Радиус вписанной в треугольник окружности через три высоты:Окружность описанная вокруг треугольника
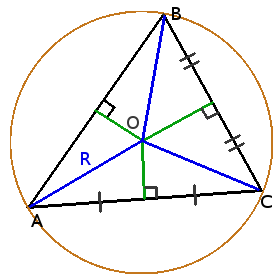
Определение. Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь: Радиус описанной окружности через площадь и три угла:R = S2 sin α sin β sin γ
Радиус описанной окружности через сторону и противоположный угол (теорема синусов):R = a2 sin α = b2 sin β = c2 sin γ
Связь между вписанной и описанной окружностями треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то.rR = 4 sinα2 sinβ2 sinγ2 = cos α + cos β + cos γ — 1
Средняя линия треугольника
Определение. Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
Свойства средней линии треугольника
1. Любой треугольник имеет три средних линии
2.
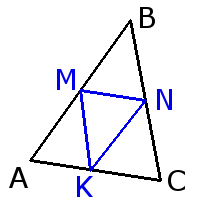Средняя линия треугольника параллельна основанию и равна его половине.MN = 12AC KN = 12AB KM = 12BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольникаS∆MBN = 14 S∆ABC
S∆MAK = 14 S∆ABC
S∆NCK = 14 S∆ABC
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
Периметр треугольника ∆ABC равен сумме длин его сторон
P = a + b + c
Формулы площади треугольника
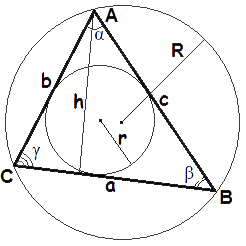
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 12a · ha
S = 12b · hb
S = 12c · hc - Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p — a)(p — b)(p — c)
где p = a + b + c2 — полупериметр треугльника. - Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S = 12a · b · sin γ
S = 12b · c · sin α
S = 12a · c · sin β - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Определение. Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Теорема 1.
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.Теорема 2.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.Теорема 3.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.Подобие треугольников
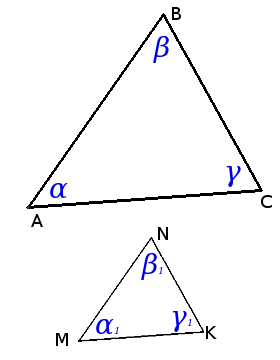Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и ABMN = BCNK = ACMK = k,
где k — коэффициент подобияПризнаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны. Свойства. Площади подобных треугольников относятся как квадрат коэффициента подобия:S∆АВСS∆MNK = k2
\[{\Large{\text{Основные сведения}}}\]
Определения
Угол – это геометрическая фигура, состоящая из точки и двух лучей, выходящих из этой точки. Градусная мера угла может принимать значения от \(0^\circ\) до \(180^\circ\) включительно.
Угол \(\alpha\) называется острым, если \(0^\circ<\alpha<90^\circ\), прямым – если \(\alpha=90^\circ\), тупым – если \(90^\circ<\alpha<180^\circ\), и развернутым – если \(\alpha=180^\circ\).
Биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.
Смежные углы – это два угла, у которых общая вершина и одна общая сторона, а две другие стороны образуют прямую.
Вертикальные углы – это два угла, образованные пересечением двух прямых и не являющиеся смежными.
Теорема
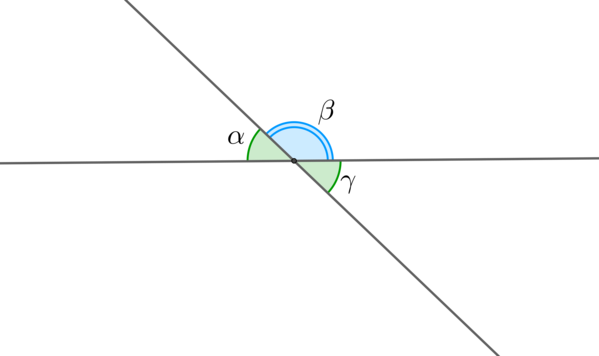
Смежные углы \(\alpha\) и \(\beta\) в сумме дают \(180^\circ\).
Вертикальные углы равны: \(\alpha=\gamma\).
Определения
Треугольник – это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой (называемых вершинами треугольника), и отрезков, соединяющих эти точки (называемых сторонами треугольника). Треугольник со своей внутренностью будем сокращенно называть также треугольником.
Угол (внутренний) треугольника – угол, образованный вершиной треугольника и двумя его сторонами.
Теоремы: признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и два прилежащих угла одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Определение
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Две прямые называются перпендикулярными, если угол между ними равен \(90^\circ\).
Перпендикуляр из точки к прямой – это отрезок, соединяющий данную точку с точкой на прямой, проведенный под углом \(90^\circ\).
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Замечание
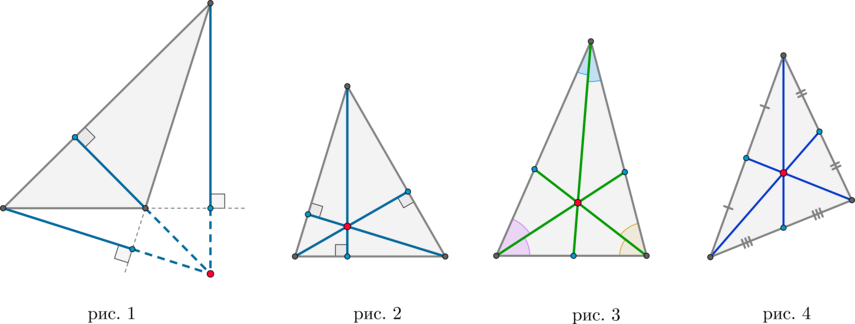
Если в треугольнике один угол тупой, то высоты, опущенные из вершин острых углов, упадут не на сторону, а на продолжение стороны (рис. 1).
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
\[{\Large{\text{Параллельные прямые}}}\]
Определение
Две различные прямые на плоскости называются параллельными, если они не пересекаются.
Замечание
Заметим, что на плоскости существует три вида взаимного расположения прямых: совпадают, пересекаются и параллельны.
Аксиома параллельных прямых
Через точку, не лежащую на данной прямой, проходит единственная прямая, параллельная данной.
Следствия из аксиомы
1. Если прямая пересекает одну из параллельных прямых, то она пересекает и другую прямую.
2. Две прямые, параллельные третьей прямой, параллельны.
Теоремы: признаки параллельности прямых
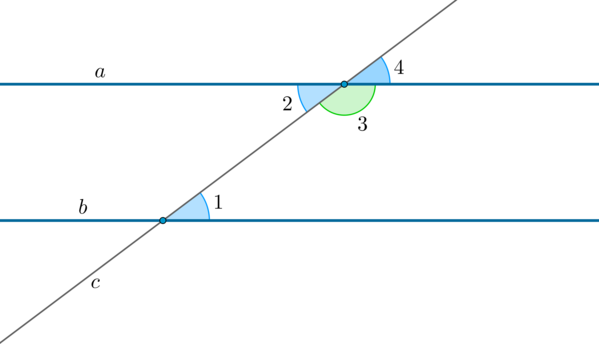
1. Если при пересечении двух прямых \(a\) и \(b\) секущей \(c\) накрест лежащие углы равны: \(\angle 1=\angle 2\), то такие прямые параллельны.
2. Если при пересечении двух прямых \(a\) и \(b\) секущей \(c\) сумма односторонних углов \(\angle 1\) и \(\angle 3\) равна \(180^\circ\), то такие прямые параллельны.
3. Если при пересечении двух прямых \(a\) и \(b\) секущей \(c\) соответственные углы равны: \(\angle 1=\angle 4\), то такие прямые параллельны.
Теоремы: свойства параллельных прямых
1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна \(180^\circ\).
3. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
\[{\Large{\text{Углы треугольника}}}\]
Определения
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один его угол тупой (остальные — острые).
Треугольник называется прямоугольным, если один его угол прямой (остальные — острые).
Теорема
Сумма внутренних углов треугольника равна \(180^\circ\).
Доказательство
Рассмотрим произвольный треугольник \(ABC\) и покажем, что \(\angle A + \angle B + \angle C = 180^\circ\).
Проведём через вершину \(B\) прямую \(a\), параллельную стороне \(AC\).
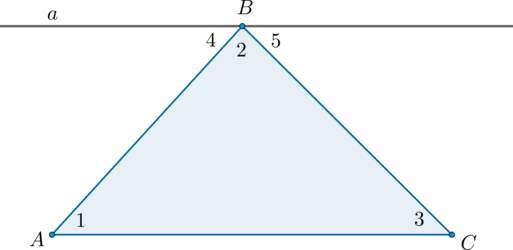
Углы \(1\) и \(4\) являются накрест лежащими углами при пересечении параллельных прямых \(a\) и \(AC\) секущей \(AB\), а углы \(3\) и \(5\) – накрест лежащими углами при пересечении тех же параллельных прямых секущей \(BC\). Поэтому \[\begin{aligned} &\angle 4 = \angle 1, \ \angle 5 = \angle 3. \qquad \qquad \qquad (1) \end{aligned}\]
Очевидно, сумма углов \(4, \ 2\) и \(5\) равна развёрнутому углу с вершиной \(B\), то есть \(\angle 4 + \angle 2 + \angle 5 = 180^\circ\). Отсюда, учитывая равенства \((1)\), получаем: \(\angle 1 + \angle 2 + \angle 3 = 180^\circ\).
Определение
Внешний угол треугольника – это угол, смежный с каким-нибудь внутренним углом треугольника.
Теорема
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: \(\angle BCD=\angle BAC+\angle ABC\).
Доказательство
Рассмотрим рисунок.
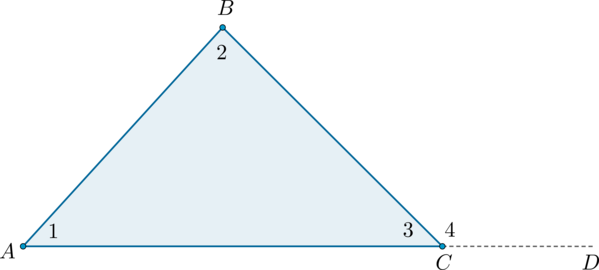
Угол \(4\) – внешний угол треугольника, смежный с углом \(3\). Так как \(\angle 4 + \angle 3 = 180^\circ\), а по теореме о сумме углов треугольника \(\angle 1 + \angle 2 + \angle 3 = 180^\circ\), то \(\angle 4 = \angle 1 + \angle 2\), что и требовалось доказать.
\[{\Large{\text{Равнобедренный треугольник}}}\]
Определения
Треугольник называется равнобедренным, если две его стороны равны.
Эти стороны называются боковыми сторонами треугольника, а третья сторона — основанием.
Треугольник называется равносторонним, если все его стороны равны.
Равносторонний треугольник, очевидно, является и равнобедренным.
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Доказательство
Пусть \(ABC\) – равнобедренный треугольник, \(AB = BC\), \(BD\) – биссектриса (проведённая к основанию).
Рассмотрим треугольники \(ABD\) и \(BCD\): \(AB = BC\), \(\angle ABD = \angle CBD\), \(BD\) – общая. Таким образом, \(\triangle ABD = \triangle BCD\) по двум сторонам и углу между ними.
Из равенства этих треугольников следует, что \(AD = DC\), следовательно, \(BD\) – медиана.
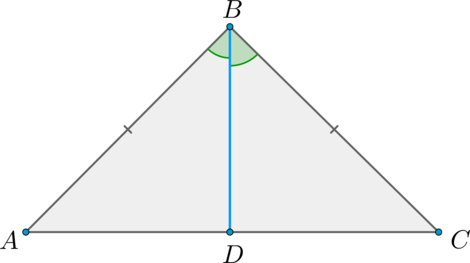
Кроме того, в равных треугольниках против равных сторон лежат равные углы, а \(AB = BC\), следовательно, \[\begin{aligned} &\angle ADB = \angle CDB, \qquad \qquad \qquad (2) \end{aligned}\] но \(\angle ADB + \angle CDB = \angle ADC\) – развёрнутый, следовательно, \(\angle ADB + \angle CDB = 180^\circ\), откуда при учёте \((2)\): \(\angle ADB = 90^\circ = \angle CDB\), то есть \(BD\) – высота.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
В равнобедренном треугольнике углы при основании равны.
Доказательство
Проведем биссектрису \(BD\) (см. рисунок из предыдущей теоремы). Тогда \(\triangle ABD=\triangle CBD\) по первому признаку, следовательно, \(\angle A=\angle C\).
Теоремы: признаки равнобедренного треугольника
1. Если в треугольнике два угла равны, то треугольник равнобедренный.
2. Если в треугольнике высота является медианой или биссектрисой, то треугольник равнобедренный.
Теорема о соотношении между сторонами и углами треугольника
В треугольнике против большей стороны лежит больший угол.
В треугольнике против большего угла лежит большая сторона.
Теорема: неравенство треугольника
В треугольнике сумма любых двух сторон больше третьей стороны.
Другая формулировка: в треугольнике разность любых двух сторон меньше третьей стороны.
\[{\Large{\text{Прямоугольный треугольник}}}\]
Определения
В прямоугольном треугольнике большая сторона (то есть сторона, лежащая напротив прямого угла) называется гипотенузой.
Две другие стороны называются катетами.
Теоремы: свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна \(90^\circ\).
2. В прямоугольном треугольнике катет, лежащий против угла \(30^\circ\), равен половине гипотенузы.
Верно и обратное: если катет равен половине гипотенузы, то он лежит против угла \(30^\circ\).
По известным координатам вершин треугольника А(4;4), В(-6;-1), С(-2;-4) записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла АВС.
Решение
Так как нам известны координаты вершин, то проще всего получить уравнение стороны в канонической форме – формула, от которого легко перейти к уравнению в общей форме. Для канонического уравнения нам нужны координаты точки, принадлежащей стороне и координаты направляющего вектора (параллельного рассматриваемому).
1. Найдем уравнение стороны АВ. В качестве точки прямой можно взять точку А с заданными координатами, а в качестве направляющего вектора – вектор АВ. Найдем координаты вектора АВ:
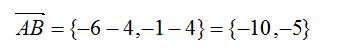
2. Тогда каноническое уравнение стороны АВ запишется:
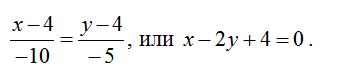
3. Аналогично можно получить уравнения остальных сторон треугольника: для стороны ВС: координаты вектора
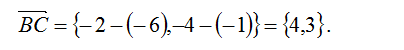4. Откуда каноническое уравнение: 
Следовательно, общее уравнение: 3x+4y+22=0.
5. Для стороны CА: координаты направляющего вектора
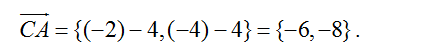
6. Каноническое уравнение:
7. Выведем общее уравнение для биссектрисы. Известно, что биссектриса делит угол пополам. Если на сторонах АВ и ВС треугольника отложить орты (соответственно a и b) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов a и b).
8. Для нахождения орта a необходимо знать координаты вектора BA:
соответственно a определится как:
9. Аналогично определим орт b:
Теперь определим их сумму:
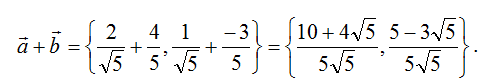
10. Тогда каноническое уравнение биссектрисы:
Уравнение высоты треугольника | Треугольники
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Пример.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
Решение:
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Составить уравнение прямой | Треугольники
Рассмотрим, как составить уравнение прямой, проходящей через две точки, на примерах.
Пример 1.
Составить уравнение прямой, проходящей через точки A(-3; 9) и B(2;-1).
Решение:
1 способ — составим уравнение прямой с угловым коэффициентом.
Уравнение прямой с угловым коэффициентом имеет вид y=kx+b. Подставив координаты точек A и B в уравнение прямой (x= -3 и y=9 — в первом случае, x=2 и y= -1 — во втором), получаем систему уравнений, из которой находим значения k и b:
Сложив почленно 1-е и 2-е уравнения, получим: -10=5k, откуда k= -2. Подставив во второе уравнение k= -2, найдём b: -1=2·(-2)+b, b=3.
Таким образом, y= -2x+3 — искомое уравнение.
2 способ — составим общее уравнение прямой.
Общее уравнение прямой имеет вид ax+by+c=0. Подставив координаты точек A и B в уравнение, получаем систему:
Поскольку количество неизвестных больше количества уравнений, система не разрешима. Но можно все переменные выразить через одну. Например, через b.
Умножив первое уравнение системы на -1 и сложив почленно со вторым:
получим: 5a-10b=0. Отсюда a=2b.
Подставим полученное выражение во второе уравнение: 2·2b -b+c=0; 3b+c=0; c= -3b.
Подставляем a=2b, c= -3b в уравнение ax+by+c=0:
2bx+by-3b=0. Осталось разделить обе части на b:
2x+y-3=0.
Общее уравнение прямой легко приводится к уравнению прямой с угловым коэффициентом:
y= -2x+3.
3 способ — составим уравнение прямой, проходящей через 2 точки.
Уравнение прямой, проходящей через две точки, имеет вид:
Подставим в это уравнение координаты точек A(-3; 9) и B(2;-1)
(то есть x1= -3, y1=9, x2=2, y2= -1):
и упростим:
По основному свойству пропорции
откуда 2x+y-3=0.
В школьном курсе чаще всего используется уравнение прямой с угловым коэффициентом. Но самый простой способ — вывести и использовать формулу уравнения прямой, проходящей через две точки.
Замечание.
Если при подстановке координат заданных точек один из знаменателей уравнения
окажется равным нулю, то искомое уравнение получается приравниваем к нулю соответствующего числителя.
Пример 2.
Составить уравнение прямой, проходящей через две точки C(5; -2) и D(7;-2).
Решение:
Подставляем в уравнение прямой, проходящей через 2 точки, координаты точек C и D:
Пример 3.
Составить уравнение прямой, проходящей через точки M (7; 3) и N (7; 11).
Решение:
90000 Solving Triangles 90001 90002 90003 «Solving» means finding missing sides and angles. 90004 90005 90006 90007 90008 90009 90008 90011 When we know any 3 of the sides or angles … 90005 90013 … we can find the other 3 90005 90009 90016 90007 90008 90009 90008 (Except for only 3 angles, because we need at least 90021 one side to find how big the triangle is.) 90009 90016 90024 90025 Six Different Types 90026 90027 If you need to solve a triangle 90028 right now 90029 choose one of the six options below: 90005 90002 Which Sides or Angles do you know already? 90003 (Click on the image or link) 90004 90005 90021 AAA 90021 Three Angles 90021 AAS 90021 Two Angles and a Side 90028 not 90029 between 90021 ASA 90021 Two Angles and a Side between 90021 SAS 90021 Two Sides and an Angle between 90021 SSA 90021 Two Sides and an Angle 90028 not 90029 between 90002… or read on to find out how you can 90028 become an expert triangle solver 90029: 90005 90025 Your Solving Toolbox 90026 90027 Want to learn to solve triangles? 90005 90002 Imagine you are «90028 The Solver 90029» … 90021 … the one they ask for when a triangle needs solving! 90005 90027 In your solving toolbox (along with your pen, paper and calculator) you have these 3 equations: 90005 90006 90065 90008 90067 1. The angles always add to 180 °: 90068 90002 A + B + C = 180 ° 90005 90027 When you know two angles you can find the third.90005 90067 90068 90067 2. Law of Sines (the Sine Rule): 90068 90002 90005 90027 When there is an angle opposite a side, this equation comes to the rescue. 90005 90027 Note: angle A is opposite side a, B is opposite b, and C is opposite c. 90005 90027 90005 90067 3. Law of Cosines (the Cosine Rule): 90068 90002 90005 90027 This is the hardest to use (and remember) but it is sometimes needed 90021 to get you out of difficult situations.90005 90027 It is an enhanced version of the Pythagoras Theorem that works 90021 on any triangle. 90005 90009 90016 90024 90027 With those three equations you can solve any triangle (if it can be solved at all). 90005 90025 Six Different Types (More Detail) 90026 90027 There are SIX different types of puzzles you may need to solve. Get familiar with them: 90005 90067 1. AAA: 90068 90027 This means we are given all three angles of a triangle, but no sides.90005 90027 90005 90027 AAA triangles are impossible to solve further since there are is nothing to show us 90028 size 90029 … we know the shape but not how big it is. 90005 90027 We need to know at least one side to go further. See Solving «AAA» Triangles. 90005 90027 90005 90067 2. AAS 90068 90027 This mean we are given two angles of a triangle and one side, which 90028 is not 90029 the side adjacent to the two given angles. 90005 90027 90005 90027 Such a triangle can be solved by using Angles of a Triangle to find the other angle, and The Law of Sines to find each of the other two sides.See Solving «AAS» Triangles. 90005 90027 90005 90067 3. ASA 90068 90027 This means we are given two angles of a triangle and one side, which 90028 is 90029 the side adjacent to the two given angles. 90005 90027 90005 90027 In this case we find the third angle by using Angles of a Triangle, then use The Law of Sines to find each of the other two sides. See Solving «ASA» Triangles. 90005 90027 90005 90067 4. SAS 90068 90027 This means we are given two sides and the included angle.90005 90027 90005 90027 For this type of triangle, we 90028 must 90029 use The Law of Cosines first to calculate the third side of the triangle; then we can use The Law of Sines to find one of the other two angles, and finally use Angles of a Triangle to find the last angle. See Solving «SAS» Triangles. 90005 90027 90005 90067 5. SSA 90068 90027 This means we are given two sides and one angle that is not the included angle. 90005 90027 90005 90027 In this case, use The Law of Sines first to find either one of the other two angles, then use Angles of a Triangle to find the third angle, then The Law of Sines again to find the final side.See Solving «SSA» Triangles. 90005 90027 90005 90067 6. SSS 90068 90027 This means we are given all three sides of a triangle, but no angles. 90005 90027 90005 90027 In this case, we have no choice. We 90028 must 90029 use The Law of Cosines first to find any one of the three angles, then we can use The Law of Sines (or use The Law of Cosines again) to find a second angle, and finally Angles of a Triangle to find the third angle. See Solving «SSS» Triangles. 90005 90025 Tips to Solving 90026 90027 Here is some simple advice: 90005 90027 When the triangle has a right angle, then use it, that is usually much simpler.90005 90027 When two angles are known, work out the third using Angles of a Triangle Add to 180 °. 90005 90027 Try The Law of Sines before the The Law of Cosines as it is easier to use. 90005 90027 90005 .90000 Triangle Formulas —The Formulas Plus links to lessons on each one 90001 90002 90003 Algebra 90004 90003 Geometry 90004 90003 Trigonometry 90004 90003 Calculus 90004 90003 Worksheets 90004 90003 Math Gifs 90004 90015 Teacher Tools 90002 90003 Test Grade Calculator 90004 90003 Graph Paper Maker 90004 90003 Number Line Maker 90004 90003 Inquality Number Line Maker 90004 90003 Math Worksheets 90004 90003 Chart Maker 90004 90029 90004 90029 90002 90003 Make a Graph 90004 90003 Graphing Calculator 90004 90029 90038 Advertisement 90039 90002 Related Links: 90003 Triangles 90004 90003 Triangle Types 90004 90003 90046 Free Triangle Worksheets 90004 90003 90046 Online Triangle Calculator (Finds all sides / angles and draws downloadable image of triangle) 90004 90029 90052 Interior Angles of A Triangle Triangle Inequality Theorem Relationship Between Sides and Angles Remote Interior Angles Area of Triangle (conventional Method) Area of Triangle (Heron’s Formula) Area of Triangle (SAS Method) 90053 90054 Formulas 90055 90056 90038 that Involve Right Triangles 90039 Sine Ratio Cosine Ratio Tangent Ratio Pythagorean Theorem 90059 (Lesson on how to use it) 90060 Geometric Mean 90059 (For Right Similar Triangles) 90060 .90000 90001 Equation of a Triangle 90002 90003 90004 90005 90006 Equation of a Triangle 90007 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 An ellipse can be expressed as the locus of points with orthogonal coordinates (x, y) such that (x / a) 90020 2 90021 + (Y / b) 90020 2 90021 = 1 for some constants a, b. However, it’s more difficult to give a succinct description of a piece-wise linear curve, e.g., a triangle.We seek a function f () such that f (x, y) = 0 if and only if the point (x, y) is on the perimeter of a given triangle. It’s not hard to see that no such function exists if we restrict ourselves to functions definable in terms of a finite number of basic arithmetical operations, i.e., additions, subtractions, multiplications, and divisions. 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 This raises the question of what other operation could be adjoined to the four basic operations that would enable us to define a general polygon.One possibility is the familiar «Absolute value» function, defined as 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 This function permits us to express a square as | x | + | Y | = 1. More general quadrilaterals can be expressed in the form 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 Two of the four vertices of this quadrilateral are on the x axis at the points x = -1 / (A-B) and x = 1 / (A + B), while the other two are on the y axis at the points y = -1 / (C-D) and y = 1 / (C + D).This 90088 nearly 90089 enables us to define a triangle by setting one of these vertices to zero; we can come arbitrarily close to zero using finite coefficients, but we can not quite define a true triangle. 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 A brute force approach would be to define three rays through the origin of the coordinate system: 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 These divide the plane into six regions.We can then construct a function that reduces to one of three lines, depending on the region. The point (x, y) is above or below the line y = Ax depending on whether the sign of y — ax is positive or negative. Therefore, a Boolean variable indicating whether (X, y) is above the line y = ax can be expressed as 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 Obviously the complement of this function 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 is a Boolean variable indicating whether (x, y) is 90088 below 90089 the line y = ax.However, these functions are undefined for points on the line, because then | y — ax | = 0. One way of removing this ambiguity is to express Q and q in terms of a function that is arguably even simpler than the absolute value, namely, the sign function 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 With this function we can define Q and q as 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 where now Q signifies that (X, y) is above 90088 or on 90089 the line y = ax.90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 Using these Boolean operators we can construct a function that reduces at any given point to the equation of one of the three edge lines of a triangle, depending on the relation of that point to the other two edge lines. For example, consider a triangle whose vertices fall on the three rays shown below 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 The edge line connecting the vertices on rays a and b should be invoked whenever (x, y) is on or above the relines a and b.The edge line connecting a and c should be invoked when (x, y) is 90088 below 90089 both of the relines a and c. The edge line connecting b and c should be invoked when (x, y) is 90088 on 90089 or 90088 above 90089 reline c and 90088 below 90089 reline b. Thus, if the equations for the individual edge lines are A 90048 1 90049 x + B 90048 1 90049 y = 1, A 90048 2 90049 x + B 90048 2 90049 y = 1, and A 90048 3 90049 x + B 90048 3 90049 y = 1, then the overall equation for the triangle can be expressed in the form 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 To illustrate, if we take the triangle given by the rays 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 with the edge lines 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 then equation (1) is satisfied by the points on the perimeter of the triangle shown below.90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 This figure assumes we have defined Q and q in terms of the «sign» function. Another way of dealing with the singularity of the absolute value versions of Q and q would be to multiply through equation (1) by the factor 4 | y — ax || y — bx || y — cx |. Letting R, S, T and r, s, t denote respectively the values and the absolute values of y — ax, y — bx, and y — cx, this gives the non-singular function 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90048 90049 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 This is equivalent to (1) except that it is also satisfied by the points on any of the three rays.Thus the solution of equation (2) is as illustrated below. 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 One interesting aspect of this «Triangle function» is that we do not need to restrict our attention to just the points (x, y) that satisfy the equation. Instead, we can assign a color to every point on the plane depending on how close it comes to satisfying the equation.This results in some striking images, such as the «Stealth fighter» shown below. 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90047 90008 90009 90010 90003 90004 90005 90008 90009 90010 90003 90004 90005 Return to MathPages Main Menu 90008 90009 90010 90471.90000 Equation of the Altitudes of a Triangle 90001 90002 To find the equation of the altitude of a triangle, we examine the following example: Consider the triangle having vertices $$ A \ left ({- 3,2} \ right) $$, $$ B \ left ({5, 4} \ right) $$ and $$ C \ left ({3, — 8} \ right) $$. 90003 90004 90005 90002 First we find the slope of side $$ AB $$: 90004 \ [\ frac {{4 — 2}} {{5 — \ left ({- 3} \ right)}} = \ frac {2} {{ 5 + 3}} = \ frac {1} {4} \] 90003 90002 The altitude $$ CD $$ is perpendicular to side $$ AB $$.90003 90002 The slope of \ [CD = — \ frac {1} {{{\ text {slope}} \, {\ text {of}} \, AB}} = — 4 \] 90003 90002 Since the altitude $$ CD $$ passes through the point $$ C \ left ({3, — 8} \ right) $$, using the point-slope form of the equation of a line, the equation of $$ CD $$ is 90004 \ [\ begin {gathered} y — \ left ({- 8} \ right) = — 4 \ left ({x — 3} \ right) \\ \ Rightarrow y + 8 = — 4x + 12 \ \ \ Rightarrow 4x + y — 4 = 0 \\ \ end {gathered} \] 90003 90002 This is the required equation of the altitude from $$ C $$ to $$ AB $$.90003 90002 90003 90002 The slope of side $$ BC $$ is 90004 \ [\ frac {{- 8 — 4}} {{3 — 5}} = \ frac {{- 12}} {{- 2}} = 6 \] 90003 90002 The altitude $$ AE $$ is perpendicular to side $$ BC $$. 90003 90002 The slope of \ [AE = — \ frac {1} {{{\ text {slope}} \, {\ text {of}} \, BC}} = — \ frac {1} {6} \] 90003 90002 Since the altitude $$ AE $$ passes through the point $$ A \ left ({- 3,2} \ right) $$, using the point-slope form of the equation of a line, the equation of $$ AE $$ is 90004 \ [\ begin {gathered} y — 2 = — \ frac {1} {6} \ left ({x — \ left ({- 3} \ right)} \ right) \\ \ Rightarrow — 6 \ left ({y — 2} \ right) = x + 3 \\ \ Rightarrow x + 6y — 9 = 0 \\ \ end {gathered} \] 90003 90002 This is the required equation of the altitude from $$ A $$ to $$ BC $$.90003 90002 90003 90002 The slope of side $$ AC $$ is 90004 \ [\ frac {{- 8 — 2}} {{3 — \ left ({- 3} \ right)}} = — \ frac {{10}} { 6} = — \ frac {5} {3} \] 90003 90002 The altitude $$ BF $$ is perpendicular to side $$ AC $$. 90003 90002 The slope of \ [BF = — \ frac {1} {{{\ text {slope}} \, {\ text {of}} \, AC}} = \ frac {3} {5} \] 90003 90002 Since the altitude $$ BF $$ passes through the point $$ B \ left ({5,4} \ right) $$, using the point-slope form of the equation of a line, the equation of $$ BF $ $ is 90004 \ [\ begin {gathered} y — 4 = \ frac {3} {5} \ left ({x — 5} \ right) \\ \ Rightarrow 5 \ left ({y — 4} \ right) = 3 \ left ({x — 5} \ right) \\ \ Rightarrow 3x — 5y + 5 = 0 \\ \ end {gathered} \] 90003 90002 This is the required equation of the altitude from $$ B $$ to $$ AC $$.90003 .