РЕШЕНИЕ БОЛЬШИХ СИСТЕМ БУЛЕВЫХ УРАВНЕНИЙ | Закревский
1. Теория дискретных управляющих устройств / Под ред. А.Д. Закревского и И.В. Прангишвили. – М.: Наука, 1982.
2. Лазарев В.Г., Пийль Е.И. Синтез управляющих автоматов. – М.: Энергия, 1970.
3. Закревский А.Д. Алгоритмы синтеза дискретных автоматов. – М.: Наука, 1971.
4. Основы технической диагностики / Под ред. П.П. Пархоменко. – М.: Энергия, 1976.
5. Чень Ч., Ли Р. Математическая логика и автоматическое доказательство теорем. М.: Наука, 1983.
6. Математические и компьютерные основы криптологии / Ю.С. Харин, В.И. Берник, Г.В. Матвеев, С.В. Агиевич. – Мн.: ООО «Новое знание», 2003.
7. Алгоритмы решения логико-комбинаторных задач: Сб. науч. тр. / Под ред. А.Д. Закревского. – Мн.: Ин-т техн. кибернетики АН БССР, 1975-1980. – Вып. 1-6.
8. Закревский А.Д. Некоторые комбинаторные задачи искусственного интеллекта // Семиотика и информатика. М.: ВИНИТИ, 1980. – Вып. 15. С. 3-17.
9. Закревский А.Д. Комбинаторика логического проектирования // Автоматика и вычислительная техника. 1990. – № 2. – С. 68-79.
Закревский А.Д. Комбинаторика логического проектирования // Автоматика и вычислительная техника. 1990. – № 2. – С. 68-79.
10. Закревский А.Д. Комбинаторные задачи над логическими матрицами в логическом проекти-ровании и искусственном интеллекте // Успехи современной радиоэлектроники. 1998. № 2. С. 59-67.
11. Поттосин Ю.В. Задачи теории графов в логическом проектировании // Логическое проектирование. – Мн.: Ин-т техн. кибернетики НАН Беларуси, 2001. – Вып. 6. – С. 106-130.
12. Распознавание образов / Под ред. П. Колерса и М. Идена. – М.: Мир, 1970.
13. Закревский А.Д., Карелина А.В., Печерский Ю.Н. Всесоюзная школа-семинар по логико-комбинаторным методам в распознавании образов // Информационные материалы: Кибернетика. – М.: АН СССР, 1978. – № 4(104). – С. 16-18.
14. Zakrevskij A.D. A common logical approach to data mining and pattern recognition // Data Mining and Knowledge Discovery Approaches Based on Rule Induction Techniques. – Dordrecht: Kluwer Academic Publishers, 2004. – P. 1-42.
– P. 1-42.
15. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. – М.: Мир, 1980.
16. Закревский А.Д. О приближенных методах решения логических задач // Вопросы синтеза цифровых автоматов. – М.: Наука, 1967. – С. 5-13.
17. Эйнгорин М.Я. О системах уравнений алгебры логики и синтезе дискретных управляющих схем с обратными связями // Известия вузов. Радиофизика. – 1958. – Т. 1. – № 2. – С. 169-184.
18. Rudeanu S. Boolean functions and equations. – Amsterdam-London-New York: North-Holland and American Elsevier, 1974.
19. Закревский А.Д. Логические уравнения. – Мн.: Наука и техника, 1975; М.: УРСС, 2003. – 2-е изд.
20. Уткин А.А. Решение логических уравнений // Автоматизация логического проектирования. – Мн.: Ин-т техн. кибернетики АН БССР, 1982. – С. 41-58.
21. Bochmann D., Zakrevskij A.D. Posthoff Ch. Boolesche Gleichungen. – Berlin: VEB Verlag Technik, 1984.
22. Закревский А.Д. Решение логических уравнений // Логическое проектирование. – Мн.: Ин-т техн. кибернетики НАН Беларуси, 2001. – Вып. 6. – С. 51-68.
– Мн.: Ин-т техн. кибернетики НАН Беларуси, 2001. – Вып. 6. – С. 51-68.
23. Закревский А.Д. Логические уравнения с приложениями в автоматизированном проектировании и управлении // Автоматика и телемеханика, 2004. – № 4. – С. 173-185.
24. Закревский А.Д. Логический синтез каскадных схем. – М.: Наука, 1981. – 416 с.
25. Закревский А.Д. ПЛМ и матричные логические уравнения // Automatentheorie und Ihre Anwendung. Seminarbericht, Sekt. Math. der Humboldt-Universitet. – Berlin, 1984 Januar. – S. 26-34.
26. Бибило П.Н. Декомпозиция булевых функций на основе решения логических уравнений // Известия Академии наук. Теория и системы управления. – 2002. – № 4. – I. – С. 53-64; 2002. – № 5. – II. – С. 57-63; 2003. – № 6. – III. – С. 88-97.
27. Zakrevskij A.D. Pattern recognition as solving logical equations. – Special Issue 1999 – SSIT’99 (AMSE). – P. 125-136.
28. Лукасевич Я. Аристотелевская силлогистика с точки зрения современной формальной логики. – М.: ИЛ, 1959.
29. Закревский А.Д. К формализации полисиллогистики // Логический вывод. – М.: Наука, 1979. – С. 300-309.
30. Закревский А.Д. Матричный аппарат логического вывода в конечных предикатах // Философские основы неклассических логик: Тр. науч.-иссл. семинара по логике. – М.: Ин-т философии АН СССР, 1990. – С. 70-80.
31. Закревский А.Д. К решению систем логических уравнений // Принципы построения сетей и систем управления. – М.: Наука, 1964. – С. 48-55.
32. Закревский А.Д. Проверка тождеств в алгебре логики // Логический язык для представления алгоритмов синтеза релейных устройств. – М.: Наука, 1966. – С. 159-163.
33. Zakrevskii A.D., Kalmykova A.Yu. The solution of systems of logical equations // LYaPAS: A programming language for logic and coding algorithms – New-York and London: Academic Press, 1969. – P. 193-206.
34. Нильсон Н. Искусственный интеллект. Методы поиска решений. – М.: Мир, 1973.
35. Zakrevskij A., Zakrevski L. Solving systems of logical equations using search tree minimization technique // Proceedings of the PDPTA’02 International Conference, June 24-27, 2002, Las Vegas, USA. – P. 1145-1150.
– P. 1145-1150.
36. Закревский А.Д., Василькова И.В. Решение больших систем логических уравнений: метод минимизации дерева поиска // Вестник Томского государственного университета. Приложение № 1 (II), сентябрь 2002. – С. 260-265.
37. Zakrevskij A., Vasilkova I. Reducing search trees to accelerate solving large systems of Boolean equations // Boolean Problems. 5th International Workshop, Sept. 19-20, 2002, Freiberg (Sachsen). – P. 71-76.
38. Закревский А.Д., Василькова И.В. Минимизация дерева поиска корней больших систем логических уравнений // Автоматика и вычислительная техника. – 2003. – № 1. – C. 3-11.
39. Cherry C., Vaswani P.K. A new type of computer in propositional logic, with greatly reduced scanning procedures // Information and control. – 1961. – V. 4. – № 3. – P. 155-168.
40. Zakrevskij A. Reduction algorithms for solving large systems of logical equations // Computer Science Journal of Moldova. – 2000. – V. 8. – № 1. – P. 3-15.
41. Zakrevskij A. , Vasilkova I. Reducing large systems of Boolean equations // 4th International Workshop on Boolean Problems, September 21-22, 2000. – Freiberg, Germany. – P. 21-28.
, Vasilkova I. Reducing large systems of Boolean equations // 4th International Workshop on Boolean Problems, September 21-22, 2000. – Freiberg, Germany. – P. 21-28.
42. Закревский А.Д., Василькова И.В. Криптоанализ машины Hagelin – метод решения системы логических уравнений // Комплексная защита информации. – Мн.: Ин-т техн. кибернетики АН Беларуси, 1999. – Вып. 2. – С. 129-138.
43. Закревский А.Д. Метод «отраженных волн» решения логических уравнений // Прикладные аспекты теории автоматов. Тр. III Междунар. семинара. Т. 1. – Варна: БАН, 1975. – С. 81-84.
44. Baumann M., Rohde R., Barthel R. Cryptoanalysis of the Hagelin M-209 Machine // 3rd International Workshop on Boolean Problems, Sept. 17-18, 1998. – Freiberg (Sachsen). – P. 109-116.
45. Закревский А.Д. Решение систем логических уравнений методом локальной редукции // Доклады НАН Беларуси, 1999. – Т. 43. – № 5. – С. 5-8.
46. Закревский А.Д., Василькова И.В. Локальная редукция больших систем логических уравнений // Логическое проектирование. – Мн: Ин-т техн. кибернетики АН Беларуси, 1999. – Вып.4.– С. 91-101.
– Мн: Ин-т техн. кибернетики АН Беларуси, 1999. – Вып.4.– С. 91-101.
47. Закревский А.Д. Редукция больших систем логических уравнений: метод силлогизмов // Автоматика и вычислительная техника. – 2000. – № 5. – С. 32-39.
48. Закревский А.Д., Торопов Н.Р. Полиномиальная реализация частичных булевых функций и систем. – Мн.: Ин-т техн. кибернетики НАН Беларуси, 2001. – 200 с.
49. Zakrevskij A.D. Looking for shortest solutions of systems of linear logical equations: theory and applications in logic design // 2 Workshop «Boolesche Probleme», 19 – 20 Septem-ber 1996. Freiberg (Sachsen). – P. 63-69.
50. Закревский А.Д., Торопов Н.Р. Поиск кратчайшего решения системы линейных логических уравнений // Автоматизация проектирования дискретных систем: Мат. Второй междунар. конф. (CAD DD’97). – Мн.: Ин-т техн. кибернетики НАН Беларуси.– Т. 2. – С. 16-23.
51. Zakrevskij A.D., Zakrevski L. Optimizing solutions in a linear Boolean space – a decomposition method // Proc. of STI ‘2003, Orlando, Florida, USA, July 2003. – P. 276-280.
– P. 276-280.
52. Закревский А.Д. Оптимизация решений в линейном булевом пространстве – методы декомпозиции // Автоматика и вычислительная техника. – 2003. – № 5. – C. 28-36.
53. Закревский А.Д. Комбинаторные методы оптимизации решений систем линейных логических уравнений // Вестник Томского государственного университета. Приложение. № 6. – Сентябрь 2003. – С. 4-8.
54. Закревский А.Д. Эффективные методы нахождения кратчайших решений систем линейных логических уравнений // Проблемы управления. – 2003. – № 4. – C. 16-22.
55. Zakrevskij A.D. Randomization of a parallel algorithm for solving undefined systems of linear logical equations // Proceedings of the International Workshop on Discrete-Event System Design – DESDes’04, 2004. – University of Zielona Gora Press, Poland. – P. 97-102.
56. Закревский А.Д., Василькова И.В. Прогнозирование затрат времени на реализацию комбинаторных алгоритмов // Методы логического проектирования. – Мн.: ОИПИ НАН Беларуси, 2003. – Вып. 2. – С. 26-32.
– Вып. 2. – С. 26-32.
57. Закревский А.Д. Метод решения несовместных систем линейных логических уравнений // Вестник Томского государственного университета. Приложение. № 9(1). Сентябрь 2004. – С. 13-18.
58. Zakrevskij A.D. Solving inconsistent systems of linear logical equations // 6th International Workshop on Boolean Problems, September 23-24, 2004. Freiberg (Sachsen). – P. 183-190.
Стохастические дифференциальные уравнения смешанного типа со стандартными и дробными броуновскими движениями с индексами Херста, большими 1/3 | Васьковский
1. Stochastic Calculus for Fractional Brownian Motion and Applications / F. Biagini [et al.]. – London: Springer-Verlag, 2008. – 330 p. https://doi.org/10.1007/978-1-84628-797-8
2. Cheridito, P. Regularizing fractional Brownian motion with a view towards stock price modeling: a dissertation … doctor of mathematics / P. Cheridito. – Zurich, 2001. – 121 p.
3. Zahle, M. Integration with respect to fractal functions and stochastic calculus. I / M. Zahle // Probability Theory and Related Fields. – 1998. – Vol. 111, № 3. – P. 333–374. https://doi.org/10.1007/s004400050171
I / M. Zahle // Probability Theory and Related Fields. – 1998. – Vol. 111, № 3. – P. 333–374. https://doi.org/10.1007/s004400050171
4. Mishura, Y. S. Stochastic calculus for fractional Brownian motion and related processes / Y. S. Mishura. – Berlin; Heidelberg: Springer-Verlag, 2008. – 398 p. https://doi.org/10.1007/978-3-540-75873-0
5. Kleptsyna, M. L. General approach to filtering with fractional Brownian noises application to linear systems / M. L. Kleptsyna, A. Le Breton, M.-C. Roubaud // Stochastics and Stochastic Reports. – 2000. – Vol. 71, № 1/2. – P. 119–140. https://doi.org/10.1080/17442500008834261
6. Vaskouski, M. Asymptotic expansions of solutions of stochastic differential equations driven by multivariate fractional Brownian motions having Hurst indices greater than 1/3 / M. Vaskouski, I. Kachan // Stochastic Anal. Appl. – 2018. – Vol. 36, № 6. – P. 909–931. https://doi.org/10.1080/07362994.2018.1483247
7. Kubilius, K. The existence and uniqueness of the solution of an integral equation driven by a p-semimartingale of special type / K. Kubilius // Stochastic Processes and their Appl. – 2002. – Vol. 98, № 2. – P. 289–315. https://doi.org/10.1016/s0304-4149(01)00145-4
Kubilius // Stochastic Processes and their Appl. – 2002. – Vol. 98, № 2. – P. 289–315. https://doi.org/10.1016/s0304-4149(01)00145-4
8. Guerra, J. Stochastic differential equations driven by fractional Brownian motion and standard Brownian motion / J. Guerra, D. Nualart // Stochastic Anal. Appl. – 2008. – Vol. 26, № 5. – P. 1053–1075. https://doi.org/10.1080/07362990802286483
9. Mishura, Y. S. Existence and uniqueness of the solution of stochastic differential equation involving Wiener process and fractional Brownian motion with Hurst index H > 1/2 / Y. S. Mishura, G. M. Shevchenko // Communications in Statistics – Theory and Methods. – 2011. – Vol. 40, № 19/20. – P. 3492–3508. https://doi.org/10.1080/03610926.2011.581174
10. Shevchenko, G. M. Mixed stochastic delay differential equations / G. M. Shevchenko // Theory of Probability and Mathematical Statistics. – 2014. – Vol. 89. – P. 181–195. https://doi.org/10.1090/s0094-9000-2015-00944-3
11. Леваков, А. А. Существование слабых решений стохастических дифференциальных уравнений со стандартным и дробным броуновскими движениями и с разрывными коэффициентами / А. А. Леваков, М. М. Васьковский // Дифференц. уравнения. – 2014. – Т. 50, № 2. – C. 187–200.
А. Леваков, М. М. Васьковский // Дифференц. уравнения. – 2014. – Т. 50, № 2. – C. 187–200.
12. Леваков, А. А. Существование слабых решений стохастических дифференциальных уравнений со стандартным и дробным броуновскими движениями, с разрывными коэффициентами и с частично вырожденным оператором диффузии / А. А. Леваков, М. М. Васьковский // Дифференц. уравнения. – 2014. – Т. 50, № 8. – C. 1060–1076.
13. Васьковский, М. М. Существование слабых решений стохастических дифференциальных уравнений с запаздыванием со стандартным и дробным броуновскими движениями / М. М. Васьковский // Вес. Нац. акад. навук Беларусi. Сер. фiз.-мат. навук. – 2015. – № 1. – С. 22–34.
14. Леваков, А. А. Существование решений стохастических дифференциальных включений со стандартным и дробным броуновскими движениями / А. А. Леваков, М. М. Васьковский // Дифференц. уравнения. – 2015. – Т. 51, № 8. – C. 997–1003.
15. Леваков, А. А. Свойства решений стохастических дифференциальных уравнений со стандартным и дробным броуновскими движениями / А. А. Леваков, М. М. Васьковский // Дифференц. уравнения. – 2016. – Т. 52, № 8. – C. 1011–1019.
А. Леваков, М. М. Васьковский // Дифференц. уравнения. – 2016. – Т. 52, № 8. – C. 1011–1019.
16. Васьковский, М. М. Устойчивость и притяжение решений нелинейных стохастических дифференциальных уравнений со стандартным и дробным броуновскими движениями / М. М. Васьковский // Дифференц. уравнения. – 2017. – Т. 53, № 2. – С. 160–173.
17. Васьковский, М. М. Методы интегрирования стохастических дифференциальных уравнений смешанного типа, управляемых дробными броуновскими движениями / М. М. Васьковский, И. В. Качан // Вес. Нац. акад. навук Беларусi. Сер. фiз.-мат. навук. – 2019. – T. 55, № 2. – С. 135–151. https://doi.org/10.29235/1561-2430-2019-55-2-135-151
18. Леваков, А. А. Стохастические дифференциальные уравнения и включения / А. А. Леваков, М. М. Васьковский. – Минск: БГУ, 2019. – 495 с.
19. Lyons, T. Differential equations driven by rough signals / T. Lyons // Revista Matematica Iberoamericana. – 1998. – Vol. 14, № 2. – P. 215–310. https://doi.org/10.4171/rmi/240
20. Gubinelli, M. Controlling rough paths / M. Gubinelli // J. Functional Anal. – 2004. – Vol. 216, № 1. – P. 86–140. https://doi.org/10.1016/j.jfa.2004.01.002
Gubinelli, M. Controlling rough paths / M. Gubinelli // J. Functional Anal. – 2004. – Vol. 216, № 1. – P. 86–140. https://doi.org/10.1016/j.jfa.2004.01.002
21. Friz, P. A Course on Rough Paths with an Introduction to Regularity Structures / P. Friz, M. Hairer. – Cham: Springer Int. Publ. AG, 2014. – 262 p. https://doi.org/10.1007/978-3-319-08332-2
22. Trees and asymptotic expansions for fractional stochastic differential equations / A. Neuenkirch [et al.] // Annales de I Institut Henri Poincaré (B) Probability and Statistics. – 2009. – Vol. 45, № 1. – P. 157–174. https://doi.org/10.1214/07-aihp159
23. Coutin, L. Stochastic analysis, rough path analysis and fractional Brownian motions / L. Coutin, Z. Qian // Probability Theory Related Fields. – 2002. – Vol. 122, № 1. – P. 108–140. https://doi.org/10.1007/s004400100158
24. Breeden, J. L. Living with CECL: Mortgage modeling alternatives / J. L. Breeden. – Middletown, 2018. – 203 p.
Самое важное уравнение во Вселенной
Научная группа НАСА / WMAP
На прошлой неделе Институт Периметра опубликовал статью, в которой они спросили 14 ученых, какое уравнение им больше всего нравится и почему. Было много отличных ответов из разных областей исследований, от термодинамики до чистой математики. Многие люди обращались к фундаментальным уравнениям, таким как закон всемирного тяготения, знаменитый закон Ньютона.0009 F = ma , или уравнение Шрёдингера, которое описывает квантовые частицы. Я имел честь быть включенным в этот список, и мой ответ не был ни одним из них. Вместо этого я выбрал очень специфическое уравнение: первое уравнение Фридмана, которое выводится из общей теории относительности Эйнштейна при определенных обстоятельствах.
Институт периметра / Harley Thronson
Когда они спросили, почему я выбрал это уравнение, я ответил:
«Первое уравнение Фридмана описывает, как, исходя из того, что находится во Вселенной, скорость ее расширения будет меняться с течением времени. Если вы хотите знать, откуда возникла Вселенная и куда она движется, все, что вам нужно измерить, — это то, как она расширяется. сегодня и что в нем. Это уравнение позволяет предсказать все остальное!»
История Фридмана, его уравнения и того, что оно говорит нам о нашей Вселенной, — это история, которую должен знать каждый энтузиаст науки.
Научное сотрудничество LIGO / T. Pyle / Caltech / MIT
В 1915 году Эйнштейн выдвинул свою общую теорию относительности, которая связала искривление пространства-времени, с одной стороны, с присутствием материи и энергии во Вселенной, с другой . Как много лет спустя выразился Джон Уилер, пространство-время указывает материи, как двигаться; материя сообщает пространству-времени, как искривляться. Теория Эйнштейна одним махом воспроизвела все предыдущие успехи ньютоновской гравитации, объяснила хитросплетения орбиты Меркурия (чего не могла сделать теория Ньютона) и сделала новое предсказание искривления звездного света, которое было блестяще подтверждено во время полной солнечное затмение 19 числа19. Единственная проблема? Чтобы предотвратить коллапс Вселенной, Эйнштейну нужно было добавить в свою теорию космологическую постоянную — 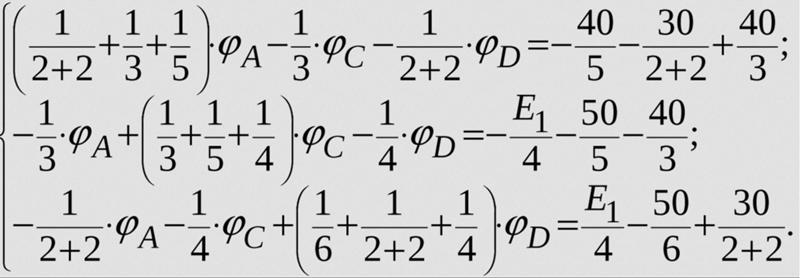 Это было уродливо, это было точно настроено, и у него не было никакой другой мотивации.
Это было уродливо, это было точно настроено, и у него не было никакой другой мотивации.
Э.А. Тропп, В.Я. Френкель и А.Д. Чернин; Издательство Кембриджского университета
Введите Friedmann. В 1922 году, всего через три года после подтверждения затмения, Фридман нашел элегантный способ спасти Вселенную, одновременно отказавшись от космологической постоянной: не предполагайте, что она статична. Вместо этого, утверждал Фридман, предположим, что он, как мы его наблюдаем, наполнен материей и излучением и может быть искривлен. Предположим далее, что оно примерно изотропно и однородно, что является математическим выражением, означающим «одинаково во всех направлениях» и «одинаково во всех местах». Если вы сделаете эти предположения, появятся два уравнения: уравнения Фридмана.
E. Siegel / Beyond the Galaxy
Что примечательно, так это то, что Фридман опубликовал это до того, как мы обнаружили, что Вселенная расширяется; еще до того, как Хаббл обнаружил, что за пределами Млечного Пути во Вселенной есть галактики! Только в следующем году Хаббл идентифицировал переменные звезды-цефеиды в Андромеде, сообщив нам расстояние до нее и поместив ее далеко за пределы нашей собственной галактики.
Э. Хаббл, НАСА, Европейское космическое агентство, Р. Гендлер, З. Левей и команда наследия Хаббла
Тем не менее, его научное наследие было неоспоримым и стало еще более неоспоримым, когда мы стали лучше понимать космологию. Первое уравнение Фридмана — самое важное из двух, поскольку его проще всего связать с наблюдениями. С одной стороны, у вас есть эквивалент скорости расширения (в квадрате), или то, что в просторечии известно как постоянная Хаббла. (На самом деле это не постоянная величина, поскольку она может меняться по мере того, как Вселенная расширяется или сжимается с течением времени.
LaTeX / общественное достояние
С другой стороны буквально все остальное. Там вся материя, излучение и любые другие формы энергии, составляющие Вселенную. Существует кривизна, присущая самому пространству, зависящая от того, является ли Вселенная закрытой (положительно изогнутой), открытой (отрицательно изогнутой) или плоской (неискривленной). А еще есть термин «Λ»: космологическая постоянная, которая может быть либо формой энергии, либо внутренним свойством пространства.
E. Siegel
В любом случае это уравнение, которое связывает количественное расширение Вселенной с тем, что составляет материю и энергию внутри нее. Измерьте, что есть в вашей Вселенной сегодня и как быстро она расширяется сегодня, и вы сможете экстраполировать вперед или назад на произвольные величины. Вы можете узнать, как расширялась Вселенная в далеком прошлом или сразу после Большого Взрыва. Вы можете знать, схлопнется ли он снова или нет (не будет), будет ли скорость расширения асимптотической к нулю (не будет) или навсегда останется положительной (будет).
Э. М. Хафф, команда SDSS-III и команда Телескопа Южного полюса; рисунок Зося Ростомян
И, пожалуй, самое впечатляющее, что вы можете добавить несовершенства на этот гладкий фон. Несовершенства плотности , которые вы вкладываете в свою Вселенную, говорят вам, как растет и формируется крупномасштабная структура, что вырастет в галактику/скопление, а что нет, и что станет гравитационно связанным, а что будет разорвано.
Все это можно вывести из одного-единственного уравнения: первого уравнения Фридмана.
НАСА / GSFC
Хотя жизнь Фридмана была короткой, его влияние невозможно переоценить.
НАСА / CXC / М. Вайс
Спустя почти столетие после его самой известной работы уравнения Фридмана были распространены на Вселенную, содержащую инфляционное происхождение, темную материю, нейтрино и темную энергию. Тем не менее, они по-прежнему полностью действительны, без каких-либо дополнений или модификаций, необходимых для объяснения этих огромных достижений. Хотя мы все можем спорить об относительных достоинствах Эйнштейна, Ньютона, Максвелла, Фейнмана, Больцмана, Хокинга и многих других, когда речь идет о расширяющейся Вселенной, вам нужно только первое уравнение Фридмана. Он связывает материю и энергию, которые присутствуют сегодня, в прошлом и будущем, и позволяет вам узнать судьбу и историю Вселенной из измерений, которые мы можем сделать сегодня. Что касается ткани нашей Вселенной, это уравнение считает корону самой важной.
Тем не менее, они по-прежнему полностью действительны, без каких-либо дополнений или модификаций, необходимых для объяснения этих огромных достижений. Хотя мы все можем спорить об относительных достоинствах Эйнштейна, Ньютона, Максвелла, Фейнмана, Больцмана, Хокинга и многих других, когда речь идет о расширяющейся Вселенной, вам нужно только первое уравнение Фридмана. Он связывает материю и энергию, которые присутствуют сегодня, в прошлом и будущем, и позволяет вам узнать судьбу и историю Вселенной из измерений, которые мы можем сделать сегодня. Что касается ткани нашей Вселенной, это уравнение считает корону самой важной.
align — Как работать с большими уравнениями? — TeX
У меня есть система уравнений, где уравнения большие (одной строки мало). Я нашел это решение (второе, от egreg. Как выровнять набор очень длинных уравнений), чтобы справиться с вопросом «как выровнять длинные уравнения?» проблема, но у меня все еще есть некоторые проблемы.
Мои уравнения представляют собой «просто» суммы различных элементов, и некоторые из этих элементов являются большими произведениями (опять же, одной строки недостаточно).
Пример (как показать результат этого кода?)
\documentclass[a4paper]{статья}
\usepackage{аммат}
\начать{документ}
\начать{выравнивать}
\начать{разделить}
A &= АААААААААААААААААААААААААААААААААААААА \cdots \\
&\qquad -BBBBBBBBBBBB\cdots\\
& +\\
&\qquad CCCCCCCCCCCCCCCCCCCCCCCCC\\
& \раз\\
&\qquad CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
\конец{разделить}
\начать{разделить}
A &= АААААААААААААААААААААААААААААААААААААА \cdots \\
&\qquad -BBBBBBBBBBBB\cdots\\
& +\\
&\qquad CCCCCCCCCCCCCCCCCCCCCCCCC\\
& \раз\\
&\qquad CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
\конец{разделить}
\end{выравнивание}
\конец{документ}
Какие соглашения в этом случае?
Если это возможно, я хочу центрировать + и x и, возможно, добавить скобки для (CCCC x CCCC), чтобы показать, что это только один элемент суммы.
Я полагаю, мне нужно вложить среду в другую, но я не знаю, в какие среды.
Некоторые попытки не увенчались успехом, но это может помочь вам понять, что я имею в виду Попробуйте 1
\documentclass[a4paper]{статья}
\usepackage{аммат}
\начать{документ}
\начать{выравнивать}
\начать{разделить}
A &= АААААААААААААААААААААААААААААААААААААА \cdots \\
&\qquad -BBBBBBBBBBBB\cdots\\
& \центр{+}\\
\ влево \ (\ начать {разделить}
&\qquad CCCCCCCCCCCCCCCCCCCCCCCCC\\
& \ центр {\ раз} \\
&\qquad CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
\конец{разделить}\вправо\)
\конец{разделить}
\end{выравнивание}
\конец{документ}
Попробуйте 2
\documentclass[a4paper]{статья}
\usepackage{аммат}
\начать{документ}
\начать{выравнивать}
\начать{разделить}
A &= АААААААААААААААААААААААААААААААААААААА \cdots \\
&\qquad -BBBBBBBBBBBB\cdots\\
& \центр{+}\\
\ влево \ (\ начать {собирать}
\qquad CCCCCCCCCCCCCCCCCCCCCCCCC\\
\ центр {\ раз} \\
\qquad CCCCCCCCCCCCCCCCCCCCCCCCCCCCC
\конец{собрать}\право\)
\конец{разделить}
\end{выравнивание}
\конец{документ}
РЕДАКТИРОВАТЬ:
В соответствии с просьбой: вот несколько фотографий, чтобы показать, что я имею в виду.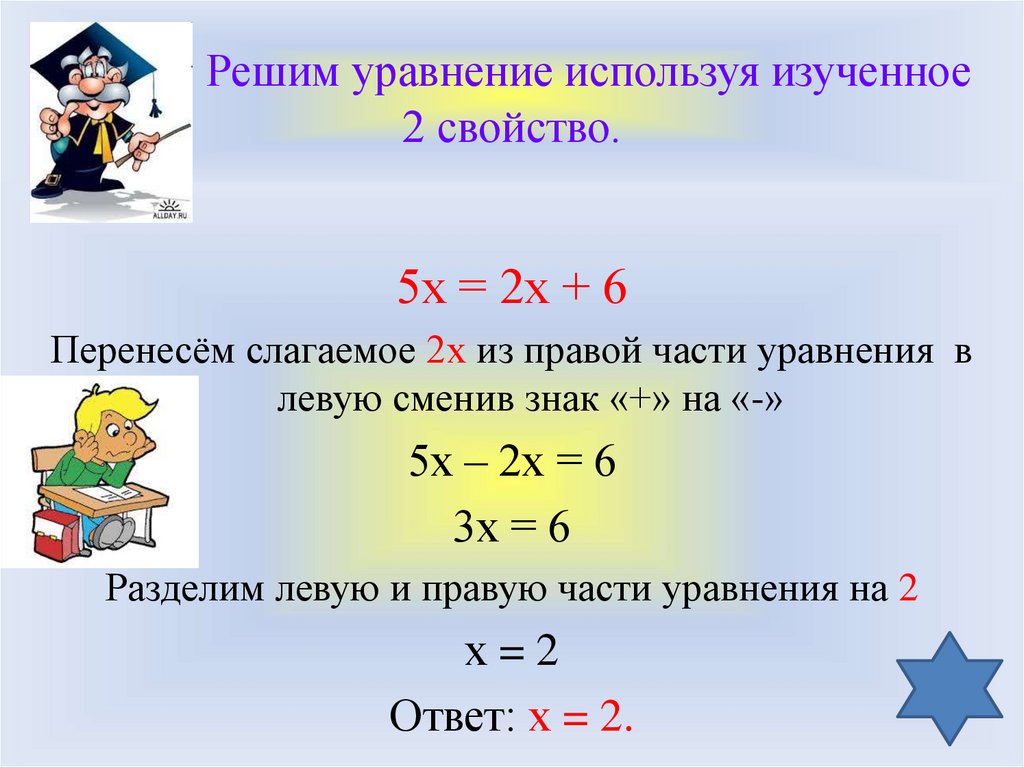

 .. [+] расширяющейся Вселенной. Первое уравнение Фридмана описывает все эти эпохи, от инфляции до Большого взрыва, настоящего и далекого будущего, совершенно точно, даже сегодня.
.. [+] расширяющейся Вселенной. Первое уравнение Фридмана описывает все эти эпохи, от инфляции до Большого взрыва, настоящего и далекого будущего, совершенно точно, даже сегодня. .. [+] первое уравнение Фридмана справа.
.. [+] первое уравнение Фридмана справа.
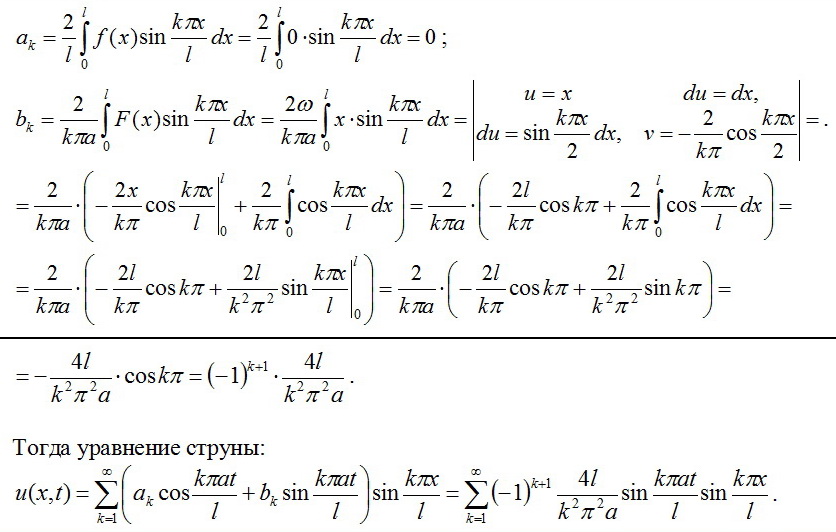 .. [+] самому пространству. Все три этих решения выводятся из уравнений Фридмана.
.. [+] самому пространству. Все три этих решения выводятся из уравнений Фридмана.