Уравнения тригонометрия формулы: Формулы тригонометрических уравнений

Тригонометрические уравнения

   Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно.  Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.

В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.  

Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.

Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.

Понимание раздела «Тригонометрия»  в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.

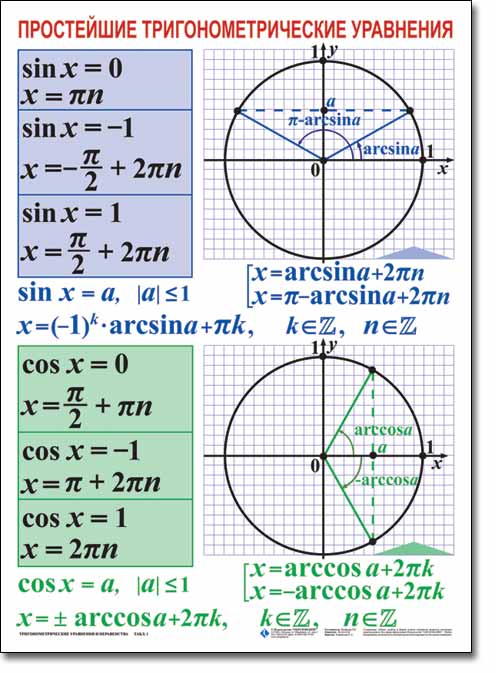
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:

Знание этих значений необходимо, это «азбука», без которой  невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да  просто вы  именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.

Алгоритм восстановления этих значений прост, он также приведён в теории,  полученной вами во втором письме после  подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».

Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с  использованием угла х для соответствующих  уравнений: cosx=a, sinx=a, tgx=a, где х может быть  и выражением. В примерах ниже у нас аргумент задан именно выражением.

Итак, рассмотрим следующие задачи:

Найдите корень уравнения:

В ответе запишите наибольший отрицательный корень.

Решением уравнения cos x = a  являются два корня:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.

Значит

Выразим x:

Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.

Общая рекомендация для всех подобных задач: для начала берите диапазон  n  от   – 2  до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x:  – 3 и 3,  – 4  и 4 и так далее.

Вычисляем:

При  n = – 2     х₁= 3 (– 2) – 4,5 = – 10,5      х₂= 3 (– 2) – 5,5 = – 11,5

При  n = – 1     х₁= 3 (– 1) – 4,5 = – 7,5        х₂= 3 (– 1) – 5,5 = – 8,5

При  n = 0        х₁= 3∙0 – 4,5 = – 4,5            х₂= 3∙0 – 5,5 = – 5,5

При  n = 1        х₁= 3∙1 – 4,5 = – 1,5            х₂= 3∙1 – 5,5 = – 2,5

При  n = 2        х₁= 3∙2 – 4,5 =  1,5              х₂= 3∙2 – 5,5 = 0,5

Получили, что наибольший отрицательный корень равен   –1,5

Ответ:  –1,5

Решите самостоятельно:

Посмотреть решение

Решите уравнение:

В ответе напишите наименьший положительный корень.

Решением уравнения sin x = a  являются два корня:

Либо (он объединяет оба указанные выше):

Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от   – 90^о до 90^о синус которого равен a.

Значит

Выразим x (умножим обе части уравнения на 4 и разделим на Пи):

Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n =  0,1,2 …

При  n = 0     х = (– 1)⁰ + 4∙0 + 3 = 4

При  n = 1     х = (– 1)¹ + 4∙1 + 3 = 6

При  n = 2     х = (– 1)² + 4∙2 + 3 = 12

Проверим при   n = –1     х = (–1)^–1 + 4∙(–1) + 3 = –2

Значит наименьший положительный корень равен 4.

Ответ: 4

Решите самостоятельно:

Посмотреть решение

Решите уравнение:

В ответе напишите наименьший положительный корень.

Решением уравнения tg x = a  является корень:

Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90^о до 90^о,  тангенс которого равен a.

Значит

Выразим x (умножим обе части уравнения на 6 и разделим на  Пи):

Найдём наименьший положительный корень. Подставим значения  n = 1,2,3…    Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:

Таким образом, наименьший положительный корень равен 0,25.

Ответ: 0,25

Решите самостоятельно:

Посмотреть решение

Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.

Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если  в ходе решения вы не сможете определить угол, например, для

то данные формулы вам помогут:

 

Спасибо за внимание, учитесь с удовольствием!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Тригонометрические уравнения – формулы в таблице, основные примеры

4.6

Средняя оценка: 4.6

Всего получено оценок: 631.

4.6

Средняя оценка: 4.6

Всего получено оценок: 631.

Тригонометрические уравнения – это весьма трудный раздел. После изучения в школьной программе, он встречается только в высшей физике и математике, в редких разделах программирования. Это делает тему несколько отдаленной и запутанной, но не менее интересной.

Что нужно знать?

Эта тема, как и любая другая, нуждается в наборе базовых знаний, которые требуются для успешного понимания вопроса. Сразу перечислим необходимые навыки, чтобы потом к этому не возвращаться:

• Умение пользоваться таблицами Брадиса.
• Знание формул-приведений. Это очень часто требуется, чтобы превратить синус в косинус или наоборот.
• Знание тригонометрических формул. Это крайне важно для решения сложных уравнений.
• Знание определений тригонометрических функций. 2)=0$$

  $$cos(x)=0$$

  $$x=({{\pi}\over2}+\pi)$$

  Что мы узнали?

  Мы узнали, что такое тригонометрические уравнения. Научились их решать и привели примеры решения для каждого из двух основных методов. Выделили основные навыки и знания, необходимые для правильного решения уравнений такого рода.

  Тест по теме

  Доска почёта

  Чтобы попасть сюда — пройдите тест.

  • Алексей Измайлов

    10/10

  • Миша Черепанов

    9/10

  • София Кристар

    9/10

  • Дмитрий Петров

    8/10

  Оценка статьи

  4.6

  Средняя оценка: 4.6

  Всего получено оценок: 631.

  ---

  А какая ваша оценка?

  Тригонометрические уравнения — формула, решение, этапы решения, примеры

  Тригонометрические уравнения включают тригонометрические функции углов в качестве переменных. Угол θ тригонометрических функций, таких как Sinθ, Cosθ, Tanθ, используется в качестве переменной в тригонометрических уравнениях.

  Подобно общим полиномиальным уравнениям, тригонометрические уравнения также имеют решения, которые называются главными решениями и общими решениями.

  Мы будем использовать тот факт, что период sin x и cos x равен 2π, а период tan x равен π, чтобы найти решения тригонометрических уравнений. Давайте узнаем больше о тригонометрических уравнениях, способах их решения и найдем их решения с помощью нескольких решенных примеров тригонометрических уравнений для лучшего понимания концепции.

  1.	Что такое тригонометрические уравнения?
  2.	Формулы тригонометрических уравнений
  3.	Решение тригонометрических уравнений
  4.	шагов для решения тригонометрических уравнений
  5.	Примеры решения тригонометрических уравнений
  6.	Часто задаваемые вопросы по тригонометрическим уравнениям

  Что такое тригонометрические уравнения?

  Тригонометрические уравнения аналогичны алгебраическим уравнениям и могут быть линейными уравнениями, квадратными уравнениями или полиномиальными уравнениями. В тригонометрических уравнениях тригонометрические отношения Sinθ, Cosθ, Tanθ представлены вместо переменных, как в обычном полиномиальном уравнении. В тригонометрических уравнениях используются следующие тригонометрические отношения: Sinθ, Cosθ или Tanθ.

  Линейное уравнение ax + b = 0 может быть записано как уравнение тригонометрии как aSinθ + b = 0, которое также иногда записывается как Sinθ = Sinα. Квадратное уравнение ax

  2 + bx + c = 0 в качестве примера тригонометрического уравнения записывается как aCos ² θ + bCosθ + c = 0. Но в отличие от обычных решений уравнений с числом решений в зависимости от степени переменной, в тригонометрических уравнениях одно и то же значение решения существует для разных значений θ. Например, мы имеем Sinθ = 1/2 = Sinπ/6 = Sin5π/6 = Sin13π/6 и т. д., поскольку значения функции синуса повторяются через каждые 2π радиан.

  Ниже приведены некоторые примеры тригонометрических уравнений.

  • Sin2x — Sin4x + Sin6x = 0
  • 2Cos ² х + 3Sinx = 0
  • Cos4x = Cos2x
  • Sin2x + Cosx = 0
  • Секунда ² 2x = 1 — Tan2x

  Формулы тригонометрических уравнений

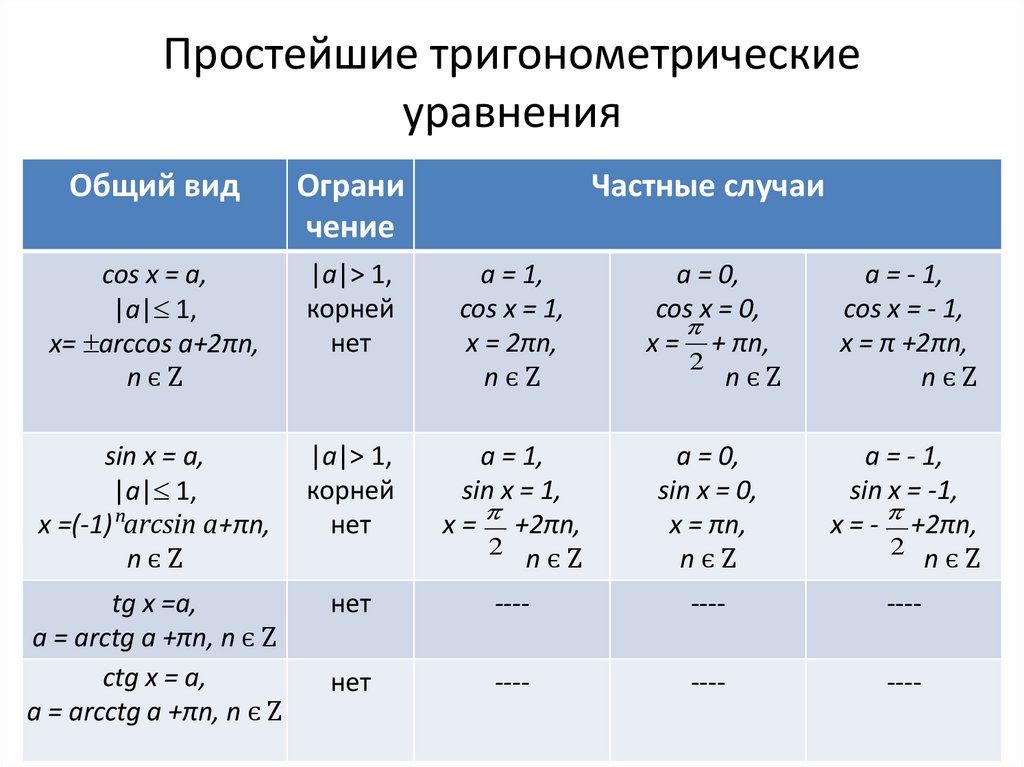
  Мы используем некоторые результаты и общие решения основных тригонометрических уравнений для решения других тригонометрических уравнений.

  Эти результаты таковы:
  • Для любых действительных чисел x и y из sin x = sin y следует x = nπ + (-1) ⁿ y, где n ∈ Z.
  • . Для любых действительных чисел x и y из cos x = cos y следует x = 2nπ ± y, где n ∈ Z.
  • Если x и y не являются нечетными кратными π/2, то tan x = tan y влечет x = nπ + y, где n ∈ Z.

  Теперь мы можем доказать эти результаты, используя тригонометрические формулы.

  Докажите, что для любых действительных чисел x и y из sin x = sin y следует x = nπ + (-1)

  ⁿ y, где n ∈ Z

  Доказательство: Если sin x = sin y, то sin x – sin y = 0

  ⇒ 2 cos (x + y)/2 sin (x − y)/2 = 0 — [Используя формулу Sin A — Sin B = 2 cos ½ (A + B) sin ½ (A — B)]

  ⇒ cos (x + y)/2 = 0 или sin (x — y) /2 = 0

  ⇒ (x + y)/2 = (2n + 1)π /2 или (x − y)/2 = nπ, где n ∈ Z —- [Поскольку sin A = 0 влечет A = nπ и cos A = 0 влечет A = (2n + 1)π/2, где n ∈ Z]

  , т. е. x = (2n + 1) π – y или x = 2nπ + y, где n ∈ Z.

  Отсюда x = (2n + 1)π + (–1) ^{2n + 1} y или x = 2nπ + (–1) ²ⁿ y, где n ∈ Z.

  Объединяя эти два результата, получаем x = nπ + (–1) ⁿ y, где n ∈ Z.

  Докажите, что для любых действительных чисел x и y из cos x = cos y следует x = 2nπ ± y, где n ∈ Z.

  Доказательство: . Если cos x = cos y, то cos x – cos y = 0

  ⇒ -2 sin (x + y)/2 sin (x − y)/2 = 0 — [Используя формулу Cos A — Cos B = — 2 sin ½ (A + B) sin ½ (A — B)]

  ⇒ sin (x + y)/2 = 0 или sin (x − y)/2 = 0

  ⇒ (x + y)/2 = nπ или (x − y)/2 = nπ, где n ∈ Z —- [Поскольку из sin A = 0 следует A = nπ, где n ∈ Z]

  т. е. x = 2nπ – y или x = 2nπ + y, где n ∈ Z.

  Следовательно, x = 2nπ ± y, где n ∈ Z.

  Докажите, что если x и y не являются нечетными кратными π/2, то из tan x = tan y следует x = nπ + y, где n ∈ Z.

  Доказательство: Если tan x = tan y, тогда тангенс x — тангенс y = 0

  ⇒ sin x / cos x — sin y / cos y = 0

  ⇒ (sin x cos y — cos x sin y) / (cos x cos y) = 0

  ⇒ sin (x — y) / (cos x cos y) = 0 —- [Используя тригонометрическую формулу sin (A — B) = sinA cosB — sinB cosA]

  ⇒ sin (x — y) = 0

  ⇒ x — y = nπ, где n ∈ Z — [Поскольку sin A = 0 влечет A = nπ, где n ∈ Z]

  ⇒ x = nπ + y, где n ∈ Z

  Решение тригонометрических уравнений

  В отличие от обычных решений алгебраических уравнений с числом решений, основанным на степени переменной, в тригонометрических уравнениях решения бывают двух типов, основанные на различном значении угла тригонометрической функции, для одного и того же решения. Например, для простого тригонометрического уравнения 2Cosθ — 1 = 0 решение дается выражением Cosθ = 1/2, а значения θ равны π/3, 5π/3, 7π/3, 11π/3 и т. д. поскольку значения функции косинуса повторяются через каждые 2π радиан, а cos x положителен в первом и четвертом квадрантах. У нас есть два типа решений тригонометрических уравнений:
  • Основное решение: Начальные значения углов для тригонометрических функций называются главными решениями. Решение Sinx и Cosx повторяется через интервал 2π, а решение Tanx повторяется через интервал π. Решения этих тригонометрических уравнений, для которых x лежит между 0 и 2π, называются главными решениями.
  • Общее решение: Значения углов для одного и того же ответа тригонометрической функции называются общим решением тригонометрической функции. Все решения тригонометрических уравнений за пределами 2π объединяются и выражаются в виде общего решения тригонометрических уравнений. Общие решения Sinθ, Cosθ, Tanθ следующие.
    • Sinθ = Sinα, и общее решение θ = nπ + (-1) ⁿ α, где n ∈ Z
    • Cosθ = Cosα, и общее решение θ = 2nπ + α, где n ∈ Z
    • Tanθ = Tanα, и общее решение θ = nπ + α, где n ∈ Z

  шагов для решения тригонометрических уравнений

  Для решения тригонометрического уравнения необходимо выполнить следующие шаги.

  • Преобразовать данное тригонометрическое уравнение в уравнение с одним тригонометрическим соотношением (sin, cos, tan)
  • Измените уравнение с тригонометрическим уравнением, имеющим кратные углы или дольные углы, в простой угол.
  • Теперь представим уравнение в виде полиномиального уравнения, квадратного уравнения или линейного уравнения.
  • Решите тригонометрическое уравнение, подобное обычным уравнениям, и найдите значение тригонометрического отношения.
  • Угол тригонометрического отношения или значение тригонометрического отношения представляет собой решение тригонометрического уравнения.

  Примеры решения тригонометрических уравнений

  Пример 1: Найдите главные решения тригонометрического уравнения sin x = √3/2.

  Решение: Чтобы найти главные решения sin x = √3/2, мы знаем, что sin π/3 = √3/2 и sin (π — π/3) = √3/2

  ⇒ sin π/3 = sin 2π/3 = √3/2

  Мы можем найти другие значения x такие, что sin x = √3/2, но нам нужно найти только те значения x, что x лежит в [0, 2π], так как главное решение лежит между 0 и 2π.

  Таким образом, основными решениями sin x = √3/2 являются x = π/3 и 2π/3.

  Пример 2: Найдите решение cos x = 1/2.

  Решение: В этом случае мы найдем общее решение cos x = 1/2. Мы знаем, что cos π/3 = 1/2, поэтому имеем

  cos x = 1/2

  ⇒ cos x = cos π/3

  ⇒ x = 2nπ + (π/3), где n ∈ Z —- [Используя Cosθ = Cosα, и общее решение θ = 2nπ + α, где n ∈ Z]

  Таким образом, общее решение cos x = 1/2 равно x = 2nπ + (π/3), где n ∈ Z.

  Важные замечания по тригонометрическим уравнениям , sin x = sin y влечет x = nπ + (-1) ⁿ y, где n ∈ Z.

  • . Для любых действительных чисел x и y из cos x = cos y следует x = 2nπ ± y, где n ∈ Z.
  • Если x и y не являются нечетными кратными π/2, то tan x = tan y влечет x = nπ + y, где n ∈ Z.
  • sin A = 0 влечет A = nπ, а cos A = 0 влечет A = (2n + 1)π/2, где n ∈ Z

  Похожие темы

  • Тригонометрические функции
  • Тригонометрическая таблица
  • Тригонометрические тождества
  • Обратные тригонометрические соотношения

  Часто задаваемые вопросы по тригонометрическим уравнениям

  Что такое тригонометрические уравнения?

  Тригонометрические уравнения аналогичны алгебраическим уравнениям и могут быть линейными уравнениями, квадратными уравнениями или полиномиальными уравнениями. В тригонометрических уравнениях вместо переменных представлены тригонометрические отношения Sinθ, Cosθ, Tanθ.

  Что такое формулы трех тригонометрических уравнений?

  Три тригонометрических уравнения основаны на трех тригонометрических функциях. Три тригонометрических уравнения: Sinθ = Sinα, Cosθ = Cosα, Tanθ = Tanα. Три формулы тригонометрических уравнений выглядят следующим образом:

  • Для любых действительных чисел x и y из sin x = sin y следует x = nπ + (-1) ⁿ y, где n ∈ Z.
  • . Для любых вещественных чисел x и y из того, что cos x = cos y, следует x = 2nπ ± y, где n ∈ Z.
  • Если x и y не являются нечетными кратными π/2, то tan x = tan y влечет x = nπ + y, где n ∈ Z.

  Приведите примеры тригонометрических уравнений.

  Вот некоторые примеры тригонометрических уравнений:

  • Sin2x — Sin4x + Sin6x = 0
  • 2Cos ² х + 3Sinx = 0
  • Cos4x = Cos2x

  Каковы шаги для решения тригонометрических уравнений?

  Следующие шаги помогут решить тригонометрическое уравнение:

  • Преобразовать данное тригонометрическое уравнение в уравнение с одним тригонометрическим соотношением.
  • Замените уравнение с тригонометрическим уравнением, имеющим кратные углы или дольные углы, на простое. угол.
  • Теперь представим уравнение в виде полиномиального уравнения, квадратного уравнения или линейного уравнения.
  • Решите тригонометрическое уравнение, подобное обычным уравнениям, и найдите значение тригонометрического отношения.
  • Угол тригонометрического отношения или значение тригонометрического отношения представляет собой решение тригонометрического уравнения.

  В чем разница между тригонометрическими уравнениями и алгебраическими уравнениями?

  Тригонометрическое уравнение и алгебраические уравнения отличаются переменной, используемой в уравнении. В тригонометрическом уравнении переменной является тригонометрическая функция, а в алгебре в качестве переменных берутся алфавиты x, y. И тригонометрические уравнения, и алгебраические уравнения имеют линейные уравнения, квадратные уравнения и полиномиальные уравнения.

  В чем разница между тригонометрическими уравнениями и тождествами?

  Тригонометрические уравнения похожи на алгебраические уравнения, где от нас требуется найти решение и найти значение переменной. С другой стороны, тригонометрические тождества — это результаты тригонометрии, которые выражают отношения между различными тригонометрическими отношениями.

  Что такое главное решение тригонометрических уравнений?

  мы знаем, что sin x и cos x повторяются через каждые 2π радиан, а tan x повторяются через каждые π радиан. Решения тригонометрического уравнения, для которых 0 ≤ x < 2π, называются главными решениями.

  Как найти общее решение тригонометрического уравнения?

  Мы можем найти общее решение тригонометрических уравнений, используя следующие три результата:

  • Для любых действительных чисел x и y, sin x = sin y, подразумевает x = nπ + (-1) ⁿ y, где n ∈ Z.
  • Для любых действительных чисел x и y из условия x = cos y следует, что x = 2nπ ± y, где n ∈ Z.
  • Если x и y не являются нечетными кратными π/2, то tan x = tan y влечет x = nπ + y, где n ∈ Z.

  Как найти общее решение тригонометрических уравнений?

  11 декабря 2020 г. by sastry

  Тригонометрические уравнения тригонометрический тождества. Тождество выполняется для каждого значения неизвестного угла

  например ., cos ² x = 1 − sin ² x истинно ∀ x ∈ R, а тригонометрическое уравнение выполняется для некоторых частных значений неизвестного угла.

  (1) Корни тригонометрического уравнения: Величина неизвестного угла (переменная величина), удовлетворяющая данному уравнению, называется корнем уравнения, например, ., cos θ = ½, корень θ = 60° или θ = 300°, потому что уравнение удовлетворяется, если положить θ = 60° или θ = 300°.

  (2) Решение тригонометрических уравнений: Значение неизвестного угла, удовлетворяющее тригонометрическому уравнению, называется его решением.
  Поскольку все тригонометрические отношения периодические по своей природе, обычно тригонометрическое уравнение имеет более одного решения или бесконечное число решений. Есть в основном три типа решений:

  1. Частное решение: Конкретное значение неизвестного угла, удовлетворяющее уравнению.
  2. Основное решение: Наименьшее численное значение неизвестного угла, удовлетворяющего уравнению (численно наименьшее частное решение).
  3. Общее решение: Полный набор значений неизвестного угла, удовлетворяющих уравнению. Он содержит все частные решения, а также главные решения.

  Тригонометрические уравнения с их общим решением

  Тригонометрическое уравнение	Общее решение
  sin θ = 0	θ = nπ
  cos θ = 0	θ = nπ + π/2
  0 тангенс θ = nπ
  sin θ = 1	θ = 2nπ + π/2
  cos θ = 1	θ = 2nπ
  sin θ = sin α	θ = n 056 α
  кос θ = cos α	θ = 2nπ ± α
  тангенс θ = тангенс α	θ = nπ ± α
  sin 2 θ = sin 2 α	θ = nπ ± α
  tan 2 α 5 tan 5 900 = tan	θ = nπ ± α
  cos 2 θ = cos 2 α	θ = nπ ± α
  sin θ = sin α cos θ = cos α	θ = nπ 9010 + α 9001 11 sin θ = sin α тангенс θ = тангенс α	θ = nπ + α
  тангенс θ = тангенс α cos θ = cos α	θ = nπ + α

  Общее решение вида a cos θ  +  b sin θ  = c

  Метод нахождения главного значения ½ , удовлетворяющее уравнению .

  
  Поскольку sin θ отрицательный, θ будет находиться в квадранте 3   или 4  . Мы можем подойти к 3-му или 4-му квадранту с двух сторон. Если мы возьмем направление против часовой стрелки, числовое значение угла будет больше, чем π. Если мы приблизимся к нему по часовой стрелке, угол будет численно меньше π. В качестве главного значения мы должны взять численно наименьший угол. Итак, по главному значению.
  (1) Если угол находится в 1-м или 2-м квадранте, мы должны выбрать направление против часовой стрелки, а если угол находится в квадранте 3 ^rd или 4 ^th , мы должны выбрать направление по часовой стрелке.
  (2) Главное значение никогда не бывает численно больше π.
  (3) Главное значение всегда лежит в первом круге (т. е. в первом вращении). По приведенным выше критериям θ будет равно −π/6 или −5π/6. Между этими двумя −π/6 имеет наименьшее числовое значение. Следовательно, −π/6 является главным значением θ, удовлетворяющим уравнению sin θ = −½.
  Исходя из приведенного выше, метод нахождения главного значения можно резюмировать следующим образом:
  1. Сначала начертите тригонометрический круг и отметьте квадрант, в котором может лежать угол.
  2. Выберите направление против часовой стрелки для квадрантов 1 ^st и 2 ^nd и выберите направление по часовой стрелке для квадрантов 3 ^rd  и 4 ^th .
  3. Найдите угол первого поворота.
  4. Выберите угол с наименьшим численным значением. Найденный таким образом угол будет главным значением.
  5. В случае, если два угла, один с положительным знаком, а другой с отрицательным знаком, соответствуют наименьшему в числовом отношении углу, то в качестве главного значения принято выбирать угол с положительным знаком.

  Задачи на тригонометрические уравнения с решениями

  1.
  
  Решение:
  
  2.
  
  
  Решение 6:6 369 3.

  No related posts.