Как решать алгебраические неравенства первой степени
- Альфашкола
- Статьи
- Как решать алгебраические неравенства первой степени
Неравенства бывают трансцендентные и алгебраические, последние делятся на неравенства первой, второй и т.д. степени (в зависимости от степени неизвестной, входящей в неравенство) и иррациональные. Рассмотрим методы решения неравенств первой степени с одним неизвестным вида ах*в, где * — один из знаков «больше» >, «меньше» <, «больше равно» >=, «меньше равно» <=.
1. Решением одного неравенства будет х*в/a, при a>0
Если неравенство имеет вид ах+в*сх+р, а не равно с, его преобразуем к уже рассмотреному неравенству и решением будет х*(р-в)/(а-с).
Если а равно с просто имеем либо правильное либо неправильное числовое неравенство.
2. Решение неравенств первой степени с одним неизвестным вида ах+в*р при а не равном нулю состоит из двух этапов:
- число b нужно перенести в правую часть неравенства, изменив знак на противоположный, что позволит перейти к равносильному неравенству;
- разделить обе части равносильного неравенства на число a. В таком случае при положительном a знак неравенства сохранится, при отрицательном a знак неравенства меняется на противоположный. В итоге получают неравенство, которое равносильно исходному неравенству первой степени.
3. Системы неравенств первой степени. Для их решения необходимо каждое неравенство решить в отдельности и найти пересечение решений. Это пересечение или сопоставление либо дает решение системы, либо свидетельствует о том, что система не имеет решений.
Примеры
1.
Решить неравество 5х>20. Имеем х>20/5 или х>4.
2. Система неравенств
5х>20
4х<40
Решением первого неравенства будет открытый интервал х>4. Решением второго неравенства будет тоже открытый интервал х<10. Пересечением этих интервалов будет интервал 4<x<10.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Светлана Валентиновна Емец
Репетитор по математике
Стаж (лет)
Образование:
Государственное образовательное учреждение высшего профессионального образования «Самарский государственный педагогический университет»
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Камо Аркадьевич Филипосян
Репетитор по математике
Стаж (лет)
Образование:
Самаркандский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Ольга Олеговна Деева
Репетитор по математике
Стаж (лет)
Образование:
Туркменский государственный университет им.
Махтумкули
Проведенных занятий:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Репетитор по алгебре
- Подготовка к ЕГЭ по математике (профильный уровень)
- Репетитор по русскому языку для подготовки к ОГЭ
- Репетитор по грамматике русского языка
- Репетитор по грамматике английского языка
- Репетитор по английскому для взрослых
- ВПР по математике
- Репетитор для подготовки к ОГЭ по обществознанию
- Репетитор по географии для подготовки к ЕГЭ
- Репетитор по информатике для подготовки к ОГЭ
Похожие статьи
- Пропорция в математике
- Декартова прямоугольная система координат, координаты точек
- Свойства скалярного произведения
- Как быстро умножить число на 2,5
- Множество целых чисел
- ЕГЭ по математике, профильный уровень.
Иррациональные неравенства - Задачи на движение по прямой (вариант 1)
- Самые необычные животные на планете
Иррациональные неравенстваНажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Как решить логарифмическое неравенство
Логарифмическое неравенство может встретиться вам в 13 задании ЕГЭ по математике. При решении логарифмического неравенства важно правильно определить область допустимых значений (ОДЗ). Как же решить логарифмическое неравенство? Давайте разберем основные правила.
- Как найти ОДЗ (область допустимых значений) логарифмического неравенства
- Решение логарифмического неравенства с основанием больше 1
- Решение логарифмического неравенства с основанием от 0 до 1
- Решение логарифмического неравенства с переменным основанием: классический подход и метод рационализации
- Видео урок: решение сложного логарифмического неравенства
Простейшее логарифмическое неравенство можно записать в виде:знак можно заменить на <, ≤ или ≥.
В логарифмическом неравенстве вначале решения нам важно определить область допустимых значений (ОДЗ).Далее мы смотрим на основание логарифма – a. Напомним, что основание логарифма должно быть положительным, и не должно равняться единице.
Если у логарифма в неравенстве а > 1, то знак неравенства не меняется.
Если у логарифма в неравенстве 0 < а < 1, то знак неравенства меняется на противоположный.
Рассмотрим, как это работает на практике.
Вначале определяем ОДЗ: 2х + 4 > 0
Решаем это простейшее неравенство и получаем х > -2.
Таким образом область допустимых значений данного неравенства х > -2.
Далее решаем непосредственно логарифмическое неравенство. Так как основание логарифмов (основание = 2) в неравенстве больше единицы, знак неравенства сохраняется:Так как логарифмы в неравенстве имеют одинаковое основание, то мы их можем просто отбросить и решить неравенство вида
Теперь вспоминаем про нашу ОДЗ и определяем окончательный ответ.
Отметим полученные значения на числовой оси:
Теперь разберем то же самое неравенство, только основание логарифма будет равно ½. Таким образом, получим:
Определяем ОДЗ, как и в прошлом примере, х > -2.
Далее смотрим на основание логарифма. В данном случае основание равно ½, т.е. находится в области от 0 < а < 1. В этом случае знак исходного неравенства меняется на противоположный. Получим:
Решаем полученное неравенство. Так как основания у логарифмов в обеих частях равны, то их можно отбросить, в результате чего получим:Вспоминаем про ОДЗ и определяем окончательный ответ.Отметим полученные точки на числовой оси:Таким образом, решением нашего неравенства является:
Такие неравенства являются простыми, так как основания логарифмов, которые присутствовали в наших неравенствах, были четко определены.
А что делать, если основание логарифма, который присутствует в неравенстве, содержит Х? То есть нельзя четко сказать а > 1 или 0 < а < 1.
Такое логарифмическое неравенство называется логарифмическим неравенством с переменным основанием. Решить его можно двумя способами – с помощью определения логарифма с переменным основанием и методом рационализации.
Давайте рассмотрим оба способа. И для наглядности решим одно логарифмическое неравенство двумя этими способами.
Итак, мы имеем неравенство
Решение логарифмического неравенства с переменным основанием: классический подходКак правило, в школе учат решать логарифмические неравенства с переменным основанием только с помощью определения логарифма, поэтому-то его и назвали классическим подходом.
Выше мы говорили о том, что при решении неравенств, содержащих логарифмы, необходимо обращать внимание на основание логарифма, которое может быть либо больше единицы, либо меньше единицы, но при этом больше ноля. И в зависимости от этого определяем знак неравенства.
С помощью такого подхода можно решить и логарифмическое неравенство с переменным основанием, то есть с основанием, которое содержит Х, и о котором невозможно сказать больше оно единицы или меньше.
В этом случае нам просто нужно рассмотреть два случая: когда исходное неравенство больше единицы, и когда исходное неравенство меньше единицы, но больше ноля.
Вернемся к нашему примеру.Для начала нам нужно преобразовать данное неравенство в такой вид, где слева и справа будут логарифмы с одинаковым основанием. Для этого вспомним такое свойство логарифмов, как логарифмическая единица:То есть в нашем примере правую часть можно преобразовать следующим образом:Таким образом наше неравенство примет вид:
Теперь нам нужно рассмотреть два случая, когда основание логарифма больше единицы и, когда основание логарифма меньше единицы, но больше нуля. При этом не забываем про область допустимых значений.
Отметим полученные точки на числовой оси:Таким образом, решением исходного неравенства является (-2/3;6) .
Метод рационализации заключается в том, что исходное неравенство видаВместо V может стоять знак: >, <, ≤ или ≥.
Далее неравенство можно переписать в виде:
В этом случае необходимо поставить тот же знак, что и в изначальном неравенстве.
Далее нам необходимо учесть область допустимых значений:
Применим метод рационализации для решения нашего неравенства:Первое, что нам нужно сделать, это привести его к виду
Для этого снова воспользуемся свойством логарифмов – логарифмическая единица:Теперь перепишем неравенство, используя метод рационализации:
Нам необходимо учесть ОДЗ, тогда получим следующую систему:Первое неравенство системы решим методом интервалов:Таким образом, решение первого неравенства -2 < х < 6
Решение второго неравенства: х > -4½
Решение третьего неравенства: х < 7
Решение четвертого неравенства: х ≠ 6
Совместим решения всех неравенств на числовой оси:
На приведенном примере мы разобрали, как решить логарифмическое неравенство двумя способами. Часто решение методом рационализации бывает более коротким, соответственно, на него вы потратите гораздо меньше драгоценного времени, отведенного на ЕГЭ.
Потому рекомендуем потренироваться в решении логарифмических неравенств этим методом, чтобы без затруднения воспользоваться им на ЕГЭ.
Видео урок: решение сложного логарифмического неравенства
В данной статье мы разобрали, как решить логарифмическое неравенство. Еще больше примеров решения логарифмических неравенств вы можете найти
Math Scene — Неравенства — Урок 1
Math Scene — Неравенства — Урок 1 — Решение неравенств 2008 Расмус Эхф | Печать |
Решение неравенства включает в себя нахождение числа или интервал действительных чисел, которые удовлетворяют заданному условию. Это условие задается с помощью любого из следующих символов неравенства:
> означает больше, чем
< означает меньше, чем
означает больше или равно
означает
меньше или равно.
Утверждение 3 > 2 (три больше двух) является верное утверждение. Если у вас есть проблемы с запоминанием, в какую сторону поворачивается знак, тогда постарайтесь запомнить, что стрелка указывает на меньшее число. Утверждение 2 < 3 (два меньше трех) также истинный.
Когда мы говорим, что х > 2, мы имеем в виду, что х — действительное число. больше двух. Используя обозначение Set, мы пишем {x R | х > 2} чтобы подчеркнуть тот факт, что x — любое действительное число.
Обозначение х 2 означает, что x любое действительное число, большее или равное 2. Разница в том, что теперь мы включить 2.
Мы часто можем использовать одни и те же методы для решения неравенств
которые мы используем для решения уравнений. Мы
можно, например, прибавить или вычесть одно и то же число с обеих сторон
неравенство так же, как и с уравнениями. Мы также можем умножать и делить
обе стороны одним и тем же числом, но только если мы используем положительные числа.
Пример 1
Решите неравенство:
Мы умножьте каждое слагаемое на 4, чтобы избавиться от дробей. Мы затем вычтите 4 из обеих частей неравенства. |
В этом примере показано неравенство, которое можно решается точно так же, как если бы это было уравнение. К сожалению, это не всегда так. Исключения возникают, когда нам нужно умножить или разделить на отрицательные числа. Посмотрите на следующую диаграмму:
Мы можем видеть из вещественная числовая линия, что a < b. Если мы умножим на −1, мы получим −а < −b. Если мы посмотрим на числовую прямую, то увидим, что это уже неверно, так как −a находится справа от −b и, следовательно, −a > −b .
Это приводит к
правило, что если мы умножаем на отрицательное число, мы должны превратить неравенство
знак раунда.
Пример 2
2 − х > 1 −x > −1 х < 1 | Вычесть 2 с обеих сторон. Сейчас умножьте на -1, не забывая перевернуть знак неравенства круглый. |
При решении уравнений мы можем поворачивать обе стороны уравнения перевернуть так, чтобы числитель и знаменатель изменились места. (например, a/x=b/c можно записать как x/a = c/b). Это больше невозможно при работе с неравенствами
Если a < b, то 1/a > 1/b, потому что когда мы делим на большее число, результат становится меньше. Мы можем сделать это однако до тех пор, пока мы не забудем повернуть знак неравенства округляется.
Пример 3
Мы
поверните дробь по обе стороны от знака неравенства по кругу и в обратном порядке
знак неравенства. Наконец мы умножаем на 2. |
Мы также можем решить этот пример следующим образом:
Есть и другие расчеты, которые мы должны остерегаться при решении неравенств. Например, мы не можем возвести в квадрат обе стороны неравенство, если одно из слагаемых отрицательно. Это то же самое, что умножить на отрицательное число. Мы должны быть очень уверены, что функции, над которыми мы работаем, с увеличиваются на интервале, с которым мы работаем, прежде чем мы сможем лечить неравенства так же, как уравнения.
Но что имеется в виду, когда мы говорим, что функция увеличивается? Ниже приведены три графика, которые мы собираемся использовать для решения неравенства.
Функции f(x)
= x 3 , g(x) = ln x и h(x)
= e 90 135 x 90 136 являются
все возрастающие. Это означает, что с увеличением x функция возрастает. Когда мы
двигаться по графику слева направо график идет вверх.
Как
мы уже видели, что функция g(x) = ln x
определяется только для положительных значений x.
Пример 4
Решить неравенство |
Здесь нет проблем, просто поднимаем оба сторон в степени 3 и получить
х 8
Пример 5
Решить неравенство ln (2x — 1) < ln 3.
Опять же, здесь нет никаких проблем. Мы поднимаем оба сторон к степени e, чтобы избавиться от ln − функции. Затем мы получаем:
2x -1 > 0 | 2x − 1 < 3 |
2x > 1 х > 1 / 2 | 2x < 4 х < 2 |
1 / 2 < х < 2
Пример 6
Решите неравенство e x > e −x .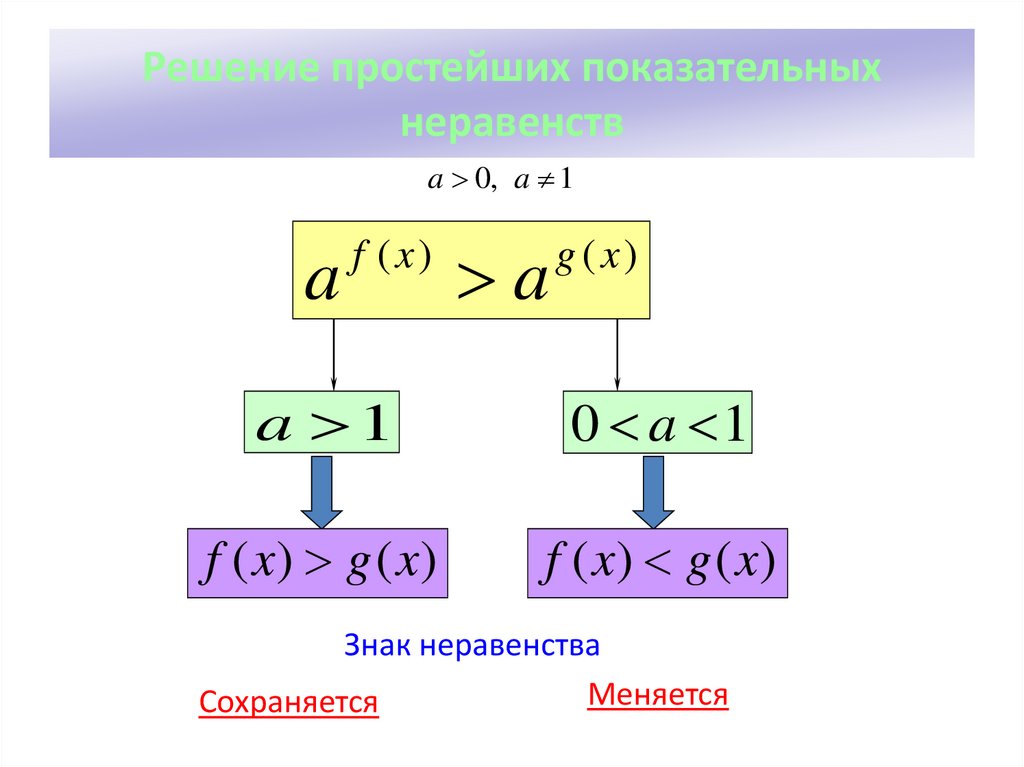
e x > e −x (e x ) 2 > 1 e 2x > 1 2x > 0 х > 0 | Умножить с обеих сторон ex , чтобы избавиться от e −x или 1/e x справа сторона. Тогда поместите ln в обе части уравнения, чтобы сократить e. |
Попробуйте пройти тест 1 по неравенствам.
Не забудьте использовать контрольный список для следить за своей работой.
Tinder: приложение для знакомств. Встретиться. Чат
На сегодняшний день Tinder® является лучшим бесплатным приложением для знакомств, и лучшим местом для знакомства с более чем 70 миллиардами совпадений.
Вы ищете настоящую любовь? Открытые отношения? Вы хотите пойти туда и найти дату, или вы просто хотите подружиться и поболтать? С Tinder вы можете встречаться с местными жителями повсюду и получать максимум удовольствия от свиданий:
Независимо от того, натурал вы, гей, бисексуал или кто-то другой, Tinder позволяет вам быть тем, кто вы есть, и найти того, кого вы хотите.
Поделитесь своими интересами и узнайте больше о своих совпадениях, чтобы начать разговор и зажечь искры.
Фото Проверенные профили: Потому что единственные сюрпризы, которые мы хотим, это цветы на первом свидании
Видеочат: Проверьте свою химию онлайн-знакомств и познакомьтесь с новыми людьми из дома!
Куда-то едете? Познакомьтесь с местными жителями и присоединитесь к сообществу людей со всего мира. Свидание в Нью-Йорке, знакомство с новыми друзьями в Майами или свидание в Лондоне: куда бы вы ни пошли, мы будем там.
Некоторые люди называют нас своим «самым надежным приложением для знакомств», некоторые люди называют нас «самым популярным в мире бесплатным сайтом знакомств» , но вы можете просто позвонить нам, когда захотите встретиться с людьми в вашем районе.
Матч, чат и свидание. Это наша мантра.
Находить новых людей в Tinder® легко и весело. Выделите свой профиль своими лучшими фотографиями и немного о себе, чтобы повысить свой потенциал поиска партнеров. Используйте функцию Swipe Right™, чтобы поставить лайк кому-то, используйте функцию Swipe Left™, чтобы отказаться. Если кто-то любит вас в ответ, это совпадение! И никакого давления: с нашей функцией двойного согласия интерес должен быть взаимным, чтобы он соответствовал. Сколько приложений для знакомств могут сказать такое?
Пока вы здесь, поднимите тост за жизнь Gold и наслаждайтесь некоторыми премиальными функциями Tinder с нашей подпиской Tinder Gold™. чувства к какому количеству новых людей, как вы хотите
Перемотать назад, чтобы вы могли отменить свой последний лайк или нет
Используйте Passport, чтобы отправиться в любую точку мира, чтобы найти людей в Интернете за пределами вашего почтового индекса минут, чтобы привлечь больше внимания
5 суперлайков доступно в неделю, потому что иногда вам очень-очень нравится кто-то
Ищете доступ ко всем премиум-функциям Tinder? Присоединяйтесь к Tinder Platinum™, чтобы ваши лайки располагались в приоритете с потенциальными совпадениями, чтобы иметь возможность отправлять сообщения перед сопоставлением и многое другое.
Есть плюс для тех, кто не готов завязать отношения с Gold или Platinum. С Tinder Plus® вы разблокируете такие функции, как неограниченные лайки, неограниченные перемотки и паспорт.
Так чего же ты ждешь? Загрузите лучшее бесплатное приложение для знакомств уже сегодня! Неважно, хотите ли вы завести друзей, познакомиться с новыми людьми или найти свою идеальную пару, Tinder — это место, где каждый может найти именно то, что ищет. — и тебе пора уже появиться.
—————————————————
Если вы решите приобрести Tinder Plus®, Tinder Gold ™ или Tinder Platinum™ будет снята с вашей учетной записи Google Play, и с вашей учетной записи будет снята плата за продление в течение 24 часов до окончания текущего периода. Автообновление можно отключить в любое время, зайдя в настройки в Play Store после покупки. Отмена текущей подписки не допускается в течение активного периода подписки. Если вы не хотите покупать Tinder Plus®, Tinder Gold™ или Tinder Platinum™, вы можете просто продолжать использовать Tinder бесплатно.