| ||||||||||||||||||||||||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
|||||||||||||||||||||||||||||||||
какова вероятность Задача 055tv Партия изготовленных деталей проверялась двумя контроллерами. Первый контроллер проверил 65% всех деталей, второй — 35%. Вероятность допустить ошибку при проверке для первого контроллера равна 0,04, для второго — 0,08.
Задача 057tv Есть два ящика. В первом ящике размещается 6 стандартных и 4 бракованных детали, второй ящик — пустой. Из первого ящика наугад берут 3 детали и кладут во второй. Какова вероятность взять из второго ящика одну стандартную деталь?
Задача 061tv Трое рабочих изготовляют однотипные детали. За смену первый рабочий изготовил 200 деталей, второй — в 5 раз меньше, чем первый, а третий — в 2 раза больше, чем второй. Среди деталей, изготовленных первым рабочим, 0,5% бракованных, вторым — 0,8%, третьим — 0,2% бракованных. Все изготовленные детали размещают в одну емкость. Взятая наугад одна деталь оказалась бракованной. Какая вероятность того, что деталь была изготовлена первым или третьим рабочим.
Задача 064tv Прибор может работать на протяжении смены в двух режимах. Первый режим наблюдается в 75% случаях, второй — в 25%. Вероятность выхода прибора из строя в первом режиме равняется 0,08; на втором — 0,1. На протяжении смены прибор вышел из строя. Какая вероятность того, что он работал в втором режиме.
Задача 067tv В первом ящике находится 7 стандартных и 3 бракованных детали, во втором — 4 стандартных и 6 бракованных. Из каждого ящика наугад берут по одной детали, а потом наугад из них берут одну деталь. Какая вероятность того, что эта деталь окажется стандартной?
Задача 937tv Случайно встреченное лицо может оказаться, с вероятностью p = 0,2 брюнетом, с p = 0,3 — блондином, с p = 0,4 — шатеном и с p = 0,1 — рыжим. Какова вероятность того, что среди трех случайно встреченных лиц: а) не менее двух брюнетов; б) один блондин и два шатена; в) хотя бы один рыжий.
Задача 939tv В квартире четыре электролампочки. Для каждой лампочки вероятность того, что она останется исправной в течении года, равна 5/6. Какова вероятность того, что в течении года придется заменить не менее половины лампочек?
Задача 986tv В квартире четыре электролампочки. Для каждой лампочки вероятность того, что она останется исправной в течении года, равна 5/6. Какова вероятность того, что в течении года прийдется заменить не менее половины лампочек?
Задача 00tv3 В приемнике имеется 6 радиоламп одного типа и 8 радиоламп другого типа. Вероятность выхода лампы из строя в течении времени Т равна 0,002 для лампы первого типа и 0,004 для лампы второго типа. Какова вероятность того, что в течении этого времени выйдет из стоя хотя бы одна лампа?
Задача 00tv5 Вероятность для изделия удовлетворять стандарту равна 0,96.
Задача 02tv3 В группе 10 мальчиков и 5 девочек, среди которых выбирают двух для участия в конференции. Какая вероятность того, что: 1) выберут одного мальчика и одну девочку; 2) выберут двух мальчиков?
Задача 03tv0 Среди 30 деталей 8 бракованных. Какова вероятность того, что взятые наугад 5 деталей будут без дефекта?
Задача 03tv5 В академической группе 26 студентов, из низ 18 девочек и 8 мальчиков. Группу наугад делят на две равные подгруппы. Какова вероятность того, что в каждой подгруппе будет по 4 мальчика?
Задача 04tv4 Победителями конкурса стали 15 женщин и 10 мужчин.
Задача 05tv6 С одного выстрела можно попасть в цель с вероятностью 0,8. Какова вероятность попасть в цель хотя бы один раз из двух выстрелов?
Задача 06tv2 Три опытных хирурга выполняют сложные операции. Вероятность отрицательного результата операции у первого составляет 0,05, в второго – 0,09, а в третьего — 0,1. Больной наугад избирает врача. Какая вероятность положительного результата?
Задача 07tv3 Хлебопекарня выпекает 70 % продукции из муки высшего и 25 % — из муки первого сорта. Какая вероятность того, что среди двух наугад избранных изделий будет: а) только одно из муки высшего сорта? б) два одного и того же сорта?
Задача 08tv4 Тираж популярной газеты печатается в двух типографиях.
Задача 09tv9 Часы изготовляют на трех заводах. Первый изготовляет 40% продукции, второй — 45% и третий — 15%. Из часов первого завода точно показывает время 95%, второго завода — 85%, третьего — 80%. Часы поступают в продажу в один магазин. Какая вероятность того, что купленные наугад часы будут точно показывать время?
Задача 10tv2 На сборку прибора поступают детали из двух бункеров: 75% — из первого и 25% — из второго. При этом детали из первого бункера в 5%, а из второго в 8% случаев имеют погрешности в размерах. Наугад взятая деталь, которая поступила на место собирания прибора, оказалась с погрешностью.
Задача 11tv0 Три бригады изготовляют соответственно 50%, 40%, 10% продукции. Брак в их работе составляет 1%, 2%, 4%. Какая вероятность того, что взятое наугад изделие будет бракованным? Какая вероятность, что бракованную деталь изготовила первая бригада?
Задача 11tv3 Вероятность того, что студент сдаст зачет с первого раза, равняется 0,9. Какая вероятность того, что среди 7 студентов зачет сдадут: а) 5 студентов? б) не меньшее 5 студентов?
Задача 11tv6 В агентство недвижимости обращаются по поводу аренды и продажи квартир в соотношении 7:5. Какова вероятность того, что среди 6 произвольно выбранных заявок будет: а) четыре по поводу продажи квартир? б) не менее четырех по поводу аренды квартир?
Задача 13tv3 Фирма не имеет в среднем 5 % деталей, представленных в каталоге.
Задача 14tv1 Локальная сеть состоит из 100 компьютеров. Вероятность возникновения сбоев в работе в течении суток для каждого из них равна 0,002. Какая вероятность того, что в течении суток сбои возникнут не более чем в 3 компьютерах?
Задача 14tv4 Энергетическая компания обслуживает 800 потребителей электроэнергии. Перебои в подачи энергии на протяжении суток возникают с вероятностью 0,005. Какая вероятность того, что на протяжении суток поступит 10 сообщений о перебоях?
Задача 14tv9 Игральный кубик подбрасывают 800 раз. Какая вероятность того, количество очков, кратное трем, появится 267 раз?
Задача 52tv2 Вероятность сдачи экзамена студентом на «5» равна 0,3; на «4» равна 0,45; на «2» — 0,1; не явиться на экзамен — 0,05.
Задача 52tv6 В группе из 30 учеников на контрольной работе 6 учеников получили оценку «отлично», 10 — «хорошо», 9 — «удовлетворительно». Какова вероятность того, что все три ученика, вызванные к доске, имеют удовлетворительные оценки по контрольной работе?
Задача 55tv9 Какова вероятность, что в первый раз будет составлен слово «РАГУ» из букв слова «ФИГУРА»?
Задача 56tv3 Из полного набора костяшек домино взяли одну за другой две косточки. Какова вероятность того, что вторую косточку можно приставить к первой, если первым был «дубль».
Задача 56tv8 Из 10 студентов, которые пришли сдавать экзамен по теории вероятностей и взяли билеты, Иванов и Петров знают 20 билетов из 30.
Задача 60tv4 Из полного набора костяшек домино взяли одну за другой две кости. Какова вероятность того, что вторую кость можно приставить к первой.
Задача 61tv4 При проверке 10000 пар мужских носков обнаружено 200 пар с дефектами. Какая вероятность того, что в партии из 300 пар число дефектных носков будет не более 5?
| ||||||||||||||||||||||||||||||||||
7.Элементы комбинаторики.
В
теории вероятностей часто используют
размещения, перестановки и сочетания. Если дано множество
,
торазмещением
(сочетанием) из
элементов
поназывается
любое упорядоченное (неупорядоченное)
подмножествоэлементов
множества.
Приразмещение
называетсяперестановкой из
элементов.Пусть,
например, дано множество.
Размещениями из трех элементов этого
множества по два являются,,,,,;
сочетаниями —,,.Два
сочетания различаются хотя бы одним
элементом, а размещения различаются
либо самими элементами, либо порядком
их следования. Число сочетаний изэлементов
повычисляется
по формуле
Если дано множество
,
торазмещением
(сочетанием) из
элементов
поназывается
любое упорядоченное (неупорядоченное)
подмножествоэлементов
множества.
Приразмещение
называетсяперестановкой из
элементов.Пусть,
например, дано множество.
Размещениями из трех элементов этого
множества по два являются,,,,,;
сочетаниями —,,.Два
сочетания различаются хотя бы одним
элементом, а размещения различаются
либо самими элементами, либо порядком
их следования. Число сочетаний изэлементов
повычисляется
по формуле
где
есть
число размещений из
элементов
по;—
число перестановок изэлементов.Пример
2. В партии из 10 деталей имеется 7 стандартных.
Найти вероятность того, что среди взятых
наудачу 6 деталей ровно 4 стандартных.Решение. Общее число возможных исходов испытания
равно числу способов, которыми можно
извлечь 6 деталей из 10, т. е. равно
—
числу сочетаний из 10 элементов по 6.
Число исходов, благоприятствующих
событию(среди
6 взятых деталей ровно 4 стандартных),
определяем так: 4 стандартные детали
можно взять из 7 стандартных деталейспособами;
при этом остальныедетали
должны быть нестандартными; взять же
2 нестандартные детали изнестандартных
деталей можноспособами. Следовательно, число благоприятствующих
исходов равно.
Исходная вероятность равна отношению
числа исходов, благоприятствующих
событию, к числу всех исходов:
Следовательно, число благоприятствующих
исходов равно.
Исходная вероятность равна отношению
числа исходов, благоприятствующих
событию, к числу всех исходов:
Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не взаимосвязанные, то остановки этих линий являются независимыми событиями.
Пример 3. Монета брошена два раза. Вероятность появления «герба» в первом испытании (событие ) не зависит от появления или не появления «герба» во втором испытании (событие ). В свою очередь, вероятность появления «герба» во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
События
называются зависимыми, если одно из
них влияет на вероятность появления
другого. Например, две производственные
установки связаны единым технологическим
циклом. Тогда вероятность выхода из
строя одной из них зависит от того, в
каком состоянии находится другая.
Вероятность одного события , вычисленная
в предположении осуществления другого
события , называется условной вероятностью
события и обозначается .
Например, две производственные
установки связаны единым технологическим
циклом. Тогда вероятность выхода из
строя одной из них зависит от того, в
каком состоянии находится другая.
Вероятность одного события , вычисленная
в предположении осуществления другого
события , называется условной вероятностью
события и обозначается .
Условие независимости события от события записывают в виде , а условие его зависимости — в виде . Рассмотрим пример вычисления условной вероятности события.
Пример 4. В ящике находятся 5 резцов: два изношенных и три новых. Производится два последовательных извлечения резцов. Определить условную вероятность появления изношенного резца при втором извлечении при условии, что извлеченный в первый раз резец в ящик не возвращается.
Решение.
Обозначим извлечение изношенного
резца в первом случае, а — извлечение
нового. Тогда . Поскольку извлеченный
резец в ящик не возвращается, то
изменяется соотношение между количествами
изношенных и новых резцов. Следовательно,
вероятность извлечения изношенного
резца во втором случае зависит от того,
какое событие осуществилось перед
этим.
Следовательно,
вероятность извлечения изношенного
резца во втором случае зависит от того,
какое событие осуществилось перед
этим.
Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятности этого события могут быть такими:
| Что такое меры распространения? Показатели разброса описывают, насколько похожи или различаются наборы наблюдаемых значений для конкретной переменной (элемента данных). Показатели разброса включают диапазон, квартили и межквартильный диапазон, дисперсию и стандартное отклонение. Когда можно измерить спред? Разброс значений может быть измерен для количественных данных, поскольку переменные являются числовыми и могут быть расположены в логическом порядке с нижним конечным значением и верхним конечным значением. Почему мы измеряем спред? Обобщение набора данных может помочь нам понять данные, особенно когда набор данных большой.
Что говорит нам каждый показатель распространения? Диапазон — это разница между наименьшим и наибольшим значениями в наборе данных.
упорядоченный набор данных на четыре равные части, и относятся к значениям точки между кварталами. Набор данных также можно разделить на квинтили (пять равных частей) или децили (десять равных частей).
Нижний квартиль (Q1) — это точка между 25% самых низких значений и 75% самых высоких значений.  Его еще называют 9.0005 25-й процентиль . Его еще называют 9.0005 25-й процентиль .Второй квартиль (Q2) — это середина набора данных. Его также называют 50-м процентилем или медианой . Верхний квартиль (Q3) — это точка между самыми низкими 75% и самыми высокими 25% значений. Его также называют 75-й процентиль .
| 100040 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 values - значение квартиля:
values - значение квартиля: Q1 = (3+4) / 2 = 3,5
Q2 = (6+6) / 2 = 6
Q3 = (8+9) / 2 = 8,5
Межквартильный диапазон | ||||||||||||||
25% of values | Q1 | 25% of values | Q2 | 25% of values | Q3 | 25% of Значения | ||||||||
Расчет межквартильного диапазона IQR для набора данных A IS = 2 IQR = Q3 — Q1 = 7 — 5 .  0006 0006 = 2 IQR для набора данных B IS = 5 |
Вариант и стандартный Deabiat As Deabiat разброса данных вокруг среднего. Они обобщают, насколько близко каждое наблюдаемое значение данных к среднему значению.
В наборах данных с небольшим разбросом все значения очень близки к среднему, что приводит к небольшой дисперсии и стандартному отклонению. Там, где набор данных более разбросан, значения разбросаны дальше от среднего, что приводит к большей дисперсии и стандартному отклонению.
Чем меньше дисперсия и стандартное отклонение, тем больше показатель среднего значения для всего набора данных. Следовательно, если все значения набора данных одинаковы, стандартное отклонение и дисперсия равны нулю.
Стандартное отклонение нормального распределения позволяет вычислить доверительные интервалы. При нормальном распределении около 68 % значений находятся в пределах одного стандартного отклонения по обе стороны от среднего значения и около 95 % оценок находятся в пределах двух стандартных отклонений от среднего значения.
The population Variance σ 2 (pronounced sigma squared ) of a discrete set of numbers is expressed by the following formula:
where:
X i представляет единицу ith , начиная с первого наблюдения и до последней
μ представляет среднюю совокупность
N представляет количество единиц в совокупности
Дисперсия образца S 2 (произносится S квадрат ) выражается немного другой формулой:
, где:
x I Представляющий ITH. начиная с первого наблюдения до последнего
x̅ представляет среднее значение выборки
n представляет количество единиц в выборке
Стандартное отклонение представляет собой квадратный корень из дисперсии. Стандартное отклонение для населения представлено σ , а стандартное отклонение для выборки представлено с.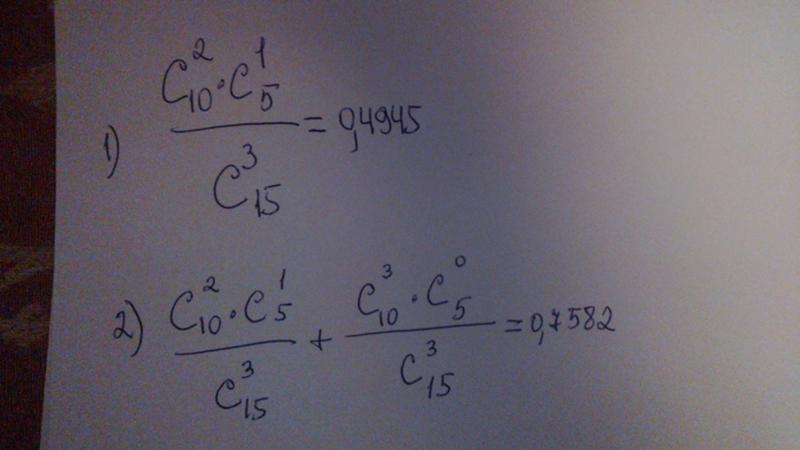
Calculating the Population Variance σ 2 and Standard Deviation σ | |||||
Dataset A Calculate the population mean ( μ ) набора данных A.(4 + 5 + 5 + 5 + 6 + 6 + 6 + 6 + 7 + 7 + 7 + 8) / 12 среднее ( μ ) = 6 Рассчитать отклонение отдельных значений от среднего путем вычитания среднего из каждого значения в наборе данных = -2, -1, -1, -1, 0, 0, 0, 0, 1, 1, 1, 2 Возведение в квадрат каждого отдельного значения отклонения = 4, 1, 1, 1, 0, 0, 0, 0, 1,1,1, 4 Вычисление среднего квадрата значений отклонения = (4 + 1 +1 +1 + 0 + 0 + 0 + 0 +1 +1 +1 + 4) / 12 Дисперсия σ 2 = 1,17 Рассчитайте квадратный корень дисперсии Стандартное отклонение σ = 1,08 | DATASET B | . Рассчитайте отклонение отдельных значений от среднее путем вычитания среднего значения из каждого значения в наборе данных Возведение в квадрат каждого отдельного значения отклонения Вычислить среднее значение квадрата отклонения Дисперсия σ 2 = 9,17 Вычислить квадратный корень из дисперсии Большая дисперсия и стандартное отклонение в наборе данных B Далее демонстрирует, что набор данных B больше диспергирован, чем набор данных A. . Внешние ссылки: КодыТрехгодичное издание Title 24, 2022 г.Кодекс строительных стандартов Калифорнии 2022 года (Cal. Code Regs., Title 24) будет опубликован 1 июля 2022 года и вступит в силу 1 января 2023 года. Сводная информация об изменениях кодекса в этом издании доступна в разделе «Ресурсы». вкладка веб-сайта CBSC. Приведенные ниже активные ссылки ведут на веб-сайт каждого издателя. Пожалуйста, свяжитесь с CBSC по адресу [email protected], если у вас возникли трудности с доступом к кодам. ЧАСТЬ 1 – АДМИНИСТРАТИВНЫЙ НОДЕКС КАЛИФОРНИИ
ЧАСТЬ 2 – СТРОИТЕЛЬНЫЙ НОДЕКС КАЛИФОРНИИ – Тома 1 и 2
Errata — Part 2, Volume 1 (несущественные исправления) Действует с 1 января 2023 г.
ЧАСТЬ 2.5 – КОДЕКС ПРОЖИВАНИЯ В КАЛИФОРНИИ
ЧАСТЬ 3. ЭЛЕКТРИЧЕСКИЙ КОД КАЛИФОРНИИ ПРИМЕЧАНИЕ . NFPA требует создания учетной записи пользователя для просмотра бесплатных онлайн-ресурсов.
ЧАСТЬ 4 – МЕХАНИЧЕСКИЙ КОД КАЛИФОРНИИ
ЧАСТЬ 5 – КАЛИФОРНСКИЙ САНТЕХНИЧЕСКИЙ НОРМ
Часть 6 — Калифорнийский энергетический код
Часть 7 — вакантный — ранее калифорнийский код строительства эф.
PART 9 – CALIFORNIA FIRE CODE
PART 10* – CALIFORNIA EXISTING BUILDING CODE
PART 11 – КОД КАЛИФОРНИЙСКИХ ЗЕЛЕНЫХ СТРОИТЕЛЬНЫХ СТАНДАРТОВ , также известный как CALGreen
ЧАСТЬ 12* – ССЫЛОЧНЫЕ СТАНДАРТЫ КАЛИФОРНИИ, КОД
*Печатные версии частей 8, 10 и 12 находятся в общей папке с частью 10. Трехгодичное издание Title 24, 2019 г. Калифорнийский кодекс строительных стандартов 2019 г. (Cal. Code Regs., Title 24) был опубликован 1 июля 2019 г. и вступил в силу 1 января 2020 г. Информационный бюллетень 19-04 и Информационный бюллетень 19-05 предоставляют подробную информацию о публикации 2019 года. Приведенные ниже активные ссылки ведут на веб-сайты каждого издателя. Пожалуйста, свяжитесь с CBSC по адресу [email protected], если у вас есть проблемы с доступом к кодам. ЧАСТЬ 1 – АДМИНИСТРАТИВНЫЙ НОДЕКС КАЛИФОРНИИ – включая обновления (HTML) (PDF) Текущая печать — часть 2, том 1 и 2 — включая обновления (HTML) Errata — Part 2, Volume 1 (несущественные исправления) Действует с 1 января 2020 г. Опечатки — часть 2, том 1 (несущественные исправления) Действует с 1 октября 2020 г. Опечатки — часть 2, том 2 (несущественные исправления) Действует с 1 января 2020 г. Опечатки — часть 2, том 2 (несущественные исправления) Действует с 1 октября 2020 г. Часть 2.5 — РЕЗИДЕНЦИАЛЬНЫЙ НОМЕР КАЛИФОРНИИ — включая обновления (HTML) (PDF)
ЧАСТЬ 3– ЭЛЕКТРИЧЕСКИЙ КОДЕКС КАЛИФОРНИИ ПРИМЕЧАНИЕ : NFPA требует создания учетной записи пользователя для просмотра своих бесплатных ресурсов.
ЧАСТЬ 4– МЕХАНИЧЕСКИЙ КОД КАЛИФОРНИИ
ЧАСТЬ 5– САНТЕХНИКА КАЛИФОРНИИ
ЧАСТЬ 6– ЭНЕРГЕТИЧЕСКИЙ КОДЕКС КАЛИФОРНИИ — включая обновления (HTML) (PDF)
Часть 8* — Калифорнийский исторический строительный кодекс — внедрение обновлений (HTML) (PDF)
.
ЧАСТЬ 10* — СУЩЕСТВУЮЩИЕ СТРОИТЕЛЬНЫЕ НОРМЫ КАЛИФОРНИИ — включая обновления (HTML) (PDF)
ЧАСТЬ 11– СТАНДАРТЫ ЗЕЛЕНОГО СТРОИТЕЛЬСТВА КАЛИФОРНИИ, КОД , также именуемый CALGreen — включая обновления (HTML) (PDF)
ЧАСТЬ 12*– ССЫЛОЧНЫЙ КОД СТАНДАРТОВ КАЛИФОРНИИ — включая обновления (HTML) (PDF)
* Печатные версии Частей 8, 10 и 12 находятся в общей папке с Частью 10. Трехгодичное издание Title 24, 2016 г. Кодекс строительных стандартов Калифорнии 2016 г. (Cal. Code Regs., Title 24) был опубликован 1 июля 2016 г. и вступил в силу 1 января 2017 г. Кроме того, промежуточное дополнение было опубликовано 1 января 2017 г. и вступило в силу. от 1 июля 2018 г. Информационные бюллетени 16-01 и 17-06 содержат подробную информацию об изменениях в публикации 2016 года. Приведенные ниже ссылки ведут на веб-сайт издателя. Пожалуйста, свяжитесь с CBSC, если у вас есть проблемы с доступом к кодам. ЧАСТЬ 1 — АДМИНИСТРАТИВНЫЙ НОДЕКС КАЛИФОРНИИ ЧАСТЬ 2 — СТРОИТЕЛЬНЫЙ НОРМ КАЛИФОРНИИ
ЧАСТЬ 2.5 — ЖИЛОЙ КОД КАЛИФОРНИИ
ЧАСТЬ 3 — ЭЛЕКТРИЧЕСКИЙ КОД КАЛИФОРНИИ
ЧАСТЬ 4 — МЕХАНИЧЕСКИЙ КОД КАЛИФОРНИИ
ЧАСТЬ 5 — САНТЕХНИКА КАЛИФОРНИИ
ЧАСТИ 6 — Калифорнийский энергетический код
Часть 7 — вакантный — ранее калифорнийский кодекс строительства лифта (см. Cal. Code. Исторический строительный кодекс
Часть 9 — Калифорнийский пожарный кодекс Часть 10* — Существующий строительный кодекс
Часть 11 — Калифорнийские стандарты Зеленого здания Код также называют Calgreen Часть 12 — . СПОСКАЗ СТАТРЫ. Трехгодичное издание Title 24, 2013 г.Приведенные ниже ссылки ведут на веб-сайт издателя. Пожалуйста, свяжитесь с CBSC, если у вас есть проблемы с доступом к кодам. Часть 1 — Административный кодекс Калифорнии Часть 2 — Строительный кодекс Калифорнии Том 1 части 2 Том 2 части 2 Часть 2.5 — Жилищный кодекс штата Калифорния Часть 3 — Электротехнический кодекс штата Калифорния
Часть 4 — Сантехнические нормы Калифорнии Часть 5 — Сантехнические нормы Калифорнии
| |||




 Предлагается система контроля, при которой вероятность принятия стандартного изделия равна 0,98, а нестандартного 0,05. Какова вероятность того, что качество взятого наудачу изделия будет оценено правильно?
Предлагается система контроля, при которой вероятность принятия стандартного изделия равна 0,98, а нестандартного 0,05. Какова вероятность того, что качество взятого наудачу изделия будет оценено правильно?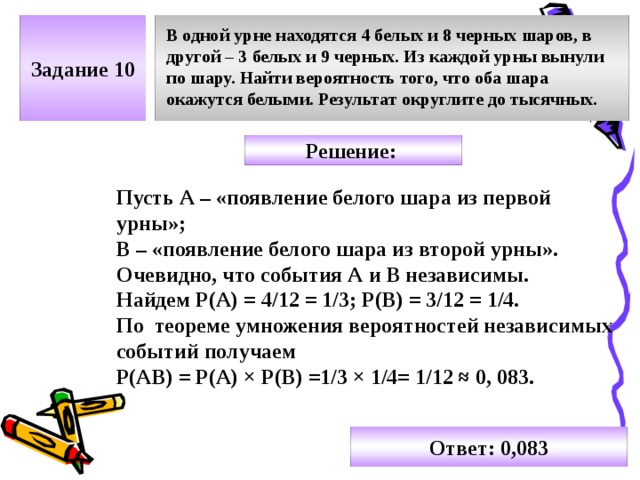
 Мощности двух типографий относятся как 3:4, причем первая дает 3,5% брака, а вторая — 2,5%. Какая вероятность того, что: а) наугад избранный экземпляр газеты будет бракованной? б) бракованный экземпляр газеты напечатан в первой типографии?
Мощности двух типографий относятся как 3:4, причем первая дает 3,5% брака, а вторая — 2,5%. Какая вероятность того, что: а) наугад избранный экземпляр газеты будет бракованной? б) бракованный экземпляр газеты напечатан в первой типографии? Какая вероятность того, что она из второго бункера?
Какая вероятность того, что она из второго бункера? Поступил заказ на 8 деталей. Какая вероятность того, что все они есть в фирме?
Поступил заказ на 8 деталей. Какая вероятность того, что все они есть в фирме? Какова вероятность того, что студент получит положительную оценку?
Какова вероятность того, что студент получит положительную оценку? Сидоров плохо подготовился и успел выучить только 15 билетов, остальные знают все 30 билетов. Экзаменатор вызывает одного из студентов. Какова вероятность того, что студент сдал экзамен, если знание билета гарантирует сдачу экзамена с вероятностью 0,85, а если студент не знает билета, он может сдать экзамен с вероятностью 0,1.
Сидоров плохо подготовился и успел выучить только 15 билетов, остальные знают все 30 билетов. Экзаменатор вызывает одного из студентов. Какова вероятность того, что студент сдал экзамен, если знание билета гарантирует сдачу экзамена с вероятностью 0,85, а если студент не знает билета, он может сдать экзамен с вероятностью 0,1. Как обсуждалось на странице «Показатели центральной тенденции», мода, медиана и среднее суммируют данные в одно значение, которое является типичным или репрезентативным для всех значений в наборе данных, но это только часть «картины», которая суммирует набор данных. Меры разброса суммируют данные таким образом, чтобы показать, насколько разбросаны значения и насколько они отличаются от среднего значения.
Как обсуждалось на странице «Показатели центральной тенденции», мода, медиана и среднее суммируют данные в одно значение, которое является типичным или репрезентативным для всех значений в наборе данных, но это только часть «картины», которая суммирует набор данных. Меры разброса суммируют данные таким образом, чтобы показать, насколько разбросаны значения и насколько они отличаются от среднего значения.


 Набор данных B.
Набор данных B.  com — Калькулятор сводки пяти чисел
com — Калькулятор сводки пяти чисел
 0007 PART 8* – CALIFORNIA HISTORICAL BUILDING CODE
0007 PART 8* – CALIFORNIA HISTORICAL BUILDING CODE 

 Part 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072. (PDF)
Part 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072 9072. (PDF)
 Если вам нужна копия нашей таблицы перекрестных ссылок, которая поможет вам идентифицировать перемещенные разделы кода, отправьте электронное письмо по адресу
Если вам нужна копия нашей таблицы перекрестных ссылок, которая поможет вам идентифицировать перемещенные разделы кода, отправьте электронное письмо по адресу  5 — Включая обновления (HTML)
5 — Включая обновления (HTML)
 находится в конце Строительного кодекса штата Калифорния, часть 2, том 2.
находится в конце Строительного кодекса штата Калифорния, часть 2, том 2. 