Правда ли что векторное умножение векторов это умножение двух матриц размерностью два и имеет геометрический смысл площади параллелограмма?
Математика и математики
Популярное
Сообщества
Правда ли что векторное умножение векторов идентично умножение двух матриц с размерностью два и имеет геометрический смысл площади параллелограмма?
МатематикаДомашние задания+3
igor simchanko
Математика и математики·
4,4 K
ОтветитьУточнитьAndronick Arutyunov
Математика
1,0 K
к.ф.м.н., преподаватель Свободного Университета, доцент МФТИ, с.н.с. Института Проблем… · 20 дек 2022
Нет, это неправда. Прежде всего векторное умножение это операция, которая определена в трехмерном пространстве R^3. 3. Иными словами, если у нас имеется два трехмерных вектора a,b, то их векторное произведение [a,b] это снова трехмерный вектор.
3. Иными словами, если у нас имеется два трехмерных вектора a,b, то их векторное произведение [a,b] это снова трехмерный вектор.
При этом, конечно, для векторного произведения в ортнормированном базисе i, j. k справедлива формула
Более подробно про формулы в других базисах можно почитать в википедии. Так что умножение двумерных матриц (т.е. видимо матриц 2х2) тут ни при чём.
В тоже время, есть и геометрические свойства. Прежде всего модуль векторного произведения |[a,b]| действительно численно равен площади параллелограмма «натянутого» на векторы a,b. Кроме того, векторное произведение ортогонально плоскости векторов a,b. Эти два свойства определяют два противоположных вектора (советую проверить это). По этому для определённости говорят, что векторы a,b, [a,b] образуют «правую тройку», это позволяет выбрать из двух векторов один.
Вообще, векторное произведение очень интересная штука: позволяет не только решать многие стереометрические задачи (например с их помощью очень просто доказывается теорема косинусов для трехранного угла), но они ещё и тесно связаны с кватернионами (см.
А значит трехмерные векторы с операцией векторного произведения образуют алгебру Ли, это очень интересный и важный пример такой алгебраической структуры.
Математика, политика, высшая школа и хейт спич
Перейти на t.me/forodirchNEWS1 эксперт согласен
igor simchanko
24 декабря 2022
Почему в двумерном пространстве нельзя произвести векторное умножение двух векторов? Результирующий вектор будет… Читать дальше
Комментировать ответ…Комментировать…
Топ-20
Александр Рябцев
Математика
217
Бог Царь Отечество · 20 дек 2022
Похоже, автор вопроса слышал что-то о векторной и тензорной алгебре, но особо не вникал.
Речь здесь должна идти об антисимметричных тензорах ранга два. Векторное произведение — это антисимметризация тензорного произведения векторов. Ранг и размерность — независимые характеристики, но антисимметричные тензоры ранга два и размерности три (и только такой) имеют три… Читать далее
Векторное произведение — это антисимметризация тензорного произведения векторов. Ранг и размерность — независимые характеристики, но антисимметричные тензоры ранга два и размерности три (и только такой) имеют три… Читать далее
igor simchanko
20 декабря 2022
Какой физический смысл имеет векторное произведение векторов . Напишите расчетные примеры примеры.
Комментировать ответ…Комментировать…
Faris Mekhdi-Zadeh
Digital marketer, researcher and data analyst · 20 дек 2022
Векторное умножение векторов, также известное как векторное произведение, это операция, которая применяется к двум векторам и возвращает вектор, который является перпендикуляром к плоскости, в которой расположены исходные векторы. Векторное произведение векторов не может быть выражено как умножение двух матриц размерностью два, так как это операция, которая имеет. .. Читать далее
.. Читать далее
Леонид Коганов
20 декабря 2022
Полагаю, что глагол «возвращает» в первой фразе несёт смысл «доставляет в конечном итоге операции (векторного… Читать дальше
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
О сообществе
Математика и математики
Сообщество практикующих математиков разного уровня. Оригинальные решения, нетворкинг и общение. Не отвечаем на школьные задачки!
Векторное умножение | это… Что такое Векторное умножение?
Содержание
|
Правые и левые тройки векторов
Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой — вторым, а какой — третьим.
Тройка некомпланарных векторов называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.
Определение
Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:
- длина вектора равна произведению длин векторов и на синус угла ; между ними
- вектор ортогонален каждому из векторов и
- вектор направлен так, что тройка векторов является правой.

Обозначение:
В различных учебных заведениях определение векторного произведения даётся по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах. А далее выводится данное выше определение.
Свойства
Геометрические свойства векторного произведения
- Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
- Модуль векторного произведения равняется площади S параллелограмма, построенного на приведённых к общему началу векторах и
- Если — единичный вектор, ортогональный векторам и , а S — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
- Если — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор, — единичный вектор, лежащий в плоскости π и ортогональный к , — единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов является правой, то для любого лежащего в плоскости π вектора справедлива формула
Алгебраические свойства векторного произведения
- (свойство антикоммутативности)
- (свойство ассоциативности относительно умножения на скаляр)
- (свойство дистрибутивности по сложению)
- (тождество Якоби)
- (формула «БАЦ минус ЦАБ», тождество Лагранжа)
- .
 Это частный случай мультипликативности нормы кватернионов
Это частный случай мультипликативности нормы кватернионов - ; значение этого выражения называют смешанным произведением векторов a, b, c и обозначают либо .
Выражение для векторного произведения в декартовых координатах
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где — символ Леви-Чивиты.
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Если представить вектор как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь

С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
- и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В 3-хмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу
A как столбец векторов, тогдаУмножение матрицы на вектор слева определяется аналогично, если представить A как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (A — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
E — единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы A вычисляется как векторное произведение матрицы A на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть D — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерности 3.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом).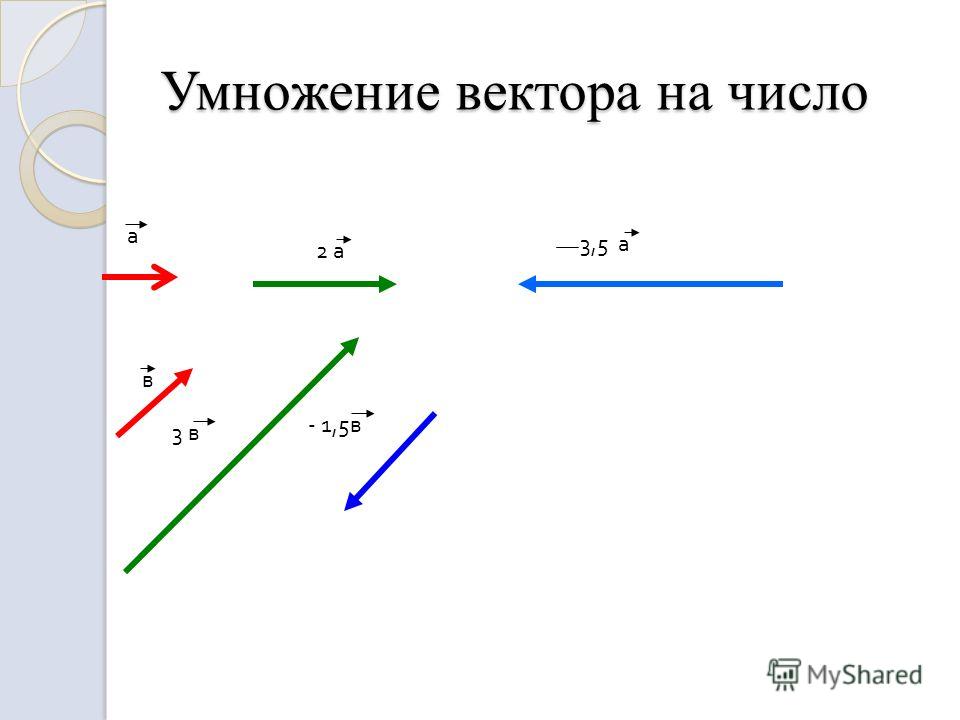 Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (D − 1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в D-мерном пространстве на операцию с D сомножителями. Используя символ Леви-Чивиты с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (D − 1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в D-мерном пространстве на операцию с D сомножителями. Используя символ Леви-Чивиты с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности (D − 1).
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при D < > 3 не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
- .

Эта конструкция называется внешним произведением.
Для двумерного случая эта операция называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат можно отождествить с псевдоскаляром.
Алгебра Ли векторов
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
- Косое произведение векторов (2D)
- Скалярное произведение векторов (2D и 3D)
- Смешанное произведение векторов (3D)
- Векторно-векторное произведение векторов (3D)
Другое
- Ротор
Ссылки
- Многомерное векторное произведение
Литература
- Кочин Н.
 Е. Введение в векторный и тензорный анализ.
Е. Введение в векторный и тензорный анализ.
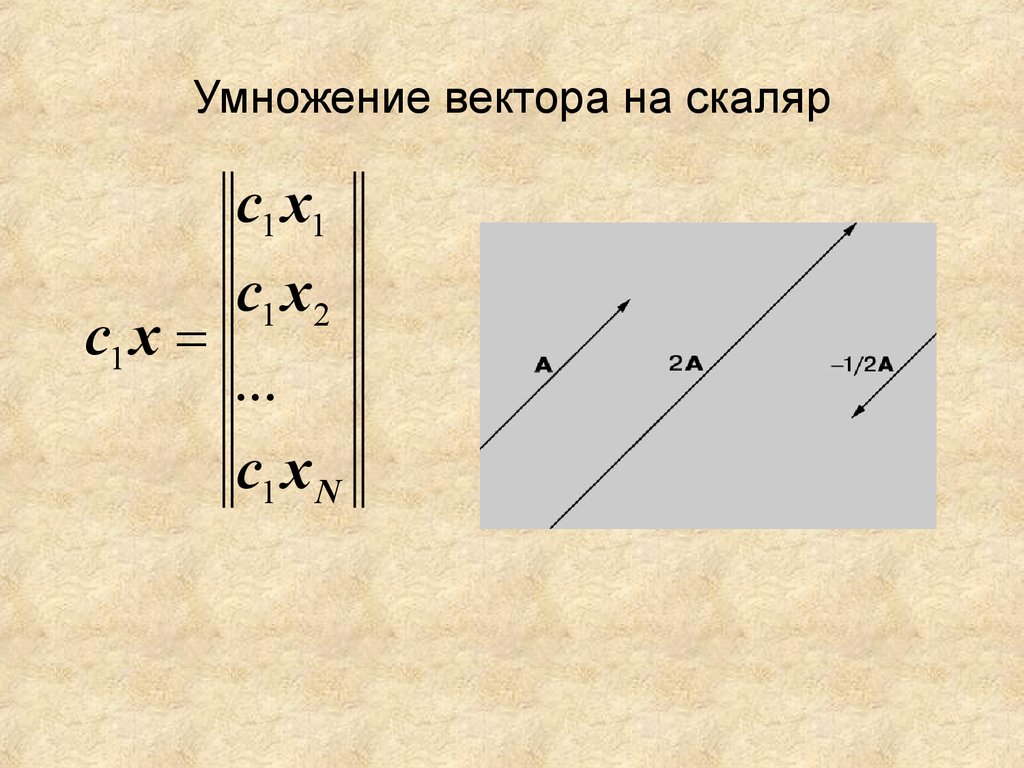
Сложение векторов и скалярное умножение
Обновлено: 27 ноября 2007 г. (дендане)
Учебник по сложению и скалярному умножению векторов. Векторы — это математические величины, используемые для представления таких понятий, как сила или скорость, которые имеют как величину, так и направление. Компоненты вектораКомпонентная форма вектора v с начальной точкой A(a1,a2) и конечной точкой B(b1,b2) определяется выражениемЕсли вектор задан как v = < v1 , v2 > , его величина || в || дан кем-то Пример 1: Найдите компоненты и модуль вектора v с начальной точкой A(2,3) и конечной точкой B(4,5).  Решение примера 1: Используйте приведенное выше определение, чтобы найти вектор v v = < v1, v2 > = < b1 - a1, b2 - a2 > = < 4 - 2 , 5 - 3 > = < 2 , 2 > и его величина || в || || в || = √(v1 2 + v2 2 ) = √(2 2 + 2 2 ) = √(8) = 2 √(2) Скалярное умножение вектораСкалярное умножение вектора v = < v1 , v2 > на действительное число k есть вектор k v, заданный выражениемк v = < к v1 , к v2 > Сложение двух векторовСложение двух векторов v(v1 , v2) и u (u1 , u2) дает вектор v + u = < v1 + u1 , v2 + u2> Ниже приведены апплеты html5, которые можно использовать для понимания геометрического объяснения сложения двух векторов.  Введите компоненты векторов A и B и используйте кнопки для рисования, добавления, увеличения и уменьшения масштаба, а также перемещения системы осей. Введите компоненты векторов A и B и используйте кнопки для рисования, добавления, увеличения и уменьшения масштаба, а также перемещения системы осей. Онлайн Калькулятор сложения векторов можно использовать для проверки любых ответов на приведенные ниже примеры. Пример 2: Векторы v и u задаются своими компонентами следующим образом 1 : v + 2 u = <-2, 3> + 2 <4, 6> = <-2, 3> + <8, 12> Пример 3: v и u — векторы, заданные формулой v + 3 u = <1, -2> + 3 = <1, -2> + <3 и1, 3 и2> Упражнения Ответы на приведенные выше упражнения Добавление вектора — апплет HTML5 Вычитание векторов — апплет HTML5 Векторные калькуляторы. |
Умножение скалярных векторов — проектирование цифровых систем
ДР. ШИРШЕНДУ РОЙ / 10 июня 2020 г. 19 февраля 2021 г. / Без рубрики
Умножение скаляра на вектор — очень важная арифметическая операция при реализации алгоритмов обработки сигналов или изображений. В этом уроке мы обсудим аппаратное обеспечение для умножения между матрицей 6X3 (A) и матрицей 3X1 (B), и результатом будет вектор-столбец 6X1 (C). Это умножение показано ниже на рисунке 1.
Рисунок 1: Умножение матрицы на вектор Это умножение может быть выполнено двумя способами: умножением вектора на вектор или умножением скаляра на вектор. При умножении на скалярный вектор один столбец матрицы и один элемент вектора-столбца B подаются на вычислительный процессор. Этот результат умножения суммируется с умножением 2-го столбца A и второго элемента B. Таким образом, матричное и векторное умножение достигается путем скалярно-векторного умножения и накопления. Умножение между A и B может быть выражено как
При умножении на скалярный вектор один столбец матрицы и один элемент вектора-столбца B подаются на вычислительный процессор. Этот результат умножения суммируется с умножением 2-го столбца A и второго элемента B. Таким образом, матричное и векторное умножение достигается путем скалярно-векторного умножения и накопления. Умножение между A и B может быть выражено как
Вычислительный блок разработан с использованием базового блока умножения и накопления (MAC). Эта единица умножает два элемента и накапливает. Схема этого блока MAC показана ниже на рисунке 2.
Рисунок 2: Схема MACОбщий вычислительный блок показан ниже на рисунке 3.
Рисунок 3: Умножитель скалярного вектора Используется шесть блоков MAC. Задержка блока MAC составляет два такта. Но после четырех тактов вычисляется вектор C. Вход сброса (первый) здесь очень важен. Регистр после сумматора в блоке MAC должен быть очищен перед умножением и перед запуском другого умножения. Временная диаграмма для вычисления блока MAC показана ниже на рисунке 4.
Здесь P — выходной сигнал блока MAC. P1 — первый выход умножения, P2 — первый выход накопления, а P3 — конечный выход. Вычислительный блок потребляет шесть умножителей и шесть сумматоров.
(посетили 1104 раза, сегодня посетили 1 раз)
Искать:Подписаться
Всего посещений сайта
363 412Категории
КатегорииВыбрать категориюASIC (3)Цифровая арифметика (6) Цифровая арифметика (6)Проекты (5) Проекты (5)Учебники (12)Без категории (87)Архивы
Архивы Выберите месяц Февраль 2023 (1) Ноябрь 2022 (1) Июль 2022 (1) Июнь 2022 (1) Март 2022 (1) Январь 2022 (3) Октябрь 2021 (2) Сентябрь 2021 (4) Июнь 2021 (1) Май 2021 ( 1) февраль 2021 г. (2) январь 2021 г. (1) август 2020 г. (2) июль 2020 г. (5) июнь 2020 г. (23) май 2020 г. (9) апрель 2020 г. (1) март 2020 г. (2) февраль 2020 г. (9) декабрь 2019 г. ( 1) июнь 2019 г. (10) май 2019 г. (10) апрель 2019 г.

 1 Кватернионы
1 Кватернионы
 Это частный случай мультипликативности нормы кватернионов
Это частный случай мультипликативности нормы кватернионов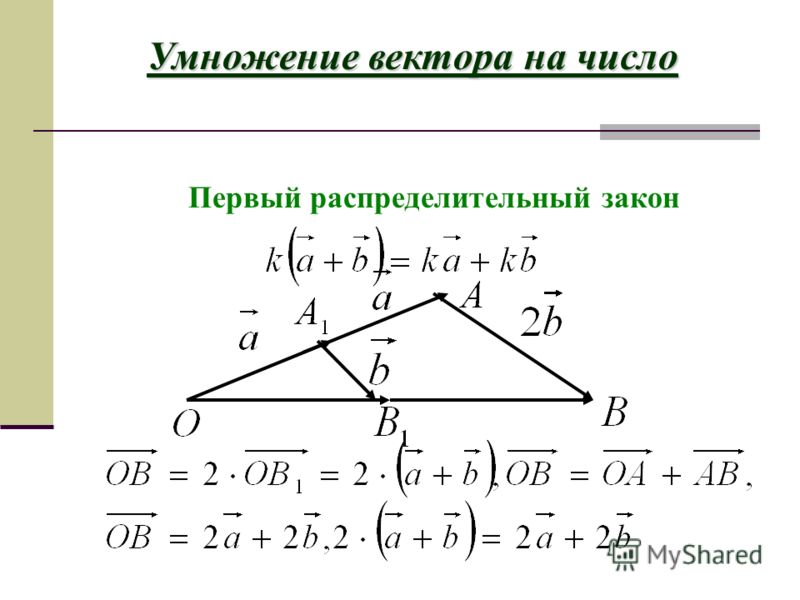
 Е. Введение в векторный и тензорный анализ.
Е. Введение в векторный и тензорный анализ.
