Векторное произведение пример: Векторное и смешанное произведения векторов

Векторное произведение векторов. Примеры решения задач

Высшая математика / Практикум по аналитической геометрии

20.03.201525.11.2015

Решения типовых задач по теме: «Векторное произведение векторов»
Задача № 1. Даны модули векторов

и , , и их скалярное произведение Вычислить модуль векторного произведения .
Решение. Так как модуль векторного произведения двух векторов равен произведению модулей данных векторов, умноженному на синус угла между векторами, то необходимо знать синус угла между векторами и .
Воспользуемся скалярным произведением данных векторов:

откуда

Тогда

Следовательно,

Ответ:
Задача № 2. Какому условию должны удовлетворять векторы и , чтобы векторы и были коллинеарны?
Решения этих задач подробно изложено в следующем видео

Задача № 3. Векторы

, и удовлетворяют условию . Доказать, что .
Задача № 4. Вычислить площадь параллелограмма, построенного на векторах и , если и
Указания. Площадь параллелограмма численно равна длине вектора, полученного в результате векторного умножения двух данных векторов, т. е.

Ответ: S параллелограмма= 157,5 кв. ед.
Решения этих задач подробно изложено в следующем видео

Задача № 5. Зная стороны треугольника

={-3; -2; 6} и = {- 2; 4; 4}, вычислить длину высоты .
Решение. I способ приведен в видеоуроке
II способ. Указания. Найти Пр и затем по теореме Пифагора вычислить высоту .
Ответ: ед. длины.
Решение этой задачи подробно изложено в следующем видео

Задача № 6. Решить самостоятельно. Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах:

{6;0;2} и {1,5; 2; 1}.
Указания. Одна из диагоналей параллелограмма будет равна сумме векторов сторон, а другая — разности векторов сторон параллелограмма (рис.1).

Рис.1

Ответ: длины диагоналей и , площадь параллелограмма 13 кв.ед.
Задача № 7. Зная, что векторы и коллинеарны, вычислить коэффициенты α и β.
Указания. Если векторы а и b коллинеарны, то их векторное произведение равно нулю, .
Ответ:
Решения этих задач подробно изложено в следующем видео

Тегивекторное произведениевекторное произведение вектороввекторное произведение векторов онлайнвекторное произведение двух вектороввекторное произведение онлайнвекторное произведение формуланайти векторное произведениенайти векторное произведение векторовсвойства векторного произведениясвойства векторного произведения векторов

Как найти векторное произведение двух векторов: формула, свойства, пример задачи

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Векторное произведение векторов

В данной публикации мы рассмотрим, каким образом можно найти векторное произведение двух векторов, приведем геометрическую интерпретацию, алгебраическую формулу и свойства этого действия, а также разберем пример решения задачи.

• Геометрическая интерпретация
• Формула векторного произведения
• Свойства векторного произведения
• Пример задачи

Геометрическая интерпретация

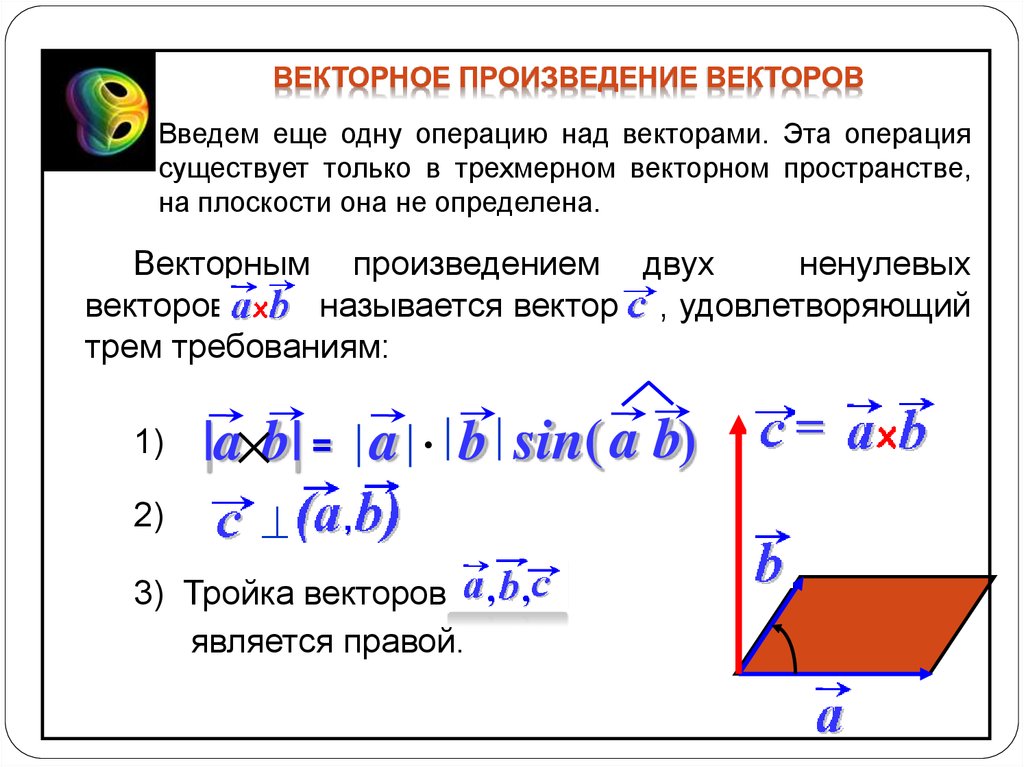
Векторное произведение двух ненулевых векторов a и b – это вектор c, который обозначается как [a, b] или a x b.

Длина вектора c равна площади параллелограмма, построенного с помощью векторов a и b.

При этом c перпендикулярен плоскости, в которой расположены a и b, и расположен так, чтобы наименьшее вращение от a к b выполнялось против часовой стрелки (с точки зрения конца вектора).

Формула векторного произведения

Произведение векторов a = {a_x; a_y, a_z} и b = {b_x; b_y, b_z} вычисляется с помощью одной из формул ниже:

Свойства векторного произведения

1.

Векторное произведение двух ненулевых векторов равняется нулю тогда и только тогда, когда эти векторы являются коллинеарными.

[a, b] = 0, если

a || b

.

2. Модуль векторного произведения двух векторов равняется площади параллелограмма, образованного этими векторами.

S_парал. = |a x b|

3. Площадь треугольника, образованного двумя векторами, равняется половине их векторного произведения.

S_Δ = ¹/₂ · |a x b|

4. Вектор, являющийся векторным произведением двух других векторов, перпендикулярен им.

c ⟂ a, c ⟂ b.

5. a x b = –b x a

6. (m a) x a = a x (m b) = m (a x b)

7. (a + b) x c = a x c + b x c

Пример задачи

Вычислим векторное произведение a = {2; 4; 5} и b = {9; -3; 1}.

Решение:

Ответ: a x b = {19; 43; -42}.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Перекрестное произведение

Вектор имеет величины (длина) и направления :

Два вектора могут быть умножены на с использованием « Cross Product

» (см. также Скалярный продукт)

Перекрестное произведение a × b двух векторов равно другому вектору , который находится под прямым углом к ​​обоим:

И все это происходит в 3-х измерениях!

Величина (длина) векторного произведения равна площади параллелограмма с векторами a и b для сторон:

Посмотрите, как он меняется под разными углами:

Перекрестное произведение ( синий ) равно:

• нулевая длина, когда векторы a и b указывают в одном или противоположном направлении
• достигает максимальной длины, когда векторы a и b находятся под прямым углом

И может указывать то в одну, то в другую сторону!

Так как же нам его рассчитать?

Расчет

Мы можем вычислить кросс-произведение следующим образом:

а × б = | и | | б | sin(θ) n

• | и | является величиной (длиной) вектора a
• | б | — величина (длина) вектора б
• θ — угол между a и b
• n — единичный вектор под прямым углом к ​​ a и b

Таким образом, длина равна: длине a умножить на длину b умножить на синус угла между a и b ,

Затем мы умножаем на вектор n , чтобы получить правильную девятку. 0003 направление (под прямым углом к ​​ a и b ).

 

ИЛИ мы можем рассчитать это так:

Когда a и b

начинаются в исходной точке (0,0,0), перекрестное произведение заканчивается на:

• c _x = a _y b _z − a _z b _y
• в _у = а _z б _x − a _x b _z
• c _z = a _x b _y − a _y b _x

Пример: перекрестное произведение

a = (2,3,4) и b = (5,6,7)

• c _x = a _y b _z − a _z б _у = 3×7 — 4×6 = -3
• с _у = а _z б _х — а _х б _г = 4×5 — 2×7 = 6
• c _z = a _x b _y − a _y b _x = 2×6 − 3×5 = −3

Ответ: a × b = (−3,6,−3)

 

В каком направлении?

Сквозное произведение может указывать в совершенно противоположном направлении и по-прежнему находиться под прямым углом к ​​двум другим векторам, поэтому мы имеем:

«Правило правой руки»

Правой рукой укажите указательным пальцем вдоль вектора a и укажите средним пальцем вдоль вектора b : векторное произведение идет в направлении большого пальца.

 

Скалярный продукт

Перекрестное произведение дает ответ вектор и иногда называется векторным произведением .

Но есть также скалярное произведение, которое дает скалярный ответ (обычное число) и иногда называется скалярным произведением .

 

Вопрос: Что получится, если скрестить слона с бананом?

Ответ: | слон | | банан | sin(θ) n

 

3038, 3039, 3905, 3040, 3041, 3906, 3907, 3908, 3042, 3043

Cross Product — Расчет 3

Все ресурсы по расчету 3

6 Диагностические тесты 373 практических теста Вопрос дня Карточки Учитесь по концепции

← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 Следующая →

Исчисление 3 Помощь » Векторы и векторные операции » Перекрестное произведение

Пусть , и .

Найти .

Возможные ответы:

Правильный ответ:

Объяснение:

Мы пытаемся найти векторное произведение между  и .

Вспомните формулу векторного произведения.

Если  , и , то

.

Теперь применим это к нашей ситуации.

Сообщить об ошибке

Пусть , и .

Найти .

Возможные ответы:

Правильный ответ:

Объяснение:

Мы пытаемся найти векторное произведение между  и .

Вспомните формулу векторного произведения.

Если  , и , то

.

Теперь применим это к нашей ситуации.

Сообщить об ошибке

Верно или неверно: перекрестное произведение можно получить только из двух трехмерных векторов.

Возможные ответы:

Неверно

Верно

Правильный ответ:

Верно

Объяснение:

Это правда.

Перекрестное произведение определяется таким образом. Однако скалярное произведение можно взять для двух векторов размерности n (при условии, что оба вектора имеют одинаковую размерность).

Сообщить об ошибке

Какой из следующих вариантов верный?

Возможные ответы:

Правильный ответ:

Объяснение:

По определению порядок скалярного произведения двух векторов не имеет значения, так как конечный результат является скаляром. Однако векторное произведение двух векторов меняет знак в зависимости от порядка их пересечения. Следовательно 

.

Сообщить об ошибке

Для каких углов выполняется перекрестное произведение ?

Возможные ответы:

Правильный ответ:

Объяснение:

У нас есть следующее уравнение, которое связывает векторное произведение двух векторов с относительным углом между ними , записанное как

.

Из этого мы видим, что числитель, или векторное произведение, будет когда угодно . Это будет верно для всех кратных . Следовательно, мы находим, что перекрестное произведение двух векторов будет для .

Report an Error

Evaluate

Possible Answers:

None of the other answers

Correct answer:

None of the other answers

Объяснение:

Невозможно получить векторное произведение -компонентных векторов. Определение перекрестного произведения гласит, что каждый из двух векторов должен иметь компоненты. Таким образом, вышеуказанная проблема невозможна.

Сообщить об ошибке

 Вычислить .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы вычислить векторное произведение, мы используем формулу определителя

Итак, мы имеем

 

. (Используйте расширение кофактора вдоль верхней строки. Обычно это делается при использовании любых перекрестных произведений)

 

Сообщить об ошибке

Оценить .

Возможные ответы:

Ни один из других ответов

Правильный ответ:

9

7 Объяснение:

Чтобы вычислить векторное произведение, мы используем формулу определителя

Итак, мы имеем

 

. (Используйте расширение кофактора вдоль верхнего ряда. Обычно это делается при использовании любых перекрестных произведений)

 

Сообщить об ошибке

Найдите векторное произведение двух векторов.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти векторное произведение, находим определитель матрицы

Определитель равен

В качестве перекрестного произведения

Сообщить об ошибке

Найти векторное произведение двух векторов.

No related posts.