Все математические формулы: Все формулы по математике — Формулы под рукой

Все формулы по математике — Формулы под рукой

Не решается задачка? Наш сайт поможет тебе в учебе, подготовке к сложным экзаменам, контрольным, олимпиадам, сессиям, ЕГЭ.

ФОРМУЛЫ ПО АЛГЕБРЕ

Формулы сокращенного умноженияСвойства степени ПропорцииСвойства квадратного корня Прогрессии  Квадратное уравнение Квадратный трехчлен Неравенства Логарифмы Сравнение логарифмов Теория соединений. Бином Ньютона

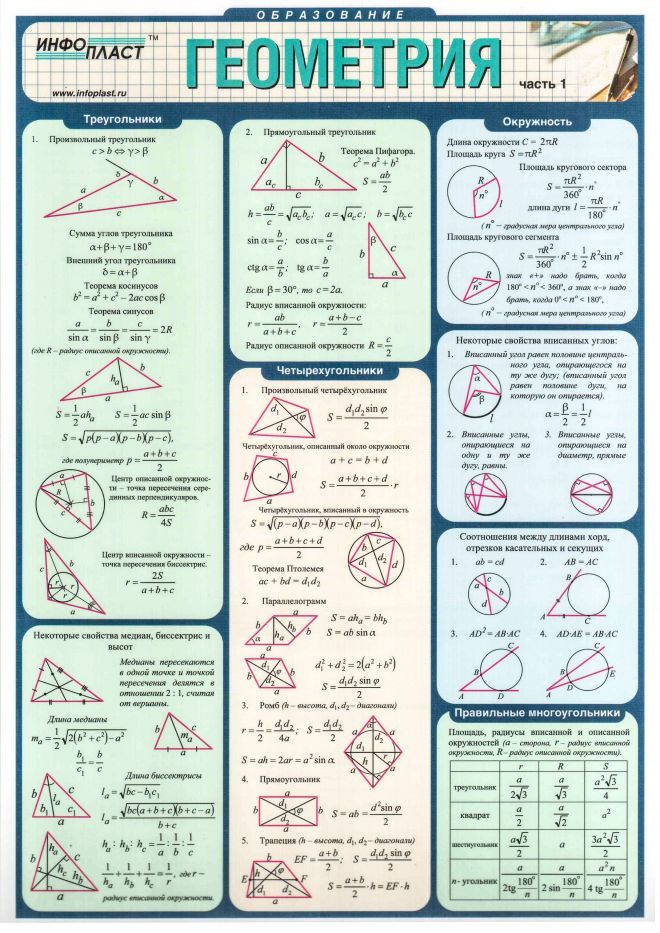
ФОРМУЛЫ ПО ГЕОМЕТРИИ

 ТреугольникиЧетырехугольникиПравильные n-угольникиОкружность и кругМногогранникиПравильные многогранникиТела вращенияВекторы

ФОРМУЛЫ ПО ТРИГОНОМЕТРИИ

Градусная и радианная мера угловТригонометрические функцииТригонометрические функции
в прямоугольном треугольникеТригонометрические тождестваВыражение одних функций тригонометрии через другиеФормулы сложения тригонометрических функцийФормулы приведения тригонометрических функцийТригонометрические функции кратных угловТригонометрические функции половинного углаПонижение степени тригонометрических функцийПроизведение тригонометрических функцийФормула дополнительного углаСоотношения между обратными тригонометрическими функциями

Обладатель премии Эйнштейна, известнейший британский исследователь в области теоретический физики Стивен Хокинг однажды рассказал, что получил должность профессора математики в Оксфордском университете, не имея специального образования. На тот момент за его плечами были лишь изрядно подзабытые школьные знания по математике. Царицу наук постигал «на ходу», читая студенческий учебник с опережением программы на две недели. Впоследствии студенты Хокинга вспоминали его занятия как исключительно познавательные и захватывающие!

Такие примеры вдохновляют, вселяют уверенность, что и каждый из нас может с таким же успехом освежить «хорошо забытое». А там и новый вектор развития появится.

Чтобы вспомнить (или освоить!) школьный материал было легче, предлагаем листать не страницы учебников и справочной литературы, а воспользоваться нашим сайтом, где удобная навигация и система поиска позволят быстро отыскать нужную формулу по предметам:

• арифметика;
• алгебра;
• геометрия;
• физика;
• химия.

От теории к практике

Бывает, что и материал знаком, да и формулы, теоремы и аксиомы по нужной теме — вот они, а задачка не поддается. Педагогический «диагноз»: нет опыта. Приобретается этот опыт при помощи решения типовых уравнений и задач. Предлагаем наиболее удачные и интуитивно понятные методики, которые уже помогли не одному ученику овладеть инструментарием точных наук!

Быстрее, выше, сильнее!

Возможно, сейчас ты и считаешь, что выучить все школьные формулы невозможно. Но на самом деле формул, необходимых для решения задач школьного уровня по математике, не более двухсот, а по физике — и того меньше! А это значит, что, заглядывая в наши справочники и освоив принципы решения типовых задач, можно постепенно запомнить все базовые формулы!

Какими бы сложными ни казались тебе задания твоих преподавателей сейчас, через какое-то время школьные, да и институтские стены могут показаться тебе тесными.

На нашем сайте собраны как часто используемые, так и гораздо более сложные формулы. Если захочешь знать больше, чем написано в школьном учебнике, начни с аксиомы — слов Марка Твена, который «никогда не позволял, чтобы школьные занятия мешали образованию!».

Все формулы по математике — Тур-инфо

Математика все формулы скачать

На этой странице собраны все формулы, необходимые для сдачи контрольных и самостоятельных работ, экзаменов по по алгебре, геометрии, тригонометрии, стереометрии и другим разделам математики.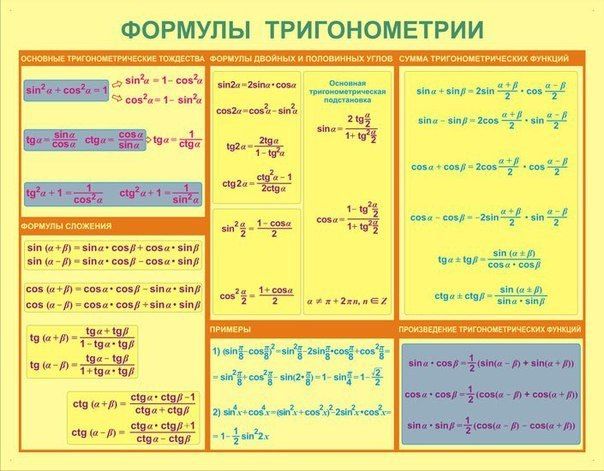

Здесь вы можете скачать или посмотреть онлайн все основные тригонометрические формулы, формулу площади круга, формулы сокращенного умножения, формула длины окружности, формулы приведения и многие другие.

Можно так же распечатать необходимые сборники математических формул.

Успехов в учебе!

Формулы Арифметики:

Формулы Алгебры:

Геометрические Формулы:

Арифметические формулы:

Законы действий над числами

Переместительный закон сложения: a + b = b + a.

Сочетательный закон сложения: (a + b) + с = a + (b + c).

Переместительный закон умножения: ab = ba.

Сочетательный закон умножения: (ab)с = a(bc).

Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.

Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.

Некоторые математические обозначения и сокращения:

Признаки делимости

Признаки делимости на «2»

Число, делящееся на «2» без остатка называется Чётным, не делящееся – Нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, 8) или ноль

Признаки делимости на «4»

Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»

Признаки делимости на «8»

Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (Пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и. т.д.)

Признаки делимости на «3» и на «9»

Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»

Признаки делимости на «5»

Признаки делимости на «25»

Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т. е. числа, оканчивающиеся на «00», «25», «50», «75»

Признаки делимости на «10», «100» и на «1 000»

Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули

Признаки делимости на «11»

Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»

Абсолютная величина — формулы ( модуль)

|a| ? 0, Причём |a| = 0 только если a = 0; |-a|=|a| |a2|=|a|2=a2 |ab|=|a|*|b| |a/b|=|a|/|b|, Причём b? 0; |a+b|?|a|+|b| |a-b|?|a|-|b|

Формулы Действия с дробями

Формула обращения конечной десятичной дроби в рациональную дробь:

Пропорции

Два равных отношения образуют Пропорцию:

Основное свойство пропорции

Ad = bc

Нахождение членов пропорции

Средние величины

Среднее арифметическое

Среднее геометрическое (среднее пропорциональное)

Среднее квадратичное

Среднее гармоническое

Некоторые конечные числовые ряды

Тождественные преобразования алгебраических и тригонометрических выражений

Свойства степеней

Свойства арифметических корней

Многочлены

Свойства числовых неравенств

1) Если a

2) Если a 0, то aс

3) Если a bс.

4) Если a 1/b.

5) Если a

6) Если a 0, b > 0, c > 0, d > 0, то ac

7) Если a 0, b > 0, то

8) Если, то

Соотношения между тригонометрическими функциями одного и того же аргумента

Формулы сложения:

Формулы двойного аргумента:

Формулы тройного аргумента:

Формулы половинного аргумента:

(для функций sin и cos – формулы понижения степени)

Формулы третьей и четвертой степени:

Формулы преобразования суммы в произведение:

Формулы преобразования произведения в сумму:

Формула приведения для преобразования выражений вида а) перед приведенной функцией ставиться тот знак, который имеет исходная функция;б) функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс. ) Например:

Формулы нахождения угла:

ТАБЛИЦА ЗНАЧЕНИЙ

Единичная окружность:

Формулы Прогрессии:

Арифметическая прогрессия

(a1 – первый член; d – разность; n – число членов; an – n-й член; Sn – сумма n первых членов):

Геометрическая прогрессия

(b1 – первый член; q – знаменатель; n – число членов; bn – n-й член; Sn – сумма n первых членов, S – сумма бесконечной геом. прогрессии):

Производная

Основные правила дифференцирования:

Производная сложной функции:

Если функция f имеет производную в точке xo, а функция g имеет производную в точке yo = f(xo), то сложная функция h(x) = g(f(x)) также имеет производную в точке xo, причем:

Производные тригонометрической функции:

Производная логарифмической функции:

Уравнение касательной к графику функции:

1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:

2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам:

3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид:

Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.

4. Общее уравнение прямой имеет вид: ax + by + c = 0.

5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид:

6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2 соответственно имеют вид:

7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид:

Представляет собой уравнение параболы с вершиной в точке, абсцисса которой

1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле:

2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам:

3. Модуль вектора заданного своими координатами, находится по формуле:

4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т. е. справедливы формулы:

5. Единичный вектор сонаправленный с вектором находится по формуле:

6. Скалярным произведением векторов называется число:

Где — угол между векторами.

7. Скалярное произведение векторов

8. Косинус угла между векторами и находится по формуле:

9. Необходимое и достаточное условие перпендикулярности векторов и имеет вид:

10. Общее уравнение плоскости, перпендикулярной вектору имеет вид:

Ax + by + cz + d = 0.

11. Уравнение плоскости, перпендикулярной вектору и проходящей через точку (xo;yo;zo), имеет вид:

A(x — xo) + b(y — yo) + c(z — zo) = 0.

12. Уравнение сферы с центром O(0;0;0) записывается в виде:

1) Число перестановок из n элементов находится по формуле:

2) Число размещений из n элементов по m находится по формуле:

3) Число сочетаний из n элементов по m находится по формуле:

4) Справедливы следующие свойства сочетаний:

5) Формула бинома Ньютона имеет вид:

Сумма показателей чисел a и b равна n.

6) (k+1)-й член находится по формуле:

7) Число сочетаний также можно найти по треугольнику Паскаля.

Треугольник Паскаля (до n=7):

8) Сумма биномиальных коэффициентов равна 2n.

9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.

Центр описанной окружности – точка пересечения серединных перпендикуляров. Центр вписанной окружности – точка пересечения биссектрис. (a, b,c – стороны: — противолежащие им углы; p – полупериметр; R – радиус описанной окружности; r – радиус вписанной окружности; S – площадь; ha – высота, проведенная к стороне a):

2. Прямоугольный треугольник:

Центр описанной окружности совпадает с центром гипотенузы. (a, b – катеты; c – гипотенуза; ac, bc – проекции катетов на гипотенузу):

3. Равносторонний треугольник:

Медиана = биссектрисе. OR = Or.

4.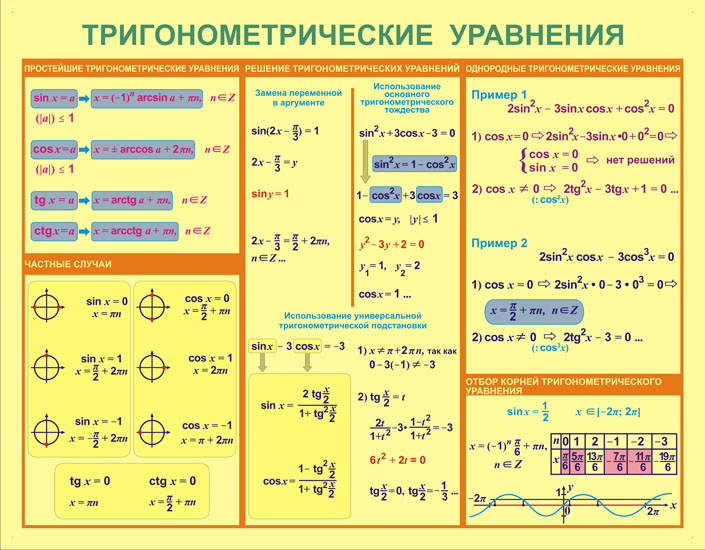 Произвольный выпуклый четырехугольник

(d1 и d2 – диагонали; – угол между ними; S — площадь):

5. Параллелограмм

(a и b – смежные стороны; – угол между ними; ha – высота, проведенная к стороне a):

6. Ромб:

В любой ромб можно вписать окружность.

7. Прямоугольник:

Около любого прямоугольника можно описать окружность.

8. Квадрат

9. Трапеция

(a и b – основания; h – расстояние между ними; l – средняя линия):

10. Описанный многоугольник

(p – полупериметр; r – радиус вписанной окружности):

S = pr. 11. Правильный многоугольник

(an – сторона правильного n-угольника; R – радиус описанной окружности; r – радиус вписанной окружности):

12. Окружность, круг

(r — радиус; C – длина окружности; S – площадь круга):

13. Сектор

(l – длина дуги, ограничивающей сектор; — градусная мера центрального угла; — радианная мера центрального угла):

(l – боковое ребро; P – периметр основания; S – площадь основания; H – высота; Pсеч – периметр перпендикулярного сечения; Sбок – площадь боковой поверхности; V — объем):

2. Прямая призма: 3. Прямоугольный параллелепипед

(a, b,c – его измерения; V — диагональ):

4. Куб

5. Произвольная пирамида

(S – площадь основания; H – высота; V — объем):

6. Правильная пирамида

(P – периметр основания; l – апофема; Sбок – площадь боковой поверхности):

7. Произвольная усеченная пирамида

(S1 и S1 – площади оснований; h – высота; V — объем):

8. Правильная усеченная пирамида

(P1 и P2 – периметры оснований; l – апофема; Sбок – площадь боковой поверхности):

9. Цилиндр

(R – радиус основания; H – высота; Sбок – площадь боковой поверхности; V — объем):

10. Конус

(R – радиус основания; H – высота; l – образующая; Sбок – площадь боковой поверхности; V — объем):

11. Шар, сфера

(R – радиус шара; S – площадь сферической поверхности; V — объем):

12. Шаровой сегмент

(R – радиус шара; h – высота сегмента; S – площадь сферической поверхности сегмента; V — объем):

13. Шаровой сектор

(R – радиус шара; h – высота сегмента; V — объем):

Полезности

Цитаты и афоризмы

“ Если хочешь узнать человека, не слушай, что о нём говорят другие, послушай, что он говорит о других.” —

Два равных отношения образуют Пропорцию: Основное свойство пропорции ad = bc

Формулы Арифметики:

Законы действий над числами

Переместительный закон сложения: a + b = b + a.

Сочетательный закон сложения: (a + b) + с = a + (b + c).

Переместительный закон умножения: ab = ba.

Сочетательный закон умножения: (ab)с = a(bc).

Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.

Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.

1) Если a 0, то aс bс.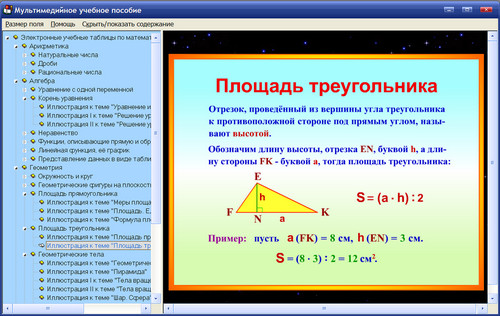 4) Если a 1/b. 5) Если a 0, b > 0, c > 0, d > 0, то ac 0, b > 0, то 8) Если, то

Формула приведения для преобразования выражений вида а) перед приведенной функцией ставиться тот знак, который имеет исходная функция;б) функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.) Например:

Производная сложной функции.

Advice-me. ru

24.07.2017 23:32:14

2017-07-24 23:32:14

Источники:

Http://advice-me. ru/vse-formuly-po-matematike/

Основные формулы по математике — Математика — Теория, тесты, формулы и задачи — Обучение Математике, Онлайн подготовка к ЦТ и ЕГЭ. » /> » /> .keyword { color: red; }

Математика все формулы скачать

Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены основные формулы по школьной математике.

Изучать основные формулы по школьной математике онлайн:

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.

Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены основные формулы по школьной математике.

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту адрес электронной почты здесь.

Educon. by

05.10.2018 3:26:48

2018-10-05 03:26:48

Источники:

Https://educon. by/index. php/formuly/formulymat

Формулы по математике – скачать бесплатно в epub, fb2, rtf, mobi, pdf или читать онлайн » /> » /> .keyword { color: red; }

Математика все формулы скачать

Книга не претендует на научные труды – в данной книге собраны по порядку все характеристики, нужные для человека, для осознанного существования. В книги вы узнаете не только характеристики, но и еще ф. Подробнее

Представьте, что вы в падающем самолете. Без паники! Из сари вашей соседки можно сделать парашют и остаться в живых, надо лишь правильно рассчитать площадь материала.

Это всего один пример того, как з. Подробнее

Новый способ выучить основные правила математики. Удобный формат «чекбук»: можно вырвать страницу и прикрепить куда угодно – материал всегда на виду. Правила математики сопровождаются примерами и зани. Подробнее

Изложен теоретический материал, указаны основные формулы, используемые для решения задач. Приведены примеры и даны типовые расчеты. Предназначено для студентов, обучающихся по направлению бакалавриата. Подробнее

Современный и удобный в использовании справочник подготовлен в соответствии с требованиями ФГОС для начальной школы. В книге в наглядном виде представлен основной теоретический материал, охватывающий. Подробнее

Учебное пособие содержит введение в финансовую математику. Оно описывает, что такое платежи, какие бывают процентные ставки наращения и дисконта, сложных и простых процентов, их связь, как рассчитываю. Подробнее

В буклете знаний «Все формулы по тригонометрии. 10–11 классы» представлены основные формулы – понижения степени, приведения и произведения функций, функции суммы и разности углов, двойного и половинно. Подробнее

В буклете знаний «Все формулы по алгебре. 6–11 классы» содержатся все формулы, которые нужно знать школьникам 6–11 классов. Благодаря удобному оглавлению в виде закладок легко и быстро найти нужную те. Подробнее

Справочник включает весь материал, входящий в программу основного курса математики высших учебных заведений. Детальная рубрикация и подробный предметный указатель позволяют читателю легко и быстро най. Подробнее

В работе представлены новые, ранее неизвестные математике функции. Даны определения этих функций, а также некоторые соотношения, формулы обращения, частные значения, производные, неопределённые интегр. Подробнее

Книга адресована учащимся выпускных классов общеобразовательных школ и окажет неоценимую помощь при подготовке к ЕГЭ. Будет полезна для студентов колледжей и вузов при подготовке к экзаменам по матема. Подробнее

Справочник содержит материал курса «Математика» в объёме, проверяемом на ОГЭ и ЕГЭ. Наглядность и доступность подачи материала в табличной форме позволяет легко и быстро обобщить, систематизировать и п. Подробнее

Справочник содержит все определения, правила, формулы и теоремы элементарной математики, а также математические таблицы. Предметный указатель и подробное содержание позволяют легко и быстро получать н. Подробнее

В книге приведены производные, неопределенные и определенные интегралы, конечные суммы, ряды и другие формулы, содержащие специальные функции. Она включает в основном новые результаты и является ценны. Подробнее

Книжка состоит примерно из двухсот задач, многие из них даны с решениями или комментариями. Эти задачи очень разнообразны – от традиционных задач, в которых нужно найти и как-то использовать то или ин. Подробнее

Справочный материал по всему школьному курсу математики в 5-11 классах сгруппирован в тематические таблицы. Весь материал распределен в соответствии с содержанием школьных предметов – математика, алге. Подробнее

В справочнике приведены все необходимые формулы школьного курса математики и высшей математики, изучаемой на первых курсах вузов. Подробнее

В буклете знаний Все формулы по алгебре.

Aldebaran. ru

23.08.2017 22:29:43

2017-08-23 22:29:43

Источники:

Https://aldebaran. ru/tags/119417/

Самый важный список математических формул

• 67,9 тыс. просмотров

 

Здесь вы найдете краткое изложение основных формул, которые вам необходимо знать. Этот список был организован не по годам обучения, а тематически. Это не исчерпывающий список, т.е. здесь представлены не все математические формулы, которые используются на уроках математики, а только те, которые были сочтены наиболее важными.

 Области

 Объемы

 Functions and Equations

 Exponents

 Radicals

 Trigonometry

 Geometry

 Logic

 Векторы

 Статистика

Последовательности

 Derivatives

 Probability and Sets

 logarithms

 Special Limits

 Integrals and primitives

Комплексные числа

 

Таблица математических формул

Таблица математических формул содержит все основные математические формулы. Таблица математических формул приведена ниже

Perimeter	Square Rectangle	P = 2a P = 2(l+b)
Circumference	Circle	C = 2 (PI) R
Область	кв.0005 Circle	A = A 2 A = L x B A = ½ (B x H) A = (B 1 +B 2 ) x) / H 2 +B 2 ) x) / H HH) / HH) / HH) / HH) / HH) / HH) / HH) / HH HO = (B 1 +B 2 9000). A = pi x r  2
Surface Area	Cube Cylinder Cone Sphere	S = 6l 2 S = 2 x pi х г х ч S = пи х г х л S = 4 x pi x r  2
Volume	Cylinder Cone Sphere	V = bh V = bh/3 V = 4 x pi x r 3  / 3
Pythagoras Theorem	a 2  + b 2  = c 2
Distance Formula	d = sqrt[(x 2  – x 1 ) 2  +(y 2  – y 1 ) 2 ]
Slope of a line	m = y 2 — Y 1 / x 2 -x 1
Средняя точка формула	M = (x 1 + X 9020 2		M = (x 1 + X 2		).  + y 2  )/ 2
Алгебраическая формула	Pythagorean Теорема Форма с наклоном в уравнении линии Формула расстояния Общая стоимость квадратичная формула Законы экспонентов 9000 Фракционные экспоненты	. 2  = c 2 y = mx + c d = rt общая стоимость = (количество единиц) × (цена за единицу) X = [-b ± sqrt(b 2 – 4ас)] /2а a m  x b  m  = (a x b) m a m  x a  n  = (a) m+n a 1/2  = sqrt a
Тригонометрические формулы	Синусоидальная функция Функция косинуса ТАНГЕННА0005

Поделиться

Javascript отключен!

Пожалуйста, включите Javascript, если вы его отключили, или используйте другой браузер, мы предпочли Google Chrome.

Пожалуйста Обновить  Страница после включения

Powered By UnCopy.

17 важных математических формул для понимания

Автор: Вирджиния | 21 июня 2022 г., 8:55

Любой школьник знает, что сложные математические задачи достаточно сложны, даже если не нужно запоминать правильную формулу. Поэтому важно иметь все нужные инструменты в заднем кармане!

Запоминание пошаговой методологии, необходимой для решения сложных математических задач, достаточно сложно для учащихся. Последнее, что им нужно, это попытаться вспомнить хитрую формулу вдобавок ко всему!

Если вашему ребенку нужно освежиться, чтобы выполнить домашнее задание, или ему нужно вспомнить основы для большого теста или викторины, эти формулы обязательно пригодятся.

Важные математические формулы

Математика может быть интересной задачей или головной болью учащихся: эти формулы будут полезны независимо от того, к какой части спектра относится ваш ребенок. Мы обеспечим вас, несмотря ни на что.

Начальная и средняя школа

Площадь прямоугольника: площадь = длина x ширина

Детям необходимо знать это на уроках алгебры и математики.

Периметр прямоугольника: 2(l + b)

Это рассчитает сумму внешних линий прямоугольника.

Площадь квадрата: a²

Возведите в квадрат длину обеих сторон, чтобы найти площадь квадрата.

Периметр квадрата: 4 x a

Умножьте длину стороны квадрата на 4, чтобы найти периметр.

Площадь круга: π x r²

Используйте это, чтобы найти общую площадь круга.

Длина окружности: 2π x  r

Эта формула вычисляет длину внешней стороны окружности.

Найти среднее: Сумма общих чисел, деленная на количество значений.

Полезен в статистике и многих других математических задачах.

Полезные математические формулы для старших классов и SAT®

Эти математические формулы для старших классов пригодятся в геометрии, алгебре, математических вычислениях и многом другом. Кроме того, когда наступит сезон SAT®, они помогут подросткам добиться успеха в сложной математической секции.

(Ищете дополнительную помощь по математике SAT®? Ознакомьтесь с 11 приложениями SAT® для ежедневной практики и подготовкой к тесту по математике.)

Квадратная формула: x = −b ± √b²-4ac/2a

Это понадобится учащимся для решения квадратных уравнений по алгебре II и выше. В качестве дополнительного легочного бонуса этот легче запомнить на мелодию «Pop Goes the Weasel».

Вероятность: количество благоприятных исходов, деленное на общее количество благоприятных исходов.

Чтобы определить вероятность события, это уравнение определяет вероятность того, что что-то произойдет.

Формула расстояния: d=√(x₁ – x₂)² + (y₁ – y₂)²

Это уравнение рассчитает расстояние между двумя точками, которое понадобится в геометрии и алгебре.

Формула наклона: Наклон = y₂ – y₁ /  x₂ – x₁

Используйте это, чтобы найти угол, соединяющий две точки на графике.

Формула пересечения наклона: y=mx+b

В алгебре это находит пересечение наклона прямой линии.

Площадь треугольника: Площадь = (1/2) (основание) (высота)

Используйте это в геометрии, чтобы найти общую площадь треугольника.

Синус (SOH): Синус = противоположность / гипотенуза

Это уравнение вычисляет неизвестные углы треугольника.

Косинус (CAH): косинус = смежный / гипотенуза

Используйте это уравнение, чтобы найти неизвестные углы треугольника.

Касательная (TOA): Касательная = противоположная / смежная

Это уравнение также можно использовать для вычисления неизвестных углов треугольника.

Теорема Пифагора: a²+b²=c²

Используется для нахождения длины гипотенузы в прямоугольном треугольнике. В любом прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов прямоугольного треугольника.

Проблемы с математикой? У нас есть математические решения!

В дополнение к беспрецедентному обучению математике iD Tech предлагает множество математических ресурсов. Вот краткий обзор:

• Интересные факты о математике
• Математические соревнования 2021
• Ежедневные способы сделать математику увлекательной
• 25 занимательных математических заданий
• Лучшие образовательные каналы YouTube

Имея в руках эти полезные советы и рекомендации, вы готовы помочь своему ученику с домашними заданиями по математике, тестами, викторинами и SAT®!

Вирджиния

Вирджиния начала работать с iD Tech в Денверском университете в 2015 году и с тех пор наслаждается каждой минутой! Бывший учитель по профессии, она имеет степень магистра в области образования и любит работать, чтобы вдохновлять следующее поколение с помощью STEM. Вне офиса вы обычно можете найти ее читающей хорошую книгу, борющейся на коврике для йоги или исследующей Скалистые горы.