Примеры решения пределами с ответами
Алгоритм решения пределов
Теорема
Пределом называется значение функции, вычисленное в точке к которой стремиться независимый аргумент.
Свойства пределов
Если
то
Если
то
Если
то
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Примеры решений пределов
Пример 1
Задача
Найти предел:
Решение
Заменим в выражении аргумент его предельным значением:
Ответ
Пример 2
Задача
Найти предел:
Решение
Заменим в выражении аргумент его предельным значением:
Ответ
Пример 3
Задача
Найти предел:
Решение
Заменим в выражении аргумент его предельным значением:
Ответ
Пример 4
Задача
Найти предел:
Решение
Проверяем, не обращается ли в нуль знаменатель дробно-рациональной функции при предельном значении аргумента.
Для этого подставим значение в
Вычисляем передел:
Ответ
Пример 5
Задача
Найти предел:
Решение
Проверяем, не обращается ли в нуль знаменатель дробно-рациональной функции при предельном значении аргумента. Для этого подставим значение в
Вычисляем предел:
Ответ
Пример 6
Задача
Найти предел:
Решение
Проверяем, не обращается ли в нуль знаменатель дробно-рациональной функции при предельном значении аргумента. Для этого подставим значение в
Вычисляем предел:
Ответ
Пример 7
Задача
Найти предел:
Решение
В данном примере знаменатель обращается в нуль при предельном значении аргумента
Преобразуем выражение
Ответ
Пример 8
Задача
Найти предел:
Решение
При числитель и знаменатель дроби обращаются в нуль.
Для решения задачи необходимо сделать подстановку Число является наименьшим общим кратным показателей корней.
Разделим числитель и знаменатель дроби
на
В итоге получим:
Ответ
Пример 9
Задача
Найти предел:
Решение
При знаменатель дроби обращается в нуль, поэтому вычислить непосредственно предел нельзя.
Рассмотрим обратную дробь
и её предел при
Т.к.
, то при функция является бесконечно малой, поэтому при является бесконечно большой, а
Ответ
Пример 10
Задача
Найти предел:
Решение
Разделим числитель и знаменатель дроби на – высшую степень , встречающуюся в дроби
При поэтому
Ответ
Средняя оценка 3 / 5.
Количество оценок: 46
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
49433
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
§ 8. Примеры вычисления пределов
Пример 1. Вычислить предел функции целочисленного
аргумента при
; .
Решение примера 1:
о
.
о
При вычислении предела в числителе и знаменателе пренебрегли постоянными слагаемыми по сравнению с бесконечно большой величиной ~ .
.
Здесь было использовано свойства бесконечности (бесконечно больших величин):
.
о о
.
о о
Здесь сначала пренебрегли постоянными в числителе и знаменателе по сравнению с бесконечно большими слагаемыми. Затем в числителе пренебрегли величиной по сравнению с бесконечно большой величиной высшего порядка . В знаменателе также, величина , которой пренебрегаем, может рассматриваться как бесконечно малая по сравнению с величиной .
о о
.
о
Здесь опять постоянной величиной пренебрегали по сравнению с бесконечно большой величиной , которая сама является бесконечно малой по сравнению с , поскольку для степеней имеет место неравенство < 2/3.
В
знаменателе по тем же причинам пренебрегли
величиной по сравнению с ее квадратом
.
Последняя является бескончно большой
величиной высшего порядка по сравнению
с величиной
.
Замечание: При сравнении порядков бесконечно больших степенных функций можно пользоваться шкалой бесконечно больших функций (см.
§7 )..
Здесь учтено, что бесконечно большие величины в отрицательной степени становятся бесконечно малыми. Действительно, например,
.
о
.
о
Здесь пренебрегли постоянными величинами по сравнению с бесконечно большими, а также учтено, что бесконечно большая величина в отрицательной степени является бесконечно малой величиной.
Пример 2. Вычислить предел функции целочисленного аргумента при .
.
Решение примера 2.
.
При раскрытии неопределенности была использована формула разности кубов:
.
Ее использование приводит к уничтожению кубических корней. Формула срабатывает после умножения и деления заданного выражения на неполный квадрат суммы.
Приведем другой способ решения, с помощью различного представления функций, эквивалентных в нуле, см § 4.
.
.
В первом слагаемом под корнем единицей можно пренебречь по сравнению с бесконечно большой величиной . При сравнении двух бесконечно больших функций и первой из них можно пренебречь как бесконечно большой, низшего порядка, поскольку 1 / 7 < 1 / 2.
.
Здесь постоянными числами в числителе и знаменателе пренебрегаем по сравнению с бесконечно большой величиной .
.
Как и в предыдущем примере, постоянными числами пренебрегаем по сравнению с бесконечно большой величиной .
.
Для
раскрытия неопределенности вида применяется стандартное преобразование
с использованием основного логарифмического
тождества в соответствии с формулой .
Для преобразования логарифмической функции использована формула эквивалентных в нуле функций (см. § 4): ,
причем в качестве бесконечно малой величины здесь берется выражение
.
Пример 3. Вычислить предел функции целочисленного аргумента
при
.
Замечание. При вычислении пределов с использованием понятия факториала помимо определения факториала:
или
(например, 5 ! = )
необходимо использовать свойства факториала, следующие из его определения:
1°
2°
3°
……………………………………………………………………….
!
Решение примера 3.
о
.
При решении было использовано второе свойство факториала, записанное в форме . Под знаком предела пренебрегли единицей по сравнению с бесконечно большой величиной .
.
Здесь было использовано первое свойство факториала, записанное в форме .
o
.
о
Здесь было использовано второе свойство факториала, записанное в форме . Кроме того, под знаком предела пренебрегли единицей по сравнению с бесконечно большой величиной ~ .
о
.
о
Здесь в числителе и знаменателе пренебрегли постоянными величинами (не зависящими от ), затем было использовано первое свойство факториала, записанное в форме .
.
Здесь
было использовано третье свойство
факториала, записанное в форме ,
а также первое свойство факториала,
записанное в форме .
.
Здесь было дважды использовано первое свойство факториала, записанное в формах и .
Пример 4. Вычислить пределы функций, если они существуют, при
.
Решение примера 4.
.
Ввиду того, что пределы слева и справа в точке х = 0 не совпадают, искомый предел не существует.
о
.
Последний предел вычисляется аналогично предыдущему. В числителе дроби пренебрегли постоянным числом по сравнению с бесконечно большим слагаемым ~ .
.
Ввиду совпадения пределов слева и справа в нуле, искомый предел также равен бесконечности: .
В
числителе пренебрегли единицей по
сравнению с бесконечно большим слагаемым
~
.
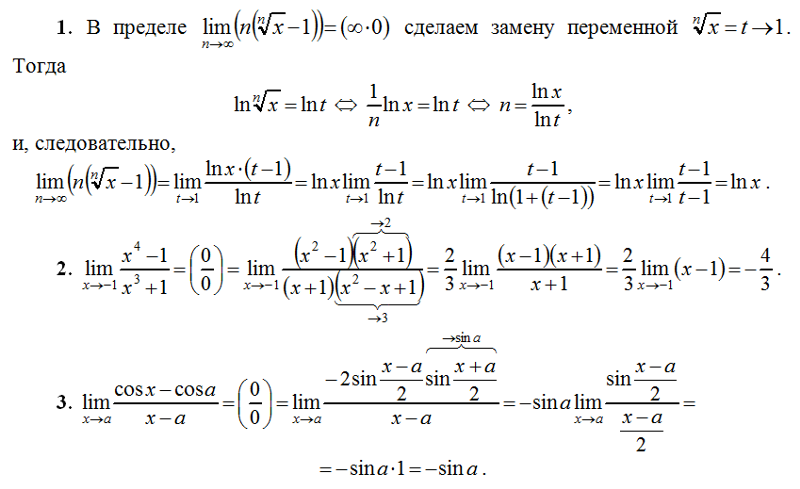
о о
.
о
В числителе пренебрегли бесконечно малыми величинами по сравнению с конечным числом два. В знаменателе пренебрегли вторым слагаемым как величиной бесконечно малой по сравнению с первым слагаемым ( известно, что при возведении числа , меньшего единицы в положительную степень, число становится тем меньше, чем больше степень).
Заметим здесь, что в этом конкретном примере пренебрегать вторым слагаемым в знаменателе было не обязательно, однако такое действие в некоторых случаях играет существенную роль.
Ввиду того, что оба вычисленных предела совпадают, искомый предел существует и равен тому же значению предела: .
о о о о
.
о о
Здесь в соответствии
со шкалой бесконечно больших функций
два первых слагаемых числителя и первое
слагаемое знаменателя являются по
сравнению с оставленными слагаемыми
бесконечно малыми величинами, которыми
можно пренебречь.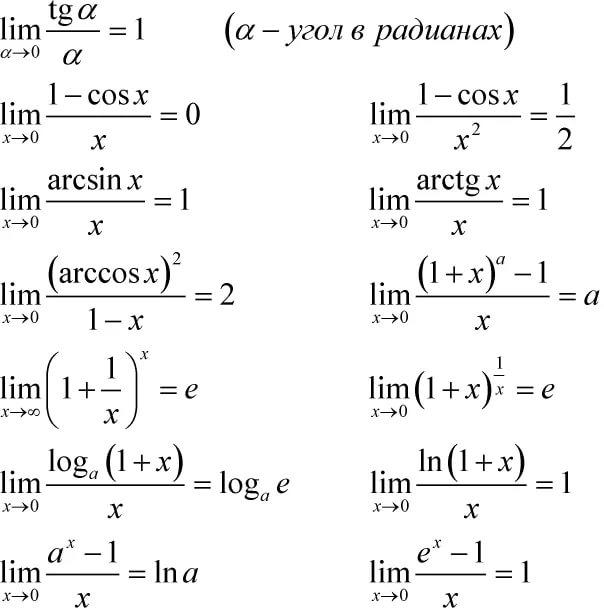
Последнее можно
объяснить и тем, что при возведении
чисел, больших единицы в положительную
степень, результат будет тем больше,
чем больше величина степени, а в нашем
случае в степень возводится сколь угодно
большая величина.
.
.
Ввиду равенства обоих пределов искомый предел существует и равен вычисленному значению предела: .
о
.
о
Здесь второе и третье слагаемые числителя взаимно уничтожаются (при любых положительных значениях ).
В знаменателе в соответствии со шкалой бесконечно больших функций слагаемым с меньшей степенью можно пренебречь. Единицей в числителе пренебрегаем по сравнению с бесконечно большим значением .
о о
.
о
Здесь
второе и третье слагаемые числителя
складываются (при любых отрицательных
значениях
),
образуя положительную величину .
Вторым слагаемое знаменателя пренебрегаем как величиной бесконечно большой низшего порядка, по сравнению с первым слагаемым (т.е. бесконечно малой по сравнению с первым слагаемым).
.
.
Ввиду того, что вычисленные пределы не совпадают, искомый предел — не существует.
о о о
.
о о
.
Оба последних предела вычисляются одинаково. Постоянными числами 1 и 4 пренебрегаем по сравнению с бесконечно большим значением .
Величиной также пренебрегаем, т. к. она является бесконечно малой: при .
Пример 5. Вычислить пределы функций, если они существуют, при и при
.
Решение
примера 5.
.
— не существует.
Последний предел не существует, т. к. под корнем в знаменателе стоит отрицательная величина. Это можно было сразу заметить, если бы мы рассмотрели область определения функции, стоящей под знаком предела.
Таким образом искомого предела функции при также не существует. Существует лишь предел слева в единице, который и был найден выше.
— предел не существует.
Последний предел не существует т. к. опять под корнем в знаменателе стоит отрицательная величина. Предела слева в точке x = 2 также не существует по тем же причинам.
.
Ввиду совпадения обоих пределов, в точке х =1, искомый предел существует и равен значению вычисленного предела:
.
.
Здесь
мы не стали вычислять отдельно левый и
правый пределы в точке х=2, ввиду того,
что скобка возводится в квадрат, и вычисления как
левого, так и правого пределов не
отличались бы друг от друга.
— не существует.
Здесь не существование предела связано с тем, окрестность точки х =1 не входит в область определения рассматриваемой функции, ввиду того, что аргумент логарифма должен быть только положительным: .
.
Предел слева в точке х = 2 не существует поскольку область определения рассматриваемой функции: . Таким образом, в точке х = 2 предел также не существует. (Существует лишь предел справа, который и был вычислен).
.
.
Поскольку в точке х = 1 пределы слева и справа не совпадают, искомый предел — не существует.
.
.
Ввиду того, что в точке х = 2 пределы справа и слева не совпадают, искомый не существует.
При вычислении значения арксинуса в нуле можно использовать график функции
y=arcsin x
-1 0 1 x
Пример
6.
Вычислить пределы функций при
Решение примера 6.
.
Здесь мы воспользовались формулами для функций, эквивалентных в нуле (см. § 4), причем для синуса и арктангенса ограничились лишь первым членом разложения в ряд Тейлора этих функций.
.
Здесь опять использованы различные формы функций, эквивалентных в нуле (см. § 4). Для синуса ограничились лишь первым членом разложения, а для показательной функции использованы ее два первых члена разложения в ряд Тейлора.
Необходимость учета именно двух членов разложения диктуется требованием, что в результате подстановки разложения под знак предела, после взаимного уничтожения слагаемых, какие то слагаемые должны оставаться. Здесь в знаменателе дроби осталось слагаемое ( ).
.
Здесь при
использовании различных форм функций,
эквивалентных в нуле (см.
§ 4), для
логарифмической функции оставлен первый
ее член разложения, а для косинуса
оставлены два его первых члена разложения
в ряд Тейлора.
Здесь в соответствии с § 4 были использованы различные формы функций, эквивалентных в нуле. При разложении функций в ряд Тейлора, слагаемыми ~ пренебрегали.
= .
Здесь в соответствии с § 4 были использованы различные формы функций, эквивалентных в нуле. При разложении функций в ряд Тейлора, слагаемыми ~ пренебрегали. Выражение, стоящее в знаменателе, преобразовывалось следующим образом:
.
Пример 7. Вычислить пределы функций, если они существуют, при
Решение примера 7.
.
Здесь
были использованы различные формы
функций, эквивалентных в нуле (см. § 4),
причем в качестве «нуля» выступала
величина .
.
Здесь были опять использованы различные формы эквивалентных в нуле функций (см. § 4), где в качестве «нуля» выступала величина .
.
Здесь были опять использованы различные формы функций, эквивалентных в нуле, а в качестве «нуля» выступала величина .
.
Здесь было использовано свойство логарифма: , где последнее равенство справедливо лишь при .
Рассмотрим теперь предел справа при :
—предел не существует,
поскольку в знаменателе дроби имеется логарифм от отрицательной величины, в то время как действительная функция логарифм определена лишь для положительных значений аргумента. Таким образом, и искомый предел не существует.
Пример 8. Вычислить пределы функций, если они существуют, при и при
Решение
примера 8.
о
.
о
Здесь пренебрегали бесконечно малой величиной в числителе по сравнению с единицей, а в знаменателе по сравнению с тройкой. Учтено также, что при возведении в бесконечно большую степень положительного числа, меньшего единицы, получается ноль.
о
.
о
Здесь в числителе и в знаменателе пренебрегли постоянными конечными числами по сравнению с бесконечно большим слагаемым ~ .
о
о
о о
о
Здесь в числителе и знаменателе, а также в показателе степени пренебрегли конечными величинами по сравнению с бесконечно большой величиной, ~ .
.
Для
раскрытия неопределенности вида воспользовались основным логарифмическим
тождеством: ,
а для освобождения от логарифма
воспользовались различными формами
функций, эквивалентных в нуле (см.
§ 4).
о
.
Для раскрытия неопределенности вида , опять воспользовались представлением
При раскрытии неопределенности вида использовали правило Лопиталя, при этом для упрощения под знаком логарифма пренебрегли единицей по сравнению с бесконечно большой величиной.
Аналогичного предела при не существует, ввиду того, что при больших отрицательных значениях основание действительной степенно-показательной функции становится отрицательным , при этом мы выходим за рамки ее области определения.
.
Здесь пренебрегалось бесконечно малыми величинами по сравнению с конечными — единицей, четверкой и двойкой.
о о
о о
.
Для
раскрытия неопределенности вида воспользовались представлением: .
Затем бесконечно малыми величинами
(двойкой по сравнению с
,
четверкой по сравнению с , единицей по сравнению с
и по
сравнению с ) пренебрегли.
Аналогичный предел при не существует, поскольку основание действительной степенно-показательной функции при больших отрицательных значениях
становится отрицательным: , что не соответствует ее области определения: .
о
.
Здесь для раскрытия неопределенности вида воспользовались представлением . Далее пренебрегли единицей по сравнению с бесконечно большой величиной . При раскрытии неопределенности вида использовали правило Лопиталя.
.
Здесь
при раскрытии неопределенности вида воспользовались представлением
.
Для разложении логарифма использовали
формы функций, эквивалентных в нуле,
см. § 4.
.
При раскрытии неопределенности вида воспользовались представлением .
Для раскрытия неопределенности вида использовали правило Лопиталя.
Искомый предел при не существует, ввиду отрицательности основания степени рассматриваемой функции .
Пример 9. Вычислить пределы функций при и при
Решение примера 9
о
.
Здесь
для удобства введена новая переменная .
Затем с помощью основного логарифмического
тождества степенная функция выражена
через показательную. Далее с учетом
шкалы бесконечно больших функций
пренебрегаем по сравнению с бесконечно большой
величиной ~
.
После раскрытия неопределенности вида по правилу Лопиталя, и представления
предела как произведения пределов,
вновь учитываем, что является величиной бесконечно малой
по сравнению с
.
.
Здесь после раскрытия неопределенности вида по правилу Лопиталя, в соответствии со шкалой бесконечно больших функций учтено, что является бесконечно малой величиной, по сравнению с .
о
.
о
Здесь неопределенности вида раскрывается по правилу Лопиталя.
о
.
о
Здесь в соответствии со шкалой бесконечно больших функций величиной пренебрегли как величиной бесконечно малой по сравнению с .
.
Здесь конечная величина обозначена как .
.
Здесь использовали различные формы функций, эквивалентных в нуле (см. § 4), в частности, при .
о
.
о
Здесь вводим новую переменную . Затем степенную функцию выражаем через показательную. Далее в соответствии со шкалой бесконечно больших функций, пренебрегаем бесконечно малой величиной по сравнению с величиной ~ . И наконец учитываем, что является бесконечно малой по сравнению и с показательной функцией .
о
.
Здесь в соответствии со шкалой бесконечно больших функций, пренебрегаем логарифмической функцией по сравнению со степенной .
о
.
Здесь бесконечно малой величиной пренебрегли по сравнению с бесконечно большой величиной .
о
.
Здесь
неопределенность вида
с помощью основного логарифмического
тождества преобразовали в неопределенность
вида
,
которую раскрывали с помощью правила
Лопиталя.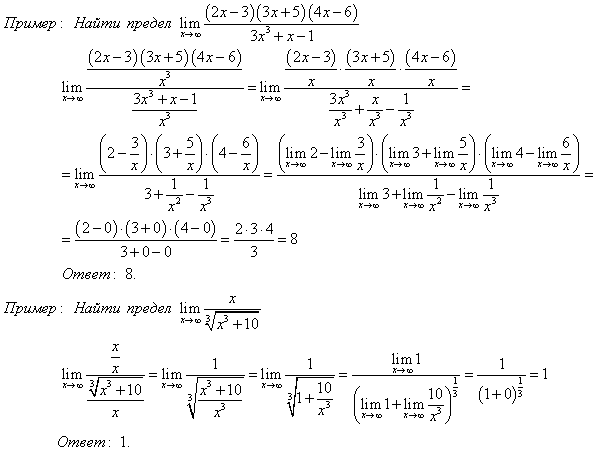
Далее в соответствии со шкалой
бесконечно больших функций учтено, что является бесконечно малой величиной
по сравнению со степенной функций
,
в результате чего, оказалось возможным
пренебречь бесконечно малой величиной
~
по сравнению с единицей.
.
.
о
Здесь пренебрегли степенной функцией по сравнению с показательной , поскольку их отношение . (Соотношение легко проверяется, если к нему применить правило Лопиталя). Затем, неопределенность вида раскрывали с использованием правила Лопиталя.
Пример 10. Вычислить указанные пределы
.
Решение примера 10.
.
Ввиду того, что пределы слева и справа в точке не совпадают, искомого предела не существует.
.
Здесь учтено, что .
о
.
Здесь после освобождения от модуля для раскрытия неопределенности вида использовано правило Лопиталя. Затем, пренебрегая единицей по сравнению с бесконечно большой величиной, и желая применить шкалу бесконечно больших функций, вводим новую переменную .
В соответствии со шкалой бесконечно больших функций, учитываем, что является бесконечно малой по сравнению с функцией.
о
Здесь после выяснения вида неопределенности мы не стали применять правило Лопиталя, т. к. оно привело бы к усложнению функции, стоящей по знаком предела.
Вместо этого, используя основное логарифмическое тождество, прологарифмировали первоначально заданную функцию. Затем, пренебрегая конечной величиной по сравнению с бесконечно большой величиной , получаем конечный результат.
Пример 11. Найти поведение функции при
Решение
примера 11.
.
.
Здесь после освобождения от модуля использована формула для эквивалентных в нуле функций: .
Поведение заданной функции определяется найденными пределами. Добавки (-0) означают, что график функции располагается ниже соответствующих значений пределов (см. Рис 1). Стрелки на графике означают исключение из области допустимых значений аргумента точки с абсциссой .
y y
1
o x
0 1 x
-1
Рис. 1 Рис. 2
.
.
Здесь
неопределенность вида раскрывалась по правилу Лопиталя.
Поведение заданной функции определяется найденными значениями пределов. Схематический рисунок графика функции в окрестности точки см. на Рис. 2. Стрелка на графике означает, что точка с абсциссой исключена из области допустимых значений аргумента.
.
Здесь для раскрытия неопределенности вида было использовано правило Лопиталя.
Предела слева в точке рассматривать нет необходимости, т. к. заданная функция определена только для положительных значений аргумента .
Поведение функции справа от нуля изобразим на Рис. 3
y y
1
o x x
Рис. 3 Рис. 4
.
Здесь
для раскрытия неопределенности вида использовали основное логарифмическое
тождество.
Затем использовали различные
формы представления функций, эквивалентных
в нуле. В частности, для логарифма
использовали формулу ,
справедливую при
.
Далее, по шкале бесконечно больших
функций определили, что логарифм
является бесконечно малой величиной
по сравнению со степенной функцией
.
Поведение заданной функции при изображено на Рис. 4.
Пределы прямой подстановки — GeeksforGeeks
Пределы являются строительными блоками исчисления. Это значения, которые, по-видимому, принимает функция, когда мы достигаем определенной точки. Они помогают вычислить скорость изменения функций. Понятие производных было определено с ограничениями. Они также помогают нам определить понятия непрерывности и дифференцируемости. Таким образом, становится важным понять их интуицию и различные методы определения пределов для различных категорий функций.
Пределы
С точки зрения геометрии предел функции в определенной точке можно легко оценить по ее графику.
Например, на приведенном ниже графике при x = 3. Функция как бы принимает значение 1. В данном случае не имеет значения, с какой стороны мы подходим — с левой и с правой стороны .
Для функции f(x) предел при x = a обозначается как
Пределы с использованием прямой подстановкиПравило подстановки для расчета пределов — это метод нахождения пределов путем простой замены значения x на точку, в которой мы хотим вычислить предел. Рассмотрим функцию f(x), цель состоит в том, чтобы найти предел функции в точке x = a. В этом методе x просто заменяется на «a» в выражении функции f(x).
Давайте рассмотрим этот метод на примере:0003
⇒
⇒
⇒
Часто с помощью этого правила можно вычислить пределы функции, если говорить формально.
Если f(x) представляет собой выражение, построенное из многочленов, корней, абсолютных значений, экспонент, логарифмов, тригонометрических функций и/или обратных тригонометрических функций с использованием композиции функций и таких операций, как x, +, -, / тогда для любого a, для которого определено f(a),
Неопределенные пределы прямой подстановкой
Существуют определенные пределы, которые нельзя рассчитать этим методом.
Например, рассмотрим функцию f(x) = , вычислите предел для этой функции при x = 1.
⇒
⇒
⇒
Этот предел не определен. В таких случаях применяется метод прямой замены.
Пределы тригонометрической функции
Иногда можно использовать прямую замену для вычисления пределов функций, включающих тригонометрические функции. Например, предположим, что у нас есть функция f(x), и мы хотим вычислить пределы для этой функции при x = 0. Давайте рассмотрим это на примере.
Пример: Рассчитайте
F (x) = sin (x) + sin (x) cos (x)
Решение:
⇒
⇒
⇒
⇒
⇒
ента ⇒ 0 × (1 + 1)
⇒ 0
Пределы кусочной функции
При работе с кусочными функциями правило подстановки, как правило, не работает в местах изменения определения функции.
Он используется немного измененным способом для этих функций. Давайте решим пример задачи, чтобы лучше понять это,
Пример. Рассчитайте значение .
Решение:
При x = 1 определение функции меняется. Поэтому не рекомендуется применять правило напрямую. В таких функциях следует искать предел с обеих сторон.
левый боковой предел
⇒
⇒1
Правосторонняя сторона
⇒
⇒0
В этом случае пределы с обеих сторон различны.
Let’s see some problems on these concepts
Sample Problems
Question 1: Calculate the
f(x) = x 2 + x + 1
Solution:
⇒
⇒
⇒ 1
Question 2: Calculate the
f(x) =
Solution:
⇒ \
⇒
⇒
Вопрос 3.
Вычислите значение .
Решение:
При x = 1 определение функции меняется. Поэтому не рекомендуется применять правило напрямую. В таких функциях следует искать предел с обеих сторон.
Левый предел
⇒
Правый предел
⇒
В этом случае пределы с обеих сторон разные.
Question 4: Calculate the
f(x) =
Solution:
⇒ \
⇒
⇒
⇒ e + 2
Question 5 : Calculate the
f(x) =
Solution:
⇒ \
⇒
⇒
⇒ e sin(1) + 2
Question 6 : Рассчитать с использованием правила подстановки.
f(x) =
Решение:
⇒ \
⇒
⇒ форма не определена.
Здесь нельзя использовать правило подстановки.
Здесь нельзя использовать правило подстановки.Вопрос 7. Рассчитайте значение .
Решение:
При x = 1 определение функции меняется. Поэтому не рекомендуется применять правило напрямую. В таких функциях следует искать предел с обеих сторон.
Левый предел
⇒
Правый предел
⇒
В этом случае пределы с обеих сторон разные.
Теоремы о пределах. Подход к исчислению
Подход
к
C A L C U L U S
Содержание | Дом
2
Раздел 2: Теоремы о пределах
Пределы многочленов
Назад к Разделу 1
Теперь мы докажем, что некоторый предел существует , а именно предел f ( x ) = x , поскольку x приближается к любому значению c . (То, что f ( x ) также приближается к c , должно быть очевидно.
)
ТЕОРЕМА. Если f ( x ) = x , то для любого значения c , которое мы могли бы назвать:
Для, если последовательность значений переменной c x приближается к x предел (определение 2.1), то последовательность значений функции f ( x ) = x также будет приближаться к c в качестве предела (определение 2.2).
Например,
Теоремы о пределах
Чтобы помочь нам вычислить пределы, можно доказать следующее.
Пусть f и g являются функциями переменной x . Тогда, если существуют следующие пределы:
| 1) | ( ж + г ) = А + Б . | ||
| 2) | ( f g ) = AB . | ||
| 3) | ж г | = | А Б | , если B не равно 0. |
Другими словами:
1) Предел суммы равен сумме пределов.
2) Предел произведения равен произведению пределов.
3) Предел частного равен частному пределов,
3) при условии, что предел знаменателя не равен 0.
Также, если c не зависит от x — если c является константой — тогда
| 4) |
Чтобы убедиться в этом, приблизите x к 4: например,
| 4 | 1 2 | 4 | 1 4 | 4 | 1 8 | 4 | 1 16 | 4 | 1 32 | . . . |
Тогда значение 5 или любая константа не изменится. Это постоянно!
Когда c является постоянным множителем, но f зависит от x , тогда
| 5) |
Постоянный коэффициент может проходить через знак ограничения . (Это следует из теорем 2 и 4.) Например,
Пример 1. Процитируйте теоремы с 1) по 5), чтобы доказать следующее:
Решение . x 2 = x · x . А мы доказали, что существует и равно 4. Следовательно, согласно теореме 2,
То есть
Из этого примера должно быть ясно, что для оценки предела любой степени x , поскольку x приближается к любому значению, просто оцените мощность при этом значении. Повторное применение теоремы 2 подтверждает это.
| Задача 2. |
Задача 3. Оцените следующие пределы и обоснуйте свои ответы, цитируя теоремы с 1 по 5.
4 3 + 4 = 64 + 4 = 68. Это следует из теоремы 1 и теоремы 2.
4 2 + 1 = 16 + 1 = 17. Это следует из теорем 1, теорем 2 и теорем 4.
5 · 4 2 = 5 · 16 = 80. Это следует из теоремы 5 и теоремы 2.
| 15 5 | = 3, |
Пределы числителя и знаменателя следуют из теорем 1, 2 и 4. Предел дроби следует из теоремы 3.
Пределы многочленов
Учащийся может подумать, что для оценки предела по мере приближения x к значению все, что мы делаем, — это оцениваем функцию при этом значении. И по большей части это правда.
Одним из наиболее важных классов функций, для которых это верно, являются многочлены. (Тема 6 Precalculus.) Многочлен от x имеет следующую общую форму:
, где n — целое число, а а п 0.
Следовательно, согласно теоремам о пределах, чтобы назвать предел многочлена, когда x приближается к любому значению c , просто оцените многочлен при этом значении.
Если P ( x ) полином, то
Сравните пример 1 и задачу 2.
(В следующем разделе мы увидим, что это эквивалентно утверждению, что многочлены являются непрерывными функциями.)
Важно еще раз отметить, что когда мы пишем
the variable x is never equal to c , and therefore P ( x ) is never equal to P ( c ) Both c and P ( c ) приближаются к предельным значениям.
Дело в том, что мы можем назвать предел, просто вычислив функцию по адресу c .
| Задача 4. Оценить |
Пусть в этом многочлене x = −1:
. 5(1) — 4(-1) + 3(1) — 2(-1) + 1
= 5 + 4 + 3 + 2 + 1
= 15,
| Задача 5. Оценить |
При замене 90 336 x 90 337 на 90 336 c с + с = 2 с .
| Задача 6. Вычислить |
[Подсказка: это многочлен от t .]
При замене t на −1:
3(−1) 2 −5(−1) + 1 = 3 + 5 + 1 = 9,
| Задача 7. Вычислите |
[Подсказка: это многочлен от ч .]
При замене ч на 0 предел равен 4 x 3 .
Однако некоторые из наиболее важных ограничений не будут полиномами.
Они будут пределами некоторых частных — и они окажутся таковыми!
Разобраться с этим будет непросто.
Пример 2. Рассмотрим функцию г ( х ) = х + 2, график которого представляет собой простую прямую линию. И просто для извращения (и для иллюстрации логического момента, к которому мы вернемся в Уроке 3), пусть следующая функция f ( x ) не определена для x = 2. То есть пусть
Другими словами, точка (2, 4) не принадлежит функции; его нет на графике.
Тем не менее предел при приближении x к 2 — слева или справа — равно 4
Ибо любая последовательность значений x , которая приближается к 2, может прийти к , близкому к 2, как нам угодно. (В любом случае предел переменной никогда не является членом последовательности; определение 2.1.) Следовательно, соответствующие значения f ( x ) будут все ближе и ближе приближаться к 4.