Вычислить сумму ряда с точностью: Вычисление суммы ряда с заданной точностью — Программирование на C, C# и Java

§4. Приближенное вычисление суммы числового ряда.

Поскольку точное значение суммы ряда удается вычислить далеко не всегда (такие задачи были нами рассмотрены), возникает проблема приближенного вычисления суммы ряда с заданной точностью.

Напомним, что -ый остаток рядаполучается из исходного рядаотбрасыванием первыхслагаемых:

.

Тогда, поскольку для сходящегося ряда ,

остаток сходящегося ряда равен разности между суммой ряда и -ой частичной суммой:

,

и для достаточно больших имеем приближенное равенство

.

Из определения остатка ряда следует, что абсолютная погрешность при замене точного неизвестного значения суммы его частичной суммойравна модулю остатка ряда:

.

Таким образом, если требуется вычислить сумму ряда с заданной точностью , то нужно оставить сумму такого числаслагаемых, чтобы для отброшенного остатка ряда выполнялось неравенство:

.

Метод приближенного вычисления суммы выбирается в зависимости от вида ряда:

если ряд положительный и может быть исследован на сходимость по интегральному признаку (удовлетворяет условиям соответствующей теоремы), то для оценки суммы используем формулу

;

если это ряд Лейбница, то применяем оценку:

.

В других задачах можно использовать формулу суммы бесконечно убывающей геометрической прогрессии.

Задача №1. Сколько нужно взять слагаемых ряда, чтобы получить его сумму с точностью 0,01.

Решение.Прежде всего отметим, что данный ряд сходится. Рассмотрим-ый остаток ряда, который и является погрешностью вычислений суммы ряда:

.

Оценим этот ряд с помощью бесконечно убывающей геометрической прогрессии. Для этого заменим в каждом слагаемом множитель на, при этом каждое слагаемое увеличится:

После вынесения общего множителя за скобку, в скобке остался ряд, составленный из членов бесконечно убывающей геометрической прогрессии, сумму которого мы и вычислили по формуле

.

Заданная точность будет достигнута, если будет удовлетворять условию

.

Решим неравенство, учитывая, что — целое.

При имеем

.

При имеем

.

В силу монотонности функции , неравенствобудет выполняться для всех.

Следовательно, если вместо точного значения суммы мы возьмем первые пять (или более) слагаемых, то погрешность вычислений не превысит 0,01.

Ответ: .

Задача №2. Оценить ошибку, получаемую при замене суммы рядасуммой первых 100 слагаемых.

Решение.Заметим, что данный ряд является сходящимся и знакопеременным. Оценивать будем ряд, состоящий из модулей исходного ряда, что сразу увеличивает погрешность вычислений. Кроме того, нам придется перейти (используя признак сравнения) к большему, более простому сходящемуся ряду:

.

Рассмотрим ряд . Поскольку этот ряд удовлетворяет условиям теоремы – интегрального признака сходимости, то для оценки погрешности вычисления суммы используем соответствующую формулу:

.

Вычислим несобственный интеграл:

,

погрешность вычислений можно оценить по формуле

,

по условию , тогда.

Ответ: .

Задача №3. Оценить ошибку, получаемую при замене суммы рядасуммой первых 10 слагаемых.

Решение.Подчеркнем еще раз, что задача о приближенном вычислении суммы имеет смысл только для сходящегося ряда, поэтому, прежде всего отметим, что данный ряд сходится. Поскольку исследуемый ряд является знакопеременным со сложным правилом изменения знака, то оценивать придется, как и в предыдущем примере, ряд из модулей данного ряда:

.

Используя тот факт, что при любом значении аргумента, имеем:

.

Оценим остаток ряда:

.

Мы получили ряд, составленный из членов бесконечно убывающей геометрической прогрессии, в которой

,

его сумма равна:

,

.

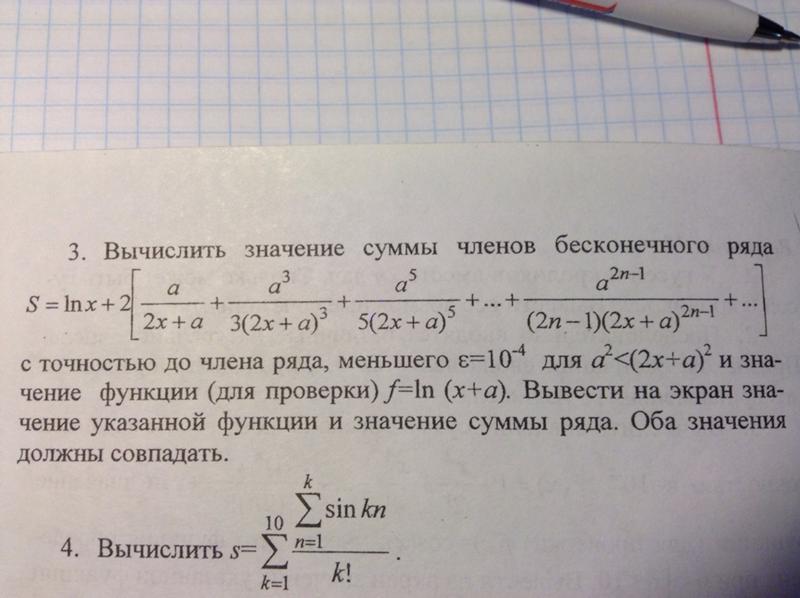
Ответ: .

Задача №4. Вычислить сумму рядас точностью 0,01.

Решение.Данный ряд является рядом Лейбница. Для оценки погрешности верна формула:

,

другими словами, погрешность вычислений меньше модуля первого отброшенного слагаемого. Подберем номер так, чтобы

.

При имеем

.

При имеем

.

Погрешность , если в качестве значения суммы возьмем сумму первых четырех слагаемых:

.

Ответ:.

Вычислить сумму ряда с точностью а=0.001 — вопрос №2576900 — Учеба и наука

Лучший ответ по мнению автора

05. 09.17 Лучший ответ по мнению автора

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

вычислить сумму ряда с точностью a=0. 001

Здравствуйте! Помогите пожалуйста с математикой: Сумма S существует и конечна. Найдите ее.

Решено

Помогите пожалуйста с математикой!!! 3 фото(пояснение) : Сумма S существует и конечна. Найдите ее. Помогите чем сможете,решить сама пробовала,но не получилось :((((

Пользуйтесь нашим приложением

python — бесконечная сумма с заданной точностью

спросил 1 год, 5 месяцев назад

Изменено 1 год, 5 месяцев назад

Просмотрено 319 раз

Я пытался решить эту бесконечную сумму с заданной точностью. Вы можете увидеть описание на картинке ниже

Вот что я пробовал до сих пор:

 импортировать математику
def infin_sum(x, eps):
    сумма = плавающая (0)
    пред = ((-1)*(х**2))/2
    я = 2
    пока верно:
        текущий = предыдущий + ((-1)**i) * (x**(2*i)) / math. factorial(2*i)
        если (абс (текущая - предыдущая) <= eps):
            печать (текущая)
            обратный ток
        предыдущий = текущий
        я+=1
 

Для данного выборочного ввода (0,2 для x и точность 0,00001) моя сумма равна 6,65777777777778e-05 и, согласно их тестам, она недостаточно близка к правильному ответу

• питон

1

Вы должны использовать math.isclose() вместо abs() для проверки сходимости (учитывая, что именно так будет проверяться результат). учитывая, что каждая итерация добавляет или вычитает определенный термин, дельта между предыдущим и следующим (Si-1 против Si) будет равна последнему добавленному термину (поэтому вам не нужно отслеживать предыдущее значение).

Эта бесконечная серия почти для косинуса (было бы, если бы я начал с нуля), поэтому вы можете проверить свой результат против math.cos(x)-1 . Кроме того, я нахожу странным, что проверка ожидаемого результата фиксируется с точностью до 0,0001, но в образце ввода указана точность 0,00001 (я думаю, более точно будет в пределах 0,0001, но тогда проверка на самом деле не проверяет правильность вывода учитывая ввод?)

 из math import isclose
def cosMinus1 (х, точность = 0,00001):
    результат = 0
    числитель = 1
    знаменатель = 1
    даже = 0
    while not isclose(numerator/denominator,0,abs_tol=precision): # достичь точности
        числитель *= -x*x # +/- для четных степеней x
        даже += 2
        знаменатель *= четный * (четный-1) # факториал четных чисел
        результат += числитель / знаменатель # сумма слагаемых
    вернуть результат
печать (cosMinus1 (0,2))
# -0,019933422222222226
импортировать математику
ожидается = math. cos(0.2)-1
print(ожидаемый, math.isclose(ожидаемый,cosMinus1(0.2),abs_tol=0.0001))
# -0.019933422158758374 Верно
 

Поскольку затенение суммой не является хорошей идеей, у вас была правильная идея назвать его current , но вы не инициализировали current значением float(0) и забыли его суммировать. Это ваш код с исправленными проблемами:

 def infin_sum(x, eps):
    текущий = плавающий (0)
    пред = ((-1) * (х ** 2)) / 2
    я = 2
    пока верно:
        текущий = текущий + (((-1) ** i) * (x ** (2 * i))) / math.factorial (2 * i)
        если (абс (текущая - предыдущая) <= eps):
            печать (текущая)
            обратный ток
        предыдущий = текущий
        я += 1
 

В качестве более общего комментария, печать внутри такой функции, вероятно, не лучшая идея - это ограничивает возможность повторного использования функции - в идеале вы хотели бы захватить возвращаемое значение и распечатать его вне функции.

1

Во-первых, вы не суммируете элементы.

Пересчитывать все с нуля очень расточительно, а точность с плавающей запятой с ограничена.

Вы можете использовать метод Хорнера для уточнения суммы:

 импорт математики
 def infin_sum(x, eps):
     всего = с плавающей запятой (0)
     е = 1
     всего = 0
     я = 1
     в то время как abs(e) >= eps:
         diff = (-1) * (x ** 2) / (2 * i) / (2 * i - 1)
                                                          
         е *= разница
         всего += е
         я += 1
                                                          
     общая сумма возврата
                                                   
                                                   
 если __name__ == "__main__":
     х = бесконечная_сумма (0,2, 0,00001)
     печать (х)
 

Не забудьте добавить результат, а не заменить его:

 пред. += текущий
 

вместо

 пред.  = текущий
 

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Теорема об оценке переменного ряда для оценки значения ряда и определения ошибки — Криста Кинг Математика

Использование теоремы об оценке переменного ряда требует от нас соблюдения двух правил.

Теорема оценки переменного ряда дает нам способ аппроксимировать сумму переменного ряда с остатком или ошибкой, которую мы можем вычислить.

Чтобы использовать эту теорему, наш ряд должен подчиняться двум правилам:

1. Ряд должен быть убывающим , ???b_n\geq b_{n+1}???

2. Предел серии должен быть равен нулю, ???\lim_{n\to\infty}b_n=0???

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Как только мы подтвердим, что наш чередующийся ряд удовлетворяет этим двум условиям, мы можем вычислить ошибку, используя

???|R_n|=|s-s_n|\le{b_{n+1}}???

Как рассчитать ошибку, используя оценку переменного ряда

Пройти курс

Хотите узнать больше об исчислении 2? У меня есть пошаговый курс для этого.

🙂

Узнать больше

Использование теоремы оценки переменного ряда для аппроксимации переменного ряда до трех знаков после запятой

Пример

Аппроксимация суммы ряда до трех знаков после запятой. 9п}???

Мы будем вычислять первые несколько членов ряда, пока не получим стабильный ответ с точностью до трех знаков после запятой.

Далее нам нужно суммировать эти члены, пока мы не увидим, что третий десятичный знак не меняется.

Сложив первые два члена вместе, мы получим

???a_1+a_2=0.1+(-0.02)???

???a_1+a_2=0,1-0,02???

???a_1+a_2=0,08???

???s_2=0.08???

Так как мы не до трех знаков после запятой, мы добавим еще один член к сумме

???a_1+a_2+a_3=0,1+(-0,02)+0,003???

???a_1+a_2+a_3=0,1-0,02+0,003???

???a_1+a_2+a_3=0,083???

???s_3=0,083???

Мы дошли до трех знаков после запятой, но нам нужно убедиться, что четвертый знак после запятой не приведет к округлению третьего знака после запятой.

???a_1+a_2+a_3+a_4=0,1+(-0,02)+0,003+(-0,0004)???

???a_1+a_2+a_3+a_4=0,1-0,02+0,003-0,0004???

???a_1+a_2+a_3+a_4=0,0826???

???s_4=0.0826??? 9{n+1}}???

Теперь мы можем вычислить первые три члена для обоих ???b_n??? и ???b_{n+1}???.

Теорема об оценке переменного ряда дает нам способ аппроксимировать сумму переменного ряда с остатком или ошибкой, которую мы можем вычислить.

Глядя на эти результаты, мы видим, что ???{b_n}\geq b_{n+1}???, поэтому ???b_n??? уменьшается.

Далее нужно показать, что ???\lim_{n\to\infty}b_n=0???. 94}???

???|R_3|\le\frac{1}{2,500}???

???|R_3|\le0.0004???

Приблизительная сумма ряда с точностью до трех знаков после запятой равна ???0,083??? с ошибкой ???|R_3|\le0.0004???.

Получить доступ к полному курсу Calculus 2

Начать

Изучайте математикуКриста Кинг 15 мая 2019 г.