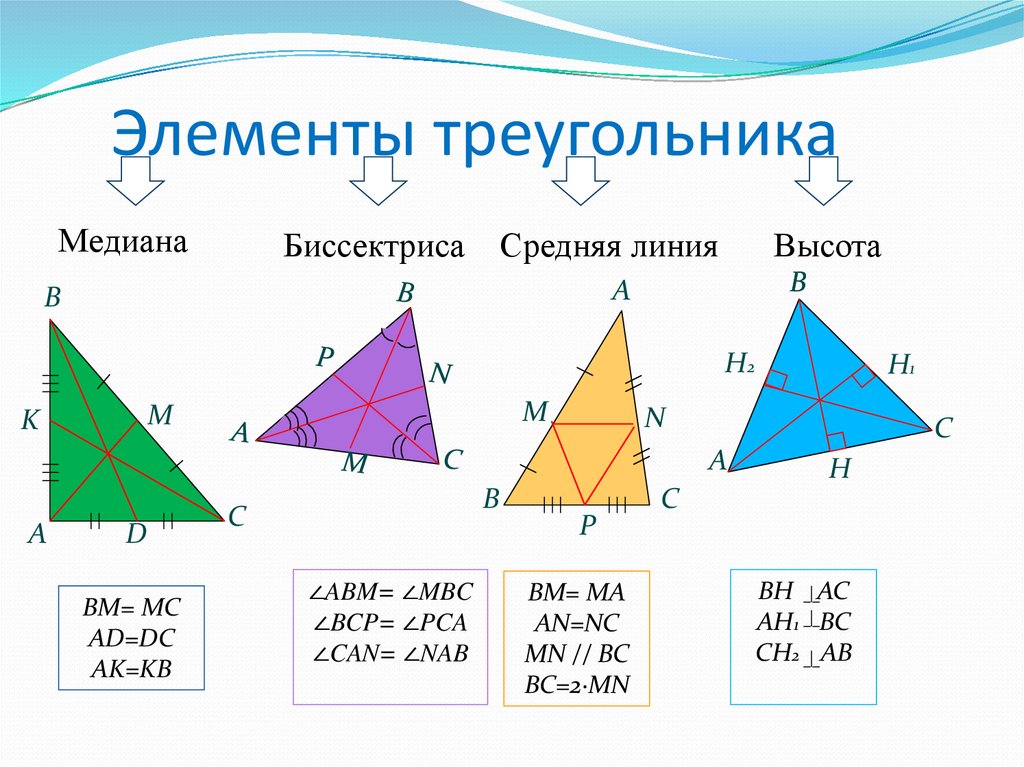
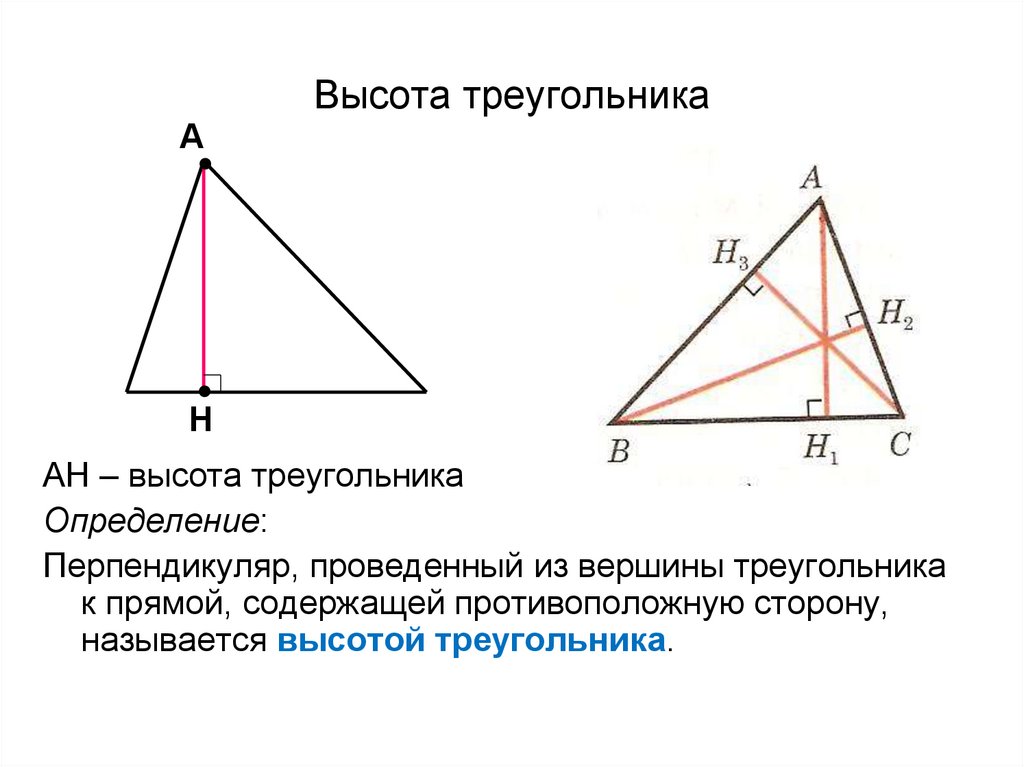
Высота треугольника, биссектриса и медиана
Содержание
Из вершин треугольника к противолежащим от вершин сторонам можно проводить различные отрезки, причем так, чтобы получать «интересные данные» внутри фигуры. К примеру, отрезок из вершины можно опустить таким образом, что в итоге он «приземлится» ровно посередине противолежащей от вершины стороны. В геометрии существует три подобных отрезка, что задают для треугольника новые геометрические параметры — высота треугольника, биссектриса треугольника и медиана треугольника.
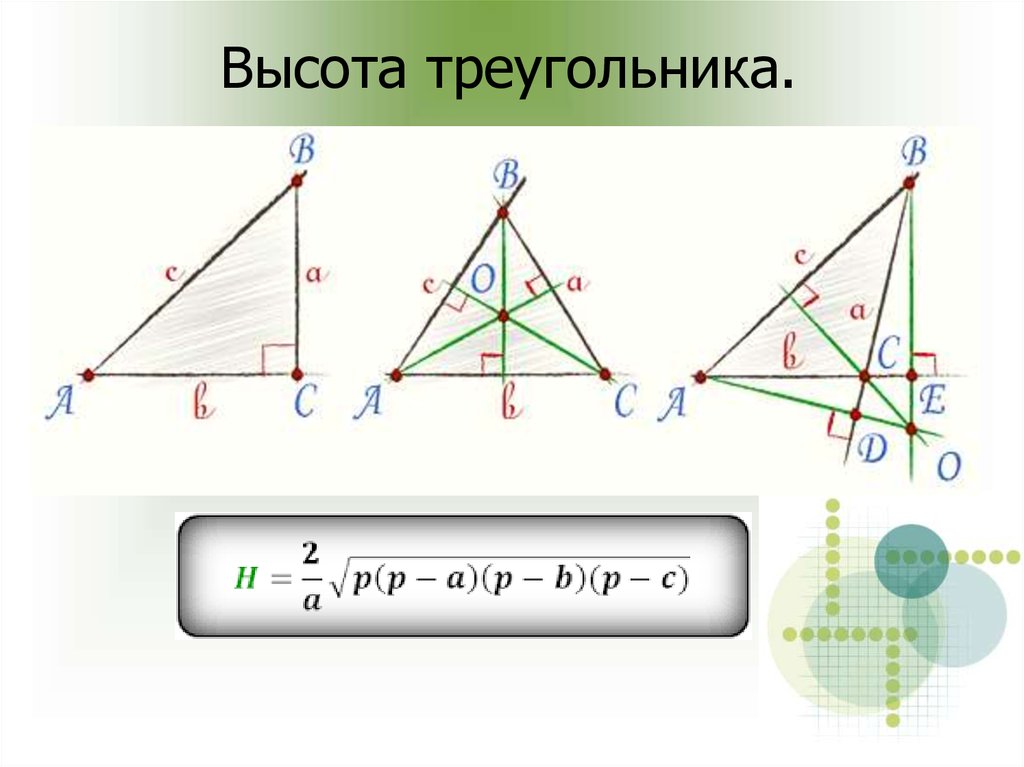
Высота треугольникаПусть нам дан треугольник $\bigtriangleup{ABC},$ где из вершины $C$ к противолежащей стороне $AB$ опущен отрезок $CD$, образующий при этом перпендикуляр к стороне $AB$. Тогда отрезок $CD$ будет являться высотой треугольника $\bigtriangleup{ABC}$. Аналогичный перпендикуляр можно опустить как из вершины $A$, так и из вершины $B$.
Получается, что:
Высота треугольника — перпендикуляр, проведенный из вершины к прямой, содержащей противолежащую сторону треугольника.
{\circ},$ — провести высоту будет уже не так интуитивно просто.
Осмотрите треугольник $\bigtriangleup{PMK}$ выше, с тупым углом $\angle{M}$.
Нам необходимо провести высоту из вершины $K$ к стороне $PM$. Подумайте, как будет располагаться отрезок, выполните чертеж и сравните свои предположения со скрытым чертежом.
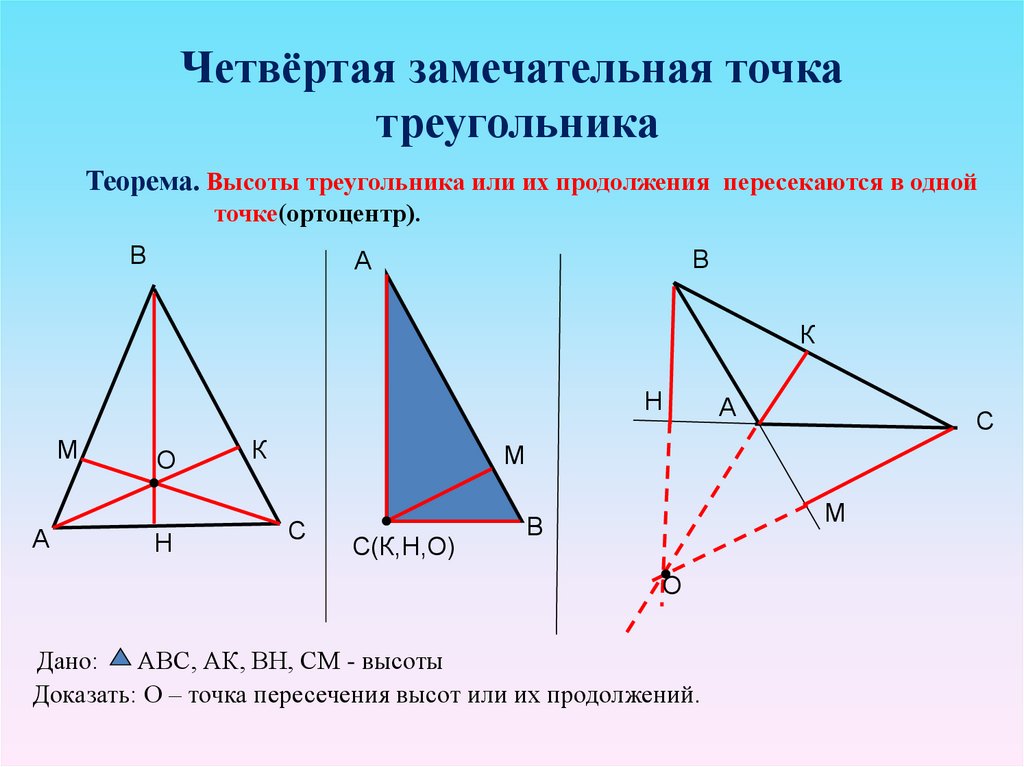
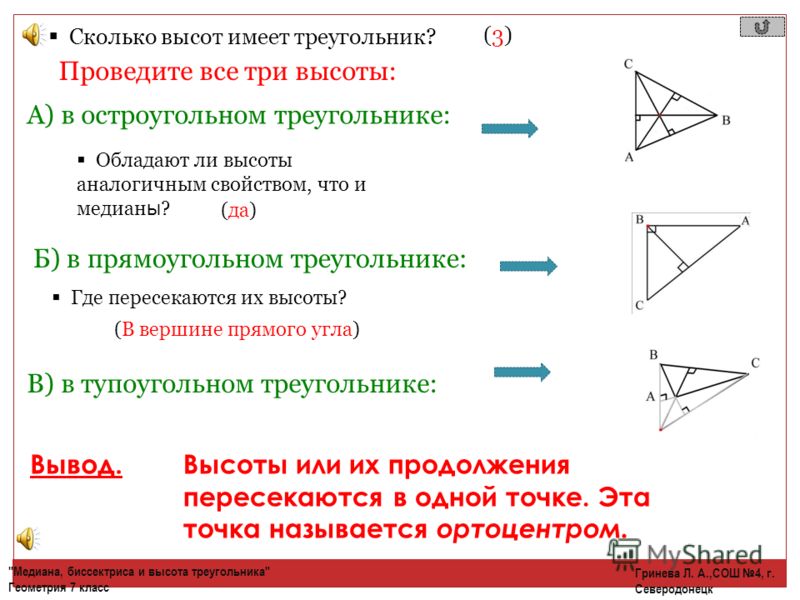
Пересечение высот: как найти высоту треугольника
Выходит, что в остроугольном треугольнике высоты пересекаются в точке, расположенной строго внутри треугольника — никаких дополнительных построений не требуется.
Высоты в тупоугольном треугольнике пересекаются в точке, расположенной вне треугольника, — чтобы найти высоту треугольника, необходимо достраивать продолжение сторон. Так, в случае с нашим тупоугольным треугольником, высоты пересекаются в точке $O$ — внимание на чертеж выше.
{"questions":[{"content":"[[image-1]] Помимо остроугольного и тупоугольного треугольника, существует треугольник прямоугольный — частный случай, когда один из углов прямой, то есть равняется $90^{\\circ}$.Биссектриса угла треугольникаЧто это за треугольник и какими свойствами он обладает, подробнее мы разберем далее в курсе геометрии. Пока что давайте просто поразмышляем: а где же будут <b>пересекаться высоты</b> в прямоугольном треугольнике? [[choice-11]]","widgets":{"image-1":{"type":"image","url":"http://obrazavr.ru/wp-content/uploads/2022/02/test-right.svg","width":"500"},"choice-11":{"type":"choice","options":["Внутри треугольника.","Внутри по центру треугольника.","Вне треугольника.","В вершине прямого угла."],"explanations":["","","","Это очень логично! <br /><br />В треугольнике $\\bigtriangleup{ABC}$ сторона $AB$ является высотой к стороне $BC$, и наоборот, ведь $\\angle{B}$ — прямой. Высота к стороне $AC$ будет выходить из вершины $B$. Так что точка пересечения высот в прямоугольном треугольнике, получается, располагается в точке $B$ — в вершине прямого угла."],"answer":[3]}}}]}
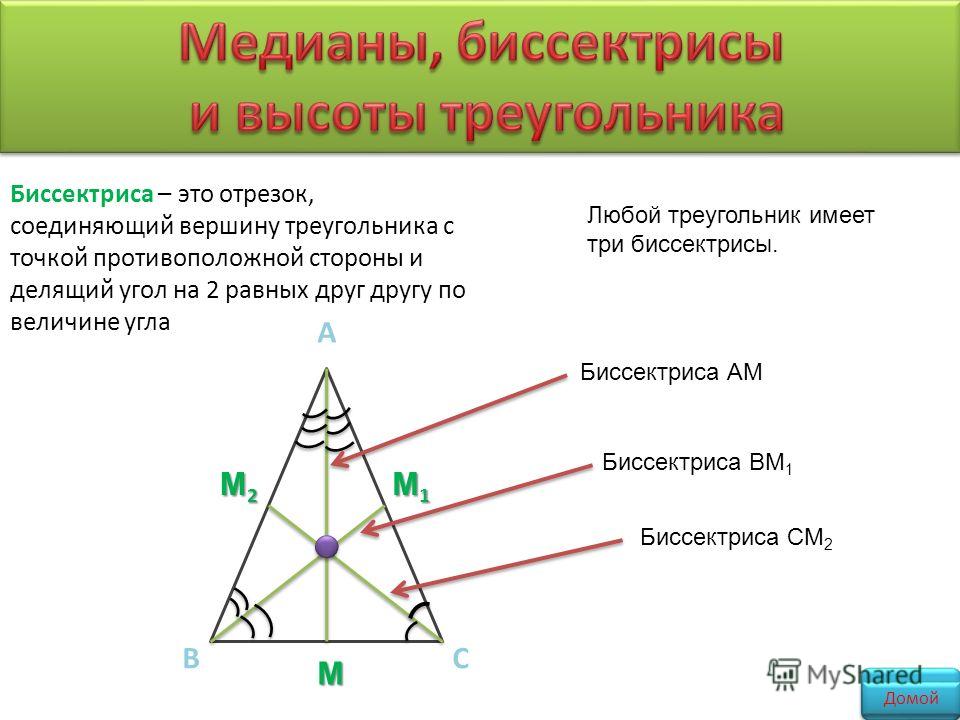
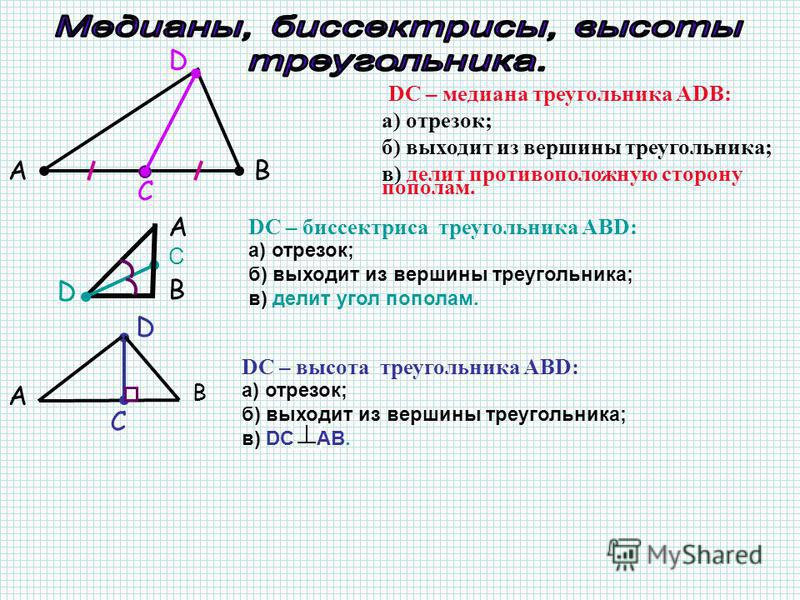
Пусть нам дан треугольник $\bigtriangleup{ABC},$ где из вершины $C$ к противолежащей стороне $AB$ опущен отрезок $CD$ таким образом, что $\angle{C}$ делится отрезком $CD$ на два равных друг другу угла.
Тогда отрезок $CD$ будет называться биссектрисой угла треугольника $\bigtriangleup{ABC}$ (от лат. ‘bi’ — «два», ‘secare’ — «резать»).
По аналогии с высотами, биссектриса угла треугольника опускается как из вершины $A$, так и из вершины $B$.
Дадим определение:
Биссектриса треугольника — отрезок, соединяющий вершину с противолежащей стороной и делящий при этом угол данной вершины пополам.
В отличие от высоты, биссектриса — понятие, теснее связанное с углом, чем с треугольником, поэтому ряд ее свойств больше определяет геометрию углов, чем геометрию треугольников. Например, одно из таких замечательных свойств связано со смежными углами. Оказывается, что биссектрисы, проведенные из смежных углов, будут образовывать прямой угол. Давайте это докажем!
Теорема о биссектрисах смежных углов. Биссектрисы смежных углов взаимно перпендикулярны.
Доказательство.
Медиана{\\circ}-\\angle{AOK}.$»,»Осталось только посчитать!»]}]}
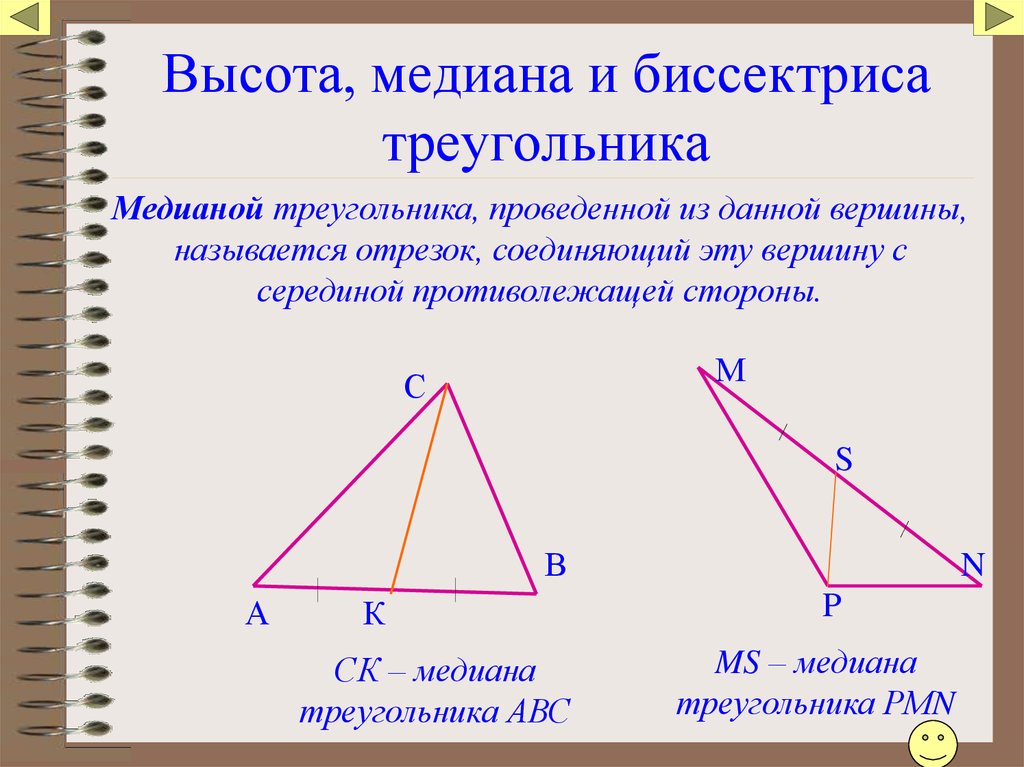
Наконец, проведем отрезок $CD$ в треугольнике $\bigtriangleup{ABC}$ из вершины $C$ к противолежащей стороне $AB$ таким образом, что сторона $AB$ поделится на два равных друг другу отрезка. Мы получили третий важный отрезок в треугольнике — медиану (от лат. ‘medianus’ — «средний»).
По определению:
Медиана треугольника — отрезок, соединяющий вершину с серединой противолежащей стороны.
{"questions":[{"content":"[[image-1]] Есть три треугольника. Есть три отрезка — медиана, высота и биссектриса. Попробуйте определить, где какой отрезок проведен. <br />[[matcher-4]]","widgets":{"image-1":{"type":"image","url":"http://obrazavr.ru/wp-content/uploads/2022/02/test-3.svg"},"matcher-4":{"type":"matcher","labels":["Треугольник «1»","Треугольник «2»","Треугольник «3»"],"items":["Биссектриса","Медиана","Высота"]}}}]}Обратили внимание?
Медианы, как и биссектрисы с высотами, пересекаются в одной точке внутри треугольника.
Исключением является тупоугольный треугольник и его высоты: высоты в тупоугольном треугольнике пересекаются вне треугольника.
Доказать это, к сожалению, нам пока не по силам, ибо требуется знание нескольких важных теорем, которые мы обязательно изучим в курсе далее. Как только, так сразу. Пока — принять, понять, поверить, что медианы треугольника пересекаются в одной точке.
Решим задачу!
В $\bigtriangleup{ABC}$ проведена медиана $AD$ к стороне $BC$. Продолжение медианы проходит через точку $E$, расположенную вне треугольника так, что $AD=DE$. Докажите, что треугольники $\bigtriangleup{ACD}$ и $\bigtriangleup{BED}$ равны.
Дано:
$\bigtriangleup{ABC}$
$CD=DB$
$AD=DE$Найти:
$\bigtriangleup{ACD}=\bigtriangleup{BED}$
Решение
Рассмотрим $\bigtriangleup{ACD}$ и $\bigtriangleup{BED}$. В них углы $\angle{ADC}$ и $\angle{BDE}$ равны как вертикальные.По заданному условию $AD=DE$. Также имеем равенство сторон $CD=DB$ — по определению медианы: отрезка, делящего противолежащую от угла сторону на два равных отрезка.
Следовательно $\bigtriangleup{ACD}= \bigtriangleup{BED}$ по первому признаку равенства треугольников: двум сторонам и углу, лежащему между ними.
Что и требовалась доказать.
Высота треугольника по углу и стороне. Высота треугольника
Треугольники.
Основные понятия.
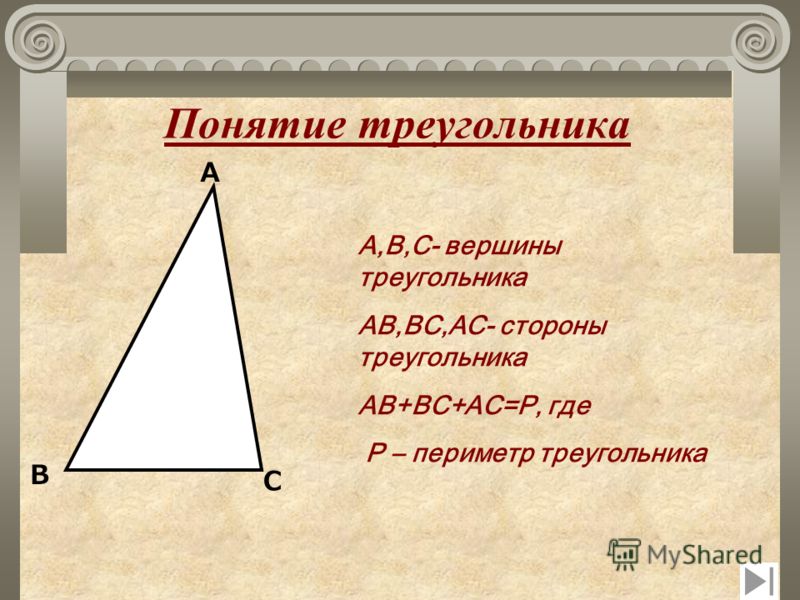
Треугольник — это фигура, состоящая из трех отрезков и трех точек, не лежащих на одной прямой.
Отрезки называются сторонами , а точки — вершинами .
Сумма углов треугольника равна 180 º .
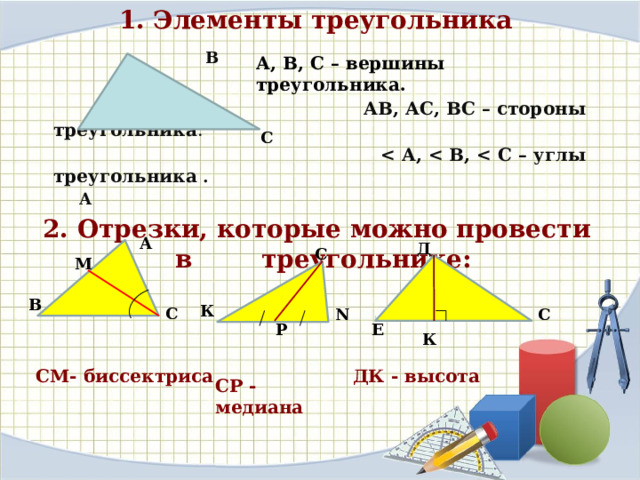
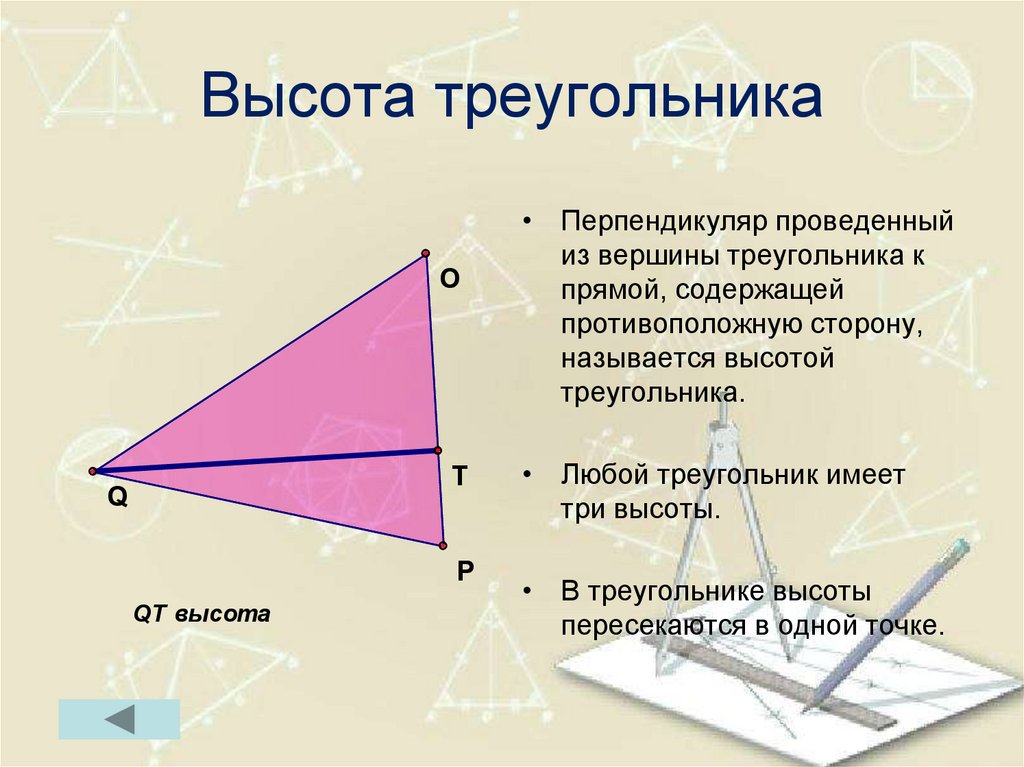
Высота треугольника.
Высота треугольника — это перпендикуляр, проведенный из вершины к противолежащей стороне.
В остроугольном треугольнике высота содержится внутри треугольника (рис.1).
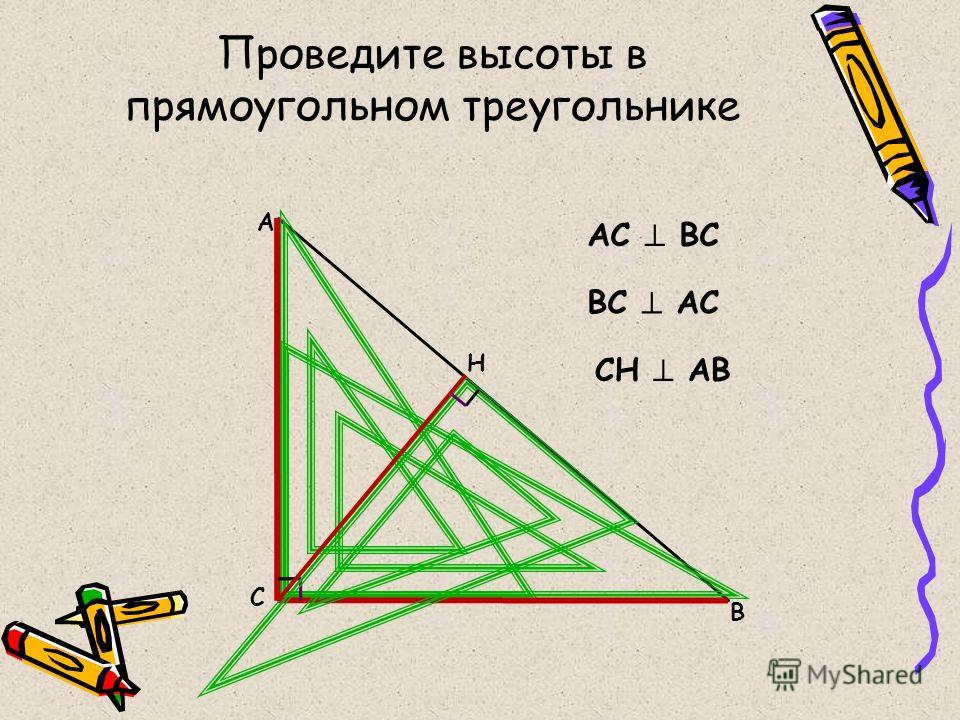
В прямоугольном треугольнике катеты являются высотами треугольника (рис.
2).
В тупоугольном треугольнике высота проходит вне треугольника (рис.3).
Свойства высоты треугольника:
Биссектриса треугольника.
Биссектриса треугольника — это отрезок, который делит угол вершины пополам и соединяет вершину с точкой на противолежащей стороне (рис.5).
Свойства биссектрисы:
Медиана треугольника.
Медиана треугольника — это отрезок, соединяющий вершину с серединой противолежащей стороны (рис.9а).
Длину медианы можно вычислить по формуле:
2b 2 + 2c 2 — a 2
m a 2 = ——————
4где m a — медиана, проведенная к стороне а .
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы:
c
m c = —
2где m c — медиана, проведенная к гипотенузе c (рис.
9в)
Медианы треугольника пересекаются в одной точке (в центре масс треугольника) и делятся этой точкой в соотношении 2:1, отсчитывая от вершины. То есть отрезок от вершины к центру в два раза больше отрезка от центра к стороне треугольника (рис.9с).
Три медианы треугольника делят его на шесть равновеликих треугольников.
Средняя линия треугольника.
Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон (рис.10).
Средняя линия треугольника параллельна третьей стороне и равна ее половине
Внешний угол треугольника.
Внешний угол треугольника равен сумме двух несмежных внутренних углов (рис.11).
Внешний угол треугольника больше любого несмежного угла.
Прямоугольный треугольник.
Прямоугольный треугольник — это треугольник, у которого есть прямой угол (рис.12).
Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой .
Две другие стороны называются катетами
.
Пропорциональные отрезки в прямоугольном треугольнике.
1) В прямоугольном треугольнике высота, проведенная из прямого угла, образует три подобных треугольника: ABC, ACH и HCB (рис.14а). Соответственно, углы, образуемые высотой, равны углам А и В.
Рис.14а
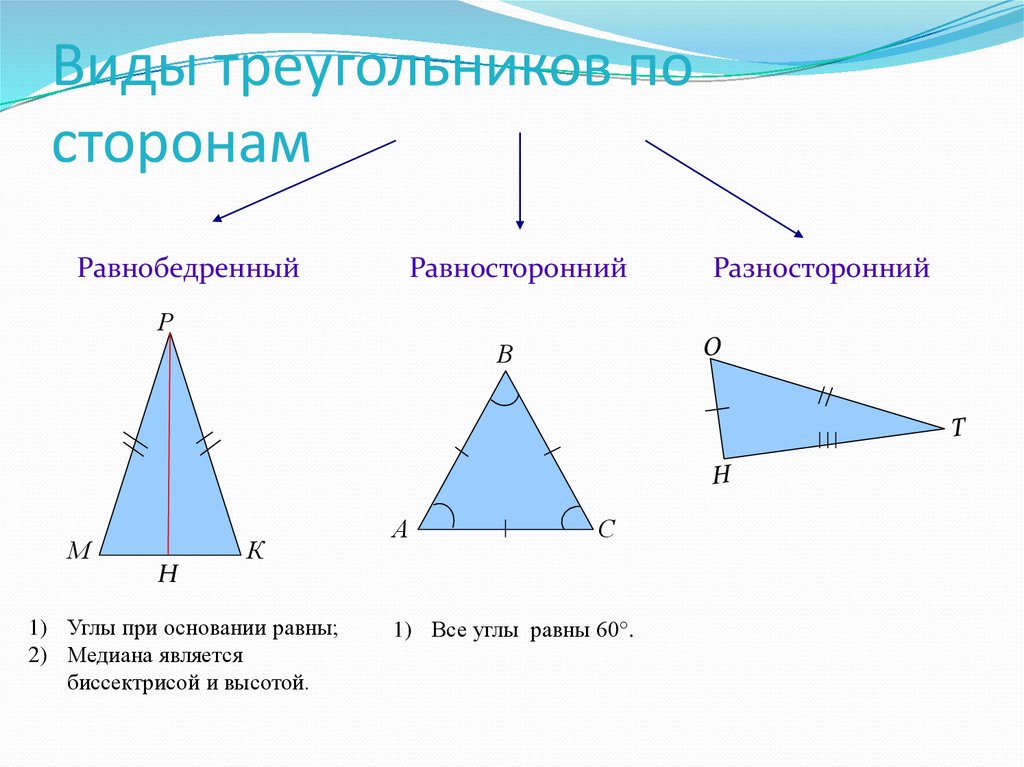
Равнобедренный треугольник.
Равнобедренный треугольник — это треугольник, у которого две стороны равны (рис.13).
Эти равные стороны называются боковыми сторонами , а третья — основанием треугольника.
В равнобедренном треугольнике углы при основании равны. (В нашем треугольнике угол А равен углу C).
В равнобедренном треугольнике медиана, проведенная к основанию, является одновременно и биссектрисой, и высотой треугольника.
Равносторонний треугольник.
Равносторонний треугольник — это треугольник, у которого все стороны равны (рис.14).
Свойства равностороннего треугольника:
Замечательные свойства треугольников.

У треугольников есть оригинальные свойства, которые помогут вам успешно решать задачи, связанные с этими фигурами. Некоторые из этих свойств изложены выше. Но повторяем их еще раз, добавив к ним несколько других замечательных особенностей:
1) В прямоугольном треугольнике с углами 90º, 30º и 60º катет b , лежащий напротив угла в 30º, равен половине гипотенузы. А катет a больше катета b в √3 раз (рис.15а ). К примеру, если катет b равен 5, то гипотенуза c обязательно равна 10, а катет а равен 5√3.
2) В прямоугольном равнобедренном треугольнике с углами 90º, 45º и 45º гипотенуза в √2 раз больше катета (рис.15b ). К примеру, если катеты равны 5, то гипотенуза равна 5√2.
3) Средняя линия треугольника равна половине параллельной стороны (рис.15с ). К примеру, если сторона треугольника равна 10, то параллельная ей средняя линия равна 5.
4) В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы (рис.9в): m c = с/2.
5) Медианы треугольника, пересекаясь в одной точке, делятся этой точкой в соотношении 2:1. То есть отрезок от вершины к точке пересечения медиан в два раза больше отрезка от точки пересечения медиан к стороне треугольника (рис.9c)
6) В прямоугольном треугольнике середина гипотенузы является центром описанной окружности (рис.15d ).
Признаки равенства треугольников .
Первый признак равенства : если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства : если сторона и прилежащие к ней углы одного треугольника равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства : если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Неравенство треугольника.
В любом треугольнике каждая сторона меньше суммы двух других сторон.
Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
c 2 = a 2 + b 2 .
Площадь треугольника.
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
ah
S= ——
22) Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними:
1
S = — AB · AC · sin A
2Треугольник, описанный около окружности.
Окружность называется вписанной в треугольник, если она касается всех его сторон (рис.16а ).
Треугольник, вписанный в окружность.
Треугольник называется вписанным в окружность, если он касается ее всеми вершинами (рис.
17a ).
Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника (рис.18).
Синус острого угла x противолежащего катета к гипотенузе.
Обозначается так: sin x .Косинус острого угла x прямоугольного треугольника — это отношение прилежащего катета к гипотенузе.
Обозначается так: cos x .Тангенс острого угла x — это отношение противолежащего катета к прилежащему катету.
Обозначается так: tg x .Котангенс острого угла x — это отношение прилежащего катета к противолежащему.
Обозначается так: ctg x .Правила:
Катет, противолежащий углу x , равен произведению гипотенузы на sin x :
b = c · sin x
Катет, прилежащий к углу x , равен произведению гипотенузы на cos x :
a = c · cos x
Катет, противоположный углу x , равен произведению второго катета на tg x :
b = a · tg x
Катет, прилежащий к углу x , равен произведению второго катета на ctg x :
a = b · ctg x .
Для любого острого угла x :
sin (90° — x ) = cos x
cos (90° — x ) = sin x
Как найти наибольшую или наименьшую высоту треугольника? Чем меньше высота треугольника, тем больше проведенная к ней высота. То есть наибольшая из высот треугольника — та, которая проведена к его наименьшей стороне. — та, которая проведена к наибольшей из сторон треугольника.
Чтобы найти наибольшую высоту треугольника , можно площадь треугольника разделить на длину стороны, к которой проведена эта высота (то есть на длину наименьшей из сторон треугольника).
Соответственно, для нахождения наименьшей высоты треугольника можно площадь треугольника разделить на длину его наибольшей стороны.
Задача 1.
Найти наименьшую высоту треугольника, стороны которого равны 7 см, 8 см и 9 см.
Дано:
AC=7 см, AB=8 см, BC=9 см.
Найти: наименьшую высоту треугольника.
Решение:
Наименьшая из высот треугольника — та, которая проведена к его наибольшей стороне. Значит, нужно найти высоту AF, проведенную к стороне BC.
Для удобства записи введем обозначения
BC=a, AC=b, AB=c, AF=ha.
Высота треугольника равна частному от деления удвоенной площади треугольника на сторону, к которой эта высота проведена. можно найти с помощью формулы Герона. Поэтому
Вычисляем:
Ответ:
Задача 2.
Найти наибольшую сторону треугольника со сторонами 1 см, 25 см и 30 см.
Дано:
AC=25 см, AB=11 см, BC=30 см.
Найти:
наибольшую высоту треугольника ABC.
Решение:
Наибольшая высота треугольника проведена к его наименьшей стороне.
Значит, нужно найти высоту CD, проведенную к стороне AB.
Для удобства обозначим
При решении различного рода задач, как сугубо математического, так и прикладного характера (особенно в строительстве), нередко требуется определить значение высоты определенной геометрической фигуры.
Как рассчитать данную величину (высоту) в треугольнике? Если мы попарно совместим 3 точки, расположенные не на единой прямой, то полученная фигура будет треугольником. Высота – часть прямой из любой вершины фигуры, которая при пересечении с противоположной стороной образует угол 90°.
Найти высоту в разностороннем треугольнике
Определим значение высоты треугольника в случае, когда фигура имеет произвольные углы и стороны.
Формула Герона
h(a)=(2√(p(p-a)*(p-b)*(p-c)))/a, где
p – половина периметра фигуры, h(a) – отрезок к стороне a, проведенный под прямым углом к ней,
p=(a+b+c)/2 – расчет полупериметра.
В случае наличия площади фигуры для определения ее высоты можно воспользоваться соотношением h(a)=2S/a.
Тригонометрические функции
Для определения длины отрезка, который составляет при пересечении со стороной a прямой угол, можно воспользоваться следующими соотношениями: если известна сторона b и угол γ или сторона c и угол β, то h(a)=b*sinγ или h(a)=c*sinβ.

Где:
γ – угол между стороной b и a,
β – угол между стороной c и a.Взаимосвязь с радиусом
Если исходный треугольник вписан в окружность, для определения величины высоты можно воспользоваться радиусом такой окружности. Центр ее расположен в точке, где пересекаются все 3 высоты (из каждой вершины) – ортоцентре, а расстояние от него и до вершины (любой) – радиус.
Тогда h(a)=bc/2R, где:
b, c – 2 другие стороны треугольника,
R – радиус описывающей треугольник окружности.Найти высоту в прямоугольном треугольнике
В данном виде геометрической фигуры 2 стороны при пересечении образуют прямой угол – 90°. Следовательно, если требуется определить в нем значение высоты, то необходимо вычислить либо размер одного из катетов, либо величину отрезка, образующего с гипотенузой 90°. При обозначении:
a, b – катеты,
c – гипотенуза,
h(c) – перпендикуляр на гипотенузу.
Произвести необходимые расчеты можно с помощью следующих соотношений:
- Пифагорова теорема:
a=√(c 2 -b 2),
b=√(c 2 -a 2),
h(c)=2S/c,т.к. S=ab/2,то h(c)=ab/c .
- Тригонометрические функции:
a= c*sinβ,
b=c* cosβ,
h(c)=ab/c=с* sinβ* cosβ.Найти высоту в равнобедренном треугольнике
Данная геометрическая фигура отличается наличием двух сторон равной величины и третьей – основанием. Для определения высоты, проведенной к третьей, отличной стороне, на помощь приходит теорема Пифагора. При обозначениях
a – боковая сторона,
c – основание,
h(c) – отрезок к c под углом 90°, то h(c)=1/2 √(4a 2 -c 2).
Треугольника) или проходить вне треугольника у тупоугольного треугольника.
Энциклопедичный YouTube
1 / 5
✪ ВЫСОТА МЕДИАНА БИССЕКТРИСА треугольника 7 класс
✪ биссектриса, медиана, высота треугольника. Геометрия 7 класс
✪ 7 класс, 17 урок, Медианы, биссектрисы и высоты треугольника
✪ Медиана, биссектриса, высота треугольника | Геометрия
✪ Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис Трушин
Субтитры
Свойства точки пересечения трех высот треугольника (ортоцентра)
E A → ⋅ B C → + E B → ⋅ C A → + E C → ⋅ A B → = 0 {\displaystyle {\overrightarrow {EA}}\cdot {\overrightarrow {BC}}+{\overrightarrow {EB}}\cdot {\overrightarrow {CA}}+{\overrightarrow {EC}}\cdot {\overrightarrow {AB}}=0}
(Для доказательства тождества следует воспользоваться формулами
A B → = E B → − E A → , B C → = E C → − E B → , C A → = E A → − E C → {\displaystyle {\overrightarrow {AB}}={\overrightarrow {EB}}-{\overrightarrow {EA}},\,{\overrightarrow {BC}}={\overrightarrow {EC}}-{\overrightarrow {EB}},\,{\overrightarrow {CA}}={\overrightarrow {EA}}-{\overrightarrow {EC}}}
В качестве точки E следует взять пересечение двух высот треугольника.
)
- Ортоцентр изогонально сопряжен центру описанной окружности .
- Ортоцентр лежит на одной прямой с центроидом , центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник .
- Центр описанной ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника .
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если О — центр описанной окружности ΔABC, то O H → = O A → + O B → + O C → {\displaystyle {\overrightarrow {OH}}={\overrightarrow {OA}}+{\overrightarrow {OB}}+{\overrightarrow {OC}}} ,
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
- Теорема Гамильтона . Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
- Следствия теоремы Гамильтона :
- Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона , имеющих равные радиусы описанных окружностей.
- Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
- В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.
Свойства высот равнобедренного треугольника
- Если в треугольнике две высоты равны, то треугольник — равнобедренный (теорема Штейнера - Лемуса), и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
- У равностороннего треугольника все три высоты равны.
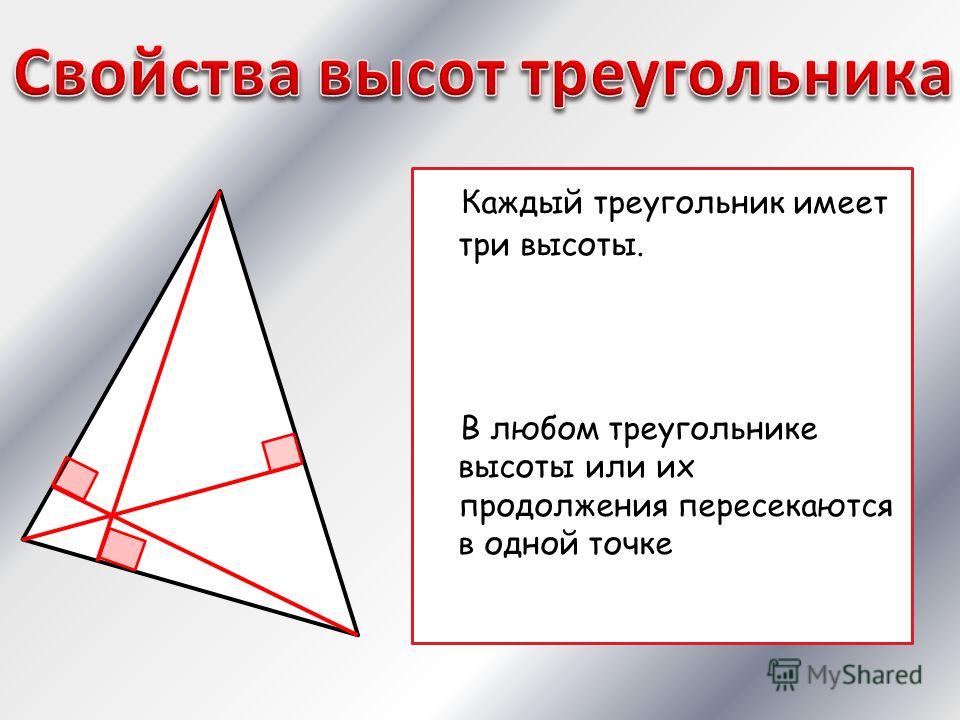
Свойства оснований высот треугольника
- Основания высот образуют так называемый ортотреугольник , обладающий собственными свойствами.
- Описанная около ортотреугольника окружность — окружность Эйлера .
На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
- Другая формулировка последнего свойства:
- Теорема Эйлера для окружности девяти точек . Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром , все лежат на одной окружности (на окружности девяти точек ).
- Теорема . В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
- Теорема . В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.
Другие свойства высот треугольника
- Если треугольник разносторонний (неравносторонний ), то его внутренняя биссектриса , проведённая из любой вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
- Высота треугольника изогонально сопряжена диаметру (радиусу) описанной окружности , проведенному из той же самой вершины.
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
- В прямоугольном треугольнике высота , проведенная из вершины прямого угла , разбивает его на два треугольника, подобных исходному.
Свойства минимальной из высот треугольника
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
- Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
- Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
- При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
- Минимальная высота в треугольнике всегда проходит внутри этого треугольника.
Основные соотношения
- h a = b ⋅ sin γ = c ⋅ sin β , {\displaystyle h_{a}=b{\cdot }\sin \gamma =c{\cdot }\sin \beta ,}
- h a = 2 ⋅ S a , {\displaystyle h_{a}={\frac {2{\cdot }S}{a}},} где S {\displaystyle S} — площадь треугольника, a {\displaystyle a} — длина стороны треугольника, на которую опущена высота .
- h a = b ⋅ c 2 ⋅ R , {\displaystyle h_{a}={\frac {b{\cdot }c}{2{\cdot }R}},} где b ⋅ c {\displaystyle b{\cdot }c} — произведение боковых сторон, R − {\displaystyle R-} радиус описанной окружности
- h a: h b: h c = 1 a: 1 b: 1 c = (b ⋅ c) : (a ⋅ c) : (a ⋅ b) .
{\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=(b{\cdot }c):(a{\cdot }c):(a{\cdot }b).}
- 1 h a + 1 h b + 1 h c = 1 r {\displaystyle {\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}={\frac {1}{r}}} , где r {\displaystyle r} — радиус вписанной окружности .
- S = 1 (1 h a + 1 h b + 1 h c) ⋅ (1 h a + 1 h b − 1 h c) ⋅ (1 h a + 1 h c − 1 h b) ⋅ (1 h b + 1 h c − 1 h a) {\displaystyle S={\frac {1}{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}} , где S {\displaystyle S} — площадь треугольника.
- a = 2 h a ⋅ (1 h a + 1 h b + 1 h c) ⋅ (1 h a + 1 h b − 1 h c) ⋅ (1 h a + 1 h c − 1 h b) ⋅ (1 h b + 1 h c − 1 h a) {\displaystyle a={\frac {2}{h_{a}{\cdot }{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}}){\cdot }({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}}){\cdot }({\frac {1}{h_{b}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{a}}})}}}}} , a {\displaystyle a} — сторона треугольника к которой опускается высота h a {\displaystyle h_{a}} .
{2}}},}
где c {\displaystyle c} — основание, a {\displaystyle a} — боковая сторона.
Теорема о высоте прямоугольного треугольника
Если высота в прямоугольном треугольнике ABC длиной h {\displaystyle h} , проведённая из вершины прямого угла, делит гипотенузу длиной c {\displaystyle c} на отрезки m {\displaystyle m} и n {\displaystyle n} , соответствующие катетам b {\displaystyle b} и a {\displaystyle a} , то верны следующие равенства.
Для решения многих геометрических задач требуется найти высоту заданной фигуры. Эти задачи имеют прикладное значение. При проведении строительных работ определение высоты помогает вычислить необходимое количество материалов, а также определить, насколько точно сделаны откосы и проемы. Часто для построения выкроек требуется иметь представление о свойствах
У многих людей, несмотря на хорошие оценки в школе, при построении обычных геометрических фигур возникает вопрос о том, как найти высоту треугольника или параллелограмма.
Причем является самым сложным. Это происходит потому, что треугольник может быть острым, тупым, равнобедренным или прямоугольным. Для каждого из существуют свои правила построения и расчета.
Как найти высоту треугольника, в котором все углы острые, графическим способом
Если все углы у треугольника острые (каждый угол в треугольнике меньше 90 градусов), то для нахождения высоты необходимо сделать следующее.
- По заданным параметрам выполняем построение треугольника.
- Введем обозначения. А, В и С будут вершинами фигуры. Углы, соответствующие каждой вершине — α, β, γ. Противолежащие этим углам стороны — a, b, c.
- Высотой называется перпендикуляр, опущенный из вершины угла к противоположной стороне треугольника. Для нахождения высот треугольника проводим построение перпендикуляров: из вершины угла α к стороне a, из вершины угла β к стороне b и так далее.
- Точку пересечения высоты и стороны a обозначим h2, а саму высоту h2. Точка пересечения высоты и стороны b будет h3, высота соответственно h3.
Для стороны c высота будет h4, а точка пересечения h4.
Высота в треугольнике с тупым углом
Теперь рассмотрим, как найти высоту треугольника, если один (больше 90 градусов). В этом случае высота, проведенная из тупого угла, будет внутри треугольника. Остальные две высоты будут находиться за пределами треугольника.
Пусть в нашем треугольнике углы α и β будут острыми, а угол γ — тупой. Тогда для построения высот, выходящих из углов α и β, надо продолжить противоположные им стороны треугольника, чтобы провести перпендикуляры.
Как найти высоту равнобедренного треугольника
У такой фигуры есть две равные стороны и основание, при этом углы, находящиеся при основании, также являются равными между собой. Это равенство сторон и углов облегчает построение высот и их вычисление.
Сначала нарисуем сам треугольник. Пусть стороны b и c, а также углы β, γ будут соответственно равными.
Теперь проведем высоту из вершины угла α, обозначим ее h2.
Для эта высота будет одновременно биссектрисой и медианой.
Для основания можно сделать только одно построение. Например, провести медиану — отрезок, соединяющий вершину равнобедренного треугольника и противоположную сторону, основание, для нахождения высоты и биссектрисы. А для вычисления длины высоты для двух других сторон можно построить только одну высоту. Таким образом, чтобы графически определить, как вычислить высоту равнобедренного треугольника, достаточно найти две высоты из трех.
Как найти высоту прямоугольного треугольника
У прямоугольного треугольника определить высоты намного проще, чем у других. Это происходит потому, что сами катеты составляют прямой угол, а значит, являются высотами.
Для построения третьей высоты, как обычно, проводится перпендикуляр, соединяющий вершину прямого угла и противоположную сторону. В итоге для того, чтобы треугольника в данном случае, требуется только одно построение.
Как построить высоту треугольника — основные способы
Для решения многих геометрических задач учащемуся нужно уметь быстро построить высоту треугольника.
Сделать это можно несколькими простыми для восприятия способами, которые подходят для фигуры разной формы и размера. Весь процесс состоит из определённой последовательности действий, правильно выполнить которые сможет каждый школьник.
Содержание
- С применением циркуля
- С помощью линейки
- В остроугольном треугольнике
- В тупоугольной фигуре
- В прямоугольном и равнобедренном
С применением циркуля
Если нужно нарисовать высоту (перпендикуляр к противоположной стороне) в произвольном треугольнике и измерить её, то лучше всего воспользоваться классическим методом построения. Он предусматривает использование циркуля в качестве основной рабочей принадлежности. Кроме этого, для работы понадобится лист бумаги, небольшая линейка, ластик и простой карандаш.
Способ начертить искомый отрезок:
- На листе бумаги чертят треугольник (можно нарисовать заранее, чтобы сэкономить время).
- Рисунок располагают так, чтобы вершина угла, из которого нужно начертить высоту, находилась сверху, а противоположная ему сторона фигуры была расположена горизонтально (по отношению к ученику).
- Иглу циркуля ставят в вершине любого угла у основания.
- Ножку с грифелем ставят в верхнюю точку треугольника, из которой проводится высота.
- Циркулем рисуют окружность и делают пометку в месте её пересечения с основанием фигуры.
- Аналогичным способом чертят круг из другого угла при основании. При этом важно определить новый радиус, который будет равен длине второй стороны треугольника.
- Делают пометку в месте пересечения начерченных окружностей.
- Ластиком стирают лишние линии, оставляя лишь поставленную точку.
- С помощью карандаша и линейки из неё проводят отрезок к вершине, который и будет высотой треугольника.
- Стирают линии, находящиеся под основанием.
Таким же способом можно с помощью циркуля построить высоту треугольника из любого другого угла.
С помощью линейки
Начертить и обозначить высоту можно и без циркуля. Для этого следует воспользоваться чертёжным угольником, 2 стороны которого перпендикулярны друг другу. Альтернативой этой школьной принадлежности могут стать 2 прямые линейки, соединённые между собой под прямым углом.
В остроугольном треугольнике
Провести высоту в треугольнике, где все углы острые (менее 90 градусов), довольно просто.
Чтобы справиться с этой задачей, нужно подготовить все необходимое и заранее начертить на бумаге геометрическую фигуру.
Правильная последовательность действий:
- Находят вершину, из которой хотят провести перпендикуляр.
- Совмещают угольник с противоположной стороной фигуры.
- Перемещают чертёжную принадлежность до тех пор, пока её перпендикулярная сторона не пройдёт через вершину.
- Простым карандашом проводят линию, которая и будет искомым отрезком.
В тупоугольной фигуре
Трёхсторонняя фигура, у которой один из углов тупой (более 90 градусов) имеет только 1 внутреннюю высоту. Для её проведения используют то же, что и в предыдущем случае.
Порядок действий:
- Располагают чертёж так, чтобы тупой угол оказался у основания.
- Угольник прикладывают к наибольшей стороне фигуры.
- Совмещают перпендикулярную сторону линейки с вершиной тупого угла.
- Соединяют 2 точки простым карандашом, получая искомую линию.
В прямоугольном и равнобедренном
В прямоугольном треугольнике нужно находить только 1 высоту. Две другие будут совпадать с катетами.
Пошаговая инструкция:
- Прикладывают одну из перпендикулярных сторон угольника к гипотенузе.
- Вторую сторону линейки совмещают с вершиной прямого угла.
- Проводят линию, которая будет высотой.
Проще всего проводить перпендикуляр из верхней точки равнобедренного треугольника.
Он будет совпадать с биссектрисой и медианой фигуры. Начертить его можно таким же способом, что и для остроугольной фигуры. Более простой метод предусматривает выполнение следующих действий:
- Линейкой замеряют длину основания.
- Эту величину делят на 2.
- Полученное значение откладывают от вершины одного из углов при основании.
- Отмечают середину стороны и соединяют её с верхней точкой фигуры.
Проведение высоты в треугольнике — это простая задача, с которой легко справится каждый ученик.
Для этого достаточно сделать чертёж геометрической фигуры и воспользоваться одним из существующих способов построения. Такая работа потребует минимум времени и не отнимет у школьника много сил.
youtube.com/embed/IMQJPa41zKs»>Предыдущая
ГеометрияБиссектриса параллелограмма — свойства, признаки и теоремы
Следующая
ГеометрияУравнение биссектрисы в треугольнике — формула, свойства и решение задач
Как найти высоту равностороннего треугольника
Освоить 7 столпов школьной успеваемости
Улучшить оценки и снизить стресс
Давайте рассмотрим еще несколько примеров нахождения высоты равностороннего треугольника .
Найдите высоту равностороннего треугольника со стороной 8 см.
8/2 = 4 4√3 = 6,928 см.
Когда вы используете десятичные дроби и когда вы используете ответ с квадратным корнем. Ответ с квадратным корнем является точным ответом. На стандартизированных тестах, таких как SAT, они ожидают точного ответа. Десятичный ответ является оценкой.
Найдите высоту равностороннего треугольника со стороной 12 единиц.

12/2 = 6, тогда 6√3 единицы = 10,392 единицы
Сторона равностороннего треугольника равна 16 единицам. Чему равна высота этого равностороннего треугольника.
16/2=8√3 единиц или 13,856 единиц
Высота равностороннего треугольника равна 10 единицам. Какова длина стороны?
h = √3/2 * a a =сторона
6 = √3/2 * A
A = 6/√3/2
A = 4√3
Стандарт Common Core 6.G.1
Треугольник Практический0002 Нахождение апофемы равностороннего треугольника
Формула высоты равностороннего треугольника
Найдите высоту треугольника со стороной 6 единиц.

Шаг 1. Возьмите 1/2 побочного времени √3
6/2* √ (3) = 3√3 = высота
1/2 основания * высоты или 1/2 ширины * высоты
Найдите площадь равностороннего треугольника со стороной 8 единиц
Шаг 1. Используйте формулу высоты: ( сторона/2 * √3 ) для расчета высоты.
высота = 8/2* √3=4√3
Шаг 2. Подставьте высоту в формулу площади 1/2b * h 16√3 = площадь треугольника
Формула периметра равностороннего треугольника
Периметр = Добавить все три стороны или 3* стороны
Каков периметр треугольника со стороной 7 единиц?
Добавить все три стороны 7+7+7 = 21 единицы
или
3 (7) = 21 единицы
.
Найдите апофему равностороннего треугольника со стороной 12 единицШаг 1.
Подключите длину боковой в Формуле
12/((2√3))
Шаг 2. Упрощение 12/(2√3) =
ЕДИНИЦА = АПОФЕМ
Длина боковой стороны
Длина
. Apothem находится на расстоянии от центра полиг.0003 Видео решение нахождения высоты
Видео решение нахождения апофемы
Апофема
середина стороны треугольника. Апофема перпендикулярна стороне треугольника и образует прямой угол.
Длина стороны
Эта формула работает для всех полигонов
s= length of one side
n = number of sides
tan = tan function in degrees
Side Length
Pre-Algebra/Expressions,Equations,Integers
Предальгебра/фракции, Percents
Алгебра/Экспоненты, уравнения, радикалы
Математические калькуляторы
Геометрия/формы
Геометрия/SAT
9000 9000/SAT
9000Геометрия/Плоскость
Хорошие навыки обучения
Геометрия/Основы
Длина стороны
Существует множество различных типов треугольников, названных по длине стороны и величине угла.
Равносторонний треугольник обладает следующими свойствами.
- Равносторонние треугольники имеют три равные длины сторон
- Равносторонние треугольники также имеют три равных угла по 60 градусов
- Они также имеют три равные высоты
- Высота равностороннего треугольника равна длине его стороны. Нет. При прочих равных условиях легко представить, что высота и длина стороны равны, но это не так.
- Высота равна стороне/2 x √3
Как найти основание треугольника
Математика является важным предметом практически для всех конкурсных экзаменов, включая SAT и ACT. Правильное понимание основ очень важно, когда дело доходит до решения сложных задач по математике. Многим учащимся трудно запомнить шаги и вспомнить математические формулы во время подготовки к экзамену. С дополнительным давлением конкурсных экзаменов беды студента удваиваются.
Основные термины, касающиеся нахождения основания треугольника:
Что такое основание?
Основание означает дно.Какова высота?
Высота любого объекта — это его длина от верха до низа.Как определить основание треугольника?
Любая из трех сторон треугольника может считаться его основанием.Как определить высоту треугольника?
Высота треугольника — это перпендикуляр, опущенный на его основание из угла, противоположного основанию.Поскольку Турито понимает эту трудность и решает проблему, мы показываем вам, как можно найти основание треугольника.
- Способ найти основание треугольника из площади треугольника:
Площадь треугольника = ½ bh
Где b- основание
h- высота
После того, как площадь треугольника найдена, формулы площади можно применить в обратном порядке2 к A=1. длина основания. Итак, формула основания треугольника равна 9.
0006
b=2A/h
2. Способы найти основание треугольника из прямоугольного треугольника:
Можно применить теорему Пифагора или использовать формулу, которая включает длину двух сторон или длину двух сторон гипотенуза. Обратная техника помогает даже в этом отношении.
Даже если значение площади неизвестно, но известна длина треугольника — эту формулу можно использовать. В прямоугольном треугольнике высота и основание имеют одинаковую длину.
3. Способ нахождения основания равнобедренного треугольника:
Известно, что в равнобедренном треугольнике две стороны имеют одинаковую длину.
а — длина двух известных равнобедренных сторон, которые эквивалентны.
4. Способ найти основание равностороннего треугольника:
У равностороннего треугольника все стороны одинаковой длины. Здесь применяется формула правильной площади треугольника
Визуализируйте равносторонний треугольник как два меньших прямоугольных треугольника, чтобы найти высоту, где длина гипотенузы равна длине стороны b .
По правилу 30-60-90, частному случаю прямоугольного треугольника, мы знаем, что основание этого меньшего прямоугольного треугольника равно, а высота этого меньшего прямоугольного треугольника равна, принимая b за гипотенузу.
Найдя высоту, используйте ее в следующей формуле, добавив значения площади и высоты:
И замените высоту:
Инструменты для нахождения основания треугольника:
Теорема Пифагора: Это уравнение показывает соотношение между тремя сторонами прямоугольного треугольника, поэтому найти площадь проще.
Треугольник, в одном из трех углов которого имеется прямой угол, равный 90 градусам, называется прямоугольным. Основанием прямоугольного треугольника является одна из сторон, прилежащая к углу 90 градусов.
Все о Пифагоре – создателе этой находчивой формулы:
Пифагора, родом из Греции, часто связывают с открытием математической теоремы, которая до сих пор используется для вычисления размеров прямоугольного треугольника.
Для выполнения расчетов необходимо знать размеры наибольшей стороны геометрической фигуры, гипотенузы, а также еще одной ее стороны.
Легендарный математик эмигрировал в Италию примерно в 532 г. до н. э. из-за политических и социальных условий в стране. Пифагор также определил значение чисел в музыке. К сожалению, большинство его работ не задокументированы, поэтому ученые не знают, был ли это сам Пифагор, который открыл теорему, или один из многих студентов или учеников, которые были членами пифагорейского братства, религиозной или мистической группы, принципы которой повлияли на творчество Платона и Аристотеля.
Эффективные советы по поиску основания треугольника:
- Сначала узнайте типы треугольников: важно знать классификацию треугольников: равнобедренный, равнобедренный, прямоугольный и разносторонний.
Равнобедренный треугольник : Из трех сторон две стороны имеют одинаковую длину для этого типа треугольника.
Эквивалентный треугольник: Три стороны этого треугольника равны по длине.
Прямоугольный: В этом треугольнике одна сторона наибольшая по сравнению с двумя другими сторонами и называется гипотенузой.
Scalene: Здесь все стороны треугольника неравны. Решение задач и нахождение площади и основания этого треугольника найти сложно.
- Запомните формулы: Ожидается, что учащийся запомнит все формулы, связанные с нахождением площади и длины треугольника. Это сэкономит время, чтобы найти решение без особых усилий.
- Думайте нестандартно: Хотя математика является предметом, который зависит от пошаговой последовательности решения проблемы, иногда возникает идея обратного проектирования, чтобы получить ответ.
Особенно, когда дело доходит до конкурсных экзаменов, время является ценным ресурсом. Следовательно, нестандартное мышление облегчит поиск решений.
Заключительное слово:
Нахождение основания треугольника зависит от типа треугольника для длины, и ожидается, что учащийся запомнит формулы, чтобы использовать их соответствующим образом для получения решения. Правильное руководство от преподавателя и запись на курс могут легко помочь студенту создать прочные основы.
Математика — это предмет, который в значительной степени зависит от концепции, и наличие прочных основ значительно поможет учащемуся в долгосрочной перспективе — будь то на конкурсных экзаменах или в карьере по этому предмету.
Решение линейных уравнений с одной переменной. | СС | 8 | 8.EE | 8.EE.C
Более конкретные темы
in Решение линейных уравнений с одной переменной.Popular Tutorials
in Решение линейных уравнений с одной переменной.
Как решить двухшаговое уравнение путем умножения на -1?
В уравнении есть отрицательная переменная? Хотите избавиться от этого отрицательного знака? В этом руководстве показано, как с помощью свойства умножения -1!
Как решить двухшаговое уравнение, комбинируя одинаковые члены?
Пытаетесь решить уравнение, в котором одна и та же переменная встречается несколько раз? Выясните, как собрать эти переменные вместе и решить уравнение с помощью этого урока!
Как найти переменную в дроби, используя сначала умножение?
Пытаетесь решить уравнение с дробью? Просто умножьте дробь, а затем выполните операции в обратном порядке! Посмотрите, как в этом уроке.
Как решить двухшаговое уравнение путем умножения на обратную величину?
Пытаетесь решить уравнение с дробью? Просто умножьте дробь на обратную, а затем выполните действия в обратном порядке! Посмотрите, как в этом уроке.
Как решить уравнение тождества?
Пытаетесь решить уравнение с переменными в обеих частях уравнения? Выясните, как собрать эти переменные вместе и решить уравнение с помощью этого урока!
Как решить уравнение без решения?
Пытаетесь решить уравнение с переменными в обеих частях уравнения? Выясните, как собрать эти переменные вместе и решить уравнение с помощью этого урока! Сюрприз! Оказывается, это уравнение не имеет решения. Посмотрите этот урок и узнайте, почему!
Как решить уравнение с переменными с обеих сторон и группировкой символов?
Пытаетесь решить уравнение с переменными по обе стороны от знака равенства и группировки символов? Посмотрите это руководство, чтобы узнать, как удалить символы группировки и объединить эти переменные для решения уравнения.
Как решить двухшаговое уравнение, сначала умножив на -1?
В уравнении есть отрицательная переменная? Хотите избавиться от этого отрицательного знака? В этом руководстве показано, как с помощью свойства умножения -1!
Как решить двухшаговое уравнение, сначала распределив дробь?
Пытаетесь решить уравнение для переменной? Мешают ли символы группировки? Посмотрите этот урок, чтобы узнать, как удалить символы группировки и решить уравнение!
Как решить текстовую задачу, используя уравнение с переменными с обеих сторон?
Словесные задачи — отличный способ увидеть математику в реальном мире! В этом уроке вы увидите, как взять текстовую задачу и использовать ее для написания и решения уравнения с переменными с обеих сторон!
Что такое уравнение тождества?
Уравнения тождества — это уравнения, которые истинны независимо от того, какое значение подставлено для переменной.
Если вы упростите тождественное уравнение, вы ВСЕГДА получите истинное утверждение. Узнайте об уравнениях тождества в этом руководстве, а затем создайте собственное уравнение тождества. Проявите творческий подход! Возможности безграничны!
Что это значит, когда уравнение не имеет решения?
Иногда уравнения не имеют решения. Это означает, что независимо от того, какое значение подставлено для переменной, вы ВСЕГДА получите противоречие. Посмотрите этот урок и узнайте, что нужно, чтобы уравнение не имело решения.
Как решить уравнение с переменными с обеих сторон и дробями?
Пытаетесь решить уравнение с переменными и дробями в обеих частях уравнения? Вы можете поспорить, что это включает в себя поиск общего знаменателя! Чтобы узнать, что для этого нужно, посмотрите этот урок.
Как решить уравнение с переменными в обеих частях?
Пытаетесь решить уравнение с переменными по обе стороны от знака равенства? Узнайте, как собрать эти переменные вместе, и найдите ответ с помощью этого руководства!
Как решить уравнение с помощью сложения?
Решение уравнения для переменной? Порядок действий выполняйте в обратном порядке! Проверьте это в этом уроке.
Как решить уравнение, в котором умножаются дроби?
Решение уравнения с несколькими дробями в разных формах не так уж и плохо. В этом уроке показано, как преобразовать смешанную дробь в неправильную, чтобы решить уравнение. Затем вы увидите, как преобразовать ответ обратно в смешанную дробь, чтобы понять его смысл. Следуйте этому руководству, чтобы увидеть, как это делается!
Как решить уравнение с помощью умножения?
Решение уравнения для переменной? Порядок действий выполняйте в обратном порядке! Проверьте это в этом уроке.
Как решить многошаговое уравнение, используя обратный порядок операций?
Пытаетесь решить уравнение с переменными и дробями? Просто выполните порядок операций в обратном порядке! Чтобы узнать, что для этого нужно, посмотрите этот урок.
Как решить многошаговое уравнение с дробями путем умножения дроби?
Пытаетесь решить уравнение с дробью? Просто умножьте дробь, а затем выполните операции в обратном порядке! Посмотрите, как в этом уроке.
Как решить многошаговое уравнение с дробями, используя обратный порядок операций и обратные величины?
Пытаетесь решить уравнение с дробью? Просто выполните порядок операций в обратном порядке! Посмотрите, как в этом уроке.
Как решить двухшаговое уравнение?
Решение уравнения для переменной? Порядок действий выполняйте в обратном порядке! Проверьте это в этом уроке.
Как решить уравнение с помощью деления?
Решение уравнения для переменной? Порядок действий выполняйте в обратном порядке! Проверьте это в этом уроке.
Как решить уравнение с помощью вычитания?
Решение уравнения для переменной? Порядок действий выполняйте в обратном порядке! Проверьте это в этом уроке.
Как решить многошаговое уравнение, используя распределительное свойство?
Пытаетесь решить уравнение, в котором одна и та же переменная встречается несколько раз? Выясните, как собрать эти переменные вместе и решить уравнение с помощью этого урока!
Как решить уравнение с дробями с одинаковыми знаменателями с помощью вычитания?
Хотите попрактиковаться в решении уравнений, содержащих дроби? Тогда посмотрите этот урок! Следуйте инструкциям и узнайте, как вычитать дроби с общими знаменателями, чтобы решить уравнение для переменной.
Как решить уравнение с дробями с одинаковыми знаменателями с помощью сложения?
Хотите попрактиковаться в решении уравнений, содержащих дроби? Тогда посмотрите этот урок! Следуйте инструкциям и узнайте, как складывать дроби с общими знаменателями, чтобы решить уравнение для переменной.
Как решить уравнение с дробями с разными знаменателями с помощью вычитания?
Хотите попрактиковаться в решении уравнений, содержащих дроби? В этом уроке вы увидите, как сначала преобразовать смешанную дробь в неправильную, а затем вычесть дроби с разными знаменателями, чтобы решить уравнение. Обязательно проверяйте свои ответы, чтобы ЗНАТЬ, что они правильные!
Как решить уравнение с дробями с разными знаменателями с помощью сложения?
Хотите попрактиковаться в решении уравнений, содержащих дроби? В этом уроке вы узнаете, как складывать дроби с разными знаменателями, чтобы решить уравнение.
Затем обязательно проверьте свои ответы, чтобы ЗНАТЬ, что они правильные!
Как решить десятичное уравнение с помощью вычитания?
Хотите узнать, как решить уравнение, содержащее десятичные дроби? Тогда посмотрите этот урок! Вы увидите, как вычитать десятичные дроби, чтобы решить уравнение для переменной. Затем узнайте, как проверить свой ответ, чтобы убедиться, что он правильный!
Как решить десятичное уравнение с помощью сложения?
Хотите узнать, как решить уравнение, содержащее десятичные дроби? Тогда посмотрите этот урок! Вы увидите, как складывать десятичные дроби, чтобы решить уравнение для переменной. Затем узнайте, как проверить свой ответ, чтобы убедиться, что он правильный!
Как решить десятичное уравнение с помощью деления?
Хотите узнать, как решить уравнение, содержащее десятичные дроби? Тогда посмотрите этот урок! Вы увидите, как делить десятичные дроби, чтобы решить уравнение для переменной.

 {\circ},$ — провести высоту будет уже не так интуитивно просто.
{\circ},$ — провести высоту будет уже не так интуитивно просто.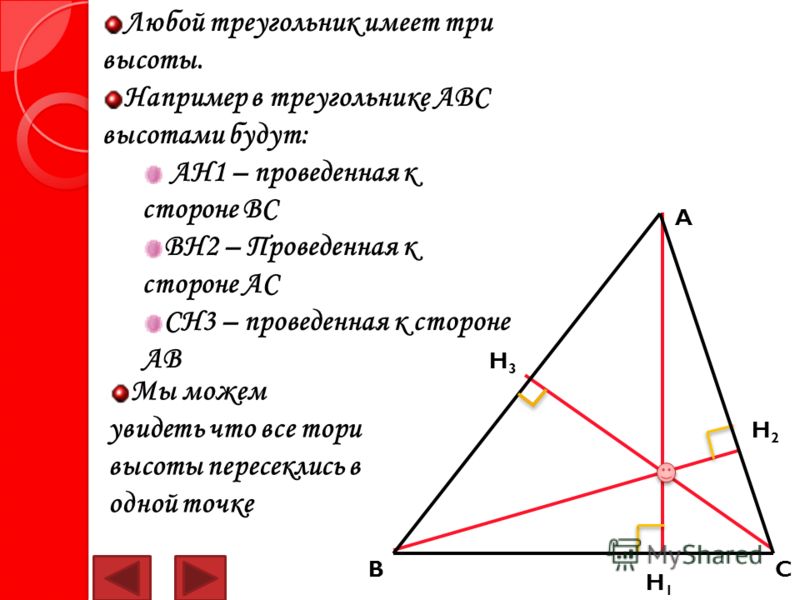 Что это за треугольник и какими свойствами он обладает, подробнее мы разберем далее в курсе геометрии. Пока что давайте просто поразмышляем: а где же будут <b>пересекаться высоты</b> в прямоугольном треугольнике? [[choice-11]]","widgets":{"image-1":{"type":"image","url":"http://obrazavr.ru/wp-content/uploads/2022/02/test-right.svg","width":"500"},"choice-11":{"type":"choice","options":["Внутри треугольника.","Внутри по центру треугольника.","Вне треугольника.","В вершине прямого угла."],"explanations":["","","","Это очень логично! <br /><br />В треугольнике $\\bigtriangleup{ABC}$ сторона $AB$ является высотой к стороне $BC$, и наоборот, ведь $\\angle{B}$ — прямой. Высота к стороне $AC$ будет выходить из вершины $B$. Так что точка пересечения высот в прямоугольном треугольнике, получается, располагается в точке $B$ — в вершине прямого угла."],"answer":[3]}}}]}
Что это за треугольник и какими свойствами он обладает, подробнее мы разберем далее в курсе геометрии. Пока что давайте просто поразмышляем: а где же будут <b>пересекаться высоты</b> в прямоугольном треугольнике? [[choice-11]]","widgets":{"image-1":{"type":"image","url":"http://obrazavr.ru/wp-content/uploads/2022/02/test-right.svg","width":"500"},"choice-11":{"type":"choice","options":["Внутри треугольника.","Внутри по центру треугольника.","Вне треугольника.","В вершине прямого угла."],"explanations":["","","","Это очень логично! <br /><br />В треугольнике $\\bigtriangleup{ABC}$ сторона $AB$ является высотой к стороне $BC$, и наоборот, ведь $\\angle{B}$ — прямой. Высота к стороне $AC$ будет выходить из вершины $B$. Так что точка пересечения высот в прямоугольном треугольнике, получается, располагается в точке $B$ — в вершине прямого угла."],"answer":[3]}}}]} Тогда отрезок $CD$ будет называться биссектрисой угла треугольника $\bigtriangleup{ABC}$ (от лат. ‘bi’ — «два», ‘secare’ — «резать»).
Тогда отрезок $CD$ будет называться биссектрисой угла треугольника $\bigtriangleup{ABC}$ (от лат. ‘bi’ — «два», ‘secare’ — «резать»).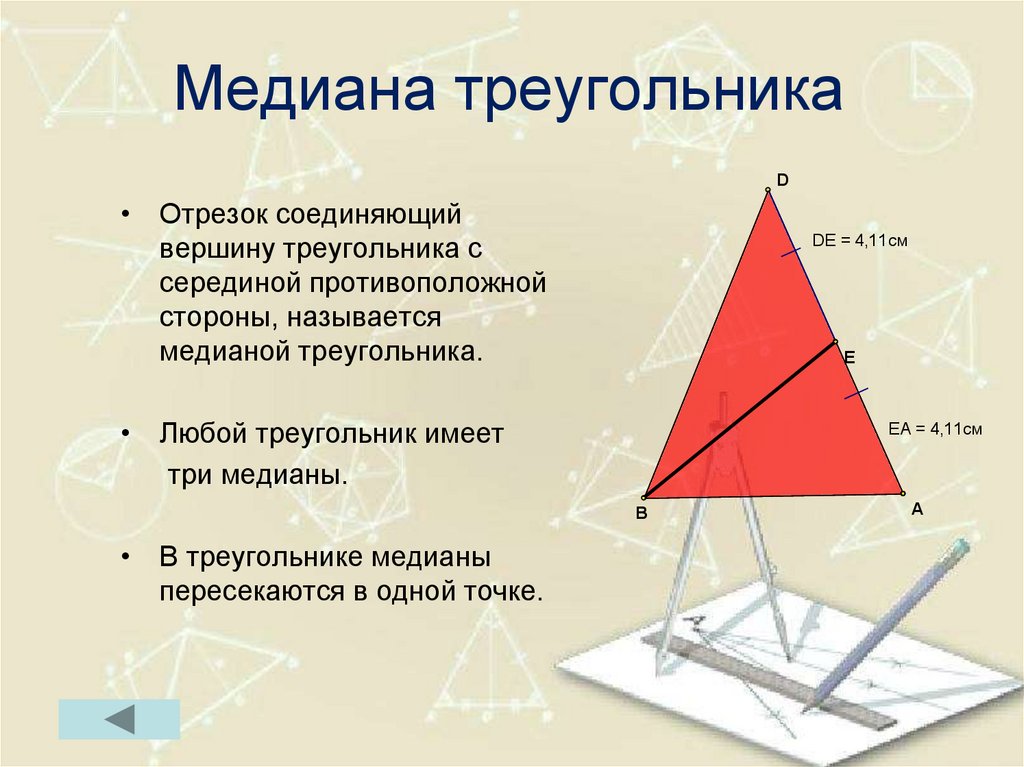 {\\circ}-\\angle{AOK}.$»,»Осталось только посчитать!»]}]}
{\\circ}-\\angle{AOK}.$»,»Осталось только посчитать!»]}]}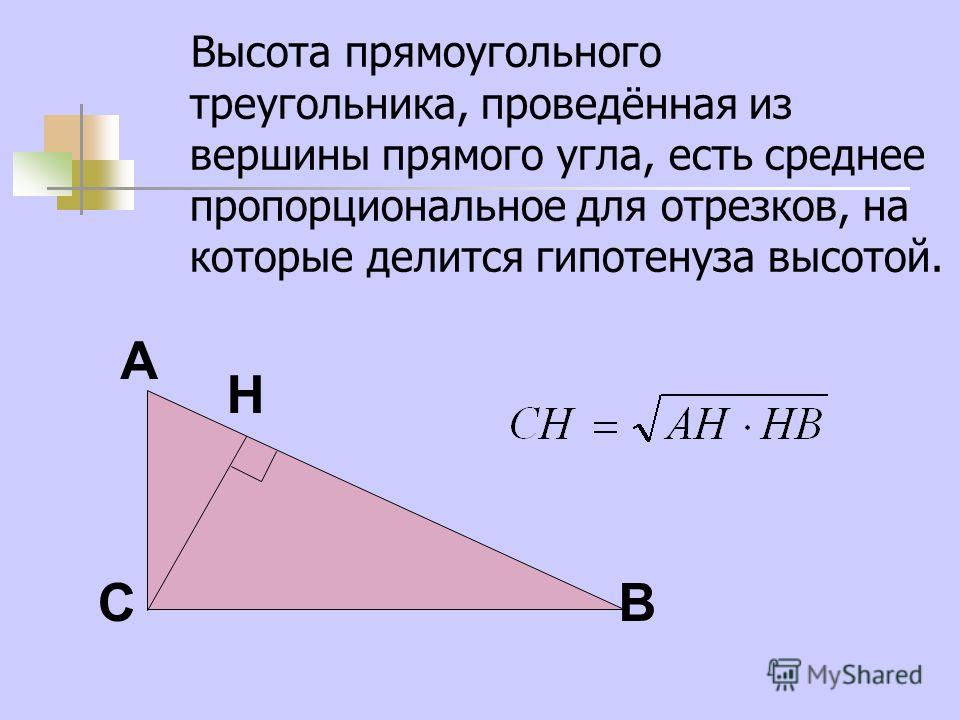 Исключением является тупоугольный треугольник и его высоты: высоты в тупоугольном треугольнике пересекаются вне треугольника.
Исключением является тупоугольный треугольник и его высоты: высоты в тупоугольном треугольнике пересекаются вне треугольника. По заданному условию $AD=DE$. Также имеем равенство сторон $CD=DB$ — по определению медианы: отрезка, делящего противолежащую от угла сторону на два равных отрезка.
По заданному условию $AD=DE$. Также имеем равенство сторон $CD=DB$ — по определению медианы: отрезка, делящего противолежащую от угла сторону на два равных отрезка. 2).
2). 9в)
9в)
 17a ).
17a ).


 к. S=ab/2,то h(c)=ab/c .
к. S=ab/2,то h(c)=ab/c . )
)

 На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.

 {\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=(b{\cdot }c):(a{\cdot }c):(a{\cdot }b).}
{\displaystyle h_{a}:h_{b}:h_{c}={\frac {1}{a}}:{\frac {1}{b}}:{\frac {1}{c}}=(b{\cdot }c):(a{\cdot }c):(a{\cdot }b).}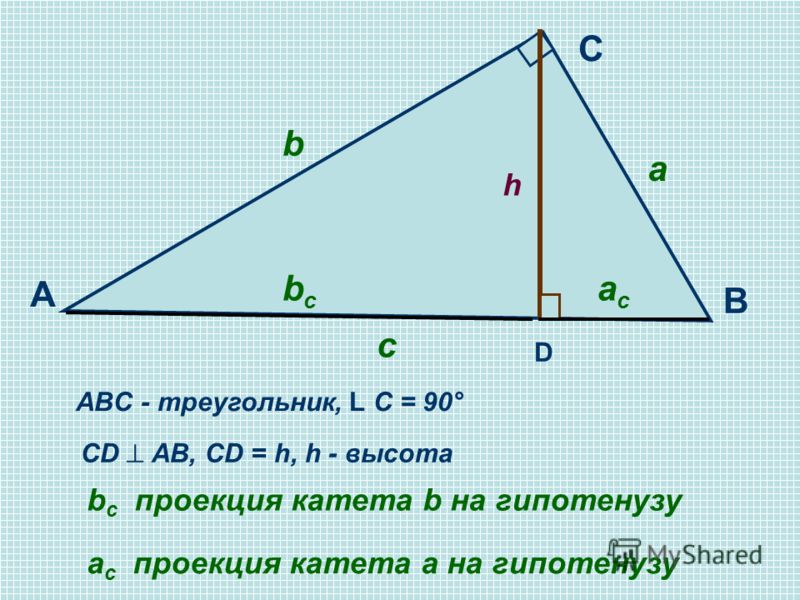 {2}}},}
{2}}},}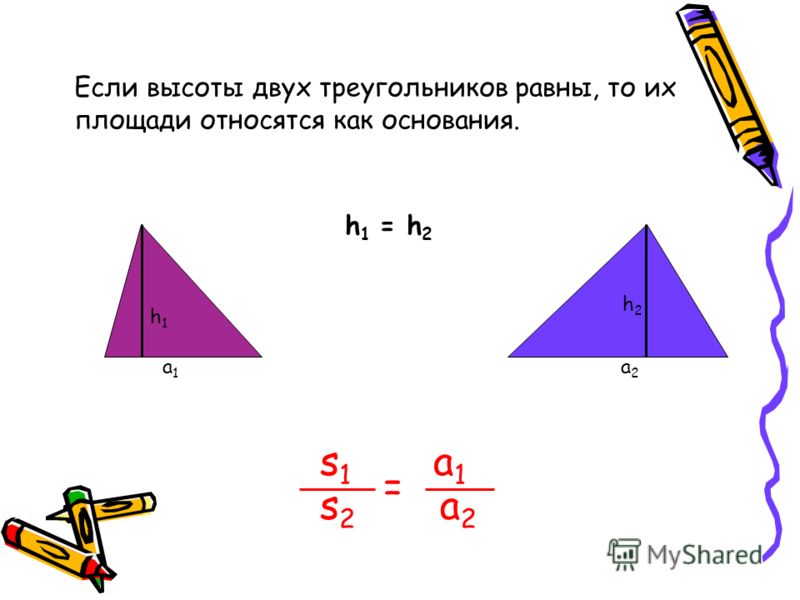 Причем является самым сложным. Это происходит потому, что треугольник может быть острым, тупым, равнобедренным или прямоугольным. Для каждого из существуют свои правила построения и расчета.
Причем является самым сложным. Это происходит потому, что треугольник может быть острым, тупым, равнобедренным или прямоугольным. Для каждого из существуют свои правила построения и расчета. Сделать это можно несколькими простыми для восприятия способами, которые подходят для фигуры разной формы и размера. Весь процесс состоит из определённой последовательности действий, правильно выполнить которые сможет каждый школьник.
Сделать это можно несколькими простыми для восприятия способами, которые подходят для фигуры разной формы и размера. Весь процесс состоит из определённой последовательности действий, правильно выполнить которые сможет каждый школьник.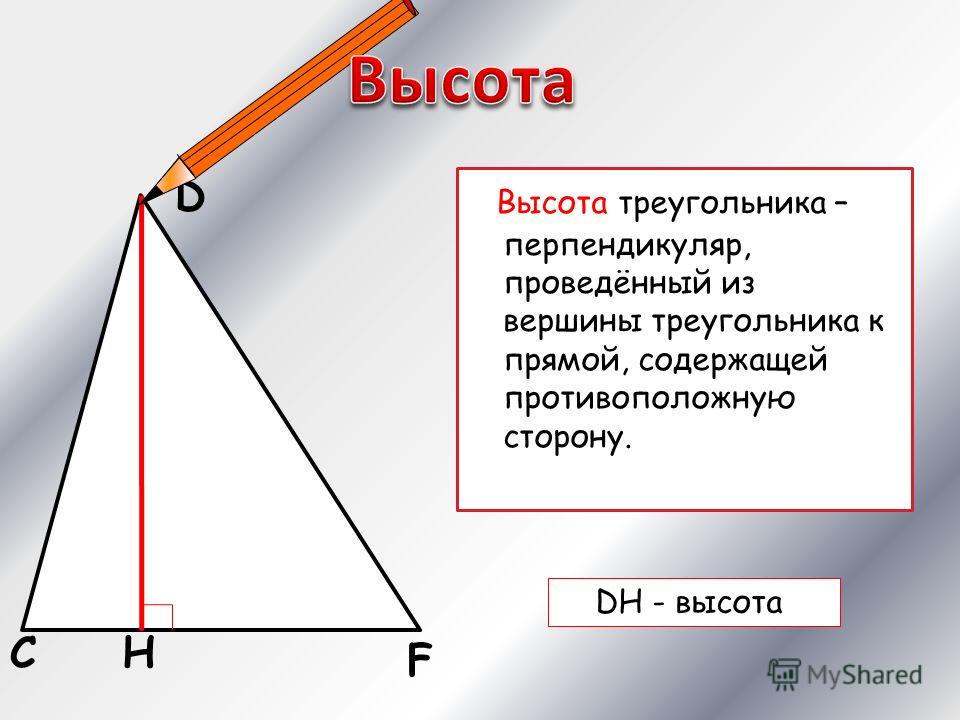


 Подключите длину боковой в Формуле
Подключите длину боковой в Формуле 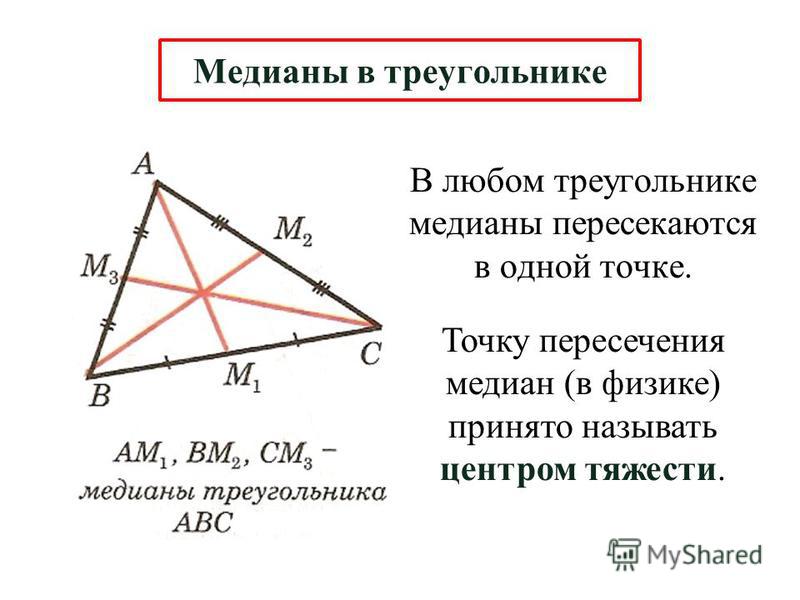 Равносторонний треугольник обладает следующими свойствами.
Равносторонний треугольник обладает следующими свойствами. 
 0006
0006 По правилу 30-60-90, частному случаю прямоугольного треугольника, мы знаем, что основание этого меньшего прямоугольного треугольника равно, а высота этого меньшего прямоугольного треугольника равна, принимая b за гипотенузу.
По правилу 30-60-90, частному случаю прямоугольного треугольника, мы знаем, что основание этого меньшего прямоугольного треугольника равно, а высота этого меньшего прямоугольного треугольника равна, принимая b за гипотенузу. Для выполнения расчетов необходимо знать размеры наибольшей стороны геометрической фигуры, гипотенузы, а также еще одной ее стороны.
Для выполнения расчетов необходимо знать размеры наибольшей стороны геометрической фигуры, гипотенузы, а также еще одной ее стороны.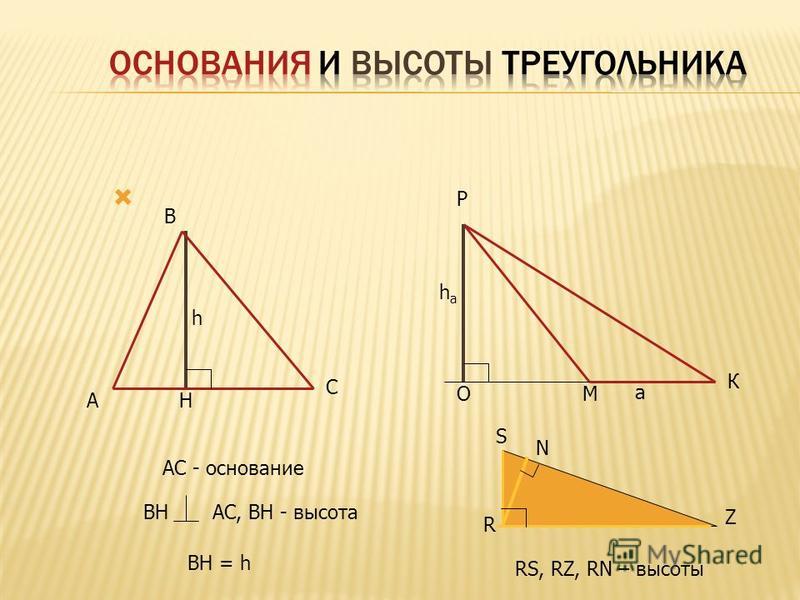
 Особенно, когда дело доходит до конкурсных экзаменов, время является ценным ресурсом. Следовательно, нестандартное мышление облегчит поиск решений.
Особенно, когда дело доходит до конкурсных экзаменов, время является ценным ресурсом. Следовательно, нестандартное мышление облегчит поиск решений.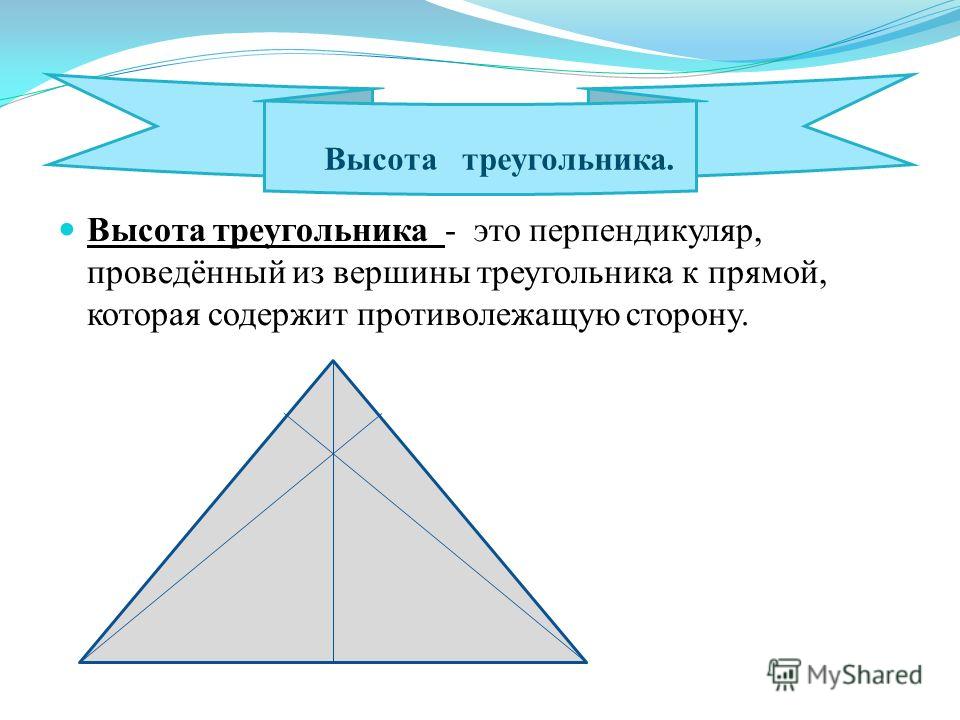
 Если вы упростите тождественное уравнение, вы ВСЕГДА получите истинное утверждение. Узнайте об уравнениях тождества в этом руководстве, а затем создайте собственное уравнение тождества. Проявите творческий подход! Возможности безграничны!
Если вы упростите тождественное уравнение, вы ВСЕГДА получите истинное утверждение. Узнайте об уравнениях тождества в этом руководстве, а затем создайте собственное уравнение тождества. Проявите творческий подход! Возможности безграничны!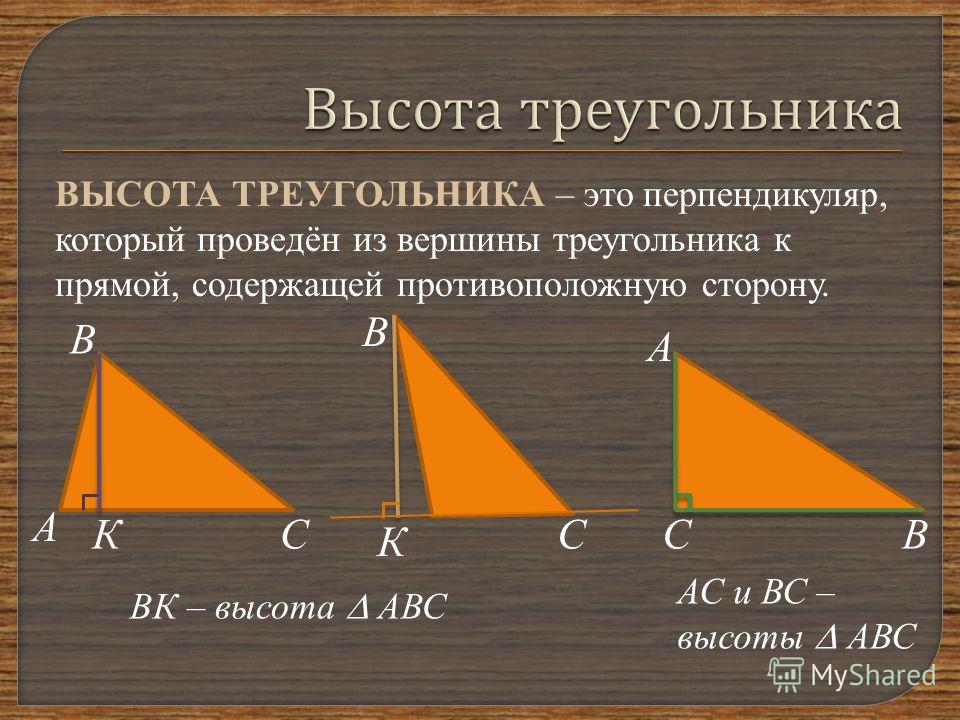

 Затем обязательно проверьте свои ответы, чтобы ЗНАТЬ, что они правильные!
Затем обязательно проверьте свои ответы, чтобы ЗНАТЬ, что они правильные!