Выяснить будут ли матрицы неособенными: Обратная матрица — нахождения обратной матрицы (теория и практика)

16, 17)) Обратная матрица

Рассмотрим квадратную матрицу.Обозначим  =det A.Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если  = 0.Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е — единичная матрица того же порядка, что и матрицы А и В.Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля/Матрица, обратная матрице А, обозначается через А^1, так что В = А^1. Обратная матрица вычисляется по формуле, где А _{i j} — алгебраические дополнения элементов a _{i j}.Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП).

Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы

18) Система м-линейных уравнений с n неизвесными(m<n)

Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида

(1)

Здесь x₁, x₂, …, x_n — неизвестные, которые надо определить. a₁₁, a₁₂, …, a_mn — коэффициенты системы — и b₁, b₂, … b_m — свободные члены — предполагаются известными. Индексы коэффициентов (a_ij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно^[1].Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b

₂ = … = b_m = 0), иначе — неоднородной.Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.Решение системы (1) — совокупность n чисел c₁, c₂, …, c_n, таких что подстановка каждого c_i вместо x_i в систему (1) обращает все её уравнения в тождества. Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.Совместная система вида (1) может иметь одно или более решений.Решения c₁⁽¹⁾, c₂⁽¹⁾, …, c_n⁽¹⁾ и c₁⁽²⁾, c₂⁽²⁾ , …, c_n⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Определение 14.10   Пусть дана матрица размеров и число , не превосходящее наименьшего из чисел и : . Выберем произвольно строк матрицы и столбцов (номера строк могут отличаться от номеров столбцов). Определитель матрицы, составленной из элементов, стоящих на пересечении выбранных строк и столбцов, называется минором порядка матриws

   Предложение 14.23   Если все миноры матрицы порядка равны нулю, то все миноры порядка , если такие существуют, тоже равны нул./. Доказательство.     Возьмем произвольный минор порядка . Это определитель матрицы порядка . Разложим его по первой строке. Тогда в каждом слагаемом разложения один из множителей будет являться минором порядка исходной матрицы. По условию миноры порядка равны нулю. Поэтому и минор порядка будет равен нулю. Определение 14.11   Рангом матрицы называется наибольший из порядков миноров матрицы , отличных от нуля. Ранг нулевой матрицы считается равным нулю.   Единое, стандартное, обозначение ранга матрицы отсутствует. Следуя учебник, мы будем обозначать его Ранг невырожденной квадратной матрицы порядка равен , так как ее определитель является минором порядка и у невырожденной матрицы отличен от нуля.  Предложение 14.24   При транспонировании матрицы ее ранг не меняется, то есть  Доказательство.     Транспонированный минор исходной матрицы будет являться минором транспонированной матрицы , и наоборот, любой минор является транспонированным минором исходной матрицы . При транспонировании определитель (минор) не меняется ( предложение 14.6). Поэтому если все миноры порядка в исходной матрице равны нулю, то все миноры того же порядка в тоже равны нулю. Если же минор порядка в исходной матрице отличен от нуля, то в есть минор того же порядка, отличный от нуля. Следовательно, . Определение 14.12   Пусть ранг матрицы равен . Тогда любой минор порядка , отличный от нуля, называется базисным минором.   Определение 14.13   Система столбцов (строк) называется линейно зависимой, если существует такой набор коэффициентов, из которых хотя бы один отличен от нуля, что линейная комбинация столбцов (строк) с этими коэффициентами будет равна нулю.    Определение 14.14   Система столбцов (строк) является линейно независимой, если из равенства нулю линейной комбинации этих столбцов (строк) следует, что все коэффициенты этой линейной комбинации равны нулю.     Верно также следующее предложение, аналогичное предложению 10.6 Предложение 14.25   Система столбцов (строк) является линейно зависимой тогда и только тогда, когда один из столбцов (одна из строк) является линейной комбинацией других столбцов (строк) этой системы.   Сформулируем теорему, которая называется теорема о базисном миноре  Теорема 14.2   Любой столбец матрицы является линейной комбинацией столбцов, проходящих через базисный минор.      Предложение 14.26   Ранг матрицы равен максимальному числу ее столбцов, образующих линейно независимую систему.    Доказательство .     Пусть ранг матрицы равен . Возьмем столбцы, проходящие через базисный минор. Предположим, что эти столбцы образуют линейно зависимую систему. Тогда один из столбцов является линейной комбинацией других. Поэтому в базисном миноре один столбец будет линейной комбинацией других столбцов. По предложениям 14.15 и 14.18 этот базисный минор должен быть равен нулю, что противоречит определению базисного минора. Следовательно, предположение о том, что столбцы, проходящие через базисный минор, линейно зависимы, не верно. Итак, максимальное число столбцов, образующих линейно независимую систему, больше либо равно .Предположим, что столбцов образуют линейно независимую систему. Составим из них матрицу . Все миноры матрицы являются минорами матрицы . Поэтому базисный минор матрицы имеет порядок не больше . По теореме о базисном миноре, столбец, не проходящий через базисный минор матрицы , является линейной комбинацией столбцов, проходящих через базисный минор, то есть столбцы матрицы образуют линейно зависимую систему. Это противоречит выбору столбцов, образующих матрицу . Следовательно, максимальное число столбцов, образующих линейно независимую систему, не может быть больше . Значит, оно равно , что и утверждалось.   Предложение 14.27   Ранг матрицы равен максимальному числу ее строк, образующих линейно независимую систему  Доказательство.     По предложению 14.24 ранг матрицы при транспонировании не меняется. Строки матрицы становятся ее столбцами. Максимальное число новых столбцов транспонированной матрицы, (бывших строк исходной) образующих линейно независимую систему, равно рангу матрицы   Предложение 14.28   Если определитель матрицы равен нулю, то один из его столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).Доказательство .     Пусть порядок матрицы равен . Определитель является единственным минором квадратной матрицы, имеющим порядок . Так как он равен нулю, то . Следовательно, система из столбцов (строк) является линейно зависимой, то есть один из столбцов (одна из строк) является линейной комбинацией остальных.              Теорема 14.3   Определитель матрицы равен нулю тогда и только тогда, когдаодин из ее столбцов (одна из строк) является линейной комбинацией остальных столбцов (строк).      Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений   Определение 14.15   Назовем элементарными преобразованиями матриц следующие действия над ними: 1) перестановка строк или столбцов; 2) умножение строки или столбца на число отличное от нуля; 3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.  Предложение 14.29   При элементарных преобразованиях ранг матрицы не меняе  Доказательство.     Пусть ранг матрицы равен ,  — матрица, получившаяся в результате выполнения элементарного преобразования.Рассмотрим перестановку строк. Пусть  — минор матрицы , тогда в матрице есть минор , который или совпадает с , или отличается от него перестановкой строк. И наоборот, любому минору матрицы можно сопоставить минор матрицы или совпадающий с , или отличающийся от него порядком строк. Поэтому из того, что в матрице все миноры порядка равны нулю, следует, что в матрице тоже все миноры этого порядка равны нулю. И так как в матрице есть минор порядка , отличный от нуля, то и в матрице тоже есть минор порядка , отличный от нуля, то есть Рассмотрим умножение строки на число , отличное от нуля. Минору из матрицы соответствует минор из матрицы или совпадающий с , или отличающийся от него только одной строкой, которая получается из строки минора умножением на число, отличное от нуля. В последнем случае . Во всех случаях или и одновременно равны нулю, или одновременно отличны от нуля. Следовательно, Пусть к -ой строке матрицы прибавлена ее -ая строка, умноженная на число . Рассмотрим миноры порядка в матрице . Если через минор не проходит -ая строка, то он совпадает с минором , расположенным в тех же строках и столбцах в матрице , и следовательно, равен нулю. Если через минор проходят и -ая и -ая строки, то онполучается из минора , расположенного в тех же строках и столбцах матрицы , прибавлением к -ой строке минора -ой строки, умноженной на . По свойству определителя . Следовательно, . Пусть через минор проходит -ая строка и не проходит -ая. Тогда отличается от -ой строкой. Эта строка в является строкой , к которой добавлены элементы -ой строки, умноженные на . По свойствам определителей , где  — минор порядка матрицы , стоящий в -ой строке и в тех же строках, что и минор , исключая -ую, а знак » » связан с возможным изменением порядка строк. Так как все миноры порядка в матрице равны нулю, то .

Итак, в матрице все миноры порядка равны нулю. Следовательно, , то есть при выполнении элементарного преобразования третьего типа ранг не может повыситься. Предположим, что , и . Тогда в матрице к -ой строке прибавим -ую строку, умноженную на число . В результате получим исходную матрицу . По только что доказанному . Получили противоречие: . Предположение не верно, следовательно, .     

Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы. Алгоритм нахождения ранга матрицы.

Пусть требуется вычислить ранг матрицы размеров . Если матрица нулевая, то по определению . В противном случае с помощью перестановки строк и столбцов матрицы добиваемся того, чтобы в левом верхнем углу матрицы стоял ненулевой элемент. Итак, считаем, что . Первую строку оставляем без изменений. Ко второй строке прибавляем первую, умноженную на число . В результате вторая строка принимает вид Затем к третьей строке прибавляем первую строку, умноженную на число . В результате третья строка принимает вид Процесс продолжаем до тех пор, пока не получим нуль на первом месте в последней строке. Преобразованная матрица имеет вид Если все строки, начиная со второй, в полученной матрице нулевые, то ее ранг равен 1, так как естьминор первого порядка, отличныйот нуля . В противном случае перестановкой строк и столбцов матрицы с номерами,большими единицы, добиваемся, чтобы второй элемент второй строки был отличен от нуля. Итак, считаем, что . Первую и вторую строки оставляем без изменений. К третьей строке прибавляем вторую, умноженную на чисо . В результате получим, что второй элемент третьей строки равен нулю. Затем к четвертой строке прибавляем вторую, умноженную на число , и т.д. В результате получаем матрицу Если все строки, начиная с третьей, нулевые, то , так как минор . В противном случае перестановкой строк и столбцов с номерами, большими двух, добиваемся, чтобы третий элемент третьей строки был отличен от нуля. Далее, добавлением третьей строки, умноженной на соответствующие числа, к строкам с большими номерами получаем нули в третьем столбце, начиная с четвертого элемента, и т. д. На каком-то этапе мы придем к матрице, у которой все строки, начиная с -ой , равны нулю (или отсутствуют при ), а минор в первых строках и первых столбцах является определителем треугольной матрицы с ненулевыми элементами на диагонали. Ранг такой матрицы равен . Следовательно, .       Замечание 14.15   В предложенном алгоритме нахождения ранга матрицы все вычисления должны производиться без округлений. Сколь угодно малое изменение хотя бы в одном из элементов промежуточных матриц может привести к тому, что полученный ответ будет отличаться от ранга исходной матрицы на несколько единиц.          Замечание 14.16   Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.  Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец b является линейной комбинацией столбцов матрицы A. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (соответственно столбец), которая является линейной комбинацией других строк (соответственно столбцов) следует, что .ДостаточностьПусть . Возьмем в матрице A какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы B. Тогда согласно теореме о базисном миноре последний столбец матрицы B будет линейной комбинацией базисных столбцов, то есть столбцов матрицы A. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы A

30) Обратная матрица

      Определение 14 . 8   Матрица   называется обратной матрицей для квадратной матрицы   , если   .          Из определения следует, что обратная матрица   будет квадратной матрицей того же порядка, что и матрица  (иначе одно из произведений   или   было бы не определено). Обратная матрица для матрицы   обозначается   . Таким образом, если   существует, то   . Из определения обратной матрицы следует, что матрица  является обратной для матрицы   , то есть   . Про матрицы   и  можно говорить, что они обратны друг другу или взаимно обратны.         Предложение 14 . 20   Если матрица   имеет обратную, то   и  .          Доказательство .     Так как определитель произведения матриц равен произведению определителей (  предложение 14.7 ), то  . По   следствию 14.1   , поэтому   , что невозможно при   . Из предыдущего равенства следует также  .      Последнее предложение можно сформулировать в следующем виде. Если определитель матрицы равен нулю, то обратная к ней не существует. Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.         Определение 14 . 9   Квадратную матрицу   назовем вырожденной или особенной матрицей , если   , и невырожденной или неособенной матрицей , если   .                  Предложение 14 . 21   Если обратная матрица существует, то она единственна.          Доказательство .     Пусть две матрицы   и   являются обратными для матрицы  . Тогда     и Следовательно,   .              Предложение 14 . 22   Если квадратная матрица  является невырожденной, то обратная для нее существует и  ( 14 .14) где    — алгебраические дополнения к элементам   .          Доказательство .     Так как для невырожденной матрицы   правая часть равенства ( 14.14 ) всегда существует, то достаточно показать, что эта правая часть является о братной матрицей для матрицы   . Обозначим правую часть равенства ( 1 4.14 ) буквой   . Тогда нужно п роверить, что  и что   . Докажем первое из этих равенств, второе доказывается аналогично. Пусть   . Найдем элементы матрицы   , учитывая, что  :   Если   , то по   предложению 14.17 сумма справа равна нулю, то есть   при   . Если  , то   Сумма справа представляет собой разложение определителя матрицы   по   -ой строке ( предложение 14. 16 ). Таким образом,  Итак, в матрице   диагональные элементы равны 1, а остальные равны нулю, то есть   .      Результаты предложений 14.20 , 14.21 , 14.22 соберем в одну теорему.         Теорема 14 . 1   Обратная матрица для квадратной матрицы   существует тогда и только тогда, когда матрица    — невырожденная, обратная матрица единственна, и справедлива формула ( 14.14 ).              Замечание 14 . 12   Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца , а второй — номер строки , в которые нужно записать вычисленное алгебраическое дополнение.                  Пример 14 . 7   Найдите обратную матрицу для матрицы   . Решение. Находим определитель  Так как  , то матрица    — невырожденная, и обратная для нее существует. Находим алгебраические дополнения:  Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй — строке:   ( 14 . 15) Полученная матрица и служит ответом к задаче.                  Замечание 14 . 13   В предыдущем примере было бы точнее ответ записать так:  ( 14 .16) Однако запись ( 14.15 ) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде ( 14.15 ) предпочтительнее, если элементы матриц — целые числа. И наоборот, если элементы матрицы    — десятичные дроби, то обратную матрицу лучше записать без множителя   впереди.                  Замечание 14 . 14   При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.                  Пример 14 .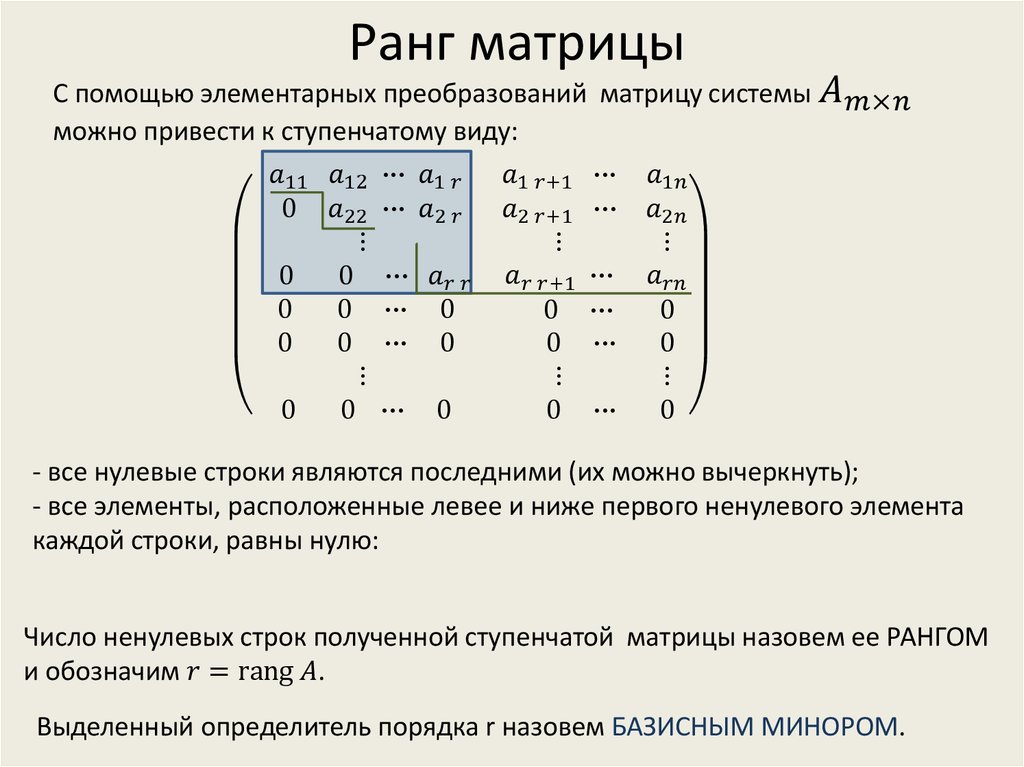 8   Найдите обратную матрицу для матрицы   . Решение.   — существует.   Ответ:   .          Нахождение обратной матрицы по формуле ( 14.14 ) требует слишком много вычислений. Для матриц четвертого порядка и выше это неприемлемо. Реальный алгоритм нахождения обратной матрицы будет приведен позже. 

Теорема существования и единственности решения задачи Коши

У кажем достаточные условия существования и единственности решения задачи Коши

                                                               .                                                             (1)

Теорема Пикара. Пусть функция непрерывна в прямоугольнике

и удовлетворяет условию Липшица по y равномерно относительно x, т.е.  , для всех x,  и .

Пусть

 ,

тогда задача Коши (1) на промежутке  имеет единственное решение .

Замечание. Условие Липшица в теореме Пикара можно заменить на требование ограниченности или непрерывности    в каждом компакте из области определения дифференциального уравнения.

Решение задачи Коши при выполнении условий теоремы Пикара можно найти как предел при   равномерно сходящейся последовательности функций  , определяемых рекуррентным соотношением

                                              .                                     (2)

Оценка погрешности, получаемой при замене точного решения y(x) n- м приближением  , выражается неравенством

.

Теорема Пеано. Пусть функция непрерывна в прямоугольнике , причем

.

Тогда задача Коши на промежутке   имеет по крайне мере одно решение  .

Система уравнений

в векторных обозначениях записывается в виде

                                                                       ,                                                                        (3)

где   и   — векторы. Непрерывность вектор — функции f  означает непрерывность всех функций  , а вместо  рассматривается матрица из частных производных   .

Рассмотренные выше теоремы остаются справедливы и для системы, записанной в виде (3). При этом |y| означает длину вектора y:  .

Рассмотрим уравнение вида

                                                                .                                                              (4)

Пусть в области D функция f и ее частные производные первого порядка по  непрерывны, и точка  лежит внутри D. Тогда при начальных условиях

уравнение (4) имеет единственное решение.

Уравнение (4) можно свести к системе вида (2), если ввести новые неизвестные функции по формулам  . Тогда уравнение (4) сводится к системе

,

которая является частным случаем системы (3) и к которой применимы все рассмотренные утверждения.

Часто решение задачи Коши существует не только на отрезке, указанном в теоремах, но и на большем отрезке.

Если функция f(x,y)  удовлетворяет в прямоугольнике   условиям теоремы Пикара, то всякое ее решение  можно продолжить до выхода на границу прямоугольника  . Если функция f(x,y) в полосе   непрерывна и удовлетворяет неравенству  , где a(x) и b(x) — непрерывные функции, то всякое решение уравнения (1) и (3) можно продолжить на весь интервал  .

Пример 1.  Построить последовательные приближения   к решению данного уравнения с данными начальными условиями:  .

Решение.

Последовательные приближения к решению данной задачи определим по рекуррентной формуле

.

Подставляя в последнюю формулу поочередно n=0,1 найдем нужные приближения:

,

.

Пример 2. Указать какой-нибудь отрезок, на котором существует решение с данными начальными условиями:  .

Решение.

Воспользуемся теоремой Пикара. В данном случае  . Функция f непрерывна в любом прямоугольнике   и удовлетворяет условию Липшица, поскольку производная   ограничена числом  . Следовательно, на сегменте  , где

существует единственное решение данной задачи. Найдем число

.

Ясно, что если на каком — то сегменте I существует единственное решение, то оно существует и на меньшем сегменте, вложенном в I. Отсюда следует, что желательно найти как можно больший отрезок I, т.е.

.

Так как функция   возрастает при  , а функция  убывает, то   достигается при условии, что  , т.е.

                                                                         .                                                                       (5)

Взяв производную по b от правой части (5), найдем, что при  достигается максимум a, который легко вычислить, подставив значение   в (5). Тогда получим

.

Таким образом, можно гарантировать существование и единственность решения данной задачи на сегменте  .

Пример 3. При каких начальных условиях существует единственное решение уравнения  .

Решение.

Поскольку функция

вместе с частными производными

непрерывна при   и  , то через каждую точку  , где   и  , проходит единственная интегральная кривая уравнения

.

Если получены два различных набора базисных неизвестных при различных способах нахождения решения одной и той же системы, то эти наборы обязательно содержат одно и то же число неизвестных, называемое рангом системы.

Вычисление обратной матрицы

Пусть A=(aij) – квадратная матрица с определителем, не равным нулю. Тогда существует обратная матрица A–1, которая вычисляется по формуле

  .

Последняя формула означает, что в i-й строке и j-м столбце обратной матрицы располагается алгебраическое дополнение элемента, стоящего в j-й строке и в i-м столбце исходной матрицы, деленное на определитель исходной матрицы.

Напомним здесь, что Apq=(–1)p+qMpq, где Mpq называется минором и представляет собой определитель, получающийся из определителя detA вычеркиванием p-й строки и q-го столбца.

Рассмотрим пример:

  detA=20+6–24=2;

    .

Еще раз подчеркнем, что обратная матрица существует только для квадратной матрицы с определителем, отличным от нуля!

Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием. Примерами эквивалентных преобразований могут служить следующие преобразования: перестановка местами двух уравнений системы, перестановка местами двух неизвестных вместе с коэффициентами у всех уравнений, умножение обеих частей какого-либо уравнения системы на отличное от нуля число.

31) Рангом системы строк (столбцов) матрицы A с m строк и nстолбцов называется максимальное число линейно независимыхстрок (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы.

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля.

Ранг матрицы — Размерность образа dim(im(A)) линейного оператора, которому соответствует матрица.

Обычно ранг матрицы A обозначается   ( ) или  . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — длянемецкого, французского и ряда других языков.

Определение.  В матрице порядка mxn минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.   Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.

            В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.

            Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается Rg А. Очень важным свойством элементарных преобразований  матриц является то, что они не изменяют ранг матрицы.

            Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.             Надо отметить, что равные матрицы и эвивалентные матрицы — понятия совершенно различные.

            Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк.

            Т.к. элементарные преобразования не изменяют ранг матрицы, то можно существенно упростить процесс нахождения ранга матрицы.

Определение. Матрица  , полученная из матрицы   при помощи элементарных преобразований, называется эквивалентной и обозначается А   В.

Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.

Матрица   называется ступенчатой если она имеет вид:

, где  ,  ,  .

Очевидно, что ранг ступенчатой матрицы равен числу ненулевых строк  , т.к. имеется минор  -го порядка, не равный нулю:

.

Пример. Определить ранг матрицы с помощью элементарных преобразований.

                  .

Ранг матрицы равен количеству ненулевых строк, т.е.  .

линейная алгебра — Доказательство невырожденности матрицы

Задавать вопрос

спросил 9 лет, 1 месяц назад

Изменено 9 лет, 1 месяц назад

Просмотрено 12 тысяч раз

$\begingroup$ 92 х = 0 х = 0 $$

$\endgroup$

$\begingroup$

Если вы сможете доказать вторую часть, то будет доказательством первой части. Матрица считается вырожденной, если она не имеет обратной. Вы доказали, что $I-A$ имеет обратное, а именно $I+A$. Следовательно, $I-A$ несингулярна.

$\endgroup$

$\begingroup$

Сравнение $|I-A|$ с характеристическим полиномом $A$: 9п$). Карта имеет правую обратную тогда и только тогда, когда она сюръективна: так, поскольку наша $L_T$ такова, что $L_S\circ L_T=id$, следует, что $L_S$ сюръективна. Но сюръективная линейная карта между двумя пространствами одной и той же размерности обязательно инъективна. Следовательно, $L_S$ имеет левую обратную (каждая карта инъективна тогда и только тогда, когда она имеет левую обратную), скажем, $G$. Но тогда, поскольку композиция отображений ассоциативна, мы имеем, что $G=L_T$: на самом деле $$G = G\circ (L_S\circ L_T)=(G\circ L_S)\circ L_T=L_T$$ Таким образом, по определению обратного $L_S$ обратимо, а его обратное — это $L_T$ ($=G$). Наконец, изоморфизм между матрицами и линейными отображениями (то, что каждой матрице $M$ ставится в соответствие отображение $x\mapsto Mx$) также дает нам, что матрица $S$ обратима, а обратная ей есть $T$.

$\endgroup$

Несингулярная матрица – формула, определение, свойства, примеры

Несингулярная матрица – это квадратная матрица, определитель которой не равен нулю. Свойство невырожденности матрицы должно быть удовлетворено, чтобы найти обратную матрицу.

Давайте узнаем больше о невырожденной матрице, как найти невырожденную матрицу, свойствах, примерах невырожденной матрицы.

1.	Что такое невырожденная матрица?
2.	Как найти невырожденную матрицу?
3.	Свойства невырожденной матрицы
4.	Термины, относящиеся к невырожденной матрице
5.	Примеры невырожденной матрицы
6.	Практические вопросы по невырожденной матрице
7.	Часто задаваемые вопросы о невырожденной матрице

Что такое невырожденная матрица?

Несингулярная матрица — это квадратная матрица, определитель которой не равен нулю. Несингулярная матрица является обратимой матрицей, и ее обратную можно вычислить, поскольку она имеет определяющее значение. Для квадратной матрицы A = \(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) условие то, что это невырожденная матрица, является определителем этой матрицы A, отличным от нуля. |А| =|объявление — до н.э.| ≠ 0,

Как найти невырожденную матрицу?

Определитель матрицы помогает определить, является ли матрица вырожденной или невырожденной матрицей. Определитель невырожденной матрицы имеет ненулевое значение. Определитель матрицы можно вычислить с помощью операций со строками или столбцами или путем нахождения определителя с использованием кофактора элементов матрицы.

Правила для операций со строками и столбцами определителя

Следующие правила полезны для выполнения операций со строками и столбцами над определителями.

• Значение определителя не изменится, если строки и столбцы поменять местами.
• Знак определителя меняется, если любые две строки или (два столбца) поменять местами.
• Если любые две строки или столбца матрицы равны, то значение определителя равно нулю.
• Если каждый элемент определенной строки или столбца умножается на константу, то значение определителя также умножается на константу.
• Если элементы строки или столбца выражены в виде суммы элементов, то определитель может быть выражен в виде суммы определителей.
• Если элементы строки или столбца сложить или вычесть с соответствующими кратными элементами другой строки или столбца, то значение определителя остается неизменным.

Для простейшей квадратной матрицы порядка 1×1, которая имеет только одно число, определитель становится самим числом. Давайте научимся вычислять определители для матриц второго и третьего порядка.

Вычисление двумерных определителей

Для любой двумерной квадратной матрицы или квадратной матрицы порядка 2×2 мы можем использовать формулу определителя для вычисления ее определителя:

C = \(\left[\begin{array}{ll} a & b \\c & d\end{массив}\right]\)

Его двумерный определитель можно вычислить как:

|C| = \(\left|\begin{array}{ll}a & b \\c & d\end{array}\right|\)

|C| = (a×d) — (b×c)

Вычисление трехмерных определителей

Для любой трехмерной квадратной матрицы или квадратной матрицы порядка 3×3 это процедура вычисления ее определителя.

\(C = \left[\begin{array}{ccc}a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_ {3} & b_{3} & c_{3}\end{массив}\right] \)

Здесь первая строка берется для вычисления определителя матрицы. Элементы \(a_1, b_1, c_1\) умножаются на их соответствующие кофакторы, и суммирование произведения элементов с их соответствующими кофакторами дает значение определителя квадратной матрицы. В качестве альтернативы элементы любой конкретной строки или столбца матрицы можно использовать для нахождения определителя матрицы.

|С| = \(a_{1} \cdot\left|\begin{array}{ll}b_{2} & c_{2} \\b_{3} & c_{3}\end{массив}\right|-b_ {1} \cdot\left|\begin{array}{cc}a_{2} & c_{2} \\a_{3} & c_{3}\end{array}\right|+c_{1} \ cdot\left|\begin{array}{ll}a_{2} & b_{2} \\a_{3} & b_{3}\end{array}\right|\)

|C| = \(a_{1}\left(b_{2} c_{3}-b_{3} c_{2}\right)-b_{1}\left(a_{2} c_{3}-a_{3 } c_{2}\right)+c_{1}\left(a_{2} b_{3}-a_{3} b_{2}\right)\)

Свойства невырожденной матрицы

Ниже приведены некоторые важные свойства невырожденной матрицы.

• Определитель невырожденной матрицы имеет ненулевое значение.
• Несингулярная матрица также называется обратимой матрицей, потому что ее определитель можно вычислить.
• Несингулярная матрица является квадратной матрицей, потому что определители можно вычислить только для невырожденных матриц.
• Произведение двух невырожденных матриц является невырожденной матрицей.
• Если A — невырожденная матрица, k — константа, то kA также невырожденная матрица.

Следующие термины полезны в процессе понимания концепции невырожденной матрицы. Давайте кратко узнаем о каждом из этих терминов.

Сингулярная матрица: Матрица, имеющая значение определителя, равное нулю, называется сингулярной матрицей. Для сингулярной матрицы A |A| = 0. Обратная сингулярная матрица не существует.

Сопряженная матрица: Сопряженная матрица является транспонированием матрицы элементов кофактора данной матрицы.

Минор: Минор определяется для каждого элемента матрицы. Минором конкретного элемента называется определитель, полученный после исключения строки и столбца, содержащих этот элемент. Для матрицы A = \(\begin{pmatrix} a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{ 33}\end{pmatrix}\), минор элемента \(a_{11}\) равен:

Минор от \(a_{11}\) = \(\left|\begin{matrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{matrix}\right|\ )

Кофактор: Кофактор элемента вычисляется путем умножения минора с -1 на показатель степени суммы элементов строки и столбца в порядке представления этого элемента.

Кофактор \(a_{ij}\) = (-1) ^{i + j} × минор \(a_{ij}\).

Определитель: Определитель матрицы — это представление единственного уникального значения матрицы. Определитель матрицы можно вычислить относительно любой строки или столбца данной матрицы. Определитель матрицы равен сумме произведения элементов и его сомножителей определенной строки или столбца матрицы.

Обратная матрица: Обратная матрица — это другая матрица, которая при умножении на данную матрицу дает мультипликативное тождество. Для матрицы порядка 2 × 2 общая формула обратной матрицы равна присоединенной к матрице, деленной на определитель матрицы. A ^-1 = \(\dfrac{1}{|A|}\) Adj A

Связанные темы

Следующие темы помогут лучше понять невырожденную матрицу.

• Порядок матрицы
• Инвертируемая матрица
• Скалярная матрица
• Матрица единиц измерения
• Симметричная матрица
• Диагональная матрица
• Ортогональная матрица
• Кососимметричная матрица
• Эрмитова матрица

Часто задаваемые вопросы о невырожденной матрице

Что называется невырожденной матрицей?

Несингулярная матрица — это квадратная матрица, определитель которой не равен нулю. Свойство невырожденности матрицы должно быть удовлетворено, чтобы найти обратную матрицу.