Wolfram alpha lim: Wolfram|Alpha Examples: Limits

Вольфрам Альфа — frwiki.wiki

Для одноименных статей см. Wolfram .

Правильное название: «  Вольфрам | Альфа  ».

Из-за технических ограничений не удалось правильно отобразить желаемую типографику заголовка.

Wolfram | Alpha (также обозначаемый как WolframAlpha, когда Wolfram и Alpha выделены двумя разными цветами) — это вычислительный инструмент на естественном языке, разработанный международной компанией Wolfram Research . Это интернет-сервис, который отвечает непосредственно на ввод фактических вопросов на английском языке, вычисляя ответ из базы данных, вместо того, чтобы предоставлять список документов или веб-страниц, которые могут содержать ответ. О его запуске было объявлено вМарт 2009 г.британским физиком и математиком Стивеном Вольфрамом, и он был запущен16 мая 2009 г. в 3 часа ночи

Wolfram | Alpha содержит около 10 миллиардов единиц информации, более 50 000 типов алгоритмов и моделей, а также языковые возможности для более чем 1000 областей.

Резюме

• 1 Операция
• 2 зоны охвата
• 3 Использование
• 4 Wolfram Alpha Pro
• 5 необычных просьб
• 6 Примечания и ссылки
• 7 См. Также
  • 7.1 Статьи по теме
  • 7.2 Внешние ссылки

Операция

Пользователи вводят вопрос или запрос на расчет. Сервис рассчитывает ответы и соответствующие визуализации на основе базы знаний .

Благодаря использованию инструмента Mathematica Wolfram | Alpha может отвечать на математические вопросы. Ответ обычно представляется в удобочитаемой форме.

• Пример: lim(x→0) x/sin x​предоставляет ожидаемый ответ, 1, а также способ получить его с помощью правила L’Hôpital .

Wolfram | Alpha также может ответить на фактические вопросы, заданные на естественном английском языке, такие как «  Где родилась Сеголен Руаяль?»  » (» Где родилась Сеголен Руаяль? «) Или более сложные вопросы, такие как »  Сколько лет было Николя Саркози в 1981 году? »  » (« Сколько лет было Николя Саркози в 1981 году? »).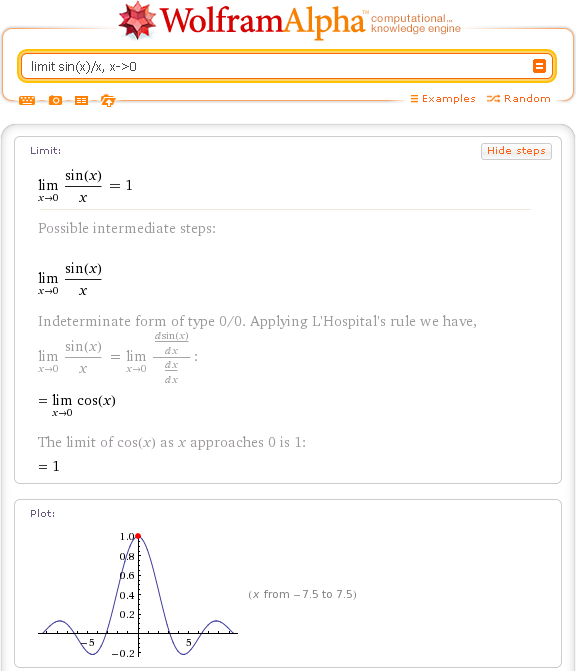

Wolfram | Alpha отображает свою интерпретацию введенного вопроса («  Входная интерпретация  »), используя стандартные предложения, например, «Ségolène Royal | место рождения »или«  возраст | Николя Саркози (политик) | в 1981 году ». (Ответ относительно Сеголен Руаяль включает разнообразную справочную информацию о Дакаре, Сенегал, его географическом положении, а также ссылки на биографию Сеголен Руаяль в Википедии.)

Wolfram | Alpha также может рассчитывать данные, скрещивая несколько источников:

• Пример: «  Какая страна занимает пятьдесят второе место по размеру ВВП на душу населения?  »(« Какая страна занимает пятьдесят второе место по величине ВВП на душу населения? ») Обеспечивает в результате16 ноября 2016 г.«  Джибути, 1814 долларов в год на человека  » («Джибути, 1814 долларов  в год на человека»).

Команда Wolfram | Alpha постепенно собирала и нормализовала данные. В 2009 году база данных охватывала сотни областей, включая данные о текущей и прошлой погоде.

Крытые площади

Wolfram | Alpha анализирует данные из самых разных дисциплин, включая математику, статистику, анализ данных, физику, химию, материаловедение, инженерию, астрономию, науки о Земле и жизни ( геология ), новые технологии, даты и время, места и географию, социально-экономические данные, метеорология, здоровье и медицина, продукты питания и питание, лингвистика, культура, СМИ, личности, история, образование, различные организации, игры и спорт, музыка, цвета и т. д.

использовать

Wolfram Alpha используется для улучшения результатов поисковых систем с помощью Bing и DuckDuckGo . Он также используется Siri и Iris .

Вольфрам Альфа Про

В 8 февраля 2012 г., Выпущен Wolfram Alpha Pro, и предлагает несколько других вариантов.

Необычные запросы

В 2013 году этот сервис использовался особым образом, чтобы пользователи Интернета могли рассчитать дату своей смерти.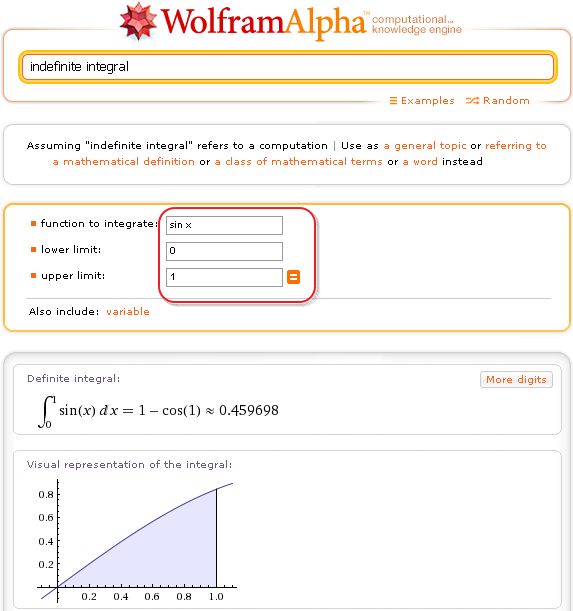

Примечания и ссылки

1. ↑ (in) Блог Wolfram | Альфа: Так много для спокойного запуска
2. ↑ (in) Блог Wolfram | Альфа: выход в эфир и интернет-трансляция
3. ↑ Кстати, на официальном сайте
4. ↑ «  Первый кусок от Wolfram Alpha  » ,18 мая 2009 г.(по состоянию на 9 ноября 2016 г. ) .
5. ↑ «  [Жуткий сайт дня] Вот дата твоей смерти / Journal du Geek  », на Journal du Geek ,20 августа 2013 г.(по состоянию на 3 октября 2020 г. ) .

Смотрите также

Статьи по Теме

• Evi (программное обеспечение  )
• Powerset

Внешние ссылки

• (in) WolframAlpha, официальный сайт
• (in) Вольфрам Альфа приближается, блог Стивена Вольфрама

Поисковые системы (сайты)
Общий	Ask. com Baidu Bing Агент Коперника Exalead Гигабласт Google HotBot Junglekey Двигатель Lycos Mozbot Naver Panguso Сезнам Поделиться Так-так Согоу V9 WebCrawler Yahoo! Яндекс Yippy
Солидарность	Ecogine (экологический) Ecosia (экологический) GoodSearch (гуманитарный) Лило (социальный / экологический)
Частная жизнь	Отключить УткаУтка Начальная страница Qwant Searx Стремится YaCy
Работа	Cadremploi HelloWork Действительно Jobboom Jobillico Келджоб Монстр Воркополис
Наука	CiteSeerX Google Scholar ScientificCommons Sci-Hub Вольфрам Альфа
Другой	Базилиг IceRocket Келкоо NexTag Qwant Junior Skyscanner Спок Ятедо
Отсутствующий	Общие: AltaVista A9. com Блекко Другое: Astalavista Doona Qwant Причины Technorati

<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

2,{x,2}] D[f[x,y],x] вычислить частную производную f(x,y) по x D[Sin[ x y],x] D[f[x,y],{x,n}] вычисляет n -ю частную производную от f(x,y) по отношению к x D[Sin[x y],{x,2}] Integrate[f[x],x] вычисляет неопределенный интеграл от f(x) по отношению к x Интегрировать[Log[x],x] Интегрировать[f[x],{x,x _min ,x _max }] вычисляет определенный интеграл2 от ) относительно x в диапазоне [ x _мин ,x _макс ] Интегрировать[Log[x],{x,1,E}] DSyequation, ,x] решает дифференциальное уравнение для функции y с независимой переменной x DSolve[y'[x]==y,y,x] Series[f[x],{x,0,n}] генерирует n +1 член разложения в Серия MacLaurin Power для f(x) Series[Exp[x],{x,0,10}] Series[f[x],{x,x ₀ ,n}] генерирует n +1 член разложения по степеням Тейлора для f(x) относительно точки x ₀ Series[Log[x],{x,1,10}] Sum[f[i],{i,i _min ,i _max }] вычисляет сумму слагаемых f(i) , где i от i min до i _max , увеличивая i на 1 на каждом шаге ,i _max ,inc}] вычисляет сумму слагаемых f(i) , где i из i min 92,х]

Неопределенный интеграл: Integrate[Log[x],x]

 

Если вы нажмете на кнопку Показать шаги , вы получите демонстрацию.

Определенный интеграл: Integrate[Log[x],{x,1,E}]

 

Дифференциальное уравнение: DSolve[y'[x]==y,y,x]

 

Если нажать на кнопку Показать шаги , вы получите демонстрацию.

Расширение серии Maclaurin: Series[Exp[x],{x,0,10}]

 

Сумма первых 11 нечетных чисел: Sum[2i+1,{i,0,10}]

 

Пределы — IB Math Stuff

Введение в пределы

Пределы являются основой для большей части вычислений. Они также очень абстрактны. Развитие исчисления застопорилось отчасти из-за неспособности математиков иметь дело с пределами. Пределы тесно связаны с идеей бесконечности (как бесконечно большой, так и малой).

Пределы, неформально, представляют собой концепцию исследования того, что происходит с функцией по мере того, как ее аргумент становится все ближе и ближе к определенному значению. Большинство функций, которые вы видели, ведут себя хорошо (и поэтому довольно скучны), но некоторые ведут себя по-другому… Но прежде чем мы перейдем к функциям, давайте посмотрим на последовательности чисел.

Ниже приведена последовательность чисел, которая приближается к значению по мере увеличения «номера термина»:

Номер термина	$n=1$	$n=2$	$n=3$	$n=4$	$n=5$
Стоимость срока	0,3	0,33	0,333	0,3333	0,33333

По мере продвижения последовательности значение члена становится больше, но значение каждого последующего члена приближается к значению. Подумайте об этом… Число становится все больше и больше, но существует ограничение в 90 299 – 90 300 на то, насколько большим может быть это число (если следовать шаблону). Независимо от того, сколько терминов вы выберете, значение термина становится все ближе и ближе к $\frac{1}{3}$! 9{-х}$. Давайте начнем со старого доброго plug-and-chug, сначала взглянем на большие положительные значения x и посмотрим, что происходит с функцией:

Значение x	2	5	10	15
Значение функции	0,25	0,03125	0,000977	0,0000305

Так что же происходит с функцией x становится все больше и больше? Ясно, что функция стремится к нулю. Это можно легко (и быстрее) увидеть, просто построив график функции на калькуляторе. На самом деле многие (но не все) вопросы об ограничениях можно решить, просто построив график функции и наблюдая, что происходит. Метод plug-and-chug также может быть использован и в разы более точен…

Обозначение предела

Опять же, в пределах мы задаем вопрос, что происходит с функцией, поскольку переменная что-то делает. Обозначение пределов выглядит примерно так: 92 = ? \end{align}

Это можно сделать графически или численно, но в этом случае численно может быть проще (ограничения по мере приближения аргумента к положительной или отрицательной бесконечности часто проще всего сделать графически).

Значение x	1	1,5	1,9	1,99
Значение функции	1	2,82	3,732	3,972 92}{х} = ? \end{align} Этот пример не простой, так как предыдущая функция не определена для $x=0$. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт