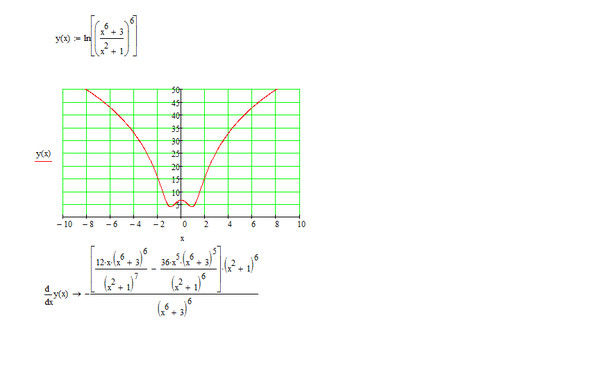
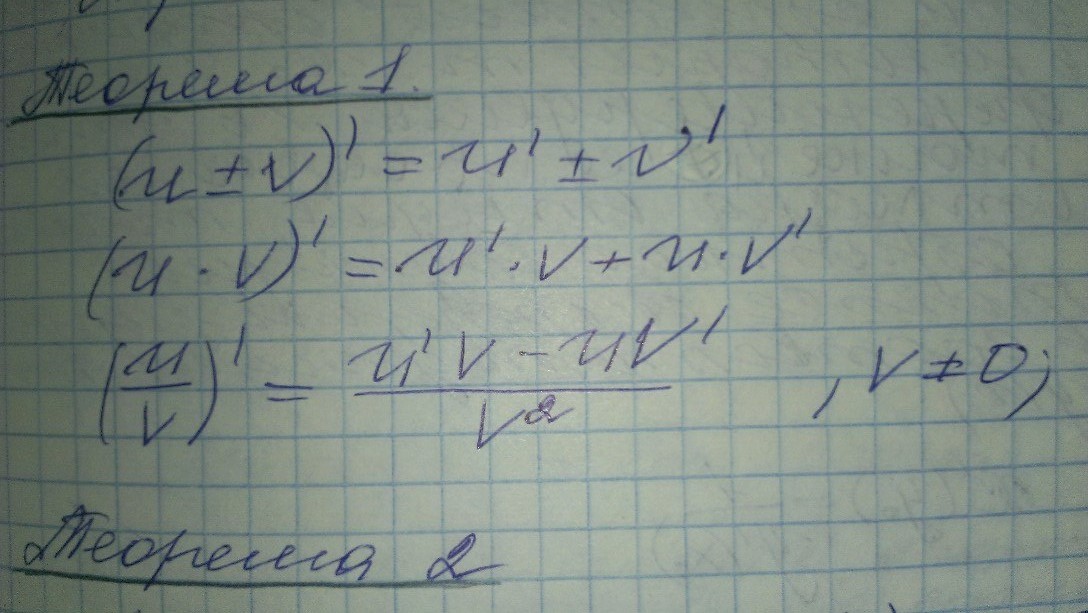ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11. 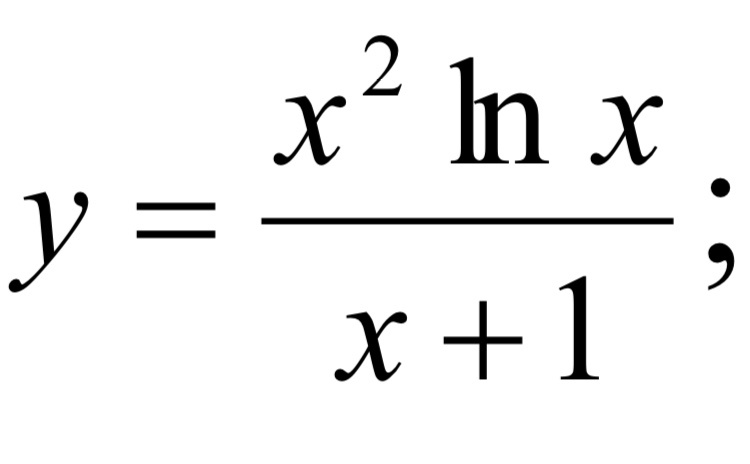 n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 23. 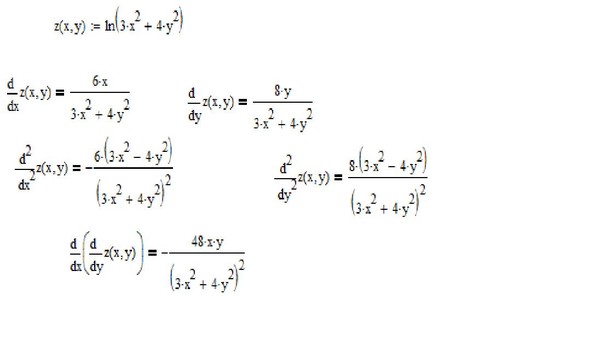 x, sin x, cos xУпражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2.  Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  Формула Чебышева§ 10. Интегралы, зависящие от параметра. Гамма-функция Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII |
11 правил естественного бревна, которые вам нужно знать
Если вы посещаете уроки математики в старшей школе или колледже, вы, скорее всего, будете изучать натуральные бревна. Но что такое натуральные бревна? Что такое лн? Почему буква е продолжает появляться?
Естественные журналы могут показаться сложными, но как только вы поймете несколько ключевых правил естественного журнала, вы сможете легко решать даже очень сложные задачи.
В этом руководстве мы объясним четыре наиболее важных правила натурального логарифма, обсудим другие свойства натурального логарифма, которые вам следует знать, рассмотрим несколько примеров разной сложности и объясним, чем натуральный логарифм отличается от других логарифмов.
Что такое ln?
Натуральный логарифм, или ln, является обратным e . Буква « e» представляет собой математическую константу, также известную как натуральный показатель степени. Как и π, e является математической константой и имеет заданное значение. Значение e приблизительно равно 2,71828.
e появляется во многих случаях в математике, включая сценарии о сложных процентах, уравнениях роста и уравнениях распада. пер( x ) — это время , необходимое для роста до x , а e x — это величина роста , которая произошла после времени x .
Поскольку e так часто используется в математике и экономике, а специалистам в этих областях часто приходится логарифмировать число по основанию e , чтобы решить уравнение или найти значение, был создан естественный логарифм как быстрый способ записи и расчета базы журнала e .
Естественный журнал просто позволяет людям, читающим задачу, знать, что вы берете логарифм с основанием 9.0016 e , номер. So ln( x ) = log e ( x ). Например, ln( 5 ) = log e ( 5 ) = 1,609.
4 ключевых правила естественного логарифма
Есть четыре основных правила, которые вам необходимо знать при работе с естественным логарифмом, и вы будете встречать каждое из них снова и снова в своих математических задачах. Знайте их хорошо, потому что они могут сбивать с толку в первый раз, когда вы их видите, и вы хотите убедиться, что у вас есть основные правила, подобные этим, до того, как перейти к более сложным темам логарифмов.
Правило продукта
- ln(x)(y) = ln(x) + ln(y)
- Натуральный логарифм произведения x и y равен сумме ln числа x и ln числа y.
- Пример: ln(8)(6) = ln(8) + ln(6)
Частное правило
- ln(x/y) = ln(x) — ln(y)
- Натуральный логарифм деления x и y равен разнице ln x и ln of y.
- Пример: ln(7/4) = ln(7) — ln(4)
Правило взаимности
- ln(1/x) = −ln(x)
- Натуральный логарифм обратной величины x противоположен ln x.
- Пример: ln(⅓)= -ln(3)
Степенное правило
- ln( x y ) = y * ln(x)
- Натуральный логарифм x, возведенный в степень y, равен y, умноженному на ln числа x.
- Пример: ln(5 2 ) = 2 * ln(5)
Ключевые свойства натурального бревна
В дополнение к четырем правилам натурального логарифма, рассмотренным выше, есть еще несколько свойств ln, которые вам необходимо знать, если вы изучаете натуральный бревно. Запомните их, чтобы вы могли быстро перейти к следующему шагу задачи, не тратя время на запоминание общих свойств ln.
| Сценарий | Л-н Имущество |
| Номер отрицательного числа | Индикация отрицательного числа не определена |
| № 0 | ln(0) не определено |
| № 1 | лн(1)=0 |
| Инфинити | ln(∞)= ∞ |
| лн е | ln(e)=1 |
| Число e, возведенное в степень x | ln( e х ) = х |
| e в степени ln | е ln(x) =x |
Как видно из последних трех строк, ln( e )=1, и это верно, даже если одно возводится в степень другого.
Это потому, что ln и e являются обратными функциями друг друга.
Примеры задач Natural Log
Теперь пришло время проверить свои навыки и убедиться, что вы понимаете правила ln, применяя их к примерам задач. Ниже приведены три примера задач. Попробуйте решить их самостоятельно, прежде чем читать объяснение.
Задача 1
Вычислить ln(7 2 /5)
Сначала воспользуемся правилом частных, чтобы получить: ln(7 2 ) — ln(5).
Затем мы используем правило степени, чтобы получить: 2ln(7) -ln(5).
Если у вас нет калькулятора, вы можете оставить уравнение в таком виде или рассчитать натуральные логарифмические значения: 2(1,946) — 1,609 = 3,891 — 1,609 = 2,282.
Задача 2
Вычислить ln( e ) /7
Для этой задачи нам нужно помнить, чем ln( e )=1
Это означает, что задача упрощается до 1/7, что и является нашим ответом. в круглых скобках вы хотите сделать e основанием, а все остальное — показателем степени e .
Тогда вы получите ln и e рядом друг с другом и, как мы знаем из правил естественного логарифма, e ln(x) =x.
С. ) = 5x-6
Следовательно, 5 x -6= e 2
Поскольку e является константой, вы можете вычислить значение , используя либо 3 , 6 e 9003 нажмите клавишу e на вашем калькуляторе или используйте оценочное значение e, равное 2,718.
5 x -6 = 7,389
Теперь мы добавим 6 к обеим сторонам
5 x = 13,389
Наконец, мы разделим обе стороны на 5.
x = 2,678
Чем натуральные логарифмы отличаются от других логарифмов?
Напоминаем, что логарифм противоположен степени. Если вы возьмете логарифм числа, вы отмените экспоненту. Основное различие между натуральным логарифмом и другими логарифмами заключается в используемом основании. Логарифмы обычно используют основание 10 (хотя это может быть другое значение, которое будет указано), в то время как натуральные журналы всегда будут использовать основание e .
Это означает, что ln(x)=log e ( x )
Если вам нужно преобразовать логарифмы в натуральные логарифмы, используйте следующие два уравнения: х ) = пер(х) / пер(10)
За исключением разницы в основании (что является большой разницей), правила логарифмирования и правила натурального логарифма одинаковы:
| Правила логарифмирования | лн Правил |
| лог(ху)=лог(х)+лог(у) | 1n(x)(y)= 1n(x)+ln(y) |
| лог(х/у)=лог(х)-лог(у) | пер (х/у) = пер (х) — пер (у) |
| журнал (x a ) = a log( x ) | ln(x a )= a ln( x ) |
| log(10 х ) = х | ln( e х )= х |
| 10 log(x) = x | е ln(x) = х |
Резюме: Правила естественного логарифма
Натуральный логарифм, или ln, является обратным числом 9.
0016 е. Правила естественного бревна поначалу могут показаться нелогичными, но как только вы их выучите, их будет довольно просто запомнить и применять к практическим задачам.
Четыре основных правила ln:
- ln(x)(y) = ln(x) + ln(y)
- ln(x/y) = ln(x) — ln(y)
- ln(1/x)=−ln(x)
- n( x y ) = y*ln(x)
Основное различие между натуральным логарифмом и другими логарифмами заключается в используемом основании.
Что дальше?
Пишете исследовательскую работу для школы, но не знаете, о чем написать? В нашем справочнике по темам для научных работ более 100 тем в десяти категориях, так что вы обязательно найдете идеальную тему для себя.
Хотите узнать самый быстрый и простой способ конвертации градусов Фаренгейта в Цельсий? Мы вас прикроем! Ознакомьтесь с нашим руководством по лучшим способам преобразования градусов Цельсия в градусы Фаренгейта (или наоборот).
Сдавать SAT или ACT? Учащимся часто труднее всего справиться с математическим разделом этих тестов, но ознакомьтесь с нашими подробными руководствами по математике SAT и ACT по математике, чтобы узнать все, что вам нужно знать, чтобы справиться с этими математическими вопросами.
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Кристин Сарикас
Об авторе
Кристин окончила Мичиганский государственный университет со степенью в области экологической биологии и географии и получила степень магистра в Университете Дьюка.
В старшей школе она набрала 99-й процентиль по SAT и была названа финалистом национальных заслуг. Она преподавала английский язык и биологию в нескольких странах.
исчисление — Is $\ln (x/y) = \ln |x| — \ln |y|$?
Задавать вопрос
спросил
Изменено 2 года, 6 месяцев назад
Просмотрено 458 раз
$\begingroup$
Если мне нужно найти $y$ следующего уравнения
$$\ln(x/y) = x + y,$$
, вы сначала попытаетесь разделить левую часть, выполнив $\ ln х — \ln у$.
У меня такой вопрос: нужно ли использовать абсолютную функцию как для $x$, так и для $y$?
Я думаю, хотя вы знаете, что $x/y > 0$, вы не знаете, больше или меньше нуля они оба.
На мой взгляд, я не думаю, что это математически правильно, поскольку и $x$, и $y$ могут быть отрицательными. Поэтому мне интересно, правильнее ли вместо этого писать так:
$$\ln |x| — \лн |у| = x + y.$$
Может ли кто-нибудь сообщить мне, действительно ли это правильный способ разделения журнала? Спасибо!
- исчисление
- алгебра-предварительное исчисление
- логарифмы
$\endgroup$
2
$\begingroup$
Выражение $\ln(x/y)$ имеет смысл только тогда, когда $x/y>0$. В данном конкретном случае имеем $x>0$ и $y>0$ или $x<0$ и $y<0$. Когда ($x>0$ и $y>0$) или ($x<0$ и $y<0$), мы можем написать,
$$\frac xy=\frac{|x|}{|y|}$$ а затем
$$\ln (x/y)=\ln |x|-\ln |y|.$$
$\endgroup$
8
$\begingroup$
Сам по себе $\ln |x| — \лн |у| = x + y$ будет давать ложные решения вида $x=-y$.