| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Уравнения Бернулли онлайн
Дифференциальное уравнениеy' +a0(x)y=b(x)yn называется уравнением Бернулли.
Так как при n=0 получается линейное уравнение, а при n=1 — с разделяющимися переменными, то предположим, что n ≠ 0 и n ≠ 1. Разделим обе части (1) на yn. Тогда Положив , имеем . Подставляя это выражение, получим , или, что то же самое, z’ + (1-n)a0(x)z = (1-n)b(x). Это линейное уравнение.
Назначение сервиса. Онлайн калькулятор можно использовать для проверки решения дифференциальных уравнений Бернулли.
- Решение онлайн
- Видеоинструкция
Пример 1. Найти общее решение уравнения y’ + 2xy = 2xy3. Это уравнение Бернулли при n=3. Разделив обе части уравнения на y3 получаем Делаем замену Тогда и поэтому уравнение переписывается в виде -z’ + 4xz = 4x. Решая это уравнение методом вариации произвольной постоянной, получаем откуда или, что то же самое, .
Пример 2. y'+y+y2=0
y’+y = -y2
Разделим на y2
y’/y2 + 1/y = -1
Делаем замену:
z=1/yn-1, т. е. z = 1/y2-1 = 1/y
е. z = 1/y2-1 = 1/y
z = 1/y
z’= -y’/y2
Получаем: -z’ + z = -1 или z’ — z = 1
Далее надо найти z и выразить через него y = 1/z.
Пример 3. xy’+2y+x5y3ex=0
Решение.
а) Решение через уравнение Бернулли.
Представим в виде: xy’+2y=-x5y3ex. Это уравнение Бернулли при n=3. Разделив обе части уравнения на y3 получаем: xy’/y3+2/y2=-x5 ex. Делаем замену: z=1/y2. Тогда z’=-2/y3 и поэтому уравнение переписывается в виде: -xz'/2+2z=-x5ex. Это неоднородное уравнение. Рассмотрим соответствующее однородное уравнение: -xz’/2+2z=0
1. Решая его, получаем: z’=4z/x
Интегрируя, получаем:
ln(z) = 4ln(z)
z=x4. Ищем теперь решение исходного уравнения в виде: y(x) = C(x)x4, y'(x) = C(x)’x4 + C(x)(x4)’
-x/2(4C(x) x3+C(x)’ x4)+2y=-x5ex
-C(x)’ x5/2 = -x5ex или C(x)’ = 2ex. Интегрируя, получаем: C(x) = ∫2exdx = 2ex+C
Интегрируя, получаем: C(x) = ∫2exdx = 2ex+C
Из условия y(x)=C(x)y, получаем: y(x) = C(x)y = x4 (C+2ex) или y = Cx4+2x4ex. Поскольку z=1/y2, то получим: 1/y2 = Cx4+2x4ex
б) решение через замену переменных
y=uv
x(u’v + uv’)+2uv+x5u3v3ex=0
v(x u’ + 2u) + xuv’+ x5u3v3ex = 0
a) xu’+2u = 0
или ln(u)=ln(x-2). Откуда u = x-2
b) xuv’+ x5u3v3ex = 0
x x-2v’+ x5 x-6v3ex = 0
v’/x+ v3ex/x = 0
v’+ v3ex = 0
или 1/y2 = Cx4+2x4ex
| 1 | Оценка с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценка с использованием заданного значения | квадратный корень из 45 | |
| 3 | Оценить | 5+5 | |
| 4 | Оценить | 7*7 | |
| 5 | Найти простую факторизацию | 24 | |
| 6 | Преобразование в смешанный номер | 52/6 | |
| 7 | Преобразование в смешанный номер | 93/8 | |
| 8 | Преобразование в смешанный номер | 34/5 | |
| 9 | График | у=х+1 | |
| 10 | Оценка с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найдите площадь поверхности | сфера (3) | |
| 12 | Оценить | 54-6÷2+6 | |
| 13 | График | г=-2x | |
| 14 | Оценить | 8*8 | |
| 15 | Преобразование в десятичное число | 5/9 | |
| 16 | Оценка с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | у=2 | |
| 18 | Преобразование в смешанный номер | 7/8 | |
| 19 | Оценить | 9*9 | |
| 20 | Решите для C | С=5/9*(Ф-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | у=х+4 | |
| 23 | График | г=-3 | |
| 24 | График | х+у=3 | |
| 25 | График | х=5 | |
| 26 | Оценить | 6*6 | |
| 27 | Оценить | 2*2 | |
| 28 | Оценить | 4*4 | |
| 29 | Оценить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Оценить | 1/3+13/12 | |
| 31 | Оценка | 5*5 | |
| 32 | Решить для d | 2д=5в(о)-вр | |
| 33 | Преобразование в смешанный номер | 3/7 | |
| 34 | График | г=-2 | |
| 35 | Найдите склон | у=6 | |
| 36 | Преобразование в проценты | 9 | |
| 37 | График | у=2х+2 | |
| 38 | 92+5х+6=0|||
| 41 | Преобразование в смешанный номер | 1/6 | |
| 42 | Преобразование в десятичное число | 9% | |
| 43 | Найти n | 12н-24=14н+28 | |
| 44 | Оценить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразование в упрощенную дробь | 43% | |
| 47 | График | х=1 | |
| 48 | График | у=6 | |
| 49 | График | г=-7 | |
| 50 | График | у=4х+2 | |
| 51 | Найдите склон | у=7 | |
| 52 | График | у=3х+4 | |
| 53 | График | ||
| 54 | График | 92-9=0||
| 58 | Оценка с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценка с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Найти простую факторизацию | 14 | |
| 61 | Преобразование в смешанный номер | 7/10 | |
| 62 | Решите для | (-5а)/2=75 | |
| 63 | Упростить | х | |
| 64 | Оценить | 6*4 | |
| 65 | Оценить | 6+6 | |
| 66 | Оценить | -3-5 | |
| 67 | Оценить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найди обратное | 1/3 | |
| 71 | Преобразование в смешанный номер | 20. 11. 11. | |
| 72 | Преобразование в смешанный номер | 7/9 | |
| 73 | Найти LCM | 11, 13, 5, 15, 14 | , , , , |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | у=-х-2 | |
| 79 | График | у=3х+7 | |
| 80 | Определить, является ли многочлен | 2x+2 | |
| 81 | График | у=2х-6 | |
| 82 | График | у=2х-7 | |
| 83 | График | у=2х-2 | |
| 84 | График | у=-2х+1 | |
| 85 | График | у=-3х+4 | |
| 86 | График | у=-3х+2 | |
| 87 | График | у=х-4 | |
| 88 | Оценить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | х+2у=4 | |
| 91 | График | х=7 | |
| 92 | График | х-у=5 | |
| 93 | Решение с использованием свойства квадратного корня 92-2x-3=0 | ||
| 95 | Найдите площадь поверхности | конус (12)(9) | |
| 96 | Преобразование в смешанный номер | 3/10 | |
| 97 | Преобразование в смешанный номер | 7/20 | 92)
Точные уравнения и интегрирующие коэффициенты
Привет! Возможно, вам захочется сначала узнать о дифференциальных уравнениях и частных производных!
Точное уравнение
«Точное» уравнение — это дифференциальное уравнение первого порядка, подобное этому:
М(х, у)dx + N(х, у)dy = 0
имеет некоторую специальную функцию I(x, y), чьи частные производные можно поставить вместо M и N следующим образом:
∂I ∂x dx + ∂I ∂y dy = 0
, и наша задача — найти эту волшебную функцию I(x, y), если она существует.
С самого начала мы можем знать, точное это уравнение или нет!
Представьте, что мы делаем следующие частные производные:
∂M ∂y = ∂ 2 I ∂y ∂x
10 ∂x = ∂ 2 I ∂y ∂x
они заканчиваются теми же ! Итак, это будет верно:
∂M ∂y = ∂N ∂x
Когда это правда, у нас есть «точное уравнение», и мы можем продолжить.
И чтобы обнаружить I(x, y) , мы делаем ЛИБО :
- I(x, y) = ∫M(x, y) dx (с x в качестве независимой переменной), ИЛИ
- I(x, y) = ∫N(x, y) dy (с y в качестве независимой переменной)
И затем есть дополнительная работа (мы покажем вам), чтобы прийти к общему решению
I(x, y) = C
Посмотрим в действии.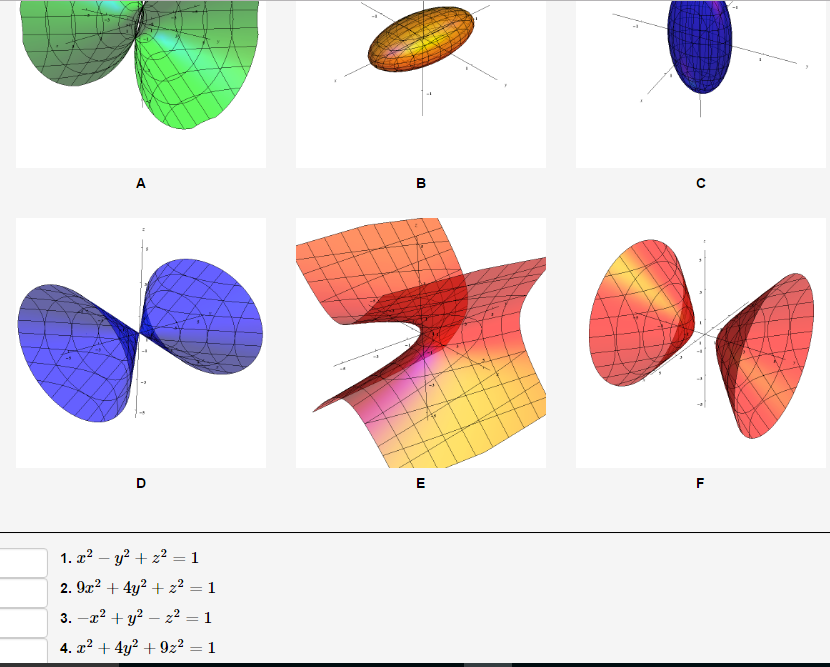
(3x 2 y 3 − 5x 4 ) dx + (y + 3x 3 y 0 2 90dy = 9 0909 В данном случае имеем:
- М(х, у) = 3х 2 у 3 — 5x 4
- N(x, y) = y + 3x 3 y 2
Мы оцениваем частные производные для проверки точности.
- ∂M ∂y = 9x 2 y 2
- ∂N ∂x = 9x 2 y 2
Они одинаковые! Итак, наше уравнение является точным.
Мы можем продолжать.
Теперь мы хотим найти I(x, y)
Проведем интегрирование с x как независимая переменная:
I (x, y) = ∫m (x, y) dx
= ∫ (3x 2 y 3 — 5x 4 ) DX
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
ER — 5x 4 ).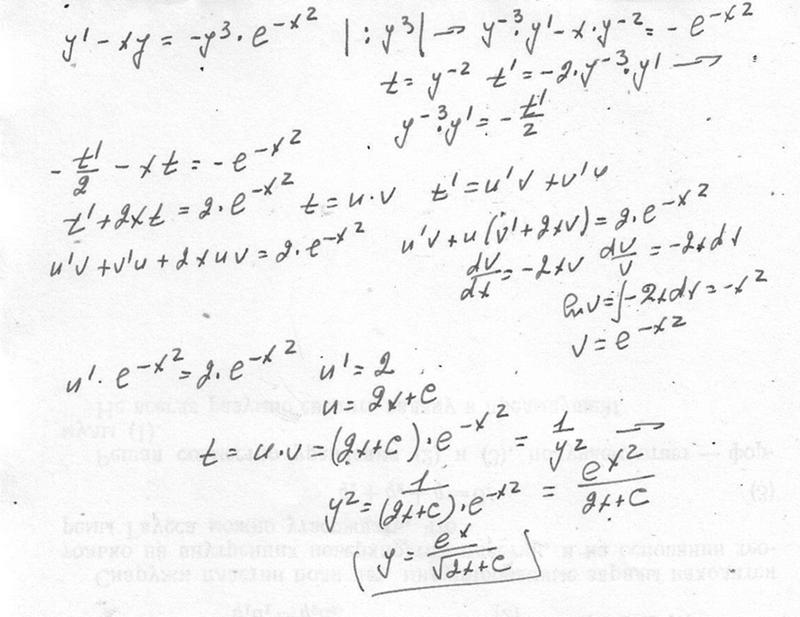 — 5x 4 ). 3 y 3 − x 5 + f(y)
— 5x 4 ). 3 y 3 − x 5 + f(y)
Примечание: f(y) — это наша версия константы интегрирования «C», потому что (из-за частной производной) у нас было y в качестве фиксированного параметра, который, как мы знаем, на самом деле является переменной.
Теперь нам нужно найти f(y)
В самом начале этой страницы мы сказали, что N(x, y) можно заменить на ∂I ∂y , поэтому:
∂I ∂y = N(x, y)
Получаем:
3x 3 y 2 + df dy = y + 3x 3 y 2 df dy = y Интегрируя обе стороны: f(y) = y 2 2 + C У нас есть f(y). Теперь просто поставьте на место: I(x, y) = x 3 y 3 − x 5 + y 2 9 6 + C 900 0 общее решение (как упоминалось перед этим примером): I(x, y) = C Упс! Это «C» может быть другим значением, чем «C» только что. Получаем: x 3 y 3 − x 5 + y 2 2 923 = C Вот как работает этот метод! Поскольку это был наш первый пример, давайте пойдем дальше и убедимся, что наше решение правильное. Выведем I(x, y) относительно
до х, то есть: Оценка ∂I ∂x Начать с: I(х, у) = х 3 у 3 − х 5 + у 2 2 Использование неявного
дифференцировав получаем ∂I ∂x = x 3 3y 2 y’
+ 3x 2 у 3 − 5x 4 + уу’ Упростить ∂I ∂x = 3x 2 y 3 − 5x 4 + y'(y + 3x 3 y 2 1) Мы используем тот факт, что y’ = dy dx и ∂I ∂x = 0, затем умножьте все на dx, чтобы в итоге получить: (у + 3x 3 у 2 )dy
+ (3x 2 y 3 — 5x 4 )dx =
0 , которое является нашим исходным дифференциальным уравнением. Итак, мы знаем, что наше решение верное. (3x 2 − 2xy + 2)dx + (6y 2 − x 2 + 3)dy = 0 Итак: Уравнение точное! Теперь найдем функцию I(x, y) На этот раз попробуем I(x, y) = ∫N(x, y)dy Итак, I(x, y) = ∫(6y 2 − х 2 + 3)dy I(x, y) = 2y 3 − x 2 y
+ 3y + g(x) (уравнение 1) Теперь продифференцируем I(x, y) по x и приравняем его к M: ∂I ∂x = M(x, y) 0 − 2xy + 0 + g'(x) = 3x 2 − 2xy + 2 −2xy + g'(x) = 3x 2 − 2xy + 2 g'(x) = 3x 2 + 2 И интегрирование дает: g(x) = x 3 +
2x + C (уравнение 2) Теперь мы можем заменить g(x) в уравнении 2 в уравнении 1: I(x, y) = 2y 3 − x 2 y + 3y + x 3 + 2x + C И общее решение имеет вид I(x, y) = C и т. 2y 3 − x 2 y + 3y + x 3 + 2x = C Решено! (xcos(y) − y)dx + (xsin(y) + x)dy = 0 Имеем: M = (xcos(y) − y) DX ∂M ∂y = −xsin (y) — 1 n = (xsin (y) + x) dy ∂n ∂x = SIN +10920 +10920 +10920 +10920 (Y) +10920 (Y) +10920 ∂NN ∂x = SIN +10920 +10920 +10920 +10920 ∂10920 (Y). Таким образом ∂M ∂y ≠ ∂N ∂x Итак, это уравнение
не точно! [y 2 − x 2 sin(xy)]dy +
[cos(xy) − xy sin(xy) + e 2x ]dx = 0 M = cos(xy) − xy sin(xy) + e 2x ∂M ∂3y 909 −x 2 y cos(xy) − 2x sin(xy) N = y 2 − x 2 sin(xy) ∂N ∂3x 90 942 г. Они одинаковы! Итак, наше уравнение является точным. На этот раз мы оценим I(x, y) = ∫M(x, y)dx I(x, y) = ∫(cos(xy) − xy sin(xy) + e 2x )dx Используя интегрирование по частям, получаем: I(x, y) = 1 y sin(xy) +
x cos(xy) − 1 y sin(xy)
+ 1 2 e 2x + f(y) I(x, y) = x cos(xy) + 1 2 e 2x 909 42 + f1090 we оценить производную по y ∂I ∂y =
−x 2 sin(xy) + f'(y) И что равно N, что равно M: ∂I ∂y = N(x, y) −x 2 sin(xy) +
f'(y) = y 2 − x 2 sin(xy) f'(y) = y 2 − x 2 sin(xy) + x 2 sin(xy) f'(y) = y 2 f(y) = 1 3 y 3 Таким образом, наше общее решение I(x, y) = C принимает вид: xcos(xy) + 1 2 e 2x + 1 3 y 3 20 = Done 3 20 = Done 0 3 20 Некоторые уравнения, которые не являются точными, могут быть умножены на некоторый коэффициент, a
функция u(x, y) , чтобы сделать их точными. Когда эта функция u(x, y) существует, она называется интегрирующим фактором .
Это сделает допустимым следующее выражение: ∂(u·N(x, y)) ∂x = ∂(u·M(x, y)) ∂y Есть несколько особых случаев: Давайте посмотрим на эти дела… ∂M ∂y = 2y + 9xy 2 2 = 1 − ху ∂N ∂x = −y Итак, ясно, что ∂M ∂y ≠ ∂N ∂x Но мы можем попытаться сделать это точным21 путем умножения каждой части
уравнение на x m y n : (x m y n y 2 + x m 1 y 9094 41 3 Что «упрощает» до: (x m y n+2 + 1x 9094 1 н+3 Теперь имеем: M = x m y n+2 + 3x m+1 y n+3 ∂929 ∂1M 90 0923 = (n + 2 )x m y n+1 + 3(n + 3)x m+1 y n+2 N = x m y n — 1 m ∂N ∂x = mx м−1 y n − (m + 1)x м 9 10 9 n n А мы хотим ∂M ∂y = ∂N ∂x Итак, давайте выберем правильные значения n n , чтобы сделать уравнение точным. Приравняем их: (n + 2)x m y n+1 + 3(n + 3)x m+1 y n+2 = mx m−1 y n − (m + 1)x m y n+1 Изменить порядок и упростить: [(m + 1) + (n + 2)]x 9Для равенства ноль, каждый коэффициент должен быть равен нулю, поэтому: Последнее, m = 0 , очень помогает! При m=0 мы можем вычислить, что n = −3 И результат: x м г н =
y −3 Теперь мы знаем, как умножить исходное дифференциальное уравнение на y −3 : (y −3 y 2 + y 3 901 x 909 909 942) дх + (y −3 − y −3 xy) dy Получается: (y −1 + 3x)dx + (y −3 − xy −2 )0dy = 090 И это новое уравнение должно быть точным , но давайте проверим еще раз: M = y −1 + 3x ∂M ∂y = −y −2 N = y ∂N Они одинаковы! Теперь наше уравнение точно равно ! Итак, продолжим: I(x, y) = ∫N(x, y)dy I(x, y) = ∫(y −3 − xy −2 )dy I(x, y) = −1 2 y −2 + xy −1 + g(x) Теперь, чтобы определить функцию g(x) мы вычисляем ∂I ∂x = y −1 + g'(x) И это равно M = y −1 + 3x, поэтому: 4 y ‘(x) = y −1 + 3x Итак: g'(x) = 3x g(x) = 3 2 x 2 Таким образом, наше общее решение I(x, y) = C: -1 2 y -2 + xy -1 + 3 2 x 2 2 = 10 x 2 Для u(x, y) = u(x) мы должны проверить это важное условие: Выражение: Z(x) = 1 N [ ∂M ∂y − ∂N ∂x ] должен , а не иметь член y , так что интегрирующий коэффициент является только функцией x u(x) = e ∫Z(x)dx Давайте попробуем пример: M = 3xy − y 2 ∂M ∂9322 − 2 года Н = х(х — у) 9 1428
Итак, наше уравнение , а не точно. Рассчитаем Z(x): Z(x) = 1 N [ ∂M ∂y − ∂N ∂x ] 2 1 10 23 N [ 3x−2y − (2x−y ) ] = x−y x(x−y) = 1 x Итак, Z(x) является функцией только от x, ура! u(x) = e ∫Z(x)dx = e ∫(1/x)dx ) 1 ln 42 = x Теперь, когда мы нашли интегрирующий коэффициент, давайте умножим
дифференциальное уравнение по нему. х[(3xy − y 2 )dx +
x(x − y)dy = 0] и мы получаем (3x 2 у — ху 2 )дх
+ (x 3 − x 2 y)dy = 0 Теперь должно быть точно. Проверим: M = 3x 2 y − xy 2 ∂M ∂y = 3x 2 909 N = − 0 2 Отменяющие термины  Но они оба означают «любую константу», так что давайте назовем их C 1 и C 2 , а затем объединим их в новый C ниже, сказав C=C 1 +C 2
Но они оба означают «любую константу», так что давайте назовем их C 1 и C 2 , а затем объединим их в новый C ниже, сказав C=C 1 +C 2 
 д. (не забывая, что две предыдущие «C» — это разные константы, которые можно свернуть в одну, используя C=C 1 +C 2 ) получаем:
д. (не забывая, что две предыдущие «C» — это разные константы, которые можно свернуть в одну, используя C=C 1 +C 2 ) получаем:
Пример 3: Решить
Пример 4: Решить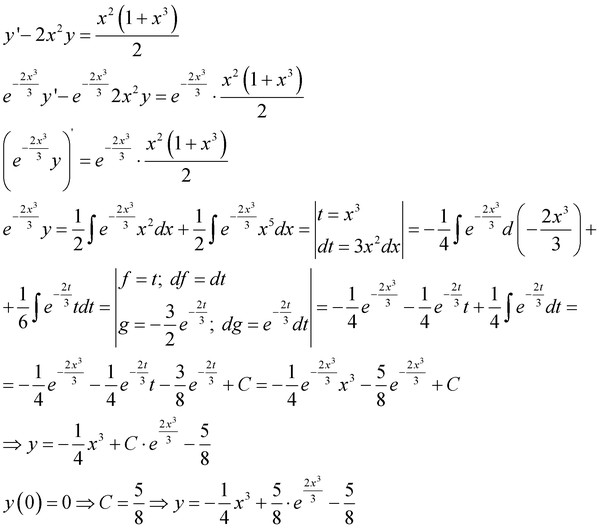 cos(xy) − 2x sin(xy)
cos(xy) − 2x sin(xy) Факторы интегрирования
Интегрирование коэффициентов с использованием u(x, y) = x
м г п Пример 5: (y 2 + 3xy 3 )dx + (1 −
xy)dy = 0
M = y 2 + 3xy 3 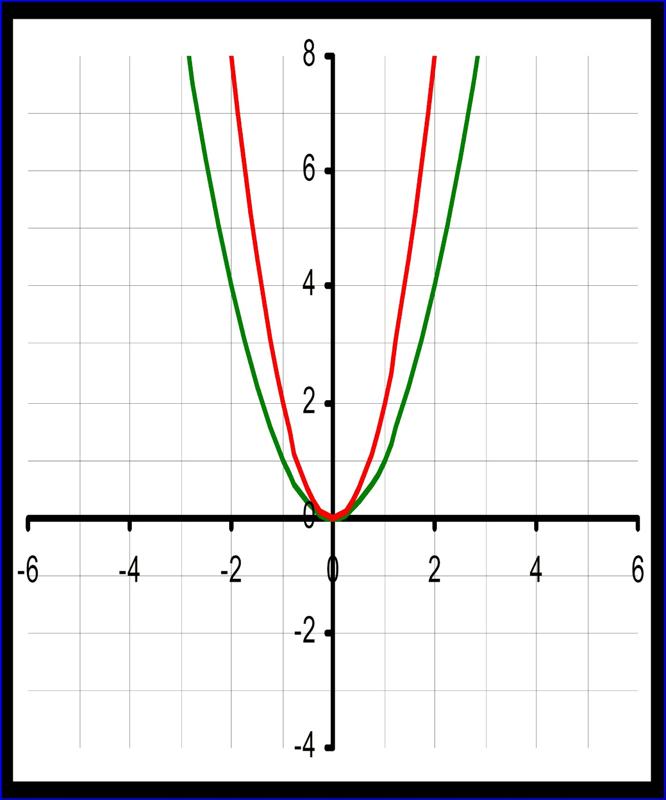
Интегрирование коэффициентов с использованием u(x, y) = u(x)
Если приведенное выше условие верно, то наш интегрирующий коэффициент равен: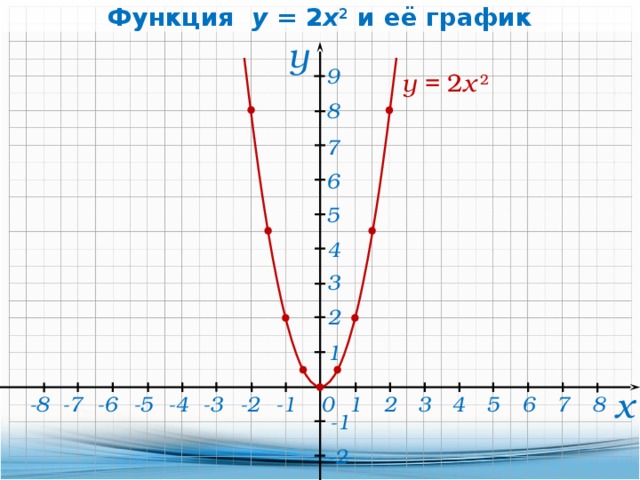
Итак, наш интегрирующий коэффициент равен
∂N ∂x = 3x 2 − 2xy
∂M ∂y = ∂ ∂N
Итак, наше уравнение точное!
Теперь решаем так же, как и в предыдущих примерах.