Y x 5 график: Постройте график функции y=x-5

2+4x-2.найти с помощью графика 1)значение у при х=-1,5 2)значение х при которых у=4 3)значение х при которых у меньше 0 4) промежуток , в котором функция возрастает — вопрос №2376012 — Учеба и наука

Ответы

19. 03.17

Елена Васильевна Читать ответы

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

задача по математике 3-й класс: в забеге участвовало несколько детей.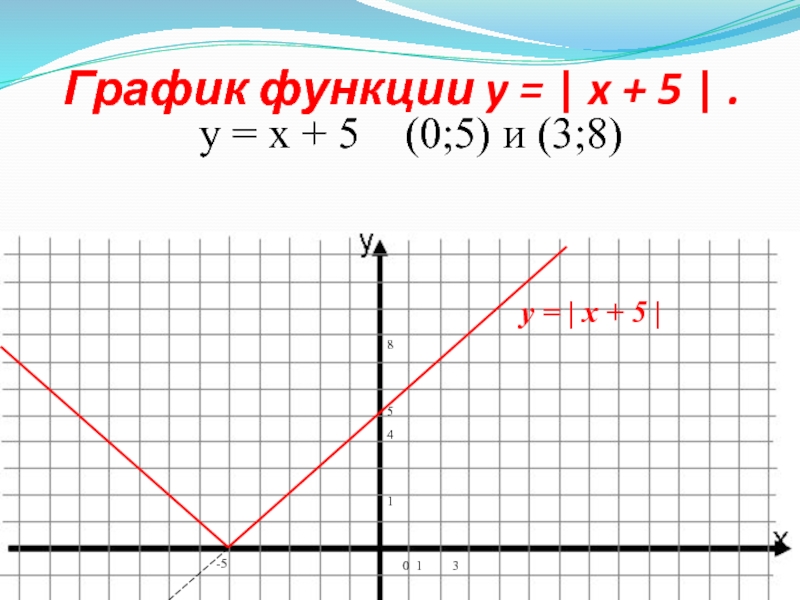 Число прибежавших раньше Миши в три раза больше тех, кто прибежал после него. А

из аэропорта на автовокзал через каждые три минуты отправляется автобус,который едет 1 час.через 2 минуты после отправления из аэропорта выехал

Решено

В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.

задача для 5 класса. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на

В ребусе КЕНГ+УРУ +2017 зашифрована сумма четырехзначного и трехзначного чисел, Разными буквами зашифрованы разные цифры,а одинаковыми — одинаковые.

Пользуйтесь нашим приложением

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т. к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике.

И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

---

Desertai be cukraus Vilniuje: tortai, pyragaičiai, saldainiai

Нарисовать график уравнения y = x+5

• Курс
  • NCERT
    • Класс 12
    • Класс 11
    • Класс 10
    • Класс 9
    9 0003 Класс 8
    • Класс 7
    • Класс 6
  • IIT JEE

• Exam
  • JEE MAINS
  • JEE ADVANCED
  • X BOARDS
  • XII BOARDS
  900 03 NEET
  • Neet Предыдущий год (по годам)
  • Физика Предыдущий год
  • Химия Предыдущий год
  • Биология Предыдущий год
  • Нет Все образцы работ
  • Образцы работ Биология
  • Образцы работ Физика
  • Образцы работ Химия

• Скачать PDF-файлы
  • Класс 12
  • Класс 11
  • Класс 10
  • Класс 9
  • Класс 8
  • Класс 7
  • Класс 6

• Экзаменационный уголок

• Онлайн-класс

• Викторина

• Задать вопрос в Whatsapp

• Поиск Сомнения

900 03 English Dictionary

• Toppers Talk

• Блог

• Скачать

• Получить Приложение

Вопрос

Обновлено: 26/04/2023

Рекомендуемые вопросы

9 видео

РЕКЛАМА

Ab Padhai karo bina ads ke

Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!

---

Похожие видео

ंचे |
x+y=0

127316778

03:36

Нарисуйте график уравнения x+y=5

318515940

01:35

90 122 समीकरण y−x=2

545846464

Текст Решение

Нарисуйте график уравнений.
x+y=3

642982014

05:22

Нарисуйте график уравнений.
x−y=4

642982015

04:03

के आलेख खींचिए :
y = — x

643082875

03:41

Нарисуйте график уравнений y-x=3.

647992257

04:33

Нарисуйте график каждого из следующих уравнений

• Рекомендуемые вопросы

• Нарисуйте график уравнения y = х+5

  02:48

• Нарисуйте график уравнения y = x+5

  02:48

• Нарисуйте график уравнения уравнение y-x=2

  01:41

• 03:37

• 03:49

900 03

Нарисовать график уравнения, x+y =0

02:16

• ित्र खींचे | у+5=0

  03:23

• ींचे | y-x=0

  02:14

• त्र खींचे | x+y=7

  02:13

1. Задайте неограниченное количество вопросов
2. Видеорешения на нескольких языках (включая хинди)
3. Видеолекции экспертов
4. Бесплатные PDF-файлы (предыдущие Ежегодники, книжные решения и многое другое )
5. Посещение специальных консультационных семинаров для IIT-JEE, NEET и экзаменов Совета директоров

Сомневающийся хочет отправлять вам уведомления. Разрешите получать регулярные обновления!

Слушаю…

Напишите уравнение для линейной функции по графику прямой | Колледж Алгебра |

Графики линейных функций

Напомним, что в разделе «Линейные функции» мы написали уравнение для линейной функции по графику. Теперь мы можем расширить наши знания о построении графиков линейных функций для более тщательного анализа графиков. Начните с рассмотрения рисунка 8. Мы сразу видим, что график пересекает y -ось в точке (0, 4), так что это точка пересечения y .

Рисунок 8

Затем мы можем рассчитать наклон, найдя подъем и уклон. Мы можем выбрать любые две точки, но давайте посмотрим на точку (-2, 0). Чтобы добраться от этой точки до перехвата y-, мы должны продвинуться на 4 единицы вверх (подъем) и вправо на 2 единицы (бег). Таким образом, наклон должен быть

м = подъем = 42 = 2 м = \ frac {\ text {подъем}} {\ text {run}} = \ frac {4} {2} = 2 м = подъем = 24 = 2

Подстановка наклона и точки пересечения y- в форму линии с пересечением наклона дает

у=2х+4у=2х+4у=2х+4

Как сделать: Имея график линейной функции, найдите уравнение, описывающее эту функцию.

1. Определите точку пересечения y- уравнения.
2. Выберите две точки для определения уклона.
3. Замените точку пересечения y- и наклон в форму линии с пересечением наклона.

Пример 4. Сопоставление линейных функций с их графиками

Сопоставьте каждое уравнение линейных функций с одной из линий на рисунке 9.

1. f(x)=2x+3f\left(x\right)=2x+3f(x)=2x+3

2. г(х)=2х-3г\влево(х\вправо)=2х — 3г(х)=2х-3

3. h(x)=−2x+3h\влево(x\вправо)=-2x+3h(x)=−2x+3

4. j(x)=12x+3j\left(x\right)=\frac{1}{2}x+3j(x)=21​x+3

Рис. 9

Решение

Проанализируйте информацию для каждой функции.

1. Эта функция имеет наклон 2 и точку пересечения y 3. Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Мы можем использовать две точки, чтобы найти наклон, или мы можем сравнить его с другими перечисленными функциями. Функция g  имеет тот же наклон, но другую точку пересечения y-. Линии I и III имеют одинаковый наклон, потому что они имеют одинаковый наклон. Линия III не проходит через (0, 3), поэтому f должно быть представлено линией I.
2. Эта функция также имеет наклон 2, но y -пересечение –3. Он должен проходить через точку (0, –3) и наклоняться вверх слева направо. Он должен быть представлен линией III.
3. Эта функция имеет наклон –2 и точку пересечения y-, равную 3. Это единственная функция, указанная с отрицательным наклоном, поэтому она должна быть представлена ​​линией IV, поскольку она наклонена вниз слева направо.
4. Эта функция имеет наклон

   12\frac{1}{2}21​

   и y- точка пересечения 3. Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Линии I и II проходят через (0, 3), но наклон j меньше, чем наклон f , поэтому линия для j должна быть более плоской. Эта функция представлена ​​линией II.

Теперь мы можем перемаркировать линии, как показано на рисунке 10.

Рисунок 10

Нахождение точки пересечения линии x

До сих пор мы находили y- точки пересечения функции: точка, в которой график функции пересекает ось y . Функция также может иметь точку пересечения x , , которая представляет собой координату x точки, в которой график функции пересекает ось x . Другими словами, это входное значение, когда выходное значение равно нулю.

Чтобы найти точку пересечения x , установите функцию f ( x ) равной нулю и найдите значение х . Например, рассмотрим показанную функцию.

f(x)=3x−6f\влево(x\вправо)=3x — 6f(x)=3x−6

Установите функцию равной 0 и найдите x .

{0=3x−66=3×2=xx=2\begin{cases}0=3x — 6\qquad \\ 6=3x\qquad \\ 2=x\qquad \\ x=2\qquad \end{cases }⎩

⎨

⎧​0=3x−66=3×2=xx=2​

График функции пересекает ось x в точке (2, 0).

Вопросы и ответы

Все ли линейные функции имеют x -перехваты?

Нет. Однако линейные функции вида y  = c , где c — ненулевое действительное число, являются единственными примерами линейных функций без пересечения x . Например, y = 5 — это горизонтальная линия, расположенная на 5 единиц выше оси x . Эта функция не имеет x -перехватов .

Рисунок 11

A Общее примечание:

x — точка пересечения

x -пересечение функции равно x , когда f ( x ) = 0. Его можно решить по уравнению 0 = m x + б .

Пример 5: Нахождение точки пересечения

x

Нахождение точки пересечения x

f(x)=12x−3f\left(x\right)=\frac{1}{2}x — 3f (x)=21​x−3

.

Решение

Установите функцию равной нулю, чтобы решить для x .

{0=12x−33=12×6=xx=6\begin{case}0=\frac{1}{2}x — 3\\ 3=\frac{1}{2}x\\ 6=x \\ x=6\end{cases}⎩

⎨

⎧​0=21​x−33=21​x6=xx=6​

График пересекает -ось x в точке (6 , 0).

Рис. 12.  График линейной функции

f(x)=12x−3f\left(x\right)=\frac{1}{2}x — 3f(x)=21​x−3

.

Попробуйте 4

Найдите точку пересечения x

f(x)=14x−4f\left(x\right)=\frac{1}{4}x — 4f(x)=41​ х−4

. Решение

Описание горизонтальных и вертикальных линий

Есть два особых случая линий на графике — горизонтальные и вертикальные линии. Горизонтальная линия указывает на постоянный выход или y -значение. На рисунке 13 мы видим, что выход имеет значение 2 для каждого входного значения. Таким образом, изменение объема производства между любыми двумя точками равно 0. В формуле наклона числитель равен 0, поэтому наклон равен 0. Если мы используем m  = 0 в уравнении

f(x)=mx+bf \влево(х\вправо)=mx+bf(x)=mx+b

, уравнение упрощается до

f(x)=bf\left(x\right)=bf(x)=b

. Другими словами, значение функции является константой. Этот график представляет функцию

f(x)=2f\left(x\right)=2f(x)=2

.

Рис. 13.  Горизонтальная линия, представляющая функцию

f(x)=2f\left(x\right)=2f(x)=2

. Рисунок 14 Мы видим, что входное значение для каждой точки на линии равно 2, но выходное значение меняется. Поскольку это входное значение сопоставляется более чем с одним выходным значением, вертикальная линия не представляет функцию. Обратите внимание, что между любыми двумя точками изменение входных значений равно нулю. В формуле наклона знаменатель будет равен нулю, поэтому наклон вертикальной линии не определен.

Обратите внимание, что вертикальная линия, такая как на рис. 15 , , имеет точку пересечения x , но не имеет точки пересечения y-, если это не линия x = 0. Этот график представляет линию x = 2.

Рис. 15. Вертикальная линия x = 2, которая не представляет функцию.

A Общее примечание: горизонтальные и вертикальные линии

Линии могут быть горизонтальными или вертикальными.

A горизонтальная линия — это линия, заданная уравнением вида

f(x)=bf\left(x\right)=bf(x)=b

.

Вертикальная линия — это линия, заданная уравнением в форме

x=ax=ax=a

.

Пример 6: Написание уравнения горизонтальной линии

Напишите уравнение линии, изображенной на рисунке 16.

Рис. 16

Решение

Для любого значения x значение y равно –4, поэтому уравнение равно г  = –4.

Пример 7: Написание уравнения вертикальной линии

Напишите уравнение линии, изображенной на рисунке 17.

Рисунок 17

Решение

Константа x -значение равно 7, поэтому уравнение x = 7.