Рациональные числа и действия с ними — что это, определение и ответ
Рациональные числа – это числа, представленные в виде отношения \(\frac{m}{n}\), где m – целое число, а n – натуральное.
Они могут быть как положительными, так и отрицательными.
Целые и дробные числа вместе образуют множество рациональных.
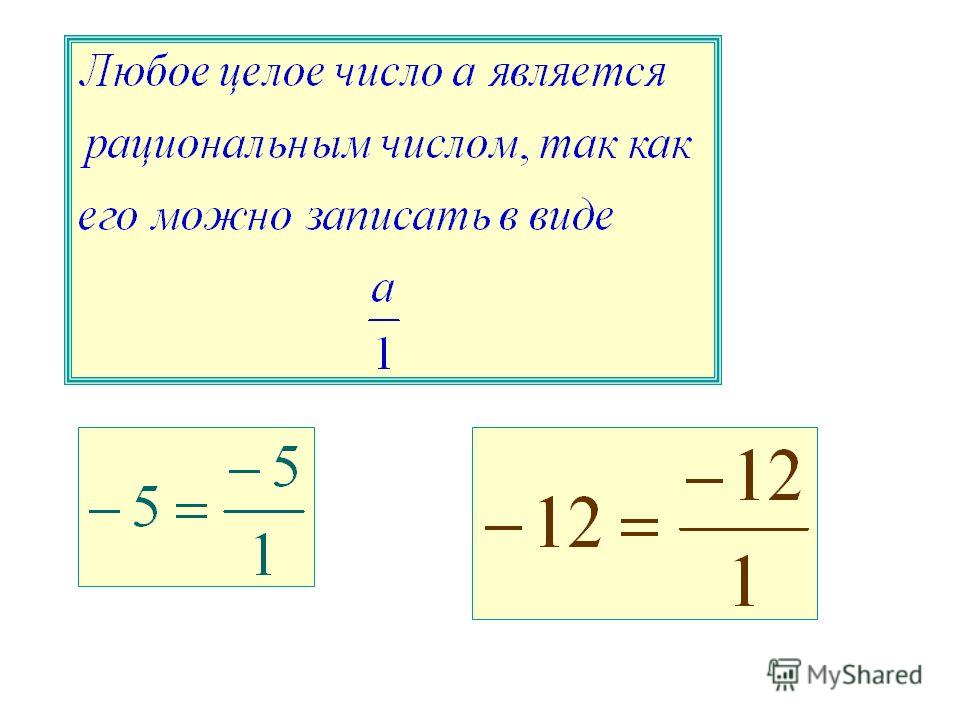
Любое целое число является рациональным, потому что его можно записать в виде \(\frac{m}{1}\).
Например:
\(–4 = \frac{- 4}{1}\)
\(2 = \frac{2}{1}\)
\(0 = \frac{0}{1}\)
Сумма, разность и произведение двух рациональных чисел – тоже рациональное число. Частное двух рациональных чисел тоже будет рациональным, если знаменатель не равен 0.
Любое рациональное число можно записать в виде десятичной или периодической дроби.
Периодическая дробь – это десятичная дробь, в записи которой бесконечное количество раз повторяется цифра или несколько цифр.
Например:
\(\frac{1}{3} = 0,33333333..\)
Повторяющиеся цифры периодической дроби записывают в скобках, например:
\(\frac{1}{3} = 0,(3)\)
\(\frac{5}{11} = 0,45454545 = 0,(45)\)
СВОЙСТВА РАЦИОНАЛЬНЫХ ЧИСЕЛ:
Сложение:
Переместительное свойство:
\(a + b = b + a\)
Сочетательное свойство:
\(a + (b + c) = (a + b) + c = (a + c) + b = a + b + c\)
Прибавление нуля не меняет рациональное число, а сумма противоположных чисел равна нулю:
\(a + 0 = a\)
\(a + ( — a) = 0\)
Умножение:
Переместительное свойство:
\(ab = ba\)
Сочетательное свойство:
\(a(bc) = (ab)c = (ac)b = abc\)
Умножение на единицу не меняет рациональное число, а произведение обратных чисел равно единице:
\(a \bullet 1 = a\)
\(a \bullet \frac{1}{a} = 1\)
Если один из множителей равен нулю, то и всё произведение равно 0:
\(a \bullet 0 = 0\)
\(0 \bullet b = 0\)
\(0 \bullet 0 = 0\)
Распределительное свойство:
\((a + b)c = ac + сb\)
ДЕЙСТВИЯ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
Так как рациональные числа включают в себя блок целых чисел и блок дробных чисел, действия, пройденные в рамках работы с целыми числами, сохраняются и для рациональных чисел. Сравнение, умножение, деление, сложение и вычитание происходит так же, как с целыми числами.
Сравнение, умножение, деление, сложение и вычитание происходит так же, как с целыми числами.
СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:
Рациональные числа можно представить на координатной прямой, где справа от нуля находятся положительные числа, а слева от нуля – обратные им, отрицательные:
Числа на такой числовой прямой возрастают слева на право, поэтому глядя на прямую можно сказать, какое числе больше.
Например:
Сравним числа 1,5 и 4:
Мы знаем, что 4 больше, чем 1,5 и еще раз убедились в этом с помощью числовой прямой.
\(4 > 1,5\)
Сравним числа 3,5 и -1:
Если положительные числа справа от нуля, а отрицательные слева, тогда любое положительное числа будет правее отрицательного, а значит будет больше.
\(3,5 > — 1\)
Сравним числа -2,5 и -3:
Конечно, 3 больше 2,5, но, когда мы смотрим на отрицательные числа, получается, что -2,5 правее -3, а значит больше.
\(- 2,5 > — 3\)
СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:
Сложение рациональных чисел так же можно представить на числовой прямой. Знак «+» означает, что мы двигаемся в положительном направлении (вправо), знак «–» означает, что мы двигаемся в отрицательном направлении (влево).
Например:
Найдем сумму положительных чисел 1 + 2,5. Значит от координаты 1 пройдем 2 полных отрезка и ещё половину отрезка в положительном направлении:
Видим, что \(1 + 2,5 = 3,5\).
Сумма положительных чисел – положительное число.
Найдем сумму отрицательных чисел -1 + (-2). От координаты -1 пройдем 2 отрезка в отрицательном направлении. При сложении можно опустить знак «+» без изменения знаков слагаемых.
Получилось, что \(- 1 + ( — 2) = — 3.\)
Сумма отрицательных чисел – отрицательное число.
Найдем разность положительных чисел 4 – 1,5.
 Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:
Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:
Получилось, что \(4\ –1,5 = 2,5.\)
Сумма положительного и отрицательного числа – положительное число, если из большего вычитают меньшее.
Найдем сумму 2 + (-4). От координаты 2пройдем 4 отрезка в отрицательном направлении:
Получим, что \(2–4 = — 2.\)
Сумма положительного и отрицательного числа – отрицательное число, если из меньшего вычитают большее.
Найдем разность 1 – (-3). Если нужно пройти в отрицательном направлении дважды, то направление движения станет положительным, то есть 1 – (-3) = 1 + 3:
Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.
Найдем сумму двух противоположных чисел 3 + (-3).
 От координаты 3 пройдем 3 отрезка в отрицательном направлении:
От координаты 3 пройдем 3 отрезка в отрицательном направлении:
Видим, что \(3 + ( — 3) = 0.\)
Сумма двух противоположных чисел \(\mathbf{= 0.}\)
УМНОЖНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:
Рациональные числа умножаются и делятся не смотря на знак.
Если перемножались или делились числа с одинаковыми знаками, то в результате получается положительное число. Если перемножались числа с разными знаками, то в результате получается отрицательное число.
Например:
\(3 \bullet 4 = 12\)
\(- 6 \bullet ( — \frac{1}{2}) = 3\)
\(7:( — 2) = — 3,5\)
\(- 12:\frac{1}{3} = — 12 \bullet 3 = — 36\)
Математика — 7
Слово «рациональный» возникло из понятия «отношение». Вам известно,
что отношение двух чисел, например, 3:4, можно записать дробью, а именно
3
4
.
Точно также отношение m:n можно записать как
m
n
Число, которое можно записать в виде дроби
m
n
называется рациональным числом.
Здесь m целое число, n — натуральное число, m ∈ Z, n ∈ N
Например,
7 рациональное число, здесь 5 и 7 — натуральные числа. — 5
7 — тоже рациональное число, здесь -5 — целое число,
7 — натуральное число.
Каждое натуральное число является рациональным числом:
7 = 7:1= 7
1 ;7 = 35:5= 35
5 ;125 = 250:2= 250
2 .
Каждое целое число является рациональным числом:
-12=-12:1=-(12:1)= — 12
1 ;0 = 0: 1 = 0
1 ;0 = 0 : 3 = 0
3 .Положительные целые и дробные числа являются положительными рациональными числами, отрицательные целые и дробные числа являются отрицательными рациональными числами.

Знак «минус», стоящий перед дробью, можно записать или перед числом, находящимся в числителе, или же перед числом, находящимся в знаменателе:
-(2:11)= — 2
11 ; -2:11= -2
11 ; 2:(-11)= 2
-11 .
ПРИМЕР: Заданные рациональные числа представьте в виде дроби с натуральным знаменателем: 0,5; 1,3; — 0,25.
РЕШЕНИЕ:
0,5 =
5
10
=
1
2
;
1,3 = 1
3
10
=
13
10
;
-0,25 =
25
100
= —
1
4
.
Множество рациональных чисел обозначается буквой Q:
Q = {
m
n
| m ∈ Z, n ∈ N }.
Множество натуральных чисел является подмножеством множества целых чисел, а множество целых чисел является подмножеством множества рациональных чисел: N ⊂ Z ⊂ Q.
Множество рациональных чисел, так же, как множество натуральных и целых чисел, является бесконечным множеством.
элементарная теория чисел — Что такое ноль? Иррациональное или рациональное или оно имеет оба свойства?
$\newcommand{\Reals}{\mathbf{R}}$У вас есть превосходные объяснения логических причин высказывания «$0$ рационально». Вот несколько дополнительных мыслей, слишком длинных для комментария:
Вот несколько дополнительных мыслей, слишком длинных для комментария:
Определения в математике существуют для , дают удобные ярлыки полезным логическим различиям
Когда два критерия (такие как «рациональный» и «иррациональный») являются логическими противоположностями по определению , никогда не будет хорошей идеей допускать, чтобы какое-то широко распространенное математическое понятие (такое как $0$) было «обоим»: , каждая теорема, применимая к этому объекту, должна содержать пункт, явно исключающий этот объект. Это неудобно. В редких случаях (см. ниже) вы можете сказать «ни то, ни другое». Но в случае $0$ лучше использовать термин «рациональный»:
Буквальное применение определения («существуют целые числа $q \neq 0$ и $p$ такие, что $0 = p/q$») говорит, что $0$ рационально.
Множество рациональных чисел обладает приятными алгебраическими свойствами (замкнуто при сложении, замкнуто при умножении) потому что $0$ рационально
. (Напротив, множество иррациональных действительных чисел не замыкается при сложении, например, $(1 — \sqrt{2}) + \sqrt{2} = 1$, или при умножении, например, $\sqrt{ 2} \cdot \sqrt{2} = 2$, независимо от того, является ли $0$ рациональным .)
(Напротив, множество иррациональных действительных чисел не замыкается при сложении, например, $(1 — \sqrt{2}) + \sqrt{2} = 1$, или при умножении, например, $\sqrt{ 2} \cdot \sqrt{2} = 2$, независимо от того, является ли $0$ рациональным .)
Чтобы доказать, что «$0$ не является рациональным», т. е. что определение «рационального числа» должно исключать $0$ , нужна веская причина, например, «формулировка полезной теоремы становится неудобной, если $0$ (считается) рациональным».
При всем уважении, возможность записи $0$ как $0/\sqrt{2}$ не является убедительной в указанном выше смысле; как объясняли другие, это представление не противоречит определению . Кроме того, полезно и не вызывает затруднений согласиться с тем, что $0$ является рациональным.
Для сравнения, вот некоторые другие «пограничные случаи», которые возникают время от времени:
Целое число $0$ является «четным» ($2$, умноженное на некоторое целое число), а не «нечетным» (оставляет остаток от $1$ при делении на $2$).
 (По алгоритму деления каждое целое число является четным или нечетным, но никакое целое число не может быть одновременно и тем, и другим. В этом случае «четное» и «нечетное» логически эквивалентны целым числам. Я упоминаю этот пример, потому что мой коллега однажды сообщил мне, что некоторые учителя считать $0$ ни четным, ни нечетным.(!!))
(По алгоритму деления каждое целое число является четным или нечетным, но никакое целое число не может быть одновременно и тем, и другим. В этом случае «четное» и «нечетное» логически эквивалентны целым числам. Я упоминаю этот пример, потому что мой коллега однажды сообщил мне, что некоторые учителя считать $0$ ни четным, ни нечетным.(!!))Нулевая функция $z: \Reals \to \Reals$ является как «четной» (для всех действительных $x$, $z(-x) = z(x)$), так и «нечетной» (для всех действительный $x$, $z(-x) = -z(x)$). Понятия «четное» и «нечетное» для функций не являются логическими противоположностями
. Более того, полезно объявить нулевую функцию одновременно четной и нечетной: множество четных функций представляет собой векторное пространство при «обычных операциях»; набор нечетных функций тоже. Если бы $z$ не было «и четным, и нечетным (как функция)», по крайней мере одна из этих полезных теорем была бы ложной.Целое число $1$ равно и не является «простым» или «составным».
 (Даже несмотря на то, что «$1$ не имеет положительных целых делителей, кроме $1$ и самого себя», мы явно исключаем $1$ из числа простых, потому что объявление $1$ «простым» нарушило бы уникальность факторизации простых чисел. С другой стороны , $1$ не является «составным», потому что $1$ не является произведением меньших положительных простых чисел.)
(Даже несмотря на то, что «$1$ не имеет положительных целых делителей, кроме $1$ и самого себя», мы явно исключаем $1$ из числа простых, потому что объявление $1$ «простым» нарушило бы уникальность факторизации простых чисел. С другой стороны , $1$ не является «составным», потому что $1$ не является произведением меньших положительных простых чисел.)
Есть более глубокий момент, который, по иронии судьбы, может показаться несовместимым с моей прежней позицией:
приводят к одним и тем же теоремам, приходится (даже полностью принимая предыдущий абзац) восхищаться феноменальной связностью логической структуры математики. Начинаешь чувствовать, что определения неизбежны. Человек становится готовым решительно бороться за правильные определения. Последнее, как я полагаю, объясняет отрицательные отзывы на ваш хороший вопрос.
Начинаешь чувствовать, что определения неизбежны. Человек становится готовым решительно бороться за правильные определения. Последнее, как я полагаю, объясняет отрицательные отзывы на ваш хороший вопрос.
Является ли нуль рациональным числом. Можете ли вы записать его в виде pq, где p и q — целые числа, а q 0…
Перейти к
- Система счисления. Упражнение 1.1.
- Система счисления. Упражнение 1.2.
- Система счисления
- Показатели действительных чисел
- Рационализация
- Алгебраические тождества
- Факторизация алгебраических выражений
- Факторизация многочленов
- Введение в геометрию Евклида
- Линии и углы
- Треугольник и его углы
- Конгруэнтные треугольники
- Координатная геометрия
- Формула цапель
- Линейные уравнения с двумя переменными
- Четырехугольники
- Площади параллелограммов и треугольников
- Круги
- Конструкции
- Площадь поверхности и объем параллелепипеда и куба
- Площадь поверхности и объем прямого кругового цилиндра
- Площадь поверхности и объем прямого круглого конуса
- Площадь поверхности и объем сферы
- Табличное представление статистических данных
- Графическое представление статистических данных
- Меры центральной тенденции
- Вероятность
Главная >
РД Шарма Решения
Класс 9Математика
>
Глава 1 — Система счисления
>
Система счисления. Упражнение 1.1.
>
Вопрос 1
Упражнение 1.1.
>
Вопрос 1
Вопрос 1 Система счисления Упражнение 1.1
Является ли ноль рациональным числом? Можете ли вы записать его в виде p/q, где p и q — целые числа, а q ≠ 0?
Ответ:
Да, ноль — рациональное число. Его можно записать в виде p/q при условии, что q≠0. Например: 0/1 или 0/3 или 0/4 и т. д.
Связанные вопросы
Найдите пять рациональных чисел между 1 и 2.
Найдите шесть рациональных чисел между 3 и 4.
Найдите пять рациональных чисел между 3/5 и 4/5.
Верны или ложны следующие утверждения? Обоснуйте свой ответ. (i) Каждое целое число есть…
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Система счисления Упражнение 1.

 Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину:
Можно представить разность чисел как сумму положительного и отрицательного числа: 4 + (-1,5). В любом случае нужно от координаты 4 пройти в отрицательном направлении 1 полный отрезок и ещё половину: От координаты 3 пройдем 3 отрезка в отрицательном направлении:
От координаты 3 пройдем 3 отрезка в отрицательном направлении:

 (Напротив, множество иррациональных действительных чисел не замыкается при сложении, например, $(1 — \sqrt{2}) + \sqrt{2} = 1$, или при умножении, например, $\sqrt{ 2} \cdot \sqrt{2} = 2$, независимо от того, является ли $0$ рациональным .)
(Напротив, множество иррациональных действительных чисел не замыкается при сложении, например, $(1 — \sqrt{2}) + \sqrt{2} = 1$, или при умножении, например, $\sqrt{ 2} \cdot \sqrt{2} = 2$, независимо от того, является ли $0$ рациональным .) (По алгоритму деления каждое целое число является четным или нечетным, но никакое целое число не может быть одновременно и тем, и другим. В этом случае «четное» и «нечетное» логически эквивалентны целым числам. Я упоминаю этот пример, потому что мой коллега однажды сообщил мне, что некоторые учителя считать $0$ ни четным, ни нечетным.(!!))
(По алгоритму деления каждое целое число является четным или нечетным, но никакое целое число не может быть одновременно и тем, и другим. В этом случае «четное» и «нечетное» логически эквивалентны целым числам. Я упоминаю этот пример, потому что мой коллега однажды сообщил мне, что некоторые учителя считать $0$ ни четным, ни нечетным.(!!)) (Даже несмотря на то, что «$1$ не имеет положительных целых делителей, кроме $1$ и самого себя», мы явно исключаем $1$ из числа простых, потому что объявление $1$ «простым» нарушило бы уникальность факторизации простых чисел. С другой стороны , $1$ не является «составным», потому что $1$ не является произведением меньших положительных простых чисел.)
(Даже несмотря на то, что «$1$ не имеет положительных целых делителей, кроме $1$ и самого себя», мы явно исключаем $1$ из числа простых, потому что объявление $1$ «простым» нарушило бы уникальность факторизации простых чисел. С другой стороны , $1$ не является «составным», потому что $1$ не является произведением меньших положительных простых чисел.)