Задача про квадрат с решением: Планиметрия в тезисах и решениях. 9 класс

Планиметрия в тезисах и решениях. 9 класс

Если а – сторона квадрата, d – его диагональ, то S = a2= d2/2.

Примеры решения задач

67. Радиус окружности, в которую вписали квадрат, равен 6. Найдите площадь квадрата (рис. 159). (1)

Рис. 159.

Решение. Очевидно, что центр описанной около квадрата окружности есть точка пересечения его диагоналей. Это означает, что ОВ – радиус окружности и ОВ = 6. Тогда АВ = 12 и по теореме Пифагора AC2+ ВС2= AB2. Обозначив длину стороны квадрата через а, получим: а2+ а2= 122; 2 ? а2= 144; а2 = 72. Sквадрата = a2= 72.

Ответ: 72.

68. Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого (2? – 4) см2. Найдите периметр квадрата (рис. 160). (2)

Рис. 160.

Решение. Площадь заштрихованного сегмента, как видно из рисунка, можно вычислить по формуле:

где а – длина стороны квадрата, R – радиус описанной окружности. Выразим R через а.

Таким образом,

С учётом условия получаем уравнение:

Рквадрата = 4a = 4 ? 4 = 16 см.

Ответ: 16 см.

69. В плоскости дан квадрат с последовательно расположенными вершинами А, В, С, D и точка О. Известно, что OB = OD = 13, ОС = 5?2 и что площадь квадрата больше 225. Найти длину стороны квадрата и выяснить, где расположена точка О – вне или внутри квадрата (рис. 161). (3)

Рис. 161.

Решение. Так как OB = OD, то точка О лежит на перпендикуляре к середине отрезка BD, т. е. на прямой АС. Обозначим через К точку пересечения диагоналей квадрата. Из условия следует, что ОВ > ОС; значит, точка О лежит по одну сторону с точкой С относительно перпендикуляра к середине отрезка ВС. Отсюда следует, что точка О лежит на луче КС.

Обозначим КО через х и АВ = CD через y. Так как

и

Применяя к прямоугольному треугольнику KOD теорему Пифагора, получаем: OD2= КО2+ KD2или 169 = х2+ 1/2 у2.

Предположим, что КО ? КС или

тогда х2 ? 1/2 у2(заметим, что числа x и y неотрицательны) и

т. е. площадь квадрата не превосходит 169, что противоречит условию. Следовательно,

т. е. КО < КС, и точка О лежит внутри квадрата. Теперь получаем

Из первого уравнения

Подставляя

вместо х во второе уравнение, после арифметических преобразований получаем уравнение у2– 10у – 119 = 0. Это квадратное уравнение имеет корни у1 = -7 и у2 = 17. Так как у есть длина отрезка, то у > 0 и, значит, y = 17.

Ответ: длина стороны квадрата равна 17; точка О лежит внутри квадрата.

Задачи для самостоятельного решения

70. Сторона квадрата равна 7 см. Определите диаметр окружности, описанной около квадрата. (1)

71. В квадрат вписан круг, а в полученный круг вписан квадрат. Найдите отношение площадей квадратов. (1)

72. Квадрат со стороной 3 см срезан по углам так, что образовался правильный восьмиугольник. Найдите сторону восьмиугольника. (2)

73. Дан квадрат ABCD. На его сторонах вовне построены равносторонние треугольники ABM, BCN, CDK, DAL. Найдите площадь четырёхугольника MNKL, если АВ = 1. (2)

Решение задач по теме «Прямоугольник. Квадрат. Ромб»

Цель урока: закрепить в процессе решения задач полученные знания и навыки.

Задачи урока:

• закрепить теоретический материал по теме “Прямоугольник. Ромб. Квадрат”;
• совершенствовать навыки решения задач;
• развитие элементов геометрического мышления и воспитание интереса к оперированию геометрическими понятиями;
• умение выполнять и оценивать выполненную работу;
• расширение кругозора, развитие чувства взаимопомощи, совершенствование навыков работы с компьютером.

Оборудование: доска, компьютеры, карточки с заданиями, тесты, справочный материал, таблицы.

Ход урока

1. Организационный момент.

– Сообщить тему урока, сформулировать цели урока.

• Какую тему мы изучаем?
• В процессе изучения темы вы должны знать:

Уметь:

Учащиеся должны:

Знать: определение прямоугольника и его свойства, определение и свойства ромба, определение квадрата и все его свойства.
Уметь: доказывать особое свойство прямоугольника и ромба, применять свойства прямоугольника, ромба и квадрата при решении задач, решать задачи, в которых рассматриваются параллелограмм, прямоугольник, ромб, квадрат.

На сегодняшний день мы

знаем: определение прямоугольника и его свойства, определение и свойства ромба, определение квадрата и все его свойства;
умеем: доказывать особое свойство прямоугольника и ромба.

Что не умеем? применять свойства прямоугольника, ромба и квадрата при решении задач, решать задачи, в которых рассматриваются параллелограмм, прямоугольник, ромб, квадрат.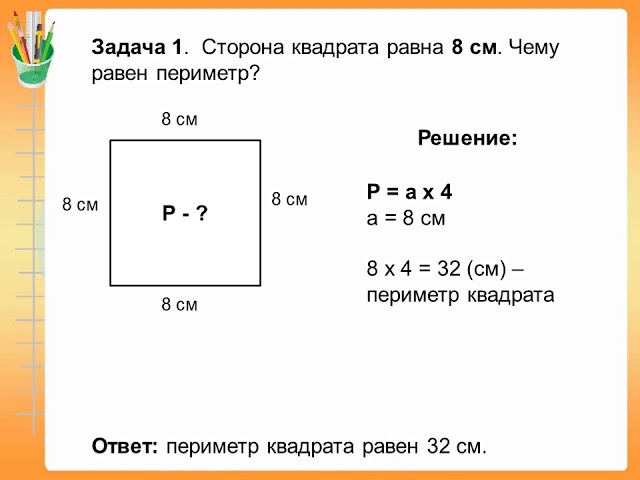

Поэтому целью нашего урока будет закрепить в процессе решения задач полученные знания и навыки.

2. Актуализация знаний учащихся.

Повторим знания, полученные на прошлом уроке. Предлагаю вам, работая в парах, дать определения параллелограмма, прямоугольника, ромба, квадрата и, вспомнив их свойства заполнить таблицу.

Теоретический опрос (работа в парах).

1. Дать определения понятиям: параллелограмм, прямоугольник, ромб, квадрат.
2. Вспомнить свойства и заполнить таблицу, отметив знаки + (да) и — (нет).

По первому вопросу оценить друг друга. Оценки выставляем в лист учета.

Свойство	Параллелограмм	Прямоугольник	Ромб	Квадрат
Противолежащие стороны параллельны и равны.
Все стороны равны.
Противолежащие углы равны, сумма соседних углов равна 180.
Все углы прямые.
Диагонали пересекаются и точкой пересечения делятся пополам.
Диагонали равны.
Диагонали взаимно перпендикулярны и являются биссектрисами его углов.

Произведите взаимопроверку и оцените друг друга.

Используя определения и свойства фигур, выполните математический диктант.

Математический диктант (графический).

Вариант 1.

1. Является ли прямоугольником параллелограмм, у которого есть прямой угол?
2. Верно ли, что каждый параллелограмм является прямоугольником?
3. Диагонали параллелограмма равны 3 см и 5 см. Является и этот параллелограмм прямоугольником?
4. Верно ли, что каждый ромб является параллелограммом?
5. Ромб АВСD имеет прямой угол. Является ли этот ромб квадратом?

Вариант 2.

1. Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол?
2. Верно ли, что каждый прямоугольник является параллелограммом?
3. Диагонали четырехугольника равны. Обязательно ли этот четырехугольник – прямоугольник?
4. Верно ли, что каждый параллелограмм является ромбом?
5. Две соседние стороны параллелограмма равны и образуют прямой угол. Называется ли такой параллелограмм — квадратом?

Проверьте правильность своих ответов и оцените свой диктант.

Итак, мы повторили определения и свойства параллелограмма, прямоугольника, квадрата, ромба. Но основной нашей целью является закрепить в процессе решения задач, полученные знания и навыки, научиться применять свойства прямоугольника, ромба и квадрата при решении задач.

Поэтому перейдем к решению задач с использованием теоретического материала.

3. Формирование умений и навыков. Решение задач.

Решение задач (устно и по готовым чертежам).(таблица 5).

1. Найдите стороны параллелограмма АВСD, зная, что его периметр равен 24 см.

Всегда ли при решении задач используем свойства?

(Определение).

Значит, для решения задач надо знать и свойства, и определения.

Выполнение задания – карточки с печатной основой (для коррекции знаний учащихся).

№ 11, 12, 14.

Решение задачи с комментированием.

1. В прямоугольнике АВСD диагонали АС и ВD пересекаются в точке О, причем, угол АОВ равен 40. Найдите угол DАО.

Обратите внимание на правильное оформление решения задачи. А теперь решим задачу с записью в тетради.

Решение задачи с комментированием в тетради. Учебник № 403.

4. Контроль за знаниями, умениями и навыками решения задач.

Мы повторили теоретический материал, разобрали решение задач с применением свойств фигур. А теперь предлагаю вам, решить самостоятельно задачи теста и задачи, предложенные компьютером.

1 вариант – у компьютера,

2 вариант – выполняет тест; затем поменялись местами.

Задания на карточках (тест, 2 варианта).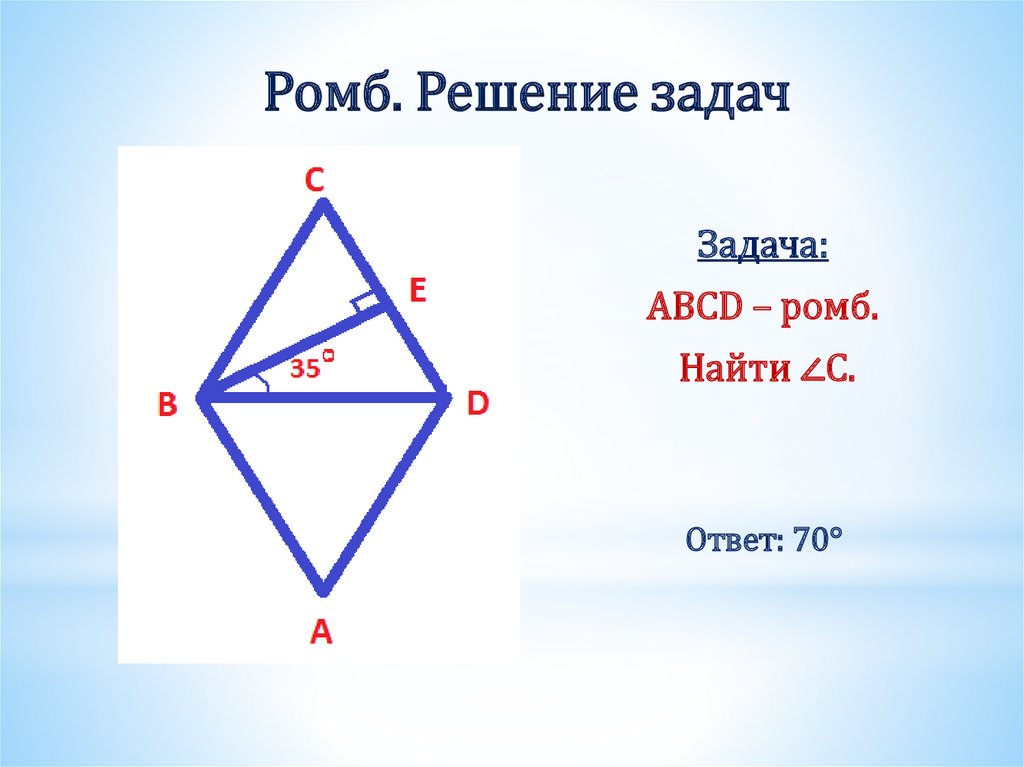

Вариант 1.

А1. Диагональ ромба образует с его стороной угол 26. Найдите наибольший угол ромба.

1) 128; 2) 154; 3) 104; 4) 52.

А2. Периметр параллелограмма равен 42 см, а одна из его сторон на 5 см больше другой. Найдите меньшую сторону параллелограмма.

1) 5 см; 2) 9 см; 3) 13 см; 4) 8 см.

А3. В прямоугольнике АВСD :  ВD = 10 см, периметр треугольника ВОС равен 16 см. Найдите длину стороны ВС.

1) 5 см; 2) 6 см; 3) 7 см; 4) 8 см.

Вариант 2.

А1. Диагональ ромба образует с его стороной угол 32. Найдите наибольший угол ромба.

1) 148; 2) 64; 3) 126; 4) 116.

А2. Периметр параллелограмма равен 56 см, а одна из его сторон в 3 раза больше другой. Найдите большую сторону параллелограмма.

1) 14 см; 2) 12 см; 3) 21 см; 4) 16 см.

А3. В прямоугольнике АВСD : АВ = 5 см, АС = 12 см. Найдите периметр треугольника АОВ.

1) 15 см; 2) 25 см; 3) 17 см; 4) 7 см.

Оцените правильность ответов теста.

Проверка верных ответов.

Вариант 1: А1. – 1), А2 – 4), А3 – 2).

Вариант 2: А1 – 4), А2 – 3), А3 – 3).

Задания на компьютере.

В программе “ Планиметрия” открыть тему “ Четырехугольники”.

В разделе “ Контрольные вопросы” решить задачу. (3, 4, 7, 8, 11).

В журнале узнать свой средний бал и записать его в лист учета.

5. Итог урока.

Самооценка своей деятельности на уроке.

Урок подходит к концу, давайте подведем итоги. Посмотрим, удалось ли нам реализовать поставленную цель?

Какая была цель?

(Закрепить в процессе решения задач полученные знания и навыки, научиться применять свойства прямоугольника, ромба и квадрата при решении задач.)

Достигли ли мы ее?

Оцените, на сколько успешно каждый из вас справился с поставленной целью. Каждый, работая на уроке, оценивал свои знания теоретического материала.

У кого оценка “5”? “4”? “3”?, а есть оценка “2”?

Если ваши знания не на “5”, то дома вам еще раз необходимо проработать п. 45, 46, и ответить на вопросы 12–15.

Оценим свои умения по решению задач.

У кого оценка “5”? “4”? “3”?, а есть оценка “2”?

Для того, чтобы вы могли лучше решать задачи, дома необходимо решить следующие задачи № 405, 401 (а).

Запишите домашнее задание в дневник.

6. Домашнее задание.

Повторить п. 45, 46, вопросы 12–15, № 405, 401 (а).

Урок окончен. Спасибо за урок.

Литература

1. Рабочая тетрадь по геометрии для 8 класса / Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков, И. И. Юдина — М.: Просвещение, 2003.
2. Геометрия, 7–9: Учебник для общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2003.
3. Современный учебно-методический комплекс “Планиметрия” 7–9. Просвещение – Медиа, 2003.
4. Упражнения по планиметрии на готовых чертежах: Пособие для учителя / С. М. Саврасова, Г. А. Ястребинецкий. – М.: Просвещение, 1987.

Площадь квадратов и прямоугольников: задачи с решениями

By Catalin David

Задача 1

Прямоугольник имеет длину 6 дюймов и ширину 4 дюйма. Район находится в ²

Задача 2

Сторона квадрата равна 5 метрам. Площадь квадрата м ²

Задача 3

Площадь квадрата равна 16 в ² . Его сторона внутри.

Задача 4

Площадь прямоугольника 45 см ² . Если его длина 9 см, то его ширина

см.

Задача 5

Периметр квадрата равен 24 см. Площадь квадрата см ²

Задача 6

Длина прямоугольника 12 см, а ширина на 5 см меньше. Площадь прямоугольника см ² .

Задача 7

Прямоугольник имеет длину 12 см и ширину в 3 раза меньше. Его площадь см ²

Задача 8

Длина прямоугольника 6 см, а ширина 4 см. Если длина больше на 2 см, какой должна быть ширина, чтобы новый прямоугольник имел такую ​​же площадь, как и первый?

Задача 9

Сколько квадратов со стороной 2 см покрывают поверхность прямоугольника длиной 24 см и шириной 8 см?

Задача 10

Квадрат со стороной 6 см и прямоугольник шириной 4 см имеют одинаковую площадь. Какова длина прямоугольника?

Задача 11

Сторона квадрата равна 5 см. Если его сторону увеличить вдвое, то во сколько раз площадь нового квадрата больше площади старого квадрата?
Ответ: раз.

Задача 12

На поле длиной 25 метров и шириной 12 метров построен дом в форме квадрата со стороной 9 метров. Какова площадь сада?

Задача 13

Какова площадь синей зоны?

Задача 14

Какова площадь красной зоны?

Задача 15

В парке, имеющем форму квадрата со стороной 30 метров, есть аллея шириной 2 метра. Какова площадь зеленой зоны?

Задача 16

Телевизор имеет длину 80 см и ширину 50 см. При толщине границы 5 см площадь экрана

Задача 17

Прямоугольник длиной 14 см и шириной 10 см покрыт черными и синими квадратами одинаковой площади. Чему равна общая площадь синих квадратов?

Задача 18

Прямоугольник ABCD имеет длину 8 см и ширину 6 см. Чему равна общая площадь синих прямоугольников?

Задача 19

Сторона квадрата 2 см, длина прямоугольника 9 см, ширина 6 см. Какова площадь красной зоны?

Задача 20

Коробка, каждая сторона которой представляет собой прямоугольник, имеет длину 10 см, ширину 6 см и высоту 8 см. Какова общая площадь коробки?

Сообщите о проблеме на этой странице.

Правильно:

Неправильно:

Нерешенные задачи:

Решение словесных задач с фигурами Квадраты и прямоугольники

Задача 1 :

Сторона квадрата больше стороны другого квадрата на 4 см, а сумма площадей двух квадратов равна 400 кв. см. Найдите размеры квадраты.

Решение :

Пусть x длина стороны одного квадрата

Сторона квадрата больше стороны другого квадрата на 4 см

Итак, длина стороны другого квадрата = x + 4

Площадь одного квадрата со стороной x = x ²

Площадь одного квадрата со стороной x + 4 равна (x + 4)²

Сумма площадей двух квадратов  =  400 кв. см

x ² + (x + 4) ² = 400

x ² + x ² + 2 ⋅ x ⋅ 4 + 4 ² = 400

2x ² + 8x + 16 — 400 = 0

2x ² + 8x — 384 = 0

Разделив все уравнение на 2, мы получим

x ² + 4x — 192  =  0

(х + 16) (х — 12) = 0

х + 16 = 0 х = -16

х — 12  =  0 х  =  12

Следовательно, сторона одного квадрата равна 12 см.

Длина стороны другого квадрата = (12 + 4) = 16 см.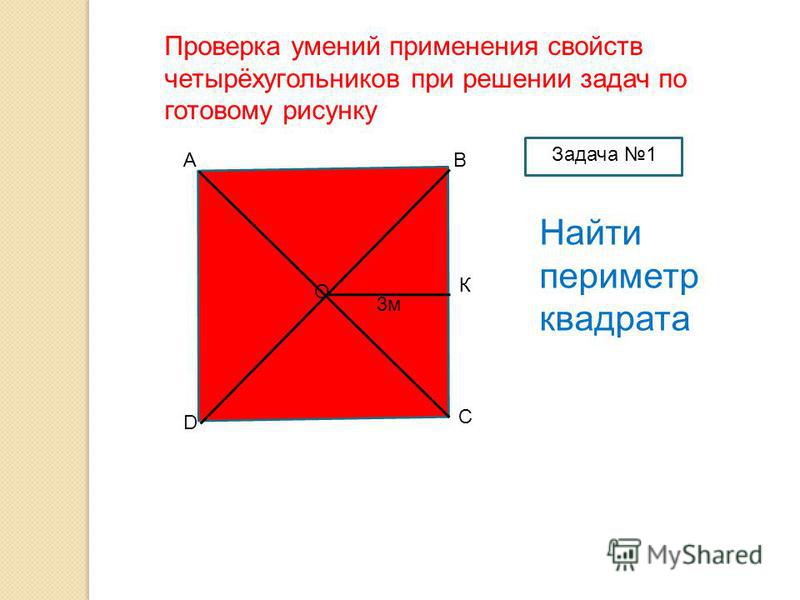

Задача 2 :

Длина прямоугольника больше ширины на 2 см, площадь прямоугольника 195 кв.см. Найдите размеры прямоугольника.

Решение:

Пусть x и y — ширина и длина прямоугольника соответственно

Длина прямоугольника больше его ширины на 2 см прямоугольник = 195 кв.см

длина ⋅ ширина = 195

х⋅(х + 2) = 195

х ² + 2х — 195 = 0

х

( ) — + () = 0

х + 15  =  0 х  =  -15

х — 13  =  0 х  =  13

Здесь x представляет ширину прямоугольника. Таким образом, отрицательное значение невозможно.

Чтобы найти значение y, мы должны применить значение x в уравнении y = x + 2

y = 13 + 2

y = 15 см

Следовательно, длина прямоугольника равна 15 см, а ширина прямоугольник 13 см.

Задача 3 :

Пешеходная дорожка одинаковой ширины проходит вокруг прямоугольного поля длиной 28 метров и шириной 22 метра. Если дорожка занимает площадь 600 м², найдите ширину дорожки.

Решение:

Пусть x будет шириной пути

Длина прямоугольного поля = 28 м

Ширина прямоугольного поля = 22 м

Длина большего прямоугольника :

  =  28 + x + x

  =  28 + 2x

Ширина большего прямоугольника :

  = 22 + x + x

  =

0 = 9000 + 2x Площадь пути Площадь большего прямоугольника — Площадь меньшего прямоугольника

600 = (28 + 2x) (22 + 2x) — 28 ⋅ 22

600 = 616 + 56x + 44x + 4x ² — 616

600 = 56x + 44x + 4x ²

600 = 56x + 44x + 4x ²

6 600 = 56x + 44x + 4x ²

6 600 = 4x ² + 100 x

4x² + 100x = 600

делят все уравнение на 4, мы получаем

x ² + 25x = 150

x² + 25x — 150 = 0

(x — 5. ) (х + 30)  =  0

х — 5  =  0 х  =  5

х + 30  =  0 х  =  -30

Отрицательное значение невозможно.

No related posts.