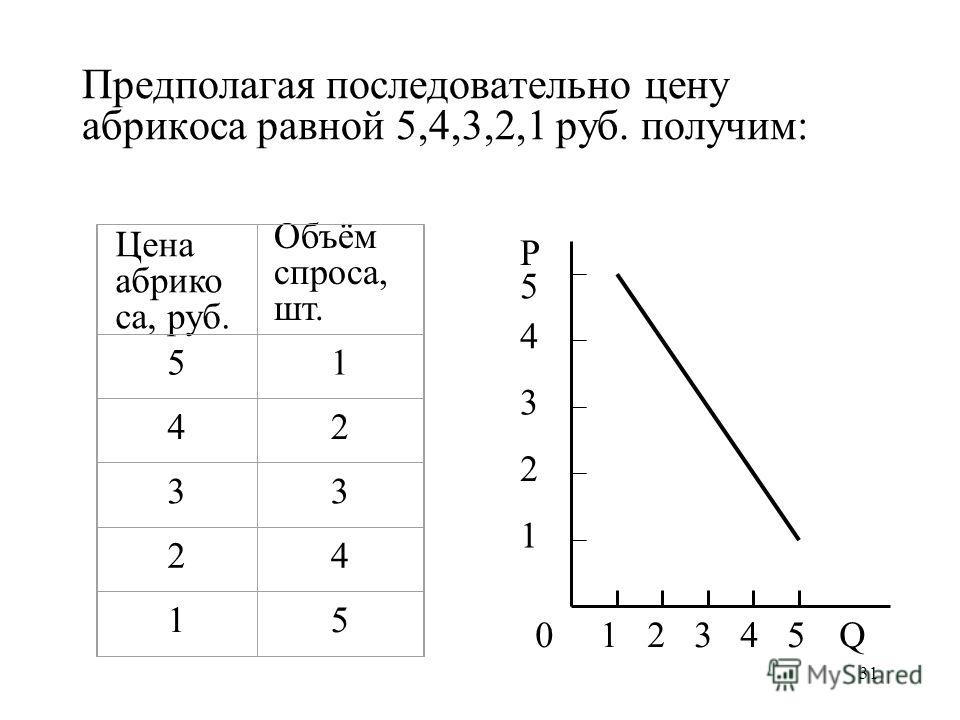
Задачи по микроэкономике. Часть 24 (потребительский выбор)
Задача №8 (расчет общей и предельной полезности)
Предположим, потребитель читает журналы и слушает музыку, записанную на диски. Ниже приведена таблица, которая показывает полезность, которую потребитель получает от потребления различного количества журналов и дисков.
|
Количество |
Полезность журналов (ютил) |
Полезность дисков (ютил) |
|
1 |
60 |
360 |
|
2 |
111 |
630 |
|
3 |
156 |
810 |
|
4 |
196 |
945 |
5 |
232 |
1050 |
|
6 |
265 |
1140 |
|
7 |
295 |
1215 |
|
8 |
322 |
1275 |
|
9 |
347 |
1320 |
|
10 |
371 |
1350 |
Цена журнала – 1,5 ден. ед., а цена диска – 7,5 ден. ед. Обычно потребитель покупает 2 диска и 10 журналов.
ед., а цена диска – 7,5 ден. ед. Обычно потребитель покупает 2 диска и 10 журналов.
Необходимо определить:
1. Сколько денег тратит потребитель на покупку этого количества дисков и журналов?
3. Какова предельная полезность, которую получает потребитель от потребления кассет и дисков? Каково отношение предельной полезности к цене для каждого из товаров?
4. Максимизирует ли потребитель полезность?
5. Какую полезность получает потребитель, если весь свой бюджет он будет тратить на покупку дисков?
6. При какой комбинации двух товаров полезность окажется максимальной?
Решение задачи:
Рассчитываем, сколько денег тратит потребитель на покупку этого количества дисков и журналов:
2*7,5+10*1,5=30 ден. ед.
Два диска приносят 630 ютил, десять журналов – 371 ютил, итого – 1001 ютил.
Для расчета предельной полезности, которую получает потребитель от потребления кассет и дисков, заполняем таблицу, в которой рассчитываем отношение предельной полезности к цене для каждого из товаров:
|
Количество |
Полезность журналов (ютил) |
Предельная полезность журналов |
Отношение предельной полезности к цене журналов |
|
1 |
60 |
— |
— |
|
2 |
111 |
111-60=51 |
51/1,5=34 |
|
3 |
156 |
156-111=45 |
45/1,5=30 |
|
4 |
196 |
196-156=40 |
40/1,5=26,7 |
|
5 |
232 |
232-196=36 |
36/1,5=24 |
|
6 |
265 |
265-232=33 |
33/1,5=22 |
|
7 |
295 |
295-265=30 |
30/1,5=20 |
|
8 |
322 |
322-295=27 |
27/1,5=18 |
|
9 |
347 |
347-322=25 |
25/1,5=16,7 |
|
10 |
371 |
|
24/1,5=16 |
|
Количество |
Полезность дискв (ютил) |
Предельная полезность дисков |
Отношение предельной полезности к цене дисков |
|
1 |
360 |
— |
— |
|
2 |
630 |
630-360=270 |
270/7,5=36 |
|
3 |
810 |
810-630=180 |
180/7,5=24 |
|
4 |
945 |
945-810=135 |
135/7,5=18 |
|
5 |
1050 |
1050-945=105 |
105/7,5=14 |
|
6 |
1140 |
1140-1050=90 |
90/7,5=12 |
|
7 |
1215 |
1215-1140=75 |
75/7,5=10 |
|
8 |
1275 |
1275-1215=60 |
60/7,5=8 |
|
9 |
1320 |
1320-1275=45 |
45/7,5=6 |
|
10 |
1350 |
1350-1320=30 |
30/7,5=4 |
Если потребитель приобретет два диска и десять журналов, он не сможет максимизировать свою полезность, поскольку не будет соблюдаться условие максимизации полезности, при котором предельные полезности приобретаемых товаров в расчете на одну денежную единицу совпадают. А в данном случае: 36?16, т.е. правило не соблюдается.
А в данном случае: 36?16, т.е. правило не соблюдается.
Если весь свой бюджет потребитель будет тратить на покупку дисков, то купит 4 диска, которые дадут 945 ютил полезности.
Полезность окажется максимальной при покупке следующей комбинации товаров: 3 диска и 5 журналов. При этом соблюдается правило максимизации полезности, речь о котором шла выше: 24=24.
Аналогичная задача приведена на с. 79-80 источника:
Микро-, макроэкономика. Практикум. / Под общ. ред. Ю.А. Огибина. – СПб.: «Литера плюс», «Санкт-Петербург оркестр», 1994. – 432 с.
Задача №36 (расчет общей и предельной полезности)
Предположим, потребитель читает журналы и слушает музыку, записанную на диски. Ниже приведена таблица, которая показывает полезность, которую потребитель получает от потребления различного количества журналов и дисков.
Количество | Полезность журналов (ютил) | Полезность дисков (ютил) |
1 | 60 | 360 |
2 | 111 | 630 |
3 | 156 | 810 |
4 | 196 | 945 |
5 | 232 | 1050 |
6 | 265 | 1140 |
7 | 295 | 1215 |
8 | 322 | 1275 |
9 | 347 | 1320 |
10 | 371 | 1350 |
Цена журнала –
1,5 ден. ед., а цена диска – 7,5 ден. ед.
Обычно потребитель покупает 2 диска и
10 журналов.
ед., а цена диска – 7,5 ден. ед.
Обычно потребитель покупает 2 диска и
10 журналов.
Необходимо определить:
Сколько денег тратит потребитель на покупку этого количества дисков и журналов?
Какую полезность получает потребитель от этой комбинации товаров?
Какова предельная полезность, которую получает потребитель от потребления кассет и дисков? Каково отношение предельной полезности к цене для каждого из товаров?
Максимизирует ли потребитель полезность?
Какую полезность получает потребитель, если весь свой бюджет он будет тратить на покупку дисков?
При какой комбинации двух товаров полезность окажется максимальной?
Решение
Рассчитываем, сколько денег тратит потребитель на покупку этого количества дисков и журналов:
2×7,5+10×1,5=30 ден. ед.
ед.
Два диска приносят 630 ютил, десять журналов – 371 ютил, итого – 1001 ютил.
Для расчета предельной полезности, которую получает потребитель от потребления кассет и дисков, заполняем таблицу, в которой рассчитываем отношение предельной полезности к цене для каждого из товаров:
Количество | Полезность журналов (ютил) | Предельная полезность журналов | Отношение предельной полезности к цене журналов |
1 | 60 | — | — |
2 | 111 | 111-60=51 | 51/1,5=34 |
3 | 156 | 156-111=45 | 45/1,5=30 |
4 | 196 | 196-156=40 | 40/1,5=26,7 |
5 | 232 | 232-196=36 | 36/1,5=24 |
6 | 265 | 265-232=33 | 33/1,5=22 |
7 | 295 | 295-265=30 | 30/1,5=20 |
8 | 322 | 322-295=27 | 27/1,5=18 |
9 | 347 | 347-322=25 | 25/1,5=16,7 |
10 | 371 | 371-347=24 | 24/1,5=16 |
Количество | Полезность дискв (ютил) | Предельная полезность дисков | Отношение предельной полезности к цене дисков |
1 | 360 | — | — |
2 | 630 | 630-360=270 | 270/7,5=36 |
3 | 810 | 810-630=180 | 180/7,5=24 |
4 | 945 | 945-810=135 | 135/7,5=18 |
5 | 1050 | 1050-945=105 | 105/7,5=14 |
6 | 1140 | 1140-1050=90 | 90/7,5=12 |
7 | 1215 | 1215-1140=75 | 75/7,5=10 |
8 | 1275 | 1275-1215=60 | 60/7,5=8 |
9 | 1320 | 1320-1275=45 | 45/7,5=6 |
10 | 1350 | 1350-1320=30 | 30/7,5=4 |
Если
потребитель приобретет два диска и
десять журналов, он не сможет максимизировать
свою полезность, поскольку не будет
соблюдаться условие максимизации
полезности, при котором предельные
полезности приобретаемых товаров в
расчете на одну денежную единицу
совпадают.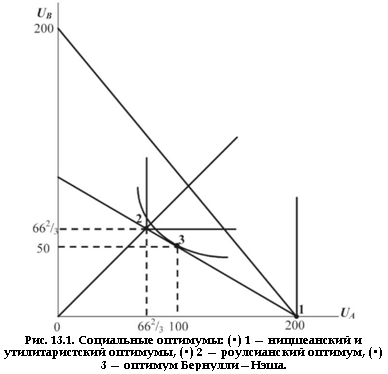 А в данном случае: 36≠16, т.е.
правило не соблюдается.
А в данном случае: 36≠16, т.е.
правило не соблюдается.
Если весь свой бюджет потребитель будет тратить на покупку дисков, то купит 4 диска, которые дадут 945 ютил полезности.
Полезность окажется максимальной при покупке следующей комбинации товаров: 3 диска и 5 журналов. При этом соблюдается правило максимизации полезности, речь о котором шла выше: 24=24.
38
промежуточный уровень. Сборник задач с решениями и ответами
- Файлы
- Академическая и специальная литература
- Финансово-экономические дисциплины org/ListItem» itemprop=»itemListElement»> Экономическая теория
- Микроэкономика
Экономическая теория
Макроэкономика
Микроэкономика
Основы экономической теории
Политэкономия
Экономика отраслевых рынков
Практикум
- формат pdf
- размер 8.
 02 МБ
02 МБ - добавлен 09 октября 2016 г.
М.: ГУ ВШЭ, 2013. — 503, [1] с. — ISBN 978-5-7598-0983-8.
Учебное пособие содержит подборку заданий по основным разделам
микроэкономики (выбор потребителя в условиях определённости и в
условиях неопределённости, поведение производителя, общее
равновесие, провалы рынка, рыночные структуры), помогающих
читателям научиться применять полученные базовые знания по
предмету. Сборник включает задачи различного уровня сложности, для
решения которых требуется знание стандартных микроэкономических
моделей. Приводятся решения некоторых задач, ответы к большинству
заданий или подсказки к решению. Многие задачи, вошедшие в пособие,
подготовлены авторами для семинаров и контрольных мероприятий по
микроэкономике на различных факультетах НИУ ВШЭ, МШЭ МГУ и
РАНХиГС.
Для студентов-бакалавров, обучающихся по направлению «Экономика», а
также специальностям, учебный план которых предусматривает изучение
микроэкономики; для абитуриентов, готовящихся поступать в
магистратуру экономических факультетов; для преподавателей
бакалаврских курсов «Микроэкономика», «Экономическая теория» и
таких дисциплин микроэкономического блока, как теория отраслевых
рынков и теория общественного выбора.
Предисловие.
Теория поведения потребителя в условиях
определённости.
Бюджетное ограничение.
Предпочтения и полезность.
Выбор потребителя и спрос. Сравнительная статика и анализ
благосостояния.
Выявленные предпочтения.
Декомпозиция Слуцкого при фиксированном доходе потребителя.
Денежная оценка благосостояния
Выбор потребителя при наличии натурального дохода: сравнительная
статика и анализ благосостояния. Межпериодный выбор. Модель
предложения труда.
Решения задач.
Ответы и подсказки.
Теория поведения производителя.
Технология, максимизация прибыли.
Максимизация прибыли и минимизация издержек. Кривые издержек.
Предложение фирмы.
Решения задач.
Ответы и подсказки.
Равновесие.
Экономика обмена: ящик Эджворта, Парето-оптимальные
распределения.
Экономика обмена: равновесие по Вальрасу, закон Вальраса,
равновесие и оптимальность.
Экономика с производством: Парето-оптимальные распределения.
Экономика с производством: равновесие по Вальрасу, закон Вальраса,
равновесие и оптимальность.
Частичное равновесие.
Решения задач.
Ответы и подсказки.
Провалы рынка.
Экономика с внешними эффектами (экстерналиями).
Экономика с общественными благами. Парето-оптимальные
распределения.
Равновесие с добровольным финансированием.
Равновесие по Линдалю.
Решения задач.
Ответы и подсказки.
Рыночные структуры: монополия и олигополия.
Максимизация прибыли монополистом, чистые потери от наличия
монополии.
Сравнительная статика: введение налога/субсидии на продукцию
монополиста.
Естественные монополии и их регулирование.
Монополия: ценовая дискриминация.
Олигополия: одновременный выбор выпусков (модель Курно).
Олигополия: последовательный выбор выпусков (модель
Штакельберга).
Олигополия: одновременный выбор цен (модель Бертрана).
Олигополия: модель ценового лидерства.
Олигополистическая конкуренция при одновременном выборе стратегий и
сговор.
Повторяющиеся взаимодействия в условиях олигополистической
конкуренции, стратегии возвращения к равновесию по Нэшу.
Задачи на разные модели олигополии.
Решения задач.
Ответы и подсказки.
Выбор потребителя в условиях неопределённости.
Денежные лотереи, отношение к риску, денежный эквивалент лотереи и
премия за риск, функция ожидаемой полезности.
Пространство контингентных благ.
Модель спроса на страховку.
Модель формирования портфеля инвестиций.
Общее равновесие в экономике с контингентными благами (равновесие
Эрроу – Дебрё).
Решения задач.
Ответы и подсказки.
Литература, рекомендуемая в качестве теоретической базы для
задачника.
Используемая литература.
Купить книгу «Микроэкономика: промежуточный уровень. Сборник задач с решениями и ответами»
Карта сайта
Главная Обучение Библиотека Карта сайта
|
Модуль 2: Коммунальные услуги – микроэкономика среднего уровня
Основная часть
«Заполнить» Derekbruff лицензирован в соответствии с CC BY-NC 2,0 The P Olicy Q UESTION : Hybrid Покупка автомобиля Налоговая кредит -IT .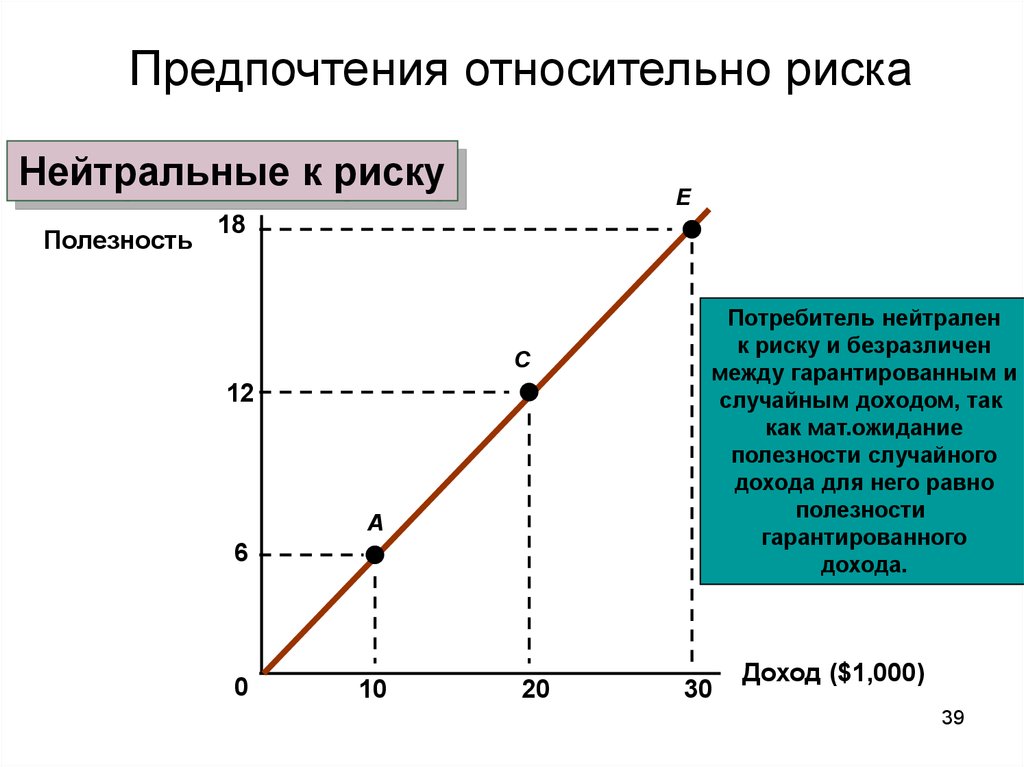 Правительство Лучший выбор для снижения потребления топлива и выбросов углерода ?
Правительство Лучший выбор для снижения потребления топлива и выбросов углерода ?
Жители США и правительство обеспокоены зависимостью от импортируемой иностранной нефти и выбросами углерода в атмосферу. В 2005 году Конгресс принял закон о предоставлении потребителям налоговых льгот на покупку электрических и гибридных автомобилей.
Этот налоговый кредит может показаться хорошим политическим выбором, но он дорогостоящий, поскольку напрямую снижает сумму доходов, собираемых правительством США. Существуют ли более эффективные подходы к снижению зависимости от ископаемого топлива и выбросов углерода? Как решить, какая политика лучше? Чтобы ответить на этот вопрос, политикам необходимо с некоторой точностью предсказать, как потребители отреагируют на эту налоговую политику, прежде чем эти политики потратят миллионы федеральных долларов.
Мы можем применить концепцию утилита на этот вопрос политики. В этом модуле мы будем изучать полезность и функции полезности. Тогда мы сможем использовать соответствующую функцию полезности для получения кривых безразличия, описывающих наш политический вопрос.
В этом модуле мы будем изучать полезность и функции полезности. Тогда мы сможем использовать соответствующую функцию полезности для получения кривых безразличия, описывающих наш политический вопрос.
Изучение вопроса политики
Предположим, что налоговая льгота для субсидирования покупки гибридных автомобилей чрезвычайно успешна и удваивает средний расход топлива всех автомобилей на дорогах США — результат, который явно нереалистичен, но полезен для наших последующих обсуждений. Как вы думаете, что произойдет с расходом топлива всех автомобилистов США? Следует ли правительству ожидать, что потребление топлива и выбросы углекислого газа от автомобилей снизятся вдвое в ответ? Почему или почему нет?
2. 1 U tility Функции
LO 2.1: Опишите вспомогательную функцию.
2.2 Вспомогательные функции и типичные предпочтения
LO 2. 2: Идентифицируйте служебные функции на основе типичных предпочтений, которые они представляют.
2: Идентифицируйте служебные функции на основе типичных предпочтений, которые они представляют.
2 .3 Относящиеся U Тилии F соединения и I80008
C urve M aps
LO 2.3: Объясните, как вывести кривую безразличия из функции полезности.
2.4 F ind ing M arginal U tility and M arginal R ate of S ubstitution
LO 2.4: Получить предельную полезность и MRS для типичных функций полезности.
2,5 . Политика Вопрос
2. 1 Полезность F функция s
1 Полезность F функция s
LO1: Опишите функцию полезности.
Наши предпочтения позволяют нам сравнивать различные потребительские пакеты и выбирать предпочтительные пакеты. Мы могли бы, например, определить порядок ранжирования всего набора пакетов на основе наших предпочтений. Функция полезности представляет собой математическую функцию, которая ранжирует наборы потребительских товаров, присваивая каждому номер, где большие числа указывают на предпочтительные наборы. Вспомогательные функции обладают свойствами, которые мы определили в Модуле 1 в отношении предпочтений. То есть: они могут упорядочивать пакеты, они полны и транзитивны, больше предпочтительнее меньшего и, в соответствующих случаях, смешанные пакеты лучше.
Число, которое функция полезности присваивает определенному набору, известно как полезность , удовлетворение, которое потребитель получает от определенного набора. Номер полезности для каждого пакета ничего не значит в абсолютном выражении; нет единой шкалы, по которой мы измеряем удовлетворенность. Это единственная цель в относительном выражении: мы можем использовать полезность, чтобы определить, какие пакеты предпочтительнее других.
Номер полезности для каждого пакета ничего не значит в абсолютном выражении; нет единой шкалы, по которой мы измеряем удовлетворенность. Это единственная цель в относительном выражении: мы можем использовать полезность, чтобы определить, какие пакеты предпочтительнее других.
Если полезность набора А выше, чем полезность набора В, это эквивалентно утверждению, что потребитель предпочитает набор А набору В. Таким образом, функции полезности ранжируют потребительские предпочтения, присваивая номер каждому набору. . Мы можем использовать функцию полезности для построения карт кривых безразличия, описанных в Модуле 1. Поскольку все наборы на одной и той же кривой безразличия обеспечивают одинаковое удовлетворение, и, следовательно, ни один из них не является предпочтительнее , каждый комплект имеет одинаковую полезность. Следовательно, мы можем нарисовать кривую безразличия, определив все наборы, которые возвращают одно и то же число из функции полезности.
Экономисты говорят, что функции полезности представляют собой порядковый номер , а не количественный . Порядковый означает, что функции полезности только ранжируют наборы — они только указывают, какой из них лучше, а не насколько он лучше другого набора. Предположим, например, что одна функция полезности указывает, что набор A возвращает 10 utils и комплект B 20 utils. Мы не утверждаем, что набор Б в два раза лучше или в 10 раз лучше, а только то, что потребитель предпочитает набор Б. Например, предположим, что друг участвовал в гонке и сказал вам, что занял третье место. Эта информация порядковая: вы знаете, что она была быстрее, чем занявшая четвертое место, и медленнее, чем занявшая второе место. Вы знаете только порядок, в котором бегуны финишировали. Индивидуальное время имеет решающее значение: если финишер, занявший первое место, пробежал гонку ровно за один час, а ваш друг финишировал за час и шесть минут, вы знаете, что ваш друг был ровно на 10% медленнее, чем самый быстрый бегун. поскольку функции полезности являются порядковыми, многие различные функции полезности могут представлять одни и те же предпочтения.
Порядковый означает, что функции полезности только ранжируют наборы — они только указывают, какой из них лучше, а не насколько он лучше другого набора. Предположим, например, что одна функция полезности указывает, что набор A возвращает 10 utils и комплект B 20 utils. Мы не утверждаем, что набор Б в два раза лучше или в 10 раз лучше, а только то, что потребитель предпочитает набор Б. Например, предположим, что друг участвовал в гонке и сказал вам, что занял третье место. Эта информация порядковая: вы знаете, что она была быстрее, чем занявшая четвертое место, и медленнее, чем занявшая второе место. Вы знаете только порядок, в котором бегуны финишировали. Индивидуальное время имеет решающее значение: если финишер, занявший первое место, пробежал гонку ровно за один час, а ваш друг финишировал за час и шесть минут, вы знаете, что ваш друг был ровно на 10% медленнее, чем самый быстрый бегун. поскольку функции полезности являются порядковыми, многие различные функции полезности могут представлять одни и те же предпочтения. Это верно до тех пор, пока порядок сохраняется.
Это верно до тех пор, пока порядок сохраняется.
Возьмем, к примеру, функцию полезности U, которая описывает предпочтения относительно наборов товаров A и B: U(A,B). Мы можем применить к этой функции любое положительное монотонное преобразование (что, по сути, означает, что мы не меняем порядок), и созданная нами новая функция будет представлять те же предпочтения. Например, мы могли бы умножить положительную константу α или добавить положительную или отрицательную константу β . Таким образом, αU(A,B)+β представляет те же самые предпочтения, что и U(A,B), потому что он упорядочивает пакеты точно так же. Этот факт весьма полезен, поскольку иногда применение положительного монотонного преобразования функции полезности облегчает решение задач.
2.2 Функции полезности и типичные предпочтения
LO2: Определение функций полезности на основе типичных предпочтений, которые они представляют яблок и бананов есть функция U(A,B). Но каковы особые предпочтения Исаака в отношении связок яблок и бананов? Предположим, что у Исаака довольно стандартные предпочтения в отношении яблок и бананов, которые приводят к нашим типичным кривым безразличия: он предпочитает больше меньшему и любит разнообразие. Функция полезности, которая представляет эти предпочтения, может быть:
Но каковы особые предпочтения Исаака в отношении связок яблок и бананов? Предположим, что у Исаака довольно стандартные предпочтения в отношении яблок и бананов, которые приводят к нашим типичным кривым безразличия: он предпочитает больше меньшему и любит разнообразие. Функция полезности, которая представляет эти предпочтения, может быть:
U(A,B) = AB
Если яблоки и бананы идеально дополняют предпочтения Исаака, функция полезности будет выглядеть примерно так:
U(A,B) = MIN[A,B],
где функция MIN просто присваивает меньшее из двух чисел в качестве значения функции.
Если яблоки и бананы являются совершенными заменителями, функция полезности является аддитивной и будет выглядеть примерно так:
U(A,B) = A + B
Класс функций полезности, известный как функции полезности Кобба-Дугласа обычно используется в экономике по двум причинам:
1. Они отражают предпочтения «хорошего поведения», такие как «чем больше, тем лучше» и предпочтение разнообразия.
2. Они очень гибкие и легко настраиваются в соответствии с реальными данными.
Функции полезности Кобба-Дугласа имеют следующую форму:
U(A,B) = A α B β
Поскольку положительные монотонные преобразования представляют одни и те же предпочтения, одно такое преобразование можно использовать для установки α + β = 1 , что, как мы увидим позже, является удобным условием, упрощающим некоторые математические расчеты в задаче потребительского выбора.
Другой способ полезного преобразования функции полезности состоит в том, чтобы взять натуральный логарифм функции, который создает новую функцию, которая выглядит следующим образом:
U(A,B) = αln(A) + βln(B )
Чтобы вывести это уравнение, просто примените правила натуральных журналов. [Мы добавим сюда ссылку, чтобы учащиеся могли нажать, чтобы увидеть, как это делается в видеоруководстве по объяснению]. Здесь важно помнить об уровне абстракции. Обычно мы не можем создавать специальные функции полезности, которые точно описывают индивидуальные предпочтения. Наверное, никто из нас не смог бы описать собственные предпочтения одним уравнением. Но пока потребители в целом имеют предпочтения, соответствующие нашим основным предположениям, мы можем довольно неплохо находить функции полезности, соответствующие реальным данным о потреблении. Мы увидим доказательства этого позже в курсе.
Наверное, никто из нас не смог бы описать собственные предпочтения одним уравнением. Но пока потребители в целом имеют предпочтения, соответствующие нашим основным предположениям, мы можем довольно неплохо находить функции полезности, соответствующие реальным данным о потреблении. Мы увидим доказательства этого позже в курсе.
В таблице 2.1 приведены настройки и служебные функции, описанные в этом разделе.
Таблица 2.1 Типы предпочтений и вспомогательные функции, которые их представляют | ||
ПРЕДПОЧТЕНИЯ | СЛУЖЕБНАЯ ФУНКЦИЯ | ТИП ПОЛЕЗНОЙ ФУНКЦИИ |
Любовь к разнообразию или хорошее поведение | U(A,B) = АВ | Кобб-Дуглас |
Любовь к разнообразию или хорошее поведение | U(A,B) = А α В β | Кобб-Дуглас |
Любовь к разнообразию или хорошее поведение | U(A,B) = αln(A) + βln(B) | Натуральное бревно Кобб-Дуглас |
Идеальное дополнение | U(A,B) = МИН[A,B] | Минимальная функция |
Идеальные заменители | U(А,В) = А + В | Добавка |
2 . . . . . . . . . . . . . . . кривая из функции полезности Кривые безразличия и функции полезности напрямую связаны. Фактически, поскольку кривые безразличия представляют предпочтения графически, а функции полезности представляют предпочтения математически, отсюда следует, что кривые безразличия могут быть получены из функций полезности. 9\frac{1}{2}[/latex] 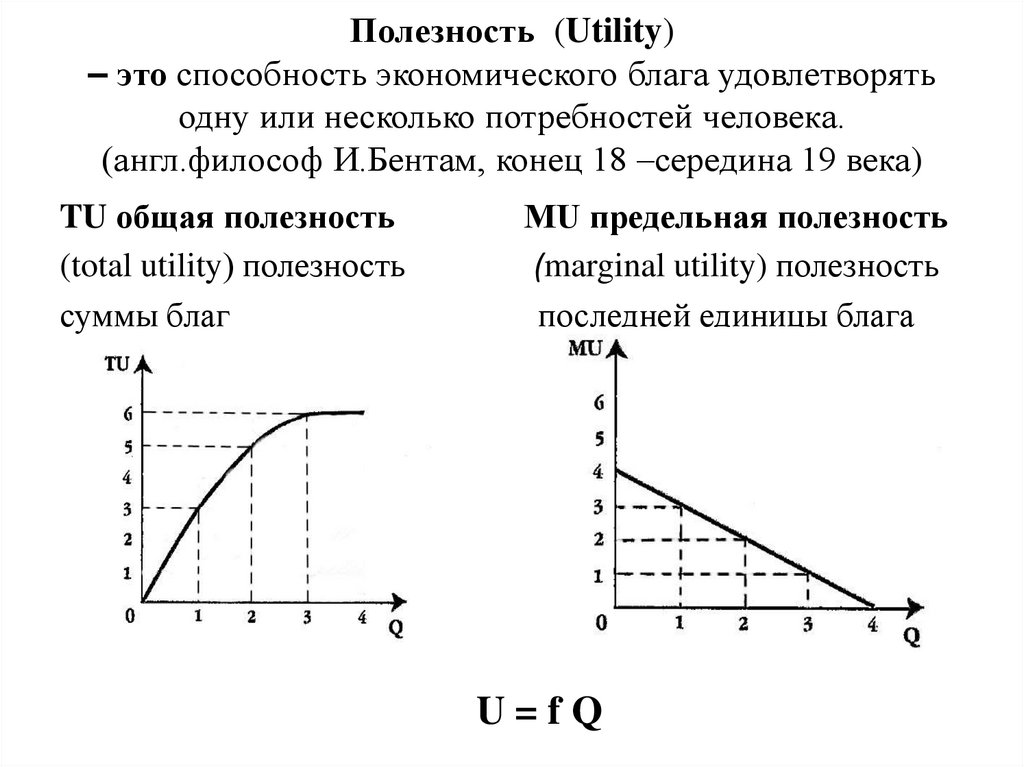 3 Отношение Утилита F ИСКЛЮЧЕНИЯ И I Ndifference C urve M 2.
3 Отношение Утилита F ИСКЛЮЧЕНИЯ И I Ndifference C urve M 2.
На рис. 2.1 ясно показано предположение, что потребители предпочитают разнообразие. Каждый пучок, содержащий определенное количество А и В, представляет собой точку на поверхности. Вертикальная высота поверхности представляет уровень полезности. Увеличивая как A, так и B, потребитель может достичь более высоких точек на поверхности.
Откуда же берутся кривые безразличия? Напомним, что кривая безразличия — это совокупность всех наборов, к которым потребитель безразличен, относительно того, какой из них потреблять. Математически это эквивалентно утверждению, что все наборы, помещенные в функцию полезности, возвращают одно и то же функциональное значение. Итак, если мы установим значение полезности Ū и найдем все наборы А и В, которые создают это значение, мы определим кривую безразличия. Обратите внимание, что это эквивалентно нахождению всех наборов, которые доставляют потребителя на одинаковую высоту на трехмерной поверхности на рис. 2.1.
Кривые безразличия представляют собой высоту (уровень полезности) на плоской поверхности. Таким образом, они аналогичны контурной линии на топографической карте. Перенося трехмерный график обратно в двумерное пространство — пространство А, В — мы можем показать контурные линии/кривые безразличия, которые представляют различные высоты или уровни полезности. Из графика на рис. 2.1 вы уже можете видеть, как эта функция полезности дает кривые безразличия, которые «изогнуты» или вогнуты к началу координат.
Из графика на рис. 2.1 вы уже можете видеть, как эта функция полезности дает кривые безразличия, которые «изогнуты» или вогнуты к началу координат.
Таким образом, кривые безразличия следуют непосредственно из функций полезности и являются удобным способом представления функций полезности на двумерном графике.
2.4 Определение предельной полезности и предельной нормы замещения
LO4: Получите предельную полезность и MRS для типичных функций полезности.
Предельная полезность — это дополнительная полезность, которую потребитель получает от потребления одной дополнительной единицы товара. Математически мы выражаем это как:
[латекс]MU_{a}=\frac{\Delta U}{\Delta A}[/latex]
или изменение полезности в результате изменения количества потребляемого А, где Δ представляет собой изменение стоимость предмета. Итак,
[латекс]MU_{a}=\frac{\Delta U}{\Delta A}=\frac{U (A+\Delta A,B)-U(A,B)}{\Delta A} [/latex]
Обратите внимание, что когда мы исследуем предельную полезность потребления A, мы считаем B постоянным.
Используя исчисление, предельная полезность равна частной производной функции полезности по A:
[латекс]MU_{A}\frac{\partial U(A,B)}{\partial A}[/latex]
Рассмотрим потребителя, который садится есть салат и пиццу. Предположим, что мы сохраняем количество салата постоянным — например, один гарнир к ужину. Теперь давайте увеличим количество кусков пиццы, предположим, что для 1 кусочка полезность равна 10, для 2 — 18, для 3 — 24 и для 4 — 28. Давайте нанесем эти числа на график, где полезность отложена по вертикальной оси, а пицца — по горизонтальной. ось (рис. 2.2).
Рисунок 2.2: График и таблица убывающей предельной полезности
Ломтики пиццы | Утилита | Предельная полезность |
1 | 10 | |
2 | 18 | 8 |
3 | 24 | 6 |
4 | 28 | 4 |
Из положительного наклона графика видно, как увеличивается полезность дополнительных кусочков пиццы. Из вогнутой формы графика видно еще одно распространенное явление: дополнительная полезность, которую потребитель получает от каждого дополнительного куска пиццы, уменьшается с увеличением количества потребляемых кусков.
Из вогнутой формы графика видно еще одно распространенное явление: дополнительная полезность, которую потребитель получает от каждого дополнительного куска пиццы, уменьшается с увеличением количества потребляемых кусков.
Тот факт, что дополнительная полезность становится меньше с каждым дополнительным куском пиццы, называется принципом убывающая предельная полезность . Этот принцип применяется к предпочтениям с хорошим поведением, когда предпочтение отдается смешанным наборам.
Предельный r s Замещение ( MRS ) – это количество одного товара, от которого потребитель готов отказаться, чтобы получить еще одну единицу другого товара. Вот почему это то же самое, что наклон кривой безразличия — поскольку мы сохраняем уровень удовлетворения постоянным, мы остаемся на той же кривой безразличия, просто двигаясь по ней, когда мы обмениваем один товар на другой. Сколько одного товара вы готовы обменять на еще один другой, зависит от предельной полезности каждого из них.
Сколько одного товара вы готовы обменять на еще один другой, зависит от предельной полезности каждого из них.
Используя наш предыдущий пример, если, съев еще один салат, ваша полезность увеличится на 10, то при текущем потреблении 4 ломтиков пиццы вы можете отказаться от 2 ломтиков пиццы и увеличить полезность с 28 до 18. На 10 дополнительных полезностей от салата и на 10 меньших полезностей за счет отказа от 2 кусков пиццы общая полезность остается неизменной, поэтому мы должны оставаться на той же кривой безразличия. Двигаясь по кривой безразличия, вы, должно быть, идете по наклонной, то есть вы должны отказываться от блага по вертикальной оси в пользу большего количества блага по горизонтальной оси, что приводит к отрицательному подъему по сравнению с положительным ходом.
Мы можем перейти непосредственно от предельной полезности к MRS, признав связь между этими двумя понятиями. В нашем случае для функции полезности [latex]U=U(A,B)[/latex] MRS представляется как:
[latex]MRS=-\frac{MU_{A}}{MU_{B} }[/latex]
Обратите внимание, что при подстановке мы можем упростить уравнение:
[latex]MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{\frac{\Delta U}{\Delta A}}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}[/latex]
Вставка вычисления, которое соответствует: 9[/ латекс]
2 . 5 Полис Вопрос
5 Полис Вопрос
В Модуле 1 мы определили, что соответствующее решение потребителя между увеличением пробега и другим потреблением, вероятно, соответствует стандартным предположениям о потребительском выборе. Следовательно, используя функцию полезности Кобба-Дугласа для представления потребителя, которому нравится водить машину, а также потреблять другие товары, и который рассматривает их как компромисс (деньги, потраченные на бензин, — это деньги, не потраченные на другие потребительские товары), хороший выбор. Он также имеет преимущества как в соответствии с предположениями, так и в гибкости: 9{\beta}[/latex] ,
, где MD = пробег в милях, а C = прочее потребление.
На самом деле, сама функция может быть взята из реальных данных, где параметры и могут быть оценены для этого рынка, рынка миль, пройденных автомобилем потребителя.
Рисунок 2.3 График кривых безразличия для примера политики
Изучение вопросов политики:
1 . Будут ли другие типы предпочтений более подходящими в этом примере?
Будут ли другие типы предпочтений более подходящими в этом примере?
2. Что должно быть верным, чтобы совершенные дополнения были подходящим типом предпочтения для анализа этой политики?
Что должно быть верно для совершенных заменителей? Учитывая, что мы рассматриваем «типичного» потребителя, который водит машину, уместно ли выбрать «типичную» функцию полезности?
4. Мы просто догадываемся или у нас есть какое-то теоретическое обоснование в поддержку нашего выбора «хорошего поведения» предпочтений или функции полезности Кобба-Дугласа?
Сводка
Обзор: темы и связанные с ними результаты обучения
2.1 Утилита F Unctions
LO 2.1: Опишите функцию утилисти. : определение функций полезности на основе типичных предпочтений, которые они представляют0008
LO 2.3: Объясните, как вывести кривую безразличия из функции полезности
2.4 Определение предельной полезности и предельной нормы замещения
LO 2. 4: Выведите предельную полезность и MRS для типичных функций полезности.
4: Выведите предельную полезность и MRS для типичных функций полезности.
2.5. Политика Вопрос
Узнайте: ключевые термины и графики
Термины
Функции двух переменных
Кардинал
Контурная линия
Убывающая предельная полезность0005
Функция
предельная скорость замены (MRS)
Уличная утилита
Оргальная
Однофакторные функции
UTIL
3DILITIE
Cobb-Douglas
Идеальные дополнения
Идеальные заменители
Бюджетное ограничение – средний уровень микроэкономики
Основной корпус
Вопрос политики : Покупка гибридного автомобиля Налоговый кредит — Лучший выбор правительства для снижения потребления топлива и выбросов углерода?
Политика правительства США по предоставлению налоговых льгот на покупку электрических и гибридных автомобилей может иметь последствия, выходящие за рамки сокращения выбросов углерода. Например, потребитель, приобретающий гибридный автомобиль, может тратить меньше денег на бензин и иметь больше денег на другие вещи. Это имеет последствия как для отдельного потребителя, так и для экономики в целом.
Например, потребитель, приобретающий гибридный автомобиль, может тратить меньше денег на бензин и иметь больше денег на другие вещи. Это имеет последствия как для отдельного потребителя, так и для экономики в целом.
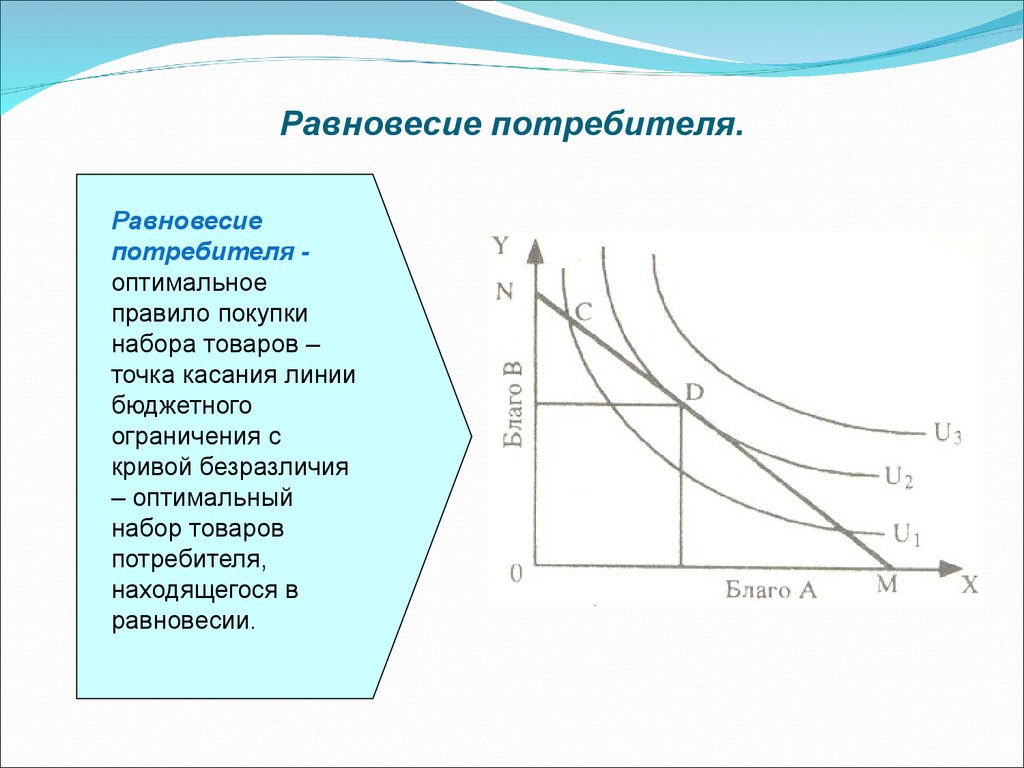
Даже самые богатые люди — от Билла Гейтса до Опры Уинфри — не могут позволить себе владеть всем на свете. У каждого из нас есть бюджет, который ограничивает объем нашего потребления. Экономисты называют это ограничение бюджетным ограничением . В нашем примере с политикой выбор человека между потреблением бензина и всем остальным ограничен его или ее текущим доходом. Любые дополнительные деньги, потраченные на бензин, — это деньги, которых нет на другие товары и услуги, и наоборот. Вот почему бюджетное ограничение называется ограничением.
Бюджетное ограничение определяется доходом, с одной стороны, тем, сколько денег потребитель может потратить на потребление, и ценами на товары, которые потребитель покупает, с другой.
Изучение вопроса политики
Каковы последствия для бюджета потребителя, владеющего гибридным автомобилем? Какие решения о покупке может принять этот потребитель, учитывая его или ее экономию на газе, и как это, в свою очередь, повлияет на цели политики налоговых субсидий?
3. 1 Описание бюджетного ограничения
1 Описание бюджетного ограничения
LO1: Определите бюджетное ограничение концептуально, математически и графически.
3.2 Наклон бюджетной линии
LO2: Интерпретация наклона бюджетной линии.
3.3 Изменения в ценах и доходах
LO3: Проиллюстрируйте, как изменения в ценах и доходах влияют на бюджетное ограничение и бюджетную строку.
3.4 Купоны, ваучеры , и налоги
LO4: Проиллюстрируйте, как купоны, ваучеры и налоги изменяют бюджетное ограничение и строку бюджета.
3,5 Пример политики : бюджеты гибридных автомобилей и бюджеты потребителей
LO1: определить ограничение бюджета, концептуально, математическое и графическое. Бюджетное ограничение — это набор всех наборов, которые потребитель может себе позволить при данном доходе этого потребителя. Мы предполагаем, что у потребителя есть бюджет — сумма денег, которую он может потратить на наборы. На данный момент мы не беспокоимся о том, откуда берутся эти деньги или доход, мы просто предполагаем, что у потребителя есть бюджет. Так что же может позволить себе потребитель? Ответ на этот вопрос зависит от цен на рассматриваемые товары. Предположим, вы идете в магазин кампуса, чтобы купить энергетические батончики и воду с витаминами. Если у вас есть 5 долларов, энергетические батончики стоят по 50 центов каждый, а витаминизированная вода стоит 1 доллар за бутылку, то вы можете купить 10 батончиков, без витаминной воды, без батончиков и 5 бутылок витаминной воды, 4 батончика и 2 витаминных воды и скоро. В этой таблице показаны возможные комбинации энергетических батончиков и воды с витаминами, которые студент может купить ровно за 5 долларов: Энергетические батончики Бутылки витаминной воды 10 0 8 1 6 2 4 3 2 4 0 5 Верно также и то, что вы можете потратить менее 5 долларов, и у вас останутся деньги. Обратите внимание, что мы фокусируемся на наборах из двух товаров, чтобы сохранить гибкость (как объяснено в модуле 1), но просто выйти за рамки двух товаров, определив один из товаров как «деньги, потраченные на все остальное». Математически общая сумма, которую потребитель тратит на два товара, A и B, равна: (3.1) , [latex]P_{A}A+P_{B}B[/latex] где [latex] P_{A}[/latex] – цена товара A, а [latex]P_{B}[/latex] – цена товара B. Если деньги, которые потребитель должен потратить на эти два товара, его доход равен задан как I, то бюджетное ограничение равно: (3.2)[latex]P_{A}A+P_{B}B\leq I[/latex] Обратите внимание на неравенство: это уравнение утверждает, что потребитель не может тратить больше, чем его доход, но может тратить меньше. Мы можем упростить это предположение, ограничив потребителя расходованием всего своего дохода на эти два товара. (3.3)[latex]P_{A}A+P_{B}B=I[/latex] Графически мы можем представить это бюджетное ограничение, как показано на рисунке 3.1. Мы называем это строкой бюджета : Строка, которая указывает возможные наборы, которые потребитель может купить, потратив весь свой доход. Рисунок 3.1 Бюджетная линия представляет собой график уравнения бюджетного ограничения (3.3). LO2: Интерпретация наклона бюджетной линии Из графика бюджетного ограничения в разделе 3.1 видно, что бюджетная линия наклонена вниз и имеет постоянный наклон по всей своей длине. Это интуитивно понятно: если вы покупаете больше одного товара, вам придется покупать меньше другого товара. (3.4) [latex]B=\frac{I}{ P_{B}}-\frac{P_{A}}{P_{B}}A[/латекс] Теперь у нас есть строка бюджета, представленная в виде точки-наклона, где: Первая часть, [latex]\frac{I}{P_{B}}[/latex], представляет собой точку пересечения по вертикали. Вторая часть,[latex]-\frac{P_{A}}{P_{B}}[/latex] , представляет собой коэффициент наклона на A. Обратите внимание, что наклон бюджетной строки представляет собой просто отношение цен, также известный как соотношение цен . Это скорость, по которой вы можете обменять один товар на другой на рынке. Чтобы убедиться в этом, давайте вернемся в магазин кампуса с 5 долларами, чтобы потратить их на энергетические батончики и воду с витаминами. Предположим, вы изначально решили купить 5 бутылок витаминной воды и положили их в корзину. Немного подумав, вы решили обменять 1 бутылку на 2 энергетических батончика. Теперь у вас в корзине 4 бутылки витаминной воды и 2 энергетических батончика. Если вы хотите еще больше батончиков, доступен тот же компромисс: можно получить еще 2 батончика, если вы откажетесь от одной бутылки витаминной воды и так далее. Наклон бюджетной линии также называют e conomic r ate of s замена ( ERS ) . Наклон бюджетной линии также представляет собой альтернативную стоимость потребления большего количества товара А, поскольку он показывает, от какого количества товара В потребитель должен отказаться, чтобы потреблять еще одну единицу товара А. o c ost чего-либо — это стоимость следующей лучшей альтернативы, от которой пришлось отказаться, чтобы получить ее. Изменения цен и доходов LO3: Проиллюстрируйте, как изменения цен и доходов влияют на бюджетное ограничение и бюджетную строку. Из нашего математического описания бюджетной линии мы можем легко увидеть, как изменения в ценах и доходе влияют на бюджетную линию и набор выбора потребителя — набор всех наборов, доступных ему при текущих ценах и доходе. Вернемся к уравнению (3.3): (3.3)[latex]P_{A}A+P_{B}B=I[/latex] Из предыдущего рисунка 3.3 мы знаем, что точка пересечения по вертикали для уравнения ( 3.3) – [латекс]\frac{I}{P_{B}}[/latex] , а точка пересечения по горизонтали – [латекс]\frac{I}{P_{A}}[/latex]. Теперь рассмотрим увеличение цены товара А. Обратите внимание на рис. 3.3, что это увеличение не влияет на точку пересечения по вертикали, а только на точку пересечения по горизонтали. По мере увеличения [latex]P_{A}[/latex] , [latex]\frac{I}{P_{A}}[/latex] уменьшается, приближаясь к исходной точке. Это изменение делает бюджетную линию «более крутой» или имеет более отрицательный наклон, как видно из коэффициента наклона: [latex]-\frac{P_{A}}{P_{B}}[/latex]. По мере увеличения [latex]P_{A}[/latex] это отношение увеличивается по абсолютной величине, поэтому наклон становится более отрицательным или более крутым. Интуитивно это означает, что цена компромисса или упущенной выгоды возросла. Теперь потребитель должен отказаться от большего количества товара B, чтобы потреблять еще одну единицу товара A9.0005 Рисунок 3.3 Изменение цены одного товара изменяет наклон бюджетной линии. Далее рассмотрим изменение дохода. Предположим, что потребитель получает дополнительную сумму денег на расходы, поэтому I увеличивается. LO4: Проиллюстрируйте, как купоны, ваучеры и налоги изменяют бюджетное ограничение и строку бюджета. Бюджетные ограничения могут меняться из-за изменений цен и доходов, но давайте теперь рассмотрим другие общие черты реального рынка, которые могут влиять на бюджетные ограничения. Мы начинаем с купонов или других методов, которые фирмы используют для предоставления скидок потребителям. Рассмотрим купон или распродажу, которая дает покупателям скидку на цену одного товара в нашей задаче об ограничении бюджета. Более сложным является купон, который дает процент от всей покупки. В этом случае процент берется из цены обоих товаров A и B в нашей задаче об ограничении бюджета. В этом случае соотношение цен, или наклон бюджетного ограничения, не меняется. Например, если цена A регулярно составляет 10 долларов, а цена B регулярно составляет 20 долларов, то при 20-процентной скидке на всю покупку новые цены составят 8 и 16 долларов соответственно. Интуитивно мы можем видеть, что это эквивалентно увеличению дохода и приводит к тому же результату: расширяя бюджетный набор, потребитель теперь может позволить себе наборы с большим количеством обоих товаров. Продукт Обычная цена Новая цена с Скидка 20% на Вся покупка 10 долларов $8 Б 20 долларов $16 Еще одна распространенная скидка — на максимальное количество товаров. Рисунок 3.4 Эффект 20% скидки на первые A̅ единицы A. Налоги имеют тот же эффект, что и купоны, но в противоположном направлении. Налог адвалорный — это налог, основанный на стоимости товара, например, процентный налог с продаж. С точки зрения бюджетного ограничения адвалорный налог на конкретный товар эквивалентен увеличению цены, как показано на рис. 3.5. Общий налог с продаж на все товары вызывает параллельный сдвиг бюджетной строки внутрь. Отметим также, что подоходный налог в данном случае функционально эквивалентен общему налогу с продаж, он вызывает параллельный сдвиг внутрь бюджетной строки. Рисунок 3.5 Адвалорный налог изменяет наклон и горизонтальную точку пересечения бюджетной линии. Ваучеры, дающие право на определенное количество товара (стоимости или количества), немного сложнее. Вернемся к вашей покупке витаминной воды и энергетических батончиков. Предположим, у вас есть ваучер на 2 бесплатных энергетических батончика. У вас есть 5 долларов Цена 1 батончика энергии 0,50 доллара Цена 1 бутылки витаминной воды 1 доллар. Как бы мы теперь изобразили вашу бюджетную линию? Начнем с простого набора, который содержит 2 энергетических батончика и 2 бутылки воды с витаминами. Обратите внимание, что отказ от 1 или 2 батончиков не позволяет учащемуся потреблять больше витаминной воды. Альтернативная стоимость этих двух баров равна 0, поэтому бюджетная линия в этой части имеет нулевой наклон. После использования ваучера, если студент хочет больше 2 батончиков, альтернативная стоимость будет такой же, как и раньше — 0,05 за бутылку воды с витаминами — и поэтому бюджетная строка с этого момента такая же, как и раньше. Новая бюджетная строка с ваучером имеет излом. 5 Пример политики : Субсидии на гибридные автомобили и бюджеты потребителей В нескольких модулях мы рассмотрели политику налогового кредита на гибридные автомобили. В Модуле 1 мы думали о различных предпочтениях вождения типичного потребителя. В Модуле 2 мы преобразовали эти предпочтения в тип функции полезности и соответствующую кривую безразличия. Теперь давайте подумаем о соответствующей строке бюджета для нашего примера политики. Для начала воспользуемся теми же двумя осями, что и для карты кривой безразличия, как показано на рис. 3.6. Другими словами, давайте поместим «пройденные мили» на горизонтальной оси, а $, то есть все деньги, потраченные на другое потребление, на вертикальной оси. Пока не будем указывать точный уровень дохода.. Теперь мы можем спросить, какова цена «другого потребления?» Поскольку мы говорим о деньгах, оставшихся после оплаты пройденных миль, цена другого потребления равна просто 1. Это потому, что мы говорим о самих деньгах и цена доллара — доллар. Но какова цена пройденной мили? Этот вопрос более сложен и включает в себя расходы на содержание и амортизацию. Однако, поскольку мы сосредоточены на эффекте увеличения количества миль за галлон бензина, давайте сосредоточимся только на затратах, связанных с покупкой бензина. В этом случае стоимость проезда в миле — это цена бензина, деленная на количество миль, пройденных автомобилем на галлон (MPG). Поскольку нас снова интересует не отдельный человек, а группа, мы можем использовать среднюю цену галлона обычного бензина, деленную на средний показатель MPG автомобилей, проезжающих в Соединенных Штатах, в качестве разумного приближения стоимости мили, пройденной в негибридный кр. Теперь у нас есть «цена» за милю; деление дохода на эту цену дает точку пересечения на оси «пройденных миль». Рисунок 3.6 Бюджетное ограничение потребителя для политики гибридных автомобилей Теперь, когда у нас есть бюджетное ограничение для нашего примера политики субсидирования электрических и гибридных автомобилей, мы можем увидеть влияние политики на ограничение. Уравнение (3.4) суммирует бюджетное ограничение для пробега в милях и других товаров. (3,4) Доход = (стр. миль riven ) (мили) + доллары, потраченные на другое потребление I Изучение Вопрос о политике S 3.1 Описание ограничения бюджета LO1: Определите ограничение бюджета 3,2 . Склон бюджетной линии 3,2 . Склон бюджетной линии 3,2 . интерпретация наклона бюджетной линии 3.3 Изменения в ценах и доходах LO3: Проиллюстрируйте, как изменения в ценах и доходах влияют на бюджетное ограничение и бюджетную строку 3,4 Купоны, ваучеры и налоги LO4: Иллюстрируйте, как купоны, ваучеры и налоги изменяют ограничение бюджета и бюджетная линия 3,5 Пример политики Адвалорный налог Бюджетное ограничение Бюджетная строка Экономическая норма замещения Альтернативная стоимость Нормальное бюджетное ограничение Бюджетное ограничение с купоном Бюджетное ограничение с ваучером Бюджетное ограничение Основная часть Пример полиса: Страхование от наводнений Большая часть страхования предоставляется частным рынком, но одним важным исключением является страхование от наводнений, которое обычно предоставляется федеральным правительством в Соединенных Штатах. Национальная программа страхования от наводнений в стране находится в ведении Федерального агентства по чрезвычайным ситуациям и обеспечивает дополнительное страхование от наводнений для домов, подверженных наводнениям, поскольку большинство полисов частных домовладельцев не покрывают ущерб от наводнения. Знакомство с вопросом о страховом полисе 23.1 Что такое Risky Ou t приходит? Задача обучения 23.1: Определить рискованные результаты и описать, как они оцениваются. 23.2 Оценка рискованных исходов Цель обучения 23.2: Объяснить ожидаемую полезность и предпочитаемый риск. 23.3 Ri s k Снижение Цель обучения 23.3: Описать, как диверсификация и страхование снижают риск. 23.4 Пример полиса: Страхование от наводнений Цель обучения 23.4: Применить знания о рисках и страховании, чтобы объяснить, как систематический риск затрудняет объединение рисков и разрушает частные рынки страхования. 23.1 Что такое Risky Ou t приходит? Задача обучения 23.1: Определить рискованные результаты и описать, как они оцениваются. Риск описывает любую экономическую деятельность с неопределенными результатами. Например, человек, который делает ставку на подбрасывание монеты, сталкивается с двумя разными исходами с равными шансами. Водитель автомобиля знает, что есть вероятность столкновения. Люди понимают, что в будущем есть вероятность, что они заболеют или получат травму, требующую медицинской помощи. Все эти сценарии являются примерами неопределенности, а неопределенность подразумевает риск. В этом модуле, как и в экономике в целом, мы используем термины «риск» и «неопределенность» как синонимы. С любым неопределенным исходом связаны вероятности. Напомним, что p вероятности — это числа от нуля до единицы, которые указывают вероятность того, что произойдёт тот или иной результат. При отсутствии известной вероятности, такой как подбрасывание монеты, экономические агенты должны оценивать. Как правило, они делают это двумя способами: они могут оценивать на основе частоты или на основе субъективной вероятности. Частота — это то, как часто происходил конкретный результат из известного количества событий. Например, человек, живущий в районе, где зимой редко выпадает снег, может задаться вопросом, каковы шансы, что этой зимой будет снег. [latex]F=\frac{k}{N}[/ латекс] Субъективная вероятность — это когда люди оценивают вероятности на основе собственного опыта и любых доступных им данных. Например, домовладелец может никогда не сталкиваться с пожаром в доме, но может сделать вывод о том, насколько вероятно, что они произошли, основываясь на своих собственных знаниях о пожарах в своем районе и сообщениях о пожарах, которые он видит в новостях. Синоптик также делает субъективную оценку вероятности при прогнозировании вероятности дождя. Они смотрят на доступные им данные и модели, но используют свой собственный опыт в качестве руководства к тому, как интерпретировать данные и прогнозы модели и делать собственную оценку. Если существует несколько возможных исходов, каждому возможному исходу можно присвоить вероятности. ожидаемое значение неопределенного исхода представляет собой сумму значений каждого возможного исхода, умноженную на вероятность того, что он произойдет. Например, рассмотрим банку со 100 шариками четырех разных цветов: красного, синего, зеленого и желтого. Если есть 40 красных шариков, 20 синих шариков, 30 зеленых шариков и 10 желтых шариков, то вероятность случайного извлечения красного шарика равна 0,4 (40/100), синего — 0,2, зеленого — 0,3 и желтый — .1. Предположим также, что красные стоят 10 долларов, синие — 50 долларов, зеленые — 20 долларов, а желтые — 100 долларов. Ожидаемое значение (EV) одного случайного розыгрыша: EV = Pr(красный) x значение(красный)+ Pr(синий) x значение(синий) + Pr(зеленый) x значение(зеленый) + Pr(желтый) x значение(желтый) или EV = 0,4 x 10 долларов + 0,2 x 50 долларов + 0,3 x 20 долларов + 0,1 x 100 долларов = 30 долларов. 23.2 Оценка рискованных результатов Задача обучения 23.2: Объяснить ожидаемую полезность и предпочтение риска. Рассмотрим следующую игру. С вероятностью 80 процентов вы выиграете 400 долларов, а с вероятностью 20 процентов вы выиграете 2500 долларов. Ожидаемая стоимость этой игры: EV = 0,6 × 1000 долл. США + 0,4 × 2500 долларов США = 1600 долларов США. честная азартная игра — это игра, в которой стоимость игры равна ожидаемой стоимости. Но сколько вы готовы заплатить за эту игру? Чтобы ответить на этот вопрос, нам нужно знать об ожидаемой полезности. Ожидаемая полезность — это средневзвешенная по вероятности полезность, которую человек получает от каждого возможного исхода неопределенной ситуации. Чтобы понять эту концепцию, мы можем применить ее к игре. Ожидаемая полезность вышеописанной игры: EU = 0,6 × U(1000 долларов) + 0,4 × U(2500 долларов) Чтобы рассмотреть конкретный пример, предположим, что полезность человека может быть выражена как функция денег следующим образом: [латекс] U(Money)=\sqrt{Money}[/latex] Тогда ожидаемая полезность от приведенной выше игры равна: [latex]EU=0,6\, x\,\sqrt{1000}+0,4\, x\,\sqrt{2500}=. Как и в случае полезности в целом, это число ничего не значит в абсолютном выражении. , только как относительная мера. Если бы вместо этого этому человеку была дана ожидаемая стоимость игры, 1600 долларов, наверняка обратите внимание, что он получил бы [latex]Y(\$1600)=\sqrt{1600}=40[/latex] Другими словами, гарантированная сумма в $1600 дает более высокую полезность, чем игра с ожидаемой стоимостью $1600. Это показывает, что человек не склонен к риску. Человек, который не желает делать честную игру, как человек выше, не склонен к риску . Человек, предпочитающий азартную игру гарантированной справедливой выплате, любит риск . Человек, который безразличен между азартной игрой и честной выплатой, равен 9.0007 нейтральный к риску Рисунок 23.2.1: График неприятия риска Рисунок 23.2.1 иллюстрирует человека с функцией полезности в отношении богатства, который не склонен к риску. Теперь рассмотрим игру, в которой подбрасывается монета, и фактическая выплата, 50 или 100 долларов, зависит от того, какая сторона монеты показывается после подбрасывания. Это означает, что у агента есть 50% шанс получить 50 долларов и 50% шанс получить 100 долларов. В ожидаемой стоимости игра стоит 75 долларов. Полезность 75 долларов для этого агента равна 130, как показано на рисунке. Ожидаемая полезность — это среднее значение уровней полезности для двух исходов, и ее можно рассматривать как среднюю точку на хорде, соединяющей две точки функции полезности. График кривой полезности, нейтральной к риску и склонной к риску Не все люди не склонны к риску. Человек с постоянной предельной полезностью богатства нейтрален к риску, а человек с возрастающей предельной полезностью богатства любит риск. Рисунок 23.2.2 иллюстрирует обе ситуации, используя тот же сценарий, что и на рисунке 23. Рисунок 23.2.2: Кривые по любви к любви и нейтральному риску. Не склонные к риску люди хотят уменьшить или полностью устранить риски, с которыми они сталкиваются. Даже нейтральные к риску люди избегают несправедливых рисков, а люди, любящие риск, могут хотеть избегать очень несправедливых рисков. Самый простой способ избежать риска — воздерживаться от рискованных действий, но это не всегда возможно. Фермер, например, не может избежать присущей погоде изменчивости. Но есть некоторые действия, которые люди могут предпринять, чтобы снизить риск: водители могут ездить более осторожно, фермеры могут сажать засухоустойчивые культуры, путешественники могут избегать авиакомпаний с плохими показателями безопасности. Часто для снижения риска путем сознательного выбора требуется информация о рисках. Например, чтобы снизить риск авиаперелетов, путешественнику потребуется доступ к записям безопасности авиакомпаний. Другой способ снизить риск — диверсификация. В простом примере фермер может посадить ряд различных культур, некоторые из которых хорошо растут в засушливых условиях, а другие — во влажных, так что независимо от того, влажный или засушливый год, у фермера будет по крайней мере один хороший урожай. Эта диверсификация требует, чтобы риски были абсолютно отрицательно коррелированы. Риски, которые в целом имеют отрицательную корреляцию, могут быть объединены для снижения общего риска. Например, рассмотрите возможность инвестирования в фондовый рынок. Инвестиции в несколько фирм в одной отрасли рискованны, потому что их риски, вероятно, положительно коррелированы. Если одна фирма в автомобильной промышленности работает плохо, это может быть связано с тем, что спрос на автомобили невелик, и, следовательно, все производители автомобилей могут в результате плохо работать. Однако, если вы инвестируете во множество фирм в самых разных отраслях, вполне вероятно, что у одних дела пойдут хорошо, а у других — плохо, и, следовательно, общий риск будет снижен. Распространенным способом снижения риска является покупка страховки. Рынки частного страхования существуют благодаря премии за риск, описанной ранее в этой главе. Люди, не склонные к риску, готовы заплатить цену, чтобы избежать или снизить риск. Люди, не склонные к риску, всегда предпочтут приобрести честную страховку. Справедливое страхование — это договор, ожидаемая стоимость которого для страховщика равна нулю, другими словами, справедливая ставка. В качестве простого примера рассмотрим полис автострахования. Предположим, что вероятность того, что водитель попадет в аварию через год, составляет 1%. В случае аварии стоимость ущерба составит 5000 долларов. Таким образом, ожидаемый убыток составляет (0,1)(5000 долларов) или 50 долларов. Справедливый страховой договор — это тот, который полностью застраховал бы от этой потери и взимал бы с водителя точно ожидаемую стоимость, или 50 долларов. Однако этот контракт не приносит никакой прибыли страховой компании. Фактически, человек, не склонный к риску, был бы готов купить страховку, которая менее чем полностью справедлива из-за премии за риск, которая порождает индустрию частного страхования. 23.4 Пример полиса: Страхование от наводнений Цель обучения 23.4: Применить знания о рисках и страховании, чтобы объяснить, как систематический риск затрудняет объединение рисков и разрушает частные рынки страхования. Домовладельцы, не склонные к риску, чьи дома расположены в районах с вероятностью затопления, будут иметь потребность в страховании до тех пор, пока договор страхования находится в пределах премии за риск, которую домовладельцы готовы платить. Но страхование от наводнения нелегко приобрести на частном рынке. Причиной этого является тот факт, что большинство людей, желающих приобрести страховку от наводнения, владеют домами в районах, подверженных наводнениям. По этим причинам федеральное правительство вышло на рынок страхования от наводнений и предоставляет субсидируемое страхование домохозяйствам, подверженным наводнениям. 23.1 Что такое Risky Ou t приходит? Задача обучения 23.1: Определить рискованные результаты и описать, как они оцениваются. 23.2 Оценка рискованных результатов Задача обучения 23.2: Объяснить ожидаемую полезность и предпочтение риска. 23.3 Ri s k Снижение Цель обучения 23.3: Описать, как диверсификация и страхование снижают риск. 23.4 Пример полиса: Страхование от наводнений Цель обучения 23.4: Применить знания о рисках и страховании, чтобы объяснить, как систематический риск затрудняет объединение рисков и разрушает частные рынки страхования. Вероятности Частота Ожидаемая стоимость Справедливая азартная игра .
3.1 Описание бюджетного ограничения 
 Таким образом, мы должны рассмотреть все возможные наборы, включая полное отсутствие потребления.
Таким образом, мы должны рассмотреть все возможные наборы, включая полное отсутствие потребления. Это позволит нам сосредоточиться на границе бюджетного ограничения. Как мы увидим в Модуле 4, это допущение согласуется с допущением «чем больше, тем лучше»: если вы можете потреблять больше (если ваш доход позволяет это), вы должны потреблять больше, потому что вы улучшите свое благосостояние. С учетом этого предположения мы можем записать бюджетное ограничение как:
Это позволит нам сосредоточиться на границе бюджетного ограничения. Как мы увидим в Модуле 4, это допущение согласуется с допущением «чем больше, тем лучше»: если вы можете потреблять больше (если ваш доход позволяет это), вы должны потреблять больше, потому что вы улучшите свое благосостояние. С учетом этого предположения мы можем записать бюджетное ограничение как: Курс, по которому вы можете обменять один товар на другой, определяется ценами на два товара, и они не меняются. 9Рисунок 3.2 сторона. Обратите внимание, что на нашем графике B — это товар на вертикальной оси, поэтому мы изменим наше уравнение, чтобы оно выглядело как стандартная функция с B в качестве зависимой переменной:
Курс, по которому вы можете обменять один товар на другой, определяется ценами на два товара, и они не меняются. 9Рисунок 3.2 сторона. Обратите внимание, что на нашем графике B — это товар на вертикальной оси, поэтому мы изменим наше уравнение, чтобы оно выглядело как стандартная функция с B в качестве зависимой переменной:
 Например, если вы решили купить еще одну бутылку витаминной воды, вам придется отказаться от двух энергетических батончиков. Обратите внимание, что альтернативные издержки не ограничиваются потреблением материальных благ. Например, альтернативной стоимостью часа сна может быть час изучения микроэкономики, которого не было из-за него.
Например, если вы решили купить еще одну бутылку витаминной воды, вам придется отказаться от двух энергетических батончиков. Обратите внимание, что альтернативные издержки не ограничиваются потреблением материальных благ. Например, альтернативной стоимостью часа сна может быть час изучения микроэкономики, которого не было из-за него.
 I положительно влияет на оба термина пересечения, поэтому при увеличении I увеличиваются как [latex]\frac{I}{P_{B}}[/latex] , так и [latex]\frac{I}{P_{A}}[/latex] или отойти от исходной точки. Но на наклон I не влияет: [latex]-\frac{P_{A}}{P_{B}}[/latex]. Таким образом, сдвиг бюджетной линии является параллельным сдвигом наружу — потребитель с дополнительным доходом может позволить себе больше и того, и другого.
I положительно влияет на оба термина пересечения, поэтому при увеличении I увеличиваются как [latex]\frac{I}{P_{B}}[/latex] , так и [latex]\frac{I}{P_{A}}[/latex] или отойти от исходной точки. Но на наклон I не влияет: [latex]-\frac{P_{A}}{P_{B}}[/latex]. Таким образом, сдвиг бюджетной линии является параллельным сдвигом наружу — потребитель с дополнительным доходом может позволить себе больше и того, и другого.
4 Купоны, Налоги , и Ваучеры  Купон, который дает предъявителю право на процентную скидку в цене, по сути является снижением цены и имеет точно такой же эффект. Например, купон на скидку 20% на товар, который обычно стоит 10 долларов, равнозначен снижению цены до 8 долларов.
Купон, который дает предъявителю право на процентную скидку в цене, по сути является снижением цены и имеет точно такой же эффект. Например, купон на скидку 20% на товар, который обычно стоит 10 долларов, равнозначен снижению цены до 8 долларов. Например, вы можете увидеть рекламу о 20-процентной скидке на покупку до трех единиц товара А. Эта скидка снижает альтернативную стоимость А в пересчете на В для первых трех единиц, но после этого возвращается к исходной альтернативной стоимости. Рисунок 3.4 иллюстрирует это.
Например, вы можете увидеть рекламу о 20-процентной скидке на покупку до трех единиц товара А. Эта скидка снижает альтернативную стоимость А в пересчете на В для первых трех единиц, но после этого возвращается к исходной альтернативной стоимости. Рисунок 3.4 иллюстрирует это.

 Итак, точка пересечения на этой оси — это просто значение I.
Итак, точка пересечения на этой оси — это просто значение I. Удвоение MPG с 20, скажем, до 40 резко снижает цену проезда за милю. Это сокращение приводит к тому, что точка пересечения «пройденных миль» смещается вверх, а все бюджетное ограничение смещается наружу. Обратите внимание, что теперь типичный потребитель может позволить себе использовать пакеты с большим количеством пройденных миль и всего остального — пакеты, которые были недоступны для них до введения политики.
Удвоение MPG с 20, скажем, до 40 резко снижает цену проезда за милю. Это сокращение приводит к тому, что точка пересечения «пройденных миль» смещается вверх, а все бюджетное ограничение смещается наружу. Обратите внимание, что теперь типичный потребитель может позволить себе использовать пакеты с большим количеством пройденных миль и всего остального — пакеты, которые были недоступны для них до введения политики. Однако в Соединенных Штатах цена дизельного топлива обычно выше, чем цена обычного газа. Каким образом только более высокая MPG сдвинет бюджетную строку на рис. 3.9? Каким образом только более дорогой газ может сдвинуть бюджетную линию на рис. 3.9? Как эти два фактора вместе взятые изменят бюджетную строку на рис. 3.9?
Однако в Соединенных Штатах цена дизельного топлива обычно выше, чем цена обычного газа. Каким образом только более высокая MPG сдвинет бюджетную строку на рис. 3.9? Каким образом только более дорогой газ может сдвинуть бюджетную линию на рис. 3.9? Как эти два фактора вместе взятые изменят бюджетную строку на рис. 3.9? РЕЗЮМЕ
Обзор: темы и связанные с ним результаты обучения
.
Графики
Уравнения
Неопределенность и риск – средний уровень микроэкономики


 При подбрасывании монеты вероятность того, что одна сторона приземлится вверх, составляет ½ или 50%. Иногда эти вероятности известны, как в примере с подбрасыванием монеты, а иногда эти вероятности неизвестны, как в примере с автомобильным столкновением. Даже когда мы не знаем вероятности, мы часто можем оценить на основе совокупных данных или какой-либо другой информации, например, если дороги покрыты снегом. В любом случае способность назначать вероятности отличает эти риски как поддающиеся количественной оценке. В этом модуле мы будем рассматривать только измеримый риск.
При подбрасывании монеты вероятность того, что одна сторона приземлится вверх, составляет ½ или 50%. Иногда эти вероятности известны, как в примере с подбрасыванием монеты, а иногда эти вероятности неизвестны, как в примере с автомобильным столкновением. Даже когда мы не знаем вероятности, мы часто можем оценить на основе совокупных данных или какой-либо другой информации, например, если дороги покрыты снегом. В любом случае способность назначать вероятности отличает эти риски как поддающиеся количественной оценке. В этом модуле мы будем рассматривать только измеримый риск. Возможно, они помнят, что за последние десять лет в трех из них выпал снег. Следовательно, они могут оценить вероятность выпадения снега в этом году на основе его годовой частоты, 3/10, или 0,3, или 30%. Формально если k равно количеству раз, когда событие произошло, а N равно возможному количеству раз, тогда частота, F , равна:
Возможно, они помнят, что за последние десять лет в трех из них выпал снег. Следовательно, они могут оценить вероятность выпадения снега в этом году на основе его годовой частоты, 3/10, или 0,3, или 30%. Формально если k равно количеству раз, когда событие произошло, а N равно возможному количеству раз, тогда частота, F , равна:
 Средний результат игры в мрамор — заработать 30 долларов.
Средний результат игры в мрамор — заработать 30 долларов. 6\,x\,31.62+.2\,x\,50\приблизительно 29[/latex]
6\,x\,31.62+.2\,x\,50\приблизительно 29[/latex]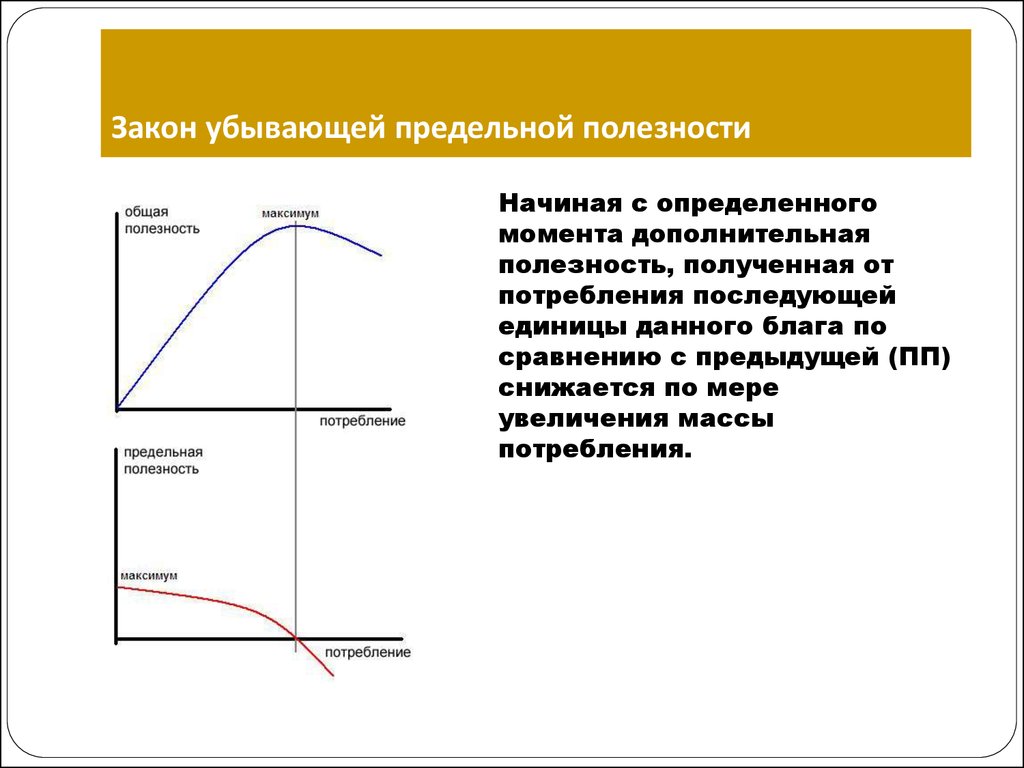 График функции полезности имеет убывающий наклон по мере увеличения благосостояния. Рассмотрим два возможных исхода: 50 и 100 долларов. График говорит нам, что полезность 50 долларов для этого агента равна 80, а полезность 100 долларов равна 140. Помните, что значение полезности не имеет абсолютного значения, оно имеет только относительное значение. Таким образом, этот агент предпочитает большее богатство меньшему, но предельная полезность богатства уменьшается. Именно это уменьшение предельной полезности богатства приводит к неприятию риска.
График функции полезности имеет убывающий наклон по мере увеличения благосостояния. Рассмотрим два возможных исхода: 50 и 100 долларов. График говорит нам, что полезность 50 долларов для этого агента равна 80, а полезность 100 долларов равна 140. Помните, что значение полезности не имеет абсолютного значения, оно имеет только относительное значение. Таким образом, этот агент предпочитает большее богатство меньшему, но предельная полезность богатства уменьшается. Именно это уменьшение предельной полезности богатства приводит к неприятию риска.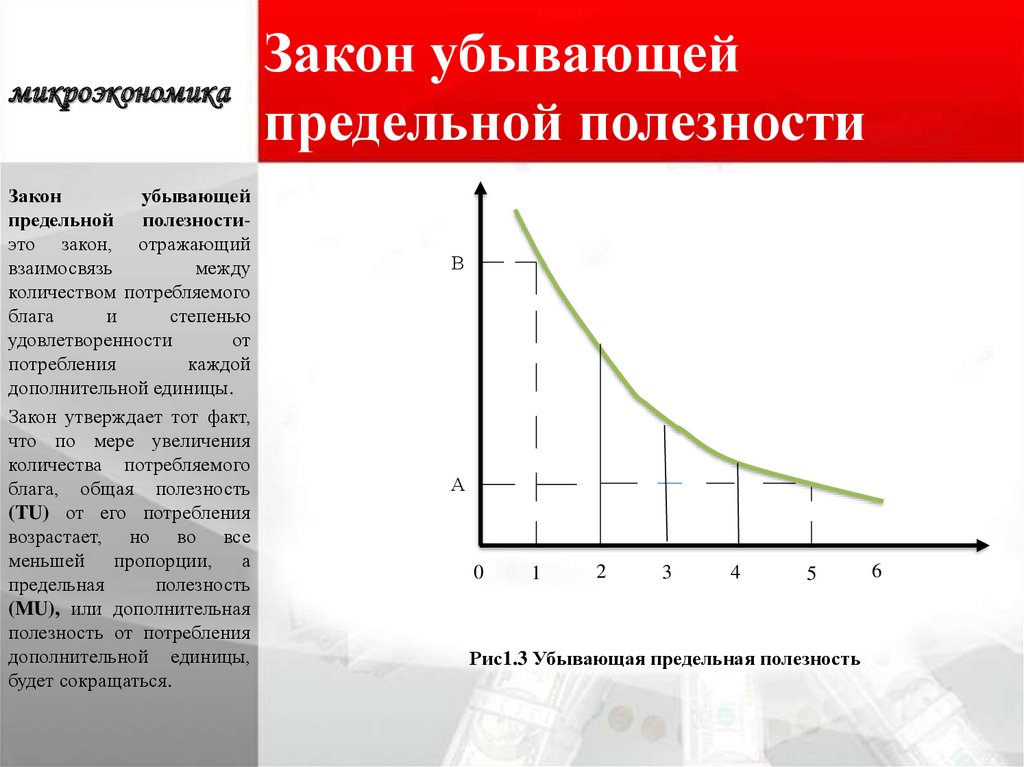 Ожидаемая полезность равна (0,5)(80)+(0,5)(140)=110. Это означает, что игра в эту рискованную игру дает этому агенту полезность 110. Какой определенный платеж принес бы агенту такую же полезность? Если мы посмотрим на рисунок, то увидим, что точка (d) на графике функции полезности находится на уровне 65 долларов. Разница между ожидаемой стоимостью игры, 75 долларов, и суммой определенного платежа, приносящего ту же полезность, что и игра, 65 долларов, называется 9.0007 премия за риск
Ожидаемая полезность равна (0,5)(80)+(0,5)(140)=110. Это означает, что игра в эту рискованную игру дает этому агенту полезность 110. Какой определенный платеж принес бы агенту такую же полезность? Если мы посмотрим на рисунок, то увидим, что точка (d) на графике функции полезности находится на уровне 65 долларов. Разница между ожидаемой стоимостью игры, 75 долларов, и суммой определенного платежа, приносящего ту же полезность, что и игра, 65 долларов, называется 9.0007 премия за риск  2.1. Обратите внимание, что нет надбавки за риск для нейтрального к риску человека, и человек, любящий риск, фактически понесет затраты на игру, если ее исключить.
2.1. Обратите внимание, что нет надбавки за риск для нейтрального к риску человека, и человек, любящий риск, фактически понесет затраты на игру, если ее исключить.


Индустрия частного страхования полагается на диверсифицированный риск, чтобы оставаться в бизнесе. Если у страховой компании 1000 клиентов, каждый из которых имеет 1%-ный риск необходимости подачи претензии, необходимо, чтобы 1%-й риск не был слишком положительно коррелирован, чтобы избежать ситуаций, в которых слишком много застрахованных предъявляют претензии в один и тот же год. Страховая компания полагается на тот факт, что она может ожидать в среднем 10 исков в год, чтобы поддерживать свой бизнес и не нести катастрофических убытков от слишком большого количества страховых исков, поданных в тот же год, что может привести к их банкротству. Возьмем, к примеру, ипотечное страхование. Страховщики покроют убытки банкам, если домовладелец с ипотечным кредитом не выполнит свои обязательства. Обычно эти риски довольно разнообразны, особенно если страховая компания страхует ипотечные кредиты в разных географических районах, чтобы экономический спад в одном городе, например закрытие крупного работодателя, не вызвал одновременно слишком много претензий. Обычно это безопасная стратегия, но жилищный кризис в Соединенных Штатах в 2006 году распространился по всей стране, что привело к глубокому кризису ряда ипотечных страховщиков, в первую очередь American International Group (AIG), которую правительство США спасло. на сумму 180 миллиардов долларов и привел к тому, что правительство взяло под свой контроль фирму.
Обычно это безопасная стратегия, но жилищный кризис в Соединенных Штатах в 2006 году распространился по всей стране, что привело к глубокому кризису ряда ипотечных страховщиков, в первую очередь American International Group (AIG), которую правительство США спасло. на сумму 180 миллиардов долларов и привел к тому, что правительство взяло под свой контроль фирму. Наводнения относительно редки, но очень дорогостоящи. Когда случается наводнение, большинство домов в зоне затопления серьезно повреждаются, поэтому риски имеют очень высокую положительную корреляцию. Это делает страхование от наводнений очень сложным для частных страховых компаний, которые изо всех сил пытаются диверсифицировать свой портфель рисков, и подвергает их опасности катастрофических выплат в случае наводнения. По этой причине цены на большую часть частного страхования превышают надбавку за риск частных домовладельцев. Это усугубляется тем фактом, что домовладельцы в зонах исследования наводнений часто являются домохозяйствами с непропорционально низкими доходами, поскольку земля, подверженная наводнениям, как правило, дешевле, чем земля в более высоких районах. Домохозяйства с более низкими доходами имеют более ограниченные ресурсы для покрытия расходов в случае наводнения, если у них нет страховки.
Наводнения относительно редки, но очень дорогостоящи. Когда случается наводнение, большинство домов в зоне затопления серьезно повреждаются, поэтому риски имеют очень высокую положительную корреляцию. Это делает страхование от наводнений очень сложным для частных страховых компаний, которые изо всех сил пытаются диверсифицировать свой портфель рисков, и подвергает их опасности катастрофических выплат в случае наводнения. По этой причине цены на большую часть частного страхования превышают надбавку за риск частных домовладельцев. Это усугубляется тем фактом, что домовладельцы в зонах исследования наводнений часто являются домохозяйствами с непропорционально низкими доходами, поскольку земля, подверженная наводнениям, как правило, дешевле, чем земля в более высоких районах. Домохозяйства с более низкими доходами имеют более ограниченные ресурсы для покрытия расходов в случае наводнения, если у них нет страховки. У федерального правительства есть ресурсы для борьбы с коррелирующими рисками и дорогостоящими выплатами, которых нет у большинства частных страховщиков.
У федерального правительства есть ресурсы для борьбы с коррелирующими рисками и дорогостоящими выплатами, которых нет у большинства частных страховщиков. РЕЗЮМЕ
Обзор: Темы и соответствующие результаты обучения
Обучение: ключевые термины и графики
Условия
Рисунок 23.2.1: График неприятия риска
Рисунок 23.2.2: Кривые полезности любви к риску и нейтральности к риску
Вспомогательная функция Определение
Что такое вспомогательная функция?
В экономике полезность представляет собой удовлетворение или удовольствие, которое потребители получают от потребления товара или услуги. Функция полезности измеряет предпочтения потребителей в отношении набора товаров и услуг.
Полезность измеряется в единицах, называемых utils (по-испански «полезный»), но расчет выгоды или удовлетворения, которые получают потребители, является абстрактным и трудно поддающимся точному определению. В результате экономисты измеряют полезность с точки зрения выявленных предпочтений, наблюдая за выбором потребителей. Оттуда экономисты упорядочивают потребительские корзины от наименее желательных до наиболее предпочтительных.
Ключевые выводы
- В экономике функция полезности является важным понятием, которое измеряет предпочтения в отношении набора товаров и услуг.
- Полезность представляет собой удовлетворение, которое потребители получают при выборе и потреблении продукта или услуги.
- Экономисты отслеживают выбор потребителей, чтобы определить полезность одного продукта по сравнению с другим и присвоить числовое значение этой полезности.
- Руководители компании исследуют потребительскую полезность для разработки планов компании по продажам и маркетингу, рекламы и предложения новых продуктов.
- Порядковая полезность ранжирует выбор по предпочтениям, а кардинальная полезность измеряет полезность, полученную от выбора.
Понимание служебной функции
В экономике функция полезности измеряет благосостояние или удовлетворение потребителя в зависимости от потребления реальных товаров, таких как продукты питания или одежда. Функция полезности широко используется в теории рационального выбора для анализа человеческого поведения.
Когда экономисты измеряют или ранжируют предпочтения потребителей, это называется порядковой полезностью. Другими словами, порядок, в котором потребители выбирают один продукт над другим, может установить, что потребители придают более высокую ценность выбранному продукту. Порядковая полезность измеряет, как потребители оценивают продукты, но не измеряет, насколько выше один из них стоит над другим.
Чтобы лучше понять порядковую полезность, рассмотрим следующий пример. Трое участников соревнуются за первое место в танцевальном конкурсе. Участник А объявляется победителем. Участник B занял второе место, а участник B занял третье место. Порядковая полезность показывает, что судьи отдавали предпочтение участнику А участникам В и С и участнику В участнику С. Чего порядковая функция не говорит нам, так это того, в какой степени один был предпочтительнее другого.
Кардинальная полезность, в основном используемая в микроэкономике, присваивает числовое значение потребительскому предпочтению, обозначая степени , в которой один выбор стоит выше другого. Кардинальная полезность будет определять, насколько участник A был предпочтительнее, чем участники B и C, и так далее.
Кардинальная полезность будет определять, насколько участник A был предпочтительнее, чем участники B и C, и так далее.
При рассмотрении полезности важно понимать понятия общей полезности и предельной полезности. Предельная полезность измеряет удовлетворение или выгоду, которую человек получает от потребления дополнительной единицы продукта или услуги. Общая полезность измеряет удовлетворение или выгоды, которые человек получает от общего потребления, включая предельную полезность, продукта или услуги.
Если потребление 10 единиц продукта дает 20 единиц полезности, а потребление одной дополнительной единицы дает 1 единицу полезности, общая полезность составляет 21 единицу полезности. Если потребление другой единицы дает 0,5 ютиля, общая полезность тогда составит 21,5 ютиля.
Экономисты считают, что количество удовлетворения, которое человек получает от каждой дополнительной единицы потребления, уменьшается с каждой единицей потребления. Эта концепция называется законом убывающей предельной полезности. Убывающая предельная полезность не означает, что потребление дополнительных единиц не сможет удовлетворить потребителя; он утверждает, что удовлетворение от потребления все большего количества единиц меньше, чем от первых дополнительных потребляемых единиц.
Убывающая предельная полезность не означает, что потребление дополнительных единиц не сможет удовлетворить потребителя; он утверждает, что удовлетворение от потребления все большего количества единиц меньше, чем от первых дополнительных потребляемых единиц.
Как рассчитать функцию полезности
Функции полезности выражаются как функция количества набора товаров или услуг. Его часто обозначают как U(X 1 , X 2 , X 3 , X n ).
Функция полезности, описывающая предпочтение одного набора товаров (X a ) по сравнению с другим набором товаров (X b ), выражается как U(X a , X b ).
Там, где есть совершенные дополнения, функция полезности записывается как U(X a , X b ) = MIN[X a , X b ], где меньшему из двух присваивается значение функции.
В определенных ситуациях товары могут считаться идеальными заменителями друг друга, и соответствующая функция полезности должна отражать такие предпочтения в форме полезности U(X a , X b) = X a + X b .
Пример вспомогательной функции
Допустим, потребитель покупает новую машину и сузил выбор до двух автомобилей. Автомобили почти идентичны, за исключением того, что второй автомобиль имеет улучшенные функции безопасности. В результате вторая машина стоит на 2000 долларов дороже первой.
Приростная или предельная полезность или удовлетворение, получаемые от второго автомобиля, могут быть представлены численно как разница в цене между двумя автомобилями в размере 2000 долларов. Другими словами, потребитель получает дополнительную или предельную полезность в размере 2000 долларов от второго автомобиля.
Кроме того, предположим, что 100 000 потребителей по всей экономике предпочитают автомобиль с номером два машине с номером один. Экономисты могут сделать вывод, что потребители в целом получили дополнительную полезность на сумму 200 миллионов долларов (100 000 x 2 000 долларов) благодаря функциям безопасности второго автомобиля. Полезность вытекает из веры потребителя в то, что у него, вероятно, будет меньше несчастных случаев из-за дополнительных функций безопасности второго автомобиля.
Преимущества и недостатки вспомогательной функции
Экономисты не могут присвоить истинное числовое значение степени удовлетворенности потребителя предпочтениями или выбором. Кроме того, может быть сложно определить причину покупки; обычно нужно учитывать много переменных.
В предыдущем примере две машины были почти идентичны. На самом деле между двумя автомобилями может быть несколько особенностей или различий. В результате присвоение значения потребительскому предпочтению может оказаться сложной задачей, поскольку один потребитель может предпочесть функции безопасности, а другой может предпочесть что-то другое.
Отслеживание и присвоение значений полезности все еще может быть полезным для экономистов. С течением времени выбор и предпочтения могут указывать на изменения в структурах расходов и полезности.
Понимание логики выбора потребителей и уровня их удовлетворенности важно не только для экономистов, но и для компаний. Руководители компаний могут использовать утилиту для отслеживания того, как потребители рассматривают их продукты.
Важно
Функция полезности — это, по сути, «модель», используемая для представления потребительских предпочтений, поэтому компании часто внедряют ее, чтобы получить преимущество в конкурентной борьбе. Например, изучение потребительской полезности может помочь руководству во всем, от маркетинга и продаж до модернизации продуктов и новых предложений.
Часто задаваемые вопросы о вспомогательной функции
Что такое вспомогательная функция?
Полезность описывает получаемые выгоды или удовлетворение от потребления товаров или услуг. Функция полезности измеряет предпочтения потребителей при потреблении товаров и услуг. Например, если потребитель предпочитает яблоки апельсинам независимо от их количества, функция полезности может быть выражена как U(яблоки) > U(апельсины).
В чем разница между функцией полезности и предельной полезностью?
Функция полезности ранжирует потребление товаров или услуг потребителями по предпочтениям. Предельная полезность измеряет изменение полезности при изменении нормы потребления (т.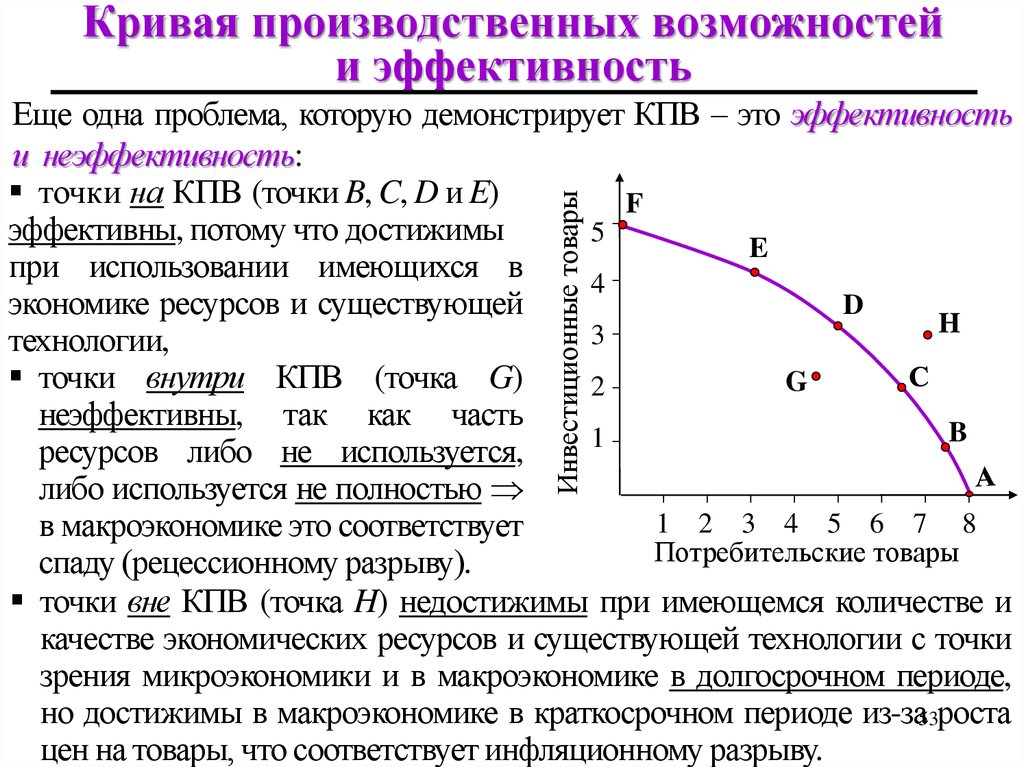 е. насколько больше удовлетворения можно получить, потребляя другую единицу товара или услуги).
е. насколько больше удовлетворения можно получить, потребляя другую единицу товара или услуги).
Почему важна вспомогательная функция?
Экономисты используют функцию полезности, чтобы лучше понять поведение потребителей, а также определить, насколько хорошо товары и услуги удовлетворяют потребителей.
Функция полезности также может помочь аналитикам определить, как распределять товары и услуги среди потребителей таким образом, чтобы реализовать общую полезность.
Компании могут использовать функцию полезности, чтобы определить, какой продукт (ы) в их продуктовой линейке (или продукции конкурента) предпочитают потребители. Знание этих предпочтений может помочь управленческим командам улучшить разработку продукта, чтобы получить конкурентное преимущество.
Практический результат
Полезность описывает выгоду или удовлетворение, получаемое от потребления товара или услуги. Единица измерения, которую экономисты используют для измерения удовлетворенности, называется полезностью. Функция полезности измеряет предпочтения потребителей в отношении набора товаров или услуг. Порядковая полезность ранжирует выбор покупателя по предпочтению, а кардинальная полезность присваивает числовое значение каждому предпочтению, чтобы определить, насколько один товар предпочтительнее другого.
Функция полезности измеряет предпочтения потребителей в отношении набора товаров или услуг. Порядковая полезность ранжирует выбор покупателя по предпочтению, а кардинальная полезность присваивает числовое значение каждому предпочтению, чтобы определить, насколько один товар предпочтительнее другого.
Энергии | Бесплатный полнотекстовый | Формализация затрат и полезности в микроэкономике
1. Введение
Микроэкономика – это изучение экономических действий отдельных лиц (потребителей) и четко определенных групп лиц (фирм) [1]. Индивидуальный анализ принятия решений лежит в основе моделирования поведения в микроэкономической теории. В экономике поведенческая экономика [2] и теория рационального выбора [3] являются двумя основными подходами к моделированию выбора, то есть товаров и услуг, потребителей и фирм. В поведенческой экономике предполагается, что на принятие решений влияют многие факторы, такие как когнитивные способности, знания или информация и предпочтения потребителя или фирмы, тогда как теория рационального выбора предполагает, что лицо, принимающее решение, всегда может предпочесть и ранжировать свои данные.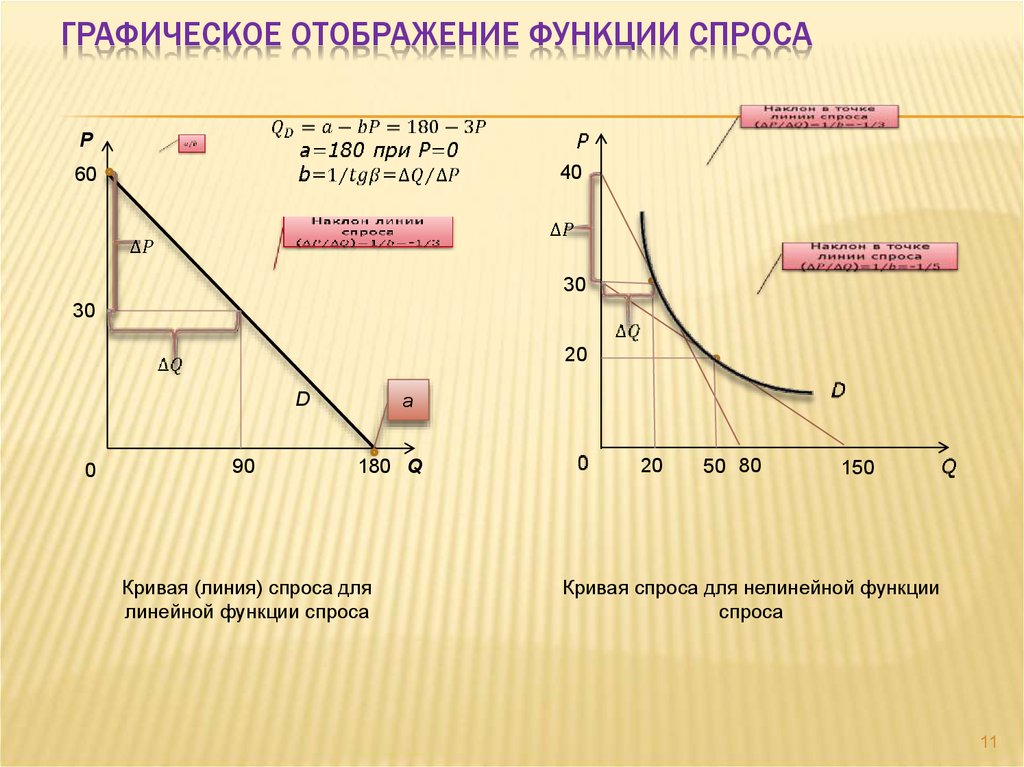 набор вариантов. Однако подход рационального выбора приводит к удобной математической структуре для проведения анализа данной экономики и, следовательно, широко используется для моделирования поведения основных лиц, принимающих решения, в микроэкономических моделях [4]. На основе модели рационального выбора разрабатываются теории потребителей и фирм для анализа потребительского (спроса) и производственного (предложения) поведения экономики [1]. В связи с этим функции затрат и полезности используются для количественной оценки и анализа последствий принятия решений фирмами и потребителями соответственно. Таким образом, моделирование затрат и полезности играет центральную роль в микроэкономическом анализе экономического рынка.
набор вариантов. Однако подход рационального выбора приводит к удобной математической структуре для проведения анализа данной экономики и, следовательно, широко используется для моделирования поведения основных лиц, принимающих решения, в микроэкономических моделях [4]. На основе модели рационального выбора разрабатываются теории потребителей и фирм для анализа потребительского (спроса) и производственного (предложения) поведения экономики [1]. В связи с этим функции затрат и полезности используются для количественной оценки и анализа последствий принятия решений фирмами и потребителями соответственно. Таким образом, моделирование затрат и полезности играет центральную роль в микроэкономическом анализе экономического рынка.
В микроэкономике математические методы предоставляют сложные инструменты для анализа экономических рынков [5]. Математически функция стоимости может быть смоделирована с использованием непрерывной, дифференцируемой, возрастающей и выпуклой функции, тогда как для моделирования полезности функция должна быть непрерывной, дифференцируемой, неубывающей и вогнутой [1]. В частности, дифференциальная теория позволяет аналитически проверять непрерывность, монотонность и выпуклый или вогнутый характер, используя тесты производных, данной функции для моделирования функций затрат и полезности. Как правило, полиномиальная, экспоненциальная и логарифмическая функции используются для моделирования стоимости и полезности в микроэкономике.
В частности, дифференциальная теория позволяет аналитически проверять непрерывность, монотонность и выпуклый или вогнутый характер, используя тесты производных, данной функции для моделирования функций затрат и полезности. Как правило, полиномиальная, экспоненциальная и логарифмическая функции используются для моделирования стоимости и полезности в микроэкономике.
Моделирование затрат и полезности позволяет изучать цены сделок и количество покупателей и продавцов на таких рынках, как электроэнергия и сельское хозяйство. В частности, микроэкономические модели и концепции имеют огромные возможности для применения в энергетике [6,7], в частности, в интеллектуальных сетях [8], которые характеризуются потоком информации наряду с электроэнергией и, таким образом, позволяют регулировать и торговля электроэнергией в сети интеллектуальных сетей [9,10,11,12,13,14]. На рынке электроэнергии функция затрат используется для моделирования затрат на производство, передачу и распределение электроэнергии конечным потребителям [15]. С другой стороны, полезное моделирование играет ключевую роль в программах реагирования на спрос (DR) [16], которые используются для формирования/изменения спроса потребителей на безопасные и надежные интеллектуальные сети.
С другой стороны, полезное моделирование играет ключевую роль в программах реагирования на спрос (DR) [16], которые используются для формирования/изменения спроса потребителей на безопасные и надежные интеллектуальные сети.
Для анализа вышеупомянутых свойств функций используются традиционные методы анализа, такие как методы проверки на бумаге и карандаше и моделирование. Методы компьютерного моделирования обычно используются для исследования функциональных свойств многих тестовых случаев. Однако моделирование не может обеспечить исчерпывающий анализ из-за связанных с этим высоких вычислительных затрат и требований к памяти. Кроме того, методы моделирования не могут моделировать непрерывное поведение функций затрат и полезности из-за компьютерного арифметического моделирования, которое приводит к ошибкам округления или усечения. Хотя методы проверки на бумаге и карандаше могут решить вышеупомянутые проблемы, эти методы подвержены человеческим ошибкам. Кроме того, бумажные и карандашные доказательства не масштабируются по отношению к сложности проблемы. Системы компьютерной алгебры (CAS), такие как Maxima [17] и Mathematica [18], также используются для исследования общих математических свойств функций-кандидатов для моделирования и анализа концепций микроэкономики [19].]. Эти методы основаны на символьных манипуляциях и, таким образом, включают в себя большие и непроверенные программы на языке программирования. Следовательно, анализ, выполненный с использованием CAS, также не может быть гарантированно точен на 100% [20]. Более того, упомянутые выше компьютерные методы позволяют проверять поведение или свойства данной функции только на заданных пользователем интервалах домена и, следовательно, не могут гарантировать исчерпывающую проверку на полном домене данной функции. Например, простая кубическая полиномиальная функция может вести себя как выпуклая или вогнутая функция в зависимости от указанной области. Вышеупомянутые недостатки традиционных методов могут привести к неточным результатам анализа, что, в свою очередь, может привести к невыносимым финансовым или человеческим потерям, особенно в случае приложений микроэкономики, важных для миссии или безопасности, таких как рынок электроэнергии.
Системы компьютерной алгебры (CAS), такие как Maxima [17] и Mathematica [18], также используются для исследования общих математических свойств функций-кандидатов для моделирования и анализа концепций микроэкономики [19].]. Эти методы основаны на символьных манипуляциях и, таким образом, включают в себя большие и непроверенные программы на языке программирования. Следовательно, анализ, выполненный с использованием CAS, также не может быть гарантированно точен на 100% [20]. Более того, упомянутые выше компьютерные методы позволяют проверять поведение или свойства данной функции только на заданных пользователем интервалах домена и, следовательно, не могут гарантировать исчерпывающую проверку на полном домене данной функции. Например, простая кубическая полиномиальная функция может вести себя как выпуклая или вогнутая функция в зависимости от указанной области. Вышеупомянутые недостатки традиционных методов могут привести к неточным результатам анализа, что, в свою очередь, может привести к невыносимым финансовым или человеческим потерям, особенно в случае приложений микроэкономики, важных для миссии или безопасности, таких как рынок электроэнергии. Чтобы преодолеть эти ограничения, мы предлагаем использовать доказательство теорем для формального анализа систем, опираясь на фундаментальные концепции микроэкономики.
Чтобы преодолеть эти ограничения, мы предлагаем использовать доказательство теорем для формального анализа систем, опираясь на фундаментальные концепции микроэкономики.
Формальные методы — это компьютерные методы для формального определения, проверки и анализа аппаратных и программных систем [21]. Эти методы используют логику для выражения модели системы на компьютерном языке, чтобы формально проверять и подтверждать свойства системы на основе дедуктивных рассуждений. Использование математической логики в этом процессе приводит к обоснованности и строгости задания и проверки свойств данной модели системы.
Формальные методы в первую очередь можно отнести к методам проверки моделей и доказательства теорем. Проверка модели позволяет моделировать поведение системы как системы с переходом состояний, а свойства системы выражаются во временной логике [22]. Однако этот метод нельзя использовать для выражения непрерывных моделей из-за его природы, основанной на состояниях. Кроме того, он склонен к проблеме взрыва пространства состояний для чрезвычайно больших систем пространства состояний. Поэтому проверку модели нельзя использовать для проверки свойств функций стоимости и полезности из-за их непрерывного характера. С другой стороны, доказательство теорем использует логику для моделирования системы и ее свойств, а взаимосвязь проверяется либо автоматически, либо интерактивно на основе разрешимости лежащей в основе логики. Однако автоматическое доказательство теорем нельзя использовать для моделирования и проверки непрерывного поведения функций стоимости и полезности, так как эти детали не могут быть охвачены разрешимой пропозициональной или полуразрешимой логикой первого порядка, в то время как интерактивное доказательство теорем [23] сильно использует выразительная логика высшего порядка для моделирования, анализа и проверки данной системы и, следовательно, способна анализировать непрерывные аспекты, относящиеся к функциям, используемым в математическом поведенческом моделировании в микроэкономике. Поэтому мы предлагаем использовать интерактивное доказательство теорем для формализации поведенческого моделирования в микроэкономике.
Поэтому проверку модели нельзя использовать для проверки свойств функций стоимости и полезности из-за их непрерывного характера. С другой стороны, доказательство теорем использует логику для моделирования системы и ее свойств, а взаимосвязь проверяется либо автоматически, либо интерактивно на основе разрешимости лежащей в основе логики. Однако автоматическое доказательство теорем нельзя использовать для моделирования и проверки непрерывного поведения функций стоимости и полезности, так как эти детали не могут быть охвачены разрешимой пропозициональной или полуразрешимой логикой первого порядка, в то время как интерактивное доказательство теорем [23] сильно использует выразительная логика высшего порядка для моделирования, анализа и проверки данной системы и, следовательно, способна анализировать непрерывные аспекты, относящиеся к функциям, используемым в математическом поведенческом моделировании в микроэкономике. Поэтому мы предлагаем использовать интерактивное доказательство теорем для формализации поведенческого моделирования в микроэкономике.
Методы формальных методов получили широкое распространение для формального анализа и проверки в энергетическом секторе [24]. Марковские модели компонентов интеллектуальных сетей наряду с резервной защитой предложены для оценки надежности с помощью средства проверки моделей PRISM [25]. В [26] компоненты интеллектуальной сети формально определены с использованием формального языка спецификации Z. Формальная проверка приложений интеллектуальных сетей на основе распределенного интеллекта была проведена с использованием средства проверки модели Symbolic Model Verifier (SMV) [27]. При доказательстве теорем стратегия деградации формализуется как проблема выполнимости по модулю теорий (SMT) и анализируется с помощью Z3 SMT-решателя [28]. Сети Петри также использовались для формального анализа надежности [29].], снижение затрат [30], обнаружение отказов [31], производительность [32,33] и возможные нарушения безопасности [34] в интеллектуальных сетях. Насколько нам известно, концепции микроэкономики никогда не были формализованы с помощью доказательства теорем, которые необходимы для формального анализа экономики рынков электроэнергии.
В микроэкономических исследованиях дифференциальная и выпуклая теории являются центральными математическими концепциями, которые используются для моделирования поведения. Многие интерактивные средства доказательства теорем, такие как HOL-Light [35], HOL4 [36] и Isabelle [37], поддерживают дифференциальный анализ; однако, помимо многомерной дифференциальной теории, HOL-Light обеспечивает обширную поддержку выпуклого анализа. В дополнение к выпуклой теории средство доказательства теорем HOL-Light наделено корневым анализом для многочленов до четвертого порядка [38], что является главным требованием для проведения формального анализа условия первого порядка на основе полиномиального типа математических функций. Поэтому в этой статье мы используем средство доказательства теорем HOL-Light для формализации математического моделирования поведения и проверки свойств этих моделей.
Основной целью данной статьи является разработка логической основы для поведенческого моделирования в микроэкономике.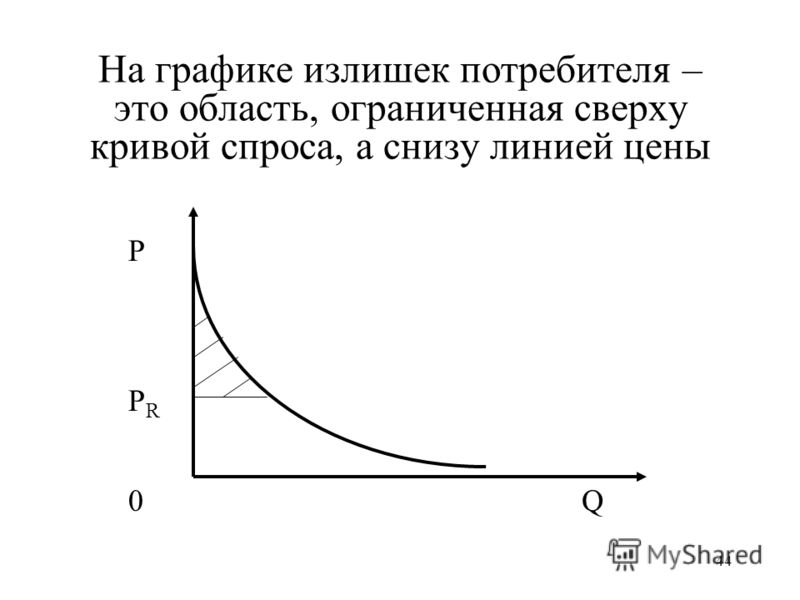 Логическая структура позволяет формально определить и обосновать модели стоимости, полезности и условий первого порядка в рамках надежного ядра средства доказательства теорем HOL-Light. Формальный анализ этих моделей в логике высшего порядка приводит к заверенным и механизированным формальным доказательствам данных моделей. В качестве примера мы предлагаем формальное моделирование и анализ поведенческого моделирования на рынке электроэнергии на основе полиномиальных функций до четвертого порядка. Формально проверенные результаты для поведенческого моделирования рынка электроэнергии обеспечивают необходимые условия для функций для точного моделирования стоимости, полезности и условий первого порядка. Наконец, мы используем это поведенческое моделирование для формальной проверки применения моделей затрат, полезности и максимизации прибыли в задачах экономической диспетчеризации и динамического ценообразования на рынке электроэнергии.
Логическая структура позволяет формально определить и обосновать модели стоимости, полезности и условий первого порядка в рамках надежного ядра средства доказательства теорем HOL-Light. Формальный анализ этих моделей в логике высшего порядка приводит к заверенным и механизированным формальным доказательствам данных моделей. В качестве примера мы предлагаем формальное моделирование и анализ поведенческого моделирования на рынке электроэнергии на основе полиномиальных функций до четвертого порядка. Формально проверенные результаты для поведенческого моделирования рынка электроэнергии обеспечивают необходимые условия для функций для точного моделирования стоимости, полезности и условий первого порядка. Наконец, мы используем это поведенческое моделирование для формальной проверки применения моделей затрат, полезности и максимизации прибыли в задачах экономической диспетчеризации и динамического ценообразования на рынке электроэнергии.
Остальная часть статьи организована следующим образом: Раздел 2 описывает некоторые предварительные сведения, относящиеся к математическому моделированию в микроэкономике, средству доказательства теорем HOL-Light и соответствующей формализации, которые необходимы для понимания остальной части статьи. В Разделе 3 представлена предлагаемая методология, и на ее основе в Разделе 4 представлена формализация теста производной второго порядка для строгой выпуклости или вогнутости, стоимости, полезности и моделей условий первого порядка в средстве доказательства теорем логики более высокого порядка. В разделе 5 используется базовая логическая структура для формального определения и проверки математического моделирования поведения в программах DR для функций моделирования полиномиального типа. Наконец, Раздел 6 завершает статью.
В Разделе 3 представлена предлагаемая методология, и на ее основе в Разделе 4 представлена формализация теста производной второго порядка для строгой выпуклости или вогнутости, стоимости, полезности и моделей условий первого порядка в средстве доказательства теорем логики более высокого порядка. В разделе 5 используется базовая логическая структура для формального определения и проверки математического моделирования поведения в программах DR для функций моделирования полиномиального типа. Наконец, Раздел 6 завершает статью.
2. Математическое моделирование в микроэкономике
Как правило, любая непрерывная, дифференцируемая, неубывающая, вогнутая или строго вогнутая функция может быть использована для моделирования функции полезности, т. е. удовлетворения или счастья потребителя от потребления товаров или услуг. Непрерывность и дифференцируемость гарантируют, что потребительские предпочтения в отношении потребления товаров и услуг никогда не исчезнут внезапно. Свойство неубывания гарантирует, что предпочтения потребителя рациональны, тогда как рациональность дополнительно накладывает такие условия, как полнота и транзитивность. Предположение о рациональности гарантирует, что потребитель всегда может предпочесть каждый товар или услугу и может ранжировать свои предпочтения товаров или услуг. С другой стороны, вогнутость или строгая вогнутость обусловлена законом убывающей предельной полезности, который гласит, что каждая дополнительная единица потребления приводит к уменьшению удовлетворения или счастья для потребителя.
Свойство неубывания гарантирует, что предпочтения потребителя рациональны, тогда как рациональность дополнительно накладывает такие условия, как полнота и транзитивность. Предположение о рациональности гарантирует, что потребитель всегда может предпочесть каждый товар или услугу и может ранжировать свои предпочтения товаров или услуг. С другой стороны, вогнутость или строгая вогнутость обусловлена законом убывающей предельной полезности, который гласит, что каждая дополнительная единица потребления приводит к уменьшению удовлетворения или счастья для потребителя.
Точно так же непрерывная, дифференцируемая, возрастающая и выпуклая или строго выпуклая функция может использоваться для моделирования функции затрат, т. е. общих затрат, связанных с производством единицы товаров или услуг. Теория продукта моделирует производство товаров или услуг с использованием набора продуктов, который содержит все возможные возможные планы производственного процесса. Для моделирования данного производственного процесса предполагается, что набор продуктов удовлетворяет определенным свойствам, например, непустоте, выпуклости, неубывающей отдаче от масштаба и т. д. Эти допущения в основном касаются входных и выходных данных возможного производственного процесса. Следовательно, предположения о взаимосвязи между входами и выходами переводятся в вышеупомянутые математические свойства функции затрат. Например, свойства монотонности и выпуклости основаны на предположениях выпуклой технологии и обеспечивают неубывающую предельную отдачу при производстве товаров или услуг, тогда как непрерывность и дифференцируемость обеспечивают существование решения задачи минимизации затрат и также позволяют выражать понятия средних и предельных затрат с помощью функции общих затрат.
д. Эти допущения в основном касаются входных и выходных данных возможного производственного процесса. Следовательно, предположения о взаимосвязи между входами и выходами переводятся в вышеупомянутые математические свойства функции затрат. Например, свойства монотонности и выпуклости основаны на предположениях выпуклой технологии и обеспечивают неубывающую предельную отдачу при производстве товаров или услуг, тогда как непрерывность и дифференцируемость обеспечивают существование решения задачи минимизации затрат и также позволяют выражать понятия средних и предельных затрат с помощью функции общих затрат.
Микроэкономическое моделирование в основном основано на математических теориях непрерывности, дифференциации и выпуклости. В частности, тесты производных, включающие производные первого и второго порядка, имеют основополагающее значение для оценки монотонности и выпуклости или вогнутости данной функции [39]. Производная первого порядка любой данной функции используется для исследования возрастания или убывания данной функции, т. Е. Монотонности. Кроме того, производные функций первого порядка также используются для нахождения стационарных или критических точек, т. Е.
Е. Монотонности. Кроме того, производные функций первого порядка также используются для нахождения стационарных или критических точек, т. Е.
Уравнение (1) также известно как условие первого порядка и используется для анализа задачи максимизации прибыли в микроэкономике [1], тогда как производная второго порядка используется для проверки выпуклости или вогнутости, которые наиболее желаемые свойства функций, чтобы претендовать на моделирование стоимости и полезности. Для выпуклой функции критерий производной второго порядка неотрицательный, т. е.
Напротив, производная второго порядка для вогнутой функции отрицательна. Строго-выпуклые и вогнутые функции имеют положительные и отрицательные производные соответственно, но соответствующие обратные соотношения неверны. Производные критерии строгой выпуклости и вогнутости формально формулируются как импликации, т. е.
Таким образом, тесты производных играют жизненно важную роль в определении математических свойств моделирующих функций в микроэкономике.
3. Основополагающая формализация микроэкономических моделей
В этом разделе представлено краткое введение в средство доказательства теорем HOL-Light и его формализация реальных теорий анализа выпуклых и полиномиальных корней, чтобы облегчить понимание остальной части статьи.
3.1. HOL-Light теорема Prover
HOL-Light [35] является интерактивным средством доказательства теорем, которое позволяет его пользователям разрабатывать новые механизированные теории, доказательства и правила вывода с поддержкой многих автоматизированных инструментов и предварительно доказанных математических теорий, таких как арифметические , множества и реальных теорий. Он широко используется для некоторых важных приложений проверки в промышленных масштабах [40,41].
Вариант строго типизированного языка функционального программирования, т. е. Objective CAML (OCaml), используется для реализации логики высшего порядка в средстве доказательства теорем HOL-Light. HOL-Light обеспечивает безопасную и надежную платформу для формальной проверки и спецификации систем. Надежное доказательство теорем обеспечивается небольшим ядром, состоящим всего из 1500 строк, включая 10 примитивных правил вывода, таких как modus ponens и рефлексивность, тогда как достоверность устанавливается за счет сходимости всех механизированных доказательств к этим правилам вывода. HOL-Light поддерживает стратегии обратного и прямого доказательства. В стратегии обратного доказательства теорема формально проверяется с использованием правил вывода, тогда как в стратегии прямого доказательства данная теорема разбивается на подцели с использованием тактики HOL-Light. Тактика — это специальная функция машинного обучения, используемая для разделения основной цели на подцели.
HOL-Light обеспечивает безопасную и надежную платформу для формальной проверки и спецификации систем. Надежное доказательство теорем обеспечивается небольшим ядром, состоящим всего из 1500 строк, включая 10 примитивных правил вывода, таких как modus ponens и рефлексивность, тогда как достоверность устанавливается за счет сходимости всех механизированных доказательств к этим правилам вывода. HOL-Light поддерживает стратегии обратного и прямого доказательства. В стратегии обратного доказательства теорема формально проверяется с использованием правил вывода, тогда как в стратегии прямого доказательства данная теорема разбивается на подцели с использованием тактики HOL-Light. Тактика — это специальная функция машинного обучения, используемая для разделения основной цели на подцели.
Мы использовали средство доказательства теорем HOL-Light для предлагаемой работы, так как оно снабжено библиотекой теории выпуклых веществ и полиномиального корневого анализа для облегчения формализации математического моделирования программ DR. В таблице 1 представлены некоторые из часто используемых функций и символов HOL-Light в этом документе, чтобы облегчить понимание формализации и проверки.
В таблице 1 представлены некоторые из часто используемых функций и символов HOL-Light в этом документе, чтобы облегчить понимание формализации и проверки.
3.2. Теория реального выпуклого анализа
Теория многомерного действительного анализа HOL-Light поддерживает выпуклый анализ для функций с действительным знаком. Эта теория в сочетании с многомерными дифференциальными и интегральными теориями обеспечивает поддержку выпуклого анализа вещественных функций. В частности, теория может быть использована для проведения теста производной второго порядка для определения выпуклости заданной функции, которая, в свою очередь, используется для формализации и проверки функции полезности в этой статье.
Вещественная выпуклая функция определяется в логике высшего порядка как:
В определении 1 real_convex_on — это функция логики высшего порядка, которая принимает вещественную функцию, f:real→real, определенную на интервале s:real→bool, тогда как s — теоретико-множественное определение вещественного интервала который представляет все подинтервалы, возможные для данного реального интервала. Функция выпукла, если для любых двух точек x и y в пределах действительного интервала s значение функции f ( u ∗ x + u ∗ y) лежит ниже отрезка, определяемого значениями функции в точках f(x) и ф(у). Переменные u и v с вещественным типом данных вместе обеспечивают все возможные линии для графика функции между f(x) и f(y).
Функция выпукла, если для любых двух точек x и y в пределах действительного интервала s значение функции f ( u ∗ x + u ∗ y) лежит ниже отрезка, определяемого значениями функции в точках f(x) и ф(у). Переменные u и v с вещественным типом данных вместе обеспечивают все возможные линии для графика функции между f(x) и f(y).
Критерий производной второго порядка широко используется для аналитической проверки выпуклости или вогнутости заданной функции. Критерий второго порядка выпуклости функции, т. е. уравнение (2), был проверен в многомерной теории действительного анализа как:
, и его производные первого и второго порядка, соответственно, определенные на произвольном интервале s. Предположение A1 исключает все действительные подинтервалы данного интервала с единственным элементом, удовлетворяющим дифференцируемости данной функции с учетом открытых интервалов. Предположения A2 и A3 гарантируют, что производные первого и второго порядка данной функции существуют в заданном интервале s, тогда как has_vector_derivative — это определение действительной производной в HOL-Light в реляционной форме. Наконец, теорема заключает об эквивалентности выпуклости данной функции и ее положительной производной второго порядка, т. е. 0 ≤ f″.
Наконец, теорема заключает об эквивалентности выпуклости данной функции и ее положительной производной второго порядка, т. е. 0 ≤ f″.
В этой статье определение 1 и теорема 1 используются для формального моделирования и обоснования свойств выпуклости и вогнутости математических функций в микроэкономике.
3.3. Теория анализа корней
Мы уже разработали формальную поддержку рассуждений для формального анализа корней для многочленов до четвертого порядка [38]. Этот формальный анализ позволяет находить нули полиномиальных функций и, кроме того, дает исчерпывающий набор предположений для стабильных корней полиномов.
Корни многочлена второго порядка формально проверяются как:
В приведенной выше теореме переменные a, b и c представляют действительные коэффициенты, тогда как x является комплексной переменной. Успенская A1 гарантирует, что порядок полинома равен 2, так как его можно уменьшить, если старший коэффициент равен нулю. Заключение теоремы формально проверяет два корня квадратного многочлена, тогда как Cx является логической функцией высшего порядка, которая отображает действительное число в эквивалентное комплексное число.
Заключение теоремы формально проверяет два корня квадратного многочлена, тогда как Cx является логической функцией высшего порядка, которая отображает действительное число в эквивалентное комплексное число.
Полиномы более высокого порядка формально проверяются путем разложения их на линейные и квадратичные множители и последующего использования приведенной выше теоремы о факторизованных полиномах для проверки их корней. Факторизация полинома кубической и четвертой степени проверяется как:
В приведенной выше теореме a, b1, c1 и r — действительные коэффициенты, соответствующие линейному и квадратичному множителям кубического многочлена. Предположения A1 – A3 связывают коэффициенты кубического многочлена с его факторизованными многочленами, тогда как x является комплексной переменной. Вывод формально проверяет факторизацию кубического многочлена для заданных коэффициентов.
В приведенной выше теореме a1, b1, c1, a2, b2 и c2 — действительные коэффициенты, соответствующие двум квадратичным множителям многочлена четвертой степени. На основе предположений A1 – A5 , Теорема 4 проверяет факторизацию данного многочлена четвертой степени.
На основе предположений A1 – A5 , Теорема 4 проверяет факторизацию данного многочлена четвертой степени.
Корни многочленов кубической и четвертой степени формально проверяются как: многочлены и их множители. Теорема дает формально проверенные результаты для трех корней кубического многочлена. Точно так же корни многочлена четвертого порядка формально проверяются как:
В этой статье теоремы 2–6 используются для формального анализа производных первого и второго порядка формальных моделей стоимости, полезности и условия первого порядка.
Определение 1 и теоремы 1–6 обеспечивают поддержку проверки свойств моделирования затрат и полезности в средстве доказательства теорем HOL-Light. Определение 1 позволяет формально проверить выпуклость или вогнутость заданной функции, тогда как теоремы 1–6 облегчают проведение формальных алгебраических манипуляций при проверке максимумов, минимумов или точек перегиба данной функции с помощью критериев производных, т. е. уравнений (1)–( 3), в доказательстве теорем логики высшего порядка. Однако структура не поддерживает формальный анализ строгой выпуклости или вогнутости, представленный в разделе 5.
е. уравнений (1)–( 3), в доказательстве теорем логики высшего порядка. Однако структура не поддерживает формальный анализ строгой выпуклости или вогнутости, представленный в разделе 5.
4. Предлагаемая методология
В этом разделе мы представляем основные этапы предлагаемой методологии, показанной на рисунке 1, для проведения формального моделирования и анализа затрат, функций полезности для потребителей или фирм и условия первого порядка для прибыли. проблемы максимизации.
В качестве первого шага мы формально моделируем реальную строгую выпуклую или вогнутую функцию в логике высшего порядка. Затем мы формально проводим тест производной второго порядка, чтобы формально определить строгую выпуклость или вогнутость действительной функции. Результаты формально проверены с использованием формальной модели строго выпуклой функции, дифференциальной, выпуклой и вещественной теории анализа HOL-Light.
На втором этапе вышеупомянутая формализация используется для формального моделирования функций стоимости и полезности в логике высшего порядка.
 Мы также формально моделируем условие первого порядка для задач максимизации прибыли, используя дифференциальную теорию HOL-Light. Эти формализации позволяют нам формально рассуждать и проверять свойства заданных функций в рамках звукового ядра средства доказательства теорем HOL-Light.
Мы также формально моделируем условие первого порядка для задач максимизации прибыли, используя дифференциальную теорию HOL-Light. Эти формализации позволяют нам формально рассуждать и проверять свойства заданных функций в рамках звукового ядра средства доказательства теорем HOL-Light.Наконец, мы используем формализацию из шагов 1 и 2, чтобы формально проверить моделирование стоимости, полезности и условий первого порядка на основе полиномиальных функций. Мы используем формализацию для формальной проверки поведенческого моделирования, используемого на рынке электроэнергии, для решения экономических задач диспетчеризации электроэнергии и DR.
5. Формализация концепций микроэкономики
В этом разделе мы представляем логическую формализацию теста производной второго порядка на строгую выпуклость или вогнутость вещественной функции. Эти формально проверенные результаты в дальнейшем используются для формального моделирования функций затрат и полезности в микроэкономике. Мы также представляем формальное моделирование условия первого порядка в средстве доказательства теорем HOL-Light.
Мы также представляем формальное моделирование условия первого порядка в средстве доказательства теорем HOL-Light.
Формализация строгой выпуклости и вогнутости
Мы формально определяем реальную строгую выпуклую функцию в HOL-Light как:
В приведенном выше определении f:real→real представляет вещественную функцию, а s:real→bool представляет действительный интервал. Приведенное выше определение отличается от определения 1 строгим неравенством.
Основываясь на определении 2, мы формально проверяем скалярное умножение и сложение двух строго выпуклых функций в HOL-Light, как: заданная функция строго выпукла. В этих условиях умножение не влияет на строгую выпуклость данной функции.
Аналогичным образом мы формально проверяем, что сложение двух строгих выпуклых функций приводит к реальному строго выпуклому поведению, как:
Теперь мы формально проверяем критерий производной второго порядка для реальных строгих функций, т. е. уравнение (3a) , в HOL-Light, как:
е. уравнение (3a) , в HOL-Light, как:
Вышеупомянутая теорема проверяется с использованием теоремы о среднем значении вместе с определением строгой выпуклости. Предположения A2–A3 гарантируют, что функция дважды дифференцируема на заданном интервале, а предположение A4 обеспечивает строго выпуклость функции. Заключение теоремы формально подтверждает, что вторая производная функции положительна.
Мы используем формализацию строгой выпуклости, чтобы формально проверить строгую вогнутость любой заданной функции. Это возможно благодаря математической связи между двумя понятиями, т. е. отрицание строго выпуклой функции строго вогнуто. Критерий производной второго порядка для строгой вогнутости, т. е. уравнение (3b), проверяется в HOL-Light, как:
Теорема 8 формально проверяется с помощью определения строгой выпуклости и производной второго порядка в HOL-Light. В предположении A4 мы используем математическую связь между строго выпуклой и строго вогнутой функциями, т. е. отрицание строгой выпуклой функции является строго вогнутой функцией. Выводом является формально проверенный результат для производной второго порядка заданной строго вогнутой функции, т. е. производная второго порядка строго вогнутой функции отрицательна. Мы использовали аналогичный подход для проверки вариантов лемм 1 и 2 для строго вогнутых функций в нашей формализации.
е. отрицание строгой выпуклой функции является строго вогнутой функцией. Выводом является формально проверенный результат для производной второго порядка заданной строго вогнутой функции, т. е. производная второго порядка строго вогнутой функции отрицательна. Мы использовали аналогичный подход для проверки вариантов лемм 1 и 2 для строго вогнутых функций в нашей формализации.
Теперь мы формально моделируем математические свойства, т. е. непрерывность, дифференцируемость, монотонность и выпуклость или вогнутость, функций стоимости и полезности в HOL-Light. Функция стоимости моделируется в логике высшего порядка как:
Аналогично, функция полезности моделируется как:
Наконец, мы формально моделируем условие первого порядка, описываемое уравнением (1), в HOL-Light, как:
В определении 7 first_order_cond — это функция логики высшего порядка, которая принимает вещественную функцию f и переменную x, тогда как real_derivative — это логическая функция высшего порядка, представляющая математическую производную данной вещественной функции.
Формализация в этом разделе обеспечивает необходимую логическую основу для формальной проверки моделей стоимости, полезности и условий первого порядка в рамках надежного ядра средства доказательства теорем HOL-Light.
6. Практический пример: формальное моделирование поведения на основе полиномиальных функций
Полиномиальные функции обычно используются в микроэкономических моделях [1,5,42]. Мы проводим формальный анализ моделирования затрат и полезности на основе полиномиального типа функций до четвертого порядка. Кроме того, мы формально проверяем условие первого порядка для функций прибыли, которые основаны на полиномиальном типе функций полезности затрат.
6.1. Полиномиальный тип функций стоимости
Мы формально проверяем квадратичную функцию стоимости как: -сингулярный интервал. Допущение A4 гарантирует, что данная функция удовлетворяет необходимым условиям для моделирования полезности с использованием определения 4. Допущение A5 гарантирует, что функция определена на заданном интервале, тогда как предположение A6–A7 представляют собой условия на область определения данной функции, −b2a < x, и на старший коэффициент, 0 < a, для формальной проверки возрастающих производных первого и второго порядка квадратичной функции в заключении.
Допущение A5 гарантирует, что функция определена на заданном интервале, тогда как предположение A6–A7 представляют собой условия на область определения данной функции, −b2a < x, и на старший коэффициент, 0 < a, для формальной проверки возрастающих производных первого и второго порядка квадратичной функции в заключении.
Затем мы формально проверяем моделирование кубической функции стоимости в средстве доказательства теорем HOL-Light следующим образом:
формально проверить свойства возрастающих производных первого и второго порядка в заключении.
В приведенной выше теореме предположения A6–A9 обеспечивают взаимосвязь между коэффициентами данного полинома четвертой степени и коэффициентами его квадратичного множителя. Предположения A10–11 налагают условия на область определения x данного полинома в терминах коэффициентов линейного и квадратичного множителей данной функции стоимости четвертой степени, чтобы формально проверить возрастающие производные первого и второго порядка в заключении теоремы.
Теоремы 9–11 являются формально проверенными результатами для квадратичной, кубической и четвертой функций стоимости, в основном, на основе определения 4, леммы 1, леммы 2 и теоремы 7, тогда как теоремы 2–6 используются для формального задания области определения заданных многочленов , в котором удовлетворяются желаемые свойства стоимостных моделей.
6.2. Функция полезности
Мы формально проверяем функции полезности, смоделированные с помощью полиномиальных функций до четвертого порядка в логике высшего порядка, как:
В приведенной выше теореме, предположение A5 моделирует необходимые условия для полезного моделирования с помощью определения 5. Допущение A6 гарантирует, что область определения заданного квадратичного многочлена, т. е. переменной x, больше, чем −b2a, чтобы удовлетворить возрастающему свойству полезного моделирования. Допущение A6 гарантирует, что старший коэффициент будет отрицательным, что, в свою очередь, подтверждает вогнутость данного квадратного многочлена. Эти предположения обеспечивают формальную проверку возрастающей производной первого порядка и убывающей производной второго порядка в заключении теоремы.
Эти предположения обеспечивают формальную проверку возрастающей производной первого порядка и убывающей производной второго порядка в заключении теоремы.
Допущения A6 и A7 накладывают условия на действительную переменную x, которая является областью определения кубической функции полезности для положительной производной первого порядка и отрицательной производной второго порядка.
Далее мы формально проверяем функцию полезности четвертой степени в логике высшего порядка следующим образом: Эти условия формально определяют факторизацию многочлена четвертой степени на основе теоремы 3. Предположения 9.1694 A10 и A11 предоставляют допустимые диапазоны области определения x заданной функции для формальной проверки положительной производной первого порядка и отрицательной производной второго порядка в заключении приведенной выше теоремы.
Теоремы 12–14 формально проверяются с помощью теоремы 1 и определения 5. Теорема 1 используется для проверки вогнутости полиномиальных функций полезности, тогда как теоремы факторизации, т. е. теоремы 2–6, используются для формального задания условий на область полиномиального типа функций полезности.
е. теоремы 2–6, используются для формального задания условий на область полиномиального типа функций полезности.
6.3. Условие первого порядка
Наконец, мы представляем формально проверенные результаты для реальных стационарных или критических точек для функций прибыли, построенных с использованием полиномиальных функций. Мы используем определение 7 для моделирования условия первого порядка для функции прибыли, где f(x)=R(x)−C(x) используется для моделирования реальной функции. Мы используем линейную функцию дохода, т. е. R(x) = r ∗ x, в которой r — тариф на электроэнергию за количество потребленной электроэнергии, т. е. x. Для моделирования функции стоимости C(x) мы последовательно рассматриваем квадратичные, кубические и полиномиальные модели четвертого порядка.
В этом отношении функция прибыли, основанная на квадратичной функции затрат или полезности, проверяется как:
В приведенной выше теореме предположение A1 гарантирует, что старший коэффициент квадратичного типа функции затрат или полезности не равен нулю.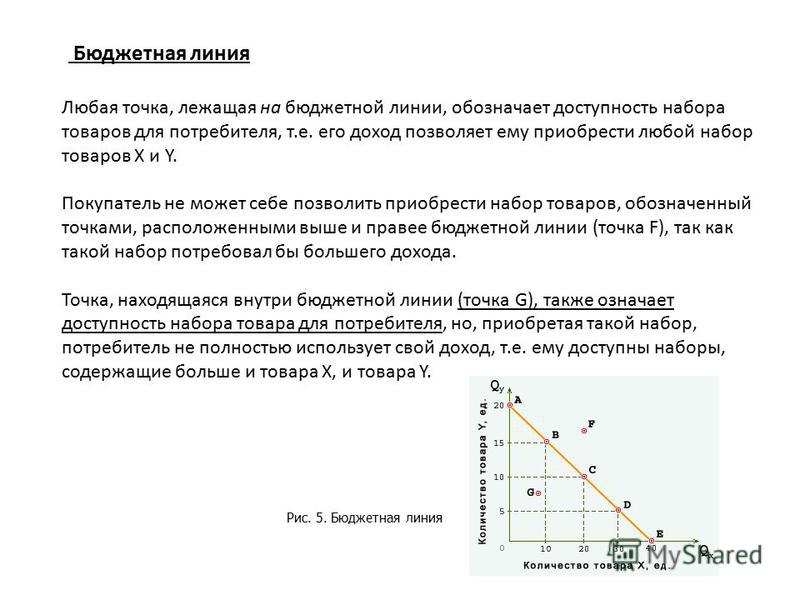 Это предположение позволяет избежать возможности случая пониженного порядка полинома. Допущение A2 определяет критическую точку данной функции прибыли в терминах тарифа на электроэнергию r и коэффициентов данной квадратичной функции затрат.
Это предположение позволяет избежать возможности случая пониженного порядка полинома. Допущение A2 определяет критическую точку данной функции прибыли в терминах тарифа на электроэнергию r и коэффициентов данной квадратичной функции затрат.
Теорема 15 формально проверяется путем взятия производной функции прибыли. Это позволяет формально проверить приведенную выше теорему, используя предположение A2 , которое является критической точкой данной функции.
Точно так же функция прибыли, основанная на кубическом типе затрат или функции полезности, формально проверяется как: критические или стационарные точки.
Наконец, мы формально проверяем условие первого порядка для функции прибыли, когда функция затрат или полезности является полиномом четвертой степени, в логике высшего порядка, как: полинома четвертой степени к соответствующему полиному третьего порядка. Допущения A2–A6 представляют отношения между коэффициентами кубической упорядоченной функции прибыли и ее коэффициентами, т. е. линейными и квадратичными. Успенская A7 дает связь между переменной x и коэффициентами для реальных стационарных точек функции прибыли.
е. линейными и квадратичными. Успенская A7 дает связь между переменной x и коэффициентами для реальных стационарных точек функции прибыли.
Предложенная фундаментальная формализация производных тестов позволила нам формально определить и проверить основанное на микроэкономике поведенческое моделирование объектов интеллектуальной сети в программах аварийного восстановления. Теоремы 9–17 представляют собой универсальные количественные результаты, которые, в отличие от традиционных методов, также содержат точный и исчерпывающий набор допущений для моделирования поведения заданных объектов. Эти результаты дают очень полезную информацию о поведении моделирующей функции по отношению к ее области для удовлетворения желаемых математических свойств. Например, предположения в теоремах 9–14 дают явные условия на область определения обычно используемого полиномиального типа функций стоимости и полезности в программах DR [42,43,44,45,46,47]. Точно так же предположения теорем 15–17 дают априорную информацию о влиянии значений коэффициентов данной функции прибыли на максимально возможную прибыль. В случае реальной функции прибыли предположения теоремы 15–17 облегчают выбор значений коэффициентов функции прибыли для реального максимума данной функции прибыли.
В случае реальной функции прибыли предположения теоремы 15–17 облегчают выбор значений коэффициентов функции прибыли для реального максимума данной функции прибыли.
Предлагаемая формализация является общей и может быть легко использована для формальной проверки и спецификации любой микроэкономической модели, основанной на различных математических функциях, таких как экспоненциальная и логарифмическая. Основные проблемы, с которыми столкнулись при предложенной формализации, заключались в том, чтобы предоставить формально проверенные теоремы, связанные со строгой выпуклостью или вогнутостью, и связанные с ними свойства таких функций, чтобы сделать возможным формализацию концепций микроэкономики. Помимо разработки фундаментальной логической основы, формальная проверка тематического исследования потребовала значительных усилий из-за строгих формальных рассуждений, необходимых для выполнения задачи с использованием доказательства теорем. Соответствующий тестовый сценарий, доступный для загрузки по адресу [48], состоит из 2000 строк кода HOL-Light и требует около 250 человеко-часов разработки.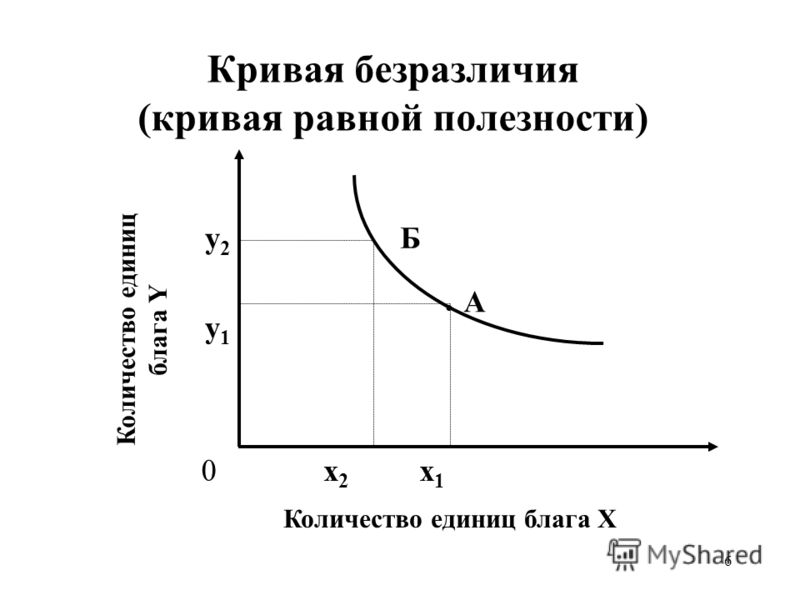
7. Приложения рынка электроэнергии
В этом разделе мы формально верифицируем квадратичные модели стоимости [49] и полезности [44], которые использовались в программах оптимального потока мощности [50] и DR [44] в электроэнергетике. рынок. В оптимальном потоке мощности полиномиальные функции используются для нахождения экономической диспетчеризации, которая обеспечивает снижение стоимости производства электроэнергии, тогда как программы DR используются для изменения поведения спроса потребителей для обеспечения безопасной и надежной работы интеллектуальной сети. В связи с этим используются стимулирующие и основанные на времени программы для изменения режима использования электроэнергии в интеллектуальных сетях.
7.1. Квадратичная полиномиальная функция стоимости для тепловых электростанций
Мы формально проверяем квадратичную полиномиальную функцию стоимости для тепловых электростанций, используя результаты раздела 6. Метауристический алгоритм в [49], называемый алгоритмом ABC, был использован для оценки коэффициентов квадратичный тип функции стоимости для задачи экономической диспетчеризации, который используется в экономике эксплуатации для снижения себестоимости производства электроэнергии. В задаче экономической диспетчеризации распределенные генераторы используются для производства электроэнергии, чтобы снизить общие эксплуатационные расходы и проблемы регулирования на рынке электроэнергии. Математическая форма функции стоимости четвертой степени:
Метауристический алгоритм в [49], называемый алгоритмом ABC, был использован для оценки коэффициентов квадратичный тип функции стоимости для задачи экономической диспетчеризации, который используется в экономике эксплуатации для снижения себестоимости производства электроэнергии. В задаче экономической диспетчеризации распределенные генераторы используются для производства электроэнергии, чтобы снизить общие эксплуатационные расходы и проблемы регулирования на рынке электроэнергии. Математическая форма функции стоимости четвертой степени:
где FCj, PGj, aoj, a1j, a2j и rj представляют функцию затрат на производство электроэнергии, количество выработанной мощности, коэффициенты и погрешность, связанные с j-м генератором. Уравнение (4) используется для оценки параметров трех различных тепловых электростанций с такими видами топлива, как уголь, нефть и газ [49]. Каждая электростанция состоит из пяти энергоблоков мощностью 10, 20, 30, 40 и 50 МВт. Оценка выполняется на фактических данных [51] и представлена в таблице 2.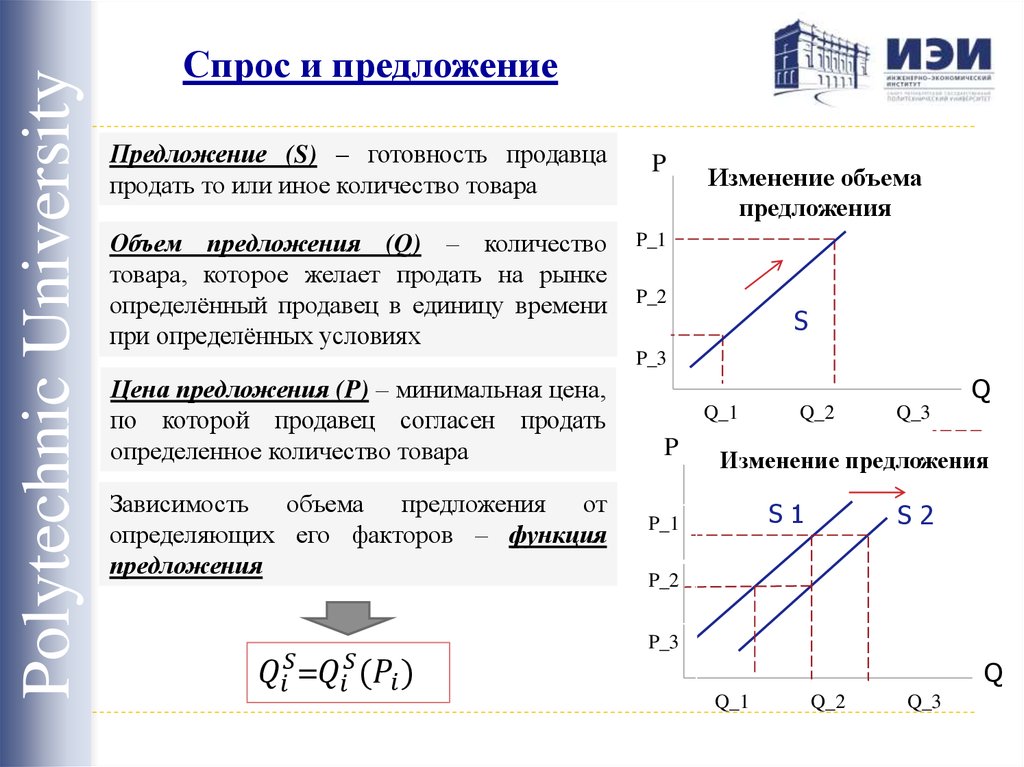
Мы формально проверяем математические свойства функции стоимости в HOL-Light как:
В приведенной выше теореме квадратичная функция стоимости для угольных, нефтяных и газовых электростанций формально проверяется с помощью теоремы 9. Благодаря нашей базовой формализации доказательство теоремы 18 потребовало всего несколько строк кода HOL-Light. Формально проверенные результаты гарантируют, что все математические свойства в определении 4 для моделирования функции стоимости удовлетворяются оцененными квадратичными полиномиальными функциями стоимости.
7.2. Функция Quadratic Utility для интеллектуальных сетей
Мы формально проверяем квадратичную функцию полезности, используя нашу формализацию, предложенную в разделе 6, которая используется в [44] для нахождения оптимальных уровней энергопотребления для пользователей интеллектуальной сети. Алгоритм, предложенный в [44], опирается на ценообразование в режиме реального времени для управления ДР, используя микроэкономическую концепцию максимизации полезности. Алгоритм рассматривает среду интеллектуальной сети, которая оснащена интеллектуальными счетчиками и сетью связи для взаимодействия между поставщиком энергии и конечными пользователями в сети интеллектуальной сети. Квадратичная функция полезности определяется как [44]:
Алгоритм рассматривает среду интеллектуальной сети, которая оснащена интеллектуальными счетчиками и сетью связи для взаимодействия между поставщиком энергии и конечными пользователями в сети интеллектуальной сети. Квадратичная функция полезности определяется как [44]:
Функция U(ω,x) представляет собой функцию полезности для разных пользователей в интеллектуальной энергосистеме, где ω варьируется среди пользователей электроэнергии в сети, чтобы различать пользователей, таких как промышленные или бытовые, а α является предварительно определенным параметром. Полезность для конкретного потребителя есть функция его потребления электроэнергии, т. е. х.
Кроме того, функция полезности также используется для расчета целевой функции благосостояния W(ω,x) отдельного потребителя, как:
где P – цена x(МВт) количества электроэнергии, потребляемой пользователем. Целевая функция благосостояния максимизируется с использованием условия первого порядка,
Мы формально проверяем поведение квадратичной функции полезности, т. е. уравнения (5), и задачи максимизации полезности, т. е. уравнения (6), для ω=4 и α=0,5 для одного потребителя в (0,ωα) интервал, как:
е. уравнения (5), и задачи максимизации полезности, т. е. уравнения (6), для ω=4 и α=0,5 для одного потребителя в (0,ωα) интервал, как:
Вышеупомянутая теорема формально проверяется с помощью теоремы 12. Допущение A1 гарантирует, что спрос на электроэнергию отдельного потребителя находится в пределах допустимых уровней потребления. Кроме того, предположения теоремы 12 также проверяются для проверки заданной функции полезности.
Аналогично, условие первого порядка для цели благосостояния формально проверяется как:
Приведенная выше теорема формально проверяется с помощью теоремы 15. цена электроэнергии, P и максимальный уровень потребления электроэнергии. Опять же, для доказательства теорем 19 и 20 потребовалось всего несколько строк кода HOL-Light, что иллюстрирует полезность и практическую эффективность предложенной формализации фундаментальных теорий. Теорема 19гарантирует, что функция полезности удовлетворяет математическим свойствам определения 6, тогда как теорема 20 дает явные условия максимизации функции благосостояния.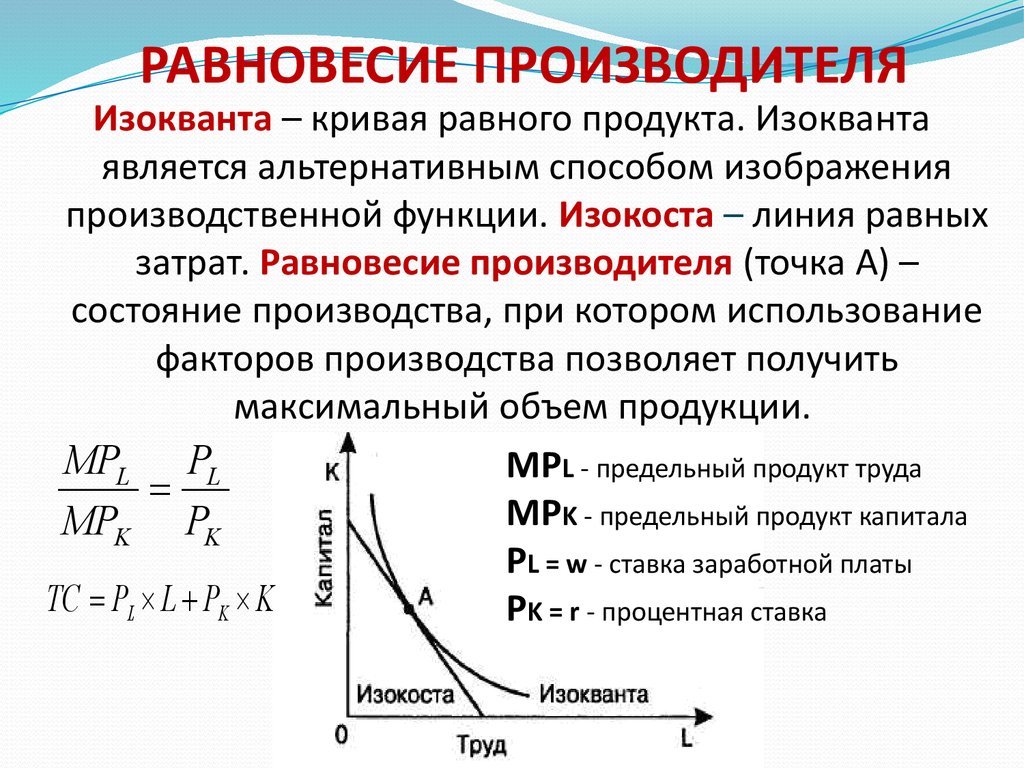
8. Выводы
В этой статье мы представили формальную методологию для проведения формального поведенческого моделирования и анализа концепций микроэкономики. Тесты производных являются основными математическими методами для определения и проверки желаемых свойств, таких как монотонность и выпуклость, функций моделирования в микроэкономике. Для формального моделирования концепций микроэкономики мы формально проверили тесты производных второго порядка на строгую выпуклость или вогнутость и, основываясь на этих результатах, предоставили формальные модели функций затрат и полезности. Кроме того, мы также разработали формальное моделирование условия первого порядка, основанное на производной первого порядка, для формального анализа функций прибыли для задач максимизации прибыли. В качестве примера формализация используется для формального моделирования поведения и анализа моделирования затрат и полезности на основе полиномиальной функции. Наконец, квадратичные функции стоимости и полезности для задачи экономической диспетчеризации и программы DR формально проверяются с использованием предложенной формализации. Отличительными чертами предлагаемой аналитической работы являются ее точные результаты благодаря привлечению надежного доказательства теорем и наличие исчерпывающего набора допущений, необходимых для достоверности результатов.
Отличительными чертами предлагаемой аналитической работы являются ее точные результаты благодаря привлечению надежного доказательства теорем и наличие исчерпывающего набора допущений, необходимых для достоверности результатов.
Предлагаемая формализация может быть легко использована для формального определения и проверки микроэкономических моделей, таких как экспоненциальные и логарифмические функции, для любого базового рыночного агента. Кроме того, формализация основана на признаках производных второго порядка, которые широко используются в выпуклой теории. Таким образом, формализация полезна и для широкого круга приложений выпуклой теории [52,53]. Представленная формализация поддерживает реальный анализ только с одной переменной и, таким образом, может быть расширена до многомерного анализа, который поддерживается средством доказательства теорем HOL-Light. Кроме того, объединение традиционных инструментов анализа, таких как Maxima [17], с средством доказательства теорем, таким как HOL-Light, также является интересным направлением для облегчения формальным неспециалистам проводить высоконадежный и точный микроэкономический анализ экономических рынков, используя предложенная формализация.
Авторские вклады
Концептуализация, F.A. и N.B.; Формальный анализ, А.А. и О.Х.; Методология, А.А. и О.Х.; Письмо — первоначальный вариант, АА; Написание — обзор и редактирование, А.А., О.Х., Ф.А. и Н.Б. Все авторы прочитали и согласны с опубликованной версией рукописи.
Финансирование
Эта работа поддерживается Фондом ИКТ ОАЭ, фонд № 21N206 в Университете ОАЭ, Аль-Айн, Объединенные Арабские Эмираты.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Ссылки
- Мас-Коллелл, А.; Уинстон, доктор медицины; Грин, Дж. Р. Микроэкономическая теория; Издательство Оксфордского университета: Нью-Йорк, штат Нью-Йорк, США, 1995; Том 1. [Google Scholar]
- Уилкинсон, Н.; Клаес, М. Введение в поведенческую экономику, третье издание; Macmillan International Higher Education: London, UK, 2017. [Google Scholar]
- Coleman, JS; Фараро, Т.
 Дж. теория рационального выбора; Sage: New York, NY, USA, 1992. [Google Scholar]
Дж. теория рационального выбора; Sage: New York, NY, USA, 1992. [Google Scholar] - Levin, J.; Милгром, П. Введение в теорию выбора. 2004, Volume 20202. Доступно в Интернете: https://web.stanford.edu/~jdlevin/Econ%20202/Choice%20Theory.pdf (по состоянию на 18 января 2020 г.).
- Хендерсон, Дж. М.; Квандт, Р.Э. Микроэкономическая теория: математический подход; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Gan, D.; Фэн, Д .; Се, Дж. Рынки электроэнергии и экономика энергосистемы; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Hasanpor Divshali, P.; Чой, Б. Дж. Управление рынком электроэнергии с учетом ограничений энергосистемы в интеллектуальных распределительных сетях. Энергии 2016 , 9, 405. [Google Scholar] [CrossRef][Green Version]
- Нафи, Н.С.; Ахмед, К.; Грегори, Массачусетс; Датта, М. Обзор архитектур интеллектуальных сетей, приложений, преимуществ и стандартизации.
 Дж. Нетв. вычисл. заявл. 2016 , 76, 23–36. [Google Scholar] [CrossRef]
Дж. Нетв. вычисл. заявл. 2016 , 76, 23–36. [Google Scholar] [CrossRef] - Сринивасан, С. Властные отношения: ценообразование на основе предельных затрат на электроэнергию и социальная устойчивость проектов по возобновляемым источникам энергии. Технол. Экон. Умные сети поддерживают. Energy 2019 , 4, 13. [Google Scholar] [CrossRef][Green Version]
- Арефин С.С.; Дас, Н. Оптимизированная гибридная ветро-дизельная энергетическая система с анализом осуществимости. Технол. Экон. Умные сети поддерживают. Энергия 2017 , 2, 9. [Google Scholar] [CrossRef][Green Version]
- Сиддики А.Н.; Томас, М.С. Технико-экономическая оценка услуги регулирования от СЭМ в системе интеллектуальных МГ. Технол. Экон. Умные сети поддерживают. Energy 2016 , 1, 15. [Google Scholar] [CrossRef][Green Version]
- Strielkowski, W. Социально-экономические последствия для интеллектуальных сетей будущего.
 Экон. соц. 2017 , 10, 310. [Google Scholar] [CrossRef][Green Version]
Экон. соц. 2017 , 10, 310. [Google Scholar] [CrossRef][Green Version] - Кеттер, В.; Коллинз, Дж.; Блок, Калифорния Экономика умных сетей: руководство по политике посредством конкурентного моделирования; Erasmus Research Institute of Management (ERIM): Роттердам, Нидерланды, 2010 г. [Google Scholar]
- Моретти, М.; Джомо, С.Н.; Азади, Х .; Мэй, К .; Де Вос, К.; Ван Пассел, С.; Виттерс, Н. Систематический обзор воздействия интеллектуальных сетей на окружающую среду и экономику. Продлить. Поддерживать. Energy Rev. 2017 , 68, 888–898. [Google Scholar] [CrossRef]
- Грир, М. Расчеты моделирования стоимости электроэнергии; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Deng, R.; Ян, З .; Чоу, М.Ю.; Чен, Дж. Обзор реагирования на спрос в интеллектуальных сетях: математические модели и подходы. IEEE транс. Инд.информ. 2015 , 11, 570–582. [Google Scholar] [CrossRef] «> Максима. 2019. Доступно в Интернете: http://maxima.sourceforge.net/l (по состоянию на 15 декабря 2019 г.).
- Вольфрам Математика. 2019. Доступно в Интернете: https://www.wolfram.com/mathematica/analysis/content/ComputerAlgebraSystems.html (по состоянию на 15 декабря 2019 г.).
- Wetzstein, ME Микроэкономическая теория, второе издание: концепции и связи; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Stoutemyer, D.R. Преступления и проступки в сфере компьютерной алгебры. Нет. Являюсь. Мат. соц. 1991 , 38, 778–785. [Google Scholar]
- Вудкок, Дж.; Ларсен, П.Г.; Бикарреги, Дж.; Фицджеральд, Дж. Формальные методы: практика и опыт. АКМ вычисл. Surv. (CSUR) 2009 , 41, 19. [Google Scholar] [CrossRef]
- Clarke, E.M.; Грумберг, О .; Лонг, Д.Э. Проверка модели и абстракция. АКМ Транс. Программа. Ланг. Сист. (ТОПЛАС) 1994 , 16, 1512–1542.
 [Google Scholar] [CrossRef]
[Google Scholar] [CrossRef] - Харрисон, Дж.; Урбан, Дж.; Видийк, Ф. История интерактивного доказательства теорем. В вычислительной логике; Северная Голландия: Оксфорд, Великобритания, 2014 г.; Том 9, стр. 135–214. [Google Scholar]
- Хакенберг, Г.; Ирлбек, М .; Куцумпас, В .; Бычков, Д. Применение формальных методов разработки программного обеспечения к интеллектуальным сетям. В материалах Первого международного семинара по проблемам разработки программного обеспечения для интеллектуальных сетей, Цюрих, Швейцария, 3 июня 2012 г .; стр. 50–56. [Google Scholar]
- Махмуд, А.; Хасан, О .; Гиллани, HR; Салим, Ю.; Хасан, С.Р. Формальный анализ надежности систем защиты в интеллектуальных сетях. В материалах симпозиума IEEE Region 10 (TENSYMP) 2016 г., Бали, Индонезия, 9–11 мая 2016 г.; стр. 198–202. [Google Scholar]
- Акрам В.; Ниази, М.А. Формальная структура спецификации для компонентов интеллектуальной сети.
 Комплекс Адапт. Сист. Модель. 2018 , 6, 5. [Google Scholar] [CrossRef]
Комплекс Адапт. Сист. Модель. 2018 , 6, 5. [Google Scholar] [CrossRef] - Патил С.; Жабелова, Г.; Вяткин, В .; Макмиллин, Б. На пути к формальной проверке распределенного интеллекта интеллектуальной сети: случай Freedm. В материалах IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Иокогама, Япония, 9–12 ноября 2015 г.; стр. 003974–003979. [Google Scholar]
- Гупта П.К.; Шетц, Б. Грациозная деградация на основе ограничений в интеллектуальных сетях. В материалах 2-го Международного семинара по разработке программного обеспечения для интеллектуальных киберфизических систем, Остин, Техас, США, 16 мая 2016 г .; стр. 8–14. [Google Scholar]
- Вахеби М.; Я позвонил.; Садегзаде, М .; Атани, Р.Э. Моделирование и анализ надежности в сети с использованием сетей Петри. Междунар. Дж. Вычисл. заявл. Технол. Рез. 2013 , 2, 726–730. [Академия Google] [CrossRef] «> Мхадби, З.; Заири, С .; Геген, К.; Зуари, Б. Проверка подхода к распределенному управлению энергопотреблением для интеллектуальной сети на основе общей модели цветных сетей Петри. J. Технология чистой энергии. 2018 , 6, 20–25. [Google Scholar] [CrossRef]
- Кальдераро, В.; Hadjicostis, CN; Пикколо, А .; Сиано, П. Идентификация сбоев в интеллектуальных сетях на основе моделирования сетей Петри. IEEE транс. Инд. Электрон. 2011 , 58, 4613–4623. [Google Scholar] [CrossRef]
- Zeineb, M.; Садже, З .; Белхассен, З. Общий подход к моделированию цветных сетей Петри для анализа производительности системы интеллектуальных сетей. В материалах 7-го Международного конгресса по возобновляемым источникам энергии (IREC) 2016 г., Хаммамет, Тунис, 22–24 марта 2016 г.; стр. 1–6. [Академия Google]
- Дей, А.; Чаки, Н .; Саньял, С. Моделирование интеллектуальной сети с использованием обобщенной стохастической сети Петри.
 arXiv 2011 , arXiv:1108.4139. [Google Scholar]
arXiv 2011 , arXiv:1108.4139. [Google Scholar] - Чен, Т. М.; Санчес-Аарнутсе, Дж. К.; Буфорд, Дж. Петри, сетевое моделирование киберфизических атак на интеллектуальные сети. IEEE транс. Smart Grid 2011 , 2, 741–749. [Google Scholar] [CrossRef][Зеленая версия]
- HOL-Light Доказательство теорем. 2019. Доступно в Интернете: https://www.cl.cam.ac.uk/~jrh23/hol-light/ (по состоянию на 15 декабря 2019 г.).).
- HOL Доказательство теорем. 2019. Доступно в Интернете: https://hol-theorem-prover.org/ (по состоянию на 15 декабря 2019 г.).
- Isabelle/HOL Доказательство теорем. 2019. Доступно в Интернете: https://isabelle.in.tum.de/ (по состоянию на 15 декабря 2019 г.).
- Ахмед А.; Хасан, О .; Аввад, Ф. Формальный анализ устойчивости систем управления. На международном семинаре по формальным методам для систем, критически важных с точки зрения безопасности; Springer: Гейдельберг, Германия, 2018 г.
 ; стр. 3–17. [Google Scholar]
; стр. 3–17. [Google Scholar] - Zill, D.; Райт, WS; Каллен, М. Р. Передовая инженерная математика; Jones & Bartlett Learning: Burlington, VT, USA, 2011. [Google Scholar]
- Хейлз, Т.; Адамс, М.; Бауэр, Г.; Данг, Т.Д.; Харрисон, Дж.; Ле Труонг, Х .; Калишик, К.; Магрон, В.; Маклафлин, С.; Нгуен, Т.Т.; и другие. Формальное доказательство гипотезы Кеплера; Форум математики, Пи; Издательство Кембриджского университета: Кембридж, Великобритания, 2017 г.; Том 5. [Google Scholar]
- Харрисон, Дж. Верификация с плавающей запятой в HOL light: экспоненциальная функция. В материалах Международной конференции по алгебраической методологии и программным технологиям, Сидней, Новый Южный Уэльс, Австралия, 13–17 декабря 1997; Springer: Берлин/Гейдельберг, Германия, 1997 г.; стр. 246–260. [Google Scholar]
- Дебертин Д.Л. Прикладная микроэкономика: потребление, производство и рынки; Независимая издательская платформа CreateSpace: Скоттс-Вэлли, Калифорния, США, 2012 г.
 [Google Scholar]
[Google Scholar] - Bessembinder, H.; Леммон, М.Л. Равновесное ценообразование и оптимальное хеджирование на форвардных рынках электроэнергии. Дж. Финанс. 2002 , 57, 1347–1382. [Google Scholar] [CrossRef]
- Самади П.; Мохсениан-Рад, А.Х.; Шобер, Р.; Вонг, В.В.; Яцкевич, Дж. Алгоритм оптимального ценообразования в реальном времени, основанный на максимизации полезности для интеллектуальной сети. В материалах Первой международной конференции IEEE 2010 г. по интеллектуальным сетям связи, Гейтерсбург, Мэриленд, США, 4–6 октября 2010 г .; стр. 415–420. [Академия Google]
- Ван, К.; Лю, Х .; Ду, Дж.; Конг Ф. Умная зарядка для электромобилей: обзор с точки зрения алгоритмов. Сообщество IEEE. Surv. Репетитор. 2016 , 18, 15:00–15:17. [Google Scholar] [CrossRef][Green Version]
- Волак, Ф.А. Идентификация и оценка функций затрат с использованием данных наблюдаемых ставок: приложение к рынкам электроэнергии; Национальное бюро экономических исследований: Кембридж, Массачусетс, США, 2001.
 [Google Scholar]
[Google Scholar] - Fahrioglu, M.; Альварадо, Ф.Л. Использование служебной информации для калибровки моделей поведения управления спросом клиентов. IEEE транс. Система питания 2001 , 16, 317–322. [Google Scholar] [CrossRef][Green Version]
- Ахмед, А. Формальное поведенческое моделирование в моделях микроэкономики. Доступно в Интернете: http://save.seecs.nust.edu.pk/projects/fcumm/ (по состоянию на 16 декабря 2019 г.).
- Sönmez, Y. Оценка параметров кривой стоимости топлива для тепловых электростанций с использованием алгоритма ABC. Турок. Дж. Электр. англ. вычисл. науч. 2013 , 21, 1827–1841 гг. [Google Scholar] [CrossRef]
- Цю, З.; Деконинк, Г.; Белманс, Р. Обзор литературы по проблемам оптимального потока мощности в контексте рынка электроэнергии. В материалах 2009 г.Конференция и выставка IEEE/PES Power Systems, Сиэтл, Вашингтон, США, 15–18 марта 2009 г.; стр.
 1–6. [Google Scholar]
1–6. [Google Scholar] - Эль-Хавари, М.; Мансур, С. Оценка эффективности алгоритмов оценки параметров для экономичной эксплуатации энергосистем. IEEE транс. Энергетический аппар. Сист. 1982 , 574–582. [Google Scholar] [CrossRef]
- Лю, X.; Лу, П.; Пан, Б. Обзор выпуклой оптимизации для аэрокосмических приложений. Астродинамика 2017 , 1, 23–40. [Академия Google] [CrossRef]
- Никулеску, К.; Перссон, Л.Э. Выпуклые функции и их приложения; Springer: Heidelberg, Germany, 2006. [Google Scholar]
Рис. 1. Предлагаемая методология для микроэкономических моделей в HOL-Light.
Рис. 1. Предлагаемая методология для микроэкономических моделей в HOL-Light.
Таблица 1. Символы и функции HOL-Light.
Таблица 1. Символы и функции HOL-Light.
| HOL Symbol | Standard Symbol | Meaning | |
|---|---|---|---|
| ∧ | and | Logical and | |
| ∨ | or | Logical or | |
| ¬ | not | Logical negation | |
| ∀ | для всех | Квантификатор всеобщности | |
| ∃ | существует0233 | λx. t t | Function that maps x to t(x) |
| real | All Real numbers | Real data type | |
| xpown | xn | Power with integer exponent |
Таблица 2. Расчетные коэффициенты кубической функции стоимости с использованием алгоритма ABC.
Таблица 2. Расчетные коэффициенты кубической функции стоимости с использованием алгоритма ABC.
| Coefficients | a0 | a1 | a2 |
|---|---|---|---|
| Estimated values (coal) | 0. 0414 0414 | 7.5874 | 96.6046 |
| Estimated values (oil) | 0.0442 | 7.8779 | 101.5360 |
| Расчетные значения (газ) | 0,0439 | 8,0991 | 101,8179 |
© 2020 авторами. Лицензиат MDPI, Базель, Швейцария. Эта статья находится в открытом доступе и распространяется на условиях лицензии Creative Commons Attribution (CC BY) (http://creativecommons.org/licenses/by/4.0/).
Модуль 2: Полезность — средний уровень микроэкономики
Перейти к содержимому
Джоэл Брюно и Клинтон Махони
- Описать функцию полезности
- Идентифицируйте функции полезности на основе типичных предпочтений, которые они представляют
- Объясните, как вывести кривую безразличия из функции полезности
- Получение предельной полезности и MRS для типичных функций полезности
P Политика Q UESTION : Hybrid Покупка автомобиля Налоговый кредит — это правительственный Лучший выбор , чтобы сократить потребление топлива и выбросы углерода ?
Жители США и правительство обеспокоены зависимостью от импортируемой иностранной нефти и выбросами углерода в атмосферу.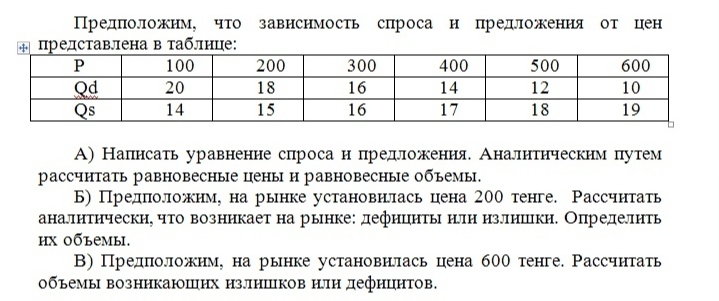 В 2005 году Конгресс принял закон о предоставлении потребителям налоговых льгот на покупку электрических и гибридных автомобилей.
В 2005 году Конгресс принял закон о предоставлении потребителям налоговых льгот на покупку электрических и гибридных автомобилей.
Этот налоговый кредит может показаться хорошим политическим выбором, но он дорогостоящий, поскольку напрямую снижает сумму доходов, собираемых правительством США. Существуют ли более эффективные подходы к снижению зависимости от ископаемого топлива и выбросов углерода? Как решить, какая политика лучше? Чтобы ответить на этот вопрос, политикам необходимо с некоторой точностью предсказать, как потребители отреагируют на эту налоговую политику, прежде чем эти политики потратят миллионы федеральных долларов.
Мы можем применить концепцию утилита на этот вопрос политики. В этом модуле мы будем изучать полезность и функции полезности. Тогда мы сможем использовать соответствующую функцию полезности для получения кривых безразличия, описывающих наш политический вопрос.
Изучение вопроса политики
Предположим, что налоговая льгота для субсидирования покупки гибридных автомобилей чрезвычайно успешна и удваивает средний расход топлива всех автомобилей на дорогах США — результат, который явно нереалистичен, но полезен для наших последующих обсуждений. Как вы думаете, что произойдет с расходом топлива всех автомобилистов США? Следует ли правительству ожидать, что потребление топлива и выбросы углекислого газа от автомобилей снизятся вдвое в ответ? Почему или почему нет?
Как вы думаете, что произойдет с расходом топлива всех автомобилистов США? Следует ли правительству ожидать, что потребление топлива и выбросы углекислого газа от автомобилей снизятся вдвое в ответ? Почему или почему нет?
2. 1 U tility Функции
LO 2.1: Опишите вспомогательную функцию.
2.2 Вспомогательные функции и типичные предпочтения
LO 2.2: Идентифицируйте служебные функции на основе типичных предпочтений, которые они представляют.
2 .3 Относящиеся U Тилии F соединения и I80008
C urve M aps
LO 2.3: Объясните, как вывести кривую безразличия из функции полезности.
2.4 F ind ing M arginal U tility and M arginal R ate of S ubstitution
LO 2. 4: Получить предельную полезность и MRS для типичных функций полезности.
4: Получить предельную полезность и MRS для типичных функций полезности.
2. 1 Полезность F функция s
LO1: Опишите функцию полезности.
Наши предпочтения позволяют нам сравнивать различные потребительские пакеты и выбирать предпочтительные пакеты. Мы могли бы, например, определить порядок ранжирования всего набора пакетов на основе наших предпочтений. — это математическая функция, которая ранжирует наборы потребительских товаров, присваивая каждому номер, где большие числа указывают на предпочтительные наборы. Вспомогательные функции обладают свойствами, которые мы определили в Модуле 1 в отношении предпочтений. То есть: они могут упорядочивать пакеты, они полны и транзитивны, больше предпочтительнее меньшего и, в соответствующих случаях, смешанные пакеты лучше.
Число, которое функция полезности присваивает определенному набору, известно как , т. е. удовлетворение, которое потребитель получает от определенного набора. Номер полезности для каждого пакета ничего не значит в абсолютном выражении; нет единой шкалы, по которой мы измеряем удовлетворенность. Это единственная цель в относительном выражении: мы можем использовать полезность, чтобы определить, какие пакеты предпочтительнее других.
е. удовлетворение, которое потребитель получает от определенного набора. Номер полезности для каждого пакета ничего не значит в абсолютном выражении; нет единой шкалы, по которой мы измеряем удовлетворенность. Это единственная цель в относительном выражении: мы можем использовать полезность, чтобы определить, какие пакеты предпочтительнее других.
Если полезность набора А выше, чем полезность набора В, это эквивалентно утверждению, что потребитель предпочитает набор А набору В. Таким образом, функции полезности ранжируют потребительские предпочтения, присваивая номер каждому набору. . Мы можем использовать функцию полезности для построения карт, описанных в Модуле 1. Поскольку все наборы на одной и той же кривой безразличия обеспечивают одинаковое удовлетворение, и, следовательно, ни один из них не является предпочтительнее , каждый комплект имеет одинаковую полезность. Следовательно, мы можем нарисовать кривую безразличия, определив все наборы, которые возвращают одно и то же число из функции полезности.
Экономисты говорят, что функции полезности равны , а не . Порядковый означает, что функции полезности только ранжируют наборы — они только указывают, какой из них лучше, а не насколько он лучше другого набора. Предположим, например, что одна функция полезности указывает, что пакет A возвращает 10 , а пакет B — 20 утилизаций. Мы не утверждаем, что набор Б в два раза лучше или в 10 раз лучше, а только то, что потребитель предпочитает набор Б. Например, предположим, что друг участвовал в гонке и сказал вам, что занял третье место. Эта информация порядковая: вы знаете, что она была быстрее, чем занявшая четвертое место, и медленнее, чем занявшая второе место. Вы знаете только порядок, в котором бегуны финишировали. Индивидуальное время имеет решающее значение: если финишер, занявший первое место, пробежал гонку ровно за один час, а ваш друг финишировал за час и шесть минут, вы знаете, что ваш друг был ровно на 10% медленнее, чем самый быстрый бегун. поскольку функции полезности являются порядковыми, многие различные функции полезности могут представлять одни и те же предпочтения. Это верно до тех пор, пока порядок сохраняется.
Это верно до тех пор, пока порядок сохраняется.
Возьмем, к примеру, функцию полезности U, которая описывает предпочтения относительно наборов товаров A и B: U(A,B). Мы можем применить к этой функции любое положительное монотонное преобразование (что, по сути, означает, что мы не меняем порядок), и созданная нами новая функция будет представлять те же предпочтения. Например, мы могли бы умножить положительную константу α или добавить положительную или отрицательную константу β . Таким образом, αU(A,B)+β представляет те же самые предпочтения, что и U(A,B), потому что он упорядочивает пакеты точно так же. Этот факт весьма полезен, поскольку иногда применение положительного монотонного преобразования функции полезности облегчает решение задач.
2.2 Функции полезности и типичные предпочтения
LO2: Определение функций полезности на основе типичных предпочтений, которые они представляют яблок и бананов есть функция U(A,B). Но каковы особые предпочтения Исаака в отношении связок яблок и бананов? Предположим, что у Исаака довольно стандартные предпочтения в отношении яблок и бананов, которые приводят к нашим типичным кривым безразличия: он предпочитает больше меньшему и любит разнообразие. Функция полезности, которая представляет эти предпочтения, может быть:
Но каковы особые предпочтения Исаака в отношении связок яблок и бананов? Предположим, что у Исаака довольно стандартные предпочтения в отношении яблок и бананов, которые приводят к нашим типичным кривым безразличия: он предпочитает больше меньшему и любит разнообразие. Функция полезности, которая представляет эти предпочтения, может быть:
U(A,B) = AB
Если яблоки и бананы идеально дополняют предпочтения Исаака, функция полезности будет выглядеть примерно так:
U(A,B) = MIN[A,B],
где функция MIN просто присваивает меньшее из двух чисел в качестве значения функции.
Если яблоки и бананы являются совершенными заменителями, функция полезности является аддитивной и будет выглядеть примерно так:
U(A,B) = A + B
Класс функций полезности, известный как функции полезности Кобба-Дугласа обычно используется в экономике по двум причинам:
1. Они отражают предпочтения «хорошего поведения», такие как «чем больше, тем лучше» и предпочтение разнообразия.
2. Они очень гибкие и легко настраиваются в соответствии с реальными данными.
Функции полезности Кобба-Дугласа имеют следующую форму:
U(A,B) = A α B β
Поскольку положительные монотонные преобразования представляют одни и те же предпочтения, одно такое преобразование можно использовать для установки α + β = 1 , что, как мы увидим позже, является удобным условием, упрощающим некоторые математические расчеты в задаче потребительского выбора.
Другой способ полезного преобразования функции полезности состоит в том, чтобы взять натуральный логарифм функции, который создает новую функцию, которая выглядит следующим образом:
U(A,B) = αln(A) + βln(B )
Чтобы вывести это уравнение, просто примените правила натуральных журналов. Здесь важно помнить об уровне абстракции. Обычно мы не можем создавать специальные функции полезности, которые точно описывают индивидуальные предпочтения. Наверное, никто из нас не смог бы описать собственные предпочтения одним уравнением. Но пока потребители в целом имеют предпочтения, соответствующие нашим основным предположениям, мы можем довольно неплохо находить функции полезности, соответствующие реальным данным о потреблении. Мы увидим доказательства этого позже в курсе.
Но пока потребители в целом имеют предпочтения, соответствующие нашим основным предположениям, мы можем довольно неплохо находить функции полезности, соответствующие реальным данным о потреблении. Мы увидим доказательства этого позже в курсе.
В таблице 2.1 приведены настройки и служебные функции, описанные в этом разделе.
Таблица 2.1 Типы предпочтений и вспомогательные функции, которые их представляют | ||
ПРЕДПОЧТЕНИЯ | СЛУЖЕБНАЯ ФУНКЦИЯ | ТИП ПОЛЕЗНОЙ ФУНКЦИИ |
Любовь к разнообразию или хорошее поведение | U(A,B) = АВ | Кобб-Дуглас |
Любовь к разнообразию или хорошее поведение | U(A,B) = А α В β | Кобб-Дуглас |
Любовь к разнообразию или хорошее поведение | U(A,B) = αln(A) + βln(B) | Натуральное бревно Кобб-Дуглас |
Идеальное дополнение | U(A,B) = МИН[A,B] | Минимальная функция |
Идеальные заменители | U(А,В) = А + В | Добавка |
2 . . . . . . . . . . . . . . . кривая из функции полезности Кривые безразличия и функции полезности напрямую связаны. Фактически, поскольку кривые безразличия представляют предпочтения графически, а функции полезности представляют предпочтения математически, отсюда следует, что кривые безразличия могут быть получены из функций полезности. 9\frac{1}{2}[/latex]  3 Отношение Утилита F ИСКЛЮЧЕНИЯ И I Ndifference C urve M 2.
3 Отношение Утилита F ИСКЛЮЧЕНИЯ И I Ndifference C urve M 2.
На рис. 2.1 ясно показано предположение, что потребители предпочитают разнообразие. Каждый пучок, содержащий определенное количество А и В, представляет собой точку на поверхности. Вертикальная высота поверхности представляет уровень полезности. Увеличивая как A, так и B, потребитель может достичь более высоких точек на поверхности.
Откуда же берутся кривые безразличия? Напомним, что кривая безразличия — это совокупность всех наборов, к которым потребитель безразличен, относительно того, какой из них потреблять. Математически это эквивалентно утверждению, что все наборы, помещенные в функцию полезности, возвращают одно и то же функциональное значение. Итак, если мы установим значение полезности Ū и найдем все наборы А и В, которые создают это значение, мы определим кривую безразличия. Обратите внимание, что это эквивалентно нахождению всех наборов, которые доставляют потребителя на одинаковую высоту на трехмерной поверхности на рис. 2.1.
Кривые безразличия представляют собой высоту (уровень полезности) на плоской поверхности. Таким образом, они аналогичны контурной линии на топографической карте. Перенося трехмерный график обратно в двумерное пространство — пространство А, В — мы можем показать контурные линии/кривые безразличия, которые представляют различные высоты или уровни полезности. Из графика на рис. 2.1 вы уже можете видеть, как эта функция полезности дает кривые безразличия, которые «изогнуты» или вогнуты к началу координат.
Из графика на рис. 2.1 вы уже можете видеть, как эта функция полезности дает кривые безразличия, которые «изогнуты» или вогнуты к началу координат.
Таким образом, кривые безразличия следуют непосредственно из функций полезности и являются удобным способом представления функций полезности на двумерном графике.
2.4 Определение предельной полезности и предельной нормы замещения
LO4: Получите предельную полезность и MRS для типичных функций полезности.
— это дополнительная полезность, которую потребитель получает от потребления одной дополнительной единицы товара. Математически мы выражаем это как:
[латекс]MU_{a}=\frac{\Delta \cup }{\Delta A}[/latex]
или изменение полезности в результате изменения количества потребляемого А, где Δ представляет собой изменение стоимости предмета. Итак,
[латекс]MU_{a}=\frac{\Delta \cup }{\Delta A}=\frac{\cup (A+\Delta A,B)-U(A,B)}{\Delta A}[/latex]
Обратите внимание, что когда мы исследуем предельную полезность потребления A, мы считаем B постоянным.
Используя исчисление, предельная полезность совпадает с частной производной функции полезности по отношению к A: }[/латекс]
Рассмотрим потребителя, который садится есть салат и пиццу. Предположим, что мы сохраняем количество салата постоянным — например, один гарнир к ужину. Теперь давайте увеличим количество кусков пиццы, предположим, что для 1 кусочка полезность равна 10, для 2 — 18, для 3 — 24 и для 4 — 28. Давайте нанесем эти числа на график, где полезность отложена по вертикальной оси, а пицца — по горизонтальной. ось (рис. 2.2).
Рисунок 2.2: График и таблица убывающей предельной полезности
Ломтики пиццы | Утилита | Предельная полезность |
1 | 10 | |
2 | 18 | 8 |
3 | 24 | 6 |
4 | 28 | 4 |
Из положительного наклона графика видно, как увеличивается полезность дополнительных кусочков пиццы. Из вогнутой формы графика видно еще одно распространенное явление: дополнительная полезность, которую потребитель получает от каждого дополнительного куска пиццы, уменьшается с увеличением количества потребляемых кусков.
Из вогнутой формы графика видно еще одно распространенное явление: дополнительная полезность, которую потребитель получает от каждого дополнительного куска пиццы, уменьшается с увеличением количества потребляемых кусков.
Тот факт, что дополнительная полезность становится меньше с каждым дополнительным куском пиццы, называется принципом . Этот принцип применяется к предпочтениям с хорошим поведением, когда предпочтение отдается смешанным наборам.
– это количество одного товара, от которого потребитель готов отказаться, чтобы получить еще одну единицу другого товара. Вот почему это то же самое, что наклон кривой безразличия — поскольку мы сохраняем уровень удовлетворения постоянным, мы остаемся на той же кривой безразличия, просто двигаясь по ней, когда мы обмениваем один товар на другой. Сколько одного товара вы готовы обменять на еще один другой, зависит от предельной полезности каждого из них.
Используя наш предыдущий пример, если, съев еще один салат, ваша полезность увеличится на 10, то при текущем потреблении 4 ломтиков пиццы вы можете отказаться от 2 ломтиков пиццы и увеличить полезность с 28 до 18. На 10 дополнительных полезностей от салата и на 10 меньших полезностей за счет отказа от 2 кусков пиццы общая полезность остается неизменной, поэтому мы должны оставаться на той же кривой безразличия. Двигаясь по кривой безразличия, вы, должно быть, идете по наклонной, то есть вы должны отказываться от блага по вертикальной оси в пользу большего количества блага по горизонтальной оси, что приводит к отрицательному подъему по сравнению с положительным ходом.
На 10 дополнительных полезностей от салата и на 10 меньших полезностей за счет отказа от 2 кусков пиццы общая полезность остается неизменной, поэтому мы должны оставаться на той же кривой безразличия. Двигаясь по кривой безразличия, вы, должно быть, идете по наклонной, то есть вы должны отказываться от блага по вертикальной оси в пользу большего количества блага по горизонтальной оси, что приводит к отрицательному подъему по сравнению с положительным ходом.
Мы можем перейти непосредственно от предельной полезности к MRS, признав связь между этими двумя понятиями. В нашем случае для функции полезности [latex]U=U(A,B)[/latex] MRS представляется как:
[latex]MRS=-\frac{MU_{A}}{MU_{B} }[/latex]
Обратите внимание, что при подстановке мы можем упростить уравнение:
[latex]MRS=-\frac{MU_{A}}{MU_{B}}=-\frac{\frac{\Delta U}{\Delta A}}{\frac{\Delta U}{\Delta B}}=-\frac{\Delta B}{\Delta A}[/latex]
Вставка вычисления, которое соответствует: 9[/ латекс]
Важное примечание. Для некоторых функций полезности MRS не определена в некоторых точках на кривой (кривых) безразличия. Например, кривая безразличия для совершенных дополнений U(A,B) = min[A,B] имеет «излом» — и, конечно, не существует ни одного наклона, касающегося излома. В любой точке, удаленной от излома, наклон равен либо (отрицательной) бесконечности, либо нулю. Поскольку наклон не уникален в изломе, для MRS не существует единого значения.
Для некоторых функций полезности MRS не определена в некоторых точках на кривой (кривых) безразличия. Например, кривая безразличия для совершенных дополнений U(A,B) = min[A,B] имеет «излом» — и, конечно, не существует ни одного наклона, касающегося излома. В любой точке, удаленной от излома, наклон равен либо (отрицательной) бесконечности, либо нулю. Поскольку наклон не уникален в изломе, для MRS не существует единого значения.
Сводка
Обзор: темы и связанные с ними результаты обучения
2.1 Утилита F Unction LO 2.1. : определение функций полезности на основе типичных предпочтений, которые они представляют0008 LO 2.3: Объясните, как вывести кривую безразличия из функции полезности 2.4 Определение предельной полезности и предельной нормы замещения LO 2.4: Выведите предельную полезность и MRS для типичных функций полезности. Трехмерная вспомогательная функция и контурная линия Кобб-Дуглас 0 Идеальное дополнение0002 Совершенные заменители Это видео с YouTube-канала «Департамент экономики» может оказаться полезным. Альтернативный текст (McAfee & Lewis), модуль 2 — развертывание утилиты Политика Вопрос В Модуле 1 мы определили, что релевантное решение потребителя между увеличением пробега и другим потреблением, вероятно, соответствует стандартным предположениям о потребительском выборе. Следовательно, используя функцию полезности Кобба-Дугласа для представления потребителя, которому нравится водить машину, а также потреблять другие товары, и который рассматривает их как компромисс (деньги, потраченные на бензин, — это деньги, не потраченные на другие потребительские товары), хороший выбор. , где MD = пробег в милях, а C = прочее потребление. На самом деле, сама функция может быть взята из реальных данных, где параметры и могут быть оценены для этого рынка, рынка миль, пройденных автомобилем потребителя. Рисунок 1: График кривых безразличия для примера политики 1 . Будут ли другие типы предпочтений более подходящими в этом примере? 2. Что должно быть верным, чтобы совершенные дополнения были подходящим типом предпочтения для анализа этой политики? 3. Что должно быть верным для совершенных заменителей? Учитывая, что мы рассматриваем «типичного» потребителя, который водит машину, уместно ли выбрать «типичную» функцию полезности? 4. Мы просто догадываемся или у нас есть какое-то теоретическое обоснование в поддержку нашего выбора «хорошего поведения» предпочтений или функции полезности Кобба-Дугласа? Лицензионный контент CC, Исходный Лицензионный контент CC, совместно используемый ранее Модуль 2: Утилита Джоэла Брюно и Клинтона Махони находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.
Learn: Основные термины и графики
Термины
Графики
Дополнительные ресурсы
 Он также имеет преимущества как в соответствии с предположениями, так и в гибкости: 9{\beta}[/latex] ,
Он также имеет преимущества как в соответствии с предположениями, так и в гибкости: 9{\beta}[/latex] , Изучение вопросов политики:
Цитаты Кандела
 Авторы : Джоэл Брюно и Клинтон Махони. Лицензия : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
Авторы : Джоэл Брюно и Клинтон Махони. Лицензия : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike Лицензия


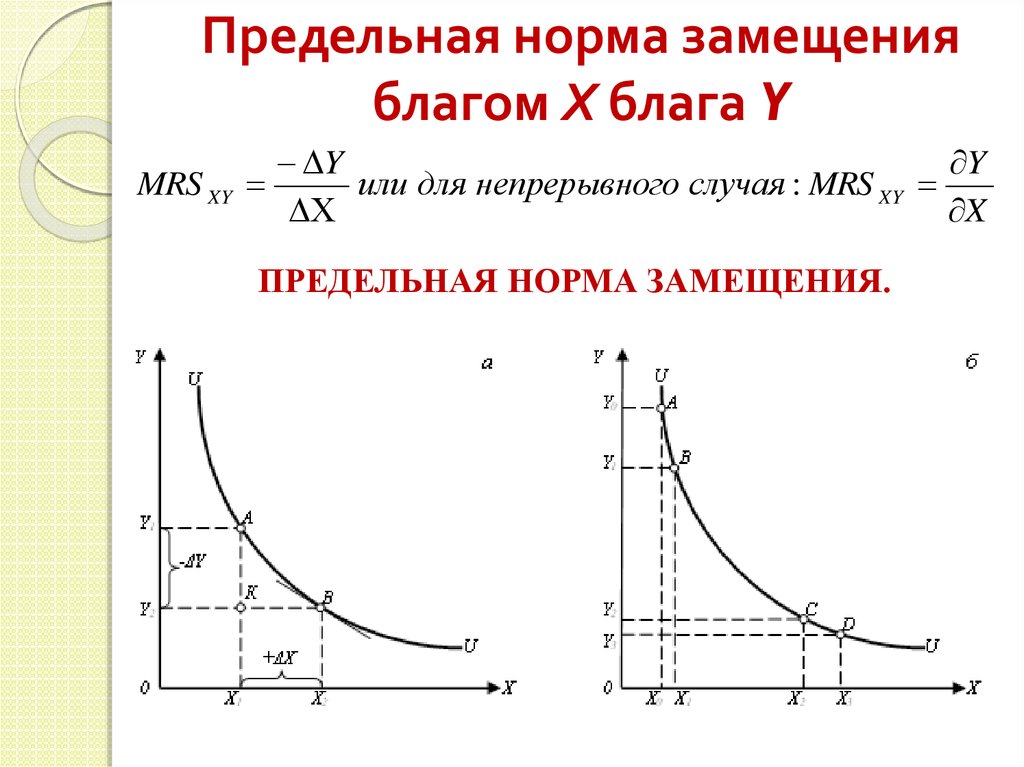 02 МБ
02 МБ Персиановский)
Персиановский)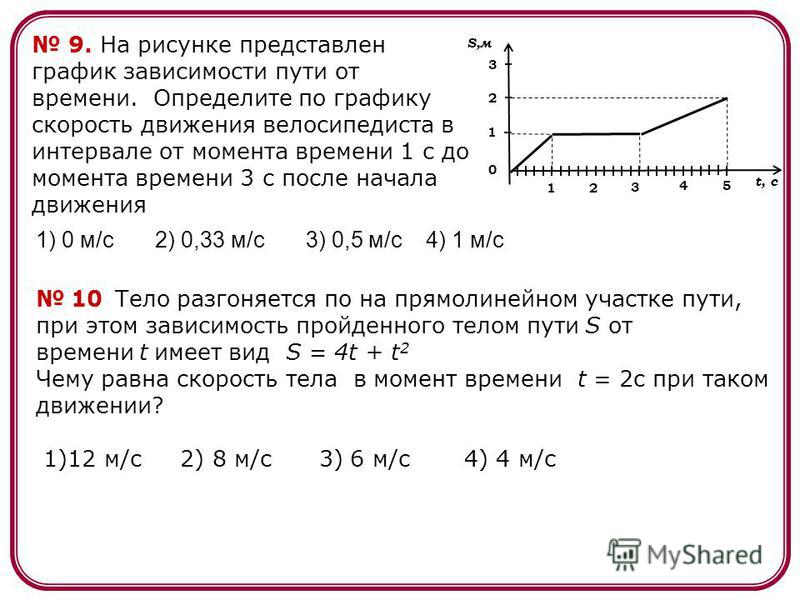 2.014.01
2.014.01 Мы также формально моделируем условие первого порядка для задач максимизации прибыли, используя дифференциальную теорию HOL-Light. Эти формализации позволяют нам формально рассуждать и проверять свойства заданных функций в рамках звукового ядра средства доказательства теорем HOL-Light.
Мы также формально моделируем условие первого порядка для задач максимизации прибыли, используя дифференциальную теорию HOL-Light. Эти формализации позволяют нам формально рассуждать и проверять свойства заданных функций в рамках звукового ядра средства доказательства теорем HOL-Light. Дж. теория рационального выбора; Sage: New York, NY, USA, 1992. [Google Scholar]
Дж. теория рационального выбора; Sage: New York, NY, USA, 1992. [Google Scholar] Дж. Нетв. вычисл. заявл. 2016 , 76, 23–36. [Google Scholar] [CrossRef]
Дж. Нетв. вычисл. заявл. 2016 , 76, 23–36. [Google Scholar] [CrossRef] Экон. соц. 2017 , 10, 310. [Google Scholar] [CrossRef][Green Version]
Экон. соц. 2017 , 10, 310. [Google Scholar] [CrossRef][Green Version] [Google Scholar] [CrossRef]
[Google Scholar] [CrossRef] Комплекс Адапт. Сист. Модель. 2018 , 6, 5. [Google Scholar] [CrossRef]
Комплекс Адапт. Сист. Модель. 2018 , 6, 5. [Google Scholar] [CrossRef] arXiv 2011 , arXiv:1108.4139. [Google Scholar]
arXiv 2011 , arXiv:1108.4139. [Google Scholar]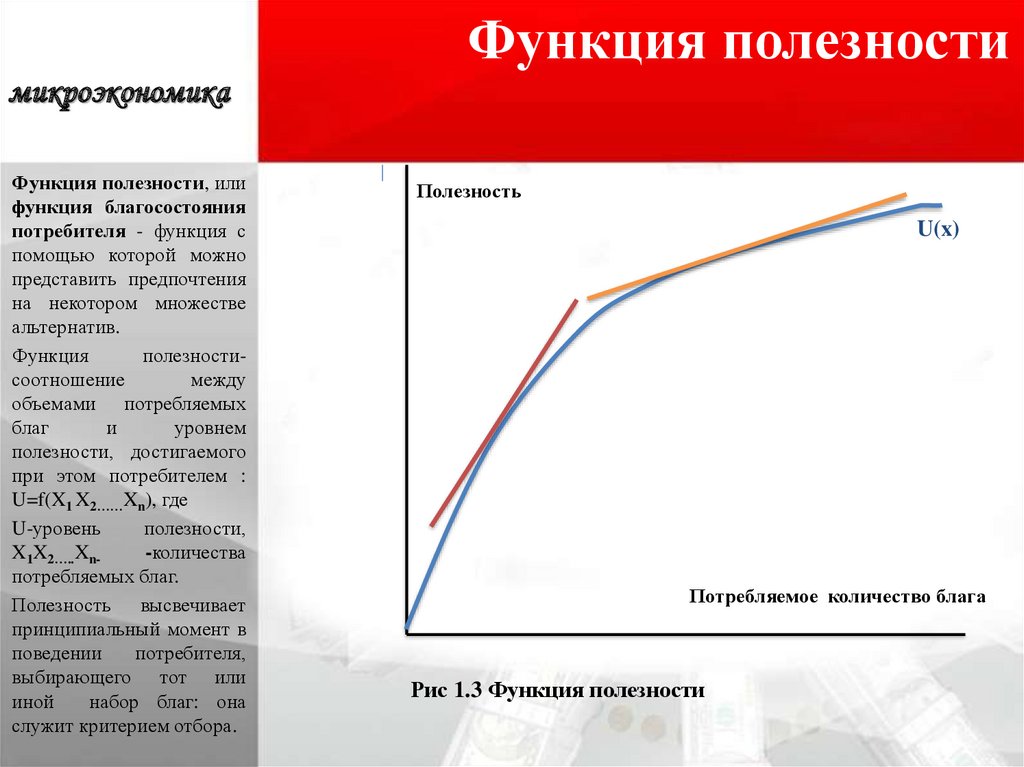 ; стр. 3–17. [Google Scholar]
; стр. 3–17. [Google Scholar] [Google Scholar]
[Google Scholar] [Google Scholar]
[Google Scholar] 1–6. [Google Scholar]
1–6. [Google Scholar]