Задачи наподобие треугольников 9 класс: Решение задач на подобие. Подобные треугольники.

Планиметрия в тезисах и решениях. 9 класс

Два треугольника подобны: по двум углам, по двум сторонам и углу между ними, по трём сторонам. Очень важно в задаче увидеть подобные треугольники или другие подобные фигуры. Для этого нужна хорошая практика решения задач.

При решении задач на прямоугольный треугольник полезно знать, что высота, проведённая из прямого угла, делит его на два подобных треугольника (рис. 180):

?ABD ~ ?ADC ~ ?ABC.

Рис. 180.

Примеры решения задач

111. Через точки М и К, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МК, параллельная стороне АС. Найдите длину СК, если ВС = 12, МК = 8 и АС = 18 (рис. 181). (1)

Рис. 181.

Решение. Обозначим КС через х. Тогда ВК = 12 – х. Из подобия треугольников ABC и МВК следует: MK/BK = AC/BC; 8/(12 – x) = 18/12; x = 20/3.

Ответ: 20/3.

112. В прямоугольный равнобедренный треугольник вписан прямоугольник так, что угол прямоугольника совпадает с углом при вершине треугольника, а вершина противолежащего угла лежит на гипотенузе.

Докажите, что периметр прямоугольника есть величина постоянная для данного треугольника (рис. 182). (1)

Рис. 182.

Решение. Пусть АВ = АС = а, DE = х; AD = у. Тогда DB = а – у; FC = а – х. Треугольник DEB подобен треугольнику FСЕ, значит, DE/DB = FC/FE; x/(a – y) = (a – x)/y; ху2= а2– ау – ах + ху; х + у = а; РADEF = 2(х + у) = 2а, т. е. не зависит от х и у.

113. В прямоугольном треугольнике ABC угол А – прямой. Опущена высота AD, равная ?5. Найдите произведение BD ? DC (рис. 183). (1)

Рис. 183.

Решение. Треугольники ADB и ADC подобны (?BAD = ?ACD, ?ABD = ?DAC). Значит, BD/AD = AD/DC; BD ? DC = AD2= (?5)2= 5.

Ответ: 5.

114. В треугольнике ABC проведены высоты AD и СЕ. Докажите, что треугольники ABC и DBE подобны. Чему равен коэффициент подобия (рис. 184)? (2)

Рис. 184.

Решение. Из прямоугольного треугольника ВСЕ: BE = ВС ? cos В. Из ?ABD: BD = АВ ? cos В. Значит, две стороны BD и BE треугольника BDE пропорциональны сторонам АВ и ВС треугольника ABC, а угол В (угол между пропорциональными сторонами) у треугольников общий.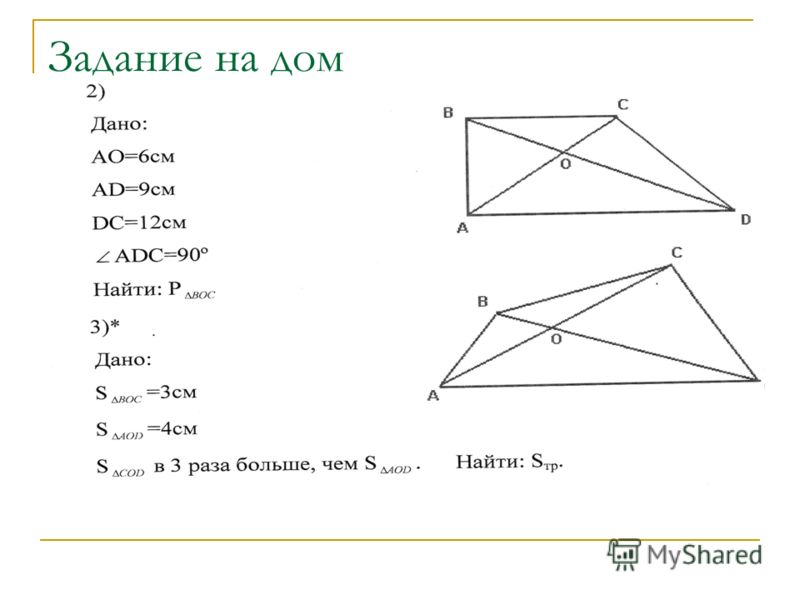 ?BDE ~ ?ABC по двум сторонам и углу между ними.

Значит,

Ответ: kподобия = cos B.

115. В равносторонний треугольник вписана окружность. Этой окружности и сторон треугольника касаются три малые окружности. Найдите сторону треугольника, если радиус малой окружности равен 1 (рис. 185). (2)

Рис. 185.

Решение. Так как в равностороннем треугольнике ABC угол ABC = 60°, то ?ОВМ = 30° (см. рис.). Из центров О и О1 проведем перпендикуляры ОМ и О1Т к стороне ВС. По условию О1Т и О1K равны 1. Длины отрезков ОМ и ОК обозначим через R. Из треугольника ВТО1 следует, что ВО1 = О1Т/sin 30° = 1/0,5 = 2. Треугольники ВТО1 и ВМО подобны по двум углам (?BTO1 = ?BMO = 90°; ?OBM – общий). Отсюда следует, что O1T/O1B = OM/OB;

Теперь мы знаем радиус вписанной в равносторонний треугольник окружности. Осталось найти длину его стороны. Из треугольника ВОМ следует ВМ = OM ? ctg ?ОВМ = 3?3. Тогда ВС = 2ВМ = 6?3.

Ответ: 6?3.

116.  Из одной точки к окружности проведены две касательные. Длина каждой касательной равна 12 см, а расстояние между точками касания 14,4 см. Определите радиус окружности (рис. 186). (2)

Рис. 186.

Решение. Пусть ОА и ОВ – касательные к окружности с центром С; А и В – точки касания. Тогда СВ ? ОВ, СА ? ОА. Кроме того, ОС ? АВ и делит эту сторону пополам. ОА = 12 см, AM = 1/2 АВ = 7,2 см.

?МОА = ?АОС (углы с взаимноперпендикулярными сторонами), значит, ?ОАС подобен ?ОАМ; тогда

Ответ: 9 см.

117. Центр О окружности радиуса длиной 3 лежит на гипотенузе АС прямоугольного треугольника ABC. Катеты треугольника касаются окружности. Найти площадь треугольника ABC, если известно, что длина отрезка ОС равна 5 (рис. 187). (3)

Рис. 187.

Решение. Пусть ABC – данный в условии задачи треугольник. Обозначим через M и N точки касания окружности соответственно со сторонами АВ и ВС. Соединив эти точки с центром О окружности, получим квадрат MBNO, и поэтому BN = ОМ = 3. Треугольник ONC прямоугольный, в нём ОС = 5, ON = 3. Следовательно,

Но тогда ВС = NC + NB = 7. Треугольники ONC и ABC подобны, поэтому AB/ON = BC/NC; AB/3 = 7/4; отсюда получаем, что AB = (ON ? BC)/NC = (3 ? 7)/4 = 21/4. Теперь находим S – площадь прямоугольного треугольника ABC:

Ответ: 147/8.

Задачи для самостоятельного решения

118. В равнобедренный треугольник вписан параллелограмм так, что угол параллелограмма совпадает с углом при вершине треугольника, а вершина противолежащего угла лежит на основании. Докажите, что периметр параллелограмма есть величина постоянная для данного треугольника. (1)

119. Из точки D, лежащей на катете АС прямоугольного треугольника ABC, на гипотенузу СВ опущен перпендикуляр DE. Найдите длину CD, если СВ = 15, АВ = 9, СЕ = 4. (1)

120. Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40 см. Найдите катеты треугольника. (1)

121.  В параллелограмме ABCD проведена диагональ BD и отрезок AF (F ? ВС), пересекающий BD в точке О. Известно, что ВО = 6, OD = 18, FB = 4. Определите сторону параллелограмма AD. (1)

122. В острый угол, равный 60°, вписаны две окружности, извне касающиеся друг друга. Радиус меньшей окружности равен 1. Найдите радиус большей окружности. (1)

123. Найдите длину стороны квадрата, вписанного в равнобедренный треугольник с основанием а и боковой стороной b так, что две его вершины лежат на основании, а две другие вершины – на боковых сторонах. (2)

124. В параллелограмме ABCD точка М– середина стороны СВ, N – середина стороны CD. Докажите, что прямые AM и AN делят диагональ BD на три равные части. (2)

125. В трапеции, основания которой равны а и b, через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найдите длину отрезка этой прямой, отсекаемого боковыми сторонами трапеции. (2)

126. В остроугольном треугольнике ABC из вершин А и С на стороны ВС и АВ опущены высоты АР и CQ. Известно, что площадь треугольника ABC равна 18, площадь треугольника BPQ равна 2, а длина отрезка PQ равна 2?2. Вычислите радиус окружности, описанной около треугольника ABC. (3)

Открытый банк заданий ОГЭ на подобие треугольников

1. Открытый банк заданий ОГЭ на подобие треугольников

Муниципальное Бюджетное Общеобразовательное Учреждение
Москаленского Муниципального района Омской области
«Гимназия имени Горького А.М.»
Открытый банк заданий
ОГЭ
на подобие треугольников
Методическое пособие
Выполнил
Латышевский
Вадим Игоревич,
9«А» Класс
Москаленки-2017

2. Оглавление

Теоритический справочник
Типы и решение задач 1 Части ОГЭ
Задачи про проектор.
Задачи про столб, фонарь, тень человека
Задачи про колодец с «журавлем» и на
шлагбаум
3.Типы и решение задач 2 Части ОГЭ.
a) Задачи на вычисление
b) Задачи на доказательство
1.
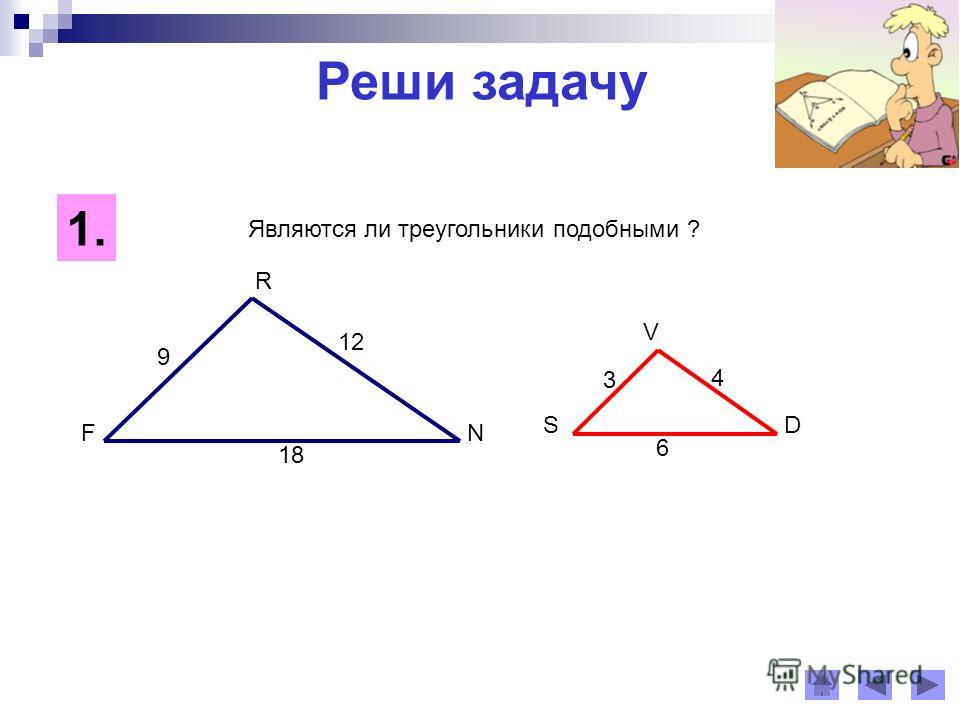
2.
a)
b)
c)

3. Раздел 1

Теоритический справочник

4. Пропорциональные отрезки

Теоритический справочник
Пропорциональные отрезки
Отношением отрезков AB и CD называется отношение их длин, т.е.
AB
CD
A
C
B
D
Отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1, если
AB A1 B1
CD C1 D1
AB A1 B1
CD C1 D1

5. Теоритический справочник

Два треугольника называются подобными, если их углы
соответственно равны и стороны одного треугольника
пропорциональны сходственным сторонам другого.
B
B1
A
C
A1
C1
Число k, равное отношению сходственных сторон треугольников,
называется коэффициентом подобия
AB
BC
AC
k
A1 B1 B1C1 A1C1

6. Теоритический справочник

Отношением площадей двух подобных треугольников равно
квадрату коэффициента подобия B
S ABC
k2
S A1B1C1
B1
A
C
A1
C1
Биссектриса треугольника делит противоположную сторону на
отрезки, пропорциональные прилежащим сторонам треугольника.
A
BD AB
BD DC
или
DC AC
AB AC
B
C
D

7. Признаки подобия треугольников

Теоритический справочник
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум
углам другого треугольника, то такие треугольники подобны
B
B1
ABC, A1B1C1,
Если A = A1, B = B1
то ABC A1B1C1
A
C
A1
C1

8. Признаки подобия треугольников

Теоритический справочник
Признаки подобия треугольников
II признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум
сторонам другого треугольника и углы, заключенные между этими
сторонами, равны, то такие треугольники подобны
ABC, A1B1C1,
B
Если A = A1 и AB AC
B1
A1 B1 A1C1
то ABC A1B1C1
A
C
A1
C1

9. Признаки подобия треугольников

Теоритический справочник
Признаки подобия треугольников
III признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем
сторонам другого треугольника, то такие треугольники подобны
B
Дано:
B1
ABC, A1B1C1,
Если
A
C
A1
C1
AB
BC
AC
A1 B1 B1C1 A1C1
То ABC
A1B1C1

10.

Свойства подобных треугольников.Теоритический справочник
Свойства подобных треугольников.
• Если треугольники
подобны, то сходственные
стороны пропорциональны.
• Если треугольники
подобны, то
соответственные
углы(лежащие против
сходственных сторон)
равны.
Если треугольники
подобны, то элементы
треугольников(высоты,
медианы, биссектрисы)
соответственно
пропорциональны
коэффициенту подобия.

11. Типы и решение задач 1 Части ОГЭ

Раздел 2
Типы и решение задач 1 Части
ОГЭ

12. Алгоритм решения задач на подобие треугольников

1. Находим пару предполагаемо
подобных треугольников.
2. Доказываем, что эти треугольники
подобны, используя признаки подобия
треугольников.
3. Определяем сходственные стороны
треугольников и составляем
соответствующую пропорцию.
4. Находим неизвестные члены этой
пропорции.

13. Задачи про проектор.

Проектор полностью освещает экран A высотой 80
см, расположенный на расстоянии 250 см от проектора. 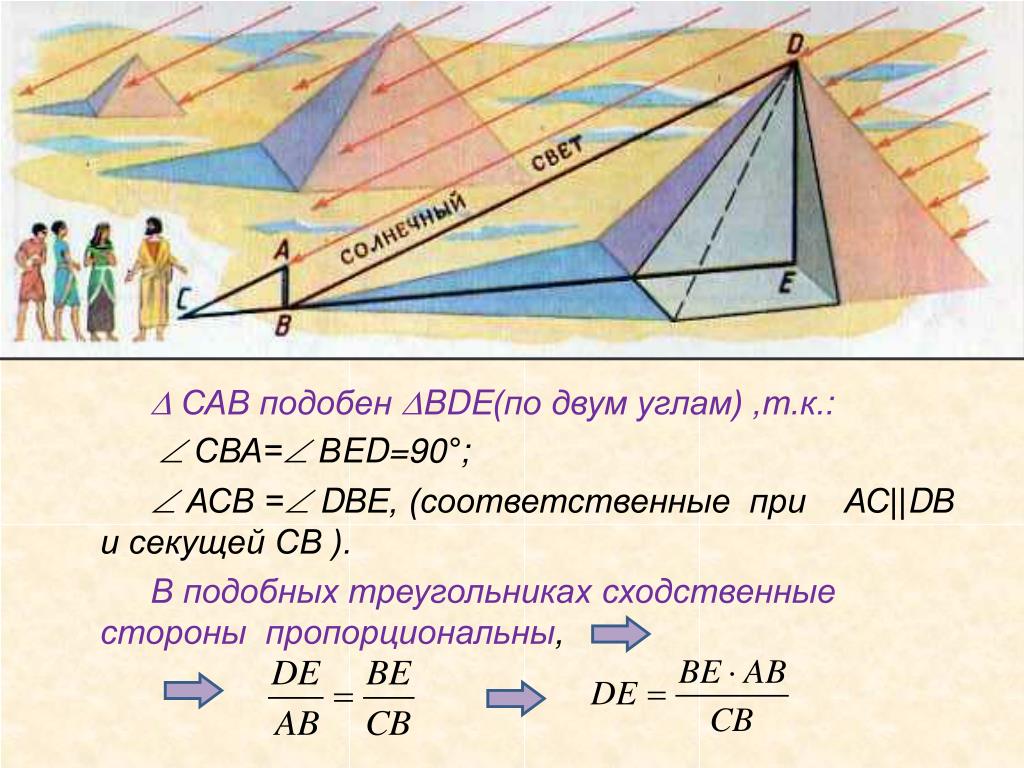На каком наименьшем расстоянии (в сантиметрах) от проектора
нужно расположить
экран B высотой 160 см,
чтобы он был полностью
освещён, если настройки
проектора остаются неизменными?
Задачи про проектор.
Дано: ДЕ=80 см, АО=160см, СВ=250см
Найти : СF
Решение :
Пусть x — искомое расстояние
∆СДЕ ~∆ САО по двум углам т. к.
∠С − общий, ∠Д = ∠А угол падения луча
Значит соответственные элементы (высоты) пропорциональны
х
160∙250
х=
=500 см Ответ: 500 см
250
80
АО
ДЕ
СF
= СВ ,
160
80
=
Задачи
про
проектор.
Задачи для самостоятельного решения
1.Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 120 см от проектора. На каком наименьшем
расстоянии (в сантиметрах) от проектора нужно расположить
экран B высотой 330 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
2. Проектор полностью освещает экран A высотой 160 см, расположенный на расстоянии 300 см от проектора. 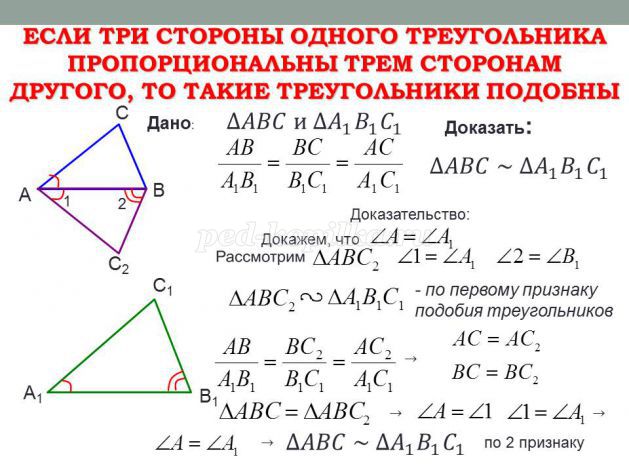На каком наименьшем
расстоянии (в сантиметрах) от проектора нужно расположить экран
B высотой 80 см, чтобы он был полностью освещён, если настройки
проектора остаются неизменными?
3. Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 110 см от проектора. На каком наименьшем
расстоянии (в сантиметрах) от проектора нужно расположить
экран B высотой 360 см, чтобы он был полностью освещён, если
настройки проектора остаются неизменными?

16. Задачи про столб, расстояние, тень человека.

• 1)Человек ростом 1,6 м стоит на
расстоянии 5 м от столба, на котором
висит фонарь на высоте 3,6 м. Найдите
длину тени человека (в метрах).
3,6м
1,6м
5м
?
Задачи про столб,
расстояние, тень человека.
Решение: По сути, в задаче нужно найти величину из
двух подобных прямоугольных треугольников (по двум
углам).
Так как треугольники подобны, то можно записать
3,6
5+х
соотношение для их сторон:
=
откуда
1,6
х
3. 6х=1.6(5+х)
3.6х=1.6х+8
3.6х-1.6х=8
2х=8/2
х=4
Ответ:4 метра.
Задачи про столб,
расстояние, тень человека.
• 2) На каком расстоянии (в метрах) от
фонаря стоит человек ростом 1,8 м, если
длина его тени равна 4 м, высота фонаря
3,6 м?
3,6 м
1,8м
?
4м
Задачи про столб,
расстояние,
тень
человека.
Решение: Обозначим человека как AB (от головы до земли) ,
фонарь как CD (от лампочки до земли) , конец тени человека
обозначим точкой O.
Тогда будем иметь два подобных прямоугольных треугольника:
OBA и ODC ( подобие по двум углам)
Так как треугольники подобны, то можно записать соотношение их
3,6 х+4
сторон: =
1,8
х
Откуда:
1.8(х+4)
3.6
1.8х+7.2
х=
3.6
х=
х=1.8х+2
0.8х=2/0.8
х=2.5
Ответ:2.5 метра.

20. Задачи про столб, расстояние, тень человека.

• 3) Человек, рост которого равен 1.2 м,
стоит на расстоянии 14 м от уличного
фонаря. При этом длина тени человека
равна 7 м. Определите высоту фонаря (в
метрах).
?
1,2м
14м
7м
Задачи про столб,
расстояние, тень человека.
Решение: Обозначим человека как AB (от головы до
земли) , фонарь как CD (от лампочки до земли) , конец
тени человека обозначим точкой O.
Тогда будем иметь два подобных прямоугольных
треугольника: OBA и ODC ( подобие по двум углам).
Так как треугольники подобны, то можно записать
соотношение их
х 14+7
1.2
7
сторон: =
Ответ:3.6 метра.
откуда х=
1.2∙(14+7) 25.2
= =3.6
7
7

22. Задачи для самостоятельного решения

Задачи про столб, расстояние, тень человека.
Задачи для самостоятельного решения
1. Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на
котором висит фонарь на высоте 7,2 м. Найдите длину тени
человека в метрах.
2. Человек ростом 1,5 м стоит на расстоянии 12 м от столба, на
котором висит фонарь на высоте 3,5 м. Найдите длину тени
человека в метрах.
3. Человек ростом 1,5 м стоит на расстоянии 13 м от столба, на
котором висит фонарь на высоте 5,4 м. Найдите длину тени
человека в метрах.
4. Человек ростом 1,9 м стоит на расстоянии 6 м от столба, на
котором висит фонарь на высоте 7,6 м. Найдите длину тени
человека в метрах.
5 Человек ростом 1,7 м стоит на расстоянии 9 м от столба, на
котором висит фонарь на высоте 6,8 м. Найдите длину тени
человека в метрах.
Задачи про столб, расстояние, тень человека.
Задачи для самостоятельного решения
• 6.На каком расстоянии (в метрах) от
фонаря стоит человек ростом 1,8 м, если
длина его тени равна 9 м, высота фонаря
5 м?
• 7.На каком расстоянии (в метрах) от
фонаря стоит человек ростом 1,8 м, если
длина его тени равна 9 м, высота фонаря
4 м?
Задачи про столб, расстояние, тень человека.
Задачи для самостоятельного решения
7.На каком расстоянии (в метрах) от
фонаря стоит человек ростом 1,8 м, если
длина его тени равна 9 м, высота фонаря
4 м?
8. 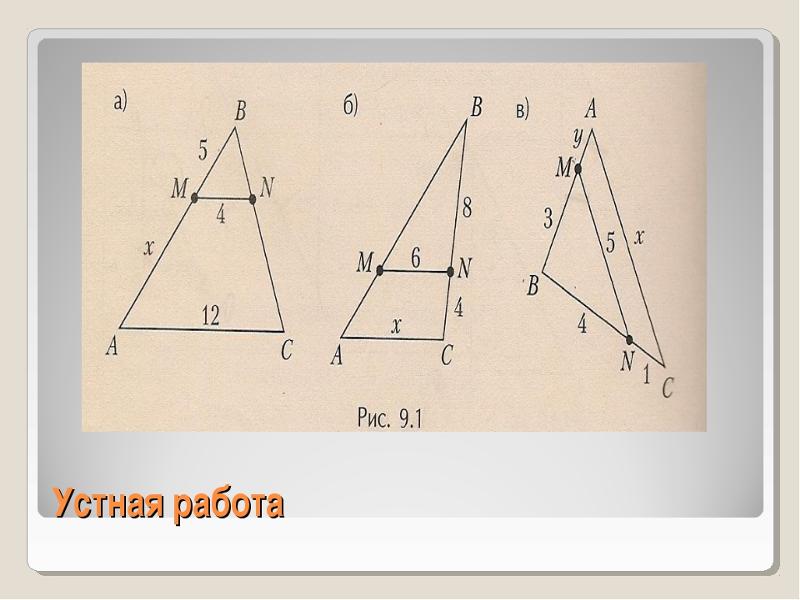Человек, рост которого равен 1,6 м,
стоит на расстоянии 17 м от уличного
фонаря. При этом длина тени человека
равна 8 м. Определите высоту фонаря (в
метрах).

25. Типы и решение задач 2 Части ОГЭ.

Раздел 3
Типы и решение задач 2
Части ОГЭ.

26. Задачи на вычисление

• Задача1Отрезки AB
и DC лежат на параллельных прямых,
а отрезки AC и BD
пересекаются в
точке M. Найдите
MC, если AB = 16,
DC = 24, AC = 25 .
Задачи на вычисление

28. Задачи на вычисление

• Задача 2 Прямая, параллельная стороне
AC треугольника
ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите
BN, если MN = 13,
AC = 65, NC = 28.

29. Задачи на вычисление

30. Задачи на вычисление

• Задача 3 Высота треугольника разбивает
его основание на два
отрезка с длинами 8
и 9. Найдите длину
этой высоты, если
известно, что другая
высота треугольника
делит ее пополам.

31.

Задачи на вычисление

32. Задачи на вычисление

• Задача 4 Окружность
пересекает стороны
AB и AC треугольника
ABC в точках K и P
соответственно и проходит через вершины
B и C. Найдите длину
отрезка KP, если
AP = 18, а сторона BC
в 1,2 раза меньше стороны AB.

33. Задачи на вычисление

34. Задачи на вычисление

Задача5 На рисунке
изображён колодец с
«журавлём». Короткое
плечо имеет длину 1 м,
а длинное плечо — 3
м. На сколько метров
опустится конец длинного плеча, когда
конец короткого поднимется на 0,5 м?

35. Задачи на вычисление

36. Задачи на вычисление

Задачи для самостоятельного решения
• 1)Отрезки AB и DC лежат на параллельных прямых, а
отрезки AC и BD пересекаются в точке M. Найдите
MC, если AB = 18, DC = 54, AC = 48
• 2)Отрезки AB и DC лежат на параллельных прямых, а
отрезки AC и  BD пересекаются в точке M. Найдите
MC, если AB = 12, DC = 48, AC = 35.
• 3)Отрезки AB и DC лежат на параллельных прямых, а
отрезки AC и  BD пересекаются в точке M. Найдите
MC, если AB = 15, DC = 30, AC = 39.

37. Задачи на вычисление

• Задачи для самостоятельного решения
• 4)Прямая, параллельная стороне AC треугольника
ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 12, AC = 42, NC
= 25.
• 5)Прямая, параллельная стороне AC треугольника
ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 17, AC = 51,
NC = 32.
• 6)Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит
через вершины B и C. Найдите длину отрезка KP,
если AP = 16, а сторона BC в 1,6 раза меньше стороны
AB.

38. Задачи на доказательство

Задача 1Высоты AA1 и
BB1 остроугольного
треугольника ABC пересекаются в точке E.
Докажите, что углы
AA1B1 и ABB1 равны.

39. Задачи на доказательство

40. Задачи на доказательство

Задача 2

41. Задачи на доказательство

Задача 3 Известно, что
около четырёхугольника ABCD можно
описать окружность и
что продолжения сторон AD и BC
четырёхугольника пересекаются в точке K.
Докажите, что треугольники KAB и KCD
подобны

42. Задачи на доказательство

43. Задачи на доказательство

• Задачи для самостоятельного решения
• 1)Известно, что около четырёхугольника ABCD
можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке
K. Докажите, что треугольники KAB и KCD подобны.
• 2)В треугольнике ABC с тупым углом ACB проведены
высоты AA1 и BB1. Докажите, что треугольники A1CB1
и ACB подобны.
• 3)Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD =16 . Докажите, что треугольники
CBD и BDA подобны.

Рабочие листы с треугольниками

Раскрашивание, обведение и рисование треугольников

Познакомьте детей с миром треугольников с помощью этой подборки рабочих листов с упражнениями, такими как определение треугольников в реальной жизни, раскрашивание, обведение и рисование треугольников и т. д., и многое другое. более увлекательные занятия.

Рабочие листы по классификации треугольников

Этот набор рабочих листов по классификации треугольников состоит из таких навыков, как определение треугольников по сторонам как равнобедренным, равносторонним и разносторонним, а по углам как острым, тупым и равносторонним. Найдите упражнения для классификации треугольников, предлагающих сочетание углов и сторон.

Периметр треугольника. Рабочие листы

Закрепите навыки работы с рабочими листами по нахождению периметра треугольника с размерами, представленными в виде целых чисел, десятичных знаков и дробей. Найдите периметр разностороннего, равнобедренного и равностороннего треугольника, определите меру сторон с помощью периметра и решите текстовые задачи.

Рабочие листы площади треугольника

Интенсифицируйте практику с помощью этого сборника рабочих листов площади треугольника, в котором представлены такие навыки, как нахождение площади разносторонних, равнобедренных и равносторонних треугольников, нахождение недостающего основания или высоты, нахождение площади с мерами, предлагаемыми в виде целых чисел, десятичные знаки, дроби и алгебраические выражения, и это лишь некоторые из них.

Углы в треугольнике. Рабочие листы

Включая множество упражнений, этот набор углов в треугольнике с рабочими листами помогает изучить применение свойства суммы углов и теоремы о внешнем угле для нахождения указанных углов с целыми числами и алгебраическими выражениями. Решите для «x» и попробуйте решить ряд сложных задач.

Рабочие листы медианы и центроида треугольника

Пройдитесь по листам медианы и центроида, предлагая широкий спектр упражнений, таких как нахождение указанной длины, нахождение середины, центроида, уравнения медиан и многое другое.

Рабочие листы по теореме о неравенстве треугольника

Рабочие листы по теореме о неравенстве треугольника включают в себя обширные навыки, такие как проверка того, образуют ли стороны треугольник или нет, нахождение диапазона возможных измерений, наименьшее и максимально возможное целочисленное измерение третьей стороны. Кроме того, включены рабочие листы для пересмотра нескольких ответов.

Теорема Пифагора о неравенстве Рабочие листы

Треугольник можно легко классифицировать, если известны меры его угла. Но можно ли определить тип треугольника по длинам его сторон? Подключитесь к нашим рабочим листам теоремы Пифагора о неравенстве и раскопайте ответ!

Рабочие листы по конгруэнтным треугольникам

Рабочие листы по конгруэнтным треугольникам помогают легко освоить понятие конгруэнтности. Этот ассортимент содержит адекватные PDF-файлы по определению конгруэнтных частей, таких как углы и стороны, написанию утверждения о конгруэнтности, идентификации постулатов, доказательству конгруэнтности прямоугольного треугольника и т. д.

Рабочие листы по подобным треугольникам

Рабочие листы по подобным треугольникам позволяют попрактиковаться в определении масштабных коэффициентов, идентификации подобных треугольников, вычислении длин сторон, написании утверждений о сходстве; поиск сходства на основе теорем SSS, SAS и AA, решение алгебраических выражений и понимание подобия прямоугольных треугольников.

Рабочие листы для упорядочивания сторон и углов треугольника

Погрузитесь в практику с этим набором рабочих листов в формате pdf и научитесь упорядочивать стороны треугольника, анализируя размеры его углов, и упорядочивать углы, анализируя длины его сторон.

Треугольники Дополнительные вопросы по математике для 9 класса Глава 7 с решениями Ответы

Здесь мы предлагаем дополнительные вопросы по математике для 9 класса Треугольники Глава 7 с ответами Решения, дополнительные вопросы для 9 класса по математике были разработаны учителями-предметниками.

Дополнительные вопросы по математике для 9 класса. Глава 7. Треугольники с решениями.
Решение:
Мы знаем, что каждый внутренний угол равностороннего треугольника равен 60°.
∴ Каждый внешний угол = 180° – 60° = 120°

Вопрос 2.
Если в ∆ABC ∠A = ∠B + ∠C, то напишите форму данного треугольника.
Решение:
Здесь ∠A = ∠B + ∠C
И в ∆ABC, по свойству суммы углов, мы имеем
∠A + ∠B + C = 180°
⇒ ∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°
Следовательно, данный треугольник прямоугольный.

Вопрос 3.
В ∆PQR, PQ = QR и ∠R = 50°, затем найдите меру ∠Q.
Решение:
Здесь, в ∆PQR, PQ = QR
⇒ ∠R = ∠P = 50° (дано)
Теперь ∠P + ∠Q  + ∠R = 180°
50° + ∠Q + 50° = 180°
⇒ ∠Q = 180° – 50° – 50°
= 80°

Вопрос 4.
Если ∆SKY ≅ ∆MON по правилу конгруэнтности SSS, то запишите три равенства соответствующих углов.
Решение:
Так как ∆SKY ≅ ∆MON по правилу конгруэнтности SSS, то три равенства соответствующих углов
равны ∠S = ∠M, ∠K = ∠O и ∠Y = ∠N.

Вопрос 5.
Возможно ли ∆ABC, если AB = 6 см, BC = 4 см и AC = 1,5 см?
Решение:
Поскольку 4 + 1,5 = 5,5 ≠ 6
Таким образом, треугольник невозможен.

Вопрос 6.
В ∆MNO, если ∠N = 90°, то укажите наибольшую сторону.
Решение:
Мы знаем, что сторона, противоположная наибольшему углу, самая длинная.
∴ Самая длинная сторона = MO.

Вопрос 7.
В ∆ABC, если AB = AC и ∠B = 70°, найти ∠A.
Решение:
Здесь в ∆ABC AB = AC ∠C = ∠B [∠s opp. равным сторонам ∆)
Теперь ∠A + ∠B + ∠C = 180°
⇒ ∠A + 70° + 70° = 180° [∵ ∠B = 70°]
⇒ ∠A = 180° – 70° – 70° = 40°

Вопрос 8.
В ∆ABC, если AD медиана, то показать, что AB + AC > 2AD.
Решение:

Произведите AD в E так, чтобы AD = DE.
В ∆ADB и ∆EDC имеем
BD = CD, AD = DE и ∠1 = ∠2
∆ADB ≅ ∆EDC
AB = CE
Теперь в ∆AEC имеем
AC + CE > AE
AC + AB > AD + DE
AB + AC > 2AD [∵ AD = DE]

Треугольники Класс 9 Дополнительные вопросы Краткий ответ Тип 1

Вопрос 1.
На данном рисунке AD = BC и BD = AC, докажите что ∠DAB = ∠CBA.
Решение:

В ∆DAB и ∆CBA имеем
AD = BC [данные]
BD = AC [данные]
AB = AB [общие]
∴ ∆DAB ≅ ∆CBA [по аксиоме конгруэнтности SSS]
Таким образом, ∠DAB =∠CBA [c.p.c.t.]

Вопрос 2.
На данном рисунке ∆ABD и ABCD равнобедренные треугольники с одним и тем же основанием BD. Докажите, что ∠ABC = ∠ADC.
Решение:

В ∆ABD имеем
AB = AD (дано)
∠ABD = ∠ADB [углы, противоположные равным сторонам равны] …(i)
В ∆BCD имеем
CB = CD
⇒ ∠CBD = ∠CDB [углы, противоположные равным сторонам, равны] … (ii)
Складывая (i) и (ii), мы получаем
∠ABD + ∠CBD = ∠ADB + ∠CDB
⇒ ∠ABC = ∠ADC

Вопрос 3.
Если на данном рисунке ∠1 = ∠2 и ∠3 = ∠4, то докажите, что BC = CD.
Решение:

В ∆ABC и ACDA имеем
∠1 = ∠2 (дано)
AC = AC [общее]
∠3 = ∠4 [дано]
Итак, используя аксиому конгруэнтности ASA,
∆ABC ≅ ∆CDA
Так как соответствующие части конгруэнтных треугольников равны
∴ BC = CD

Вопрос 4.
На данном рисунке ∠B < ∠A и ∠C < ∠D. Докажите, что AD < BC.

Решение:
Здесь ∠B < ∠A
⇒ AO < BO …..(i)
и ∠C < ∠D
⇒ OD < CO …..(ii)
[∴ сторона, противоположная большему углу, длиннее]
Добавление (i) и (ii), получаем
AO + OD < BO + CO
AD < BC

Вопрос 5.
На данном рисунке AC > AB и D — точка на AC такая, что AB = AD. Докажите, что BC > CD.
Решение:

Здесь, в ∆ABD, AB = AD
∠ABD = ∠ADB
[∠s opp. равным сторонам ∆]
In ∆BAD
доб. ∠BDC = ∠BAD + ∠ABD
⇒ ∠BDC > ∠ABD ….(ii)
Также в ∆BDC .
доб. ∠ADB > ∠CBD …(iii)
Из (ii) и (iii) мы имеем
∠BDC > CD [∵ сторон напротив. к большему углу больше]

Вопрос 6.
В треугольнике ABC точка D является серединой стороны AC, так что BD = \(\frac{1}{2}\) AC. Докажите, что угол ∠ABC прямой.
Решение:

Здесь, в ∆ABC, D — середина AC.
⇒ AD = CD = \(\frac{1}{2}\)AC …(i)
Кроме того, BD = \(\frac{1}{2}\)AC… (ii) [дано]
From (i) и (ii), мы получаем
AD = BD и CD = BD
⇒ ∠2 = ∠4 и ∠1 = ∠3 …. .(iii)
В ∆ABC имеем
∠ABC + ∠ACB + ∠CAB = 180°
⇒ ∠1 + ∠2 + ∠3 + ∠ 4 = 180°
⇒ ∠1 + ∠2 + ∠1 + ∠2 = 180° [используя (iii)]
⇒ 2(∠1 + ∠2) = 180°
⇒ ∠1 + ∠2 = 90°
Следовательно, ∠ABC = 90°

Треугольники Класс 9 Дополнительные вопросы Краткий ответ Тип 2

Вопрос 1.
ABC — равнобедренный треугольник, в котором AB = AC. P и Q — точки на AB и AC соответственно, такие, что AP = AQ. Докажите, что CP = BQ.
Решение:

В ∆ABQ и ∆ACP имеем
AB = AC (данные)
∠BAQ = ∠CAP [общие]
AQ = AP (данные)
∴ По критериям соответствия SAS имеем
∆ABQ ≅ ∆ACP
CP = BQ

Вопрос 2.
На данной фигуре ∆ABC и ∆DBC — два равнобедренных треугольника на одном основании BC, а вершины A и D лежат на одной стороне BC, AD продолжается до пересечения BC в точке P. Покажите, что: (i) ∆ABD ≅ ∆ACD (ii) ∆ABP ≅ ∆ACP

Решение:
(i) В ∆ABD и ∆ACD
AB = AC [данные]
BD = CD [данные]
AD = AD [общие]
∴ По аксиоме конгруэнтности SSS имеем
∆ABD ≅ ∆ACD
(ii) В ∆ABP и ∆ACP
AB = AC [дано]
∠BAP = ∠CAP [c. p.cit. как ∆ABD ≅ ∆ACD]
AP = AP [общий]
∴ По аксиоме конгруэнтности SAS имеем
∆ABP ≅ ∆ACP

Вопрос 3.
На данном рисунке дано, что AE = AD и BD = СЕ. Докажите, что ∆AEB ≅ ∆ADC.

Решение:
Имеем AE = AD … (i)
и CE = BD … (ii)
При добавлении (i) и (ii)
имеем AE + CE = AD + BD
⇒ AC = AB
Теперь, в ∆AEB и ∆ADC,
имеем AE = AD [дано]
AB = AC [доказано выше]
∠A = ∠A [общее]
∴ По аксиоме конгруэнтности SAS имеем
∆AEB = ∆ ADC

Вопрос 4.
На данном рисунке в ∆ABC ∠B = 30°, ∠C = 65° и биссектриса ∠A пересекается с BC в X. Расположите AX, BX и CX в порядке возрастания величины.

Решение:
Здесь AX делит пополам ∠BAC.
∴ ∠BAX = ∠CAX = x (скажем)
Теперь ∠A + ∠B + C = 180° [свойство суммы углов треугольника]
⇒ 2x + 30° + 65° = 180° 9{\circ}}{2}\) = 42,59
В ∆ABX имеем x > 30°
BAX > ∠ABX
⇒ BX > AX (сторона против большего угла больше)
⇒ AX < BX
Также , в ∆ACX имеем 65° > x
⇒ ∠ACX > ∠CAX
⇒ AX > CX [сторона опп. к большему углу больше]
⇒ CX > AX … (ii)
Следовательно, из (i) и (ii) имеем
CX < AX < BX

Вопрос 5.
На рисунке «S» — это любая точка на стороне QR APQR. Докажите, что PQ + QR + RP > 2PS.

Решение:
В ∆PQS имеем
PQ + QS > PS …(i)
[∵ сумма любых двух сторон треугольника больше третьей стороны]
В ∆PRS имеем
RP + RS > PS …( ii)
Добавляя (i) и (ii), мы имеем
PQ + (QS + RS) + RP > 2PS
Следовательно, PQ + QR + RP > 2PS. [∵ QS + RS = QR]

Вопрос 6.
Если два равнобедренных треугольника имеют общее основание, докажите, что прямая, соединяющая их вершины, делит их пополам под прямым углом.
Решение:
Здесь два треугольника ABC и BDC имеют общую
по основанию BC, так что AB = AC и DB = DC.
Теперь в ∆ABD и ∆ACD

AB = AC [данные]
BD = CD [данные]
AD = AD [общие]
∴ ΔABD ≅ ΔΑCD [по аксиоме конгруэнтности SSS]
⇒ ∠1 [данные] c.p.c.t.]
Опять же, в ∆ABE и ∆ACE имеем
AB = AC [дано]
∠1 = ∠2 [доказано выше]
AE = AE [общее]
∆ABE = ∆ACE [по аксиоме конгруэнтности SAS]
BE = CE [c. p.c.t.]
и ∠3 = ∠4 [c.p.c.t.]
Но ∠3 + ∠4 = 180° [линейная пара]
⇒ ∠3 = ∠4 = 90°
Следовательно, AD делит BC пополам справа углы.

Треугольники Класс 9 Дополнительные вопросы Тип полного ответа

Вопрос 1.
На данном рисунке AP и DP являются биссектрисами двух смежных углов A и D четырехугольника ABCD. Докажите, что 2 ∠APD = ∠B + 2C.

Решение:
Здесь AP и DP являются биссектрисами углов ∠A и ∠D
∴ ∠DAP = \(\frac{1}{2}\)∠DAB и ∠ADP = \(\frac{1}{ 2}\)∠ADC ……(i)
In ∆APD, ∠APD + ∠DAP + ∠ADP = 180°
⇒ ∠APD + \(\frac{1}{2}\) ∠DAB + \(\ frac{1}{2}\)∠ADC = 180°
⇒ ∠APD = 180° – \(\frac{1}{2}\)(∠DAB + ∠ADC)
⇒ 2∠APD = 360° – (∠DAB + ∠ADC) ……(ii)
Кроме того, ∠A + ∠B + C + ∠D = 360°
∠B + 2C = 360° – (∠A + ∠D)
∠B + C = 360° – (∠DAB + ∠ADC) ……(iii)
Из (ii) и (iii) получаем
2∠APD = ∠B + ∠C

Вопрос 2
На рисунке ABCD — квадрат, EF параллелен диагонали BD и EM = FM. Докажите, что
(i) DF = BE (i) AM делит пополам ∠BAD.

Решение:
(i) EF || BD = ∠1 = ∠2 и ∠3 = ∠4 [соответствующие ∠s]
Кроме того, ∠2 = ∠4
⇒ ∠1 = ∠3
⇒ CE = CF (стороны напротив равны ∠s ∆)
∴ DF = BE [∵ BC – CE = CD – CF)

(ii) В ∆ADF и ∆ABE имеем
AD = AB [стороны квадрата]
DF = BE [доказано выше]
∠D = ∠B = 90°
⇒ ∆ADF ≅ ∆ABE [по аксиоме конгруэнтности SAS]
⇒ AF = AE и ∠5 = ∠6 … (i) [c.p.c.t.]
In ∆AMF и ∆AME
AF = AE [доказано выше]
AM = AM [общий]
FM = EM (дано)
∴ ∆AMF ≅ ∆AME [по аксиоме конгруэнтности SSS]
∴ ∠7 = ∠8 …(ii) [c.p.c.t.]
Добавление (i) и ( ii) имеем
∠5 + ∠7 = ∠6 + ∠8
∠DAM = ∠BAM
∴ AM делит пополам ∠BAD.

Вопрос 3.
В прямоугольном треугольнике ABC, прямоугольном в точке C, M является серединой гипотенузы AB. C соединяется с M и приводится в точку D так, что DM = CM. Точка D соединяется с точкой B (см. рис.). Покажите, что: (i) ∆AMC ≅ ∆BMD (ii) ∠DBC = 90° (ii) ∆DBC ≅ ∆ACB (iv) CM = \(\frac{1}{2}\)AB

Решение:
Дано: ∆ACB, где 4C = 90°, а M — середина AB.
Доказать:
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC = 90°
(iii) ∆DBC ≅ ∆ACB
(iv) CM = \(\frac{1}{2}\)AB
Доказательство: Рассмотрим ∆AMC и ∆BMD,
имеем AM = BM [дано]
CM = DM [по построению]
∠AMC = ∠BMD [вертикально противоположные углы]
∴ ∆AMC ≅ ∆BMD [по аксиоме конгруэнтности SAS]
⇒ AC = DB …(i) [по c.p.c.t.]
и ∠1 = ∠2 [по c.p.c.t.]
Но ∠1 и ∠ 2 — альтернативные углы.
⇒ БД || CA
Сейчас, BD || CA и BC трансверсальны.
∴ ∠ACB + ∠CBD = 180°
⇒ 90° + CBD = 180°
⇒ ∠CBD = 90°
В ∆DBC и ∆ACB,
имеем CB = BC [общий]
DB = AC [используя (i)]
∠CBD = ∠BCA
∴ ∆DBC ≅ ∆ACB
⇒ DC = AB
⇒ \(\frac{1}{2}\)AB = \(\frac{1 }{2}\)DC
⇒ \(\frac{1}{2}\)AB = CM или CM = \(\frac{1}{2}\)AB (∵ CM = \(\frac{1 }{2}\)DC)

Вопрос 4.
На рисунке треугольник ABC равнобедренный, AB = AC. D — точка внутри ∆ABC такая, что ∠BCD = ∠CBD. Докажите, что AD делит ∠BAC пополам на ∆ABC.

Решение:
В ∆BDC имеем ∠DBC = ∠DCB (дано).
⇒ CD = BD (стороны напротив равны ∠s ∆DBC)
Теперь, в ∆ABD и ∆ACD,
имеем AB = AC [данные]
BD = CD [доказано выше]
AD = AD [общие]
∴ Используя аксиому конгруэнтности SSS, мы получаем
∆ABD ≅ ∆ACD
⇒ ∠BAD = ∠CAD [c.p.ç.t.]
Следовательно, AD делит ∠BAC пополам на ∆ABC.

Вопрос 5.
Докажите, что два треугольника равны, если любые два угла и сторона, прилежащая к ним, одного треугольника равны любым двум углам и стороне, прилежащей к другому треугольнику.
Решение:

Дано: два как ABC и DEF, в которых
∠B = ∠E,
∠C = ∠F и BC = EF
Доказать: ∆ABC = ∆DEF
Доказательство: У нас есть три возможности
Случай I. Если AB = DE,
, мы имеем AB = DE,
∠B = ∠E и BC = EF.
Итак, по аксиоме конгруэнтности SAS имеем ∆ABC ≅ ∆DEF

Случай II. Если AB < ED, то возьмем точку Mon ED
такую, что EM = AB.
Присоединиться к MF.
Теперь в ∆ABC и ∆MEF,
мы имеем
AB = ME, ∠B = ∠E и BC = EF.
Итак, по аксиоме конгруэнтности SAS,
мы имеем ΔΑΒC ≅ ΔΜEF
⇒ ∠ACB = ∠MFE
Но ∠ACB = ∠DFE
∴ ∠MFE = ∠DFE

Что возможно только тогда, когда FM совпадает с B FD, т. е. M совпадает с D.
Таким образом, AB = DE
∴ В ∆ABC и ∆DEF имеем
AB = DE,
∠B = ∠E и BC = EF
Итак, согласно аксиоме конгруэнтности SAS, мы имеем
∆ABC ≅ ∆DEF
Случай III. Когда AB > ED
Возьмем точку M на ED, произведенную
так, что EM = AB.
Join MF
Действуя как в случае II, можно доказать, что
∆ABC = ∆DEF
Отсюда во всех случаях имеем
∆ABC = ∆DEF.

Вопрос 6.
На данном рисунке сторона QR доведена до точки S. Если биссектрисы ∠PQR и ∠PRS пересекаются в точке T,
докажите, что ∠QTR = \(\frac{1}{2}\ ) ∠КПР.

Решение:
Здесь QT — биссектриса угла ∠PQR

Треугольники Класс 9 Дополнительные вопросы HOTS

Вопрос 1.
Покажите, что разность любых двух сторон треугольника меньше, чем разность третьей стороны.
Решение:

Рассмотрим треугольник ABC
Доказать:
(i) AC – AB < BC
(ii) BC – AC < AB
(iii) BC – AB < AC
Построение: Возьмем точку D на AC
так, что AD = AB.
Присоединиться к BD.
Доказательство: В ∆ABD имеем ∠3 > ∠1 …(i)
[∵ внешний ∠ больше, чем каждый из внутренних противоположных углов в ∆]
Аналогично, в ∆BCD имеем
∠2 > ∠4 …..(ii) [∵ доб. ∠ больше внутреннего opp. угол в a ∆]
В ∆ABD имеем
AD = AB [по построению]
∠1 = ∠2 …(iii) [углы опп. равные стороны равны в треугольнике]
Из (i), (ii) и (iii) имеем
⇒ ∠3 > ∠4 =
⇒ BC > CD
⇒ CD < BC
AC – AD < BC
AC – AB < BC [∵ AD = AB]
Следовательно, AC – AB < BC
Аналогично можно доказать
BC – AC < AB
и BC – AB < AC

Вопрос 2.
На рисунке O – внутренняя точка ∆ABC. BO встречается с AC в точке D. Покажите, что OB + OC < AB + AC.

Решение:
В ∆ABD, AB + AD > BD …(i)
∵ Сумма любых двух сторон треугольника больше третьей стороны. А еще у нас
BD = BO + OD
AB + AD > BO + OD ….(ii)
Аналогично, в ∆COD имеем
OD + DC > OC … (iii)
При сложении (ii) и (iii) мы Имеем
АБ + АД + ОД + ДС > БО + ОД + ОС
⇒ АБ + АД + ДС > БО + ОС
⇒ АБ + АС > ОВ + ОС
или ОБ + ОС < АБ + АС
Следовательно, доказано.

Треугольники, класс 9, дополнительные вопросы, основанные на ценности (VBQ)

Вопрос 1.
Добровольцы математического клуба начинают кампанию по развитию школы и ее окружения под руководством Свахха Бхарата Абхияна. Они сделали свой собственный логотип для этой кампании. Какие ценности приобретает математический клуб?
Если дано, что ∆ABC ≅ ∆ECD, BC = AE.
Докажите, что ∆ABC ≅ ∆CEA.

Решение:
Здесь дано, что
∆ABC ≅ ∆ECD
AB = CE [c.p.c.t.]
BC = CD [c.p.c.t.]
AC = ED [c.p.c.t.]
Теперь, в ∆07CEA9 0 AE [дано]
AB = EC [доказано выше]
AC = AC [общее]
∴ Используя аксиому конгруэнтности SSS, мы имеем
∆ABC ≅ ∆CEA
Ценность: Чистота и социальная забота.