Произведение двух событий. Условная вероятность. Теорема умножения вероятностей. Теория вероятностей
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Произведение событий
Произведением двух событий и называют событие , состоящее в совместном появлении (совмещении) этих событий. Например, если – деталь годная, – деталь окрашенная, то – деталь годна и окрашена.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если – появление герба соответственно в первом, втором и третьем бросаниях монеты, то – выпадение герба во всех трех испытаниях.
Условная вероятность
Случайное событие определено как
событие, которое при осуществлении совокупности условий
может произойти или не произойти.
Если при вычислении вероятности события никаких других ограничений, кроме
условий
, не налагается, то такую вероятность называют безусловной;
Условной вероятностью называют вероятность события , вычисленную в предположении, что событие уже наступило.
Теорема умножения вероятностей
Рассмотрим два события:
и
; пусть вероятности
и
известны. Как
найти вероятность совмещения этих событий, т.
е. вероятность того, что появится и событие
и событие
? Ответ на этот вопрос
дает теорема умножения.
Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Независимые события.
Теорема умножения вероятностей для независимых событий
Пусть вероятность события не зависит от появления события .
Событие называют независимым от события , если появление события не изменяет вероятности события , то есть если условная вероятность события равна его безусловной вероятности:
Если событие не зависит от события , то и событие не зависит от события – это означает, что свойство независимости событий взаимно.
Для независимых событий теорема умножения вероятностей имеет вид:
Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
Смежные темы решебника:
- Классическая вероятность.
Вероятность случайного события - Теорема сложения вероятностей
- Формула полной вероятности и формула Байеса
Вероятность случайного событияПримеры решения задач
Пример 1
В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие ), если при первом испытании был извлечен черный шар (событие .
Решение
После первого испытания в урне осталось 5 шаров, из них 3 белых.
Искомая условная вероятность:
Этот же результат можно получить по формуле:
Вероятность появления белого шара при первом испытании:
Найдем вероятность того, что в первом испытании появится черный шар, а во втором – белый. Общее число исходов, совместного появления двух шаров, безразлично какого цвета, равно числу размещений:
Из этого
числа исходов событию
благоприятствует
исходов.
Следовательно:
Искомая условная вероятность:
Ответ: .
Пример 2
У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков – конусный, а второй – эллиптический.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Вероятность того, что первый валик окажется конусным (событие ):
Вероятность того, что второй валик окажется эллиптическим (событие ), вычисленная в предположении, что первый валик – конусный, то есть условная вероятность:
По теореме умножения вероятностей, искомая вероятность:
Ответ:
.
Пример 3
Слово «арифметика» разрезали на буквы, 5 из них выложили в ряд. Какова вероятность того, что получится слово «фирма»?
Решение
Вероятность вытащить первой букву Ф из 10 равна 1/10
Вероятность вытащить букву И из оставшихся 9 букв, две из которых И, равна 2/9
Вероятность вытащить букву Р из оставшихся 8 букв равна 1/8
Вероятность вытащить букву М из оставшихся 7 букв равна 1/7
Вероятность вытащить букву А из оставшихся 6 букв, две из которых А, равна 2/6
Воспользуемся теоремой умножения вероятностей. Так как имеем независимые события, то искомая вероятность:
Ответ:
Пример 4
Для
сигнализации об аварии установлены три независимо работающих сигнализатора. Два
из них срабатывают с вероятностью 0,8, а 1 – с вероятностью 0,95. Найти
вероятность того, что при аварии сигнализация сработает.
Решение
События:
– сработал 1-й сигнализатор;
– сработал 2-й сигнализатор;
– сработал 3-й сигнализатор;
Для того, чтобы сработала сигнализация, необходимо, чтобы сработал хотя ба один сигнализатор
Пусть событие – сработал хотя бы один сигнализатор
Противоположное событие – не сработал ни один сигнализатор
Ответ:
Пример 5
Две фотомодели снимаются для журнала мод, первая – с вероятностью 0,9, вторая – с вероятностью 0,7. Какова вероятность того, что в следующем номере журнала появятся снимки: а) обеих девушек; б) только первой; в) хотя бы одной из них?
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Пусть события:
– первая фотомодель появилась в журнале;
– вторая фотомодель появилась в журнале;
а) Пусть событие – в журнале появились обе девушки
б) Пусть событие – в журнале появилось фото только первой девушки
в) Пусть событие – в журнале появилось фото хотя бы одной девушки. Противоположное событие – в журнале фото обеих девушек не напечатали
Тогда искомая вероятность:
Ответ: а) ; б) ; в) .
Пример 6
В задаче приведены схемы элементов, образующих цепь с одноим входом и одним выходом.
Предполагается, что
отказы элементов являются независимыми в совокупности событиями. Отказ любого
из элементов приводит к прерыванию сигнала в той ветви цепи, где находится
данный элемент.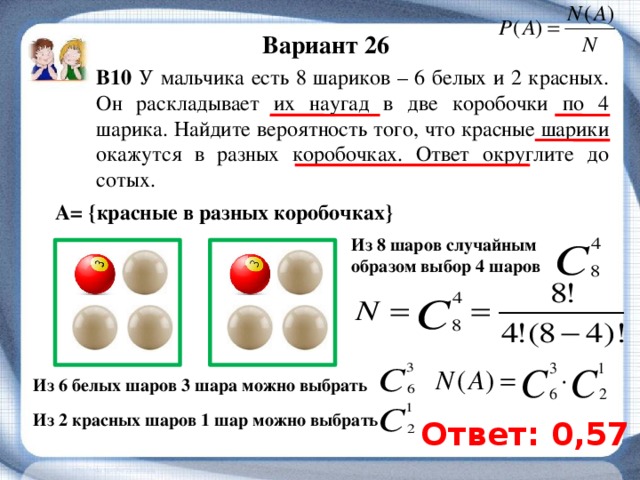
Решение
Все элементы цепи соединены последовательно. Сигнал пройдет со входа на выход только в том случае, если безотказно работают все 5 элементов. Найдем вероятность безотказной работы для каждого элемента.
Вероятность того, что сигнал пройдет со входа на выход:
Ответ: .
Пример 7
Приведены схемы
соединения элементов, образующих цепь с одним входом и одним выходом.
Предполагается, что отказы элементов являются независимыми в совокупности
событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви
цепи, где находится данный элемент.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Пусть событие -сигнал пройдет со входа на выход. -сигнал не пройдет со входа на выход. Это произойдет в том случае, если откажут все 5 элементов.
Тогда:
Так как события и образуют полную группу событий, то:
Ответ: .
Пример 8
Приведены схемы
соединения элементов, образующих цепь с одним входом и одним выходом.
Предполагается, что отказы элементов являются независимыми в совокупности
событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви
цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5
соответственно равны
;
;
;
;
. Найти вероятность того, что сигнал пройдет со входа
на выход.
Решение
Пусть событие -сигнал пройдет со входа на выход
-сигнал не пройдет со входа на выход
-сигнал не пройдет участок из элементов 1,2,3
-сигнал не пройдет участок из элементов 4,5
Вероятность того, что сигнал пройдет со входа на выход:
Ответ: .
Задачи контрольных и самостоятельных работ
Задача 1
Клиент
выбирает банк для получения ипотечного кредита по нескольким показателям:
стабильность банка, процентная ставка, условия досрочного погашения кредита.
Статистика показывает, что клиенты данного банка удовлетворены первым
показателем с вероятностью 0.7, вторым – с вероятностью 0.6, третьим – с
вероятностью 0.8. Какова вероятность того, что клиент, обратившись в банк,
будет удовлетворен:
а) всеми тремя показателями;
б) только двумя показателями;
в) хотя бы одним из показателей?
Задача 2
Найти вероятности указанных событий, пользуясь правилами сложения и умножения вероятностей.
В ящике находятся 15 деталей, 5 из которых бракованные. Наудачу отобраны 3 детали. Какова вероятность, что все они не окажутся бракованными.
Задача 3
Каждую букву слова написали на одной карточке. Карточки смешивают и вынимают без возврата по одной. Какова вероятность, что карточки будут вынуты в порядке следования букв в слове «теория»?
Задача 4
Устройство
состоит из трех элементов, работающих независимо. Вероятность безотказной
работы (за время t) первого, второго и третьего элементов
соответственно равны 0,6; 0,7; 0,8.
Найти вероятность того, что за время t безотказно будут работать: а)только один
элемент, б)только два элемента, в) все три элемента.
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Задача 5
Сколько надо бросить игральных костей, чтобы с вероятностью, меньше 0,3, можно было ожидать, что ни одной из выпавших граней не появится шесть очков?
Задача 6
При изготовлении детали заготовка должна пройти три операции. Предполагая появление брака на отдельных операциях событиями независимыми, найти вероятность изготовления стандартной детали, если вероятность брака на первой операции равна 0,02, на второй 0,01, на третьей 0,03.
Задача 7
Слово
«СТАТИСТИКА» составлено из карточек, на каждой из которых написана одна буква.
Затем карточки смешивают и вынимают без возврата по одной. Найти вероятность
того, что буквы вынимаются в порядке слова «ТИСКИ».
Задача 8
В схеме, изображенной на рисунке, элементы k1, k2, k3, k4, k5 работают независимо друг от друга и пропускают электрический ток с вероятностями p1=0.9; p2=0.8; p3=0.7; p4=0.6; p5=0.5 соответственно. С какой вероятностью ток пройдет от A к B?
Задача 9
Решить задачу, используя теоремы сложения и умножения вероятностей.
Вычислительный центр, который должен производить непрерывную обработку информации, располагает двумя вычислительными устройствами. Известно, что вероятность отказа каждого из них за время равна 0,1. Найти вероятность безотказной работы за время : а) каждого устройства; б) хотя бы одного устройства; в) одного устройства.
Задача 10
Из колоды
в 36 карт наудачу извлекаются 3 карты.
Найти вероятность того, что все
извлеченные карты разных мастей.
Задача 11
В урне имеется 5 шаров с номерами от 1 до 5. Извлекают по одному без возвращения 3 шара. Найти вероятность последовательно появляются шары с номерами 1,2,3.
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Решение задач по теории вероятности. Условная вероятность
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике.
Базовый уровень Сложные задачи
Решение задач по
теории вероятности
Условная вероятность
Выполнила :ЗУБАРЕВА ЕЛЕНА АЛЕКСАНДРОВНА
Учитель математики МБОУ
Останкинской СШ
Задача 1. На столе лежат 4 синих и 3 красных карандаша.Редактор
дважды наугад
берет по одному карандашу и обратно их не
кладет.Найти вероятность того,что вторым был взят красный
карандаш при условии ,что первым был синий
События А-первым вынут синий карандаш
В-вторым был взят красный карандаш
После извлечения со стола первым синего карандаша (произошло
событие А)там останутся 3 синих и 3 красных карандаша.
В/А-вторым был взят красный карандаш
при условии , что первым был синий
3
1
P ( В / А)
6
2
Задача 2.В барабане находится 10 лотерейных билетов,из них
2 выигрышных .Из барабана 2 раза вынимают по одному
билету ,не возвращая их обратно.Какова вероятность
того,что:в первый раз был вынут выигрышный билет,а во
второй раз-билет без выигрыша.
Событие А-первым вынут выигрышный билет
В-второй вынут билет без выигрыша
Вероятность того,что сначала вынут выигрышный билет
р(А)=0,2
Вероятность того ,что вторым вынут билет без выигрыша
(произошло событие В)вычисляется при условии,что первым
уже вынули выигрышный билет Р(В/А)=8/9
АВ -первый раз был вынут выигрышный билет,а во
второй раз-билет без выигрыша.
Р(АВ)=р(А)р(В/А)=8/45
Задача3
В вазе лежат 7 яблок и 4 груши.Не глядя из вазы
последовательно берут 2 фрукта,не возвращая их обратно.Какова
вероятность того,что вторым будет извлечено яблоко,при условии,что
первой была извлечена груша?
События А-первой извлечена груша
В-вторым извлечено яблоко
После извлечения из вазы первой груши там останутся 7 яблок и 3
груши.
Появлению яблока вторым из десяти оставшихся
благоприятствуют семь исходов
Р(В/А)=0,7
Задача 4.Из ящика,содержащего 4 белых и 5 красных шаров,2 раза
наугад извлекают по одному шару,не возвращая их обратно.
Найти
вероятность того,что вторым извлечен красный шар при условии,что
первым также оказался красный шар
События А-первым вынут красный шар
В-вторым вынут красный шар
После извлечения из ящика первым красного шара(произошло
событие А)там останутся 4 белых и 4 красных шара
Появлению красного шара
благоприятствуют 4 события
Р(В/А)=0,5
вторым
из
8
оставшихся
Задача 5.Из колоды в 36 карт последовательно наугад вынимаются и
не возвращаются 2 карты.Какова вероятность того,что оба раза
извлекались карты красной масти
События А-первой извлекли карту красной масти
В-второй извлекли карту красной масти
Всего исходов 36,т.к. всего 36 карт.
Исходов , благоприятствующих наступлению события А,равно
18,т.к.всего 18 карт красной масти.
18 1
Р(А)= 36 2
После извлечения из колоды карты красной масти (произошло
событие А)там останутся 18 карт черной масти и 17 карт красной масти.
Появлению карты красной масти второй из 35
оставшихся благоприятствует 17 событий
Р(В/А)= 17
35
Р(АВ)=р(А)Р(В/А)=
17
70
Источник материала:
Учебник :Алгебра и начала математического
анализа 11 класс
Автор :Ю.
М.Колягин,М.В.Ткачева,Н.Е.Федорова,
М.И.Шабунин
English Русский Правила
Решенные задачи условной вероятности
В этой статье вы узнаете, что такое условная вероятность и как решать вопросы, связанные с этим понятием. Итак, давайте начнем.
Условная вероятность
В нашей жизни случайным образом происходят два типа событий:
а) Независимые события
На эти события не влияют другие события. Например, бросая кости по полу. На это событие не влияет никакое другое событие; поэтому оно называется независимым событием. В математике у нас есть обозначения для всего. Обозначим простую вероятность как:
P(A)
b) Зависимые события
Эти события зависят от других событий, т. е. на них влияют другие события.
Предположим, вы выбрали шар из набора из 8 цветных шаров и не заменяете его. В следующий раз вы выбираете другой мяч из набора. Во второй раз вероятность меняется, потому что в начале общее количество шаров было 8, а в следующий раз осталось 7 шаров.
Следовательно, второе событие зависит от первого. Однако если есть условие, что мяч заменяется каждый раз, когда его выбирают, то события будут независимыми.
Условная вероятность определяет вероятность события, которое зависит от другого события.
Математическое обозначение условной вероятности:
P(A|B)
Читается как вероятность события A при данном событии B . Формула для нахождения условной вероятности двух событий A и B приведена ниже:
Мы также можем поменять местами стороны этой формулы в соответствии с вопросом следующим образом:
Теперь мы решим несколько примеров условной вероятности, чтобы лучше понять концепцию.
Лучшие репетиторы по математике
Поехали
Пример 1
Какова вероятность выбрать две дамы из колоды из 52 карт?
Решение
Чтобы решить проблемы, связанные с картами в колоде, вы должны знать, какие типы карт присутствуют в каждой колоде.
Свойства колоды приведены ниже:
- В колоде четыре масти
- Две масти с черными картами и две красные
- В каждой масти по 13 карт. К этим 13 картам относятся дама, король, валет, туз, 2, 3, 4, 5, 6, 7, 8, 9 и 10.
В колоде из 52 карт есть 4 карты дамы. Так как нам нужно выбрать две карты из колоды, значит, сначала найдем вероятность выбора первой карты из колоды.
Количество карт дам в колоде = 4
Общее количество карт в колоде = 52
Вероятность выбора дамы из колоды =
Теперь вычислим вероятность выбора второй карты из колоды.
Количество карт дамы, оставшихся в колоде = 3
Общее количество карт, оставшихся в колоде = 51
Вероятность подобрать карту дамы, учитывая, что карта дамы уже была выбрана =
In В этом примере нам нужно определить вероятность того, что выпадут две дамы, поэтому мы умножим приведенные выше вероятности:
=
Пример 2
Какова вероятность выбрать две черные карты из колоды из 52 карт?
Решение
Обратитесь к типам карт, присутствующих в колоде.
Из 52 карт в колоде две масти черные, а две красные. Колода делится на 4 масти, в каждой масти 13 карт.
В колоде из 52 карт 26 черных карт. Так как нам нужно выбрать две карты из колоды, значит, сначала найдем вероятность выбора первой карты из колоды.
Количество черных карт в колоде = 26
Общее количество карт в колоде = 52
Вероятность выбора черной карты из колоды =
Теперь вычислим вероятность вторая карта из колоды.
Количество черных карт, оставшихся в колоде = 25
Общее количество карт, оставшихся в колоде = 51
Вероятность подбора черной карты при условии, что одна черная карта уже выбрана =
В этом примере мы должны определить вероятность того, что обе выбранные карты черные. Следовательно, мы будем умножать вероятности следующим образом:
=
=
Пример 3
В пуле 12 шаров. 6 шаров синие, остальные красные. Два шара вынимаются из пула без возврата. Какова вероятность выбрать из пула два красных шара?
Решение
Рассчитаем вероятность первого шара.
Общее количество шаров в пуле = 12
Вероятность того, что случайно выбранный шар красный =
Теперь вычислим вероятность второго шара.
Общее количество шаров, оставшихся в пуле = 11
Количество красных шаров, оставшихся в пуле = 5
Вероятность выбора красного шара во второй раз =
Вероятность того, что два случайно выбранных шара красного цвета = Р(А) х Р(В|А) =
=
Пример 4
В упаковке 8 синих, 7 зеленых и 6 красных ручек. Предположим, вы вытащили из пачки 2 ручки наугад и не вернули их обратно. Затем вы рисуете еще одну ручку. Какова вероятность того, что две вытащенные ручки зеленые, а одна красная?
Решение
Сначала найдем вероятность вытащить из пачки одну зеленую ручку.
Количество зеленых ручек в упаковке = 7
Общее количество ручек в упаковке = 21
Вероятность вытащить из пачки одну зеленую ручку =
Теперь вычислим вероятность того, что во второй раз вытащим зеленую ручку.
Количество зеленых ручек, оставшихся в пакете = 6
Общее количество ручек, оставшихся в пакете = 20
Вероятность взять зеленую ручку во второй раз =
Нам нужно выбрать три ручки. Следовательно, мы также вычислим вероятность того, что из пачки будет взята красная ручка после того, как были выбраны две зеленые ручки.
Количество красных ручек в пачке = 6
Общее количество оставшихся ручек в пачке = 19
Вероятность подобрать третью красную ручку =
Вероятность подобрать две зеленые и одну красную pen =
Пример 5
В классе 35% учеников изучают естествознание и историю. 65% студентов изучают естественные науки. Какова вероятность того, что студент будет изучать историю, если он уже изучает естествознание?
Решение
Доля студентов, изучающих естественные науки и историю = 35%
Вероятность студентов, изучающих естественные науки и историю = P(S и H) = 0,35
Доля студентов, изучающих естественные науки = 65%
Вероятность студентов, изучающих науку = P(S) = 0,65
Условная вероятность | Понимание решения задачи Монти Холла
Обзор
- Узнайте, что такое Проблема Монти Холла.
- Понять условную вероятность с помощью задачи Монти Холла.
Введение
Меня увлек проект, в котором мы стремимся прогнозировать аукционные цены IPL для игроков в крикет таким образом, чтобы каждая франшиза получала максимум своего выбора в своей команде, а каждый игрок получал оптимизированную цену в соответствии с его калибром. Здесь мы использовали классификацию на основе правил, основанную на «условной вероятности».
С тех пор я начал изучать условную вероятность и несколько дней назад столкнулся с очень интересной головоломкой под названием «Проблема Монти Холла». Проблема Монти Холла стала всемирно известной в 1990 году, когда «Мэрилин Вос Савант» дала простое, но логичное решение в популярная еженедельная колонка «Спросите Мэрилин» в журнале Parade в ответ на следующий вопрос-
» Предположим, вы участвуете в игровом шоу и вам предоставляется выбор из трех дверей: за одной дверью стоит машина; позади остальных, козлы.
Вы выбираете дверь, скажем, № 1, и хозяин, который знает, что находится за дверью, открывает другую дверь, скажем, № 3, в которой есть коза. Затем он говорит вам: «Вы хотите выбрать дверь № 2?» Выгодно ли вам изменить свой выбор?»И, как обычно, многие статистики насмехались над ней, говоря, что женщины не понимают статистику, но потом все эти критики съели скромный пирог и оценили «Мэрилин Вос Савант». Все забыли, что на тот момент она была человеком с самым высоким IQ по шкале 9.0243 Книга рекордов Гиннесса
Итак, в этой статье я подробно объясню вам концепцию условной вероятности, используя задачу Монти Холла.
Если вы хотите изучить эти концепции и начать свое путешествие в области науки о данных, ознакомьтесь со следующим курсом: «Введение в науку о данных»
.
Содержание
- Проблема Монти Холла
- Интуитивное объяснение
- Объяснение ситуации
- Подробное объяснение
- Объяснение с условной вероятностью
Проблема Монти Холла
Рассмотрим такой сценарий.
Предположим, вы участвуете в игровом шоу, и вам дают три двери.
Они были в клетке.
За одной дверью машина, а за двумя другими дверями козы. (Но вы не знаете, какая дверь что имеет).
Теперь ведущий игрового шоу просит вас выбрать одну дверь. Обратите внимание, что он знает, что за какой дверью.
Предположим, вы выбрали одну из этих трех дверей. Теперь из оставшихся двух дверей ведущий открывает одну дверь, за которой стоит коза.
И делает вам очень интересное предложение.
Он спрашивает вас, хотите ли вы придерживаться выбора своей двери или хотите выбрать дверь, которая еще не открыта?
Что вы думаете? Вы хотите изменить дверь по своему выбору или хотите придерживаться своего предыдущего выбора? Вы, должно быть, думаете, что это не имеет значения. Потому что осталось всего 2 двери и у каждой из них 0,5 вероятность наличия машины? Верно?
Но это не правильно, давайте разбираться как.
Интуитивное объяснение
Давайте сначала подумаем об этом когнитивно.
Допустим, вместо трех дверей у вас теперь 1000 дверей, из которых только за одной стоит машина, а за 999 будет коза. Вас просят выбрать снова, и вы выбираете дверь. Затем ведущий открывает 998 дверей (из оставшихся 999 дверей), за которыми стоят козы. Две двери все еще остаются закрытыми — одна из них та, которую вы выбрали ранее. Что бы вы сделали?
Вы хотите переключиться сейчас? Вероятно, ответ да, но в чем причина перехода именно сейчас?
Это самоосознание или какая-то познавательная мысль, возникающая в статистическом уме.
Причина, по которой вы хотите переключиться сейчас, заключается в том, что вы поняли, что вероятность выбора двери, за которой стоит машина, при первом предположении составляет 1/1000. Поэтому, если вы не переключитесь, у вас есть только 1/1000 шансов на выигрыш
Объяснение ситуации
Взгляните на изображение ниже, на котором показаны три возможных сценария.
Предположим, за дверью 1 стоит машина, а за двумя другими дверями — козы.
- В первом случае вы выбрали первую дверь
- Хотя во втором случае вы выбрали вторую дверь
- И в третьем случае вы выбрали третью дверь.
Ситуация 1: Вы выбираете первую дверь с первого раза. Ведущий может открыть дверь 2 или 3, потому что у них обоих есть козы. Предположим, ведущий открывает дверь 3, за которой стоит коза. Теперь, если вы переключитесь на дверь 2, вы проиграете.
Ситуация 2: Что, если изначально вы выбрали дверь 2? У двери 1 есть машина, поэтому ведущий не может ее открыть, он должен открыть дверь 3, у которой есть коза. Теперь, если вы переключитесь на дверь 1 с двери 2, вы выиграете.
Ситуация 3: Точно так же, если изначально вы выбрали дверь 3? Опять же, в этом случае, поскольку у двери 1 есть машина, поэтому ведущий не может ее открыть, он должен открыть дверь 2, у которой есть коза.
Теперь, если вы переключитесь на дверь 1 с двери 3, вы снова выиграете.
Таким образом, в случае переключения вы выигрываете 2 случая из 3. Таким образом, вероятность выигрыша после переключения составляет ⅔, а вероятность выигрыша при исходном выборе составляет ⅓.
Подводя итог, можно сказать, что если вы не переключитесь, вы выиграете машину, только если вы правильно угадали дверь изначально Prob = ⅓ = 0,33
Если вы переключитесь, вы выиграете машину, только если вы ошиблись в угадывании правильной двери изначально = ⅔ = 0,66.
Подробное объяснение
Давайте теперь разберемся в этой проблеме с понятиями Вероятности. Типичный случайный эксперимент включает в себя несколько случайно определенных величин.
- Дверь, скрывающая машину.
- Дверь, изначально выбранная игроком.
- Дверь, которую хозяин открывает, чтобы увидеть козу.
Как вы можете видеть выше, эта древовидная диаграмма представляет все возможности этой головоломки.
Местонахождение автомобиля, предположение игрока и открытые двери определяют результат. Все возможные значения результата составляют выборочное пространство. Давайте разберемся, что представляет собой каждый из этих результатов. Например, BAC здесь означает, что машина находится позади B, ваше первоначальное предположение — A, а Хозяин открыл дверь C.
Как вы будете определять события из этого пространства выборки? Например, событие, состоящее в том, что приз находится за дверью C, представляет собой набор исходов:
.{(С,А,В),(С,В,А),(С,С,А),(С,С,В)}
Потому что первая буква представляет местоположение автомобиля в нашей древовидной диаграмме.
Событие, по которому вы изначально выбрали дверь, скрывающую приз, представляет собой набор исходов:
{(А,А,В),(А,А,С),(В,В,А),(В,В,С),(С,С,А),(С,С,В)
Поскольку первая буква представляет местонахождение автомобиля, а вторая буква представляет ваш выбор, который должен быть одинаковым для этого события (изначально выбрана дверь, скрывающая приз), то на самом деле нам нужен набор результатов события, который игрок выигрывает, переключаясь:
{(А,В,С),(А,С,В),(В,А,С),(В,С,А),(С,А,В),(С,В,А) }
Почему? Давайте посмотрим на любой из этих результатов,
CBA означает, что у C есть машина, B был выбран вами, а A раскрыт.
Таким образом, переключение приведет вас к двери C от двери B, у которой на самом деле есть машина. Следовательно, вы выигрываете. Точно так же все эти исходы заставляют вас выигрывать в случае переключения.
Анализируя нашу древовидную диаграмму, мы замечаем, что отмечена ровно половина исходов, а это означает, что игрок выигрывает, переключаясь на половину всех исходов. У вас может возникнуть соблазн заключить, что игрок, который переключается, выигрывает с вероятностью 1/2.
Это неправильно. Причина в том, что эти исходы не равновероятны. Как видите, исход ABC и исход BBA имеют разные вероятности. Почему?
Чемодан 1
Давайте проанализируем, сначала ABC, что означает:
- Автомобиль находится за дверью А
- Вы выбрали дверь B
- И Хозяин открыл дверь C.
- Автомобиль находится за дверью А, имеет вероятность ⅓, потому что Автомобиль может быть за любой из этих трех дверей с равной вероятностью.
- Вероятность того, что вы выбрали дверь B, также равна ⅓, потому что вы могли выбрать любую из дверей.
Таким образом, этот исход имеет вероятность ⅓ * ⅓ = 1/9. - Теперь у хоста есть двери A и C. Хост не может открыть дверь A, потому что за ней стоит машина, поэтому он должен выбрать дверь C, чтобы открыть ее. Таким образом, вероятность здесь равна 1.
Таким образом, этот исход имеет вероятность ⅓ * ⅓ = 1/9.
Чемодан 2
В случае BBA, BBA означает:
- Автомобиль находится за дверью B
- Вы выбрали дверь B
- И Хозяин открыл дверь А
- Автомобиль находится за дверью B, имеет вероятность ⅓, потому что автомобиль может быть за любой из этих трех дверей с равной вероятностью.
- Вероятность того, что вы выбрали дверь B, также равна ⅓, потому что вы могли выбрать любую из дверей.
- Теперь у хоста есть двери A и C. Хост может открыть любую из дверей A и C, потому что за обеими стоит козел, поэтому вероятность выбора хостом двери A равна 1/2.
Таким образом, этот исход имеет Вероятность ⅓ * ⅓ * ½ = 1/18, как указано в древовидной диаграмме. Таким образом, теперь ясно, что не все эти исходы равновероятны.
Рассчитаем вероятность выигрыша в случае переключения. Таким образом, используя концепции пространства выборки, событий и древовидной диаграммы
Мы заключаем, что:-
Вероятность (выигрыш при переключении) = (P{A,B,C} + P{A,C,B} + P{B,A,C} + P{B,C,A} + P{C,A, В} + Р{С, В, А})
= 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9= ⅔
Причина, по которой это не ½, заключается в том, что каждый раз после вашего выбора хост открывает дверь, за которой стоит коза, и это конкретное условие влияет на вероятность окончательных результатов в нашем тестовом пространстве.
Объяснение с условной вероятностью
Условная вероятность — это вероятность любого события А при условии, что другое событие В уже произошло. Идея здесь заключается в том, что вероятность события «может быть» зависит от того, произошли ли другие события.
Термин «условный» относится к тому факту, что у нас будут дополнительные условия, ограничения или другая информация, когда нас попросят рассчитать этот тип вероятности.
Обозначается следующим образом – «представляющая Вероятность того, что произошло А при условии, что произошло В»
Условная вероятность может быть рассчитана как вероятность пересечения A с B, деленная на вероятность события B
P(A | B) = P(A ∩ B) / P(B)
Начнем анализировать эту задачу, когда участник выбрал дверь 1. Предположим, что P(призовая дверь i) = ⅓, для i = 1, 2, 3
Если приз находится за дверью 1, то ведущий шоу откроет дверь 2 или дверь 3 с вероятностью 1/2.
Итак, у нас есть P(призовая дверь 1 и главная дверь 2) = 1/3 × 1/2 = 1/6
P(призовая дверь 1 и главная дверь 3) = 1/3 × 1/2 = 1/6
С другой стороны, если приз находится за дверью 2 или дверью 3, то у хозяина есть только одна дверь, которую он может открыть, а именно дверь 3 или дверь 2.
P(призовая дверь 2 и главная дверь 3) = 1/3 × 1 = 1/3
P(призовая дверь 3 и главная дверь 2) = 1/3 × 1 = 1/3
Мы описали все возможности, начиная с того, что участник уже выбрал одну дверь. Так как приз может быть за любой дверью с одинаковой вероятностью, не имеет значения, какая дверь выбрана. Учитывая, что ведущий открывает дверь 3, вероятность выиграть приз, сохранив дверь, равна условной вероятности
P(Сохранить и выиграть) = P(призовая дверь 1 | принимающая дверь 3)
= P(призовая дверь 1 и хост-дверь 3)/ P(хозяйская дверь 3)
= (1/6) /P(главная дверь 3)
в то время как
P (оставить и освободить) = P (призовая дверь 2 | главная дверь 3)
= P(призовая дверь 2 и главная дверь 3)/ P(хозяин дверь3)
= 1/3 P/(главная дверь 3)
Таким образом, в два раза больше шансов выиграть путем переключения, и поэтому мы имеем: —
P(Сохранить и выиграть) = 1/3
P(Оставить и освободить) = ⅔
Если кто-то хочет вычислить вероятность того, что ведущий откроет дверь 3, то ее можно найти, определив местонахождение приза:
P(главная дверь 3) = P(главная дверь 3| призовая дверь 1)P(призовая дверь 1)
+P(главная дверь 3|призовая дверь 2)P(призовая дверь 2)
+P (главная дверь 3|призовая дверь 3)P(призовая дверь 3)
= 1/2 × 1/3 + 1 × 1/3 + 0 × 1/3 = 1/2
На этом мы завершаем объяснение проблемы Монти Холла с использованием условной вероятности.