Задайте функцию обратную данной постройте ее график: № 3.4 ГДЗ Алгебра 10-11 класс Мордкович. Помогите с обратной функцией – Рамблер/класс

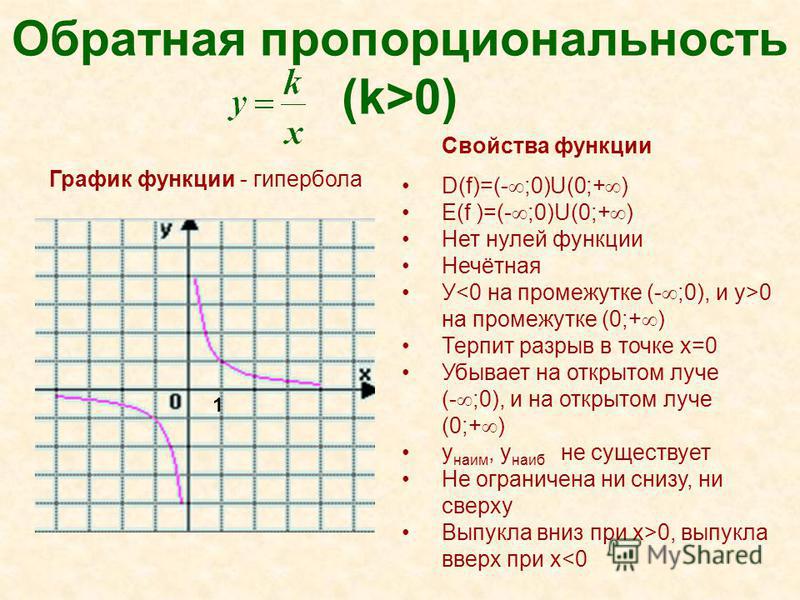
№ 3.4 ГДЗ Алгебра 10-11 класс Мордкович. Помогите с обратной функцией – Рамблер/класс

№ 3.4 ГДЗ Алгебра 10-11 класс Мордкович. Помогите с обратной функцией – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

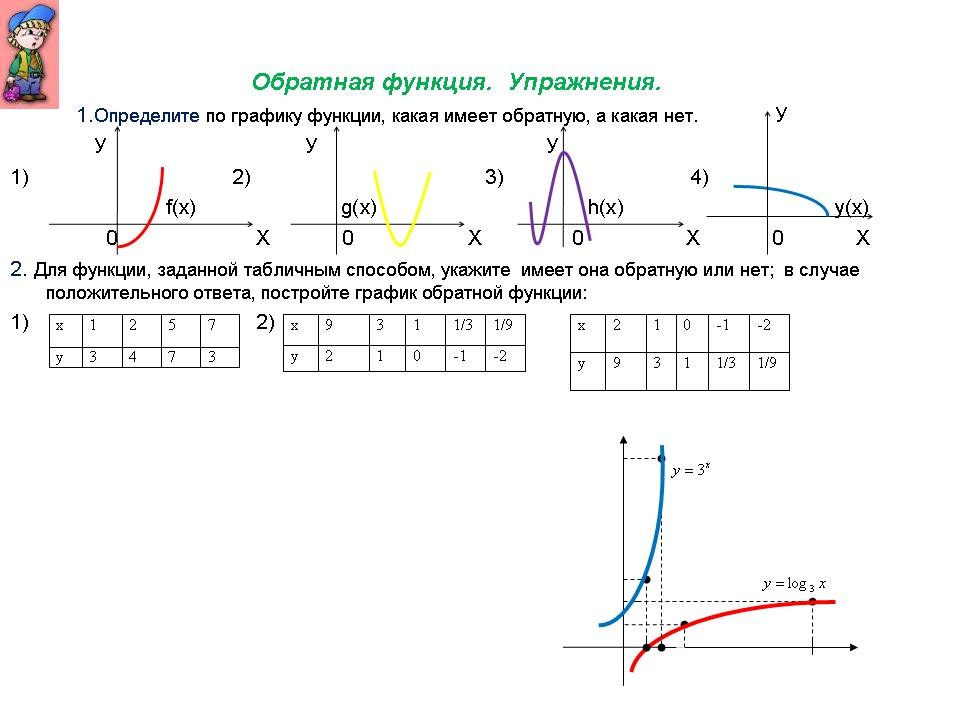
Для заданной функции найдите обратную; постройте график заданной функции и обратной функции:

а) у = х³;
б) у = (х — 2)³;
в) у = 1 — х³;
г) у = (х + 3)³ ≥ — 1.

ответы

Привет. Помогу тебе:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

9 класс

похожие вопросы 5

Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра

10. При каких значениях р уравнение  -х 2 + 6х — 2 = р:
а)    не имеет корней;
б)    имеет один корень; (Подробнее…)

ГДЗМордкович А.Г.Алгебра8 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. 2

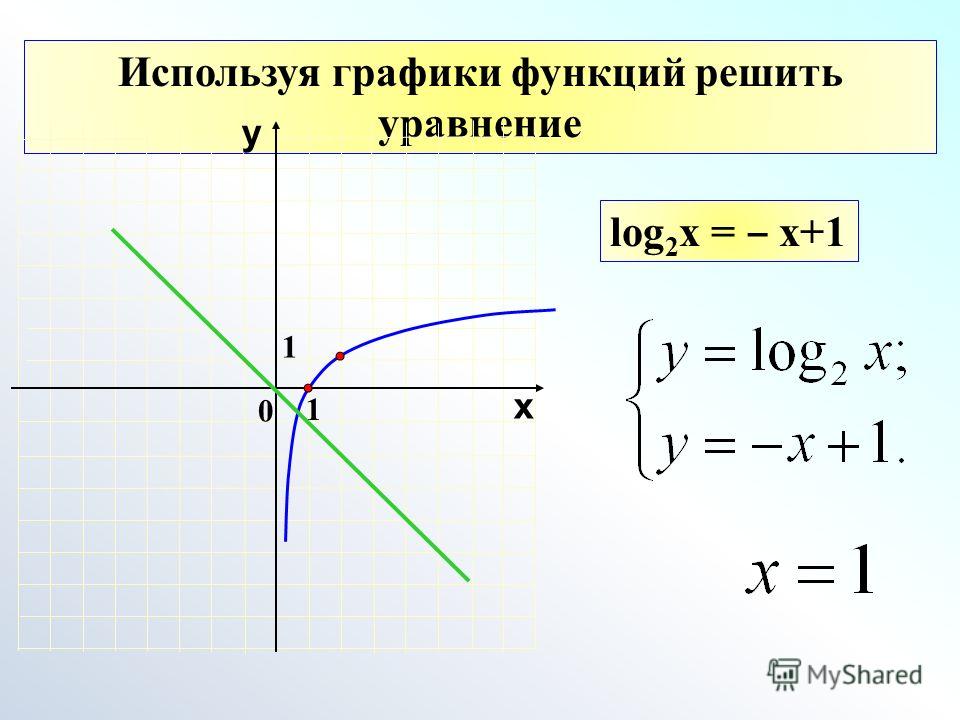
Как построить график обратной функции

Если вас попросят построить график обратной функции, вы можете сделать это, запомнив один факт: функция и ее обратная функция отражаются на линии y = x. Эта линия проходит через начало координат и имеет наклон 1.

Когда вас попросят нарисовать функцию и обратную ей функцию, вы можете нарисовать эту линию в виде пунктирной линии; таким образом, он действует как большое зеркало, и вы можете буквально видеть точки функции, отражающиеся на линии и становящиеся точками обратной функции. Отражение над этой линией переключает x и y и дает вам графический способ найти обратное без построения множества точек.

Лучший способ понять эту концепцию — увидеть ее в действии. Например, предположим, что вы знаете, что эти две функции обратны друг другу:

Чтобы увидеть, как x и y меняются местами, выполните следующие действия:

1. Возьмите число (любое, какое захотите) и подставьте его в первую заданную функцию .

   Допустим, вы выбрали –4. Когда вы оцениваете f (-4), вы получаете -11. В виде точки это записывается (-4, -11).

2. Возьмите значение из шага 1 и вставьте его в другую функцию.

   В этом случае нужно найти г (–11). Когда вы это сделаете, вы снова получите -4. Как точка, это (-11, -4). Вау!

Это работает с любым числом и с любой функцией и ее обратной: точка ( a, b ) в функции становится точкой ( b, a ) в обратном порядке. Но пусть вас не смущает эта терминология. Поскольку они по-прежнему являются точками, вы рисуете их так же, как всегда рисовали точки.

Весь домен и диапазон меняются местами с функции на обратную. Например, зная, что всего несколько точек из заданной функции f ( x ) = 2 x – 3 включают (–4, –11), (–2, –7) и (0, – 3), вы автоматически знаете, что точки на обратном g ( x ) будут (-11, -4), (-7, -2) и (-3, 0).

Поэтому, если вас попросили построить график функции и ее обратной функции, все, что вам нужно сделать, это построить график функции, а затем поменять местами все значения x и y в каждой точке, чтобы построить график обратной функции. Просто взгляните на все эти значения, которые меняются местами с функции f ( x ) на обратную g ( x ) (и обратно), отраженную на линии y = x.

Теперь вы можете построить график функции

f ( x ) = 3 x – 2 и обратное число, даже не зная, что такое обратное. Поскольку данная функция является линейной функцией, вы можете построить ее график, используя форму пересечения наклона.

Во-первых, график у = х. Форма пересечения наклона дает вам точку пересечения y- в точке (0, –2). Поскольку наклон равен 3=3/1, вы перемещаетесь вверх на 3 единицы и более чем на 1 единицу, чтобы оказаться в точке (1, 1). Если вы снова подниметесь на 3 единицы и более чем на 1 единицу, вы получите очко (2, 4). Таким образом, обратная функция проходит через (–2, 0), (1, 1) и (4, 2). Здесь показаны как функция, так и обратная ей.

Эта статья взята из книги:

• Предварительное исчисление для чайников,

Об авторе книги:

Мэри Джейн Стерлинг.

более 30 лет. Она является автором нескольких книг для чайников, , в том числе Рабочая тетрадь по алгебре для чайников, Алгебра II для чайников, и Рабочая тетрадь по алгебре II для чайников.

Эту статью можно найти в категории:

• Предварительное исчисление,

Объяснение урока: Графики, обратные функции

В этом объяснении мы узнаем, как использовать график, чтобы найти обратную функцию и анализировать графики обратной функции.

Отношение или отображение преобразует элементы из одного набора в элементы из другого. Если каждый вход в этом отображении имеет ровно один выход, это называется функцией 9.0122 .

Определение: Функции

Функция отображает каждых элементов из входного набора в ровно один элемент из выходного набора. Функции могут быть либо «один к одному» (один вход имеет один выход), либо «многие к одному» (многие входы отображаются на один и тот же выход).

Если функция 𝑓 отображает элементы множеств 𝑋 в 𝑌, мы можем использовать следующее обозначение: 𝑓∶𝑋⟶𝑌.

Набор значений, которые могут быть введены в функцию, называется доменом, а набор выходных элементов называется диапазоном.

Если 𝑓 является взаимно однозначной функцией, говорят, что она обратима. Другими словами, существует обратная к этой функции, определенная 𝑓 такая, что справедливо следующее определение.

Определение: обратные функции

Пусть 𝑓 — функция, областью определения которой является множество 𝑋, а область значений — 𝑌. 𝑓 является обратной функцией 𝑓 с областью определения 𝑌 и диапазоном 𝑋, если 𝑓(𝑓(𝑥))=𝑥𝑥𝑋,𝑓𝑓(𝑦)=𝑦𝑦𝑌. отменяет» исходную функцию. Возьмем, к примеру, функцию 𝑓(𝑥)=2𝑥. 𝑓 принимает значения 𝑥 и умножает их на 2. Функция, обратная 𝑓, «отменяет» этот процесс; следовательно, 𝑓(𝑥)=𝑥2. Обратите внимание, что, хотя существуют алгебраические процессы для вычисления обратной функции, их более подробное изучение выходит за рамки этого объяснения.

Нарисовав график 𝑦=2𝑥 и 𝑦=𝑥2 на одном и том же наборе осей, мы можем определить единственное преобразование, связывающее график функции и ее обратную функцию.

Граф 𝑦=2𝑥 отображается на график 𝑦=𝑥2 одним отражением в линии 𝑦=𝑥. Это можно обобщить для любой обратимой функции 𝑓.

Свойство: график обратного уравнения

Если 𝑓 обратимо, то график 𝑦=𝑓(𝑥) совпадает с графиком уравнения 𝑥=𝑓(𝑦). Это получается путем отражения графика 𝑦=𝑓(𝑥) через прямую 𝑦=𝑥.

Это эквивалентно перестановке ролей 𝑥 и 𝑦 в функции, поэтому любую координату для обратной функции можно найти, поменяв местами 𝑥- и 𝑦-координаты соответствующей точки на графике исходной функции. Например, точка с координатами (5,10) лежит на графике 𝑦=2𝑥, поэтому образ этой точки на графике 𝑦=𝑥2 имеет координаты (10,5).

В нашем первом примере мы покажем, как распознать график обратной функции по графику исходной функции.

Пример 1. Определение графика обратной функции

Ниже приведен график 𝑓(𝑥)=2𝑥−1.

Какой из них является графиком обратной функции 𝑓(𝑥)?

Ответ

Напомним, что для функции 𝑓 график 𝑦=𝑓(𝑥) получается отражением графика 𝑦=𝑓(𝑥) в строке 𝑦=𝑥. Это эквивалентно переключению 𝑥- и 𝑦-координат каждой точки, лежащей на прямой 𝑦=𝑓(𝑥).

Начнем с определения любых трех точек на прямой 𝑦=2𝑥−1. Мы выберем (0,−1), (1,1) и (2,3).

Чтобы найти соответствующие координаты на графике, обратном 𝑓, мы поменяем местами 𝑥- и 𝑦-координаты. Таким образом, изображение точек равно (−1,0), (1,1) и (3,2) соответственно. Добавляя прямую через эти точки, мы получаем график обратного, 𝑦=𝑓(𝑥). Из следующего эскиза видно, что это отражение графика 𝑓(𝑥)=2𝑥−1 через пунктирную линию 𝑦=𝑥.

Правильный ответ (А).

В нашем предыдущем примере мы продемонстрировали, что, применяя определение обратной функции, мы можем связать точки на графике функции с изображением этих точек на графике обратной. В нашем следующем примере мы выполним аналогичный процесс для кубической функции.

Пример 2. Связь графика функции с графиком ее обратной функции

Показан график 𝑓(𝑥)=5𝑥+6. Найдите пересечение обратной функции 𝑓(𝑥) с осью 𝑥.

Ответ

Напомним, что график обратной функции находится путем отражения графика исходной функции через прямую 𝑦=𝑥. При этом роли 𝑥 и 𝑦 меняются местами. Это означает, что если координата 𝑦-перехвата на графике 𝑦=𝑓(𝑥) равна (0,𝑎) для некоторого вещественного 𝑎, образ этой точки на графике 𝑦=𝑓(𝑥) есть (𝑎,0). Это значение 𝑥-перехвата. Итак, чтобы найти пересечение обратной функции 𝑓(𝑥) с осью 𝑥, найдем координаты 𝑓(𝑥) с осью 𝑦 и поменяем роли 𝑥 и 𝑦.

График 𝑦=𝑓(𝑥) проходит через ось 𝑦 в точке (0,6). Это означает, что график 𝑦=𝑓(𝑥) проходит через ось 𝑥 в точке (6,0).

Покажем это графически. График 𝑓(𝑥)=5𝑥+6 отражен пунктирной линией 𝑦=𝑥, как показано. 𝑥-перехват равен 6, как и ожидалось.

В нашем предыдущем примере мы видели, что если координата 𝑦-перехвата на графике 𝑦=𝑓(𝑥) равна (0,𝑎) для некоторого реального 𝑎, образ этой точки на графике 𝑦= 𝑓(𝑥) равно (𝑎,0). Отсюда следует, что должно быть верно и обратное. Аналогично, если координата 𝑥-перехвата на графике 𝑦=𝑓(𝑥) равна (𝑏,0) для некоторого действительного 𝑏, образ этой точки на графике 𝑦=𝑓(𝑥) равен ( 0,𝑏).

На самом деле, мы могли бы даже вывести больше информации о области определения и диапазоне функций и их обратных функций. Поскольку выходы 𝑓 являются входами 𝑓, диапазон 𝑓 также является доменом 𝑓. Точно так же, поскольку входы 𝑓 являются выходами 𝑓, доменом 𝑓 является диапазон 𝑓. Кроме того, если у функции нет обратной, можно было бы ограничить область определения этой функции так, чтобы эта новая функция действительно имела обратную функцию .

Например, рассмотрим функцию 𝑓(𝑥)=𝑥, график которой показан. Эта функция не проходит тест горизонтальной линии, как показано ниже, поэтому она не является однозначной.

Это означает, что если мы отразим график функции в строке 𝑦=𝑥, то полученный график не пройдет тест вертикальной линии; это отображение «многие к одному» и, следовательно, не является графиком функции. Таким образом, 𝑓(𝑥)=𝑥 не имеет обратного.

Однако, ограничивая область определения 𝑓 до [0,∞[ функция пройдет тест горизонтальной линии и теперь будет обратимой. График его обратного находится путем отражения 𝑦=𝑓(𝑥) через прямую 𝑦=𝑥, так что диапазон 𝑓 является областью определения 𝑓, [0,∞[.

Свойство: Область определения и область значений обратных функций

Область значений взаимно однозначной функции 𝑓(𝑥) является областью определения обратной функции 𝑓(𝑥).

Домен 𝑓(𝑥) — это диапазон 𝑓(𝑥).

В нашем следующем примере мы покажем, как применить отношение между графиком функции и графиком ее обратной функции, чтобы найти их точки пересечения.

Пример 3. Использование связи между функцией и ее обратной функцией для поиска неизвестных

Графики функции 𝑓(𝑥)=𝑥+𝑏 и ее обратной функции 𝑓(𝑥) пересекаются в трех точках, одна из которых  45,45.

1. Определите значение 𝑏.
2. Найдите 𝑥-координату точки 𝐴, отмеченной на рисунке.
3. Найдите 𝑥-координату точки 𝐵, отмеченной на рисунке.

Ответ

Часть 1

Так как график 𝑦=𝑓(𝑥) проходит через точку 45,45, мы можем подставить 𝑥=45 и 𝑓(𝑥)=45 в уравнение 𝑥 𝑥)=𝑥+𝑏, чтобы найти значение 𝑏: 𝑓(𝑥)=𝑥+𝑏45=45+𝑏45=64125+𝑏.

Решение для 𝑏, 𝑏=45−641361=.

Часть 2

На рисунке показан график 𝑓(𝑥)=𝑥+36125 и обратный ему. Поскольку значение 𝑦-перехвата 𝑦=𝑓(𝑥) равно 36125>0, красный график равен 𝑦=𝑓(𝑥). Это означает, что синий график равен 𝑦=𝑓(𝑥). Следовательно, мы можем найти координаты точки 𝐴, которая является 𝑥-пересечением обратной функции, найдя координаты 𝑦-пересечения исходной функции и перестановкой 𝑥 и 𝑦. Это эквивалентно отражению этой точки через прямую 𝑦=𝑥.

𝑦-перехват 𝑓(𝑥) равен 0,36125. Таким образом, 𝑥-перехват 𝑓(𝑥) равен 36125,0

Следовательно, 𝑥-координата точки 𝐴 равна 36125.

Часть 3

Напомним, что график 𝑦=𝑓(𝑥) строка 𝑦=𝑥. Поскольку точка 𝐵 является точкой пересечения 𝑦=𝑓(𝑥) и 𝑦=𝑓(𝑥), она должна лежать на прямой 𝑦=𝑥.

Таким образом, точку пересечения можно найти, решив систему уравнений 𝑦=𝑥+36125,𝑦=𝑥. 0.

Поскольку одна из точек пересечения имеет значение 𝑥=45, мы знаем, что (5𝑥−4) является множителем 𝑥−𝑥+36125.

Разделив 𝑥−𝑥+36125 на 5𝑥−4, мы получим коэффициент 112525𝑥+20𝑥−9. Следовательно, наше предыдущее уравнение можно записать как 1125(5𝑥−4)25𝑥+20𝑥−9=0.

Наконец, применяя квадратную формулу к уравнению 25𝑥+20𝑥−9=0, мы находим решения быть 𝑥=√13−25,𝑥=−√13−25.

Поскольку точка пересечения лежит в первом квадранте, ее 𝑥-координата должна быть положительной.

Следовательно, 𝑥-координата точки 𝐵 равна 𝑥=√13−25.

Теперь давайте продемонстрируем, как применить свойства графиков обратных функций для наброска функции и ее обратной функции.

Пример 4. Нахождение графика функции, обратной самой себе

Нарисовав графики следующих функций, какая из них является обратной самой себе?

1. 1𝑥
2. 𝑥
3. 𝑥
4. 1𝑥

Ответ

Чтобы ответить на этот вопрос, мы нарисуем график каждой функции, начиная с графика 𝑦 = 1𝑥.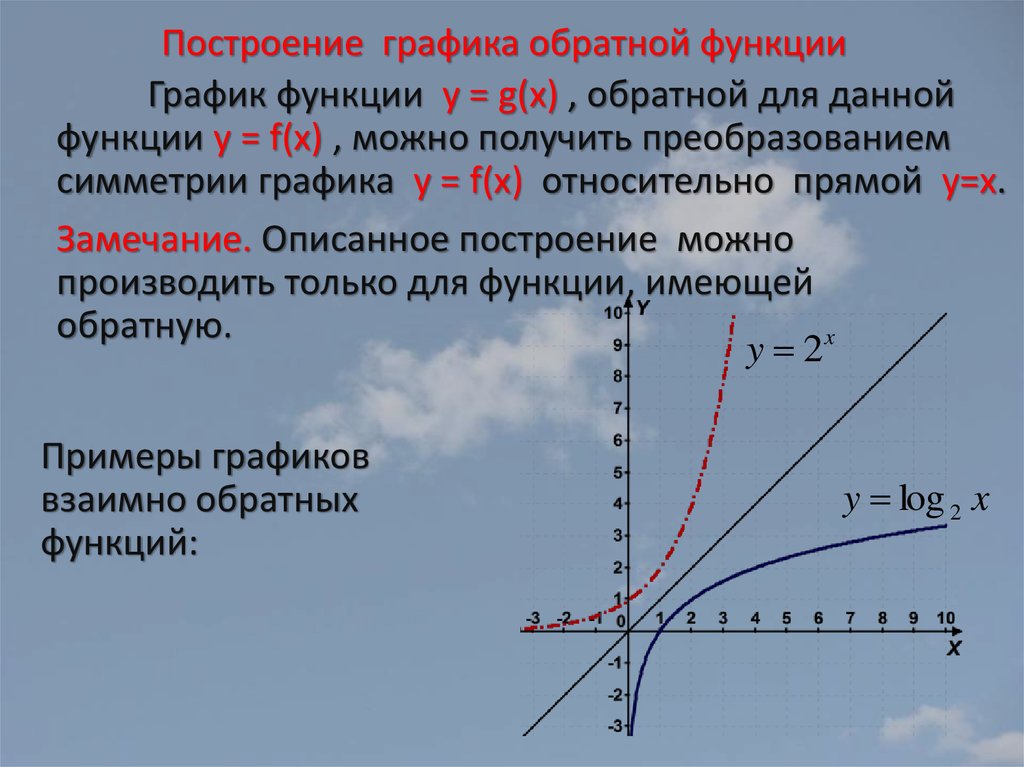 Это обратная функция с асимптотами при 𝑦=0 и 𝑥=0.

Поскольку нахождение обратного эквивалентно перестановке ролей 𝑥 и 𝑦 в функции, асимптоты обратного 1𝑥 будут 𝑥=0 и 𝑦=0. Чтобы нарисовать график обратной функции, мы отразим график исходной функции через прямую 𝑦=𝑥.

Это отражение отображает график 𝑦=1𝑥 на себя, поэтому ответ равен A.

Мы проверим это, проверив три другие функции, начиная с 𝑥. 𝑥 является функцией «многие к одному» и, следовательно, необратима без выполнения некоторых ограничений на ее область определения. Точно так же 1𝑥 является функцией «многие к одному» и не имеет обратной.

Далее идет функция 𝑥. Это кубическая функция, проходящая через начало координат.

Отражение графика функции в строке 𝑦=𝑥 дает следующую цифру:

Поскольку график функции не отображается на график обратной функции, ответ не может быть C.

Правильный ответ A , 1𝑥.

В нашем последнем примере мы покажем, как ограничение области определения функции может сделать ее обратимой.

Пример 5. Рисование графиков функций для определения их обратности

Нарисовав графики 𝑓(𝑥)=2𝑥 и 𝑔(𝑥)=𝑥2 для 𝑥≥0, определите, являются ли они обратными функциями.

Ответ

Функция 𝑓(𝑥)=2𝑥 является функцией «многие к одному», то есть несколько входов этой функции будут иметь одинаковый выход. Это означает, что это необратимая функция. Однако его домен был ограничен 𝑥≥0, тем самым создавая взаимно-однозначную функцию, в которой имеет обратную функцию .

Поскольку функция 2𝑥 является квадратичной с положительным старшим коэффициентом, она представляет собой U-образную параболу, проходящую через начало координат. Ограничение этого значения значениями 𝑥≥0 дает следующий рисунок.

Теперь мы нарисуем график 𝑦=𝑥2 на тех же осях. Это преобразование графика 𝑦=√𝑥 на горизонтальное растяжение с масштабным коэффициентом 2. Его график показан ниже.

Кажется, что эти функции обратны друг другу, так как кажется, что они были отражены через линию 𝑦=𝑥.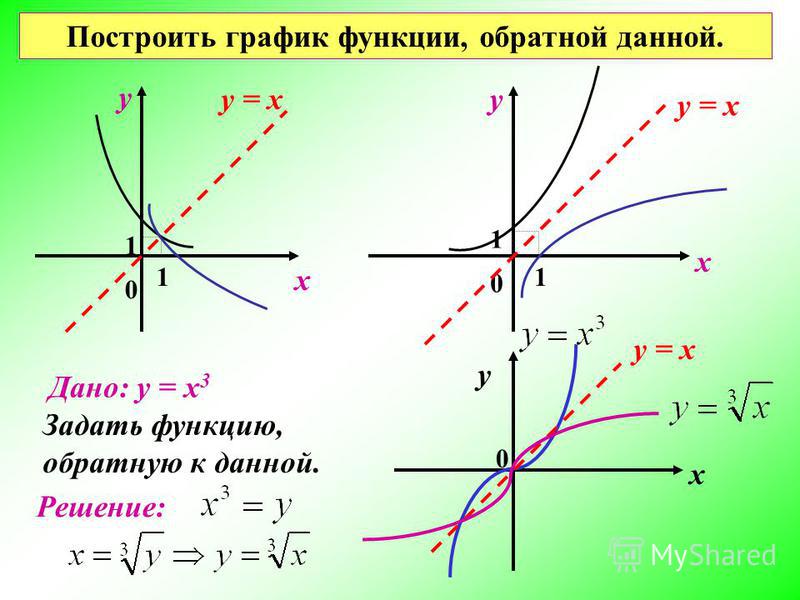 Мы проверим, посмотрев на их точку пересечения. Если он лежит на прямой 𝑦=𝑥, то его 𝑥- и 𝑦-координаты будут равны.

Чтобы найти эту точку, решим 2𝑥=𝑥2: 4𝑥=𝑥28𝑥−𝑥=0𝑥8𝑥−1=0.

Решениями этого уравнения являются 𝑥=0 или 𝑥=18=12.

Подстановка 𝑥=12 в любую функцию дает 𝑦=2×12=12. Поскольку 𝑥- и 𝑦-значения одинаковы, мы знаем, что точка пересечения кривых лежит на прямой 𝑦=𝑥.

Аналогично, подстановка 𝑥=0 в любую функцию дает 𝑦=0. Точка (0,0) также лежит на прямой 𝑦=𝑥, как показано на следующем рисунке.

Мы также можем проверить, являются ли эти функции обратными друг другу, взглянув на пару точек на каждой линии.

Точка (1,2) лежит на кривой 𝑦=2𝑥. Образ этой точки после отражения через 𝑦=𝑥 равен (2,1). Если это лежит на кривой 𝑦=𝑥2, подстановка 𝑥=2 в это уравнение даст 𝑦=1: 𝑦=𝑥2=22=√1=1.

Образ точки (1,2) после отражения через 𝑦=𝑥 лежит на кривой 𝑦=𝑥2. Следовательно, оказывается, что 𝑓(𝑥)=2𝑥 и 𝑔(𝑥)=𝑥2 для 𝑥≥0 обратны друг другу.

Конечно, хотя мы рассмотрели несколько точек, этого недостаточно. Мы могли бы проверить это, используя графическое программное обеспечение для построения графиков и их отражений по 𝑦=𝑥.

В нашем предыдущем примере мы продемонстрировали, как идентифицировать серию точек после отражения через прямую 𝑦=𝑥 и использовать эту информацию, чтобы определить, была ли пара функций обратными друг другу.

Мы могли бы проверить результат более строго, используя определение обратной функции; если 𝑓 — функция, областью определения которой является множество 𝑋, а область значений — 𝑌, 𝑓 является обратной функцией 𝑓 с областью определения 𝑌 и диапазоном 𝑋, если 𝑓(𝑓(𝑥))=𝑥𝑥𝑋,𝑓𝑓(𝑦)= 𝑦𝑦𝑌.forallinforallin

Вычисление составной функции 𝑓(𝑔(𝑥)), дает 𝑓(𝑔(𝑥))=𝑓𝑥2=2𝑥2=2𝑥2=𝑥.

Аналогично, 𝑔(𝑓(𝑥))=𝑔2𝑥=2𝑥 

Это обратные функции.

Давайте закончим повторением ключевых понятий из этого объяснения.

Ключевые моменты

• Если 𝑓 — функция, областью определения которой является множество 𝑋, а диапазон — 𝑌, 𝑓 является обратной функцией 𝑓 с областью определения 𝑌 и диапазоном 𝑋, если 𝑓(𝑓(𝑥))=𝑥𝑥 𝑓(𝑦)=𝑦𝑦𝑌.

  No related posts.