| 1. |
Определение разложения степени бинома
Сложность: среднее |
4 |
| 2. |
Слагаемое в разложении степени бинома
|
3 |
| 3. |
Сумма/разность слагаемых в разложении
Сложность: среднее |
4 |
| 4. |
Слагаемое, содержащее данную переменную, в разложении степени бинома
Сложность: среднее |
4 |
| 5. | Сложность: среднее |
4 |
| 6. |
Число рациональных слагаемых
Сложность: среднее |
2 |
| 7. |
Алгебраическая сумма коэффициентов многочлена
Сложность: сложное |
3 |
| 8. |
Слагаемое, не содержащее х
Сложность: сложное |
3 |
| 9. |
Наибольшее слагаемое в разложении бинома Ньютона
Сложность: сложное |
4 |
www.yaklass.ru
Методическая разработка занятия по теме «Бином Ньютона»
Тема: «Бином Ньютона»
Изучаемые вопросы 1. Понятие бинома Ньютона
2. Свойства бинома и биномиальных коэффициентов
3. Типовые задачи по теме «Бином Ньютона»
4. Задачи, сводящиеся к использованию формулы бинома Ньютона (нестандартные задачи по теме «Бином Ньютона»)
Понятие бинома Ньютона
Биномом Ньютона называют разложение вида:
Но, строго говоря, всю формулу нельзя назвать биномом, так как «бином» переводится как «двучлен». Кроме того, формула разложения была известна еще до Ньютона, Исаак Ньютон распространил это разложение на случай n<0 и n – дробного.
Цель изучения бинома Ньютона – упрощение вычислительных действий.
Компоненты формулы «бином Ньютона»:
правая часть формулы – разложение бинома;
– биномиальные коэффициенты, их можно получить с помощью треугольника Паскаля (пользуясь операцией сложения).
Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.
Например, четвертая строчка треугольника как раз наглядно демонстрирует биномиальные коэффициенты для бинома четвертой степени:Альтернатива треугольнику Паскаля:
перемножить почленно четыре скобки:
;
вспомнить разложение бинома Ньютона четвертой степени:
где Т – член разложения; 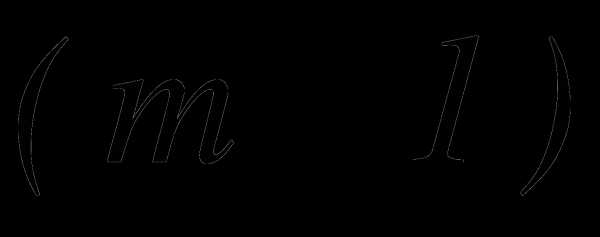 – порядковый номер члена разложения.
– порядковый номер члена разложения.
– 2 –
Свойства бинома и биномиальных коэффициентов
Число всех членов разложения на единицу больше показателя степени бинома, то есть равно

Сумма показателей степеней
Доказательство
Рассмотрим 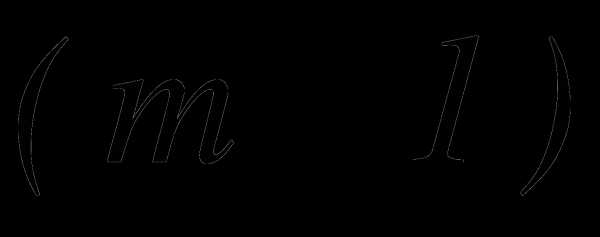 -й член разложения:
-й член разложения:
Сумма показателей степеней a и b:
Ч.т.д.
Биномиальные коэффициенты членов разложения, равноотстоящих от концов разложения, равны между собой: (правило симметрии)
Сумма биномиальных коэффициентов всех членов разложения равна

Доказательство
Пусть , тогда:
Тогда: 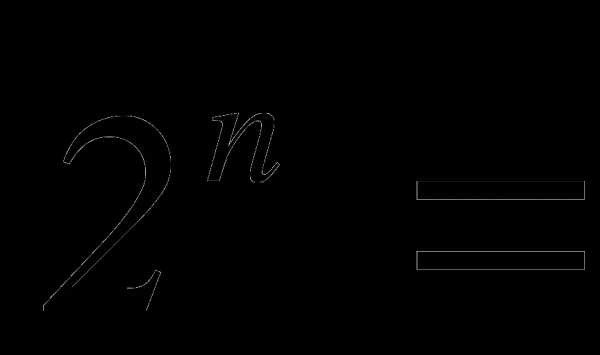
Ч.т.д.
- Сумма биномиальных коэффициентов, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах и равна

Правило Паскаля:
Доказательство – самостоятельно
Любой биномиальный коэффициент, начиная со второго, равен произведению предшествующего биномиального коэффициента и дроби

Доказательство – самостоятельно
– 3 –
Типовые задачи по теме «Бином Ньютона»
К типовым (стандартным) заданиям по данной теме можно отнести задачи на вычисление, среди которых:
Найти член (номер члена) разложения бинома
Вывести бином по известным членам разложения (по известной сумме)
Вычислить сумму биномиальных коэффициентов разложения бинома
и другие.
Продемонстрируем на примерах (их решение несложное, поэтому большинство предлагаем решить самостоятельно).
Пример 1
Разложить по формуле бином 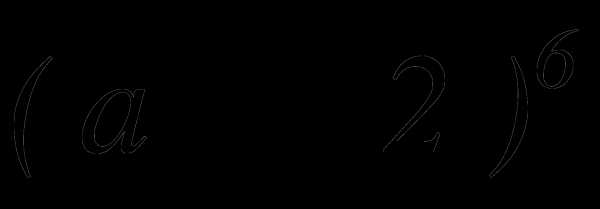
Решение – самостоятельно
ОБРАТИТЕ ВНИМАНИЕ на знакочередование!
Пример 2
Найти шестой член разложения 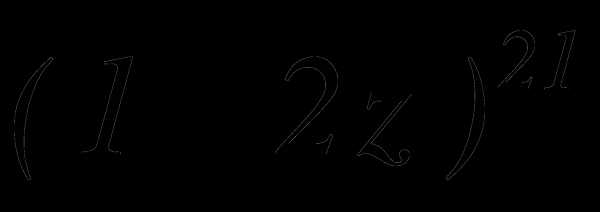
Решение – самостоятельно
ОБРАТИТЕ ВНИМАНИЕ на знак!
Лучше начинать рассуждения со следующего:
Пример 3
Найдите два средних члена разложения
Решение – самостоятельно
ОБРАТИТЕ ВНИМАНИЕ на то, что эти члены равноотстоят от конца, поэтому их биномиальные коэффициенты будут равны.
НЕ ЗАБУДЬТЕ в процессе решения проводить преобразования степеней с одинаковыми основаниями (то есть упрощать).
Пример 4
В биномиальном разложении 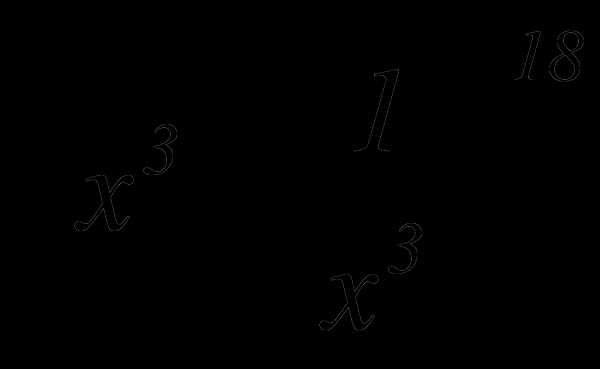 найти член разложения, не содержащий х
найти член разложения, не содержащий х
Решение
Так как в разложении мы ищем член не содержащий х, то
Тогда
Ответ: 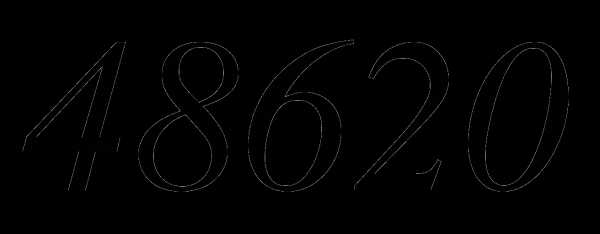
– 4 –
Задачи, сводящиеся к использованию формулы бинома Ньютона
(нестандартные задачи по теме «Бином Ньютона»)
К нестандартным заданиям по данной теме можно отнести такие, в которых нет явного намека на необходимость использования бинома. Однако в итоге, решение сводится к нему и выглядит очень интересным.
Пример 5
Доказать, что для любых  и для любых
и для любых 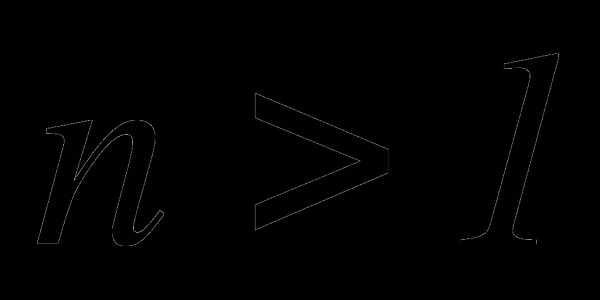 верно неравенство Бернулли:
верно неравенство Бернулли:
Доказательство
Пусть
Так как  , то
, то
Переформулируем требование: Доказать, что , где
Так как , значит в разложении как минимум три члена разложения, тогда:
Это означает, что
Ч.т.д.
Пример 6
Доказать, что 
Доказательство – самостоятельно
(Подсказка: используйте неравенство Бернулли)
Пример 7
Доказать, что при любом натуральном n число делится на 9
Доказательство
1 способ:
Ч.т.д.
2 способ:
Начнем рассматривать бином в общем виде:
Тогда
Ч.т.д.
Пример 8
Решить уравнение
Решение
Осуществим замену:
Тогда уравнение перепишем:
Применим формулу бинома к левой части уравнения:
В итоге
Ответ:
Дополнительные задания для самостоятельного выполнения
Найти номер члена разложения бинома
 , не содержащего х.
, не содержащего х.Найти пятый член разложения бинома
 .
.Найти сумму биномиальных коэффициентов членов, стоящих на нечетных местах в разложении бинома
 , если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена.
, если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена.Найти седьмой член разложения бинома
 , если биномиальный коэффициент третьего члена равен 36.
, если биномиальный коэффициент третьего члена равен 36.Сколько членов разложения бинома являются целыми числами?
Вычислить сумму .
Найти алгебраическую сумму коэффициентов многочлена относительно х, получаемого в разложении бинома
 .
.Сумма нечетных биномиальных коэффициентов разложения
 равна 512. Найти слагаемое, не содержащее х.
равна 512. Найти слагаемое, не содержащее х.При каких значениях х четвертое слагаемое разложения
 больше двух соседних с ним слагаемых?
больше двух соседних с ним слагаемых?При каком значении х четвертое слагаемое разложения в двадцать раз больше m, если биномиальный коэффициент четвертого слагаемого относится к биномиальному коэффициенту второго слагаемого как 5 : 1?
В какую наибольшую степень следует возвести бином
 чтобы отношение четвертого слагаемого разложения к третьему было равно
чтобы отношение четвертого слагаемого разложения к третьему было равно  ?
?
infourok.ru
Практическое занятие по теме: «Треугольник Паскаля. Бином Ньютона»
Максимова Р.П.
Занятие для студентов 1 курса по теме: « Бином Ньютона. Треугольник Паскаля» (по учебной дисциплине)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данный конспект занятия по теме: « Бином Ньютона. Треугольник Паскаля» составлено в соответствии с рабочей программой и относится к разделу «Комбинаторика», занятие № 115. Оно предназначено для подготовки студентов первого курса дневного отделения. Материал занятия состоит из методических указаний и упражнений, которые необходимы для усвоения и закрепления изученного материала.
В результате изучения студент должен:
иметь представление о:
знать:
уметь:
Занятие изучения и первичного закрепления новых знаний
Цель занятия – изучение и первичное осознание нового учебного материала, осмысление связей и отношений в объектах изучения. Познакомить с биномом Ньютона, показать его связь с треугольником Паскаля.
Оборудование занятия: презентация, учебник, приложение.
Cодержание занятия
1. Организационный момент
Проверка готовности группы к занятию
2 Тема, цель и задачи занятия
Цель занятия.
— обучающая – организовать самостоятельную деятельность учащихся по усвоению понятий – комплексные числа;
создать проблемную ситуацию для следующего урока
— развивающая — формировать умение применять приемы сравнения, обобщения, и навыки воображения учащихся при работе с понятием комплексного числа;
— воспитывающая – формировать умения аккуратного и точного (в соответствии с условиями задания) изображения
Тема занятия “Бином Ньютона. Треугольник Паскаля”.(тему студенты попробуют определить самостоятельно, выполняя задания:
(a+b)1 . (a+b)2 . (a+b)3 . (a+b)4 . (a+b)5 . …(a+b)10 . …
Сегодня на занятии мы должны обобщить и повторить пройденный материал. Полученные знания и навыки в применении биноминальных формул, закрепим на решении математических задач. В течение урока работать будем по группам, затем подведём итог урока, и вы получите домашнее задание.
На экране слайд Актуализация знаний: проверка домашнего задания,
устная работа
Проверка домашнего задания (наличие)
Пример 1.Найти третий член разложения 
Пример 2 Разложить по формуле бином куб разности 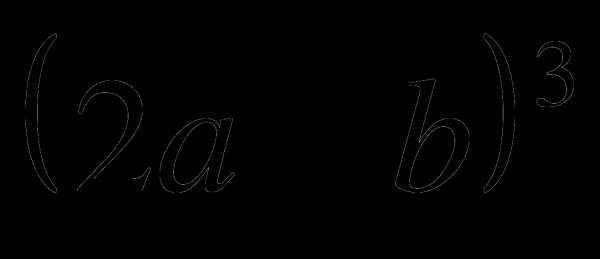
Пример 3. Замените * одночленом, чтобы получилось верное равенство:

— Какими формулами вы пользовались в данном задании?
Давайте назовём их и сформулируем.
1. Формулы квадрата суммы и разности двух выражений
2. Формула разности квадратов
3. Формулы суммы и разности кубов
Объяснение нового материала
Формулы сокращённого умножения являются частным случаем бинома Ньютона. Сегодня на занятии обобщим полученные знания и познакомимся с формулами:
Формула бинома Ньютона. Как возвести в степень n сумму двух слагаемых?
Рассмотрим некоторые сведения:
Исаак Ньютон был поистине Великим физиком своего времени, а может быть и величайшим физиком всех времен и народов. Но мы не будем судить об этом. Однако следует заметить, что Ньютон был еще и прекрасным математиком. Кстати формула бинома Ньютона была выгравирована на надгробии его могилы, как самое великое открытие современности того времени!
Кроме формулы бинома Ньютона, со школьной скамьи всем известна формула Ньютона-Лейбница. Таким образом, великий Ньютон вместе с Лейбницем заложили основы дифференциального и интегрального исчисления. Основы теории пределов и строгий подход в математическом анализе был начат и развивался в трудах таких гениев как Огюстен Коши, Георг Кантор, Карл Вейерштрасс. Нельзя, конечно, обойти стороной имя Леонарда Эйлера.
Но мы отвлеклись здесь от основной линии рассуждений. Ведь Формула бинома Ньютона относится к алгебре, а также к ветви математики, называемой комбинаторикой!
Вы спросите: а почему, собственно, формула бинома, и что такое бином вообще. Здесь употребляется алгебраическая терминология: в алгебре есть понятие многочлена. Многочлен это Полином — другими словами — сумма произвольного числа слагаемых называется полином.
Например — это полином!
А сумма двух слагаемых называется Бином! То есть  — это бином, или например ( x+y) — тоже бином. Здесь x и y предполагаются неизвестными переменными величинами! Но формула бинома Ньютона на самом деле это не просто формула бинома (иначе, что это за формула такая, которая состоит из суммы двух произвольных слагаемых?). Что же он тогда изобрел?
— это бином, или например ( x+y) — тоже бином. Здесь x и y предполагаются неизвестными переменными величинами! Но формула бинома Ньютона на самом деле это не просто формула бинома (иначе, что это за формула такая, которая состоит из суммы двух произвольных слагаемых?). Что же он тогда изобрел?
Ньютон изобрел формулу, которая позволяет возвести сумму двух слагаемых в степень с любым показателем, а не только с показателем равным 2! Невозможно переоценить значение формулы бинома Ньютона при решении многих заданий. Поэтому правильно формула, о которой идет здесь речь, называется Формулой Ньютона для степени бинома. Мы не будем сразу писать эту формулу в общем виде, а вначале обратимся к школьной алгебре!
Вспомним из школьного курса что:
Это и есть формула квадрата суммы или формула квадрата двучлена, или формула второй степени бинома! Возведем в третью степень сумму двух слагаемых или вычислим бином третьей степени.
Скобки раскрываем аналогично, используя распределительный или дистрибутивный закон алгебры: Мы доказали формулу суммы кубов. Она нам хорошо известна из школьного курса алгебры.
Пойдем дальше, возведем бином в четвертую степень! Но возводить мы будем, воспользовавшись предыдущей формулой для третьей степени бинома:
Более подробное раскрытие скобок студенты выполняют самостоятельно, проверяем результат раскрытия, так как вычисления аналогичны тому, как это уже проделали при получении формул (а + b)2 u (a+ b)3.
Итак, мы получили формулу для четвертой степени бинома! Попытаемся возвести в пятую степень бином! Для возведения бинома в пятую степень надо умножить результат возведения бинома в четвертую степень на известный нам бином! Вот в чем заключалась гениальная идея Ньютона!
=
(вместо четвертой степени бинома мы подставляем вычисленное ранее выражение (a+b) 4 и снова раскрываем скобки, опуская подробные вычисления, поскольку они выполнялись при вычислении третьей и второй степени бинома.) А сколько же можно так продолжать увеличивать порядок степени возведения бинома? Ответ: до бесконечности можно! Точно также, например при n=101 умножим результат возведения в степень 100 на (а+b), тогда получим результат возведения в степень 100.
Но мы не будем расписывать все это выражение, поскольку после приведения подобных членов оно имеет 101 слагаемое и не уместится в одну строчку, а в десять строчек прочтение будет очень затруднительно!
Но гениальность Ньютона в том и заключалось, что он смог записать эту формулу в общем виде в одну строчку для любого n, то есть формулу вида:
Здесь можно сделать вывод: чтобы получить формулу для степени n, надо знать эту формулу для (n-1). Чтобы знать формулу для (n-1) надо получить ее (n-1) раз так, как мы это делали для 2,3,4, и 5-й степени, то есть умножали уже известный результат для степени на единицу меньшей заданной степени на степень равную единице!
А теперь второй вывод: все эти действия, которые приводят к формуле бинома для степени ( n-1) можно записать более кратко?! Тогда можно будет не переписывать (n-1) раз фактически одни и те же вычисления для 2, 3, 4, 5, 6,…,n-1 степени бинома, а записать их одной формулой, умножить эту формулу еще раз на первую степень бинома и полностью доказать искомую формулу! Вот вам и алгоритм рассуждений Ньютона!
Здесь мы выделили последние предложения жирным шрифтом, поскольку они являются основой доказательства формулы бинома Ньютона и наиболее серьезным и сложным шагом во всех наших рассуждениях — метод математической индукции один из наиболее важных методов математики. Но как же записать общую формулу для степени бинома, равной n-1? Для ответа используем уже доказанные формулы степени бинома, равные 2, 3,4,и 5.
Обратим внимание, что коэффициенты крайних слагаемых равны 1, показатели степени — наивысшие (n). Показатели степени переменных изменяются в обратной зависимости, а вот определить коэффициенты достаточно сложно. Имеет смысл вернуться к определению сочетания из n элементов по m, где
n – степень бинома, а m является номером слагаемого, начиная с 0. Тогда для 3 степени бинома мы получим следующие коэффициенты:
Можно, конечно, привести вывод формулы бинома, что не входит в нашу программу, поэтому запишем эту формулу без доказательства и используем ее для получения общей формулы:
где — сигма, знак суммы слагаемых от 0 до n.
Итак, Если мы имеем бином (а — b) ⁿ, то знаки слагаемых чередуются.
Однако, вычислять коэффициенты через сочетания достаточно сложно. Чтобы облегчить эти вычисления, используют: Треугольник Паскаля:
Каждому студенту даем Раздаточный материал
Треугольник Паскаля
1
1
1
1 2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
7
21
35 35
21
7
1

Треугольник Паскаля Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:
Или треугольник Паскаля можно переписать и в виде: Слайды презентации на экранеЗакрепление. Продолжить формулу, используя бином Ньютона и треугольник Паскаля. (Решается у доски преподавателем с помощью студентов.)
1.
Ответ.
2.
Ответ.
3.Вычислить
Ответ
4.Используя треугольник Паскаля, найти разложение двучлена: (2а +3 b)4
Решение
Самостоятельная работа по вариантам
1 вариант
1. Найдите значение:
2. Вычислите значение бинома:
1)
3. Запишите, как называется многочлен вида (c + b)n __________
4. Как располагаются биноминальные коэффициенты _____________
5. Запишите коэффициенты разложения двучлена (2а + 3)4 в виде треугольника Паскаля
2 Вариант
1. Найдите значение:
2. Вычислите значение бинома:
1)
3. Запишите, как называется многочлен вида (а — b)n __________
4. Как располагаются биноминальные коэффициенты ____________
5. Запишите коэффициенты разложения двучлена (3а + 2)4 в виде треугольника Паскаля
3 Вариант
1. Найдите значение:
2. Вычислите значение бинома:
1)
3. Запишите, как называется многочлен вида (а + 3 b)n __________
4. Как располагаются биноминальные коэффициенты _____________
5. Запишите коэффициенты разложения двучлена (3а + 2)4 в виде треугольника Паскаля
4 Вариант
1. Найдите значение :
2. Вычислите значение бинома:
1)
3 Запишите, как называется многочлен вида (а + 3 b)n _______________
4. Как располагаются биноминальные коэффициенты ________________
5. Запишите коэффициенты разложения двучлена (5а + 2)4 в виде треугольника Паскаля
Критерии оценивания работы:
1. (а — г) – 1 балл, всего 5 баллов
2. – по 4 балла, всего 16 баллов
3. — 1 балл
4. — 1 балл
5. 1 балл Итого: 24 балла
Баллы снижаются: 1) плохая дисциплина (шум, некорректность в поведении)
2) небрежность в оформлении работы За проверку работы соседней группы и анализ ее выполнения 6 баллов.maxƩ = 30 баллов
ОТВЕТЫ НА РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАНИЙ:
1 вариант
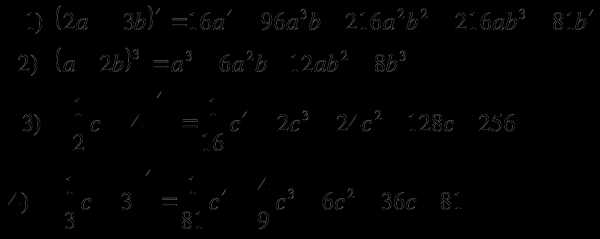
2 вариант
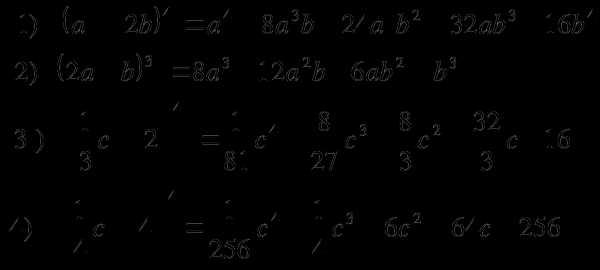
3 вариант
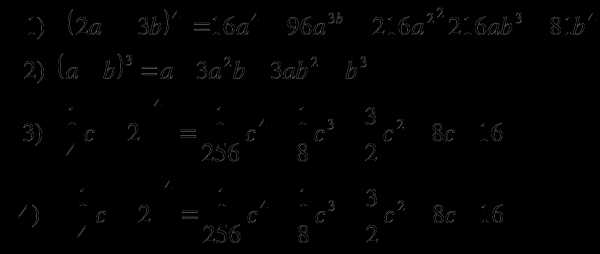
4 вариант
1) 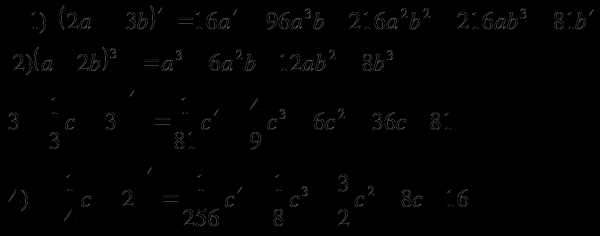
Работа по вариантам.
По каждому варианту есть консультант – студент В каждом варианте есть задания:
а) по теории (тестовые вопросы разные в каждом варианте )
б) практика (решение примеров)- задания разные
Задания помогают решать консультанты – студенты ( они оценивают работу студентов)
Затем студенты составляют задания и попарно обмениваются своими заданиями, а затем и проверяют их, тем самым студенты проверяют работы друг друга и дают им свою оценку по определенным критериям.
В первую очередь оценивается взаимодействие и слаженность работы, дисциплина в группе. Качество работы (скорость и точность).
Подведение итогов, рефлексия
Используем метод незаконченных предложений.
Сегодня на занятии я узнал(а) …
Мне оказались непонятны следующие моменты …
Мне понравилось на занятии …
Я понял(а), что надо еще раз посмотреть тему …
Покажите на графике свое эмоциональное состояние на занятии
Студенты обмениваются выполненными заданиями и проверяют работы друг друга.
Оценивают работы по критериям:
«5» — 28-30 б.
«4» — 22-27 б.
«3» — 12-21 б.
Домашнее задание (задание на листочках каждому студенту)
Составить 2 задачи на сочетания и 2 примера на Бином Ньютона с решением.
образец выполнения в печатном варианте получает каждый студент.
Автор Алимов. Учебник 10-11 класса. Стр. 319-320 §31 — теоретический материал знать.
Вычислите степени бинома:
Спасибо за занятие.
Заключение.
Современный специалист, независимо от профессиональной области должен владеть суммой знаний как гуманитарных, так и естественнонаучных дисциплин.
Чтобы быть конкурентоспособным специалистом, прежде всего, необходимо владеть навыками самостоятельной работы и работы в команде.
Целью учебно-методического занятия является ознакомление и получение навыков в разложении бинома, возведения в любую степень двучлена.
В конспекте занятия предложен теоретический и практический материал. В теоретической части даны достаточно подробные сведения, необходимые для получения основных сведений об изучаемой теме, в практической части – задания, в которых приведены подробные инструкции по их выполнению.
Методика, которая положена в основу пособия, позволяет существенно ускорить процесс закрепления знаний, полученных при изучении дисциплины, освоить новый материал, необходимый для осуществления профессиональной деятельности, а также приобрести опыт работы в команде.
Конспект занятия может быть рекомендовано в помощь преподавателям естественнонаучных дисциплин.
Цель занятия достигнута, учащиеся справились с заданием и затруднений не возникло.
Структура занятия соответствует его типу и цели. Материал дан последовательно, этапы занятия взаимосвязаны:
— проверка домашнего задания;
— устные упражнения;
— объяснение нового материала;
— закрепление;
— самостоятельная групповая работа;
— рефлексия и т.д.
Использованная литература
Алгебра и начала математического анализа: учеб.для 10-11 кл. общеобразоват. Учреждений/[ Ш.А, Алимов, Ю.М. Колягин, Ю.В. Сидоров и др]– М.: Просвещение.- 2012 г
infourok.ru
Использование Бинома Ньютона для решения задач — КиберПедия
Цель: Знать методы решения задач при помощи формулы бинома Ньютона, уметь применять ее при решении соответствующих заданий.
Методические рекомендации
Формула бинома Ньютона для натуральных n имеет вид:
где — биномиальные коэффициенты, представляющие из себя сочетания из n по k.
Выражение в правой части бинома Ньютона называют разложением выражения , а выражение — (k + 1) — м членом разложения.
Для коэффициентов бинома Ньютона справедливы следующие свойства:
· коэффициенты, равноудаленные от начала и конца разложения, равны между собой (правило симметрии)
· ;
· сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона: ;
· сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах, и равна
Первые два свойства являются свойствами числа сочетаний.
Биномиальные коэффициенты разложения удобно представлять в виде треугольника Паскаля:
Используя предложенные методические рекомендации и методические рекомендации к самостоятельной работе №12, выполните задания:
1) Написать разложение ;
2) Найти коэффициент разложения для пятого члена разложения
3) Найти восьмой член разложения в выражении
4) Разложить по формуле бином ;
5) Вычислить сумму ;
6) Доказать, что при любом натуральном n число делится на 9
Раздел 5. Координаты вектора.
Самостоятельная работа № 13.
Действия над векторами
Цель: Развитие интереса к предмету.
Форма самостоятельной деятельности: создание презентации по заявленной теме.
Работа должна соответствовать методическим рекомендациям по созданию презентации.
Самостоятельная работа № 14.
Решение задач по теме: «Векторы»
Цель: Знать правила действия над векторами и уметь применять их при вычислениях.
Методические рекомендации
Теоретический материал
Отложим вектор так, чтобы его начало совпало с началом координат. Тогда координаты его конца называются координатами вектора. Обозначим векторы с координатами (1, 0, 0), (0, 1, 0), (0, 0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем изображать эти векторы, отложенными от начала координат и называть их координатными векторами.
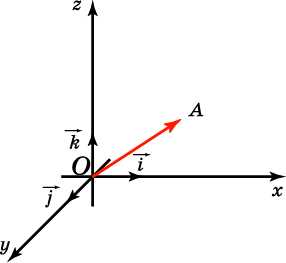
Теорема.Вектор имеет координаты (x, y, z) тогда и только тогда, когда он представим в виде .
Вариант 1
Вариант 2
cyberpedia.su
Электронный конспект для проведения урока+самостоятельная работа по теме «Формула бинома Ньютона»
Формула бинома Ньютона
Возведение выражения (a + b) в степень n может быть произведено по формуле называемой разложением бинома Ньютона:
(a + b)n = an + C1n an — 1 b + C2n an — 2 b2 +…+Ckn an — k bk +… + Cn — 1n abn — 1 + Cnnbn
Если k-й элемент разложения степени бинома обозначать через ТK , то
Тк =
— биноминальные коэффициенты
Примеры:
Примеры
№1
Разложите на множители:
(a + b)5 = ?
(a + b)n = an + C1n an — 1 b + C2n an — 2 b2 +…+Ckn an — k bk +… + Cn — 1n abn — 1 + Cnnbn
№ 2
Раскрыть скобки:
(a + b)n = an + C1n an — 1 b + C2n an — 2 b2 +…+Ckn an — k bk +… + Cn — 1n abn — 1 + Cnnbn
………
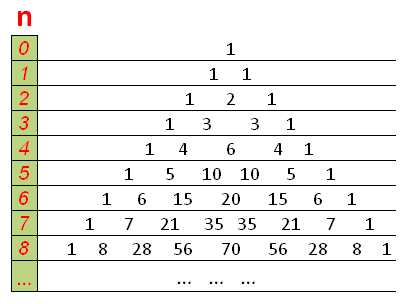
Треугольник Паскаля
№ 3
Найдите коэффициент при :
Решение:
Р(х) = …….+ 10х3∙22 +…..-(4∙(2х)3∙11)…..= …+40х3 …-(4∙8х3)+…= …+ 40х3…..- 32х3
Ответ: 40; -32
Подсчет биноминальных коэффициентов. Самостоятельная работа
№ 1
Вычислить:
а) C52; б) C83; г) C76; д) C104; e) C65
№ 2
Раскройте скобки в выражении:
А) В)
Б) Г)
№ 3
Вычислить по формуле бинома Ньютона:
а) (√5 — √2 )4; б) (√6 + √2 )4; в) (√6 — √2)5; г) (√10 — √2)5.
№ 4
Найдите коэффициент при первой степени переменной x:
А)
Б)
№ 5
Найдите коэффициент при :
А)
Б)
Внеаудиторная самостоятельная работа. Решение задачи по теме «Бином Ньютона».
№ 1
Возведите в четвертую степень выражение (х + 2у)
№ 2
infourok.ru
Урок алгебры по теме: «Бином Ньютона»
Урок алгебры в 10 классе
Тема: Бином Ньютона
Цель урока:
Введение понятия степень двучлена, формулы Бином Ньютона. Вычисление биномиальных коэффициентов. Представление степени двучлена в виде многочлена по формуле Бином Ньютона.
Развитие логического мышления, мыслительных операций, таких как синтез и анализ, обобщение и сравнение.
Создание условий для формирования информационной культуры учащихся.
Оборудование: интерактивная доска, проектор, презентация
Ход урока
1. Мотивационный момент.
Сообщение темы, целей урока, практической значимости рассматриваемой темы.
2. Проверка домашнего задания
Перестановки
1) Сколько трехсловных предложений можно составить из трех слов: сегодня, дождь, идет?
Р3 = 3! = 6
2) Сколькими способами 6 человек могут сесть на 6 стульев? Р6 = 6! = 720
Размещение
1) В чемпионате участвуют 12 команд. Сколькими различными способами могут быть распределены 3 различные медали? 1320
Сочетания
В группе 30 человек. Надо выбрать троих для работы на компьютере. Сколькими способами можно это сделать? 4060
Сколькими способами можно составить команду из 4 человек для соревнований по бегу, если имеются 7 бегунов? С47 = 35
3. Актуализация опорных знаний и постановка проблемы.
Вопросы к учащимся:
прочитайте выражения: (х +2у)2, (а- b)3, (c — d)2
(квадрат суммы двух выражений х и 2у; куб разности двух выражений а и b; квадрат разности двух выражений с и d.)
Что общего в заданных выражениях?
(каждый случай является какой либо степенью многочлена из двух выражений или степенью двучлена.)
Представьте каждую степень двучлена в виде многочлена. Какими формулами воспользуетесь?
Формулами квадрата суммы и разности, куба суммы
(х +2у)2 = х2 +4ху + 4у2
(а — 2)3 = а3 — 3а2 2 +3а 22 — 23= а3 — 6а2+12а -8.
4. Введение нового материала.
Открываем тетради и записываем новую тему «Бином Ньютона».
Бином Ньютона — это отношение, позволяющая представить выражение (a + b)n (n ∈ Z+) в виде многочлена.
С помощью следующей таблицы можно определить значения биномиальных коэффициентов для любой степени. Строится он следующим образом — любое число образуется суммой рядом стоящих чисел над ним. Именно потому эта таблица имеет название треугольник Паскаля.
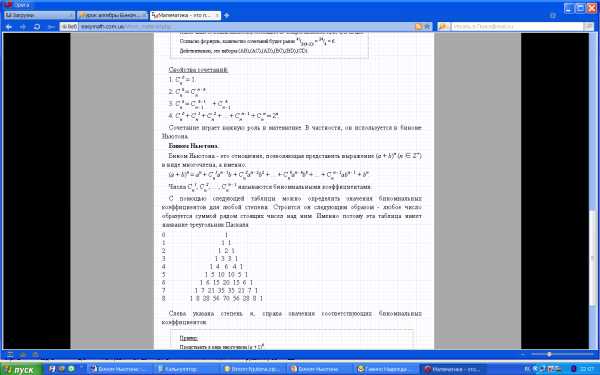
Слева указана степень n, справа значения соответствующих биномиальных коэффициентов.
Столько раз эти слагаемые встретились при приведении подобных слагаемых в многочлене. Количество этих слагаемых есть не что иное, как число сочетаний С, где n — степень двучлена, m — степень второго выражения.
Степень одного из множителей в одночленах с3а или са3 равна 1, количество таких слагаемых, по определению сочетания, равно С = ==4, что подтверждается вашими вычислениями.
Проверим нашу гипотезу на слагаемом 6с2а2 : С = ==6, что также верно.
Заметим, что первое и последнее слагаемое стоит с коэффициентом 1, так как степень одного из выражений в этом одночлене равна 0, а по свойствам сочетаний С= С= 1.
Объединим ваши замечания в следующие правила:
Каждый одночлен является произведением первого и второго выражения в различных степенях и некоторого числа;
Степени всех одночленов раны степени двучлена в условии;
Степень первого выражения одночлена в разложении убывает, начиная со степени двучлена и заканчивая нулевой;
Степень второго выражения одночлена в разложении возрастает, начиная с нулевой и заканчивая степенью двучлена.
Коэффициенты при слагаемых многочлена равны числу сочетаний С, где n — степень двучлена , m — переменная величина, пробегающая значения от 0 до n и соответствующая степени второго выражения.
А теперь запишем формулу бинома Ньютона — формулу представления степени двучлена в многочлен.
Определение:
Д
ля каждого натурального числа n и произвольных чисел a и b имеет место равенство
Равенство называется формулой бинома Ньютона, числа С- биномиальными коэффициентами.
Запишем пример, используя бином Ньютона:
(х -2)5 = Сх5 + Сх4(-2)1 + Сх3 (-2)2 + Сх2 (-2)3 +Сх1 (-2)4 +С(-2)5=
Посчитаем биномиальные коэффициенты, используя определение и свойства числа сочетаний:
С= С=1; С= С==5; С= С===10.)
=х5 -5 х4 2+ 10х3 22 — 10х2 23 +5х 24-25= х5 -10х4 + 40х3 — 80х2 +80х -32.
Как видите, мы достигли того же результата, но гораздо быстрее.
И можем добавить ещё одно правило
Что ещё, связанное с коэффициентами вы заметили?
Крайние коэффициенты равны 1, и все коэффициенты симметричны, относительно середины.
Добавим ещё одно правило, связанное со знаками между одночленами, в формуле бином Ньютона задана сумма, у нас же появились минусы.
Степень разности будет представлена в виде многочлена, знаки в котором чередуются, начиная со знака +, так как нечётная степень отрицательного выражения будет отрицательной, чётная степень всегда положительна.
Вы видите, насколько рационализируется работа по возведению двучлена в степень, если использовать бином Ньютона. Но на самом деле нашу работу можно ещё упростить. Достаточно долго вы вычисляли биномиальные коэффициенты, а коэффициенты — это сочетания. Посмотрите внимательно, все ли свойства сочетаний, которые были ранее введены, мы использовали?
4. Практическая работа.
1). Составьте формулы бинома Ньютона, используя первую, вторую и третью строки.
Для n=1 а+b = a+b — получается вполне естественное тождество.
Для n=2 (а + b)2 = a2 + 2ab+b2;
Для n=3 (а + b)3 = a3 + 3a2b + 3ab2 + b3;
Какой вывод вы сможете сделать?
Известные формулы квадрата и куба суммы или разности двух выражений являются частным случаем формулы бином Ньютона для n =2;3.
5. Обучающая самостоятельная работа с последующей проверкой
1. Представьте степень двучлена в виде многочлена, используя бином Ньютона
а) (х+у)6
б) (1- 2а)4
Решение:
1а) (х+у)6= х6 +6х5у +15х4 у2 +20х3у3 +15х2у4 +6ху5 +у6.
1б) (1- 2а)4 = 1 * 14 (2а)0 – 4* 13 2а + 6*12 (2а)2 — 4 * 11 * (2а)3 + 1 * 10(2а)4 == 1 — 8а + 24а2 — 32а3 + 16а4.
6. Подведение итогов самостоятельной работы.
7. Подведение итогов урока. Можно ещё раз повторить выводы
8. Домашнее задание:
Выучить формулу бином Ньютона.
Представить в виде многочлена: (х — 1)7 (2х — 3)4
Учитель: Послушайте рассказ и сделайте вывод о полезности комбинаторики: «Однажды Шерлок Холмс и доктор Ватсон отправились в путешествие на воздушном шаре.
Вдруг шар понесло ветром, затем он стал терять высоту. Увидев неподалеку человека, путешественники решили поинтересоваться, куда их занесло.
— Господин, скажите, пожалуйста, хотя бы приблизительно, где мы находимся? — спросил Холмс.
— Почему же приблизительно? Я могу сказать вам совершенно точно. Вы находитесь в корзине воздушного шара.
В этот момент порывом ветра шар унесло снова ввысь.
— Вот черт! Угораздило же попасть именно на математика, — пробормотал Холмс.
— Я, как всегда, восхищен вами, Холмс. Но как вы узнали, что этот человек — математик? — удивился Ватсон.
— Это элементарно, его ответ настолько же точен, насколько и бесполезен.
4
kopilkaurokov.ru
«БиномНьютон а»
Муниципальное общеобразовательное учреждение
Школа-интернат лицей-интернат
Реферат
«Б и н о м Н ь ю т о н а»
Работу выполнил:
ученик 11 класса «А»
Зыбко Иван
Руководитель
Еремина
Людмила Александровна
Калининград
2008 год
С о д е р ж а н и е.
Понятие бинома Ньютона.
Биномом Ньютона называют разложение вида:
Но, строго говоря, всю формулу нельзя назвать биномом, так как «бином» переводится как «двучлен». Кроме того, формула разложения была известна еще до Ньютона, Исаак Ньютон распространил это разложение на случай n<0 и n – дробного.
Цель изучения бинома Ньютона – упрощение вычислительных действий.
Компоненты формулы «бином Ньютона»:
— правая часть формулы – разложение бинома;
—
– биномиальные коэффициенты, их можно получить с помощью треугольника Паскаля (пользуясь операцией сложения).Практическая значимость треугольника Паскаля заключается в том, что с его помощью можно запросто восстанавливать по памяти не только известные формулы квадратов суммы и разности, но и формулы куба суммы (разности), четвертой степени и выше.
Например, четвертая строчка треугольника как раз наглядно демонстрирует биномиальные коэффициенты для бинома четвертой степени:
Альтернатива треугольнику Паскаля:
1) перемножить почленно четыре скобки:
;2) вспомнить разложение бинома Ньютона четвертой степени:
— общий член разложения бинома n-й степени:
,где Т – член разложения;
– порядковый номер члена разложения.Свойства бинома и биномиальных коэффициентов.
1.
2. Число всех членов разложения на единицу больше показателя степени бинома, то есть равно
3. Сумма показателей степеней a и b каждого члена разложения равна показателю степени бинома, то есть n
Доказательство
Рассмотрим
-й член разложения:Сумма показателей степеней a и b :
Ч.т.д.
4. Биномиальные коэффициенты членов разложения, равноотстоящих от концов разложения, равны между собой:
(правило симметрии)5. Сумма биномиальных коэффициентов всех членов разложения равна
Доказательство
Пусть
, тогда:o левая часть равна
;o правая часть равна
Тогда:
Ч.т.д.
6. Сумма биномиальных коэффициентов, стоящих на нечетных местах, равна сумме биномиальных коэффициентов, стоящих на четных местах и равна
7. Правило Паскаля:
8. Любой биномиальный коэффициент, начиная со второго, равен произведению предшествующего биномиального коэффициента и дроби
Типовые задачи по теме «Бином Ньютона».
К типовым (стандартным) заданиям по данной теме можно отнести задачи на вычисление, среди которых:
1. Найти член (номер члена) разложения бинома
2. Вывести бином по известным членам разложения (по известной сумме)
3. Вычислить сумму биномиальных коэффициентов разложения бинома
и другие.
Продемонстрируем на примере.
Пример 1
В биномиальном разложении
найти член разложения, не содержащий хРешение
Так как в разложении мы ищем член не содержащий х , то
Тогда
Ответ:
Задачи, сводящиеся к использованию формулы бинома Ньютона
(нестандартные задачи по теме «Бином Ньютона»).
К нестандартным заданиям по данной теме можно отнести такие, в которых нет явного намека на необходимость использования бинома. Однако в итоге, решение сводится к нему и выглядит очень интересным.
Пример 1
Доказать, что для любых
и для любых верно неравенство Бернулли :Доказательство
Пусть
Так как
, тоПереформулируем требование: Доказать, что
, гдеmirznanii.com


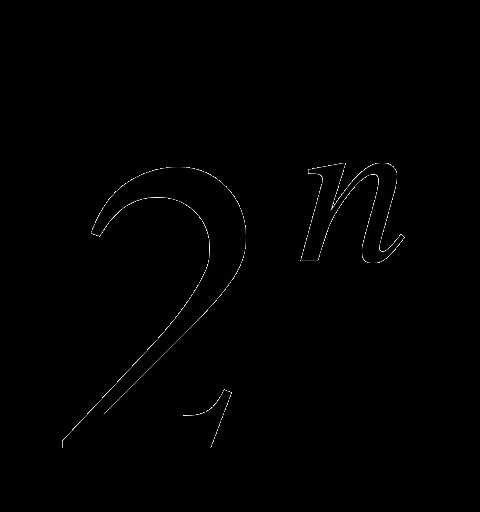
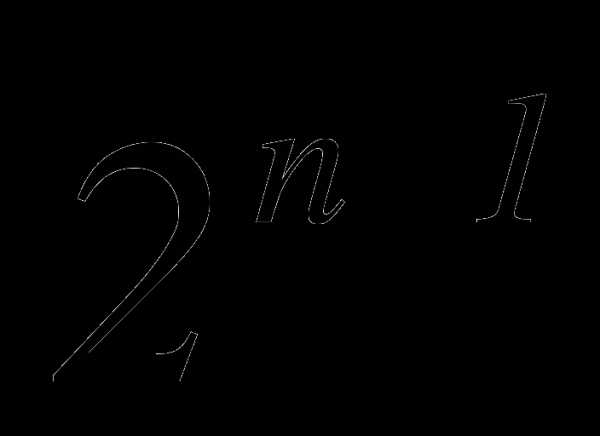
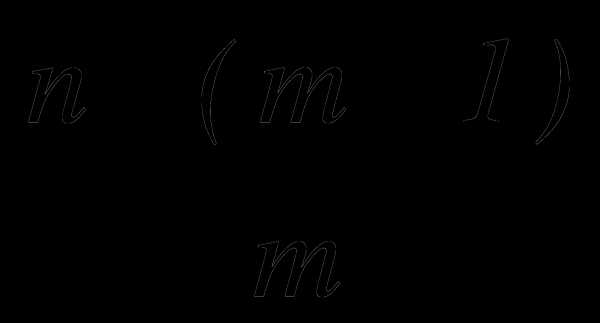
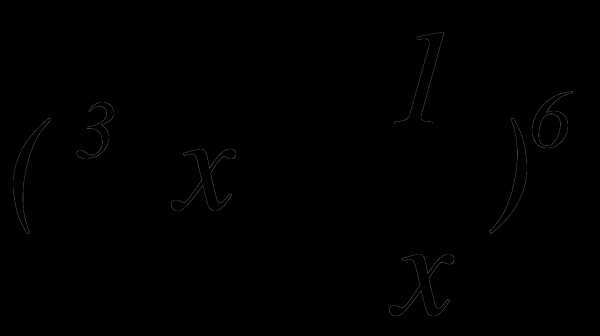 , не содержащего х.
, не содержащего х.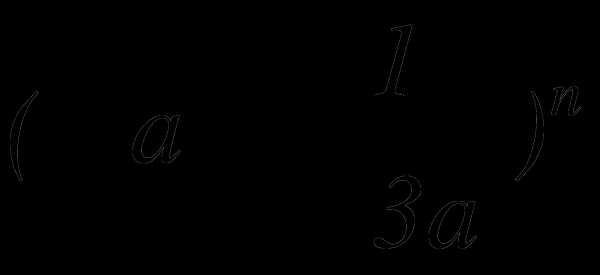 .
. , если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена.
, если биномиальный коэффициент третьего члена на 9 больше биномиального коэффициента второго члена. , если биномиальный коэффициент третьего члена равен 36.
, если биномиальный коэффициент третьего члена равен 36.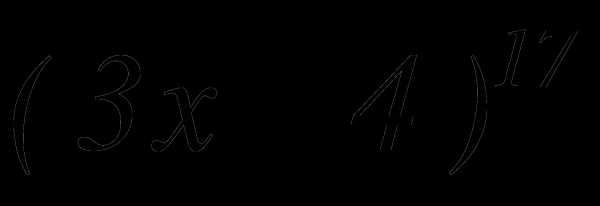 .
.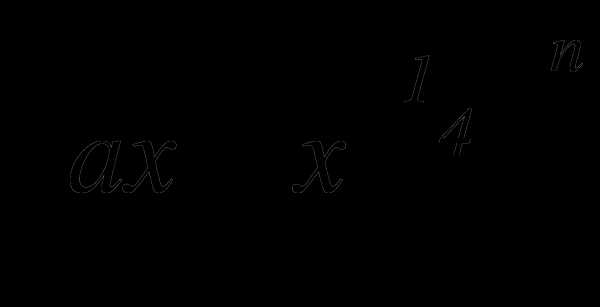 равна 512. Найти слагаемое, не содержащее х.
равна 512. Найти слагаемое, не содержащее х.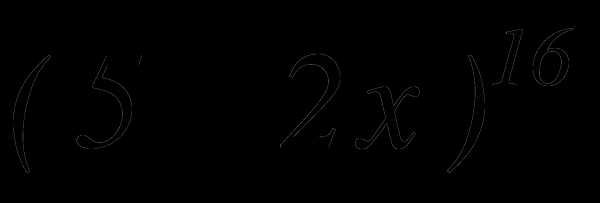 больше двух соседних с ним слагаемых?
больше двух соседних с ним слагаемых? чтобы отношение четвертого слагаемого разложения к третьему было равно
чтобы отношение четвертого слагаемого разложения к третьему было равно  ?
?