Взаимосвязь производной и функции | План-конспект урока по алгебре (11 класс):
1
Взаимосвязь свойств функций и графиков производных.
Цель:
Образовательная –повторить с обучающимся различные взаимосвязи между графиками функций, свойствами производных, графиками производных функции, свойствами функции; научить ориентироваться в разнообразии заданий, связанных с этой взаимосвязью
Развивающая – развивать познавательный интерес учащихся, умение выделять главное, сравнивать, анализировать
Воспитательная – воспитание умения работать в сотрудничестве в парах и группе, оценивать работу товарища.
Оборудование и материалы для урока: компьютер, проектор, экран, презентация для сопровождения урока, листы с заданиями для учащихся.
Ход урока.
- Постановка цели урока — 2мин
Вы изучали тему «Исследование функций с помощью производной»: находили критические точки, производную, определяли свойства и строили график функции.
Сегодня мы рассмотрим задания, в которых по графику производной функции нужно определить свойства самой функции, и наоборот (по графику функции определить поведение производной). То есть задания типа В8, которые, к сожалению, наш учебник не предлагает, но они включаются в тесты Единого Государственного Экзамена.
Поэтому нам сегодня необходимо дойти до самой сути взаимосвязи свойств функции и графика её производной. Наша задача — научиться ориентироваться в разнообразии заданий, связанных с графиками функций и их производных.
- Повторение — 4 мин.
— Давайте вспомним, а какие свойства функции связаны с её производной?
(возрастание, убывание, экстремумы функции).
Рассмотрим график некоторой функции у=f(х),
будем считать, что она определена на всей числовой прямой. (слайд 2)
Назовите точки экстремума данной функции.
ОТВЕТЫ 2 и 5 или хmax=2, xmin=5 (слайд 2)
Напомните мне необходимое условие существования точек экстремума
ОТВЕТЫ: если точка х0 является точкой экстремума, то производная в этой
точке равна нулю или не существует.
А как мы определяем характер точек экстремума (максимум или минимум) достаточное условие:
если в точке х0 функция непрерывна и при переходе через х0
производная меняет знак с + на –, то х0 – точка максимума функции;.
если в точке х0 функция непрерывна и при переходе через х0
производная меняет знак с — на +, то х0 – точка минимума функции.
Определите промежутки возрастания и убывания нашей функции
на промежутках (-∞;2]; [5;+ ∞) функция возрастает,
на промежутке [2;5] функция убывает. ( слайд 2)
А как через производную мы определяем, что функция убывает или возрастает на промежутках
признак монотонности функции:
если f ‘(x)>0 в каждой точке интервала, то функция возрастает на этом интервале.
если f ‘(x)
2
Итак, давайте ещё раз кратко повторим эти свойства:
— если производная больше 0,то…. .
.
функция возрастает
— производная меньше 0,то…..
функция убывает
— если производная равна нулю или не существует в некоторых точках …
то в этих точках возможны точки экстремума
— если производная меняет знак при переходе через точку с + на — , то…
то это точка максимума
— а если с — на +, …
то это точка минимума.
III Основная часть — 15 мин.
1). Можно поставить и обратную связь. Закончите мою мысль
- Если функция возрастает, то производная…..
больше 0
- Если функция убывает, то ……..
производная меньше 0
- Если функция имеет точку максимума, то ……
в этой точке производная равна нулю или не существует
и меняет знак с + на -.
- Если функция имеет точку минимума, то……..
в этой точке производная равна нулю или не существует
и меняет знак с – на +.
- А если график функции имеет точку перегиба ,то…….
в этой точке производная равна нулю или не существует,
но производная не поменяла свой знак.
Итак, имея график функции, мы можем определить свойства производной функции.
2). Рассмотрим задания, связывающие график функции и свойства производной.
Приготовьте лист под № 2, задание № 1. (СЛАЙД –3)
Поработайте в паре, помогите друг другу дойти до самой сути задания.
ПРОВЕРКА через 3 мин.,…ОТВЕТЫ : (СЛАЙД -3)
По графику функции у=f(х) укажите:
1) при каких значениях x производная функции f ‘(x)=0 ;
2) при каких значениях x производная функции f ‘ (x)
3) при каких значениях f ‘(x)>0.
3
3). Учтем тот момент, что производная сама является функцией, значит, у неё имеется свой график.
Учтем тот момент, что производная сама является функцией, значит, у неё имеется свой график.
Давайте установим зависимость поведения графика производной от свойств функции. (слайд – 4)
Приготовьте лист № 1.
Рассмотрим таблицу «Взаимосвязь свойств функции и её производной».
Обратите внимание:
— в первой колонке указано свойство функции,
— во второй колонке – необходимо поставить знак производной,
— далее идёт колонка, где вы должны схематично изобразить поведение графика производной функции.
Давайте первое свойство разберём вместе.
Функция возрастает
Функция возрастает, значит, производная имеет знак больше 0
Т.к производная – это функция, которая больше 0, то где будет расположен её график на интервале (а;b)? (выше оси Х)
Главное, чтобы график был выше оси Х.
Попробуйте сами заполнить дальше таблицу, рассуждая аналогично. Не забудьте о точках максимума, минимума и точах перегиба графика функции.
ПРОВЕРКА через 5мин…. ОТВЕТЫ….ПОЧЕМУ?
Ответы – слайды 5,6.
Давайте ещё раз уточним цепочку взаимосвязи
график производной — свойства функции.
- Если график производной расположен выше оси Х на интервале, то функция …. ( возрастает на этом интервале)
- Если график производной расположен ниже оси Х на интервале, то….
(функция убывает на этом интервале)
- Если график производной пересекает ось Х в точке х0, располагаясь сначала выше, потом ниже оси Х, то х0 для функции является…..
(точкой максимума)
- Если график производной пересекает ось Х в точке х0, располагаясь сначала ниже, потом выше оси Х, то х0 для функции является……
(точкой минимума)
- Если точка х0 лежит на оси Х , график производной проходит через эту точку и расположен выше или ниже оси Х, то для графика функции эта точка будет являтся … (точкой перегиба)
Наша задача научиться выполнять различные задания, связанные с этой взаимосвязью.
4
- Закрепление (5 мин).
- Приготовьте лист № 2, задание №2
Функция определена на множестве действительных чисел. На рисунке изображён
график её производной y=f ‘ (x).
1) Сколько точек экстремума имеет функция у=f(x)?
2) Укажите точку минимума функции у=f(x)
3) Исследуйте функцию y=f(x) на монотонность и укажите количество промежутков, на которых функция возрастает;
4)Укажите длину промежутка убывания функции y=f(x).
ПРОВЕРКА через 5мин…. ОТВЕТЫ….ПОЧЕМУ?
ОТВЕТЫ: СЛАЙД -7
- Тест 5 мин
Давайте проверим, как вы поняли суть взаимосвязи графиков и свойств функции и её производной. Выполним разноуровневый тест.
Каждый возьмите лист № 3, выполняем задания самостоятельно.
ПРОВЕРКА через 5мин. Быстрая, только ответы. (слайд 9)
VI. Итог урока ( 1 мин).
Сегодня на уроке мы установили различные взаимосвязи и рассмотрели разнообразные задания, связанные с графиками функций и графиками производных и их свойствами. Эти задания хороши тем, что на их выполнение можно потратить очень мало времени, т.к. они не требуют решений и вычислений: посмотрел на график – оценил – записал ответ. А на Едином Государственном Экзамене это очень важно быстро и правильно отвечать на вопросы.
Дома проверьте, как вы разобрались во взаимосвязях графиков функций и производных, решая задания типа В8 на сайте РЕШУЕГЭ.РУ.
ОглавлениеПРЕДИСЛОВИЕ ТИТУЛЬНОГО РЕДАКТОРАПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ Глава 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА Глава 2. ВЕЩЕСТВЕННЫЕ ЧИСЛА 2. Недостаточность рациональных чисел для измерения отрезков числовой оси. 3. Упорядочение множества бесконечных десятичных дробей. § 2. ОГРАНИЧЕННЫЕ СВЕРХУ (ИЛИ СНИЗУ) МНОЖЕСТВА ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ 2. Существование точных граней. § 3. ПРИБЛИЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ, РАЦИОНАЛЬНЫМИ ЧИСЛАМИ § 4. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ. ОПИСАНИЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ 2. Существование и единственность суммы и произведения вещественных чисел.  § 5. СВОЙСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ 2. Некоторые часто употребляемые соотношения. 3. Некоторые конкретные множества вещественных чисел. § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 2. Аксиоматическое введение множества вещественных чисел. § 7. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ 2. Операции над множествами. 3. Счетные и несчетные множества. Несчетность сегмента [0, 1]. Мощность множества. 4. Свойства операций над множествами. Отображение множеств. Глава 3. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ 2. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности. 3. Основные свойства бесконечно малых последовательностей. 4. Сходящиеся последовательности и их свойства. § 2. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ 2. Теорема о сходимости монотонной ограниченной последовательности. 4. Примеры сходящихся монотонных последовательностей. § 3. ПРОИЗВОЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ 2. Расширение понятий предельной точки и верхнего и нижнего пределов.  3. Критерий Коши сходимости последовательности. § 4. ПРЕДЕЛ (ИЛИ ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ) ФУНКЦИИ 2. Предел функции по Гейне и по Коши. 3. Критерий Коши существования предела функции. 4. Арифметические операции над функциями, имеющими предел. 5. Бесконечно малые и бесконечно большие функции. § 5. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО БАЗЕ Глава 4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 1. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ 2. Арифметические операции над непрерывными функциями. 3. Сложная функция и ее непрерывность. § 2. СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ 2. Понятие обратной функции. § 3. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 2. Логарифмическая функция. 3. Степенная функция. 4. Тригонометрические функции. 5. Обратные тригонометрические функции. 6. Гиперболические функции. § 4. ДВА ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛА 2. Второй замечательный предел. § 5. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ 2. О точках разрыва монотонной функции. § 6. ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ 2.  Глобальные свойства непрерывных функций. Глобальные свойства непрерывных функций.3. Понятие равномерной непрерывности функции. 4. Понятие модуля непрерывности функции. § 7. ПОНЯТИЕ КОМПАКТНОСТИ МНОЖЕСТВА 2. О покрытиях множества системой открытых множеств. 3. Понятие компактности множества. Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 1. ПОНЯТИЕ ПРОИЗВОДНОЙ 2. Определение производной. 3. Геометрический смысл производной. § 2. ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ 2. Дифференцируемость и непрерывность. 3. Понятие дифференциала функции. § 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ И ОБРАТНОЙ ФУНКЦИИ 2. Дифференцирование обратной функции. 3. Инвариантность формы первого дифференциала. 4. Применение дифференциала для установления приближенных формул. § 5. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 2. Производная логарифмической функции. 3. Производные показательной и обратных тригонометрических функций.  4. Производная степенной функции. 5. Таблица производных простейших элементарных функций. 6. Таблица дифференциалов простейших элементарных функций. 7. Логарифмическая производная. Производная степенно-показательной функции. § 6. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 2. n-ые производные некоторых функций. 3. Формула Лейбница для n-й производной произведения двух функций. 4. Дифференциалы высших порядков. § 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ § 8. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ Глава 6. ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ § 1. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ § 2. ТЕОРЕМА О НУЛЕ ПРОИЗВОДНОЙ § 3. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА ЛАГРАНЖА) § 4. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА 2. Условия монотонности функции на интервале. 3. Отсутствие разрывов первого рода и устранимых разрывов у производной. 4. Вывод некоторых неравенств. § 5. ОБОБЩЕННАЯ ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА КОШИ) § 6.  РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ (ПРАВИЛО ЛОПИТАЛЯ) РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ (ПРАВИЛО ЛОПИТАЛЯ)2. Раскрытие неопределенности вида oo/oo 3. Раскрытие неопределенностей других видов. § 7. ФОРМУЛА ТЕЙЛОРА § 8. РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА. ФОРМУЛА МАКЛОРЕНА 2. Другая запись формулы Тейлора. 3. Формула Маклорена. § 9. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА. РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 2. Разложение по формуле Маклорена некоторых элементарных функций. 2. Доказательство иррациональности числа е. 3. Вычисление значений тригонометрических функций. 4. Асимптотическая оценка элементарных функций и вычисление пределов. Глава 7. ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ И ОТЫСКАНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИИ § 1. ОТЫСКАНИЕ СТАЦИОНАРНЫХ ТОЧЕК 2. Отыскание стационарных точек. 3. Первое достаточное условие экстремума. 4. Второе достаточное условие экстремума. 5. Третье достаточное условие, экстремума. 6. Экстремум функции, недифференцируемой в данной точке.  7. Общая схема отыскания экстремумов. § 2. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ § 3. ТОЧКИ ПЕРЕГИБА 2. Первое достаточное условие перегиба. 3. Некоторые обобщения первого достаточного условия перегиба. 4. Второе достаточное условие перегиба. 5. Третье достаточное условие перегиба. § 4. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ § 6. ГЛОБАЛЬНЫЕ МАКСИМУМ И МИНИМУМ ФУНКЦИИ НА СЕГМЕНТЕ. КРАЕВОЙ ЭКСТРЕМУМ 2. Краевой экстремум. 3. Теорема Дарбу. ДОПОЛНЕНИЕ Алгоритм отыскания экстремальных значений функции, использующий только значения этой функции Глава 8. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Неопределенный интеграл. 3. Основные свойства неопределенного интеграла. 4. Таблица основных неопределенных интегралов. § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование по частям. § 3. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ в ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Краткие сведения о корнях алгебраических многочленов. 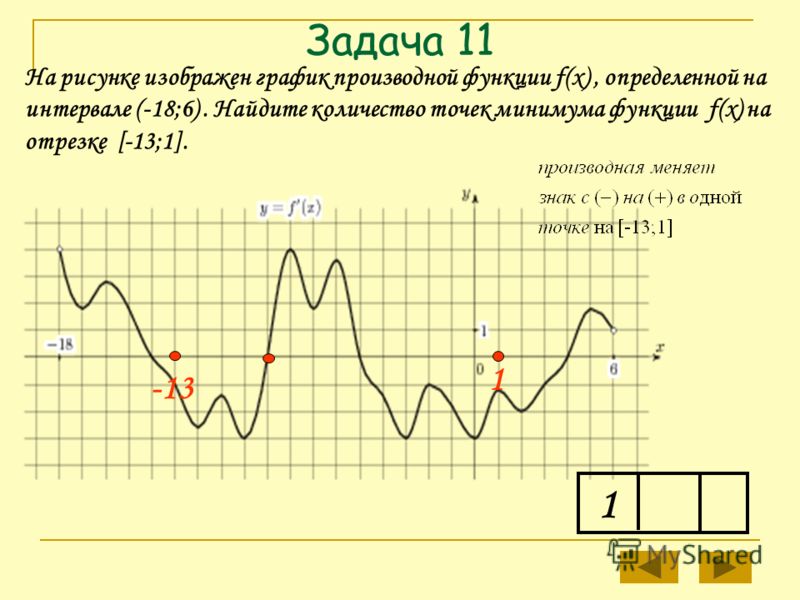 3. Разложение алгебраического многочлена с вещественными коэффициентами на произведение неприводимых множителей. 4. Разложение правильной рациональной дроби на сумму простейших дробей. 6. Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений. § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА ИНТЕГРАЛ РИМАНА: § 2. ВЕРХНИЕ И НИЖНИЕ СУММЫ И ИХ СВОЙСТВА 2. Основные свойства верхних и нижних сумм. § 3. ТЕОРЕМЫ О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ УСЛОВИЯХ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ. КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ 2. Классы интегрируемых функций. § 4. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ОЦЕНКИ ИНТЕГРАЛОВ. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ 2. Оценки интегралов. § 5. ПЕРВООБРАЗНАЯ НЕПРЕРЫВНОЙ ФУНКЦИИ. ПРАВИЛА ИНТЕГРИРОВАНИЯ ФУНКЦИЙ 2. Основная формула интегрального исчисления. 3. Важные правила, позволяющие вычислять определенные интегралы.  4. Остаточный член формулы Тейлора в интегральной форме. § 6. НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ 2. Неравенство Гёльдера для сумм. 3. Неравенство Минковского для сумм. 4. Неравенство Гёльдера для интегралов. 5. Неравенство Минковского для интегралов. § 7. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ РИМАНА 2. Критерий интегрируемости Лебега. ДОПОЛНЕНИЕ 1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Критерий Коши сходимости несобственного интеграла первого рода. 3. Абсолютная и условная сходимость несобственных интегралов. 4. Замена переменных под знаком несобственного интеграла и формула интегрирования по частям. § 2. Несобственные интегралы второго рода § 3. Главное значение несобственного интеграла ДОПОЛНЕНИЕ 2. Интеграл Стилтьеса 2. Свойства интеграла Стилтьеса. Глава 10. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. ДЛИНА ДУГИ КРИВОЙ 2. Понятие параметризуемой кривой. 3. Длина дуги кривой. Понятие спрямляемой кривой. 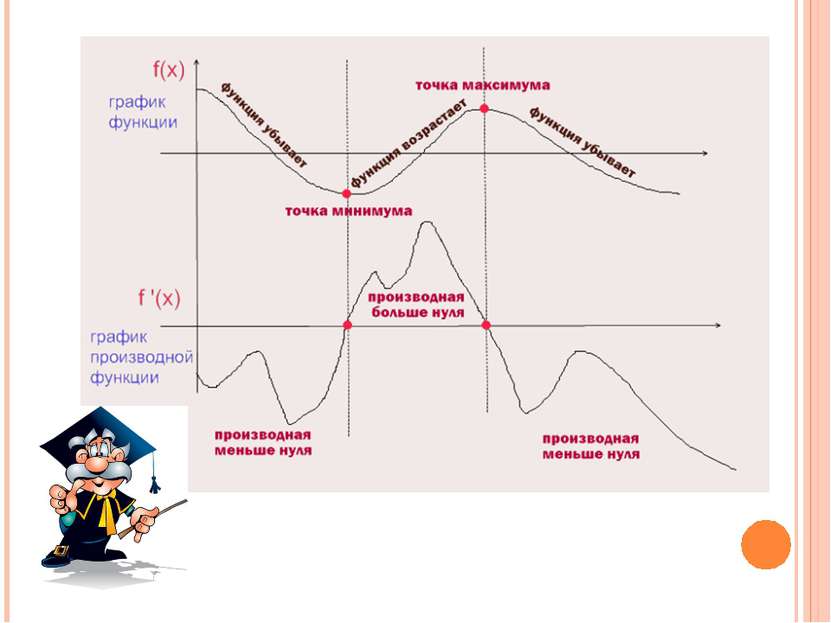 3. Предел функции m переменных. 4. Бесконечно малые функции m переменных. 5. Повторные пределы. § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ m ПЕРЕМЕННЫХ 2. Непрерывность функции m переменных по одной переменной. 3. Основные свойства непрерывных функций нескольких переменных. § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Дифференцируемость функции нескольких переменных. 3. Геометрический смысл условия дифференцируемости функции двух переменных. 4. Достаточные условия дифференцируемости. 5. Дифференциал функции нескольких переменных. 6. Дифференцирование сложной функции. 7. Инвариантность формы первого дифференциала. 8. Производная по направлению. Градиент. § 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 2. Дифференциалы высших порядков. 3. Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме. 4. Формула Тейлора с остаточным членом в форме Пеано. § 6. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ m ПЕРЕМЕННЫХ 2.  Достаточные условия локального экстремума функции m переменных. Достаточные условия локального экстремума функции m переменных.3. Случай функции двух переменных. ДОПОЛНЕНИЕ 1. Градиентный метод поиска экстремума сильно выпуклой функции 1. Выпуклые множества и выпуклые функции. 2. Существование минимума у сильно выпуклой функции и единственность минимума у строго выпуклой функции. 3. Поиск минимума сильно выпуклой функции. ДОПОЛНЕНИЕ 2. Метрические, нормированные пространства 2. Открытые и замкнутые множества. 3. Прямое произведение метрических пространств. 4. Всюду плотные и совершенные множества. 5. Сходимость. Непрерывные отображения. 6. Компактность. 7. Базис пространства. Топологические пространства Линейные нормированные пространства, линейные операторы ДОПОЛНЕНИЕ 3. Дифференциальное исчисление в линейных нормированных пространствах 2. Формула Лагранжа конечных приращений. 3. Связь между слабой и сильной дифференцируемостью. 4. Дифференцируемость функционалов. 5. Интеграл от абстрактных функций.  6. Формула Ньютона — Лейбница для абстрактных функций. 7. Производные второго порядка. 8. Отображение m-мерного евклидова пространства в n-мерное. 9. Производные и дифференциалы высших порядков. 10. Формула Тейлора для отображений одного нормированного пространства в другое. Исследование на экстремум функционалов в нормированных пространствах 2. Достаточные условия экстремума. Глава 13. НЕЯВНЫЕ ФУНКЦИИ § 1. СУЩЕСТВОВАНИЕ И ДИФФЕРЕНЦИРУЕМОСТЬ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ 2. Вычисление частных производных неявно заданной функции. 3. Особые точки поверхности и плоской кривой. 4. Условия, обеспечивающие существование для функции y=f(x) обратной функции. § 2. НЕЯВНЫЕ ФУНКЦИИ, ОПРЕДЕЛЯЕМЫЕ СИСТЕМОЙ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ 2. Вычисление частных производных функций, неявно определяемых посредством системы функциональных уравнений. 3. Взаимно однозначное отображение двух множеств m-мерного пространства. § 3. ЗАВИСИМОСТЬ ФУНКЦИЙ 2. Функциональные матрицы и их приложения.  § 4. УСЛОВНЫЙ ЭКСТРЕМУМ 2. Метод неопределенных множителей Лагранжа. 3. Достаточные условия. 4. Пример. ДОПОЛНЕНИЕ Отображения банаховых пространств. Аналог теоремы о неявной функции 2. Случай конечномерных пространств. 3. Особые точки поверхности в пространстве n измерений. Обратное отображение. 4. Условный экстремум в случае отображений нормированных пространств. |
онлайн-книга по исчислению
Глава 8. Понимание производнойГлава 8. Понимание производной
- Раздел 8.1 — Использование первой производной
- Раздел 8.2 — Использование второй производной
- Раздел 8.3 — Систематическое использование производных финансовых инструментов
Раздел 8.1 — Использование первой производной
В этой главе мы подробно рассмотрим
посмотрите на определение производной и ее связь с ее
антипроизводная. Мы увидим, каким может быть график антипроизводной. точно описать, просто взглянув только на производную функцию.
точно описать, просто взглянув только на производную функцию.
Из определения производной является производной от функция . Производная функции говорит нам, насколько быстро f изменяется относительно независимой переменной x. Таким образом, производная относится в частности, скорость изменения антипроизводной функции по отношению к Икс. Скорость изменения также является синонимом наклона касательной к график в определенной точке.
Таким образом, функция и ее производная тесно связаны и знание только производной может многое сказать нам о поведении ее антипроизводная. Поскольку производная функции получается из определение производной как: , мы можем работать с определением, чтобы найти антипроизводную когда известна только производная. Вспомните также, как дифференциация основана на процесс ограничения или вычитания и деления; поэтому работает в обратном направлении сказал бы нам, что мы должны складывать и умножать.
Мы будем развивать это позже, однако, давайте сначала посмотрим, как
мы можем использовать f(x) для получения точек равновесия на графике
антипроизводная или f(x).
точек равновесия определение, точки на графике относятся к статическим ситуациям где скорость изменения равна нулю. Таким образом, изменение независимой переменной не приводит к изменению зависимой переменной. Состояние равновесия в целом возникает, когда ситуация достигает критического максимального значения, а затем снижается или когда ситуация достигла критического минимального значения, затем увеличивается.
Равновесие и критические значения функция может относиться к разным вещам в зависимости от того, какие явления изучал. Поэтому ограничимся геометрической интерпретацией равновесия как точки на графике, где скорость изменения равна нулю. Поскольку скорость изменения равна нулю, касательная к графику в этой точке будет быть горизонтальной линией.
Горизонтальная касательная говорит нам, что значение производной в точке равновесия равно нулю. Такие ситуации случаются когда график достигает максимального или минимального значения.
Также может существовать горизонтальная касательная,
но не обязательно, когда изменяется вогнутость графика.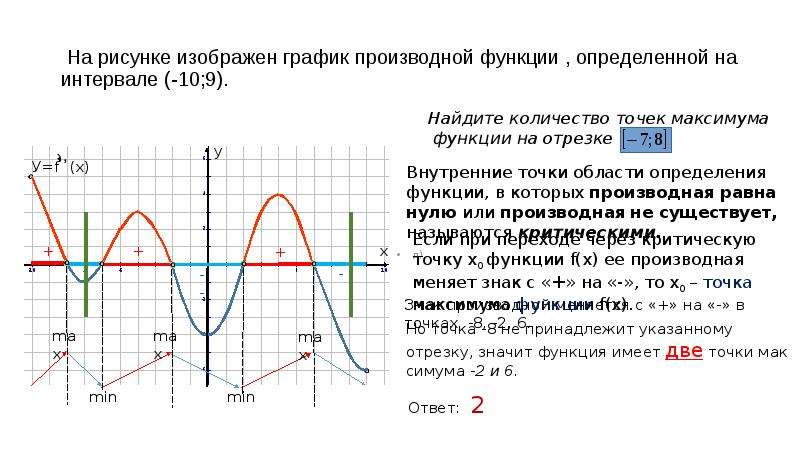
Изменение вогнутости происходит на точки на графике называются перегиба точки. Как мы вскоре узнаем, значение производной на перегибе не изменяется. должны быть равны нулю. Поэтому мы ограничим наше определение равновесия точек для отображения максимальных или минимальных значений на графике.
Например, чтобы найти равновесие баллы за функцию, . нам сначала нужно дифференцировать его, чтобы получить, . производная, , сообщает нам мгновенную скорость изменение функции, , в любой точке х. Так как мы хотим найти точки, где скорость изменения f(x) равно нулю, нам нужно набор равным нулю, чтобы найти те значения x, которые удовлетворяют уравнению, . Делая это для результат:
Это говорит нам о том, что и при x=0, и при x=2/3 существует точка равновесия, что подтверждается графиком функция,
Наличие
найдены критические точки, как мы можем классифицировать их как максимумы или
минимумы? Очевидно, это можно сделать, просто взглянув на график , но цель этой главы состоит в том, чтобы понять, как использовать только
производная, приблизить
поведение функции .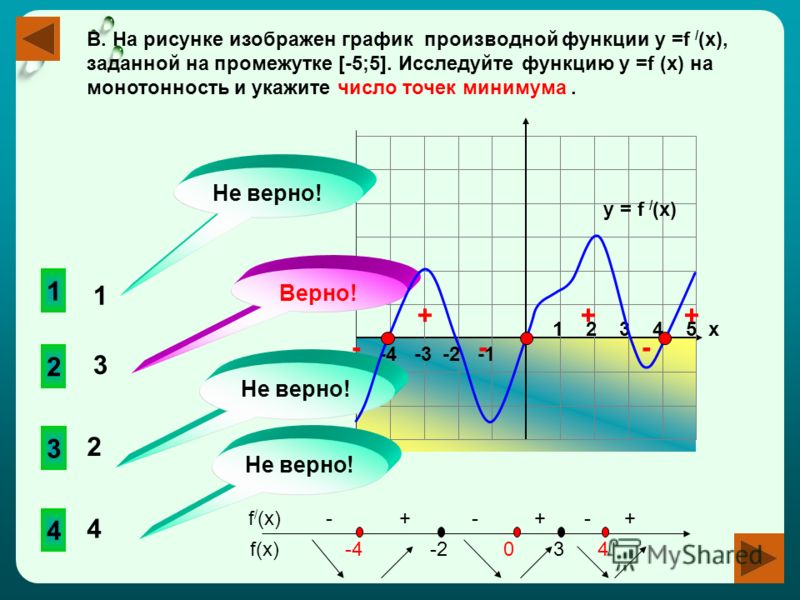 Чтобы определить, являются ли наши точки равновесия либо
максимум или минимум нам нужно оценить точки слева и справа от
точки равновесия, чтобы определить, где функция, , увеличивается или уменьшается.
Чтобы определить, являются ли наши точки равновесия либо
максимум или минимум нам нужно оценить точки слева и справа от
точки равновесия, чтобы определить, где функция, , увеличивается или уменьшается.
Минимум определяется как нижняя часть U-образного или вогнутого вверх графика. Если график вогнутый, то наклон или скорость изменения положительны. справа от точки равновесия, а функция возрастает справа от эта точка. Слева от точки равновесия наклон отрицателен, что означает, что функция убывает до он достигает точки равновесия. Чтобы лучше понять это, посмотрите на следующий график вогнутой части графика. Обратите внимание, как функция снижается, пока не достигнет точки равновесия, а после ее прохождения возрастает.
Аналогично, если скорость изменения были отрицательными на
с правой стороны и положительным с левой стороны точки равновесия, то получим
перевернутый U-образный или вогнутый вниз график. Таким образом, вогнутый вниз график отражает
максимальное значение в точке равновесия.
Если наклон положительный или отрицательно по обе стороны от точки равновесия, то мы получаем перегиб точка, которая представляет, где вогнутость изменяется от U форму перевернутой буквы U формы или наоборот. Следующий график обобщает сделанные выше выводы.
Следующий раздел -> Раздел 8.2 — Использование второй производной
Определение производной | Calc Medic
Цели обучения
Критерии успеха
Я могу объяснить, что представляет собой точка на графике производной.
Я могу использовать предельное определение производной для вычисления наклона касательной для любого значения x.
Я могу написать уравнение касательной.
Краткий план урока
Обзор
Это один из наших самых любимых уроков! В этом уроке мы переходим от неформального понятия «график наклонов» к формальному понятию производной. Учащиеся покидают класс сегодня с твердым, осязаемым, хорошо концептуализированным пониманием производной как функции, а не только как отдельных наклонов. Артефакты этого урока хранятся на наших стенах в течение года и будут упоминаться во многих будущих уроках.
Учащиеся покидают класс сегодня с твердым, осязаемым, хорошо концептуализированным пониманием производной как функции, а не только как отдельных наклонов. Артефакты этого урока хранятся на наших стенах в течение года и будут упоминаться во многих будущих уроках.
Советы преподавателям
В начале каждого урока присваивайте каждому ученику целое число от -12 до 12. Важно, чтобы у каждого ученика было свое число (увеличьте диапазон, если ваш класс большой). Это число будет их x-значением на протяжении всего урока. Они могут заполнить это поле, когда увидят x=_____ на уроке. Если ваш класс небольшой, вам придется самостоятельно заполнить некоторые точки, чтобы учащиеся начали видеть некоторые закономерности на «графике уклонов». Это не будет отвлекать от урока, пока каждый учащийся рассчитывает свою мгновенную скорость изменения по своему личному значению x.
Мы рекомендуем сделать паузу, чтобы подвести итоги после вопроса 4, сделать несколько первых замечаний о том, почему все точки образуют горизонтальную линию, а затем позволить учащимся продолжить. Мы предлагаем не использовать слово «производная» вместо «график наклонов» до конца опыта.
Мы предлагаем не использовать слово «производная» вместо «график наклонов» до конца опыта.
Поскольку этот урок довольно длинный, мы настоятельно рекомендуем, когда вы дойдете до вопроса 5, поручить половине учащихся ответить на вопрос 5а, а половине учащихся — на вопрос 6а (более сильным ученикам можно предложить решить производную кубической функции) . Таким образом, они решают только одну задачу с длинной производной вместо двух. Это означает, что у вас будет только половина точек на бумаге, но в классе среднего размера это все равно даст вам хорошее представление об общей форме этой кривой. . Если ваши ученики сильнее, вы можете попросить их сделать и то, и другое. Важно, чтобы КАЖДЫЙ учащийся скопировал графики и «график уклонов» для всех трех функций.
При подведении итогов добавьте f’(x), g’(x) и h’(x) к вашим точечным функциям, которые раньше назывались просто «графики наклонов».
После того, как точки/наклоны нанесены, укажите на конкретную точку и спросите, кто из учащихся отвечает за расстановку этой точки.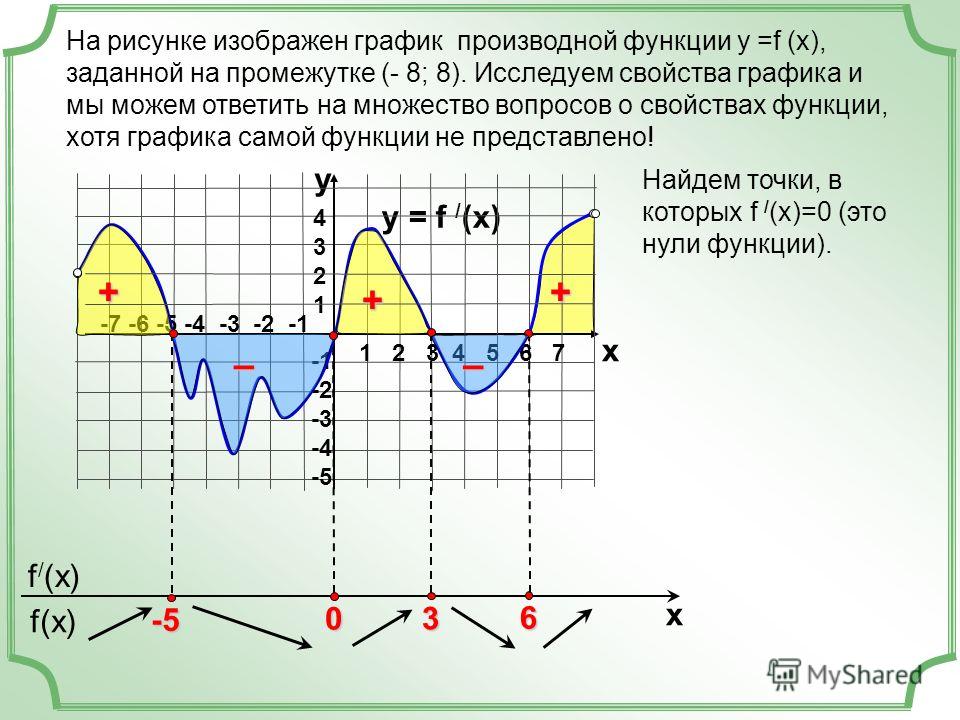 Попросите учащихся объяснить, что представляет их точка. Сделайте это несколько раз в течение урока и в последующие дни, чтобы учащиеся ознакомились с идеей о том, что точка на производной представляет собой наклон исходной кривой при x=___». Настаивайте на слове «наклон», конкретном значении x и на том, что наклон исходной функции. Очень важно, чтобы учащиеся не использовали расплывчатые формулировки, такие как «это», «график» или даже «наклон». Научите своих учеников использовать точный язык, такой как «график f» или «наклон исходной кривой, f (x)».
Попросите учащихся объяснить, что представляет их точка. Сделайте это несколько раз в течение урока и в последующие дни, чтобы учащиеся ознакомились с идеей о том, что точка на производной представляет собой наклон исходной кривой при x=___». Настаивайте на слове «наклон», конкретном значении x и на том, что наклон исходной функции. Очень важно, чтобы учащиеся не использовали расплывчатые формулировки, такие как «это», «график» или даже «наклон». Научите своих учеников использовать точный язык, такой как «график f» или «наклон исходной кривой, f (x)».
Exam Insights
Это гарантированный контент AP Test как в разделах множественного выбора, так и в разделах бесплатных ответов. Время, которое вы потратите на то, чтобы заложить основу (графическую, аналитическую и вербальную) для концепции производной, окупится тем, что учащиеся удержат, поймут и сдадут тест AP! Когда вы просматриваете прошлые вопросы AP, обратите внимание на разные представления, разные переменные и различные обозначения, представленные учащимся.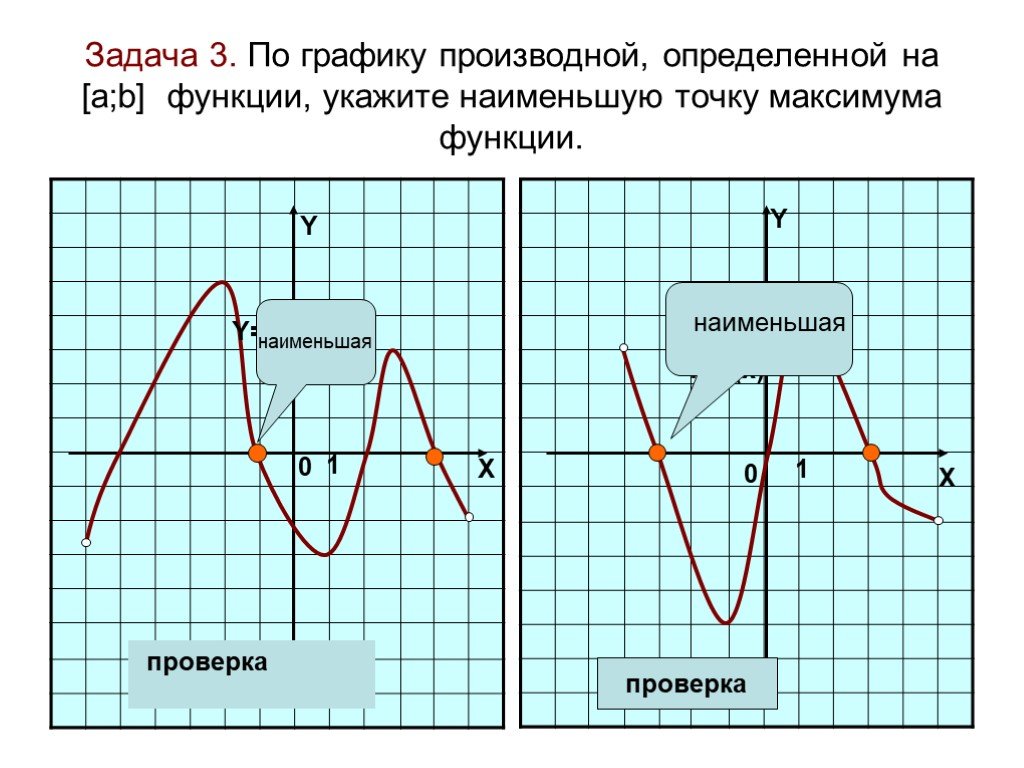

 Книга включает в себя теорию вещественных чисел, теорию пределов, теорию непрерывности функций, дифференциальное и интегральное исчисления функций одной переменной и их приложения, дифференциальное исчисление функций многих переменных и теорию неявных функций.
Книга включает в себя теорию вещественных чисел, теорию пределов, теорию непрерывности функций, дифференциальное и интегральное исчисления функций одной переменной и их приложения, дифференциальное исчисление функций многих переменных и теорию неявных функций.