Исследование функции с помощью производной /qualihelpy
Рассмотрим функции и , которые непрерывны на отрезке и дифференцируемы на интервале .Теорема Ферма : если функция в точке имеет локальный экстремум, то .
Геометрический смысл теоремы: касательная к графику функции в точке параллельна оси абсцисс.
Теорема Лагранжа: , где .
Геометрический смысл теоремы: касательная к графику функции в точке параллельна секущей, соединяющей концы графика этой функции.
Теорема Ролля: если и , то .
Геометрический смысл теоремы: у графика функции существует точка, в которой касательная параллельна оси абсцисс.
Теорема Коши: если , то .
Исследование функции с помощью первой производной
С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.
Достаточное условие возрастания (убывания) функции:
а) если на заданном промежутке , то функция возрастает на этом промежутке;
б) если , то функция убывает на этом промежутке.
Экстремум функции
Максимумом (минимумом) функции называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.
Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 6.4).
Максимум и минимум функции называются экстремумом функции . Значение аргумента, при котором достигается экстремум, называется точкой экстремума . На рисунке 6.4 значения , , , и являются точками экстремума рассматриваемой функции.
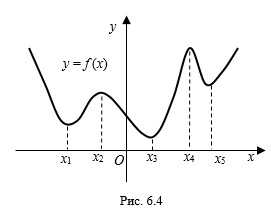
Критическими точками функции называют те значения аргумента, при которых производная функции равна нулю или не существует. Критические точки функции находят, решая уравнение: .
Алгоритм нахождения точек экстремума функции:
1) находим область определения функции ;
2) находим ;
3) находим критические точки функции, решая уравнение ;
4) наносим критические точки на область определения функции;
5) определяем знак производной функции на полученных промежутках;
6) определяем точки экстремума функции по правилу:
Рассмотрим функцию на отрезке . Свое наибольшее и наименьшее значение она может принимать либо на концах отрезка, либо в точках экстремума.
Алгоритм нахождения наибольшего и наименьшего значений функции на заданном отрезке:
1) находим ;
2) находим критические точки функции, решая уравнение ;
3) находим значение функции на концах отрезка и в критических точках, принадлежащих данному отрезку;
4) определяем наибольшее и наименьшее значение из полученных.
Исследование функции с помощью второй производной
Критическими точками второго рода
функции называют те значения аргумента, при которых вторая производная этой функции равна нулю или не существует.Критические точки второго рода функции находят, решая уравнение .
Если при переходе через критическую точку второго рода вторая производная функции меняет знак, то имеем точку перегиба графика функции.
Если на некотором промежутке выполняется неравенство , то функция вогнута на этом промежутке, а если , то функция выпукла на этом промежутке.
helpy.quali.me
Урок-зачет по теме «Исследование функции с помощью производной»
Разделы: Математика
Цель урока: проверка умений и навыков
Теоретическая часть зачета.
Вопросы
Определение точки минимума и точки максимума.
Теоретическая часть зачета
Ответы
1) Определение точки минимума.
Если функция определена в некоторой окрестности точки Х0 , то точка Х0 называется точкой минимума функции f(х), если существует такая окрестность точки Х0 ,что для всех хх0 из этой окрестности выполняется неравенство f(х)>f(х0).
Определение точки максимума.
Если функция определена в некоторой окрестности точки Х0 , то точка Х0 называется точкой максимума функции f(х),если существует такая окрестность точки Х0 , что для всех х?х0 из этой окрестности выполняется неравенство f(х)<f(х0).
2) Определение критических точек.
Критические точки – это внутренние точки области определения функции в которых производная не существует или равна нулю.
3) Необходимое условие, чтобы Х0 была точкой экстремума: эта точка должна быть критической.
4) Алгоритм нахождения критических точек.
1. Найти область определения функции.
2. Найти производную функции.
3. Найти область определения производной данной функции.(Чтобы определить есть ли точки в которых производная не существует. Если такие точки есть, то проверить являются ли они внутренними точками области определения функции.
4. Найти точки, в которых производная равна нулю, решив уравнение: f ‘(х)=0.
Проверить являются ли найденные точки внутренними точками области определения функции.
5) Стационарные точки — точки, в которых производная функции равна нулю.
6) Теорема Ферма. (Необходимое условие экстремума функции.)
у=f(х)-функция, которая определена в некоторой окрестности точки Х0, и имеет производную в этой точке.
Теорема: если Х0-точка экстремума дифференцируемой функции f(х), то f ‘(х)=0.
7) Достаточные условия существования экстремума функции в точке.
y=f(х) определена на (а;в). Х0-критическая точка.
Если функция f непрерывна в точке Х0, а f '(х)>0 на интервале (а;х0) и f ‘(х)<0 на интервале (х0;в), то точка х0 является точкой максимума функции f.
(Упрощенная формулировка: если в точке Х0 производная меняет знак с “+” на “ _”, то Х0есть точка максимума.)
Если функция f непрерывна в точке Х
(Упрощенная формулировка: если в точке Х0 производная меняет знак с “_” на “+”, то Х0 есть точка минимума.)
8) Достаточный признак возрастания, убывания функции.
Если f ‘(х)>0 для всех х из промежутка (а; в), то функция возрастает на промежутке (а; в).
Если f ‘(х)<0 для всех х из промежутка (а; в), то функция убывает на промежутке (а; в).
(Если функция непрерывна на конце промежутка, то его можно присоединить к промежутку возрастания (убывания) функции.)
9) Точки экстремума, экстремум функции.
Х0 — точка максимума, Х0
–точка минимума называются точками экстремума.f(х0) — максимум функции,
f(х0) — минимум функции называются экстремумами функции.
10) Алгоритм нахождения экстремумов функции.
1. Находим область определения функции.
2. Находим производную функции.
3. Находим критические точки.
4. Определим знак производной на каждом из интервалов, на которые критические точки разбивают область определения.
5. Найдем точки экстремума, учитывая характер изменения знака производной.
6. Найдем экстремумы функций.
11) Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке.
1. Найти значения функции на концах отрезка [а; в].
2. Найти значения функции в тех критических точках, которые принадлежат интервалу (а; в).
3. Из найденных значений выбрать наибольшее и наименьшее.
Практическая часть зачета
“Исследование функций с помощью производной.
Наибольшее и наименьшее значения функций на отрезке”
Найти:
а) критические точки функций,
б) экстремумы функций
в) наибольшее и наименьшее значения функций на указанном промежутке
г) построить график.
| 1. у=(х-3)2(х-2). | [1;4] | 11. у=2х4-х. | [-1;1] |
| 2. у=1/3х3+х2 | [-4;1] | 12. у=х2-2/х. | [-3;-0,5] |
| 3. у=1/3х3-х2-3х | [-2;6] | 13. у=1/(х2+1). | [-1;2] |
| 4. у=-1/4х4+2х2+1. | [-3;3] | 14. у=3х-х3. | [-1,5;1,5] |
| 5. у=х4-8х2-9. | [-3;3] | 15. у=2х2-х4. | [-2;1,5] |
| 6. у=(х-2)(х+1)2. | [-1,5;1,5] | 16. у=3х2/3-х2. | [-8;8] |
| 7. у=-2/3х3+2х-4/3. | [-1,5;1,5] | 17. у=3х1/3-х. | [-8;8] |
| 8. у=3х5-5х4+4. | [-1;1] | 18. у=х3-1,5х2-6х+4. | [-2;3] |
| 9. у=9х2-9х3. | [-0,5;1] | 19. у=(1-х)/(х2+3). | [-2;5] |
| 10. у=1/3х3-4х. | [-3;3] | 20. у= -х4+2х2+3. | [-0,5;2] |
Ответы к практической части зачета (Приложение1)
12.03.2008
xn--i1abbnckbmcl9fb.xn--p1ai
Разработка урока по алгебре на тему «Исследование функции с помощью производной и построение её графика» (10 класс)
Урок на тему: «Исследование функции с помощью производной и построение её графика».
Ф.И.О. учителя: Банникова Дарья Дмитриевна
Дата проведения: 25.02.13
Класс: 10 «Б»
Цели урока:
Усвоить алгоритм исследования функции с помощью производной
Формировать навыки прикладного использования производной
Развивать умение обобщать, абстрагировать и конкретизировать знания при исследовании функции
Воспитывать познавательный интерес к математике
Тип урока: урок объяснения нового материала
Структура урока: 1. Организационный момент – 2 мин.
2. Актуализация знаний – 10 мин.
3. Ознакомление с новым материалом – 10 мин.
4. Первичное осмысление изученного на практике – 16 мин.
5. Постановка задания на дом – 2 мин.
6. Подведение итогов. – 5 мин.
Ход урока.
Деятельность учителя
Деятельность учащихся
1. Организационный момент.
Проверка готовности класса к уроку. Сообщение темы и цели урока.
2. Актуализация знаний.
Самостоятельная работа одного учащегося у доски. Задание написать все формулы производной сложной функции.
Устная работа с классом.
1.Назовите промежутки убывания функции
2.Назовите точку максимума функции
3.Найти производную функции у=3х2 – cosx + 2
4.Найти область определения функции
5.Найти область определения функции
6.Найти область определения функции
Четность и нечетность функции.
Как определить четность функции?
График чётной функции
симметричен относительно
оси ординат.
График нечётной функции
симметричен относительно
начала координат.
Какие еще функции есть помимо четных и нечетных?
Как найти точки пересечения с осями координат?
[-3;2]
6
y‘= 6x+sinx
[0;2) & (2;∞)
х ≠ 5
(-∞;2) & (2;∞)
f(-х)=f (х)
f (-х)= — f (х)
Функции общего вида и периодические.
С осью ОУ: х=0
С осью ОХ: у=0
3. Ознакомление с новым материалом.
Запишем алгоритм исследования функции с помощью производной в тетрадь.
1. Найти область определения
функции.
2. Определить четность,
нечетность и периодичность
функции.
3. Найти координаты точек
пересечения графика функции
с осями координат.
4. Найти промежутки
знакопостоянства функции.
5. Найти промежутки возрастания, убывания и экстремумы функции.
6. Занесите все полученные данные в таблицу.
7. Построить график
функции.
8. Найти дополнительные точки.
9. Найти множество значений функции.
Разбор устно у доски. Ответить на вопросы появившиеся у класса.
4. Первичное осмысление изученного на практике.
Решение задач с объяснением у доски.
f(x)=
Исследовать функцию y=x3+6x2+9x и построить график.
Исследовать функцию y=x2/(x-2) и построить график.
Исследовать функцию y=(6(x-1))/(x2+3) и построить график.
y=x3+6x2+9x
1) D(y)=R
2) Определим вид функции:
y(-x)=(-x)3+6(-x)2+9(-x)=-x+6×2-9x функция общего вида.
3) Найдем точки пересечения с осями:
Oy: x=0, y=0 (0;0) – точка пересечения с осью y.
Ox: y=0,
x3+6x2+9x=0
x(x2+6x+9)=0
x=0 или x2+6x+9=0
D=b2-4ac
D=36-36=0
D=0, уравнение имеет один корень.
x=(-b+D)/2a
x=-6+0/2
x=-3
(0;0) и (-3;0) – точки пересечения с осью х.
4) Найдем производную функции:
y’=(x3+6x2+9x)’=3x2+12x+9
5) Определим критические точки:
y’=0, т.е. 3x2+12x+9=0 сократим на 3
x2+4x+3=0
D=b2-4ac
D=16-12=4
D>0, уравнение имеет 2 корня.
x1,2=(-b±√D)/2a, x1=(-4+2)/2 , x2=(-4-2)/2
x1=-1 x2=-3
6) Обозначим критические точки на координатной прямой и определим знак функции:
+ — +
-3 -1
x=-4, y’=3*16-48+9=9>0
x=-2, y’=12-24+9=-3<0
x=0, y’=0+0+9=9>0
7) Найдем xmin и xmax:
xmin=-1
xmax=-3
8) Найдем экстремумы функции:
ymin=y(-1)=-1+6-9=-4
ymax=y(-3)=-27+54-27=0
9) Построим график функции:
10)Дополнительные точки:
y(-4)=-64+96-36=-4
y=x2/(x-2)
Найдем область определения.
1) D(y)=R \ {2}
2)Определим вид функции.
y(-x)=(-x)2/(-x-2)=x2/(-x-2), функция общего вида.
3)Найдем точки пересечения с осями.
Oy: x=0, y=0 (0;0) – точка пересечения с осью y.
Ox: y=0,
x2/(x-2)=0
x3-2x2=0
x2(x-2)=0
x=0 или x=2 (2;0) – точка пересечения с осью х
4) Найдем производную функции:
y’=(2x(x-2)-x2)/(x-2)2=(2x2-4x-x2)/(x-2)2=(x(x-4))/(x-2)2=(x2-4x)/(x-2)2
5) Определим критические точки:
x2-4x=0 x(x-4)=0
y’=0, (x2-4x)/(x-2)2=0 <=> <=>
(x-2)2≠ 0 x≠ 2
x2-4x=0, а (x-2)2≠ 0, т.е. х≠ 2
x(x-4)=0
x=0 или x=4
6) Обозначим критические точки на координатной прямой и определим знак функции.
+ — — +
0 2 4
x=-1, y’=(1+4)/9=5/9>0
x=1, y’=(1-4)/1=-3<0
x=3, y’=(9-12)/1=-3<0
x=5, y’=(25-20)/9=5/9>0
7) Найдем точки минимума и максимума функции:
xmin=4
xmax=0
8) Найдем экстремумы функции:
ymin=y(4)=16/2=8
ymax=y(0)=0
9) Построим график функции:
10) Дополнительные точки:
y(-3)=9/-5=-1,8 y(3)=9/1=9
y(1)=1/-1=-1 y(6)=36/4=9
1) Найдем область определения функции:
D(y)=R
2) Определим вид функции:
y(-x)=(6(-x-1))/(x2+3)=-(6(x+1))/(x2-3) – функция общего вида.
3) Найдем точки пересечения с осями:
Oy: x=0, y=(6(0-1))/(0+3)=-2, (0;-2) – точка пересечения с осью y.
(6(x-1))/(x2+3)=0
Ox: y=0, <=>
x2+3≠ 0
6x-6=0
6x=6
x=-1
(1;0) – точка пересечения с осью х
4) Найдем производную функции:
y’=(6(x-1)/(x2+3))’=6(x2+3-2x2+2x)/(x2+2)2=-6(x+1)(x-3)/(x2+3)2
5) Определим критические точки:
y’=0, т.е. -6(x+1)(x-3)/(x2+3)2=0
-6(x+1)(x-3)=0
y’=0, если х1=-1 или х2=3 , значит х=-1 и х=3, критические точки.
6) Обозначим критические точки на координатной прямой и определим знак функции:
— + —
-1 3
x=-2, y’=-6(-2+1)(-2-3)/(4+3)2=-30/49<0
x=0, y’=-6(0+1)(0-3)/(0+3)2=2>0
x=4, y’=-6(4+1)(4-3)/(16+3)2=-30/361<0
7) Найдем точки минимума и максимума:
xmin=-1
xmax=3
8) Найдем экстремумы функции:
ymin=y(-1)=(6(-1-1))/(1+3)=-12/4=-3
ymax=y(3)=(6(3-1))/(9+3)=12/12=1
9) Построим график функции:
10) Дополнительные точки:
y(-3)=(6(-3-1))/(9+3)=-24/12=-2
y(6)=(6(6-1))/(36+3)=30/39=10/13≈ 0,77
5. Постановка задания на дом.
Задания а) – среднего уровня,
б)- уровня выше среднего,
в) – высокого уровня
1 вариант
а) у=(х+1)3 (х-2)
б) у=
в) у=
2 вариант
а) у=(х+2)2 (х-2)
б) у=
в)у=
6. Подведение итогов.
Повторение этапов алгоритма.
Выставление оценок.
www.metod-kopilka.ru
Практическое занятие «Исследование функции с помощью производной» (для студентов СПО)
Практическая работа №16 (естественно-научный профиль)
Тема: «Исследование функций с помощью производной»
Цели: научиться проводить исследование функции с помощью производной и .строить графики функций; закрепить основные признаки возрастания (убывания ) функции, условия существования точек экстремума; проводить исследование функции по графику производной.
Краткая теоретическая справка

1. Находим область определения D(f) функции y = f(x).
2. Проверяем функцию на четность.
Если f(-x) = f(x), то функция четная, график функции симметричен относительно оси OY.
Если f(-x) = — f(x), то функция нечетная, график нечетной функции симметричен относительно начала координат.
В противном случае функция является ни четной, ни нечетной.
3. Если функция периодическая, то находим период функции.
4. Находим точки пересечения графика с осями координат.
Находим нули функции — это точки пересечения графика функции с осью абсцисс (Ox).
Для этого мы решаем уравнение f(x) = 0.
Находим точку пересечения графика функции с осью ординат (Oy). Для этого ищем значение функции при x=0.
5. Находим промежутки знакопостоянства функции, то есть промежутки, на которых функция сохраняет знак. Это нам потребуется для контроля правильности построения графика.
Чтобы найти промежутки знакопостоянства функции, нам нужно решить неравенства f(x) >0 и f(x) <0 .
6. Исследуем функцию с помощью производной: находим промежутки возрастания и убывания функции, а также точки максимума и минимума.
Для этого мы следуем привычному алгоритму.
а) Находим производную
б) Приравниваем производную к нулю и находим корни уравнения
— это стационарные точки.
в) Находим промежутки знакопостоянства производной. Промежутки, на которых производная положительна, являются промежутками возрастания функции.
Промежутки, на которых производная отрицательна, являются промежутками убывания функции.
Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.
Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.
7. Найти значения функции в точках экстремума.
8. По данным исследования построить график функции.
Пример 1. Исследовать функцию и по результатам исследования построить график.
Решение.
1) D(f): R
2) Проверим функцию на чётность/нечётность:
, значит, данная функция не является чётной или нечётной.
3) Функция непериодическая.
4) Нули функции.
С осью Оy:
Чтобы найти точки пересечения с осью Ox (нули функции) требуется решить уравнение f(x) = 0:
5) Таким образом, на интервалах график расположен ниже оси абсцисс f(x)<0, а на интервалах – выше данной оси f(x) >0.
6) Возрастание, убывание.
Найдём критические точки:
Отложим их на числовой прямой и определим знаки производной:
1
Следовательно, функция возрастает на и убывает на .
7). Экстремумы функции
точка максимума, так как при переходе через нее производная меняет знак с «+» на «-»
. точка минимума, так как при переходе через нее производная меняет знак с «-» на «+».
8).
: .
9) Строим график функции.
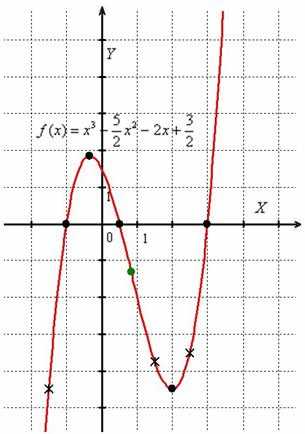
Пример 2. На рисунке изображен график производной функции , определенной на интервале . В какой точке отрезка принимает наибольшее значение.
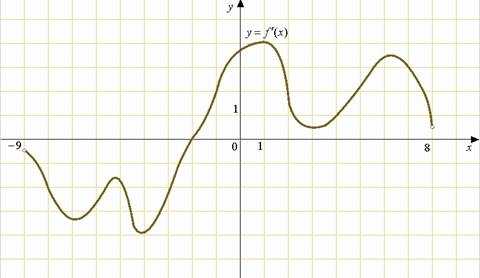
Решение. На отрезке [-7;-3] график производной расположен ниже оси Ох, это означает, что , то есть сама функция на данном отрезке монотонно убывает. Таким образом, убывающая функция принимает наибольшего значения на левом конце промежутка, то есть в точке x=-7.
Ответ. -7.
Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
Найти производную функции.
Определить критические точки (те точки, в которых производная функции обращается в ноль или не существует).
Выбрать из найденных точек те, которые принадлежат данному отрезку.
Вычислить значения функции (не производной!) в этих точках и на концах отрезка.
Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 3. Найдите наименьшее значение функции y = x3 – 18x2 + 81x + 23 на отрезке [8; 13].
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
y’ = 3x2 – 36x + 81.
y’ = 3x2 – 36x + 81 = 0
x2 – 12x + 27 = 0,
x = 3 и x = 9
x = 9 [8; 13].
y = x3 – 18x2 + 81x + 23 = x(x-9)2+23:
y(8) = 8 · (8-9)2+23 = 31;
y(9) = 9 · (9-9)2+23 = 23;
y(13) = 13 · (13-9)2+23 = 231.
Ответ. ;
Порядок выполнения работы.
Внимательно изучите теоретическую справку по теме.
Решите следующие задания по учебнику №9.40А(2в, 2г), №9.41Б(1в) , № 9.44А(2), №9.43А(6)
Выполните разбор примеров 3-7.
Пример 4. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите длину наибольшего из них.
Пример 5. На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек экстремума функции на отрезке .
Пример 6. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.
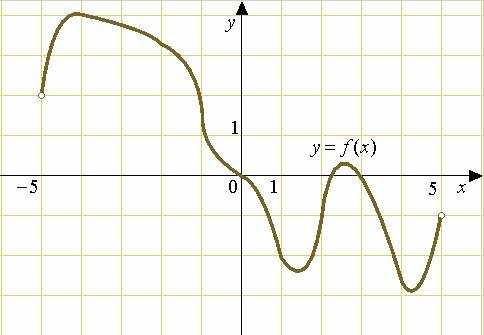
Пример 7. На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна.
Пример 8. На рисунке изображен график производной функции , определенной на интервале . Найдите количество точек максимума функции на отрезке .
Пример 9. На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции положительна.
Задание на дом:
№9.40А(2а,2б), №9.44А(1) №9.41Б(1а,1б) , № 9.44А(2)
№9.43А(1-5), №9.44А(3) №9.45А(1-4) №9.44А(9)
Выполните самостоятельно по вариантам.
Самостоятельная работа.
Задание №1. Исследуйте функцию с помощью производной и постройте ее график1
11
2
12
3
13
4
14
5
15
6
16
7
17
8
18
9
19
10
20
Задание №2. Найдите наибольшее и наименьшее значение функции на отрезке
1
,
11
,
2
,
12
,
3
,
13
,
4
,
14
,
5
,
15
,
6
,
16
,
7
,
17
,
8
,
18
,
9
,
19
,
10
,
20
,
infourok.ru
«Исследование функций с помощью производной»
«Исследование функций и построение графиков с помощью производной»
Тип урока: комбинированный.
Цели урока:
ОЦ: формировать навыки прикладного использования аппарата производной; выявить уровень овладения учащимися комплексом знаний и умений по исследованию функции и ликвидировать пробелы в знаниях в соответствии с требованиями к математической подготовке учащихся.;
ВЦ: воспитывать познавательный интерес к математике, самостоятельность, способность к коллективной работе, внимательности;
РЦ: развивать навыки коррекции собственной деятельности через применение информационных технологий, логическое мышление; самостоятельность.
Методы обучения: ОИ, РМ.
Ход урока.
1.В организационной части урока учитель мобилизирует учебную деятельность учащихся: доброжелательный настрой учащихся, быстрое включение класса в деловой ритм, организация внимания всех учащихся, полная готовность класса и оборудования к работе, повторение правил техники безопасности работы на компьютере.
Ролевая игра: для подготовки компьютерного класса, загрузки учебного ПО, смены дидактических материалов на компьютерах из числа учащихся выбирается подготовленный системный администратор.
I этап.
Актуализация ЗУН учащихся, необходимых для творческого применения знаний:
Проверка домашнего задания: выявление факта выполнения домашнего задания у всех учащихся, обнаружение причин невыполнения домашнего задания отдельными учащимися, устранение типичных ошибок.
Проводится опрос по этапам исследования функции по графику её производной и по схеме исследования функции.
Вопросы показаны на слайде презентации “Исследование функций и построение графиков с помощью производной” и предлагаются учащимся для устных ответов с места. После ответа учащегося иллюстрируется для сравнения ответ на слайде.
2. Вопросы к теоретической части (слайды 5–20, приложение №1).
Необходимое условие возрастания и убывания функции.
Достаточное условие возрастания функции.
Достаточное условие убывания функции.
Необходимое условие экстремума.
Признак максимума функции.
Признак минимума функции.
Достаточные условия выпуклости и вогнутости графика функции.
Учитель анализирует компетентность учащихся в теоретических вопросах темы.
На этом этапе ребята могут совещаться, консультироваться с товарищем, отвечать хором. Такой опрос плавно подведет нас к диагностическому тестированию для выявления у учащихся готовности к усвоению новых знаний.
Инструкция по выполнению теста:
В тестировании дано 1 задание, в котором учащиеся должны установить соответствие, соединив стрелками данную функцию и ее поведение на заданном отрезке. На выполнение теста дано 8 минут.
Критерии оценивания теста:
За каждый правильный ответ ставится 1 балл, за неправильный — 0 баллов. Таким образом, если 5 баллов — отметка «5»; 4 балла — отметка «4»; 3 балла — отметка «3».
Перед началом использования теста учитель просит учащихся внимательно ознакомиться с инструкцией по выполнению теста, с критериями оценивания теста. Затем предлагает ребятам составить план действий по прохождению данного теста, т. е. первыми выполнить те соответствия, которые для учащего кажутся самыми легкими, выполнять по мере возрастания трудности. В результате такой работы у учащихся развивается умение анализировать, составлять план действий.
Диагностическое тестирование:
то y
Если
Монотонно убывает
Монотонно возрастает
Имеет максимум во внутренней точке
Имеет минимум во внутренней точке
Постоянна
Ключ диагностического тестирования:
то y
Если
Монотонно убывает
Монотонно возрастает
Имеет максимум во внутренней точке
Имеет минимум во внутренней точке
Постоянна
+
+
+
+
+
II этап.
Усвоение образца комплексного применения ЗУН (Слайды 23-29)
Практическая работа с применением электронного учебного пособия “Математика – практикум 5–11” и по индивидуальным заданиям на местах. За компьютер сначала рассаживаются 7 учащихся, остальные за парты. По мере выполнения заданий ребята меняются местами.
Задания учащимся отличаются по объёму, по их сложности, по их содержанию. Имеют 4 уровня сложности: средний, выше среднего, высокий, творческий. Учащиеся, слабо владеющие алгоритмом исследования функции, приглашаются за компьютер и начинают работать с программой “Исследование функций с помощью производной”, где они выполняют задание по образцу — алгоритму, предлагаемому компьютером, аналогичное тому с которым не справились при выполнении самостоятельной работы, проводимой на прошлом уроке, или допустили ошибки. Выполнив работу над ошибками, тем самым, повторив алгоритм исследования функции, получают карточку с новым заданием, которое уже выполняется самостоятельно и проверяется с помощью программы на компьютере. Цель этих заданий отработка практических навыков в построении графиков.
Часть учащихся, хорошо усвоивших данный материал, получив карточки с индивидуальным заданием, отрабатывают практический навык, используя самоконтроль, с применением программы, где проверяется только конечный результат — построение графика, выполняя задания 1–3 уровня сложности. В случае затруднения при исследовании функции ученик может сесть за компьютер, где в режиме “Самостоятельная” программы “Исследование функций с помощью производной” выполнит своё задание.
Учащиеся, выполнившие задания 1–3-го уровня продолжают работу, получив задание более сложного уровня, творческого характера, где необходимо применить самостоятельность, логическое и образное мышление в новых условиях.
Все работы оцениваются. Работы, выполненные только с применением программы “Исследование функций с помощью производной”, оцениваются отметкой “3”, задания сложности 1-го уровня отметкой “4”, творческие задания и задания 2–3-го уровней отметкой “5”.
Таблица
Работа на компьютерах в группах (3 учащихся) по ролям: оператор, аналитик, конструктор.
Задание. Исследовать функцию на выпуклость, вогнутость.
3. Мини-исследовательская работа (слайд 30).
На данном этапе урока при проведении мини-исследовательской работы применяются методы контроля и самоконтроля, а также самоуправления учебными действиями. Обучение на немногочисленных, но хорошо подобранных задачах решаемых школьниками в основном самостоятельно, способствует вовлечению их в творческую исследовательскую работу, последовательно проводя через этапы научного поиска.
4. Индивидуальные задания для мини-исследовательской работы.
По 6 карточек к каждому из вариантов:
1, 2 вариант – задания среднего уровня.
3, 4 вариант – задания уровня выше среднего.
5, 6 вариант — задания высокого уровня.
Задание: исследовать и построить график функции.
1.
3.
5.
2.
4.
6.
5. Творческое задание (слайд 32).
Интерактивные кроссворд и тесты по теме “Производная функции” выполняются учащимися на интерактивной доске.
6. Подведение итогов урока.
Подвести итоги усвоения материала по уровням понимания учащимися, выделив учащихся со структурным пониманием, т.е. тех, кто работал по алгоритму; тех, кто решал по образцу; и тех, кто может применить свои знания в новых условиях. Выставляется отметка каждому ученику за блиц — опрос, и за практическую работу. Сообщается учащимся, кому и на какие вопросы необходимо обратить внимание, при подготовке к контрольной работе.
Задание на дом: № 45, 41 (устно), 39 (31) (слайд 33).
Презентация к занятию 1
Слайд 1: Урок на тему : «Исследование функции с помощью производной» с использованием компьютерных технологий.
Слайд 2: 
Слайд 3: 
Слайд 4: 
Слайд 5: 
Слайд 6: 
Слайд 7: 
Слайд 8: 
Слайд 9: 
Слайд 10: 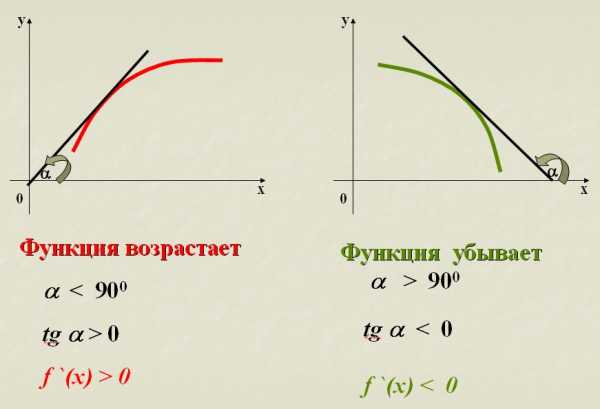
Слайд 11: 
Слайд 12: 
Слайд 13: 
Слайд 14: 
Слайд 15: 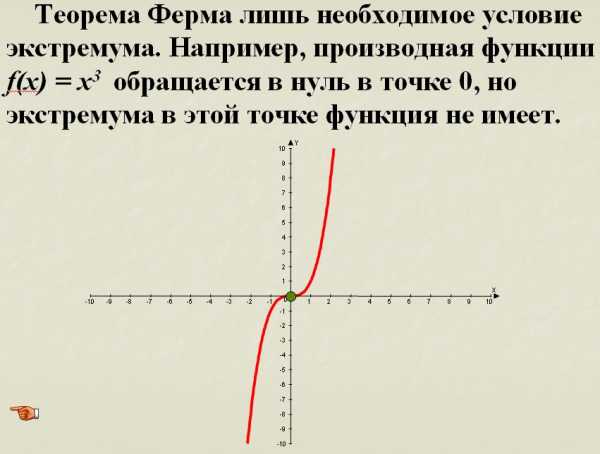
Слайд 16: 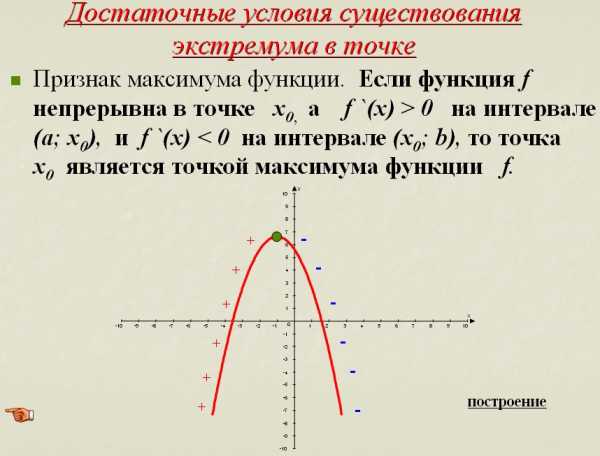
Слайд 17: 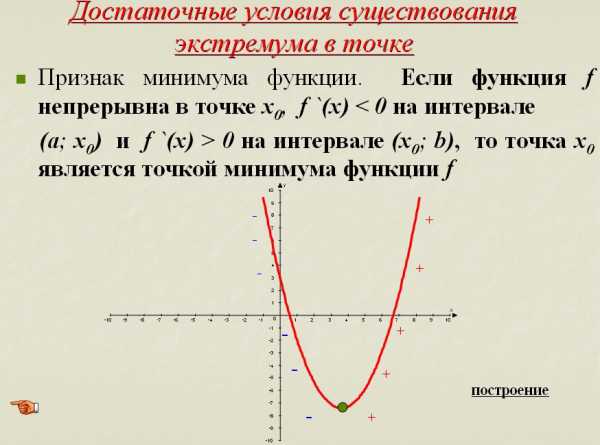
Слайд 18: 
Слайд 19: 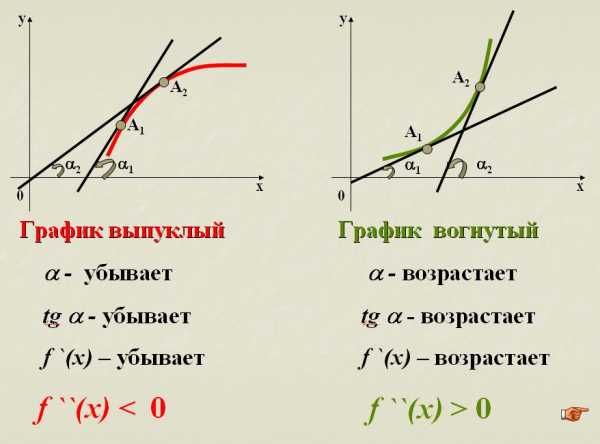
Слайд 20: 
Слайд 21: 
Слайд 22: 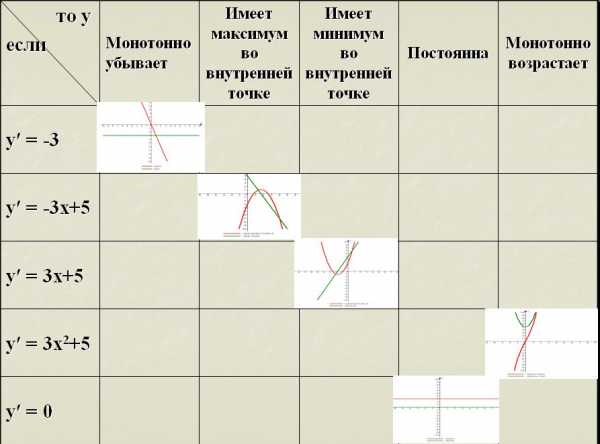
Слайд 23: 
Слайд 24: 
Слайд 25: 
Слайд 26: 
Слайд 30: 
Слайд 31: 
Слайд 32: 
Слайд 33:
Тесты к слайду 32:


Кроссворд к слайду 32:
infourok.ru
11.6. Общая схема исследования функций
Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и характере ее графика необходимо отыскать:
Область существования функции.
Это понятие включает в себя и область значений и область определения функции.
Точки разрыва. (Если они имеются).
Интервалы возрастания и убывания.
Точки максимума и минимума.
Максимальное и минимальное значение функции на ее области определения.
Области выпуклости и вогнутости.
Точки перегиба.(Если они имеются).
Асимптоты.(Если они имеются).
Построение графика.
Применение этой схемы рассмотрим на примере.
Пример. Исследовать функцию и построить ее график.
Находим область существования функции. Очевидно, что областью определения функции является область (-; -1) (-1; 1) (1; ).
В свою очередь, видно, что прямые х = 1, х = -1 являются вертикальными асимптотами кривой.
Областью значений данной функции является интервал (-; ).
Точками разрыва функции являются точки х = 1, х = -1.
Находим критические точки.
Найдем производную функции
Критические точки: x = 0; x = -;x = ;x = -1; x = 1.
Найдем вторую производную функции
.
Определим выпуклость и вогнутость кривой на промежутках.
- < x < -,y < 0, кривая выпуклая
-<x < -1, y < 0, кривая выпуклая
-1 < x < 0, y > 0, кривая вогнутая
0 < x < 1, y < 0, кривая выпуклая
1 < x < ,y > 0, кривая вогнутая
< x < , y > 0, кривая вогнутая
Находим промежутки возрастания и убывания функции. Для этого определяем знаки производной функции на промежутках.
- < x < -,y > 0, функция возрастает
-<x < -1, y < 0, функция убывает
-1 < x < 0, y < 0, функция убывает
0 < x < 1, y < 0, функция убывает
1 < x < ,y < 0, функция убывает
< x < , y > 0, функция возрастает
Видно, что точка х = -является точкоймаксимума, а точка х = является точкойминимума. Значения функции в этих точках равны соответственно 3/2 и -3/2.
Про вертикальные асимптоты было уже сказано выше. Теперь найдем наклонные асимптоты.
Итого, уравнение наклонной асимптоты – y = x.
Построим график функции:
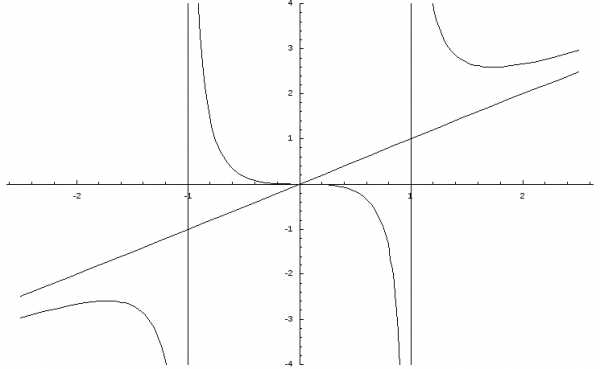
Ниже рассмотрим несколько примеров исследования методами дифференциального исчисления различных типов функций.
Пример: Методами дифференциального исчисления исследовать функцию и построить ее график.
1. Областью определения данной функции являются все действительные числа (-; ).
2. Функция является функцией общего вида в смысле четности и нечетности.
3. Точки пересечения с координатными осями: c осью Оу: x = 0; y = 1;
с осью Ох: y = 0; x = 1;
4. Точки разрыва и асимптоты: Вертикальных асимптот нет.
Наклонные асимптоты: общее уравнение y = kx + b;
Итого: у = -х – наклонная асимптота.
5. Возрастание и убывание функции, точки экстремума.
. Видно, что у 0 при любом х 0, следовательно, функция убывает на всей области определения и не имеет экстремумов. В точке х = 0 первая производная функции равна нулю, однако в этой точке убывание не сменяется на возрастание, следовательно, в точке х = 0 функция скорее всего имеет перегиб. Для нахождения точек перегиба, находим вторую производную функции.
y = 0 при х =0 и y = при х = 1.
Точки (0,1) и (1,0) являются точками перегиба, т.к. y(1-h) < 0; y(1+h) >0; y(-h) > 0; y(h) < 0 для любого h > 0.
6. Построим график функции.
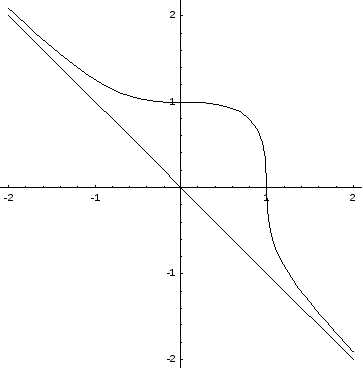
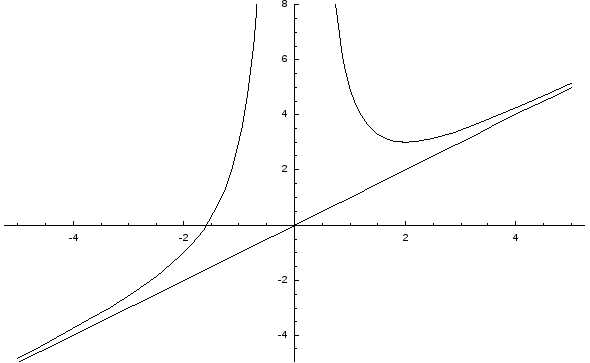
Пример: Исследовать функцию и построить ее график.
1. Областью определения функции являются все значения х, кроме х = 0.
2. Функция является функцией общего вида в смысле четности и нечетности.
3. Точки пересечения с координатными осями: c осью Ох: y = 0; x =
с осью Оу: x = 0; y – не существует.
4. Точка х = 0 является точкой разрыва , следовательно, прямая х = 0 является вертикальной асимптотой.
Наклонные асимптоты ищем в виде: y = kx + b.
Наклонная асимптота у = х.
5. Находим точки экстремума функции.
; y = 0 при х = 2, у = при х = 0.
y > 0 при х (-, 0) – функция возрастает,
y < 0 при х (0, 2) – функция убывает,
у > 0 при х (2, ) – функция возрастает.
Таким образом, точка (2, 3) является точкой минимума.
Для определения характера выпуклости/вогнутости функции находим вторую производную.
> 0 при любом х 0, следовательно, функция вогнутая на всей области определения.
6. Построим график функции.
Пример: Исследовать функцию и построить ее график.
Областью определения данной функции является промежуток х (-, ).
В смысле четности и нечетности функция является функцией общего вида.
Точки пересечения с осями координат: с осью Оу: x = 0, y = 0;
с осью Ох: y = 0, x = 0, x = 1.
Асимптоты кривой.
Вертикальных асимптот нет.
Попробуем найти наклонные асимптоты в виде y = kx + b.
— наклонных асимптот не существует.
Находим точки экстремума.
Для нахождения критических точек следует решить уравнение 4х3 – 9х2 +6х –1 = 0.
Для этого разложим данный многочлен третьей степени на множители.
Подбором можно определить, что одним из корней этого уравнения является число
х = 1. Тогда:
4x3 – 9x2 + 6x – 1 x — 1
4x3 – 4x2 4x2 – 5x + 1
— 5x2 + 6x
— 5x2 + 5x
x — 1
x — 1
0
Тогда можно записать (х – 1)(4х2 – 5х + 1) = 0. Окончательно получаем две критические точки: x = 1 и x = ¼.
Примечание. Операции деления многочленов можно было избежать, если при нахождении производной воспользоваться формулой производной произведения:
Найдем вторую производную функции: 12x2 – 18x + 6. Приравнивая к нулю, находим:
x = 1, x = ½.
Систематизируем полученную информацию в таблице:
(- ; ¼) | 1/4 | (¼; ½) | 1/2 | ( ½ ; 1 ) | 1 | (1 ; ) | |
f(x) | + | + | + | 0 | — | 0 | + |
f(x) | — | 0 | + | + | + | 0 | + |
f(x) | убывает вып. вниз | min | возрастает вып. вниз | перегиб | возрастает вып.вверх | перегиб | возрастает вып. вниз |
Построим график функции.
studfiles.net
План урока по теме «Исследование функции с помощью производной»
Тема: Исследование функции с помощью производной
УРОК: 1Школа: Набережная средняя
Дата:
имя учителя: Кузьмич Марина Ивановна
Класс: 10
количество отсутствующих:
присутствующих: 2
Цели обучения, которые необходимо достичь на данном уроке
Ознакомить с алгоритмом исследования функции с помощью производной
Цели урока
Все учащиеся смогут:
— владеть навыками нахождения области определения функции, промежутков возрастания, убывания, знакопостоянства функции, экстремумов функции.
Большинство учащихся сможет:
— исследовать функцию с помощью производной и строить ее график.
Некоторые учащиеся смогут:
— анализировать функцию на основе ее свойств и графика.
Языковая цель
Учащиеся могут: использовать и понимать терминологию
Применять алгоритм исследования функции, на основе этого строить график
Словарный запас и терминология на конкретную тему:
— исследование;
— производная;
— промежутки возрастания, убывания функции; знакопостоянства;
— производная;
— функция;
— область определения функции.
Словарная работа: производная, функция, ОДЗ, график, промежутки.
Полезные фразы для построения высказывания:
— я исследовал функцию по алгоритму;
— я знаю свойства данной функции;
— я умею строить график функции, учитывая ее свойства.
Предыдущее обучение
Производная, таблица производных
Промежутки возрастания, убывания функции;
Критические точки.
План
Запланированные сроки
Запланированные мероприятия
ресурсы
Начало урока
1 минута
3 минута
2 минуты
2 минуты
Оргмомент
Краткое повторение теории:
— определение производной;
— таблица производных;
— понятие промежутков возрастания, убывания функции;
— критические точки.
Стратегия «Только минута». В парах учащиеся в течение минуты рассказывают друг другу определение производной, правила дифференцирования
Обратная связь
-Что же такое критические точки?
— Как найти критические точки?
Сообщение целей урока.
Презентация
Графики функции
Середина урока
10 минут
7 минут
2 минуты
4 минуты
10 минут
Задание 1
Прочитать, обратить внимание на алгоритм исследования функции;
Рассмотреть пример 1, записать в тетрадь
Критерии оценивания:
КритерийДескрипотор
Баллы
Понимать смысл исследования функции
Формулируют алгоритм, называют свойства функции
3
Исследовать функцию
Последовательно записывают в тетради свойства функции
3
На основе исследований строить график функции
Построение графика
3
Обсуждение:
— алгоритм нахождения промежутков возрастания, убывания функции;
— алгоритм нахождения критических функций.
Задание 2
Рассмотреть по учебнику пример. Записать исследования в тетрадь.
Критерии оценивания:
КритерийДескрипотор
Баллы
Формулируют алгоритм исследования функции
Используют в речи новую терминологию
2
Обратная связь
Какие качеств человека проявляются при исследовании функции.
Закрепление знаний
Решение упражнений: № 241
Учебник, стр 116
Учебник
Учебник
Конец урока
3 минуты
1 минута
Рефлексия
1.Сегодня я узнал -______________________ ________________________________________
2.Было интересно__________________________________________
3.Было трудно_____________________________________________
4. У меня получилось_______________________________________
Домашнее задание № 243, выучить алгоритм исследования функции
Учебник
Дифференциация – как вы будете предоставлять больше поддержки? Какие задания вы будете давать
Оценивание – как вы планируете отслеживать прогресс/знания учащихся?
Междисциплинарные связи здоровье и безопасность поддержка ИКТ
Используйте это место для записи ваших наблюдений по уроку.
Ответьте на вопросы о вашем уроке, написанные в левом столбике.
Назовите два наиболее успешных момента (как преподавания, так и обучения)? 1:
Назовите два момента, которые бы способствовали улучшению урока (как преподавания, так и обучения)?
Что нового я узнал о классе и его отдельных учащихся и как это отразится на проведении моего следующего урока?
infourok.ru
