Центральный момент – 5.3. Начальные и центральные моменты

5.3. Начальные и центральные моменты

Начальным моментом k-го порядка случайной величины X называется математическое ожидание величины X^k:

. (5.10)

В частности,

Центральным моментом k-го порядка случайной величины X называется математическое ожидание величины [X–M(X)]^k:

. (5.11)

В частности,

Воспользовавшись определениями и свойствами математического ожидания и дисперсии, можно получить, что

,

,

.

Моменты более высоких порядков применяются редко.

Предположим, что распределение случайной величины симметрично относительно математического ожидания. Тогда все центральные нечетного порядка равны нулю. Это можно объяснить тем, что для каждого положительного значения отклонения X–M[X] найдется (в силу симметричности распределения) равное ему по абсолютной величине отрицательное значение, причем их вероятности будут одинаковыми. Если центральный момент равен нечетного порядка не равен нулю, то это говорит об асимметричности распределения и чем больше момент, тем больше асимметрия. Поэтому в качестве характеристики асимметрии распределения разумнее всего взять какой-нибудь нечетный центральный момент. Так как центральный момент 1-го порядка всегда равен нулю, то целесообразно для этой цели использовать центральный момент 3-го порядка. Однако принять этот момент для оценки асимметричности неудобно потому, что его величина зависит от единиц, в которых измеряется случайная величина. Чтобы устранить этот недостаток, 

3 делят на ³ и таким образом получают характеристику.

Коэффициентом асимметрии A называется величина

. (5.12)

Рис. 5.1

Если коэффициент асимметрии отрицателен, то это говорит о большом влиянии на величину₃ отрицательных отклонений. В этом случае кривые распределения более пологи слева от M[X]. Если коэффициент A положителен, то кривая более пологи справа.

Как известно, дисперсия (2-й центральный момент) служит для характеристики рассеивания значений случайной величины вокруг математического ожидания. Чем больше дисперсия, тем более полога соответствующая кривая распределения. Однако нормированный момент 2-го порядка 

2/₂ не может служить характеристикой «плосковершинности» или «островершинности» распределения потому, что для любого распределения D[x]/₂=1. В этом случае используют центральный момент 4-го порядка.

Эксцессом E называется величина

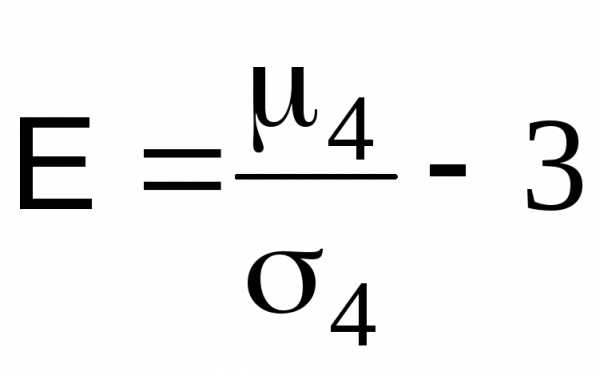. (5.13)

Ч

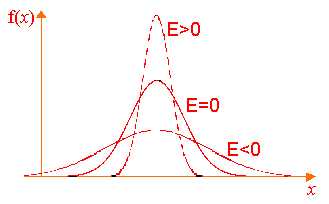
Рис. 5.2

исло 3 здесь выбрано потому, что для наиболее распространенного нормального закона распределения₄/₄=3. Поэтому эксцесс служит для сравнения имеющихся распределе­ний с нормальным, у которого экс­цесс равен нулю. Это означает, что если у распределения эксцесс положителен, то соответствующая кривая распределения более «островершина» по сравнению с кривой нормального распределения; если у распределения эксцесс отрица­телен, то соответствующая кривая более «плосковершина».

Пример 5.6. ДСВ X задана следующим законом распределения:

X	1	3	5	7	9
P	0,1	0,4	0,2	0,2	0,1

Найти коэффициент асимметрии и эксцесс.

Рис. 5.4

Решение. Предварительно найдем начальные моменты до 4-го порядка

Теперь вычислим центральные моменты:

Таким образом,

Пример 5.7. НСВ X задана следующей плотностью распределения:

Найти коэффициент асимметрии и эксцесс.

Рис. 5.5

Решение. Предварительно найдем начальные моменты до 4-го порядка

Теперь вычислим центральные моменты:

.

Таким образом,

studfiles.net

Моменты случайных величин.

Для характеристики различных свойств случайных величин используются начальные и центральные моменты.

Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k-й степени этой величины:

α_К = М [X^К].

Для дискретной случайной величины

α_К =

Для непрерывной случайной величины

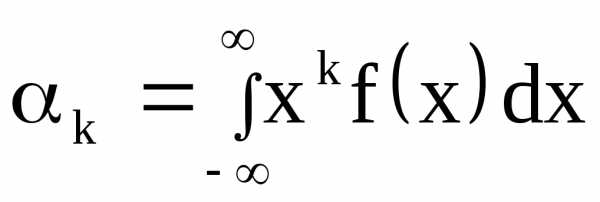
Ц

₀

Х = Х – М[Х]

ентрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:

Условимся отличать центрированную с.в. значком ⁰ наверху.

Центральным моментом

S-го порядка называется математическое ожидание S-й степени центрированной случайной величины

_S = M [(X – m_x)^S].

Для дискретной случайной величины

_S = 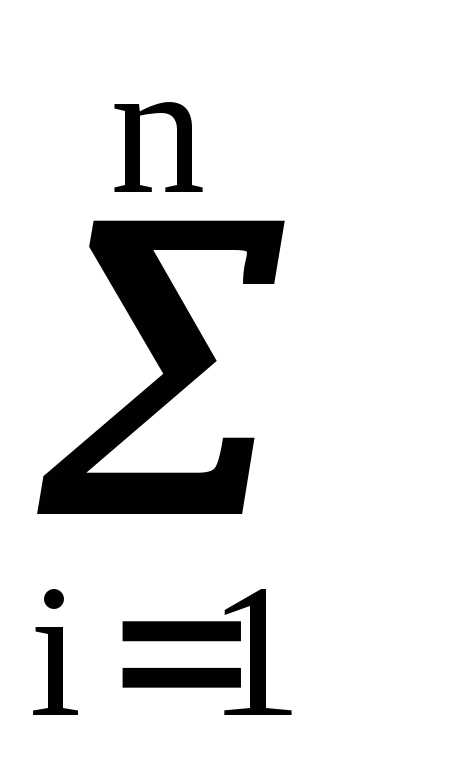(x_i – m_x)^S p_i.

Для непрерывной случайной величины

.

Свойства моментов случайных величин

1. начальный момент первого порядка равен математическому ожиданию (по определению):

α₁ = М [X¹] = m_x.

2. центральный момент первого порядка всегда равен нулю (докажем на примере дискретной с. в.):

₁ = M [(X – m_x)¹] =

(x_i – m_x)p_i =x_i p_i –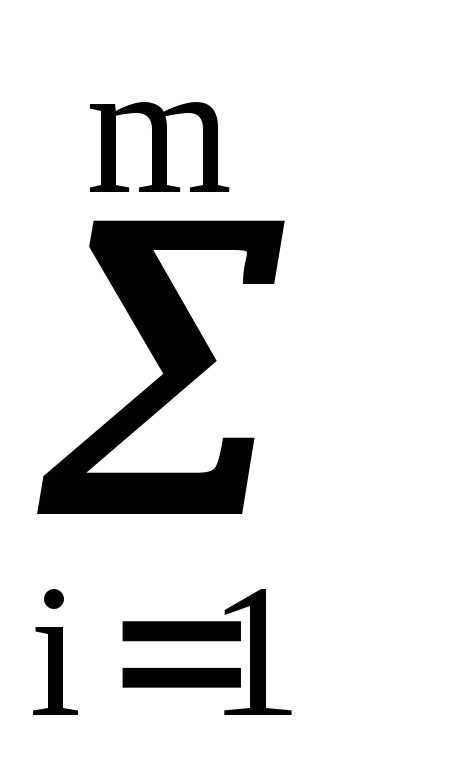m_x p_i = m_x–m_x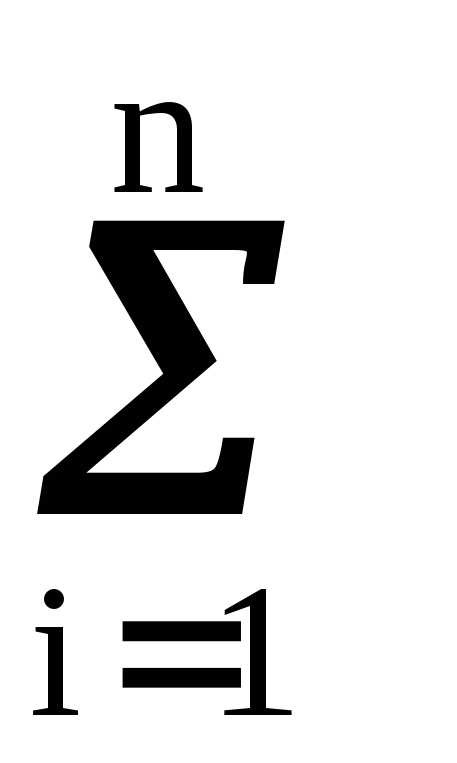p_i =m_x–m_x= 0.

3. центральный момент второго порядка характеризует разброс случайной величины вокруг ее математического ожидания.

Центральный момент второго порядка называется дисперсией с. в. и обозначается D[X] или D_x

Дисперсия имеет размерность квадрата случайной величины.

4. Среднее квадратическое отклонение σ_х = √D_x.

σ_х – также как и D_x

характеризует разброс случайной величины вокруг ее математического ожидания но имеет размерность случайной величины.

5. второй начальный момент α₂ характеризует степень разброса случайной величины вокруг ее математического ожидания, а также смещение случайной величины на числовой оси

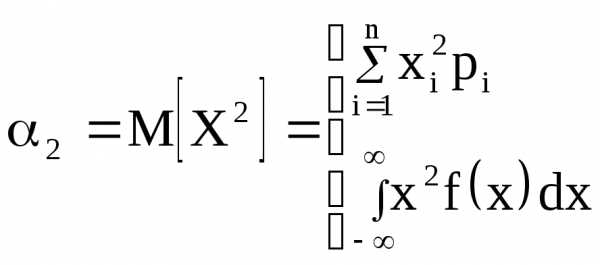
Связь первого и второго начальных моментов с дисперсией (на примере непрерывной с. в.):

6. третий центральный момент характеризует степень разброса случайной величины вокруг математического ожидания, а также степень асимметрии распределения случайной величины.

f(x_ср) > f(-x_ср)

Для симметричных законов распределения m

3 = 0.

Для характеристики только степени асимметрии используется так называемый коэффициент асимметрии

Sk = m₃ /σ³

Для симметричного закона распределения Sk = 0

7. четвертый центральный момент характеризует степень разброса случайной величины вокруг математического ожидания, а также степень островершинности закона распределения.

Для характеристики только степени островершинности распределения используется эксцесс (обозначается ε_х):

ε_х = m₄ /σ⁴ – 3

ε_х2 = 0;(нормальный закон распределения) ε_х1  0; ε_х3  0.

Задача. Случайна величина Х задана плотностью распределения вероятности

f(x) =

Найти: F(x), m_x, α₂, D_x, σ_x и построить графики функций f(x) и F(x).

Математическое ожидание:

Второй начальный момент:

Дисперсия: D_x = α₂ – m_x² = 1/2 – 4/9 = 1/18

Средне квадратичное отклонение: σ_х = √D_x = √(1/18) = √2/6.

studfiles.net

Центральный момент — 17 Мая 2013 — Примеры решений задач

Теоретические моменты Начальным моментом порядка k случайной величины X называют математическое ожидание величины Хk: В частности, начальный момент первого порядка равен матема­тическому ожиданию:   ν1 = M(X). Центральным моментом порядка k случайной величины X на­зывают математическое ожидание величины [X—М{Х)]k: μk=M[X-M(X)]k В частности, центральный момент первого порядка равен нулю: μ1=M[X-M(X)]=0 Центральный момент второго порядка равен дисперсии: μ2=M[X-M(X)]2=D(X) Центральные моменты целесообразно вычислять, используя формулы, выражающие центральные моменты через начальные: μ2=ν2-ν12 μ3=ν3-3ν1ν2+2ν13 μ4=ν4-4ν1ν3+6ν1ν2-3ν14 Пример решения задачи. Дискретная случайная величина X задана зако­ном распределения: X     1      3 р  0,4   0,6 Найти начальные моменты первого, второго и третьего порядков. Пример решения задачи. Дискретная случайная величина X задана зако­ном распределения: X   1     2    4 р 0,1 0,3 0,6 Найти центральные моменты первого, второго, третьего и четвертого порядков. Задачи: 1. Дискретная случайная величина X задана зако­ ном распределения X 3 5 р 0,2 0,8 80 Найти центральные моменты первого, второго, третьего и четвертого порядков. Указание . Найти предварительно начальные моменты и выра­ зить через них центральные моменты. 2. Доказать, что центральный момент второго по­ рядка (дисперсия) μ2=M[X-M(X)]2=D(X) меньше обычного момента второго порядка  μ‘2=M[X-M(X)]2 при любом С не равном m. 3. Доказать, что центральный момент третьего по­ рядка связан с начальными моментами равенством μ3=ν3-3ν1ν2+2ν13 4. Доказать, что центральный момент четвертого порядка связан с начальными моментами равенством μ4=ν4-4ν1ν3+6ν1ν2-3ν14

www.reshim.su

Начальные и центральные моменты. Задачи, формулы

Обобщенными числовыми характеристиками для случайных величин в теории вероятностей а также математической статистике являются начальные и центральные моменты. Задачи на отыскание моментов являются неотъемлемой частью теории вероятностей и математической статистики. Начальным моментом k-го порядка случайной величины Х называют математическое ожидание от величины в k-ой степени

Когда
Когда и т. д.

Для дискретной случайной величины начальные моменты определяют зависимостью

для непрерывной интегрированием

Если непрерывная величина задана интервалом , то моменты вычисляют по формуле

Центральным моментом k-го порядка называют математическое ожидание от величины

Когда

для имеем

при

при

и так далее.

Для дискретной случайной величины центральные моменты вычисляют по формуле

для непрерывной по следующей

Если случайная величина определена интервалом , то центральные моменты определяют интегрированием

Рассмотрим пример отыскания приведенных величин.

————————————

Пример 1. Задана функция плотности вероятностей

Вычислить начальные и центральные моменты второго и третьего порядка .
Решение. Для вычисления начальных моментов выполним интегрирование по вышеприведенным формулам

Промежуточные операции при интегрировании пропущены, они занимают много места, а Вам главное иметь инструкцию для вычислений, так как примеры у Вас будут другие.
Для вычисления центральных моментов инерции необходимо знать математическое ожидание случайной величины, поэтому определяем его первее

Найдено математическое ожидание подставляем в формулу центральных моментов. В случае получим

и при будем иметь

На этом решения примера завершено, функция плотности вероятностей приведена на графике

————————————

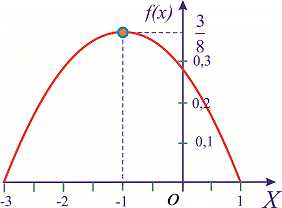
Примеры нахождения начальных и центральных моментов будут рассмотрены в следующей статье. Задачи совсем не сложные, а вычисления величин сводится к возведения в степень, интегрирование, умножение и суммирование.

yukhym.com

Вопрос 13.Характеристики случайной величины: центральный момент и дисперсия

следует, что центральный момент первого порядка всегда равен нулю:

• Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С, а отклонение от центра не меняется: Х – m = (Х – С) – (m – С).

Теперь очевидно, что дисперсия – это центральный момент второго порядка:

Здесь m = М ( Х ).

Свойства дисперсии:

Вопрос14.

1)Биноминальное распределение:

2)Геометрическое распределение.

3)Распределение Пуасона.

15. Законы распределения – равномерный, показательный.

Равномерный закон распределения. Непрерывная случайная величину Х имеет равномерный закон распределения (закон постоянной плотности) на отрезке [a; b], если на этом отрезке функция плотности вероятности случайной величины постоянна, т.е. f(x) имеет вид:

Функция плотности Функция распределения F(x)

вероятности f(x)

Вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал ), принадлежащий,( целиком отрезку [a, b]:

 Пример. Время ожидания ответа на телефонный звонок – случайная величина, подчиняющаяся равномерному закону распределения в интервале от 0 до 2 минут. Найти интегральную и дифференциальную функции распределения этой случайной величины.

Непрерывная случайная величина Х имеет Показательный (экспоненциальный) закон распределения с параметром λ, если ее плотность вероятности имеет вид

Функция распределения случайной величины, распределенной по показательному закону, равна

Кривая распределения Р(Х) и график функции распределения приведены на рис. 8.13.

Рис. 8.13

Для случайной величины, распределенной по показательному закону

; .

Вероятность попадания в интервал непрерывной случайной величины Х, распределенной по показательному закону

. Пример. Непрерывная величина Х распределена по показательному закону

Найти вероятность попадания значений величины Х в интервал .

Решение. Поскольку , то

16. Нормальный закон распределения. Параметры нормального закона. Свойства. Нормальный закон распределения. Нормальный закон распределения (закон Гаусса). Непрерывная случайная величина Х имеет нормальный закон распределения с параметрами и(обозначают), если ее плотность вероятности имеет вид:где,.

Нормальный закон распределения случайной величины Х с параметрами и(обозначается N(0;1)) называется стандартным или нормированным, а соответствующая нормальная кривая – стандартной или нормированной.

Для практических целей очень важны свойства случайной величины, имеющей нормальный закон распределения.

1.     Если , то для нахождения вероятности попадания этой величины в заданный интервал (х1;х2) используется формула:

.

2.     Вероятность того, что отклонение случайной величины от ее математического ожиданияне превысит величину(по абсолютной величине), равна:

.

3.     «Правило трех сигм». Если случайная величина , то практически достоверно, что ее значения заключены в интервале (). (Вероятность выхода за эти границы составляет 0,0027.) Правило позволяет, зная параметры (и), ориентировочно определить интервал практических значений случайной величины. Пример 5. Случайная величина распределена нормально с параметрами,. Найти вероятность того, что случайная величина в результате опыта примет значение, заключенное в интервале (12,5; 14).

.

studfiles.net

Центральные моменты случайной величины — это… Что такое Центральные моменты случайной величины?



Центральные моменты случайной величины

Моме́нт случа́йной величины́ — числовая характеристика распределения данной случайной величины.

Определения

Если дана случайная величина определённая на некотором вероятностном пространстве, то:

• -м нача́льным моментом случайной величины где называется величина

если математическое ожидание в правой части этого равенства определено;

• -м центра́льным моментом случайной величины называется величина

• -м факториальным моментом случайной величины называется величина

если математическое ожидание в правой части этого равенства определено.

Замечания

• Если определены моменты -го порядка, то определены и все моменты низших порядков
• В силу линейности математического ожидания центральные моменты могут быть выражены через начальные, и наоборот. Например:

и т. д.

Геометрический смысл некоторых моментов

• равняется математическому ожиданию случайной величины и показывает относительное расположение распределения на числовой прямой.
• равняется дисперсии распределения и показывает разброс распределения вокруг среднего значения.
• , будучи соответствующим образом нормализован, является числовой характеристикой симметрии распределения. Более точно, выражение

называется коэффициентом асимметрии.

• контролирует, насколько ярко выражена вершина распределения в окрестности среднего. Величина

называется коэффициентом эксцесса распределения

Вычисление моментов

если

а для дискретного распределения с функцией вероятности

если

• Если распределение таково, что для него в некоторой окрестности нуля определена производящая функция моментов то моменты могут быть вычислены по следующей формуле:

Обобщения

Можно также рассматривать нецелые значения k. Момент, рассматриваемый как функция от аргумента k, называется преобразованием Меллина.

Можно рассматривать моменты многомерной случайной величины. Тогда первый момент будет вектором той же размерности, второй — тензором второго ранга (см. матрица ковариации) над пространством той же размерности (хотя можно рассматривать и след этой матрицы, дающий скалярное обобщение дисперсии). Итд.

Wikimedia Foundation. 2010.

• Центральные Полинезийские Спорады
• Центральный (cтадион, Актобе)

Смотреть что такое «Центральные моменты случайной величины» в других словарях:

• Моменты случайной величины — Момент случайной величины  числовая характеристика распределения данной случайной величины. Содержание 1 Определения 2 Замечания …   Википедия

• Центральная — Центральный  прилагательное к существительному «центр». Входит в состав многих сложных терминов. Не следеут путать его с термином «централ». Содержание 1 Географические названия 1.1 Регионы мира 1.2 Государства …   Википедия

• Центрально — Центральный  прилагательное к существительному «центр». Входит в состав многих сложных терминов. Не следеут путать его с термином «централ». Содержание 1 Географические названия 1.1 Регионы мира 1.2 Государства …   Википедия

• Центральный (Нижегородская область) — Центральный  прилагательное к существительному «центр». Входит в состав многих сложных терминов. Не следеут путать его с термином «централ». Содержание 1 Географические названия 1.1 Регионы мира 1.2 Государства …   Википедия

• Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… …   Энциклопедия инвестора

• Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… …   Энциклопедия инвестора

• МНОГОМЕРНОЕ РАСПРЕДЕЛЕНИЕ — распределение вероятностей на алгебре борелевских множеств s мерного евклидова пространства . О М. р. обычно говорят как о распределении многомерной случайной величины или случайного вектора , понимая под этим совместное распределение… …   Математическая энциклопедия

• ЭКСЦЕССА КОЭФФИЦИЕНТ — эксцесс, скалярная характеристика островершинности графика плотности вероятности унимодального распределения, к рую используют в качестве нек рой меры отклонения рассматриваемого распределения от нормального. Э. к. определяется по формуле где… …   Математическая энциклопедия

• ЭДЖВОРТА РЯД — ряд, определяемый выражением Здесь f(x) плотность распределения случайной величины независимы и одинаково распределены), плотность стандартного нормального распределения, Коэффициенты bk,k+2l не зависят от пи представляют собой многочлены… …   Математическая энциклопедия

• ГРАМА — ШАРЛЬЕ РЯД — ряд, определяемый выражением или где х нормированное значение случайной величины. Ряд (1) наз. Г. Ш. р. типа А;здесь есть k я производная от , к рую можно представить в виде где многочлены Чеб …   Математическая энциклопедия

dic.academic.ru

8. Эмпирические центральные и начальные моменты

Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда.

Эмпирическим начальным моментом (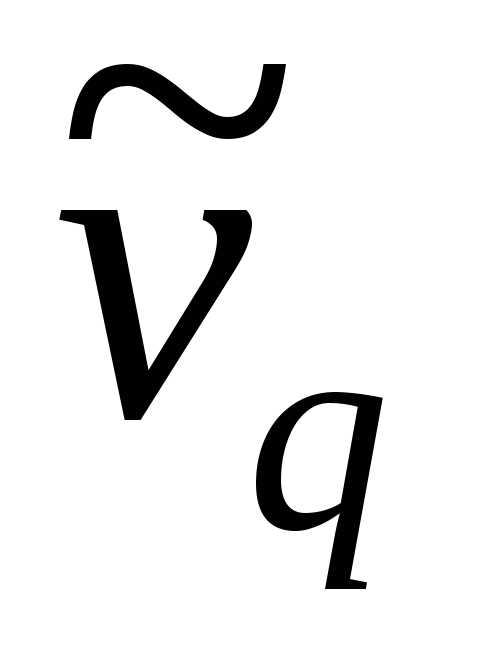) порядка q называют взвешенную среднюю арифметическую q—x степеней вариантов, т.е.

(20)

Эмпирический начальный момент нулевого порядка

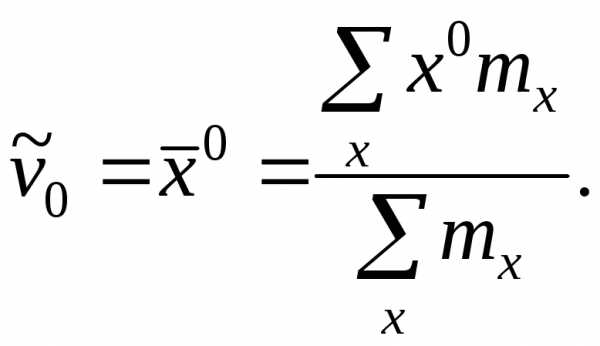
Эмпирический начальный момент первого порядка

Эмпирический начальный момент второго порядка 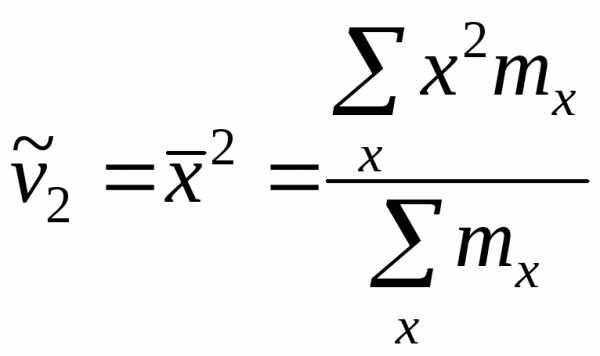и т.д.

Эмпирическим центральным моментом () порядкаq называют взвешенную среднюю арифметическую q—x степеней отклонений вариантов от их средней арифметической, т.е.

(21)

Эмпирический центральный момент нулевого порядка

Эмпирический центральный момент первого порядка

(в силу свойства 1° средней арифметической).

Эмпирический центральный момент второго порядка

В дальнейшем для краткости величину 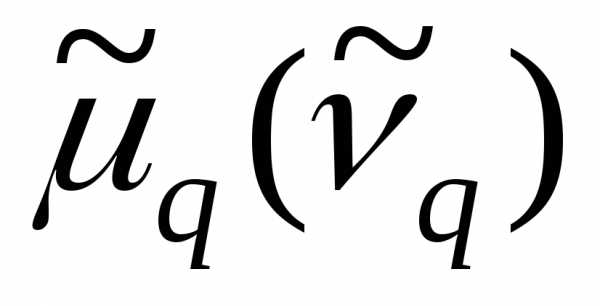часто будем называть просто центральным моментом (начальным моментом), не употребляя термин «эмпирический».

Используя формулу бинома Ньютона, разложим в ряд выражение для центрального момента q—го порядка:

В проведенных тождественных преобразованиях использованы свойства 5° и 3° средней арифметической; — число сочетаний из q элементов по р элементов (p≤.q).

Итак, центральный момент q—го порядка выражается через начальные моменты следующим образом:

(22)

Полагая q = 0, 1, 2,…, можно получить выражения центральных моментов различных порядков через начальные моменты:

;

₍₂₃₎

₍₂₄₎

₍₂₅₎

и т.д.

Заметим, что формула (23) для центрального момента второго порядка, как и следовало ожидать, аналогична формуле (18) для дисперсии.

Рассмотрим свойства центральных моментов, которые позволят значительно упростить их вычисление.

1°. Если все варианты уменьшить (увеличить) на одно и то же число с, то центральный момент q-го порядка не изменится.

Доказательство. Если все варианты уменьшить на число с, то средняя арифметическая для измененного ряда равна —с, поэтому центральный момент q—го порядка

Аналогично можно показать, что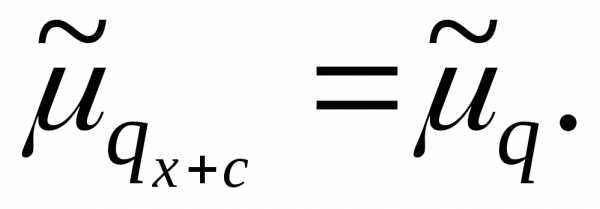

2°. Если все варианты уменьшить (увеличить) в одно и то же число k раз, то центральный момент q-го порядка уменьшится (увеличится) в 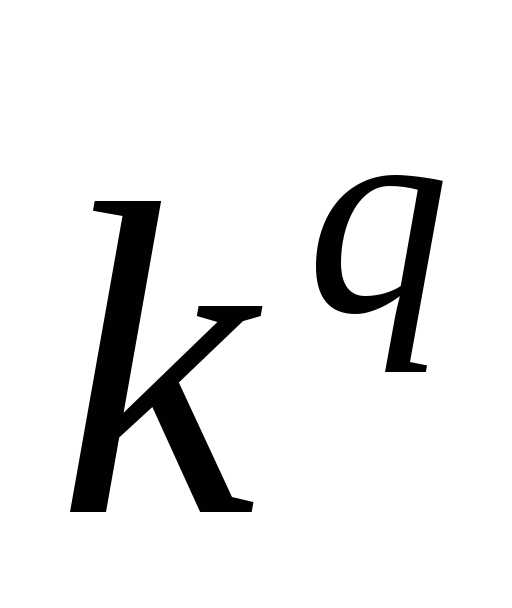раз.

Доказательство. Если все варианты уменьшить в одно и то же число k раз, то средняя арифметическая для измененного вариационного ряда равна 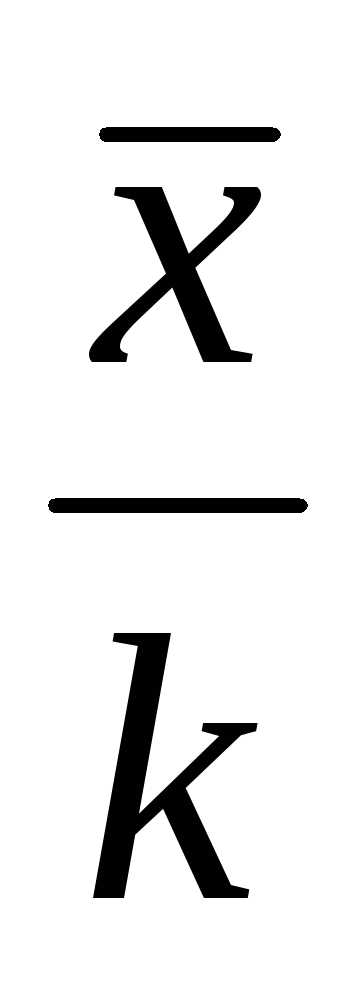, поэтому центральный момент q-гo порядка

Аналогично можно показать, что

Для облегчения расчётов центральные моменты вычисляют не по первоначальным вариантам х, а по вариантам х’=(х — с)/k. Зная 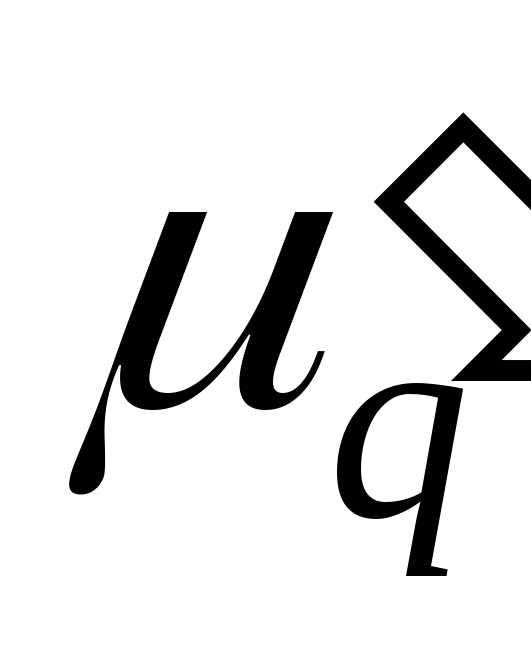(центральный момент q—го порядка для измененного ряда), легко вычислить центральный момент q-го порядка для первоначального ряда:

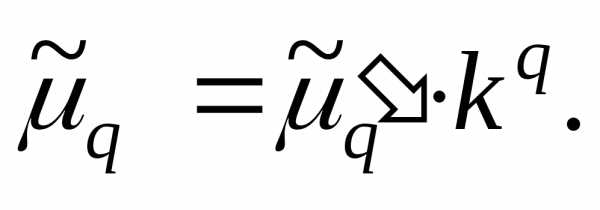(26)

Действительно, принимая во внимание свойства центрального момента, получаем

откуда следует, что

9. Эмпирические асимметрия и эксцесс

Эмпирическим коэффициентом асимметрии называют отношение центрального момента третьего порядка к кубу среднеквадратического отклонения:

. (27)

Если полигон вариационного ряда скошен, т.е. одна из его ветвей, начиная от вершины, зримо длиннее другой, то такой ряд называют асимметричным. Из формулы (27) следует, что если в вариационном ряду преобладают варианты, меньшие , то эмпирический коэффициент асимметрии отрицателен; говорят, что в этом случае имеет место левосторонняя асимметрия. Если же в вариационном ряду преобладают варианты, большие , то эмпирический коэффициент асимметрии положителен; в этом случае имеет место правосторонняя асимметрия. При левосторонней асимметрии левая ветвь полигона длиннее правой. При правосторонней, более длинной является правая ветвь.

Эмпирический коэффициент асимметрии не имеет ни верхней, ни нижней границы, что снижает его ценность как меры асимметрии. Практически коэффициент асимметрии редко бывает особенно велик, а для умеренно асимметричных рядов он обычно меньше единицы.

Эмпирическим эксцессом или коэффициентом крутости называют уменьшенное на 3 единицы отношение центрального момента четвертого порядка к четвертой степени среднеквадратического отклонения:

. (28)

За стандартное значение эксцесса принимают нуль-эксцесс так называемой нормальной кривой (см. рис. 1).

Кривые, у которых эксцесс отрицательный, по сравнению с нормальной менее крутые, имеют, более плоскую вершину и называются «плосковершинными» Кривые с положительным эксцессом более крутые по сравнению с нормальной кривой, имеют более острую вершину и называются «островершинными».

Заключение по лекции:

В лекции мы рассмотрели характеристики вариационного ряда. В ходе подготовки к последующей лекции и практическим занятиям вы должны самостоятельно при углубленном изучении рекомендованной литературы и решения предложенных задач дополнить свои конспекты лекций.

Приложения

studfiles.net