Cos sin формула – формулы cos, sin, tg, ctg

alexxlab / / Школьная жизнь

Содержание

Формулы тригонометрии Википедия

№ФормулаДопустимые значения аргумента
1.1sin2⁡α+cos2⁡α=1{\displaystyle \operatorname {sin} ^{2}\alpha +\operatorname {cos} ^{2}\alpha =1}∀α{\displaystyle \forall \alpha }
1.2tg2⁡α+1=1cos2⁡α=sec2⁡α{\displaystyle \operatorname {tg} ^{2}\alpha +1={\frac {1}{\cos ^{2}\alpha }}=\operatorname {sec} ^{2}\alpha }α≠π2+πn,n∈Z{\displaystyle \alpha \neq {\frac {\pi }{2}}+\pi n,n\in \mathbb {Z} }
1.3ctg2⁡α+1=1sin2⁡α=cosec2⁡α{\displaystyle \operatorname {ctg} ^{2}\alpha +1={\frac {1}{\sin ^{2}\alpha }}=\operatorname {cosec} ^{2}\alpha }α≠πn,n∈Z{\displaystyle \alpha \neq \pi n,n\in \mathbb {Z} }
1.4tg⁡α⋅ctg⁡α=1{\displaystyle \operatorname {tg} \alpha \cdot \operatorname {ctg} \alpha =1}

ru-wiki.ru

Основные тригонометрические формулы

В самом начале этой статьи мы с Вами рассмотрели понятие тригонометрических функций. Основное назначение их назначение – это изучение основ тригонометрии и исследование периодических процессов. И тригонометрический круг мы не зря рисовали, потому что в большинстве случаев тригонометрические функции определяются, как отношение сторон треугольника или его определенных отрезков в единичной окружности. Так же я упоминал о неоспоримо огромном значении тригонометрии в современной жизни. Но наука не стоит на месте, в результате мы можем значительно расширить область применения тригонометрии и перенести ее положения на вещественные, а иногда и на комплексные числа.

Формулы тригонометрии бывают нескольких видов. Рассмотрим их по порядку.

  1. Соотношения тригонометрических функций одного и того же угла

    2. Здесь мы подошли к рассмотрению такого понятия как основные тригонометрические тождества.

    Тригонометрическое тождество — это равенство, которое состоит из тригонометрических соотношений и которое выполняется для всех значений величин углов, которые входят в него.

    Рассмотрим наиболее важные тригонометрические тождества и их доказательства:

    Первое тождество вытекает из самого определения тангенс.

    Возьмем прямоугольный треугольник, в котором имеется острый угол х при вершине А.

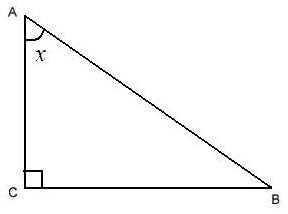
    Для доказательства тождеств необходимо воспользоваться теоремой Пифагора:

    (ВС) 2 + (АС) 2 = (АВ)

    2

    Теперь разделим на (АВ) 2 обе части равенства и припомнив определения sin и cos угла, мы получаем второе тождество:

    (ВС) 2/(AB) 2 + (AC) 2/(AB) 2 = 1

    sin x = (BC)/(AB)

    cos x = (AC)/(AB)

    sin2 x + cos2 x = 1

    Для доказательства третьего и четвертого тождеств воспользуемся предыдущим доказательством.

    Для этого обе части второго тождества разделим на cos2 x:

    sin2 x/ cos2 x + cos2 x/ cos2 x = 1/ cos2 x

    sin2 x/ cos2 x + 1 = 1/ cos2 x

    Исходя из первого тождества tg x = sin х /cos x получаем третье:

    1 + tg2 x = 1/cos2 x

    Теперь разделим второе тождество на sin2 x:

    sin2 x/ sin2 x + cos2 x/ sin2 x = 1/ sin2 x

    1+ cos2 x/ sin

    2 x = 1/ sin2 x

    cos2 x/ sin2 x есть не что иное, как 1/tg2 x, поэтому получаем четвертое тождество:

    1 + 1/tg2 x = 1/sin2 x

    Пришла пора вспомнить теорему о сумме внутренних углов треугольника, которая гласит, что сумма углов треугольника = 1800. Получается, что при вершине В треугольника находится угол, величина которого 1800 – 900 – х = 900 – х.

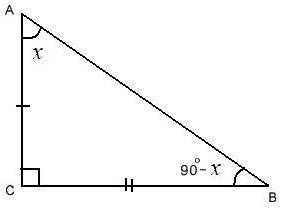
    Опять вспомним определения для sin и cos и получаем пятое и шестое тождества:

    sin x = (BC)/(AB)

    cos(900– x ) = (BC)/(AB)

    cos(900– x ) = sin x

    Теперь выполним следующее:

    cos x = (AC)/(AB)

    sin(900– x ) = (AC)/(AB)

    sin(900– x ) = cos x

    Как видите – здесь все элементарно.

    Существуют и другие тождества, которые используются при решении математических тождеств, я приведу их просто в виде справочной информации, потому как все они проистекают из вышерассмотренных.

  2. Выражения тригонометрических функций друг через друга

    (выбор знака перед корнем определяется тем, в какой из четвертей круга расположен угол ?)

  3. Далее следуют формулы сложения и вычитания углов:

  4. Формулы двойных, тройных и половинных углов.

    Замечу, что все они проистекают из предыдущих формул.

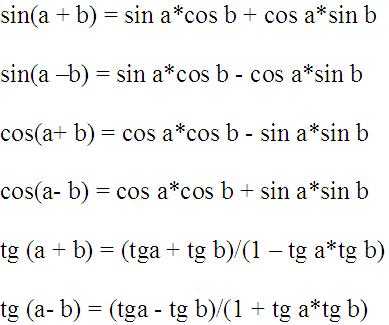
    5. sin 2х =2sin х*cos х

    cos 2х =cos2х -sin2х =1-2sin2х =2cos2х -1

    tg 2x = 2tgx/(1 — tg2 x)

    сtg 2x = (сtg2 x — 1) /2сtg x

    sin3х =3sin х — 4sin3х

    cos3х =4cos3х — 3cos х

    tg 3x = (3tgx – tg3 x) /(1 — 3tg2 x)

    сtg 3x = (сtg3x – 3сtg x) /(3сtg2 x — 1)

  5. Формулы преобразования тригонометрических выражений:

Когда-то, будучи школьником, я с удовольствием применял эти формулы для решения различного рода задач, как то упростить выражение или решить уравнение. Главное разглядеть — куда и какую формулу необходимо применить, и тогда многоярусная конструкция превращается в обычное числовое выражение. Очень полезная штука для развития логического мышления!


Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

reshit.ru

Формулы тригонометрии Вики

Тригонометрические тождества — математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента (из общей области определения).

Основные тригонометрические формулы[ | код]

  • Формула (1.1) является следствием теоремы Пифагора.
  • Формулы (1.2) и (1.3) получаются из формулы (1.1) делением на cos2⁡α{\displaystyle \cos ^{2}\alpha } и sin2⁡α{\displaystyle \sin ^{2}\alpha } соответственно.
  • Формула (1.4) следует из определений тангенса и котангенса.

Замечание[ | код]

Есть и другие тригонометрические функции.

Формулы сложения и вычитания аргументов[ | код]

№Формулы сложения и вычитания аргументов
2.1sin⁡(α±β)=sin⁡αcos⁡β±cos⁡αsin⁡β{\displaystyle \sin \left(\alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta }
2.2cos⁡(α±β)=cos⁡αcos⁡β∓sin⁡αsin⁡β{\displaystyle \cos \left(\alpha \pm \beta \right)=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta }
2.3tg⁡(α±β)=tg⁡α±tg⁡β1∓tg⁡αtg⁡β{\displaystyle \operatorname {tg} \left(\alpha \pm \beta \right)={\frac {\operatorname {tg} \alpha \pm \operatorname {tg} \beta }{1\mp \operatorname {tg} \alpha \operatorname {tg} \beta }}}
2.4ctg⁡(α±β)=ctg⁡αctg⁡β∓1ctg⁡β±ctg⁡α{\displaystyle \operatorname {ctg} \left(\alpha \pm \beta \right)={\frac {\operatorname {ctg} \alpha \operatorname {ctg} \beta \mp 1}{\operatorname {ctg} \beta \pm \operatorname {ctg} \alpha }}}

Формула (2.3) получается при делении (2.1) на (2.2). А формула (2.4) — при делении (2.2) на (2.1).

Вывод формул для sin⁡(α+β), cos⁡(α+β){\displaystyle \sin(\alpha +\beta ),\ \cos(\alpha +\beta )}

Формулы двойного угла и половинного угла[ | код]

Формулы двойного угла выводятся из формул (2.1)—(2.4) , если принять, что угол β равен углу α:

Примечания

для формулы tg⁡2α{\displaystyle \operatorname {tg} 2\alpha }:

  • α≠π4+π2n,n∈Z,{\displaystyle \alpha \not ={\frac {\pi }{4}}+{\frac {\pi }{2}}n,n\in \mathbb {Z} ,}
  • α≠π2+πn,n∈Z,{\displaystyle \alpha \not ={\frac {\pi }{2}}+\pi n,n\in \mathbb {Z} ,}

для формулы ctg⁡2α{\displaystyle \operatorname {ctg} 2\alpha }: α≠π2+πn,n∈Z.{\displaystyle \alpha \not ={\frac {\pi }{2}}+\pi n,n\in \mathbb {Z} .}

Из формулы двойного угла для косинуса (3.2) выводятся формулы половинного угла:

№Формулы половинного угла
3.5sin⁡α2=±1−cos⁡α2{\displaystyle \sin {\alpha \over 2}=\pm {\sqrt {1-\cos \alpha \over 2}}}
3.6cos⁡α2=±1+cos⁡α2{\displaystyle \cos {\alpha \over 2}=\pm {\sqrt {1+\cos \alpha \over 2}}}
3.7tg⁡α2=±1−cos⁡α1+cos⁡α=sin⁡α1+cos⁡α=1−cos⁡αsin⁡α{\displaystyle \operatorname {tg} {\alpha \over 2}=\pm {\sqrt {1-\cos \alpha \over 1+\cos \alpha }}={\sin \alpha \over 1+\cos \alpha }={1-\cos \alpha \over \sin \alpha }}

Формулы тройного угла[ | код]

Формулы тройного угла выводятся из формул (2.1)—(2.4) , если принять, что угол β равен углу 2α:

№Формулы тройного угла
4.1sin⁡3α=3sin⁡α−4sin3⁡α{\displaystyle \sin 3\alpha =3\sin \alpha -4\sin ^{3}\alpha }
4.2cos⁡3α=4cos3⁡α−3cos⁡α{\displaystyle \cos 3\alpha =4\cos ^{3}\alpha -3\cos \alpha }
4.3tg⁡3α=3tg⁡α−tg3⁡α1−3tg2⁡α{\displaystyle \operatorname {tg} 3\alpha ={\frac {3\operatorname {tg} \alpha -\operatorname {tg} ^{3}\alpha }{1-3\operatorname {tg} ^{2}\alpha }}}
4.4ctg⁡3α=3ctg⁡α−ctg3⁡α1−3ctg2⁡α{\displaystyle \operatorname {ctg} 3\alpha ={\frac {3\operatorname {ctg} \alpha -\operatorname {ctg} ^{3}\alpha }{1-3\operatorname {ctg} ^{2}\alpha }}}

Примечания

для формулы tg⁡3α{\displaystyle \operatorname {tg} 3\alpha }: α≠π6+π3n,n∈Z{\displaystyle \alpha \not ={\frac {\pi }{6}}+{\frac {\pi }{3}}n,n\in \mathbb {Z} }
для формулы ctg⁡3α{\displaystyle \operatorname {ctg} 3\alpha }: α≠π3n+πn,n∈Z{\displaystyle \alpha \not ={\frac {\pi }{3}}n+\pi n,n\in \mathbb {Z} };

Формулы понижения степени[ | код]

Формулы понижения степени выводятся из формул (3.2):

№Произведение
5.9sin2⁡αcos2⁡α=1−cos⁡4α8{\displaystyle \sin ^{2}\alpha \cos ^{2}\alpha ={\frac {1-\cos 4\alpha }{8}}}
5.10sin3⁡αcos3⁡α=3sin⁡2α−sin⁡6α32{\displaystyle \sin ^{3}\alpha \cos ^{3}\alpha ={\frac {3\sin 2\alpha -\sin 6\alpha }{32}}}
5.11sin4⁡αcos4⁡α=3−4cos⁡4α+cos⁡8α128{\displaystyle \sin ^{4}\alpha \cos ^{4}\alpha ={\frac {3-4\cos 4\alpha +\cos 8\alpha }{128}}}
5.12sin5⁡αcos5⁡α=10sin⁡2α−5sin⁡6α+sin⁡10α512{\displaystyle \sin ^{5}\alpha \cos ^{5}\alpha ={\frac {10\sin 2\alpha -5\sin 6\alpha +\sin 10\alpha }{512}}}

Формулы преобразования произведения функций[ | код]

№Формулы преобразования произведений функций
6.1sin⁡αsin⁡β=cos⁡(α−β)−cos⁡(α+β)2{\displaystyle \sin \alpha \sin \beta ={\frac {\cos(\alpha -\beta )-\cos(\alpha +\beta )}{2}}}
6.2sin⁡αcos⁡β=sin⁡(α−β)+sin⁡(α+β)2{\displaystyle \sin \alpha \cos \beta ={\frac {\sin(\alpha -\beta )+\sin(\alpha +\beta )}{2}}}
6.3cos⁡αcos⁡β=cos⁡(α−β)+cos⁡(α+β)2{\displaystyle \cos \alpha \cos \beta ={\frac {\cos(\alpha -\beta )+\cos(\alpha +\beta )}{2}}}

Вывод формул преобразования произведений функций

Формулы преобразования произведения функций выводятся из формул сложения аргументов (2.1) и (2.2). Например, из формулы (2.1) следует:

sin⁡(α+β)+sin⁡(α−β)=sin⁡αcos⁡β+cos⁡αsin⁡β+sin⁡αcos⁡β−cos⁡αsin⁡β={\displaystyle \sin(\alpha +\beta )+\sin(\alpha -\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta +\sin \alpha \cos \beta -\cos \alpha \sin \beta =}
=2sin⁡αcos⁡β{\displaystyle =2\sin \alpha \cos \beta }.

То есть:

sin⁡αcos⁡β=sin⁡(α+β)+sin⁡(α−β)2{\displaystyle \sin \alpha \cos \beta ={\frac {\sin(\alpha +\beta )+\sin(\alpha -\beta )}{2}}}    — формула (6.2).

Остальные формулы преобразования произведений функций выводятся аналогично.

Формулы преобразования суммы функций[ | код]

Вывод формул преобразования суммы функций

Преобразование суммы синусов 3-x разных углов в произведение при :α +β +γ =360∘{\displaystyle \alpha \ +\beta \ +\gamma \ =360^{\circ }} :

sin⁡α+sin⁡β+sin⁡γ=4sin⁡α2 sin⁡β2 sin⁡γ2{\displaystyle \sin \alpha +\sin \beta +\sin \gamma =4\sin {\frac {\alpha }{2}}\ \sin {\frac {\beta }{2}}\ \sin {\frac {\gamma }{2}}} (7.6)

Решение простых тригонометрических уравнений[ | код]

  • sin⁡x=a.{\displaystyle \sin x=a.}
Если |a|>1{\displaystyle |a|>1} — вещественных решений нет.
Если |a|⩽1{\displaystyle |a|\leqslant 1} — решением является число вида x=(−1)narcsin⁡a+πn; n∈Z.{\displaystyle x=(-1)^{n}\arcsin a+\pi n;\ n\in \mathbb {Z} .}
  • cos⁡x=a.{\displaystyle \cos x=a.}
Если |a|>1{\displaystyle |a|>1} — вещественных решений нет.
Если |a|⩽1{\displaystyle |a|\leqslant 1} — решением является число вида x=±arccos⁡a+2πn; n∈Z.{\displaystyle x=\pm \arccos a+2\pi n;\ n\in \mathbb {Z} .}
  • tgx=a.{\displaystyle \operatorname {tg} \,x=a.}
Решением является число вида x=arctga+πn; n∈Z.{\displaystyle x=\operatorname {arctg} \,a+\pi n;\ n\in \mathbb {Z} .}
  • ctgx=a.{\displaystyle \operatorname {ctg} \,x=a.}
Решением является число вида x=arcctga+πn; n∈Z.{\displaystyle x=\operatorname {arcctg} \,a+\pi n;\ n\in \mathbb {Z} .}

Универсальная тригонометрическая подстановка[ | код]

Тождества имеют смысл, только когда существуют обе части (то есть при α≠π+2πn{\displaystyle \alpha \neq \pi +2\pi n}).

sin⁡α=2tgα21+tg2⁡α2{\displaystyle \sin \alpha ={\frac {2\,{\operatorname {tg} }\,{\frac {\alpha }{2}}}{1+\operatorname {tg} ^{2}{\frac {\alpha }{2}}}}}cos⁡α=1−tg2⁡α21+tg2⁡α2{\displaystyle \cos \alpha ={\frac {1-\operatorname {tg} ^{2}{\frac {\alpha }{2}}}{1+\operatorname {tg} ^{2}{\frac {\alpha }{2}}}}}
tgα=2tgα21−tg2⁡α2{\displaystyle \operatorname {tg} \,\alpha ={\frac {2\,{\operatorname {tg} }\,{\frac {\alpha }{2}}}{1-\operatorname {tg} ^{2}{\frac {\alpha }{2}}}}}ctgα=1−tg2⁡α22tgα2{\displaystyle \operatorname {ctg} \,\alpha ={\frac {1-\operatorname {tg} ^{2}{\frac {\alpha }{2}}}{2\,{\operatorname {tg} }\,{\frac {\alpha }{2}}}}}
sec⁡α=1+tg2⁡α21−tg2⁡α2{\displaystyle \sec \alpha ={\frac {1+\operatorname {tg} ^{2}{\frac {\alpha }{2}}}{1-\operatorname {tg} ^{2}{\frac {\alpha }{2}}}}}cosecα=1+tg2⁡α22tgα2{\displaystyle \operatorname {cosec} \,\alpha ={\frac {1+\operatorname {tg} ^{2}{\frac {\alpha }{2}}}{2\,{\operatorname {tg} }\,{\frac {\alpha }{2}}}}}

Вспомогательный аргумент (формулы сложения гармонических колебаний)[ | код]

Сумма двух гармонических колебаний с одинаковой частотой будет вновь гармоническим колебанием. В частности,

asin⁡x+bcos⁡x=a2+b2sin⁡(x+φ){\displaystyle a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\sin(x+\varphi )}

где a,b∈R{\displaystyle a,b\in \mathbb {R} }, a{\displaystyle a} и b{\displaystyle b} не равны нулю одновременно, φ{\displaystyle \varphi } — это угол, называемый вспомогательным аргументом, который может быть найден из системы уравнений:

{sin⁡φ=ba2+b2,cos⁡φ=aa2+b2.{\displaystyle \left\{{\begin{matrix}\sin \varphi ={\dfrac {b}{\sqrt {a^{2}+b^{2}}}},\\\cos \varphi ={\dfrac {a}{\sqrt {a^{2}+b^{2}}}}.\end{matrix}}\right.}

Примечание. Из вышеприведённой системы следует, что tgφ=ba{\displaystyle \mathrm {tg} \,\varphi \,=\,{\tfrac {b}{a}}}, однако нельзя всегда считать, что φ=arctgba{\displaystyle \varphi \,=\,\mathrm {arctg} \,{\tfrac {b}{a}}}. Нужно учитывать знаки a{\displaystyle a} и b{\displaystyle b} для определения, к какой четверти принадлежит угол φ{\displaystyle \varphi }.

Полезные тождества[ | код]

В приведённых ниже формулах числа k{\displaystyle k} и n{\displaystyle n} целые.

sin⁡(π4+x)=cos⁡(π4−x).{\displaystyle \sin \left({\frac {\pi }{4}}+x\right)=\cos \left({\frac {\pi }{4}}-x\right).}

sin⁡(π4−x)=cos⁡(π4+x).{\displaystyle \sin \left({\frac {\pi }{4}}-x\right)=\cos \left({\frac {\pi }{4}}+x\right).}

1±sin⁡x=2sin2⁡(π4±x2).{\displaystyle 1\pm \sin x=2\sin ^{2}\left({\frac {\pi }{4}}\pm {\frac {x}{2}}\right).}

1+cos⁡x=2cos2⁡(x2).{\displaystyle 1+\cos x=2\cos ^{2}\left({\frac {x}{2}}\right).}

1−cos⁡x=2sin2⁡(x2).{\displaystyle 1-\cos x=2\sin ^{2}\left({\frac {x}{2}}\right).}

sin2⁡x=11+ctg2⁡x.{\displaystyle \sin ^{2}x={\frac {1}{1+\operatorname {ctg} ^{2}x}}.}

cos2⁡x=11+tg2⁡x.{\displaystyle \cos ^{2}x={\frac {1}{1+\operatorname {tg} ^{2}x}}.}

sin2⁡x−sin2⁡y=sin⁡(x−y)⋅sin⁡(x+y).{\displaystyle \sin ^{2}x-\sin ^{2}y=\sin(x-y)\cdot \sin(x+y).}

cos2⁡x−cos2⁡y=−sin⁡(x−y)⋅sin⁡(x+y).{\displaystyle \cos ^{2}x-\cos ^{2}y=-\sin(x-y)\cdot \sin(x+y).}

cos2⁡x−sin2⁡y=cos⁡(x−y)⋅cos⁡(x+y).{\displaystyle \cos ^{2}x-\sin ^{2}y=\cos(x-y)\cdot \cos(x+y).}

sin⁡2x+sin⁡2y=2cos⁡(x−y)⋅sin⁡(x+y).{\displaystyle \sin 2x+\sin 2y=2\cos(x-y)\cdot \sin(x+y).}

sin⁡2x−sin⁡2y=2sin⁡(x−y)⋅cos⁡(x+y).{\displaystyle \sin 2x-\sin 2y=2\sin(x-y)\cdot \cos(x+y).}

cos⁡2x+cos⁡2y=2cos⁡(x−y)⋅cos⁡(x+y).{\displaystyle \cos 2x+\cos 2y=2\cos(x-y)\cdot \cos(x+y).}

cos⁡2x−cos⁡2y=−2sin⁡(x−y)⋅sin⁡(x+y).{\displaystyle \cos 2x-\cos 2y=-2\sin(x-y)\cdot \sin(x+y).}

sin⁡2x+cos⁡2y=2sin⁡(π4+x−y)⋅sin⁡(π4+x+y).{\displaystyle \sin 2x+\cos 2y=2\sin \left({\frac {\pi }{4}}+x-y\right)\cdot \sin \left({\frac {\pi }{4}}+x+y\right).}

sin⁡2x−cos⁡2y=−2sin⁡(π4−x−y)⋅sin⁡(π4−x+y).{\displaystyle \sin 2x-\cos 2y=-2\sin \left({\frac {\pi }{4}}-x-y\right)\cdot \sin \left({\frac {\pi }{4}}-x+y\right).}

sin3⁡x+cos3⁡x=(sin⁡x+cos⁡x)(1−sin⁡xcos⁡x).{\displaystyle \sin ^{3}x+\cos ^{3}x=(\sin x+\cos x)(1-\sin x\cos x).}

sin4⁡x+cos4⁡x=1−2sin2⁡xcos2⁡x=1−12sin2⁡(2x)=34+14cos⁡(4x).{\displaystyle \sin ^{4}x+\cos ^{4}x=1-2\sin ^{2}x\,\cos ^{2}x=1-{\frac {1}{2}}\sin ^{2}(2x)={\frac {3}{4}}+{\frac {1}{4}}\cos(4x).}

sin6⁡x+cos6⁡x=1−3sin2⁡xcos2⁡x=1−3sin2⁡x+3sin4⁡x=1−34sin2⁡(2x)=58+38cos⁡(4x).{\displaystyle \sin ^{6}x+\cos ^{6}x=1-3\sin ^{2}x\,\cos ^{2}x=1-3\sin ^{2}x+3\sin ^{4}x=1-{\frac {3}{4}}\sin ^{2}(2x)={\frac {5}{8}}+{\frac {3}{8}}\cos(4x).}

1±tg⁡x=2sin⁡(π4±x)cos⁡x.{\displaystyle 1\pm \operatorname {tg} x={\frac {{\sqrt {2}}\sin \left({\frac {\pi }{4}}\pm x\right)}{\cos x}}.}

1±ctg⁡x=2sin⁡(π4±x)sin⁡x.{\displaystyle 1\pm \operatorname {ctg} x={\frac {{\sqrt {2}}\sin \left({\frac {\pi }{4}}\pm x\right)}{\sin x}}.}

tg⁡x=sin⁡2xcos⁡2x+1=1−cos⁡2xsin⁡2x.{\displaystyle \operatorname {tg} x={\frac {\sin 2x}{\cos 2x+1}}={\frac {1-\cos 2x}{\sin 2x}}.}

ctg2⁡x−tg2⁡x=4cos⁡2xsin2⁡2x.{\displaystyle \operatorname {ctg} ^{2}x-\operatorname {tg} ^{2}x={\frac {4\cos 2x}{\sin ^{2}2x}}.}

sin⁡3x=4sin⁡x⋅sin⁡(π3+x)⋅sin⁡(π3−x).{\displaystyle \sin 3x=4\sin x\cdot \sin \left({\frac {\pi }{3}}+x\right)\cdot \sin \left({\frac {\pi }{3}}-x\right).}

ru.wikibedia.ru

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *