Тригонометрические формулы — шпаргалка
Здесь можно найти тригонометрические формулы в удобном виде. А тригонометрические формулы приведения можно посмотреть на другой странице.
Основные тригонометрические тождества
— математические выражения для тригонометрических функций, выполняемые при каждом значении аргумента.
- sin² α + cos² α = 1
- tg α · ctg α = 1
- tg α = sin α ÷ cos α
- ctg α = cos α ÷ sin α
- 1 + tg² α = 1 ÷ cos² α
- 1 + ctg² α = 1 ÷ sin² α
Формулы сложения
- sin (α + β) = sin α · cos β + sin β · cos α
- sin (α — β) = sin α · cos β — sin β · cos α
- cos (α + β) = cos α · cos β — sin α · sin β
- cos (α — β) = cos α · cos β + sin α · sin β
- tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β)
- tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β)
- ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α)
- ctg (α — β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)
https://uchim.org/matematika/trigonometricheskie-formuly — uchim.org
Формулы двойного угла
- cos 2α = cos² α — sin² α
- cos 2α = 2cos² α — 1
- cos 2α = 1 — 2sin² α
- sin 2α = 2sin α · cos α
- tg 2α = (2tg α) ÷ (1 — tg² α)
- ctg 2α = (ctg² α — 1) ÷ (2ctg α)
Формулы тройного угла
- sin 3α = 3sin α — 4sin³ α
- cos 3α = 4cos³ α — 3cos α
- tg 3α = (3tg α — tg³ α) ÷ (1 — 3tg² α)
- ctg 3α = (3ctg α — ctg³ α) ÷ (1 — 3ctg² α)
Формулы понижения степени
- sin² α = (1 — cos 2α) ÷ 2
- sin³ α = (3sin α — sin 3α) ÷ 4
- cos² α = (1 + cos 2α) ÷ 2
- cos³ α = (3cos α + cos 3α) ÷ 4
- sin² α · cos² α = (1 — cos 4α) ÷ 8
- sin³ α · cos³ α = (3sin 2α — sin 6α) ÷ 32
Переход от произведения к сумме
- sin α · cos β = ½ (sin (α + β) + sin (α — β))
- sin α · sin β = ½ (cos (α — β) — cos (α + β))
- cos α · cos β = ½ (cos (α — β) + cos (α + β))
Мы перечислили довольно много тригонометрических формул, но если чего-то не хватает, пишите.
Всё для учебы » Математика в школе » Тригонометрические формулы — шпаргалка
Чтобы добавить страницу в закладки, нажмите Ctrl+D.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/trigonometricheskie-formuly
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):
uchim.org
?Тригонометрические формулы (более 100 шт.)
На этой странице вы найдете все основные тригонометрические формулы, которые помогут вам решать многие упражнения, значительно упростив само выражение.
Тригонометрические формулы — математические равенства для тригонометрических функций, которые выполняются при всех допустимых значениях аргумента.
Формулами задаются соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом, котангенсом.
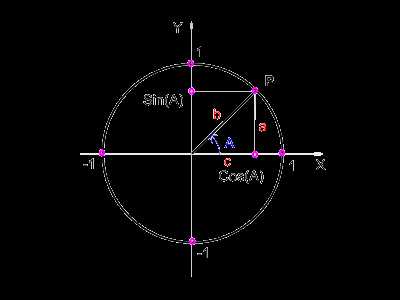
Синус угла – это координата y точки (ордината) на единичной окружности. Косинус угла – это координата x точки (абсцисса).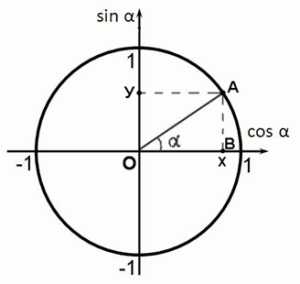
Тангенс и котангенс – это, соответственно, соотношения синуса к косинусу и наоборот.
`sin \ \alpha, \ cos \ \alpha`
`tg \ \alpha=\frac{sin\ \alpha}{cos \ \alpha},` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`ctg \ \alpha=\frac{cos\ \alpha}{sin\ \alpha},` ` \alpha\ne\pi+\pi n, \ n \in Z`
И две, которые используются реже – секанс, косеканс. Они обозначают соотношения 1 к косинусу и синусу.
`sec \ \alpha=\frac{1}{cos\ \alpha},` ` \alpha\ne\frac\pi2+\pi n,\ n \in Z`
`cosec \ \alpha=\frac{1}{sin \ \alpha},` ` \alpha\ne\pi+\pi n,\ n \in Z`
Из определений тригонометрических функций видно, какие знаки они имеют в каждой четверти. Знак функции зависит только от того, в какой из четвертей располагается аргумент.
Содержание статьи:
Тригонометрические функции угла `(-\alpha)`
При изменении знака аргумента с «+» на «-» только функция косинус не меняет своего значения. Она называется четной. Ее график симметричен относительно оси ординат.
Остальные функции (синус, тангенс, котангенс) нечетные. При смене знака аргумента с «+» на «-» их значение также изменяется на отрицательное. Их графики симметричны относительно начала координат.
`sin(-\alpha)=-sin \ \alpha`
`cos(-\alpha)=cos \ \alpha`
`tg(-\alpha)=-tg \ \alpha`
`ctg(-\alpha)=-ctg \ \alpha`
Основные тригонометрические тождества
Основные тригонометрические тождества – это формулы, устанавливающие связь между тригонометрическими функциями одного угла (`sin \ \alpha, \ cos \ \alpha, \ tg \ \alpha, \ ctg \ \alpha`) и которые позволяют находить значение каждой из этих функций через любую известную другую.
`tg \ \alpha \cdot ctg \ \alpha=1, \ \alpha\ne\frac{\pi n} 2, \ n \in Z`
`1+tg^2 \alpha=\frac 1{cos^2 \alpha}=sec^2 \alpha,` ` \alpha\ne\frac\pi2+\pi n, \ n \in Z`
`1+ctg^2 \alpha=\frac 1{sin^2 \alpha}=cosec^2 \alpha,` ` \alpha\ne\pi n, \ n \in Z`
Формулы суммы и разности углов тригонометрических функций
Формулы сложения и вычитания аргументов выражают тригонометрические функции суммы или разности двух углов через тригонометрические функции этих углов.
`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta`
`sin(\alpha-\beta)=` `sin \ \alpha\ cos \ \beta-cos \ \alpha\ sin \ \beta`
`cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`
`cos(\alpha-\beta)=` `cos \ \alpha\ cos \ \beta+sin \ \alpha\ sin \ \beta`
`tg(\alpha+\beta)=\frac{tg \ \alpha+tg \ \beta}{1-tg \ \alpha\ tg \ \beta}`
`tg(\alpha-\beta)=\frac{tg \ \alpha-tg \ \beta}{1+tg \ \alpha \ tg \ \beta}`
`ctg(\alpha+\beta)=\frac{ctg \ \alpha \ ctg \ \beta-1}{ctg \ \beta+ctg \ \alpha}`
`ctg(\alpha-\beta)=\frac{ctg \ \alpha\ ctg \ \beta+1}{ctg \ \beta-ctg \ \alpha}`
Формулы двойного угла
`sin \ 2\alpha=2 \ sin \ \alpha \ cos \ \alpha=` `\frac {2 \ tg \ \alpha}{1+tg^2 \alpha}=\frac {2 \ ctg \ \alpha}{1+ctg^2 \alpha}=` `\frac 2{tg \ \alpha+ctg \ \alpha}`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha=` `1-2 \ sin^2 \alpha=2 \ cos^2 \alpha-1=` `\frac{1-tg^2\alpha}{1+tg^2\alpha}=\frac{ctg^2\alpha-1}{ctg^2\alpha+1}=` `\frac{ctg \ \alpha-tg \ \alpha}{ctg \ \alpha+tg \ \alpha}`
`tg \ 2\alpha=\frac{2 \ tg \ \alpha}{1-tg^2 \alpha}=` `\frac{2 \ ctg \ \alpha}{ctg^2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac{ctg^2 \alpha-1}{2 \ ctg \ \alpha}=` `\frac { \ ctg \ \alpha-tg \ \alpha}2`
Формулы тройного угла
`sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`
`tg \ 3\alpha=\frac{3 \ tg \ \alpha-tg^3 \alpha}{1-3 \ tg^2 \alpha}`
`ctg \ 3\alpha=\frac{ctg^3 \alpha-3 \ ctg \ \alpha}{3 \ ctg^2 \alpha-1}`
Формулы половинного угла
`sin \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}2}`
`cos \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}2}`
`tg \ \frac \alpha 2=\pm \sqrt{\frac {1-cos \ \alpha}{1+cos \ \alpha}}=` `\frac {sin \ \alpha}{1+cos \ \alpha}=\frac {1-cos \ \alpha}{sin \ \alpha}`
`ctg \ \frac \alpha 2=\pm \sqrt{\frac {1+cos \ \alpha}{1-cos \ \alpha}}=` `\frac {sin \ \alpha}{1-cos \ \alpha}=\frac {1+cos \ \alpha}{sin \ \alpha}`
Формулы половинных, двойных и тройных аргументов выражают функции `sin, \ cos, \ tg, \ ctg` этих аргументов (`\frac{\alpha}2, \ 2\alpha, \ 3\alpha,… `) через эти ж функции аргумента `\alpha`.
Вывод их можно получить из предыдущей группы (сложения и вычитания аргументов). Например, тождества двойного угла легко получить, заменив `\beta` на `\alpha`.
Формулы понижения степени
Формулы квадратов (кубов и т. д.) тригонометрических функций позволяют перейти от 2,3,… степени к тригонометрическим функциям первой степени, но кратных углов (`\alpha, \ 3\alpha, \ …` или `2\alpha, \ 4\alpha, \ …`).
`sin^2 \alpha=\frac{1-cos \ 2\alpha}2,` ` (sin^2 \frac \alpha 2=\frac{1-cos \ \alpha}2)`
`cos^2 \alpha=\frac{1+cos \ 2\alpha}2,` ` (cos^2 \frac \alpha 2=\frac{1+cos \ \alpha}2)`
`sin^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}4`
`cos^3 \alpha=\frac{3cos \ \alpha+cos \ 3\alpha}4`
`sin^4 \alpha=\frac{3-4cos \ 2\alpha+cos \ 4\alpha}8`
`cos^4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`
Формулы суммы и разности тригонометрических функций
Формулы являют собой преобразования суммы и разности тригонометрических функций разных аргументов в произведение.
`sin \ \alpha+sin \ \beta=` `2 \ sin \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`sin \ \alpha-sin \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2`
`cos \ \alpha+cos \ \beta=` `2 \ cos \frac{\alpha+\beta}2 \ cos \frac{\alpha-\beta}2`
`cos \ \alpha-cos \ \beta=` `-2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\alpha-\beta}2=` `2 \ sin \frac{\alpha+\beta}2 \ sin \frac{\beta-\alpha}2`
`tg \ \alpha \pm tg \ \beta=\frac{sin(\alpha \pm \beta)}{cos \ \alpha \ cos \ \beta}`
`ctg \ \alpha \pm ctg \ \beta=\frac{sin(\beta \pm \alpha)}{sin \ \alpha \ sin \ \beta}`
`tg \ \alpha \pm ctg \ \beta=` `\pm \frac{cos(\alpha \mp \beta)}{cos \ \alpha \ sin \ \beta}`
Здесь происходит преобразование сложения и вычитаний функций одного аргумента в произведение.
`cos \ \alpha+sin \ \alpha=\sqrt{2} \ cos (\frac{\pi}4-\alpha)`
`cos \ \alpha-sin \ \alpha=\sqrt{2} \ sin (\frac{\pi}4-\alpha)`
`tg \ \alpha+ctg \ \alpha=2 \ cosec \2\alpha;` `tg \ \alpha-ctg \ \alpha=-2 \ ctg \2\alpha`
Следующие формулы преобразовывают сумму и разность единицы и тригонометрической функции в произведение.
`1+cos \ \alpha=2 \ cos^2 \frac{\alpha}2`
`1-cos \ \alpha=2 \ sin^2 \frac{\alpha}2`
`1+sin \ \alpha=2 \ cos^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1-sin \ \alpha=2 \ sin^2 (\frac {\pi} 4-\frac{\alpha}2)`
`1 \pm tg \ \alpha=\frac{sin(\frac{\pi}4 \pm \alpha)}{cos \frac{\pi}4 \ cos \ \alpha}=` `\frac{\sqrt{2} sin(\frac{\pi}4 \pm \alpha)}{cos \ \alpha}`
`1 \pm tg \ \alpha \ tg \ \beta=\frac{cos(\alpha \mp \beta)}{cos \ \alpha \ cos \ \beta};` ` \ ctg \ \alpha \ ctg \ \beta \pm 1=\frac{cos(\alpha \mp \beta)}{sin \ \alpha \ sin \ \beta}`
Формулы преобразования произведений функций
Формулы преобразования произведения тригонометрических функций с аргументами `\alpha` и `\beta` в сумму (разность) этих аргументов.
`sin \ \alpha \ sin \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}`
`sin\alpha \ cos\beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}`
`cos \ \alpha \ cos \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}`
`tg \ \alpha \ tg \ \beta =` `\frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)} =` `\frac{tg \ \alpha + tg \ \beta}{ctg \ \alpha + ctg \ \beta}`
`ctg \ \alpha \ ctg \ \beta =` `\frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)} =` `\frac{ctg \ \alpha + ctg \ \beta}{tg \ \alpha + tg \ \beta}`
`tg \ \alpha \ ctg \ \beta =` `\frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}`
Универсальная тригонометрическая подстановка
Эти формулы выражают тригонометрические функции через тангенс половинного угла.
`sin \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha\ne \pi +2\pi n, n \in Z`
`cos \ \alpha= \frac{1 — tg^{2}\frac{\alpha}{2}}{1 + tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z`
`tg \ \alpha= \frac{2tg\frac{\alpha}{2}}{1 — tg^{2}\frac{\alpha}{2}},` ` \alpha \ne \pi +2\pi n, n \in Z,` ` \alpha \ne \frac{\pi}{2}+ \pi n, n \in Z`
`ctg \ \alpha = \frac{1 — tg^{2}\frac{\alpha}{2}}{2tg\frac{\alpha}{2}},` ` \alpha \ne \pi n, n \in Z,` `\alpha \ne \pi + 2\pi n, n \in Z`
Формулы приведения
Формулы приведения можно получить, используя такие свойства тригонометрических функций, как периодичность, симметричность, свойство сдвига на данный угол. Они позволяют функции произвольного угла преобразовать в функции, угол которых находится в пределе между 0 и 90 градусами.
Для угла (`\frac {\pi}2 \pm \alpha`) или (`90^\circ \pm \alpha`):
`sin(\frac {\pi}2 — \alpha)=cos \ \alpha;` ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha`
`cos(\frac {\pi}2 — \alpha)=sin \ \alpha;` ` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`
`tg(\frac {\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):
`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Для угла (`\frac {3\pi}2 \pm \alpha`) или (`270^\circ \pm \alpha`):
`sin(\frac {3\pi}2 — \alpha)=-cos \ \alpha;` ` sin(\frac {3\pi}2 + \alpha)=-cos \ \alpha`
`cos(\frac {3\pi}2 — \alpha)=-sin \ \alpha;` ` cos(\frac {3\pi}2 + \alpha)=sin \ \alpha`
`tg(\frac {3\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {3\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {3\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {3\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Выражение одних тригонометрических функций через другие
`sin \ \alpha=\pm \sqrt{1-cos^2 \alpha}=` `\frac{tg \ \alpha}{\pm \sqrt{1+tg^2 \alpha}}=\frac 1{\pm \sqrt{1+ctg^2 \alpha}}`
`cos \ \alpha=\pm \sqrt{1-sin^2 \alpha}=` `\frac 1{\pm \sqrt{1+tg^2 \alpha}}=\frac {ctg \ \alpha}{\pm \sqrt{1+ctg^2 \alpha}}`
`tg \ \alpha=\frac {sin \ \alpha}{\pm \sqrt{1-sin^2 \alpha}}=` `\frac {\pm \sqrt{1-cos^2 \alpha}}{cos \ \alpha}=\frac 1{ctg \ \alpha}`
`ctg \ \alpha=\frac {\pm \sqrt{1-sin^2 \alpha}}{sin \ \alpha}=` `\frac {cos \ \alpha}{\pm \sqrt{1-cos^2 \alpha}}=\frac 1{tg \ \alpha}`
Тригонометрия в буквальном смысле переводится, как «измерение треугольников». Она начинает изучаться еще в школе, и продолжается более детально в ВУЗах. Поэтому основные формулы по тригонометрии нужны, начиная еще с 10 класса, а также для сдачи ЕГЭ. Они обозначают связи между функциями, а поскольку этих связей много, то и самых формул есть немало. Запомнить их все нелегко, да и не надо – при необходимости их все можно вывести.
Тригонометрические формулы применяются в интегральном исчислении, а также при тригонометрических упрощениях, вычислениях, преобразованиях.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Формулы тригонометрии
Взаимосвязь основных тригонометрических функций, каких как косинус и синус, тангенс и котангенс — называется формулы тригонометрии. Из-за того что взаимосвязей очень большое количество, соответственно и формул не меньше. Часть формул объединяет тригонометрические функции в зависимости от угла, который может быть либо кратным, либо одинаковым. Так же может выражаться от тангенса половинного угла. Так же через понижение степени.
Мы разберем самые основные из тригонометрических формул. С помощью которых можно решить большинство тригонометрических заданий. Для большего удобства объединим их по значению, по таблицам.
Начнем с тригонометрических тождеств.
Основы в тригонометрических тождествах определяют взаимосвязь косинуса и синуса, тангенса и котангенса в одном угле. И выходят из их определения и единичной окружности. Дают возможность выделить через любую функцию другую.
Далее рассмотрим тригонометрические формулы приведения.
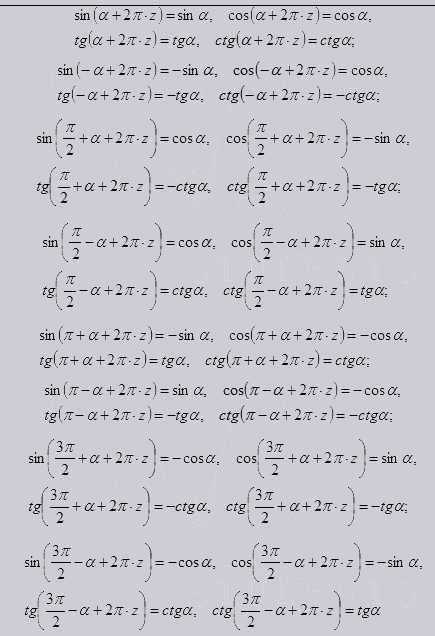
Они вытекают из свойств синусов, косинусов, котангенсов и тангенсов. Тем самым выражают такие свойства функции как: периодичность, симметричность и сдвиг к рассматриваемому углу. так же дают возможность работать с углами в радиусе до 90 градусов и произвольные углы.
Формулы на сложение.
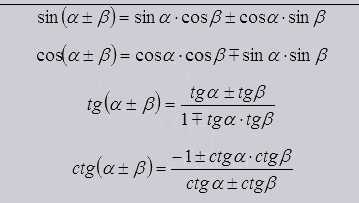
Из данных формул видно что функции на сумму или разность от 2 углов выводятся из их же тригонометрических функций. Так же являются основой для формул двойных, тройных и других углов.
Формула для двойных, тройных и других углов.
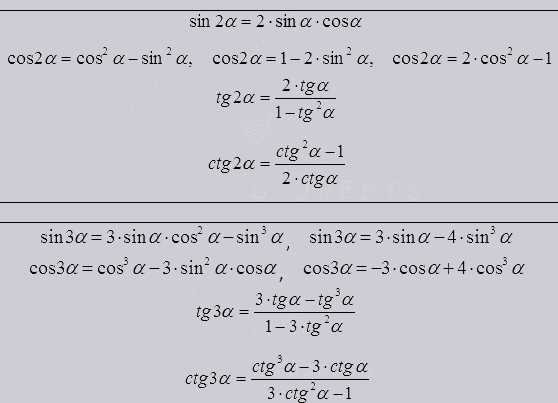
Из них видно что тригонометрическая функция двойного, тройного или какого то ни было угла выводится из т.ф. одинарных углов.
Так же как и одинарные, двойные, тройные и т.д. существуют и половинные углы
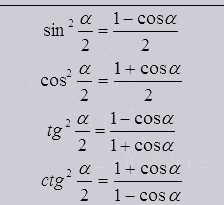
Из формул половинного угла видно, что он выходит из косинуса угла целого.
Так же существуют методы понижения степени выглядят они как:
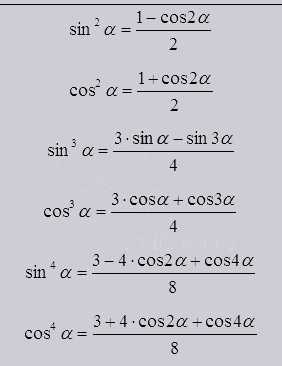

С помощью их использования возможно понизить функцию до первой степени. Взаимодействуя с натуральными степенями функций переводить до синусов и косинусов только кратных углов, в первую степень.
Сумма и разность в тригонометрической функции.
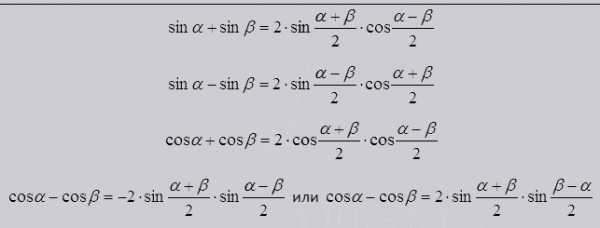
Помогают упростить тригонометрическое выражение, и разложить на множители синусы и косинусы.
Произведение синуса, косинуса, и одно на другое.
Метод универсальной тригонометрической подстановки.
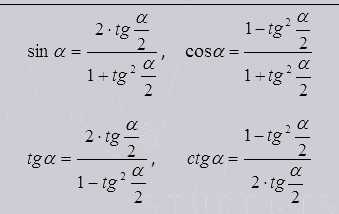
Такая подстановка удобна тем, что функции получаются без корней.
Заметка: Актуальные предложения, участие в тендерах на строительство бесплатное! Перейдите по ссылке строительно монтажные тендеры (http://www.b2bsearch.ru/tenders/stroy) узнайте подробнее.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Формулы приведения в тригонометрии: примеры, таблицы, доказательства
Формулы приведения — это соотношения, которые позволяют перейти от тригонометрических функций синус, косинус, тангенс и котангенс с углами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно.
Содержание статьи:
Формулы приведения: список и таблицы
Всех вместе формул приведения есть 32 штуки. Они несомненно пригодятся на ЕГЭ, экзаменах, зачетах. Но сразу предупредим, что заучивать наизусть их нет необходимости! Нужно потратить немного времени и понять алгоритм их применения, тогда для вас не составит труда в нужный момент вывести необходимое равенство.
Сначала запишем все формулы приведения:
Для угла (`\frac {\pi}2 \pm \alpha`) или (`90^\circ \pm \alpha`):
`sin(\frac {\pi}2 — \alpha)=cos \ \alpha;` ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha`
`cos(\frac {\pi}2 — \alpha)=sin \ \alpha;` ` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`
`tg(\frac {\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):
`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Для угла (`\frac {3\pi}2 \pm \alpha`) или (`270^\circ \pm \alpha`):
`sin(\frac {3\pi}2 — \alpha)=-cos \ \alpha;` ` sin(\frac {3\pi}2 + \alpha)=-cos \ \alpha`
`cos(\frac {3\pi}2 — \alpha)=-sin \ \alpha;` ` cos(\frac {3\pi}2 + \alpha)=sin \ \alpha`
`tg(\frac {3\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {3\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {3\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {3\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:
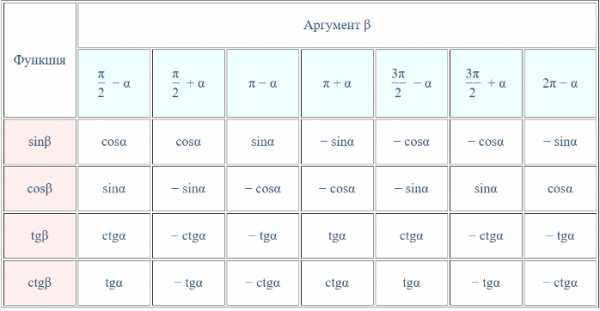
Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.
И вторая, аналогичная таблица, где углы записаны в градусах:
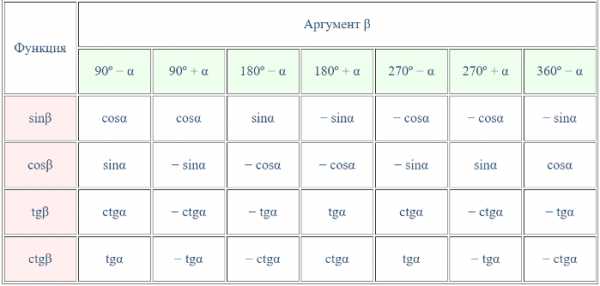
Мнемоническое правило формул приведения или как их запомнить
Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности. Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.Само привило содержит 3 этапа:
- Аргумент функции должен быть представлен в виде `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, причем `\alpha` — обязательно острый угол (от 0 до 90 градусов).
- Для аргументов `\frac {\pi}2 \pm \alpha`, `\frac {3\pi}2 \pm \alpha` тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов `\pi \pm \alpha`, `2\pi \pm \alpha` функция не меняется.
- Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:
1. ` cos(\pi + \alpha)`.
Функция на противоположную не меняется. Угол ` \pi + \alpha` находится в III четверти, косинус в этой четверти имеет знак «-» , поэтому преобразованная функция будет также со знаком «-» .
Ответ: ` cos(\pi + \alpha)= — cos \alpha`
2. `sin(\frac {3\pi}2 — \alpha)`.
Согласно мнемоническому правилу функция изменится на противоположную. Угол `\frac {3\pi}2 — \alpha` находится в III четверти, синус здесь имеет знак «-» , поэтому результат также будет со знаком «-» .
Ответ: `sin(\frac {3\pi}2 — \alpha)= — cos \alpha`
3. `cos(\frac {7\pi}2 — \alpha)`.
`cos(\frac {7\pi}2 — \alpha)=cos(\frac {6\pi}2+\frac {\pi}2-\alpha)=cos (3\pi+(\frac{\pi}2-\alpha))`. Представим `3\pi` как `2\pi+\pi`. `2\pi` — период функции.
Важно: Функции `cos \alpha` и `sin \alpha` имеют период `2\pi` или `360^\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac{\pi}2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac{\pi}2-\alpha)= — cos (\frac{\pi}2-\alpha)= — sin \alpha`.
Ответ: `cos(\frac {7\pi}2 — \alpha)=- sin \alpha`.
Лошадиное правило
Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?
Итак, мы имеем функции с аргументами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac {\pi}2`, `\pi`, `\frac {3\pi}2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac {\pi}2` и `\frac {3\pi}2` на вертикальной оси ординат.
Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.
То есть для аргументов с ключевыми точками, расположенными на горизонтальной оси, мы отвечаем «нет», мотая головой в стороны. А для углов с ключевыми точками, расположенными на вертикальной оси, мы отвечаем «да», кивая головой сверху вниз, как лошадь 🙂
Рекомендуем посмотреть видеоурок, в котором автор подробно объясняет, как запомнить формулы приведения без заучивания их наизусть.
Практические примеры использования формул приведения
Применение формул приведения начинается еще в 9, 10 классе. Немало задач с их использованием вынесено на ЕГЭ. Вот некоторые из задач, где придется применять эти формулы:
- задачи на решение прямоугольного треугольника;
- преобразования числовых и буквенных тригонометрических выражений, вычисление их значений;
- стереометрические задачи.
Пример 1. Вычислите при помощи формул приведения а) `sin 600^\circ`, б) `tg 480^\circ`, в) `cos 330^\circ`, г) `sin 240^\circ`.
Решение: а) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;
б) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac{\sqrt 3}3`;
в) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac{\sqrt 3}2`;
г) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac{\sqrt 3}2`.
Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac {9\pi}8` и `cos \frac {9\pi}8`; 2) `sin \frac {\pi}8` и `cos \frac {3\pi}10`.
Решение: 1)`sin \frac {9\pi}8=sin (\pi+\frac {\pi}8)=-sin \frac {\pi}8`
`cos \frac {9\pi}8=cos (\pi+\frac {\pi}8)=-cos \frac {\pi}8=-sin \frac {3\pi}8`
`-sin \frac {\pi}8> -sin \frac {3\pi}8`
`sin \frac {9\pi}8>cos \frac {9\pi}8`.
2) `cos \frac {3\pi}10=cos (\frac {\pi}2-\frac {\pi}5)=sin \frac {\pi}5`
`sin \frac {\pi}8<sin \frac {\pi}5`
`sin \frac {\pi}8<cos \frac {3\pi}10`.
Доказательство формул приведения
Докажем сначала две формулы для синуса и косинуса аргумента `\frac {\pi}2 + \alpha`: ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha` и` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.
Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на 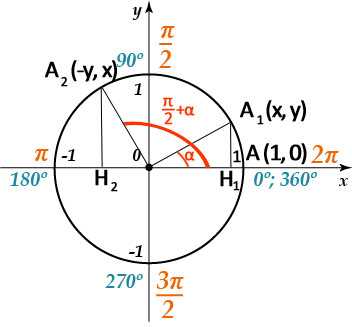 угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac {\pi}2 + \alpha` в точку `А_2(-у,х)`. Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac {\pi}2 + \alpha` в точку `А_2(-у,х)`. Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
Выходя из определения тангенса и котангенса, получим ` tg(\frac {\pi}2 + \alpha)=\frac {sin(\frac {\pi}2 + \alpha)}{cos(\frac {\pi}2 + \alpha)}=\frac {cos \alpha}{-sin \alpha}=-ctg \alpha` и ` сtg(\frac {\pi}2 + \alpha)=\frac {cos(\frac {\pi}2 + \alpha)}{sin(\frac {\pi}2 + \alpha)}=\frac {-sin \alpha}{cos \alpha}=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac {\pi}2 + \alpha`.
Чтобы доказать формулы с аргументом `\frac {\pi}2 — \alpha`, достаточно представить его, как `\frac {\pi}2 + (-\alpha)` и проделать тот же путь, что и выше. Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac {\pi}2 +(\frac {\pi}2+\alpha)` и `\frac {\pi}2 +(\frac {\pi}2-\alpha)` соответственно.
А `\frac {3\pi}2 + \alpha` и `\frac {3\pi}2 — \alpha` как `\pi +(\frac {\pi}2+\alpha)` и `\pi +(\frac {\pi}2-\alpha)`.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Тригонометрические формулы
Тригонометрические формулы и их вывод. Мы знаем, что их много и что их нужно учить, что эту информацию очень сложно запомнить и её периодически требуется повторять. Так, верно! Ниже представлен вывод этих формул, думаю, пригодится. Если запомнить принципы вывода, то когда будет необходимо — вы всегда «вспомните» нужную формулу. В любом случае информация будет полезна — кому-то проще выучить, кому-то вывести.
Сначала сами формулы, это ещё не все, будет продолжение.
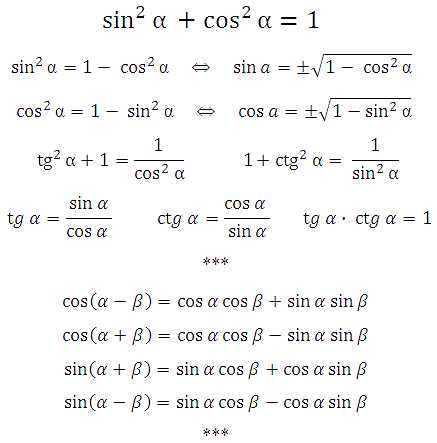
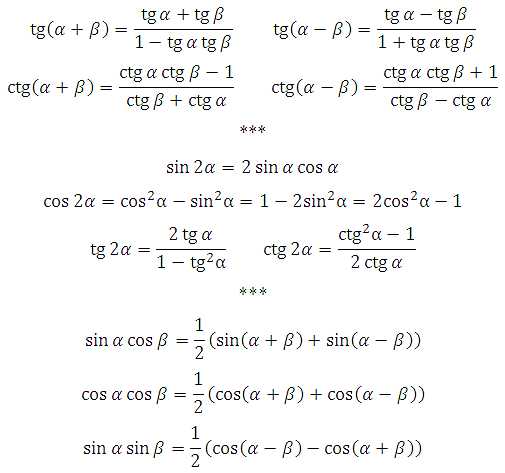
Основное тригонометрическое тождество, его запомнить нетрудно – формула «красивая»:
Откуда взялась? Посмотрите, здесь всё подробно описано.
Из неё следуют:
*Простые алгебраические преобразования.
Так же из неё получаем две другие необходимые формулы путём деления на квадрат синуса и квадрат косинуса:
Формулы тангенса и котангенса. Их проще выучить:
Что дальше? Разберём некоторые группы формул! Рассмотрим эскиз:
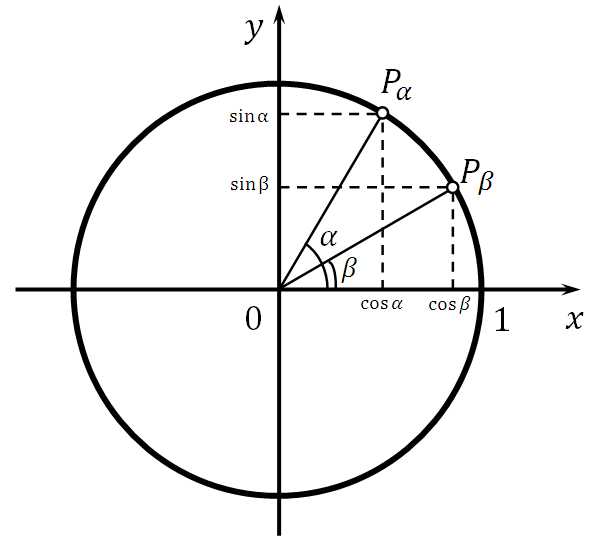
Теорема! Косинус разности двух углов равен произведению косинусов этих углов сложенному с произведением синусов:
Доказательство:
Рассмотрим единичную окружность с углами α и β, которые образованы векторами
И положительным направлением оси ох. Угол между векторами равен:
Выразим скалярное произведение векторов по формуле:
Следовательно
Так как векторы имеют длину равную единице, а именно:
Теперь вычислим это же скалярное произведение по формуле:
Так как
Мы получили, что
Следовательно
Что и требовалось доказать!
Косинус суммы >>
Сумму α + β представляем как разность α–(–β) и подставляем a формулу для косинуса разности:
Так функция косинуса чётная а функция синуса нечётная
Значит
Синус суммы >>
Воспользуемся одной из формул приведения:
Теперь по формуле косинуса разности (1):
Получили
Синус разности >>
*Функция косинуса чётная, функция синуса нечётная
Следовательно
Получили группу формул:
Тангенс суммы >>
Используя формулу тангенса делим формулу (3) на (2):
Далее разделим числитель и знаменатель на cosα∙cosβ, получим:
Получили
Тангенс разности >>
Используя формулу тангенса делим формулу (4) на (1):
Также разделим числитель и знаменатель на cosα∙cosβ, получим:
Получили
Котангенс суммы >>
Используя формулу котангенса делим формулу (2) на (3):
Далее разделим числитель и знаменатель на sinα∙sinβ, получим:
Получили
Котангенс разности >>
Используя формулу котангенса делим формулу (1) на (4):
Далее разделим числитель и знаменатель на sinα∙sinβ, получим:
Получили
Пожалуйста, ещё группа:

Синус двойного угла >>
Используем формулу (3) — синуса суммы:
Косинус двойного угла >>
Используем формулу (2) — косинуса суммы:
Если из основного тригонометрического тождества выразим:
И подставим в (10), то получим:
Если выразим:
И подставим в (10), то получим:
Тангенс двойного угла >>
Используем формулу (5):
Котангенс двойного угла >>
Используем формулу (7):
Можем выделить группу формул:
Преобразование произведения тригонометрических функций в сумму и разность.
Возьмём формулы синуса суммы и синуса разности:
Сложим их почленно, то есть правую и левую части:
Возьмём формулы косинуса суммы и косинуса разности:
Сложим их почленно, то есть правую и левую части:
Теперь из cos (α–β) вычтем cos (α+β):
Получим:
Вот и ещё одна группа формул готова:
К этой статье будет дополнение-продолжение, разобрали ещё не всё, не пропустите! Успеха вам!
Скачать материал в формате PDF
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
1. Число пиЧисло пи — одна из главных математических постоянных. Его значение объясняется большой ролью, которую играет в науке и технике окружность и связанные с ней функции синус и косинус. Без синуса и косинуса невозможно описание волновых процессов в электронике, электротехнике, гидродинамике, механике. Например, ток и напряжение в электрической розетке описывается синусом или косинусом.Число пи равно отношению длины окружности к удвоенному радиусу (диаметру). Оно выражается бесконечной непериодической десятичной дробью. Такие бесконечные числа называются иррациональными. Долгое время в математике существовала задача построения с помощью циркуля и линейки квадрата, площадь которого равна площади круга данного радиуса. Это так называемая задача о квадратуре круга. Она не может быть решена, т.к. отношение длины окружности к диаметру (или радиусу) не может быть выражено числом конечной длины. Число пи с точностью 17 верных знаков равно 3.14159265358979328. 2. РадианРадиан определяется следующим образом. Возьмем окружность произвольного радиуса, тогда угол в один радиан есть центральный угол, у которого длина дуги равна радиусу окружности. Учитывая определение числа пи, можно заключить, что углу в 360 градусов равен угол 2 * пи радиан.3. Формула перевода радиан в градусыИз определения числа пи, зная, что углу 2 * пи соответствует угол 360 градусов:
Где Ad — угол в градусах, Ar — угол в радианах. 4. Формула перевода градусов в радианыИз определения числа пи, зная, что углу 360 градусов соответствует угол 2 * пи:Ar = Ad * пи / 180Где Ad — угол в градусах, Ar — угол в радианах. 5.Тригонометрические функции. Прямоугольный треугольникРассмотрим прямоугольный треугольник, показанный на рисунке.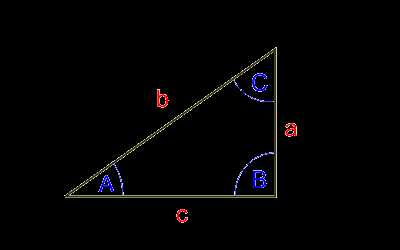 Буквами A, B, C обозначены углы, буквами a, b, c — стороны,
противолежащие углам A, B, C соответственно. Угол B = 90° (прямой).
Тогда тригонометрические функции определяются следующим образом: Буквами A, B, C обозначены углы, буквами a, b, c — стороны,
противолежащие углам A, B, C соответственно. Угол B = 90° (прямой).
Тогда тригонометрические функции определяются следующим образом:Синус: sin(A) = a/b.Косинус: cos(A) = c/b.Тангенс: tg(A) = a/c.Котангенс: ctg(A) = c/a.6. Тригонометрические формулы для прямоугольного треугольникаa = b * sin(A)c = b * cos(A) a = c * tg(A)7. Тригонометрические функции. Единичная окружность.Дадим еще одно, более общее, определение тригонометрических функций. Рассмотрим окружность единичного радиуса с центром в начале координат, показанную на рисунке.Синус угла A: При использовании тригонометрических функций принято измерять углы в радианах. Применяя определения числа пи и радиана, получим:
8. Некоторые простые соотношения тригонометрических функций tg(A) = sin (A) / cos (A). 9. Свойства тригонометрических функций9.1. Свойства синуса-1 ≤ sin (A) ≤ 1Синус — нечетная функция, sin (-A) = - sin (A).Синус — периодическая функция, период равен 2 * пи (360°). 9.2. Свойства косинуса-1 ≤ cos(A) ≤ 1Косинус — четная функция, cos (-A) = cos (A).Косинус — периодическая функция, период равен 2 * пи (360°). 9.3. Свойства тангенсаФункцияtg(A)=a/с имеет разрыв для угла пи/2 (90°) и углов, отличающихся от него на ±N*пи/2 (±N*180°), т.е. когда c обращается в 0.Тангенс — нечетная функция, tg(-A) = -tg(A).Тангенс — периодическая функция, период равен пи (180°). 9.4. Свойства котангенсаФункцияctg(A)=c/a, имеет разрыв для угла 0° и углов, отличающихся от него на ±N*пи/2 (±N*180°), т.е. когда a обращается в 0.Котангенс — нечетная функция, ctg (-A) = - ctg (A).Котангенс — периодическая функция, период равен пи (180°). 10. Основные формулы треугольникаОбозначения:A, B, C — углы треугольника, a, b, c — противолежащие стороны, R — радиус описанной окружности, r — радиус вписанной окружности, p — полупериметр, (a + b + c) / 2, S — площадь треугольника. 10.1. Теорема синусовa/sin(A) = b/sin(B) = c/sin(C) = 2*R10.2. Теорема косинусовCos(A) = (b2+c2-a2)/(2*b*c)10.3. Площадь треугольника (1)S = b*c*sin(A)/210.4. Площадь треугольника (2)S = p * (p-a) * tg (A/2)несколько простых доказательств теоремы. 10.5. Радиус описанной окружности (1)R = a/(2*sin(A))10.7. Радиус описанной окружности (2)R= a*b*c /(4*S )10.8. Радиус вписанной окружности (1)R = S/p10.9. Радиус вписанной окружности (2)R = (p-a)*tg(A/2)11. Обратные тригонометрические функции11.1. Функция arcsin — арксинусАрксинус X, это угол, синус которого равен X. Иными словами:Если X = sin(A), тоarcsin(X) = A.Функция arcsin (X) определена для -1 ≤ X ≤ 1. 11.2. Функция arccos — арккосинус.Арккосинус X, это угол, косинус которого равен X. Иными словами:Если X = cos(A), тоarccos (X) = A.Функция arccos (X) определена для -1 ≤ X ≤ 1. 11.3. Функция arctg — арктангенс.Арктангенс X, это угол, тангенс которого равен X. Иными словами:Если X = tg(A), тоarctg(X) = A .11.4. Функция arcctg — арккотангенс.Арккотангенс X, это угол, котангенс которого равен X. Иными словами:Если X = ctg(A), тоarcctg(X) = A. |
alexlat.ucoz.ru
Формулы тригонометрии Википедия
Тригонометрические тождества — математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента (из общей области определения).
Основные тригонометрические формулы
- Формула (1.1) является следствием теоремы Пифагора.
- Формулы (1.2) и (1.3) получаются из формулы (1.1) делением на cos2α{\displaystyle \cos ^{2}\alpha } и sin2α{\displaystyle \sin ^{2}\alpha } соответственно.
- Формула (1.4) следует из определений тангенса и котангенса.
Замечание
Есть и другие тригонометрические функции.
Формулы сложения и вычитания аргументов
| № | Формулы сложения и вычитания аргументов |
|---|---|
| 2.1 | sin(α±β)=sinαcosβ±cosαsinβ{\displaystyle \sin \left(\alpha \pm \beta \right)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta } |
| 2.2 | cos(α±β)=cosαcosβ∓sinαsinβ{\displaystyle \cos \left(\alpha \pm \beta \right)=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta } |
| 2.3 | tg(α±β)=tgα±tgβ1∓tgαtgβ{\displaystyle \operatorname {tg} \left(\alpha \pm \beta \right)={\frac {\operatorname {tg} \alpha \pm \operatorname {tg} \beta }{1\mp \operatorname {tg} \alpha \operatorname {tg} \beta }}} |
| 2.4 | ctg(α±β)=ctgαctgβ∓1ctgβ±ctgα{\displaystyle \operatorname {ctg} \left(\alpha \pm \beta \right)={\frac {\operatorname {ctg} \alpha \operatorname {ctg} \beta \mp 1}{\operatorname {ctg} \beta \pm \operatorname {ctg} \alpha }}} |
Формула (2.3) получается при делении (2.1) на (2.2). А формула (2.4) — при делении (2.2) на (2.1).
Вывод формул для sin(α+β), cos(α+β){\displaystyle \sin(\alpha +\beta ),\ \cos(\alpha +\beta )}Формулы двойного угла и половинного угла
Формулы двойного угла выводятся из формул (2.1)—(2.4) , если принять, что угол β равен углу α:
Примечания
для формулы tg2α{\displaystyle \operatorname {tg} 2\alpha }:
- α≠π4+π2n,n∈Z,{\displaystyle \alpha \not ={\frac {\pi }{4}}+{\frac {\pi }{2}}n,n\in \mathbb {Z} ,}
- α≠π2+πn,n∈Z,{\displaystyle \alpha \not ={\frac {\pi }{2}}+\pi n,n\in \mathbb {Z} ,}
для формулы ctg2α{\displaystyle \operatorname {ctg} 2\alpha }: α≠π2+πn,n∈Z.{\displaystyle \alpha \not ={\frac {\pi }{2}}+\pi n,n\in \mathbb {Z} .}
Из формулы двойного угла для косинуса (3.2) выводятся формулы половиного угла:
| № | Формулы половинного угла |
|---|---|
| 3.5 | sinα2=±1−cosα2{\displaystyle \sin {\alpha \over 2}=\pm {\sqrt {1-\cos \alpha \over 2}}} |
| 3.6 | cosα2=±1+cosα2{\displaystyle \cos {\alpha \over 2}=\pm {\sqrt {1+\cos \alpha \over 2}}} |
| 3.7 | tgα2=±1−cosα1+cosα=sinα1+cosα=1−cosαsinα{\displaystyle \operatorname {tg} {\alpha \over 2}=\pm {\sqrt {1-\cos \alpha \over 1+\cos \alpha }}={\sin \alpha \over 1+\cos \alpha }={1-\cos \alpha \over \sin \alpha }} |
Формулы тройного угла
Формулы тройного угла выводятся из формул (2.1)—(2.4) , если принять, что угол β равен углу 2α:
| № | Формулы тройного угла |
|---|---|
| 4.1 | sin3α=3sinα−4sin3α{\displaystyle \sin 3\alpha =3\sin \alpha -4\sin ^{3}\alpha } |
| 4.2 | cos3α=4cos3α−3cosα{\displaystyle \cos 3\alpha =4\cos ^{3}\alpha -3\cos \alpha } |
| 4.3 | tg3α=3tgα−tg3α1−3tg2α{\displaystyle \operatorname {tg} 3\alpha ={\frac {3\operatorname {tg} \alpha -\operatorname {tg} ^{3}\alpha }{1-3\operatorname {tg} ^{2}\alpha }}} |
| 4.4 | ctg3α=3ctgα−ctg3α1−3ctg2α{\displaystyle \operatorname {ctg} 3\alpha ={\frac {3\operatorname {ctg} \alpha -\operatorname {ctg} ^{3}\alpha }{1-3\operatorname {ctg} ^{2}\alpha }}} |
Примечания
для формулы tg3α{\displaystyle \operatorname {tg} 3\alpha }: α≠π6+π3n,n∈Z{\displaystyle \alpha \not ={\frac {\pi }{6}}+{\frac {\pi }{3}}n,n\in \mathbb {Z} }
для формулы ctg3α{\displaystyle \operatorname {ctg} 3\alpha }: α≠π3n+πn,n∈Z{\displaystyle \alpha \not ={\frac {\pi }{3}}n+\pi n,n\in \mathbb {Z} };
Формулы понижения степени
Формулы понижения степени выводятся из формул (3.2):
| № | Произведение |
|---|---|
| 5.9 | sin2αcos2α=1−cos4α8{\displaystyle \sin ^{2}\alpha \cos ^{2}\alpha ={\frac {1-\cos 4\alpha }{8}}} |
| 5.10 | sin3αcos3α=3sin2α−sin6α32{\displaystyle \sin ^{3}\alpha \cos ^{3}\alpha ={\frac {3\sin 2\alpha -\sin 6\alpha }{32}}} |
| 5.11 | sin4αcos4α=3−4cos4α+cos8α128{\displaystyle \sin ^{4}\alpha \cos ^{4}\alpha ={\frac {3-4\cos 4\alpha +\cos 8\alpha }{128}}} |
| 5.12 | sin5αcos5α=10sin2α−5sin6α+sin10α512{\displaystyle \sin ^{5}\alpha \cos ^{5}\alpha ={\frac {10\sin 2\alpha -5\sin 6\alpha +\sin 10\alpha }{512}}} |
Формулы преобразования произведения функций
| № | Формулы преобразования произведений функций |
|---|---|
| 6.1 | sinαsinβ=cos(α−β)−cos(α+β)2{\displaystyle \sin \alpha \sin \beta ={\frac {\cos(\alpha -\beta )-\cos(\alpha +\beta )}{2}}} |
| 6.2 | sinαcosβ=sin(α−β)+sin(α+β)2{\displaystyle \sin \alpha \cos \beta ={\frac {\sin(\alpha -\beta )+\sin(\alpha +\beta )}{2}}} |
| 6.3 | cosαcosβ=cos(α−β)+cos(α+β)2{\displaystyle \cos \alpha \cos \beta ={\frac {\cos(\alpha -\beta )+\cos(\alpha +\beta )}{2}}} |
Вывод формул преобразования произведений функций
Формулы преобразования произведения функций выводятся из формул сложения аргументов (2.1) и (2.2). Например, из формулы (2.1) следует:
- sin(α+β)+sin(α−β)=sinαcosβ+cosαsinβ+sinαcosβ−cosαsinβ={\displaystyle \sin(\alpha +\beta )+\sin(\alpha -\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta +\sin \alpha \cos \beta -\cos \alpha \sin \beta =}
- =2sinαcosβ{\displaystyle =2\sin \alpha \cos \beta }.
То есть:
- sinαcosβ=sin(α+β)+sin(α−β)2{\displaystyle \sin \alpha \cos \beta ={\frac {\sin(\alpha +\beta )+\sin(\alpha -\beta )}{2}}} — формула (6.2).
Остальные формулы преобразования произведений функций выводятся аналогично.
Формулы преобразования суммы функций
Вывод формул преобразования суммы функций
Преобразование суммы синусов 3-x разных углов в произведение при :α +β +γ =360∘{\displaystyle \alpha \ +\beta \ +\gamma \ =360^{\circ }} :
- sinα+sinβ+sinγ=4sinα2 sinβ2 sinγ2{\displaystyle \sin \alpha +\sin \beta +\sin \gamma =4\sin {\frac {\alpha }{2}}\ \sin {\frac {\beta }{2}}\ \sin {\frac {\gamma }{2}}} (7.6)
Решение простых тригонометрических уравнений
- sinx=a.{\displaystyle \sin x=a.}
- Если |a|>1{\displaystyle |a|>1} — вещественных решений нет.
- Если |a|⩽1{\displaystyle |a|\leqslant 1} — решением является число вида x=(−1)narcsina+πn; n∈Z.{\displaystyle x=(-1)^{n}\arcsin a+\pi n;\ n\in \mathbb {Z} .}
- cosx=a.{\displaystyle \cos x=a.}
- Если |a|>1{\displaystyle |a|>1} — вещественных решений нет.
- Если |a|⩽1{\displaystyle |a|\leqslant 1} — решением является число вида x=±arccosa+2πn; n∈Z.{\displaystyle x=\pm \arccos a+2\pi n;\ n\in \mathbb {Z} .}
- tgx=a.{\displaystyle \operatorname {tg} \,x=a.}
- Решением является число вида x=arctga+πn; n∈Z.{\displaystyle x=\operatorname {arctg} \,a+\pi n;\ n\in \mathbb {Z} .}
- ctgx=a.{\displaystyle \operatorname {ctg} \,x=a.}
- Решением является число вида x=arcctga+πn; n∈Z.{\displaystyle x=\operatorname {arcctg} \,a+\pi n;\ n\in \mathbb {Z} .}
Универсальная тригонометрическая подстановка
Тождества имеют смысл, только когда существуют обе части (то есть при α≠π+2πn{\displaystyle \alpha \neq \pi +2\pi n}).
| sinα=2tgα21+tg2α2{\displaystyle \sin \alpha ={\frac {2\,{\operatorname {tg} }\,{\frac {\alpha }{2}}}{1+\operatorname {tg} ^{2}{\frac {\alpha }{2}}}}} | cosα=1−tg2α21+tg2α2{\displaystyle \cos \alpha ={\frac {1-\operatorname {tg} ^{2}{\frac {\alpha }{2}}}{1+\operatorname {tg} ^{2}{\frac {\alpha }{2}}}}} |
| tgα=2tgα21−tg2α2{\displaystyle \operatorname {tg} \,\alpha ={\frac {2\,{\operatorname {tg} }\,{\frac {\alpha }{2}}}{1-\operatorname {tg} ^{2}{\frac {\alpha }{2}}}}} | ctgα=1−tg2α22tgα2{\displaystyle \operatorname {ctg} \,\alpha ={\frac {1-\operatorname {tg} ^{2}{\frac {\alpha }{2}}}{2\,{\operatorname {tg} }\,{\frac {\alpha }{2}}}}} |
| secα=1+tg2α21−tg2α2{\displaystyle \sec \alpha ={\frac {1+\operatorname {tg} ^{2}{\frac {\alpha }{2}}}{1-\operatorname {tg} ^{2}{\frac {\alpha }{2}}}}} | cosecα=1+tg2α22tgα2{\displaystyle \operatorname {cosec} \,\alpha ={\frac {1+\operatorname {tg} ^{2}{\frac {\alpha }{2}}}{2\,{\operatorname {tg} }\,{\frac {\alpha }{2}}}}} |
Вспомогательный аргумент (формулы сложения гармонических колебаний)
Сумма двух гармонических колебаний с одинаковой частотой будет вновь гармоническим колебанием. В частности,
- asinx+bcosx=a2+b2sin(x+φ){\displaystyle a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\sin(x+\varphi )}
где a,b∈R{\displaystyle a,b\in \mathbb {R} }, a{\displaystyle a} и b{\displaystyle b} не равны нулю одновременно, φ{\displaystyle \varphi } — это угол, называемый вспомогательным аргументом, который может быть найден из системы уравнений:
- {sinφ=ba2+b2,cosφ=aa2+b2.{\displaystyle \left\{{\begin{matrix}\sin \varphi ={\dfrac {b}{\sqrt {a^{2}+b^{2}}}},\\\cos \varphi ={\dfrac {a}{\sqrt {a^{2}+b^{2}}}}.\end{matrix}}\right.}
Примечание. Из вышеприведённой системы следует, что tgφ=ba{\displaystyle \mathrm {tg} \,\varphi \,=\,{\tfrac {b}{a}}}, однако нельзя всегда считать, что φ=arctgba{\displaystyle \varphi \,=\,\mathrm {arctg} \,{\tfrac {b}{a}}}. Нужно учитывать знаки a{\displaystyle a} и b{\displaystyle b} для определения, к какой четверти принадлежит угол φ{\displaystyle \varphi }.
Полезные тождества
В приведённых ниже формулах числа k{\displaystyle k} и n{\displaystyle n} целые.
sin(π4+x)=cos(π4−x).{\displaystyle \sin \left({\frac {\pi }{4}}+x\right)=\cos \left({\frac {\pi }{4}}-x\right).}
sin(π4−x)=cos(π4+x).{\displaystyle \sin \left({\frac {\pi }{4}}-x\right)=\cos \left({\frac {\pi }{4}}+x\right).}
1±sinx=2sin2(π4±x2).{\displaystyle 1\pm \sin x=2\sin ^{2}\left({\frac {\pi }{4}}\pm {\frac {x}{2}}\right).}
1+cosx=2cos2(x2).{\displaystyle 1+\cos x=2\cos ^{2}\left({\frac {x}{2}}\right).}
1−cosx=2sin2(x2).{\displaystyle 1-\cos x=2\sin ^{2}\left({\frac {x}{2}}\right).}
sin2x=11+ctg2x.{\displaystyle \sin ^{2}x={\frac {1}{1+\operatorname {ctg} ^{2}x}}.}
cos2x=11+tg2x.{\displaystyle \cos ^{2}x={\frac {1}{1+\operatorname {tg} ^{2}x}}.}
sin2x−sin2y=sin(x−y)⋅sin(x+y).{\displaystyle \sin ^{2}x-\sin ^{2}y=\sin(x-y)\cdot \sin(x+y).}
cos2x−cos2y=−sin(x−y)⋅sin(x+y).{\displaystyle \cos ^{2}x-\cos ^{2}y=-\sin(x-y)\cdot \sin(x+y).}
cos2x−sin2y=cos(x−y)⋅cos(x+y).{\displaystyle \cos ^{2}x-\sin ^{2}y=\cos(x-y)\cdot \cos(x+y).}
sin2x+sin2y=2cos(x−y)⋅sin(x+y).{\displaystyle \sin 2x+\sin 2y=2\cos(x-y)\cdot \sin(x+y).}
sin2x−sin2y=2sin(x−y)⋅cos(x+y).{\displaystyle \sin 2x-\sin 2y=2\sin(x-y)\cdot \cos(x+y).}
cos2x+cos2y=2cos(x−y)⋅cos(x+y).{\displaystyle \cos 2x+\cos 2y=2\cos(x-y)\cdot \cos(x+y).}
cos2x−cos2y=−2sin(x−y)⋅sin(x+y).{\displaystyle \cos 2x-\cos 2y=-2\sin(x-y)\cdot \sin(x+y).}
sin2x+cos2y=2sin(π4+x−y)⋅sin(π4+x+y).{\displaystyle \sin 2x+\cos 2y=2\sin \left({\frac {\pi }{4}}+x-y\right)\cdot \sin \left({\frac {\pi }{4}}+x+y\right).}
sin2x−cos2y=−2sin(π4−x−y)⋅sin(π4−x+y).{\displaystyle \sin 2x-\cos 2y=-2\sin \left({\frac {\pi }{4}}-x-y\right)\cdot \sin \left({\frac {\pi }{4}}-x+y\right).}
sin3x+cos3x=(sinx+cosx)(1−sinxcosx).{\displaystyle \sin ^{3}x+\cos ^{3}x=(\sin x+\cos x)(1-\sin x\cos x).}
sin4x+cos4x=1−2sin2xcos2x=1−12sin2(2x)=34+14cos(4x).{\displaystyle \sin ^{4}x+\cos ^{4}x=1-2\sin ^{2}x\,\cos ^{2}x=1-{\frac {1}{2}}\sin ^{2}(2x)={\frac {3}{4}}+{\frac {1}{4}}\cos(4x).}
sin6x+cos6x=1−3sin2xcos2x=1−3sin2x+3sin4x=1−34sin2(2x)=58+38cos(4x).{\displaystyle \sin ^{6}x+\cos ^{6}x=1-3\sin ^{2}x\,\cos ^{2}x=1-3\sin ^{2}x+3\sin ^{4}x=1-{\frac {3}{4}}\sin ^{2}(2x)={\frac {5}{8}}+{\frac {3}{8}}\cos(4x).}
1±tgx=2sin(π4±x)cosx.{\displaystyle 1\pm \operatorname {tg} x={\frac {{\sqrt {2}}\sin \left({\frac {\pi }{4}}\pm x\right)}{\cos x}}.}
1±ctgx=2sin(π4±x)sinx.{\displaystyle 1\pm \operatorname {ctg} x={\frac {{\sqrt {2}}\sin \left({\frac {\pi }{4}}\pm x\right)}{\sin x}}.}
tgx=sin2xcos2x+1=1−cos2xsin2x.{\displaystyle \operatorname {tg} x={\frac {\sin 2x}{\cos 2x+1}}={\frac {1-\cos 2x}{\sin 2x}}.}
ctg2x−tg2x=4cos2xsin22x.{\displaystyle \operatorname {ctg} ^{2}x-\operatorname {tg} ^{2}x={\frac {4\cos 2x}{\sin ^{2}2x}}.}
sin3x=4sinx⋅sin(π3+x)⋅sin(π3−x).{\displaystyle \sin 3x=4\sin x\cdot \sin \left({\frac {\pi }{3}}+x\right)\cdot \sin \left({\frac {\pi }{3}}-x\right).}
tg3x=tgx⋅tg(π3+x)⋅tg(π3−x).{\displaystyle \operatorname {tg} 3x=\operatorname {tg} x\cdot \operatorname {tg} \left({\frac {\pi }{3}}+x\right)\cdot \operatorname {tg} \left({\frac {\pi }{3}}-x\right).}
sin5x=16sinx⋅sin(π5+x)⋅sin(π5−x)⋅sin(2π5+x)⋅sin(2π5−x).{\displaystyle \sin 5x=16\sin x\cdot \sin \left({\frac {\pi }{5}}+x\right)\cdot \sin \left({\frac {\pi }{5}}
wikiredia.ru