Сложение и вычитание целых чисел с разными знаками
Сложение
При сложении двух целых чисел с одинаковым знаком складываются их абсолютные величины и перед суммой ставится их общий знак.
Примеры:
(+3) + (+7) = 10
(-3) + (-7) = -10
Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.
При сложении двух целых чисел с разными знаками нужно взять их абсолютные величины и из большей вычесть меньшую, в результате ставится знак того числа, у которого абсолютная величина больше.
Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:
Примеры:
(-4) + (+11) = 7, так как 11 — 4 = 7
(-5) + (+2) = -3, так как 5 — 2 = 3
Из данных примеров следует, что
Сумма двух противоположных чисел равна нулю:
(-7) + 7 = 0
Вычитание
Вычитание одного целого числа из другого можно заменить сложением, при этом уменьшаемое берётся со своим знаком, а вычитаемое с противоположным:
(+6) — (+5) = (+6) + (-5) = 1
(+6) — (-5) = (+6) + (+5) = 11
(-6) — (-5) = (-6) + (+5) = -1
(-6) — (+5) = (-6) + (-5) = -11
Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
При решении выражений, содержащих и сложение и вычитание, можно сначала заменить вычитание сложением, затем отдельно сложить положительные и отрицательные слагаемые, а потом найти сумму получившихся чисел.
Пример:12 — 18 + 41 — 9
Заменим вычитание на сложение:
12 + (-18) + 41 + (-9)
сгруппируем слагаемые по их знакам и сложим отдельно положительные и отрицательные числа:
(12 + 41) + ((-18) + (-9)) = 53 + (-27)
Теперь осталось только найти сумму двух получившихся результатов:
53 + (-27) = 26, значит 12 — 18 + 41 — 9 = 26
naobumium.info
Арифметические действия с числами разных знаков.
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА МОСКВЫ
СТРОИТЕЛЬНЫЙ ТЕХНИКУМ №30
Предметная (цикловая) комиссия
«Общеобразовательная подготовка»
Арифметические действия
с числами разных знаков
У Ч Е Б Н О Е П О С О Б И Е — П Р А К Т И К У М
Рекомендуется для использования в качестве учебного пособия по учебной дисциплине «Математика» для обучающихся первых курсов
Москва 2015
22.130я722
Х24
Арифметические действия с числами разных знаков:учеб. пособие/ сост. Т. Г. Хасянова . – М: Изд-во ГБПОУ Строительный техникум №30, 2015 . – 15 с.
Учебное пособие-практикум «Арифметические действия с числами разных знаков» составлено Хасяновой Т.Г., преподавателем математики.
Учебное пособие-практикум рассмотрено и одобрено на заседании предметной (цикловой) комиссии «Общеобразовательная подготовка», протокол № 8 от
28 мая 2015 г.Настоящее издание представляет собой часть базового курса дисциплины «Математика», который изучается обучающимися первых курсов техникума
ГБПОУ Строительный техникум №30, 2015
СОДЕРЖАНИЕ
Стр.
Введение …………………………………………………………………
3
1 Основные понятия, правила и действия с отрицательными и положительными числами…………………………………….………………
6
2 Практикум ……………………………………………………………….
8
3. Рефлексия ………………………………………………………………
13
4. Список использованных источников …………………………………
14
Введение
Современный уровень развития науки и техники требует глубоких и прочных математических знаний. Математические расчеты, основанные на использовании алгоритмов основных математических действий, являются составной частью трудовой деятельности рабочего, инженера и других. Одним из важнейших умений, которые обязано дать математическое образование, является сознательное, быстрое и безошибочное выполнение действий над числами. Однако, учение о действиях с отрицательными числами вызывает затруднения у учащихся. И не потому, что устанавливаемые правила действий сложны.
Напротив, они очень просты. Но неясными остаются два вопроса.
Зачем вводятся отрицательные числа?
Почему над ними совершаются действия по таким правилам, а не по иным? В частности, очень плохо понимается, почему при умножении и делении отрицательного числа на отрицательное результат есть положительное число.
Все эти вопросы возникают потому, что с отрицательными числами учащихся обычно знакомят до того, как они начали решать уравнения, и больше не возвращаются к правилам действий с отрицательными числами. Между тем лишь в связи с решением уравнений выясняется ответ на оба поставленных выше вопроса. Исторически отрицательные числа возникли именно в этой связи. Не будь уравнений, не было бы нужды и в отрицательных числах.
На два выше поставленных вопроса нужно ответить следующим образом:
Отрицательные числа вводятся затем, чтобы устранить ряд трудностей, возникающих прежде всего при решении уравнений.
Правила действий над ними вытекают из необходимости согласовать результаты, полученные с помощью отрицательных чисел, с теми результатами, которые могли быть получены и без них.
Опираясь на свой многолетний опыт, в учебном пособии-практикуме предельно просто изложена задача изучения этой темы: в примерах использованы только целые числа с целью сознательного усвоения именно законов и свойств арифметических действий с числами разных знаков, не отвлекая внимание на сложную работу с самими числами.
Особое внимание уделено необходимости применять теоретические знания (правила) в практике вычислений.
Первое время рекомендуется проговаривать выполняемое действие , так как это позволяет не торопиться и помогает добиться осознанных умений рациональной организации вычислений. Таким образом, у обучающихся быстрее развивается числовая наблюдательность, помогающая им проникнуть в особенности чисел и правил действий над ними. Сами приемы должны быть как можно однообразнее.
Полезно напомнить обучающимся, что цифры надо писать четко, располагать при соответствующих вычислениях по вертикали одну под другой, не пропускать математические знаки. Обучающимся следует напоминать о том, что скорость и точность вычисления зависят от того, как ведется оформление вычислительных работ на бумаге. Письменные вычисления являются основным видом вычислительной работы на уроках физики, химии и других учебных дисциплин.
В настоящем учебном пособии-практикуме изложены рекомендации, разработанные автором в помощь преподавателям математики, родителям и обучающимся с целью повышения вычислительной культуры и формирования сознательных и прочных навыков вычисления чисел с разными знаками.
1.Основные понятия, правила и действия с отрицательными и положительными числами
1.1.Абсолютная величина (модуль)
Абсолютная величина (модуль ). Для отрицательного числа – это положительное число, получаемое от перемены его знака с « – » на « + »; для положительного числа и нуля – само это число. Для обозначения абсолютной величины (модуля) числа используются две прямые черты, внутри которых записывается это число.
П р и м е р ы : | – 5 | = 5, | 7 | = 7, | 0 | = 0.
1.2. Сложение
при сложении двух чисел с одинаковыми знаками складываются их абсолютные величины и перед суммой ставится общий знак.
П р и м е р ы :
( + 6 ) + ( + 5 ) = 11 ;
( – 6 ) + ( – 5 ) = – 11 .
при сложении двух чисел с разными знаками их абсолютные величины вычитаются ( из большей меньшая ) и ставится знак числа с большей абсолютной величиной.
П р и м е р ы :
( – 6 ) + ( + 9 ) = 3 ;
( – 6 ) + ( + 3 ) = – 3 .
1.3. Вычитание
Можно заменить вычитание двух чисел сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с противоположным знаком.
П р и м е р ы :
( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3;
( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;
( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;
( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13;
1.4. Умножение
При умножении двух чисел их абсолютные величины умножаются, а произведение принимает знак « + » , если знаки сомножителей одинаковы, и знак « – » , если знаки сомножителей разные.
Полезна следующая схема (правила знаков при умножении):
+ · + = +
+ · – = –
– · + = –
– · – = +
При умножении нескольких чисел ( двух и более ) произведение имеет знак « + » , если число отрицательных сомножителей чётно, и знак « – » , если их число нечётно.
П р и м е р :
1.5. Деление
При делении двух чисел абсолютная величина делимого делится на абсолютную величину делителя, а частное принимает знак « + » , если знаки делимого и делителя одинаковы, и знак « – » , если знаки делимого и делителя разные.
Здесь действуют те же правила знаков, что и при умножении:
+ : + = +
+ : – = –
– : + = –
– : – = +
П р и м е р : ( – 12 ) : ( + 4 ) = – 3 .
2. Практикум
2.1. Сложение отрицательных чисел
2.2. Сложение чисел с разными знаками
2.3. Вычитание чисел с разными знаками
2.4. Умножение и деление чисел с разными знаками
2.5. Примеры на все действия
3. Рефлексия
Для закрепления данной темы, рекомендуется ответить на вопросы:
Что называют модулем числа?
Какие числа называют противоположными?
Сформулируйте правило сложения чисел с разными знаками.
Сформулируйте правило сложения отрицательных чисел.
Сформулируйте правило умножения отрицательных чисел.
Сформулируйте правило умножения чисел с разными знаками.
Чему равна сумма противоположных чисел?
Какое число противоположно нулю?
Какие числа называют взаимно обратными?
Как умножить смешанные числа?
Сформулируйте правило деления отрицательных чисел.
Сформулируйте правило деления чисел, имеющих разные знаки
Список используемых источников
1.http://www.bymath.net/ «Средняя математическая интернет школа»
2. «Справочник по элементарной математике», Москва, 1986г.
Учебное издание
Арифметические действия
с числами разных знаков
Ответственный за выпуск С.В. Михайлов
Верстка – А. Фадеев
______________________________
Подписано в печать 22.06.2015.
Формат 60х90/16. Бумага офсетная мелованная.
Печ. л. 1,8. Тираж 60 экз.
infourok.ru
Сложение и вычитание отрицательных и положительных чисел. Решение примеров.
Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:
- Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.
\((-2)+(-3)=-5\)
- Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:
\((-8)+4=4-8=-4\)
\(9+(-4)=9-4=5\)
Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:
\(-9+9=0\) \(7,1+(-7,1)=0\)
- При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.
\((-7)-(-6)=(-7)+6=(-1)\)
- Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.
\(7-9=-2\) так как \(9>7\)
- Также не стоит забывать минус на минус дает плюс:
\(7-(-9)=7+9=16\)
Задача 1. Вычислите:
- \(4+(-5)\)
- \(-36+15\)
- \((-17)+(-45)\)
- \(-9+(-1)\)
Решение:
- \(4+(-5)=4-5=-1\)
- \(-36+15=-21\)
- \((-17)+(-45)\) \(=-17-45=-62\)
- \(-9+(-1)=-9-1=-10\)
Задача 2. Вычислите:
- \(3-(-6)\)
- \(-16-35\)
- \(-27-(-5)\)
- \(-94-(-61)\)
Решение:
- \(3-(-6)=3+6=9\)
- \(-16-35=-51\)
- \(-27-(-5)=-27+5=-22\)
- \(-94-(-61)=-94+61=-33\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Сложение и вычитание чисел с разными знаками
На действиях с положительными и отрицательными числами основан практически весь курс математики. Ведь как только мы приступаем к изучению координатной прямой, числа со знаками «плюс» и «минус» начинают встречаться нам повсеместно, в каждой новой теме. Нет ничего проще, чем сложить между собой обычные положительные числа, нетрудно и вычесть одно из другого. Даже арифметические действия с двумя отрицательными числами редко становятся проблемой.
Однако многие путаются в сложении и вычитании чисел с разными знаками. Напомним правила, по которым происходят эти действия.
Сложение чисел с разными знаками
Если для решения задачи нам требуется прибавить к некоторому числу «а» отрицательное число «-b», то действовать нужно следующим образом.
- Возьмем модули обоих чисел — |a| и |b| — и сравним эти абсолютные значения между собой.
- Отметим, какой из модулей больше, а какой меньше, и вычтем из большего значения меньшее.
- Поставим перед получившимся числом знак того числа, модуль которого больше.
Это и будет ответом. Можно выразиться проще: если в выражении a + (-b) модуль числа «b» больше, чем модуль «а», то мы отнимаем «а» из «b» и ставим «минус» перед результатом. Если больше модуль «а», то «b» вычитается из «а» — а решение получается со знаком «плюс».
Бывает и так, что модули оказываются равны. Если так, то на этом месте можно остановиться — речь идет о противоположных числах, и их сумма всегда будет равна нулю.
Вычитание чисел с разными знаками
Со сложением мы разобрались, теперь рассмотрим правило для вычитания. Оно тоже довольно простое — и кроме того, полностью повторяет аналогичное правило для вычитания двух отрицательных чисел.
Для того, чтобы вычесть из некоего числа «а» — произвольного, то есть с любым знаком — отрицательное число «с», нужно прибавить к нашему произвольному числу «а» число, противоположное «с». Например:
- Если «а» — положительное число, а «с» — отрицательное, и из «а» нужно вычесть «с», то записываем так: а – (-с) = а + с.
- Если «а» — отрицательное число, а «с» — положительное, и из «а» нужно вычесть «с», то записываем следующим образом: (- а )– с = — а+ (-с).
Таким образом, при вычитании чисел с разными знаками в итоге мы возвращаемся к правилам сложения, а при сложении чисел с разными знаками — к правилам вычитания. Запоминание данных правил позволяет решать задачи быстро и без труда.
Примеры сложения и вычитания чисел с разными знаками

Похожие статьи
infoogle.ru
Правила знаков
Минус и плюс – это признаки отрицательных и положительных чисел в математике. Они по-разному взаимодействую с собой, поэтому при выполнении каких-либо действий с числами, например, деление, умножение, вычитание, сложение и т.д., необходимо учитывать правила знаков. Без этих правил вы никогда не сможете решить даже самую простую алгебраическую или геометрическую задачу. Без знания этих правил, вы не сможете изучить не только математику, но и физику, химию, биологию, и даже географию.
Рассмотрим подробней основные правила знаков.
Деление.
Если мы делим «плюс» на «минус», то получаем всегда «минус». Если мы делим «минус» на «плюс», то получаем всегда также «минус». Если мы делим «плюс» на «плюс», то получаем «плюс». Если же мы делим «минус» на «минус», то получим, как ни странно, также «плюс».
Умножение.
Если мы умножаем «минус» на «плюс», то получаем всегда «минус». Если мы умножаем «плюс» на «минус», то получаем всегда также «минус». Если мы умножаем «плюс» на «плюс», то получаем положительно число, то есть «плюс». Тоже самое касается и двух отрицательных чисел. Если мы умножаем «минус» на «минус», то получим «плюс».
Вычитание и сложение.
Они базируются уже на других принципах. Если отрицательное число будет больше по модулю, чем наше положительное, то результат, конечно же, будет отрицательный. Наверняка, вам интересно, что же такое модуль и зачем он тут вообще. Все очень просто. Модуль – это значение числа, но без знака. Например -7 и 3. По модулю -7 будет просто 7 , а 3 так и останется 3. В итоге мы видим, что 7 больше, то есть выходит, что наше отрицательное число больше. Вот и выйдет -7+3 = -4. Можно сделать еще проще. Просто на первое место ставить положительное число, и выйдет 3-7 = -4, возможно кому-то так более понятно. Вычитание действуют полностью по такому же принципу.
Правила при умножении (делении) чисел | |||||||||||||||
| |||||||||||||||
mateshka.ru
Вычитание отрицательных чисел — Kid-mama
Сейчас мы рассмотрим на примерах вычитание отрицательных чисел, и вы убедитесь, что это очень легко. Нужно просто помнить правило : два минуса, стоящие рядом, дают плюс.
Пример 1. Вычитание отрицательного числа из положительного числа
56 – (–34) = 56 + 34 = 90
Как видим, чтобы вычесть из положительного числа отрицательное число, нужно просто сложить их модули.
Пример 2. Вычитание отрицательного числа из отрицательного числа
– 60 – (– 25) = – 60 + 25 = – 35
– 15 – (– 30) = – 15 + 30 = 15
Таким образом, при вычитании отрицательного числа из отрицательного мы действуем по правилу сложения чисел с разными знаками, и у нас может получиться как положительное, так и отрицательное число.
Существует единое правило, определяющее вычитание любых чисел: как отрицательных, так и положительных, и звучит оно так:
| Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому. a — b = a + (-b) |

Для того, чтобы избавиться от лишних скобок при вычитании отрицательных чисел, мы можем воспользоваться правилом знаков. Это правило гласит:
| Если перед скобками стоит знак «+» , то при раскрытии скобок знак числа не изменяется. Если перед скобками стоит знак «-», то при раскрытии скобок знак числа меняется на противоположный. |
Например:
| 5 + (-7) = 5-7 | 9-(-5) = 9 + 5 | |
| -10 + (-6) = -10-6 | -4- (-6) = -4 + 6 |
Правило знаков действует также, если в скобках стоит несколько чисел. При этом,если перед скобками стоит минус, изменяются знаки у всех чисел:
Примеры:
a+(b-c-d)=a+b-c-d
a-(b-c-d)=a-b+c+d
a+(-b+c-d)=a-b+c-d
a-(-b+c-d)=a+b-c+d
Это правило обычно запоминают так:
| Минус на минус дает плюс, Плюс на минус дает минус |
А теперь пройдите тест и проверьте себя!
Сложение и вычитание отрицательных чисел
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
Выполните сложение или вычитание и введите ответ. Минус вводите при помощи дефиса (кнопка между «0» и «=» на клавиатуре). Ответ вводите без пробела (например: -3,4)
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
kid-mama.ru
Вычитание чисел с разными знаками
В курсе арифметики установлено, что вычитание есть действие, обратное сложению, при помощи которого по данной сумме и по одному слагаемому находят другое слагаемое.
Пользуясь этим определением, мы должны разобрать, как надо выполнять вычитание относительных чисел.
Пусть надо из (+8) вычесть (–3), т. е. пусть надо
Первое данное число выражает данную сумму, второе – данное слагаемое, а над найти другое слагаемое (для него оставлено место после знака равенства), т. е. надо решить вопрос: какое число надо сложить с (–3), чтобы в сумме получилось (+8)? Этот вопрос запишем в такой форме:
(?) + (–3) = +8.
Но сразу этот вопрос решить трудно, а поэтому сначала решим более простой, вспомогательный вопрос: какое число надо сложить с (–3), чтобы в сумме получился нуль ?, т. е.
(?) + (–3) = 0.
На этот вопрос ответ ясен: надо взять для неизвестного слагаемого число, имеющее ту же абсолютную величину, как и данное слагаемое, но обратный знак, – в данном случае надо для неизвестного слагаемого взять число +3. Теперь перейдем к решению главного вопроса: мы взяли для неизвестного слагаемого число + 3 и в сумме получился нуль, но нам надо получить в сумме число +8, поэтому надо чтобы и в другое слагаемое вошло это же число +8. Следовательно, неизвестное слагаемое должно состоять: 1) из +3, чтобы в сумме получился нуль и 2) из +8, чтобы эту сумму «нуль» довести до требуемой +8. Поэтому на месте неизвестного слагаемого пишем + 3 + 8:
(+ 8) – (– 3) = + 3 + 8 = + 11.
Последнее (= + 11) написано на том основании, что числа + 3 и + 8 надо соединить в одно или сложить.
Вот еще примеры:
(– 7) – (+ 5) = – 5 – 7 = – 12.
Искомое слагаемое должно состоять: 1) из –5, чтобы в сумме получился нуль и 2) из –7, чтобы дополнить этот нуль до требуемой суммы, до –7. Сложив числа –5 и –7, получим –12.
(– 3) – (– 8) = + 8 – 3 = + 5.
Искомое слагаемое должно состоять: 1) из +8, чтобы в сумме получился нуль и 2) из –3, чтобы дополнить этот нуль до требуемой суммы, до –3. Сложив числа +8 и –3, получим +5.
(+7) – (+9) = –9 + 7 = –2.
Искомое слагаемое должно состоять: 1) из –9, чтобы в сумме получился нуль и 2) +7, чтобы дополнить этот нуль до требуемой суммы, до +7; сложив числа –9 и +7, получим –2.
Из этих примеров видим, что вычитание в алгебре состоит лишь в умении раскрывать скобки: надо второе число (данное слагаемое или вычитаемое) написать с обратным знаком, а первое число (данную сумму или уменьшаемое) написать с тем же знаком. После того, как это сделано, т. е., когда скобки раскрыты, дело сводится к сложению, так как написаны числа рядом с их знаками, напр., в последнем примере: – 9 + 7.
Так как сумма не изменяется от перестановки слагаемых, то можно числа, полученные в разобранных примерах после раскрытия скобок, переставить, чтобы порядок был согласен с порядком данных чисел:
(+ 8) – (– 3) = + 8 + 3; (– 7) – (+ 5) = – 7 – 5;
– 3 – (– 8) = – 3 + 8; (+ 7) – (+ 9) = + 7 – 9.
Итак,
чтобы раскрыть скобки при вычитании, надо первое число (уменьшаемое) написать без изменения и приписать к нему второе число (вычитаемое) с обратным знаком.
Заметим еще, что при обозначении вычитания первое число пишется часто без скобок, а если оно положительное, то, как уже известно, знак + можно впереди не писать.
Например,
– 3 – (– 5) = – 3 + 5 = + 2; 1 – (– 6) = 1 + 6 = 7;
3 – (+ 3) = 3 – 3 = 0.
14. Примеры на сложение и вычитание. Пусть требуется вычислить:
1 – {3 + [5 – (3 – 5 – 6)]}.
Мы станем руководствоваться следующим порядком: если внутри какой-либо пары скобок нет других скобок и нет действия, то эти скобки можно раскрыть; если же внутри этих скобок есть действие (сложение), то надо сначала его выполнить. В нашем примере такой порядок: сначала выполним сложение чисел, написанных внутри маленьких скобок, потом надо эти скобки раскрыт, выполнить сложение внутри квадратных скобок, раскрыть квадратные скобки, выполнить сложение внутри витых скобок, раскрыть эти скобки и, наконец, сложить полученные числа:
1 – {3 + [5 – (3 – 5 – 6)]} = 1 – {3 + [5 – (– 8)]} = 1 – {3 + [5 + 8]} =
= 1 – {3 + [+13]} = 1 – {3 + 13} = 1 – {+ 16} = 1 – 16 = – 15.
Конечно, при навыке можно сразу выполнять несколько действий и, следовательно, укоротить вычисление.
Еще пример:
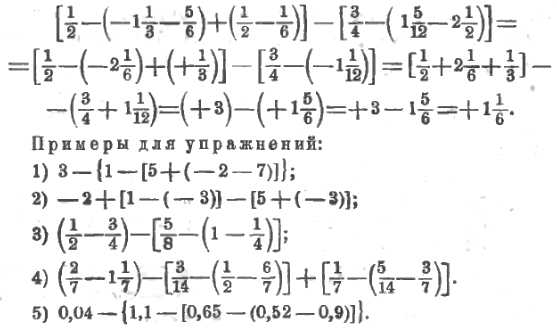
Пусть еще требуется вычислить выражение:
a – {(b – c) – [d + (e + f)]} при a = – 3; b = 1; c = 4; d = – 5; e = – 7; f = 2.
Выполним вычисления по действиям:
1) b – c = + 1 – (+ 4) = 1 – 4 = – 3;
2) e + f = (– 7) + (+ 2) = – 7 + 2 = – 5;
3) d + (– 5) = – 5 + (– 5) = – 5 – 5 = – 10;
4) (– 3) – (– 10) = – 3 + 10 = + 7;
5) – 3 – (+ 7) = – 3 – 7 = – 10.
Примеры для упражнений:
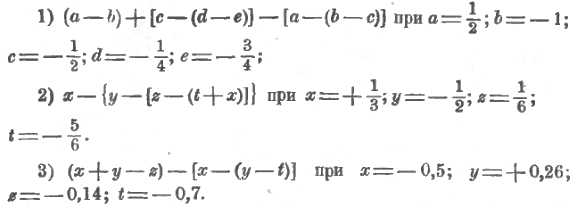
Если взять число нуль и прибавлять к нему по +1, то получим ряд постепенно увеличивающихся целых чисел:
0, +1, +2, +3, +4, +5, …..
Этот ряд совпадает (см. конец п. 10) с натуральным рядом чисел, т. е. с
0, 1, 2, 3, 4, 5 …..
Если мы, взяв число нуль, вычтем из него (+1), затем еще раз вычтем (+1) и т. д., то, согласно с тем, как мы это понимали в арифметике по отношению к натуральному ряду чисел, мы теперь признаем, что и здесь станем получать все уменьшающиеся целые числа:
1) 0 – (+ 1) = – 1; 2) (– 1) – (+ 1) = – 1 – 1 = – 2;
3) (– 2) – (+ 1) = – 3 и т. д.
Получим, идя от нуля налево, ряд уменьшающихся относительных чисел:
….., – 5, – 4, – 3, – 2, – 1, 0.
Соединяя этот ряд с предыдущим, получим полный ряд относительных чисел:
….., – 6, – 5, – 4, – 3, – 2, – 1, 0, +1, +2, +3, +4, +5, +6 …..
Этот ряд и вправо и влево идет без конца.
Всякое число в этом ряду больше другого, которое стоит левее и меньше любого, стоящего правее его. Так +1 > –3; 0 > –6; –5 < 0; –3 < +2 и т. д.
В промежутках между целыми числами этого ряда можно вставить бесконечно много дробных чисел.
maths-public.ru
