Дифференцирование под знаком интеграла
В этой главе мы познакомимся с необычным методом вычисления интегралов. Его упоминает в своей автобиографии Ричард Фейнман. Хотя применять этот метод для взятия более-менее простых интегралов не стоит (это как палить из пушки по воробьям), он может помочь при вычислении сложных (или вообще не берущихся другими методами) интегралов. Особенно, если подынтегральная функция содержит экспоненту, логарифм, арккосинус и прочие «неудобные» функции.
Фейнман рассказывает, что данный метод практически не упоминался в MIT, когда он учился там (и вообще, университеты мало акцентировали внимание на нем). Сам Фейнман прочел о нем в какой-то книге. Тут стоит отметить, что он настолько наловчился пользоваться этим методом, что зачастую и не прибегал к другим, несмотря на то, что это требует определенного мастерства и опыта.
Теория
Дифференцирование под знаком интеграла применимо только для вычисления определенных и несобственных интегралов. Метод опирается на две следующие теоремы, которые здесь приводятся без доказательства.
Теорема (*). Пусть функция ( , ) определена и непрерывна на прямоугольнике [ , ]×[ , ], на котором также определена и непрерывна первая частная производная ′( , ). Тогда справедливо равенство
|
| ′( , ) . |
∫ | ( , ) = ∫ | |
|
|
|
Для случая несобственных интегралов нужно ввести вспомогательное определение. Пусть( , ) непрерывна по на [0, +∞). Тогда если
+∞
∫
( ) R[0, +∞), ( ) →: [ , ], > 0 | ( , )| 6 ( ),
0
+∞
∫
то интеграл ( , ) равномерно сходится на [ , ], а функция ( ) называется домини-
0
рующей на [ , ].
Теорема (**). Пусть функция ( , ) | вместе с ее частной производной ′( , ) определены | ||||||||
|
|
|
|
|
|
| +∞ |
|
|
|
|
|
|
|
|
|
|
| |
и непрерывны на [ , ] | [0, + |
| ). Тогда если | ∫0 | ′ | ( , ) равномерно сходится на [ , ], то | |||
справедливо равенство× |
| ∞ |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
| ∫ | ( , ) = ∫ | ′( , ) . | ||||
|
|
|
|
|
|
|
|
|
|
studfiles.net
Собственные интегралы, зависящие от параметра, и их свойства — ПриМат
$\Box$ Рассмотрим производную заданной функции по определению
$${ J }^{ \prime }\left( y \right) =\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }.$$
Тогда для доказательства теоремы нам необходимо убедиться в равенстве
$$\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } } =\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \Rightarrow$$ $$\Rightarrow \lim _{ \Delta y\rightarrow 0 }{ \left( \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right) } =0\quad \left( 1 \right).$$
Для дальнейшей работы проанализируем отношение
$${ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }=\intop _{ a }^{ b }{ \frac { f\left( x,y+\Delta y \right) -f\left( x,y \right) }{ \Delta y } dx }.$$
Так как функция $f$ и ее производная – дифференцируемые на заданном прямоугольнике функции, то мы имеем право воспользоваться теоремой Лагранжа о среднем значении*
$${ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } }=\intop _{ a }^{ b }{ \frac { f\left( x,y+\Delta y \right) -f\left( x,y \right) }{ \Delta y } dx }=$$ $$ =\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) dx },\quad { \theta }_{ x }\in \left( 0,1 \right).$$
Вернемся к отношению находящемуся под знаком предела формулы $(1)$:
$$\frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } =$$ $$ =\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) dx }-\intop_{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx }=$$ $$ =\intop_{ a }^{ b }{ \left( \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x }\Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right) dx }.$$
Аналогично доказательству предыдущего свойства, так как $\frac { \partial }{ \partial y } f\left( x,y \right)$ непрерывна на заданном прямоугольнике, то по теореме Кантора она равномерно непрерывна на нем же. Тогда запишем условие равномерной непрерывности, что поможет оценить нам выражение под знаком предела формулы $(1)$:
$$\forall \varepsilon > 0 \quad \exists { \delta }_{ \varepsilon }>0:\forall x\in \left[ a,b \right] ; \forall y,y+\Delta y\in \left[ c,d \right]:\left| y+\Delta y-y \right|=$$ $$=\left| \Delta y \right| <{ \delta }_{ \varepsilon }\Rightarrow \left| \frac { \partial }{ \partial y } f\left( x,y+\Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| <\frac { \varepsilon }{ b-a }.$$
Принимая во внимание тот факт, что ${ \theta }_{ x } \in \left( 0,1 \right)$, автоматически при тех же условиях будет выполняться неравенство
$$\left| \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| <\frac { \varepsilon }{ b-a }.$$
Тогда можем записать
$$\left| \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right| =$$ $$=\left| \intop _{ a }^{ b }{ \left( \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right) dx } \right| \le$$ $$\le \intop _{ a }^{ b }{ \left| \frac { \partial }{ \partial y } f\left( x,y+{ \theta }_{ x } \Delta y \right) -\frac { \partial }{ \partial y } f\left( x,y \right) \right| dx } \le \left( b-a \right) \frac { \varepsilon }{ b-a } =\varepsilon.$$
Отсюда следуя определению предела функции по Коши
$$\lim _{ \Delta y\rightarrow 0 }{ \left( \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } -\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } \right) } =0\Rightarrow$$ $$\Rightarrow\lim _{ \Delta y\rightarrow 0 }{ \frac { J\left( y+\Delta y \right) -J\left( y \right) }{ \Delta y } } =\intop _{ a }^{ b }{ \frac { \partial }{ \partial y } f\left( x,y \right) dx } ={ J }^{ \prime }\left( y \right). \blacksquare$$
[свернуть]
ib.mazurok.com
ИНТЕГРАЛЫ С ПАРАМЕТРОМ | sibac.info
Корнеев Антон Александрович
студент 3 курса, факультет точных наук и инновационных технологий МГГУ им. Шолохова, г. Москва
E—mail: predsedatel_2012@mail.ru
Дорошкевич Ольга Александровна
канд. физ.-мат. наук, доцент МГГУ им. Шолохова, г. Москва
Вводные замечания
Пусть — функция двух переменных, заданная в некоторой замкнутой области , где .
Теорема 9. Если для функции существует двойной предел равный константе
и повторный предел равный константе
то допустим предельный переход
Данная теорема, является следствием теоремы [3, с. 361], справедливость которой доказана лишь для конечных и . В этой теореме из равенства двойного и повторного предела константам следует, что . В дальнейшем мы убедимся, что теорема 9 неверна для бесконечных и .
Предельный переход и дифференцирование под знаком интеграла
Следующие теоремы решают вопросы, связанные с допустимостью предельного перехода и дифференцирования в точке под знаком собственных и несобственных интегралов второго рода. Пусть — функция двух переменных, заданная в некоторой области , где .
Теорема 10. Если функция интегрируема по на конечном промежутке и для её первообразной существуют повторный и двойной пределы при и , где , равные константам
то имеет место формула
Справедливость этой теоремы следует из справедливости теоремы 9.
1)Проверим допустимость предельного перехода под знаком следующего интеграла
В силу того, что условия теоремы 10 не выполнены, а именно
предельный переход под знаком интеграла при недопустим.
Теорема 11. Если функция интегрируема по на конечном промежутке и имеет частную производную по , и для производной её первообразной существуют повторный и двойной пределы при и , где , равные константам
то имеет место формула
Справедливость этой теоремы следует из справедливости теоремы 10.
2)Проверим допустимость дифференцирования под знаком интеграла при
В силу того, что условия теоремы 11 не выполнены, а именно
Предел
не существует, дифференцирование под знаком интеграла при недопустимо.
Теорема 12. Если функция интегрируема по на конечном промежутке и для её первообразной существуют простой и двойной пределы при и , где , равные нулю
то имеет место формула
Справедливость этой теоремы следует из справедливости теоремы 2 [1].
3)Проверим допустимость предельного перехода при под знаком следующего интеграла
В силу того, что условия теоремы 12 выполнены, а именно
предельный переход под знаком интеграла при допустим.
4)Проверим допустимость предельного перехода при под знаком следующего интеграла
В силу того, что условия теоремы 12 не выполнены, а именно
предельный переход под знаком интеграла при недопустим.
Теорема 13. Если функция интегрируема по
то имеет место формула
Справедливость этой теоремы следует из справедливости теоремы 12.
Теорема 14. Если функция интегрируема по на бесконечном промежутке и для её первообразной существуют простой и двойной пределы при и , где , равные константам
и первообразная как предельная функция поточечно равномерно непрерывна в точке
то имеет место формула
Справедливость этой теоремы следует из справедливости теоремы 2 [1] и теоремы 9.
5)Проверим допустимость предельного перехода под знаком интеграла при
В силу того, что условия теоремы 14 не выполнены, а именно
Предел
не существует, предельный переход под знаком интеграла при не допустим.
Теорема 15. Если функция интегрируема по на бесконечном промежутке и имеет частную производную по и для производной её первообразной существуют простой и двойной пределы при и , где , равные константам
и производная первообразной как предельная функция равномерно непрерывна при
то имеет место формула
Справедливость этой теоремы следует из справедливости теоремы 14.
Теорема 16. Если функция интегрируема по на бесконечном промежутке и её первообразная как предельная функция поточечно равномерно непрерывна на этом промежутке
то имеет место формула
Справедливость этой теоремы следует из справедливости теоремы 2 [1].
6)Проверим допустимость предельного перехода под знаком интеграла при
В силу того, что условия теоремы 16 не выполнены
предельный переход под знаком интеграла при недопустим.
Теорема 17. Если функция интегрируема по на промежутке и имеет частную производную по и производная её первообразной как предельная функция поточечно равномерно непрерывна на этом промежутке
то имеет место формула
Справедливость этой теоремы следует из справедливости теоремы 16.
Список литературы:
1.Корнеев А.А., Дорошкевич О.А. Теория предельных функций // Вопросы естественных и математических наук: мат-лы междунар. науч.-практ. конф.
2.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления: учебник: в 3 т. Т. 1. — 9-е изд., стер. — СПб.: Лань, 2009. — 608 с.: ил. — (Учебники для вузов. Специальная книга).
sibac.info
§3 Интегрирование по параметру под знаком интеграла
Теорема. Пусть
функция 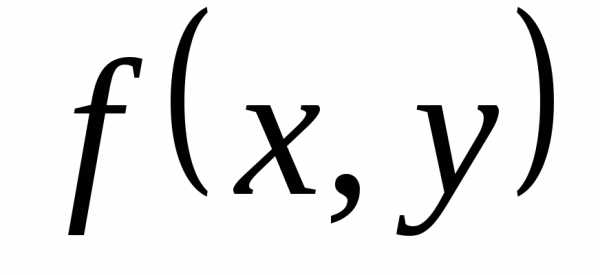 непрерывна в области
непрерывна в области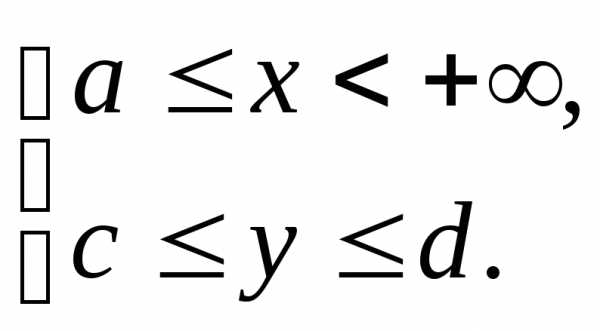
 сходится равномерно
относительно у на
сходится равномерно
относительно у на  .
.
Тогда справедливо равенство:
, (1)
причем несобственный интеграл, стоящий в правой части равенства (1) сходится.
Доказательство.
Возьмем произвольное e
> 0. По условию теоремы 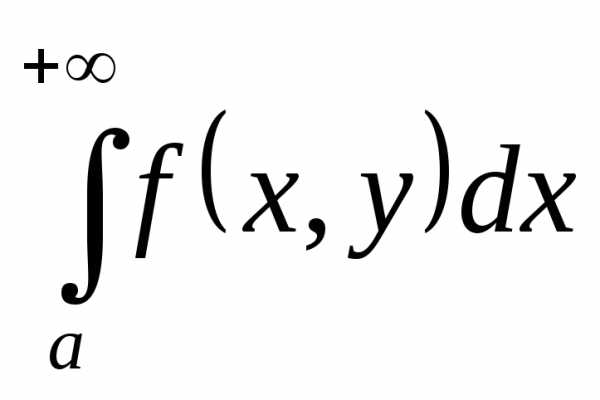
 , поэтому для выбранного e
> 0 найдется число М>0, зависящее только
от e,
такое, что как только возьмем число А>M,
то сразу для всех
, поэтому для выбранного e
> 0 найдется число М>0, зависящее только
от e,
такое, что как только возьмем число А>M,
то сразу для всех 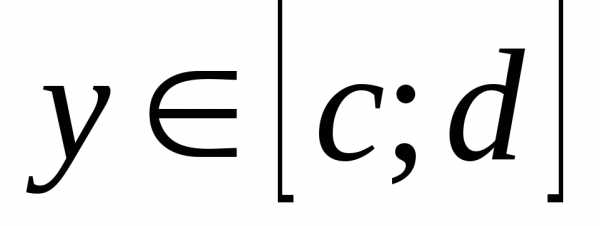 будет выполняться неравенство
будет выполняться неравенство 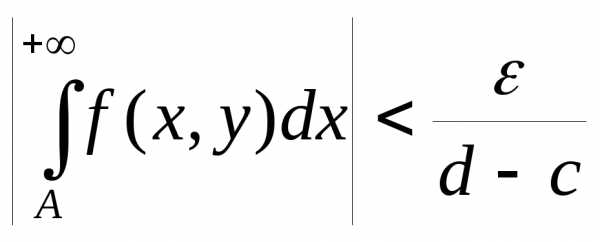 .
.
Зафиксируем
некоторое число А, удовлетворяющее
неравенству А>M.
Вводя как и раньше обозначения 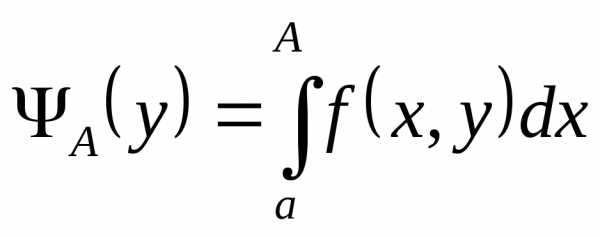 ,
сразу для всех
,
сразу для всех 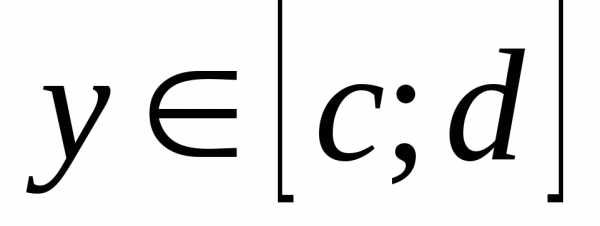 неравенство можно записать в виде
неравенство можно записать в виде
Так как функции 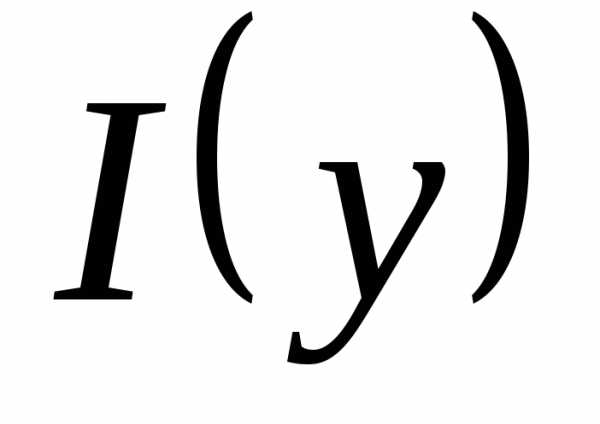
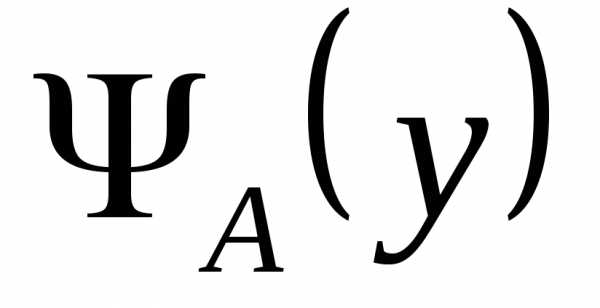 непрерывны на отрезке
непрерывны на отрезке 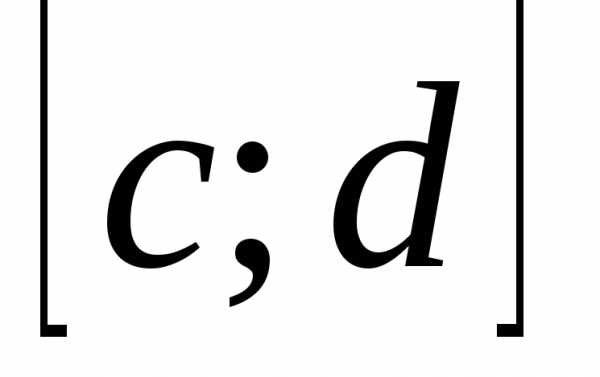 , то они и интегрируемы на нем. В силу
свойств интегралов
, то они и интегрируемы на нем. В силу
свойств интеграловтогда
Мы получили, для любого e > 0 существует число М, что при любом А>M, выполняется неравенство
.
Это означает что
, (2)
но 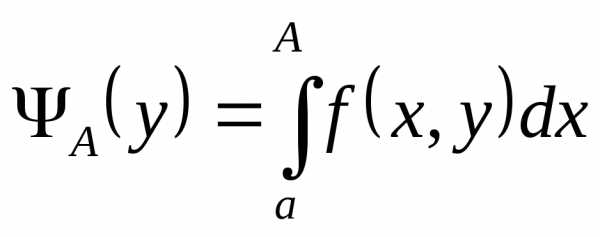 — собственный интеграл, зависящий от
параметрау. По теореме
об интегрировании по параметру
собственного интеграла можем записать
— собственный интеграл, зависящий от
параметрау. По теореме
об интегрировании по параметру
собственного интеграла можем записать
.
Тогда равенство (2) можно записать в виде
Ранее мы доказали существование предела, следовательно можно его записать иначе
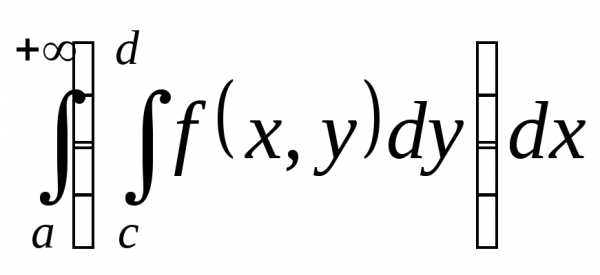
Следовательно доказана сходимость интеграла, из правой части равенства (1) и справедливость самого равенства.
Теорема доказана.
§ 4 Дифференцирование по параметру под знаком интеграла
Теорема.
Пусть функция
 непрерывна в области
непрерывна в области и имеет в ней непрерывную частную
производную
и имеет в ней непрерывную частную
производную ;
; сходится при
каждом
сходится при
каждом  ;
; сходится равномерно
относительно у на
сходится равномерно
относительно у на  ;
;
Тогда:
 существует при
каждом
существует при
каждом  ;
;, т.е. ;
 непрерывна на
непрерывна на  .
.
Доказательство:
Так как 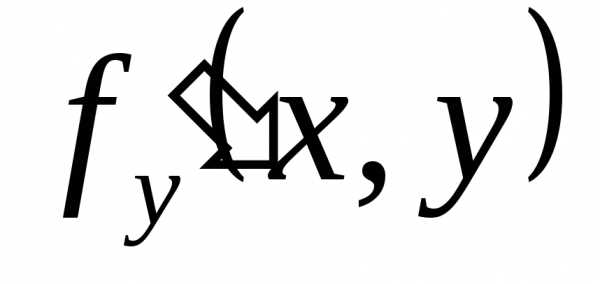 непрерывна в области
непрерывна в области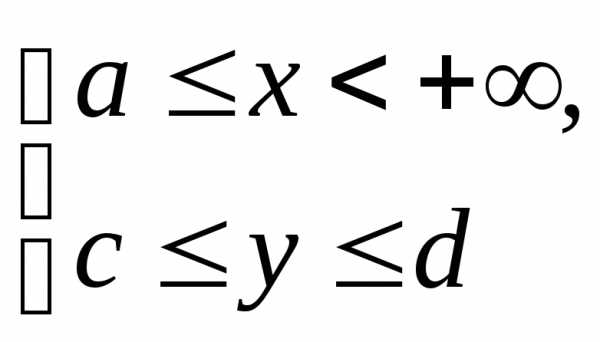 и
и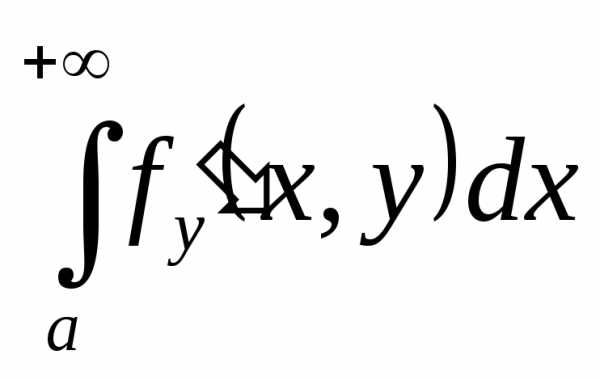 сходится равномерно относительноу на
сходится равномерно относительноу на 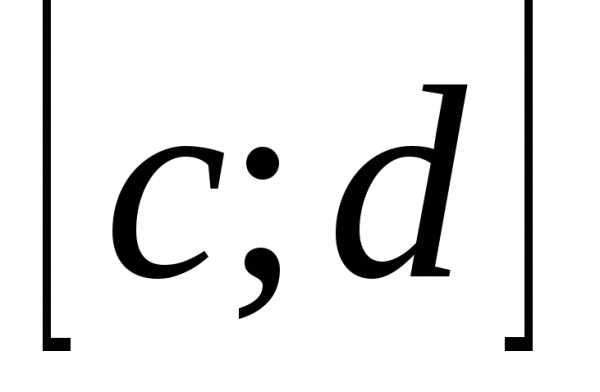 то по теореме из §2 и
то по теореме из §2 и 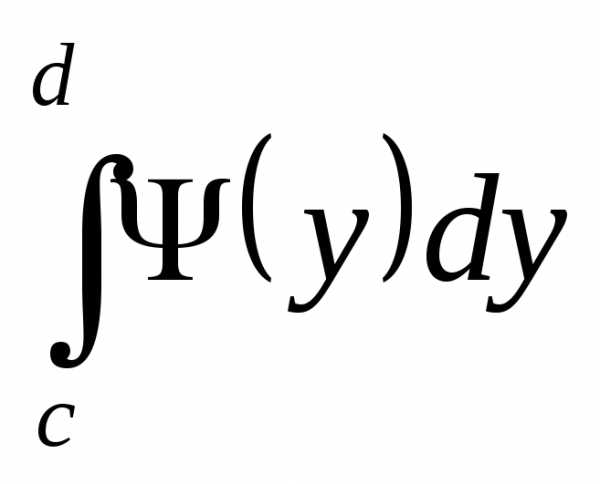 существует. В частности существует
интеграл
существует. В частности существует
интеграл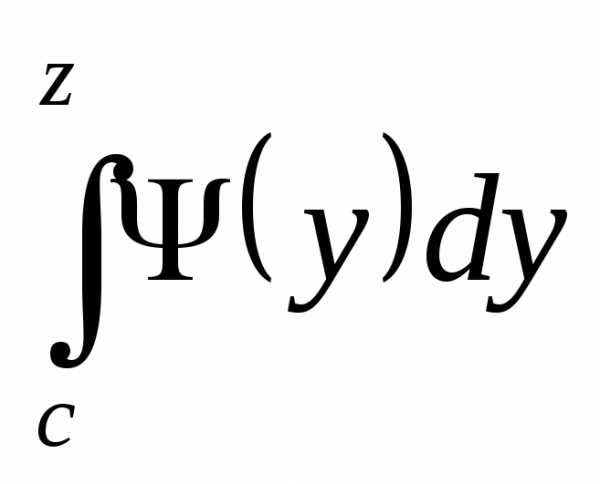 для любого
для любого ,
удовлетворяющего условиюПо теореме из §3 имеем
,
удовлетворяющего условиюПо теореме из §3 имеем
.
Но . Поэтому
,
следовательно
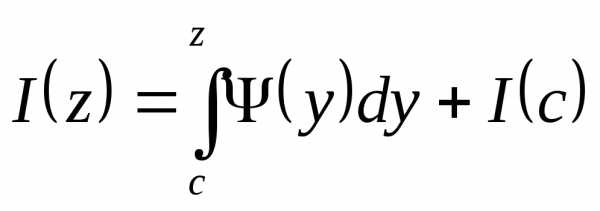
В правой части последнего равенства стоит интеграл с переменным верхним пределом от непрерывной функции, тогда по теореме Барроу
.
Последнее равенство
справедливо для любого 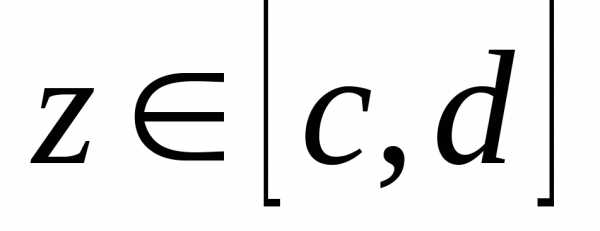 .
Таким образом доказано
.
Таким образом доказано
 существует при
каждом
существует при
каждом  ;
;,
 ;
;
3.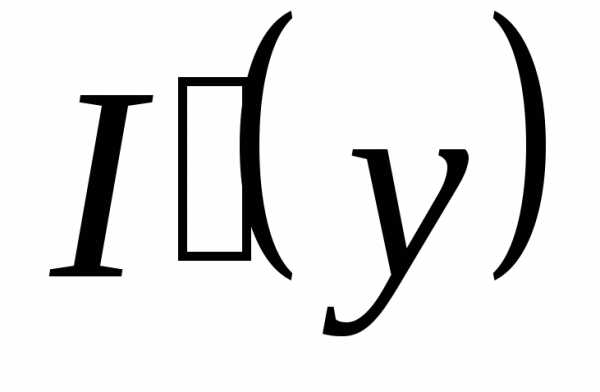 непрерывна на
непрерывна на 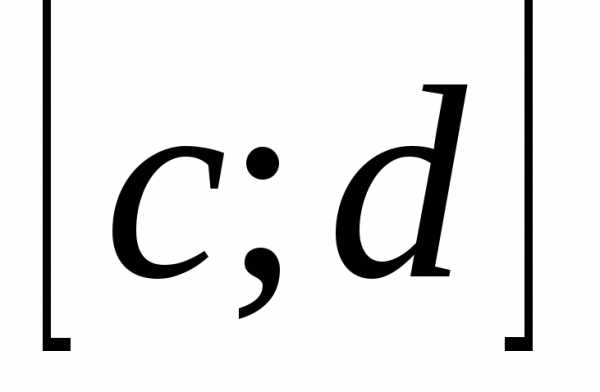 т.к.
т.к. 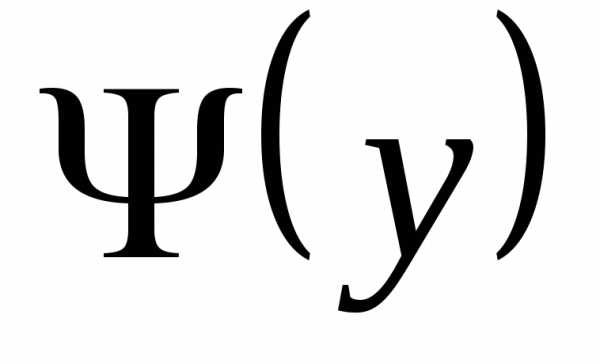 непрерывна на
непрерывна на 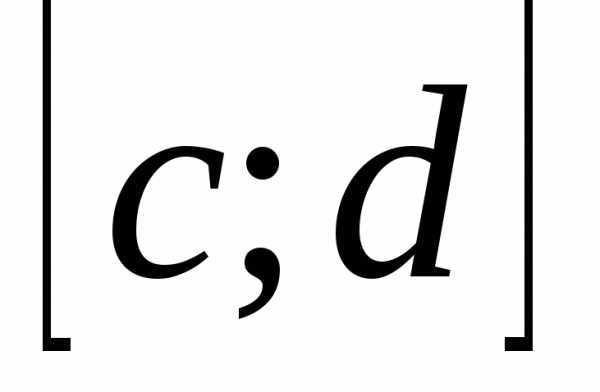 .
.
§5 Признак равномерной сходимости несобственных интегралов
Теорема.
Пусть функция
 непрерывна в области
непрерывна в области
Функция
 определена и непрерывна на
определена и непрерывна на ;
;при всех значениях
 и
.
и
.
Тогда, если
несобственный интеграл 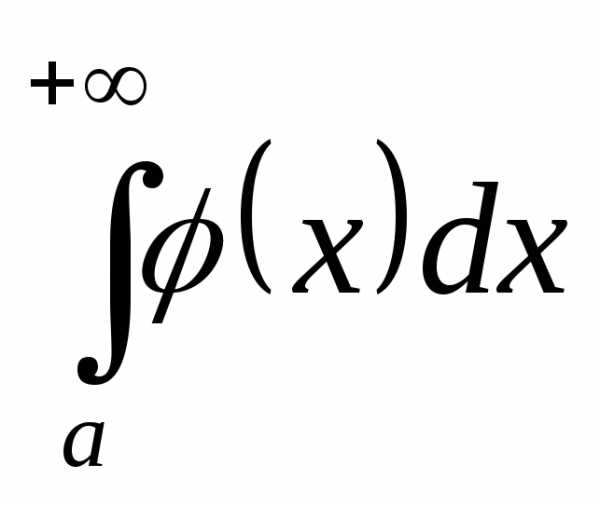 сходится, то несобственный интеграл
сходится, то несобственный интеграл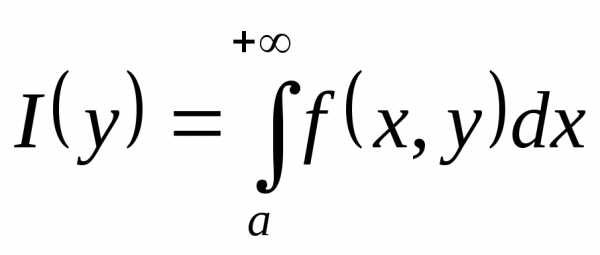 сходится равномерно относительноу на
сходится равномерно относительноу на 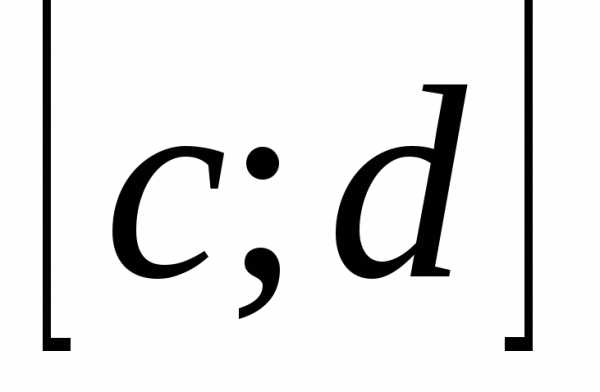 .
.
Утверждение примем без доказательства.
Замечание. Для несобственных интегралов второго рода, зависящих от параметра имеют место теоремы, аналогичные вышеизложенным.
studfiles.net
Дифференцирование интеграла по параметру под знаком интеграла
,
и вспомнить, что интеграл есть предел интегральных сумм, то из формулы будет следовать, что функция f(z) может быть представлена как предел линейных комбинаций простейших функций . Оба эти качества формулы Коши широко используются.
Заметим, что если точка a лежит вне контура Г, то есть ,то внутри Г функция будет голоморфна. По теореме Коши-Гурса интеграл от нее по Г равен 0. Таким образом, если заменить a на z, то получаем:
(6.2)
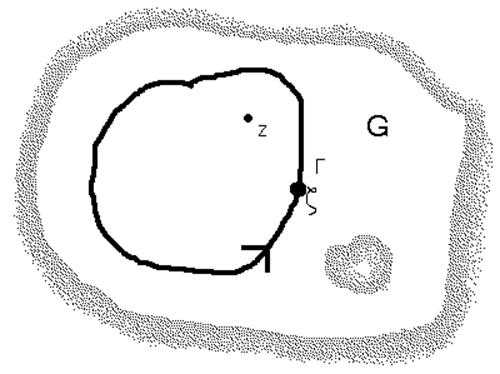
Дифференцирование интеграла по параметру под знаком интеграла.
Лемма. Пусть G и Г такие же, как и выше, функция непрерывна по совокупности переменных , и при каждом фиксированном голоморфна по . Пусть, кроме того непрерывна по совокупности переменных и .
Тогда функция
(6.3)
голоморфна в G и
(6.4)
Доказательство можно провести, сведя интеграл по комплексной переменной к интегралу по вещественной переменной, и к дифференцированию по x и y и к теореме Коши—Римана.
Интегральные формулы для производных голоморфной функции.
Вернемся к интегральной формуле Коши
(6.5)
Если это равенство формально продифференцировать по z, то получим серию формул
; (6.6)
Чтобы обосновать дифференцирование под знаком интеграла, достаточно сослаться на лемму, если положить
и отметить, что
Очевидно, что все эти функции непрерывны по совокупности переменных поскольку в числителе и знаменателе стоят непрерывные функции и знаменатель не обращается в нуль при внутри и . Таким образом, формулы (6.6) для производных обоснованы. В частности, нами доказано, что голоморфная в области функция имеет производные всех порядков.
Интеграл типа Коши. При проверке выполнения условия леммы о дифференцировании по параметру под знаком интеграла не использовалось то, что функция голоморфна. Достаточно было только, чтобы функция была непрерывной по .
Поэтому, если -непрерывная на Г функция, то интеграл
(6.7)
можно дифференцировать по z под знаком интеграла.
Следовательно, этот интеграл будет определять голоморфную функцию внутри области G ограниченной кривой Г. Более того, так же проверяется, что функция (6.7) будет голоморфной и вне контура Г. Интеграл (6.7) называется интегралом типа Коши. Он порождает две голоморфные функции: одну внутри Г и одну вне Г. Если — голоморфная в G функция, то, как это следует из (6.2), внешняя функция тождественно равна нулю. Поэтому при переходе через Г функция терпит скачок. Аналогичное явление происходит и с интегралом типа Коши в общем случае.
7. ФОРМУЛА ТЕЙЛОРА
Пусть функция голоморфна в точке . Тогда она голоморфна и в некоторой окрестности точки . Окружим эту точку контуром Г, лежащим в указанной окрестности.
Внутреннюю область, ограниченную Г, обозначим через U.
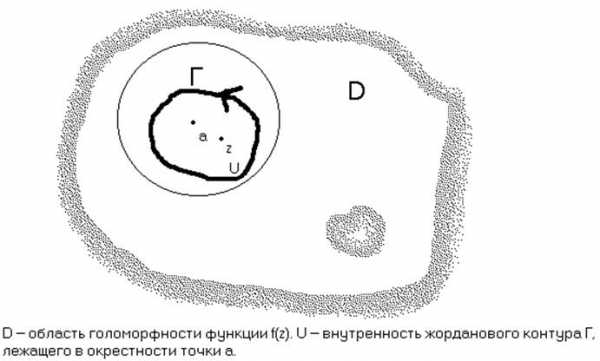
Запишем интегральную формулу Коши
при .
Преобразуем
Воспользуемся формулой для суммы геометрической прогрессии
.
Отсюда
.
Применим последнюю формулу, полагая . Тогда
.
Воспользуемся формулами (6.6) из §6 для производных, тогда получим формулу Тейлора
matematiku5.ru
Интегрирование по параметру — МегаЛекции
Глава 7
Собственные интегралы (Римана), зависящие от параметра
Пусть f(x,y) – функция двух переменных, определённая на прямоугольнике
Если для любого существует интеграл , то этот интеграл является функцией от переменной y (которая и называется здесь параметром):
Таким образом, мы получаем новый способ задания функции – в виде интеграла, зависящего от параметра, т.е. определяемые т.о. функции часто используют в математических рассуждениях и приложениях.
Следует иметь ввиду, что

Пример 1. Рассмотрим функцию
В этом примере интеграл легко вычислить:
Значит, можно задать и обычным способом:
Однако часто встречаются интегралы, которые не выражаются через элементарные функции. Тогда приходится работать с функцией, заданной в виде интеграла с параметром. Значит, нужно научиться работать с такими функциями – в частности, знать правила их дифференцирования и интегрирования.
Возможна и более сложная ситуация, когда от параметра зависит не только подынтегральная функция, но и пределы интегрирования:
Основные теоремы
Предельный переход под знаком интеграла
Теорема 1 (о непрерывности интеграла с параметром).
Если функция f(x,y) непрерывна на прямоугольнике то
функция непрерывна на отрезке
Доказательство. По теореме Кантора, непрерывная на компактном множестве ∆ функция является равномерно непрерывной, т.е.
Возьмём Тогда из равномерной непрерывности следует:
Оценим теперь приращение функции I(y):
Итак, что и означает непрерывность функции I(y).
Замечание. В теореме 1 требуется, чтобы f(x,y) была непрерывной по обеим переменным в совокупности, т.е. чтобы
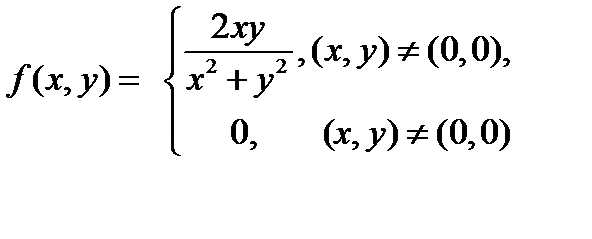 Недостаточно, чтобы f(x,y) была непрерывной по каждой из переменных. Например, функция
Недостаточно, чтобы f(x,y) была непрерывной по каждой из переменных. Например, функция
непрерывна по x (при любом фиксированном y), и непрерывна по y (при любом фиксированном x). Однако она не является непрерывной в точке (0,0) функцией (по совокупности переменных): предел не
существует. В данном случае не справедлив и вывод теоремы 1; например, функция
разрывна в точке y = 0.
Так как непрерывность в точке I(y) означает, по определению, что
в любой точке y0, то непосредственно из теоремы 1
вытекает
Теорема 2 (о предельном переходе под знаком интеграла).
Если f(x,y) непрерывна на то для любого
Если – непрерывные функции , а f(x,y) непрерывна на множестве
то можно доказать, что
Это утверждение усиливает теоремы 1 и 2.
Ещё одно усиление теорем 1,2 связано с заменой требования непрерывности f(x,y) более слабым условием.
Теорема 3. Если f(x,y) непрерывна по x (при любом фиксированном y) и f(x,y) равномерно сходится к функции g(x) при y→y0, то
Равномерная сходимость: означает:
Доказательство. просто – оно проводится с помощью той же оценки, что и доказательство теоремы 1.
Теорема 3 справедлива также в случае y → ∞, лишь определение равномерной сходимости имеет другой вид:
Пример 2. Вычислить .
Решение. Так как функция непрерывны при любых
x,y, то возможен предельный переход под знаком интеграла:
Пример 3. Вычислить .
Решение. Подынтегральная функция непрерывна при любых x, y и y→∞ стремится к g(x)=x:
Эта система равномерная, так как
,
если только . Значит, возможен переход к пределу под
знаком интеграла:
.
Дифференцирование по параметру
Дифференцируемость интеграла зависящего от параметра (Правило Лейбница)
Пусть для интеграла , в котором подынтегральная функция зависит от некоторого параметра «у» будет меняться, то будет меняться и значение определенного интеграла.
Т.о. определенный интеграл есть функция от «у» поэтому мы его можем обозначить через
Теорема 4. Предположим, что и ,
Доказательство
Найдем производную интеграла по параметру «у». Для и приращение таких, что
. Тогда производная
Заметим, что
Поделим обе части последнего равенства на « »
Применяя теорему Лагранжа к подынтегральной функции, будем иметь:
, где
Т.к.
Осталось доказать, что можно перейти к пределу под знаком интеграла. Чтобы воспользоваться теоремой 3, докажем, что ( — замкнутая область)
, где зависит от стремится к нулю при
Т.о.
Переходя к пределу при получаем:
Или
Эта формула называется формулой Лейбница.
(Замечание: Подынтегральная функция в интеграле стремится к нулю при . Из того, что подынтегральная функция в каждой (.) стремится к нулю, не всегда следует, что интеграл также стремится к нулю. Однако в данном случае при . Этот факт мы принимаем без доказательства.)
Пример 4. Найти производную функции в точке y = 2.
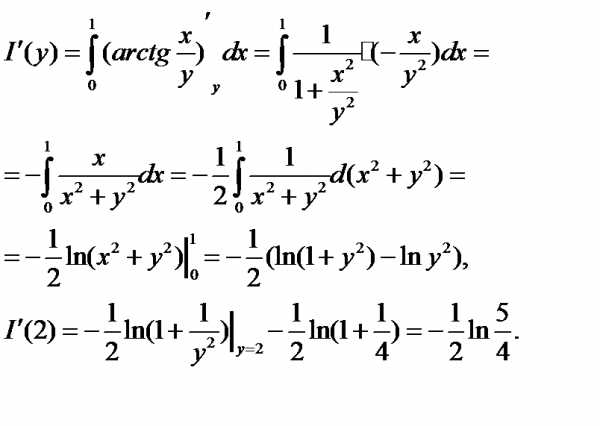 Решение. Можно, вычислив интеграл, найти явное выражение для функции I(y), а затем продифференцировать. Проще, однако, применить теорему 4:
Решение. Можно, вычислив интеграл, найти явное выражение для функции I(y), а затем продифференцировать. Проще, однако, применить теорему 4:
При и значениях y, близких к 2, функция и её частная
производная , очевидно, непрерывны.
Пример 5. Вычислить
Решение. Найдём производную интеграла по параметру . Легко проверить, что требования теоремы 4 соблюдены, поэтому
Применим подстановку t = tg x. Тогда
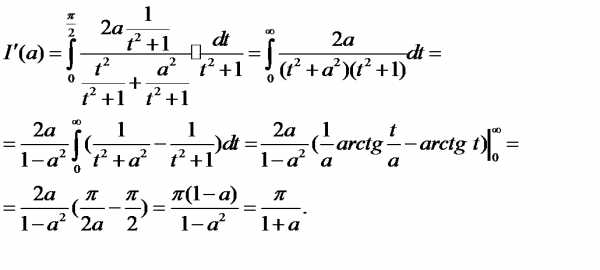
Теперь, вычисляя интеграл, получим:
Константу C найти легко, так как
.
.
Научимся теперь вычислять производные в случае, если от параметра зависит не только подынтегральная функция, но и пределы интегрирования.
Теорема 5.
Доказательство. Возьмём произвольную точку и воспользуемся аддитивностью интеграла:
Найдём производную 3-го слагаемого по определению:
Мы воспользовались теоремой о среднем для определённого интеграла, а затем – непрерывностью f(x,y) и дифференцируемостью β(y). В точности так же вычисляется и производная 1-го слагаемого:
.
Производная 2-го слагаемого вычисляется по теореме 4:
.
Складывая все 3 слагаемые, получим требуемую формулу.
Пример 6. Найти производную функции .
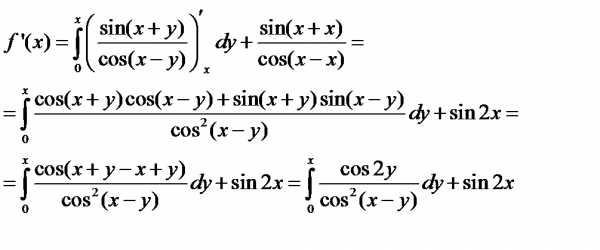 Решение. Здесь требуется дифференцировать интеграл по параметру x. Действуем по формуле теоремы 5:
Решение. Здесь требуется дифференцировать интеграл по параметру x. Действуем по формуле теоремы 5:
.
Интегрирование по параметру
Теорема 7. Пусть функция f(x,y) непрерывна в прямоугольнике
Рассмотрим . Тогда
.
Или, что то же самое,
.
Доказательство. Докажем более общее соотношение. Пусть t – произвольная точка отрезка [c, d]. Докажем, что
. (*)
Найдем производную по t от каждой части этого равенства. Применяя теорему 5 (иди давно известную нам теорему об интеграле с переменным верхним пределом), получим:
В правой части равенства (*) – интеграл, зависящий от параметра t. Дифференцируем его, применяя теорему 4:
Одинаковые результаты говорят о том, что функции в левой и правой частях равенства (*) отличаются лишь на константу:
.
Это верно. В частности, при t = c получим: 0 = 0 + C, т.е.
С = 0, и равенство доказано. Если применить его при t = d, получим утверждение теоремы.
Теорема 7’. Пусть
Тогда
Доказательство
Заметим, что если , тогда интеграл в скобках – непрерывная функция на . Поэтому все интегралы в утверждении теоремы определены.
Для каждого положим , .
Поскольку то , . Функция ,
при непрерывна по «х» на , согласно теоремы 3 (о непрерывности I(y))
Для любой точки и . Поэтому согласно теоремы 4, для . Т.о. , . Причем . Следовательно .
Доказываемое равенство получим при .
Пример 7. Вычислить интеграл
Решение. Интегрирование в указанном порядке затруднительно:
Пользуясь теоремой 6, изменим порядок интегрирования.
.
Интеграл вычислен. Попутно получено соотношение:
.
Приведём пример, показывающий, что при нарушении непрерывности подинтегральной функции изменение порядка интегрирования может привести к другому результату.
Пример 8. Вычислим интеграл:
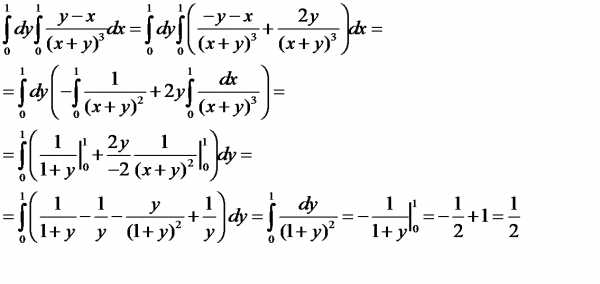
.
При вычислении в другом порядке можно заметить, что если сменить знак подинтегральной функции, то получится уже рассмотренный интеграл:
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Интегрирование и дифференцирование интегралов, зависящих от параметра
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Пермский государственный педагогический университет
Кафедра математиче ского анализа
Курсовая работа
Интегрирование и дифференцирование интегралов, зависящих от параметра
Пермь 2010
Оглавление
Введение
1. Регулярность интегралов, зависящих от параметра
2. Интеграл коши на кривой
3. Интеграл коши на области
3.1 Аналитическая зависимость от параметра
3.2 Существование производных всех порядков у аналитической функции
3.3 Вывод формулы Коши
3.2 Следствия из формулы Коши
Заключение
Список литературы
Понятие «интеграл» непосредственно связано с интегральным исчислением − разделом математики, занимающимся изучением интегралов, их свойств и методов вычисления. Вместе с дифференциальным исчислением интегральное исчисление составляет основу математического анализа.
Так как целью моей прошлой курсовой работы являлось изучение некоторых аспектов темы, таких как интегрирование и дифференцирование интегралов, зависящих от параметра.
Цель данной курсовой работы является изучение новых аспектов по теме «интегралы, зависящие от параметров» и накопление материалов для следующих работ по данной тематике.
В данной курсовой работе я рассмотрел интегралы Коши по кривой
и интегралы Коши по плоскости , также была рассмотрена аналитическая функция, аналитическая зависимость от параметра.Для достижения цели необходимо решить следующие задачи:
· Найти и изучить литературу по данной теме
· Накопить и систематизировать полученную информацию по теме
· Изучить основные понятия.
Объектом исследования являются различные виды интегралов зависящих от параметра в курсе ВУЗов.
В работе использованы следующие методы исследования:
1. Анализ научной литературы по теме «интегралы, зависящие от параметров»
2. Синтез полученных знаний
3. Обобщение полученных знаний
Работа насчитывает 26 страницы, состоит из введения, четырех глав, заключения, библиографического списка используемой литературы и содержащего 10 наименований, вспомогательные указатели, а также содержит 2 иллюстрации.
Рассмотрим интеграл
.(1)Теорема 1. [7, c. 111] Пусть выполнены условия:
1)
— конечная кусочно-гладкая кривая;2) функция
непрерывна по при , где — область в комплексной плоскости;3) при каждом фиксированном
функция регулярна по в области .Тогда интеграл (1) есть регулярная в области
функция.Доказательство. В силу условий 1, 2 функция
mirznanii.com

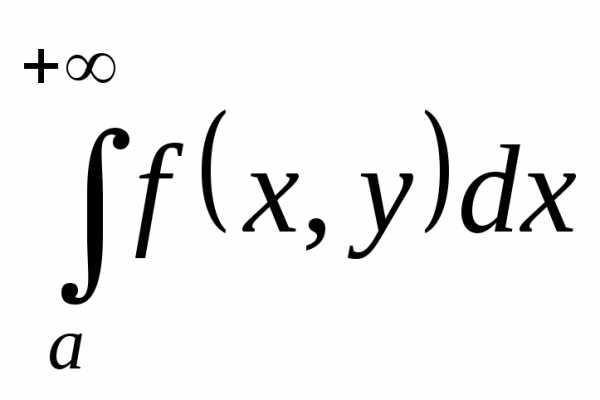 сходится равномерно
относительно у на
сходится равномерно
относительно у на 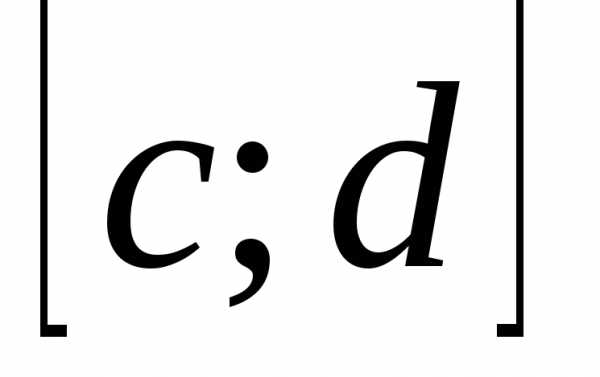 .
.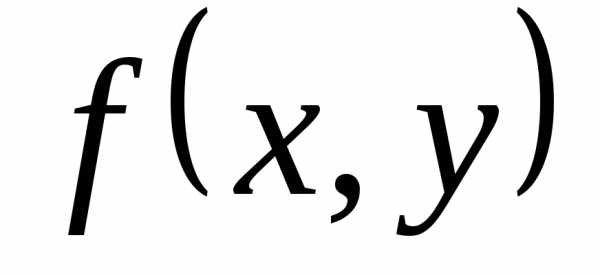 непрерывна в области
непрерывна в области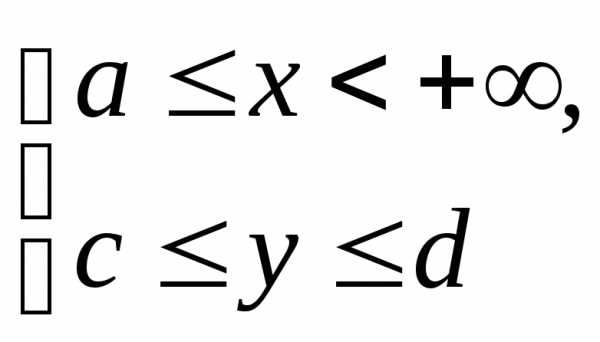 и имеет в ней непрерывную частную
производную
и имеет в ней непрерывную частную
производную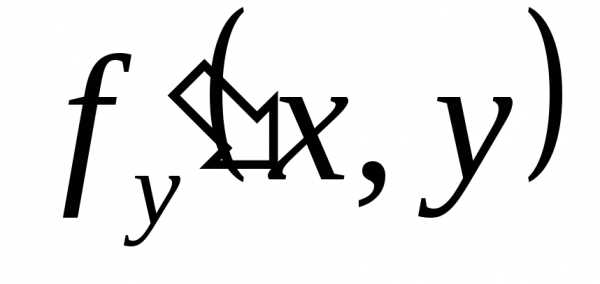 ;
;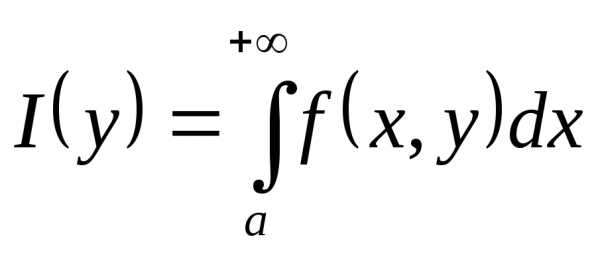 сходится при
каждом
сходится при
каждом 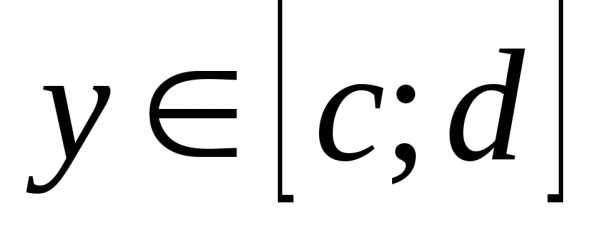 ;
;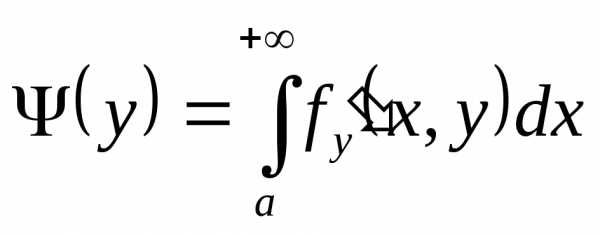 сходится равномерно
относительно у на
сходится равномерно
относительно у на 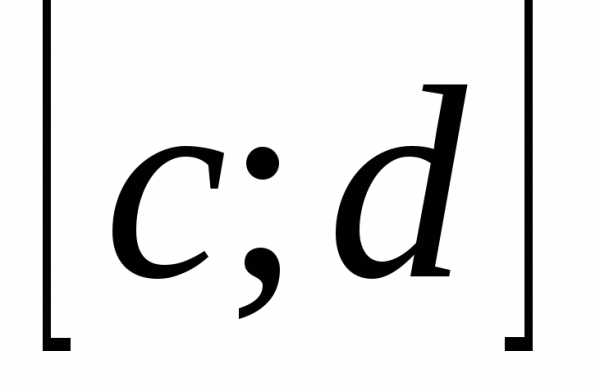 ;
;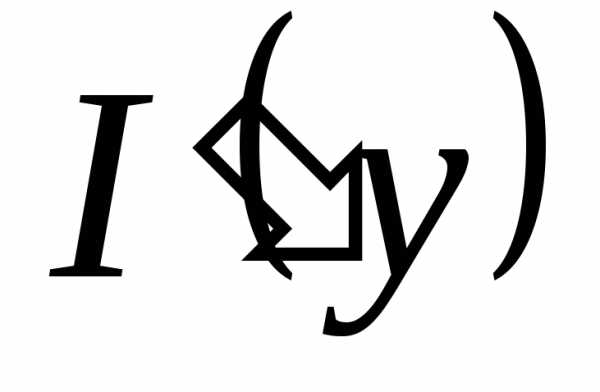 существует при
каждом
существует при
каждом 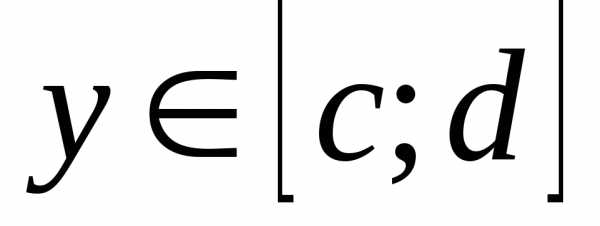 ;
;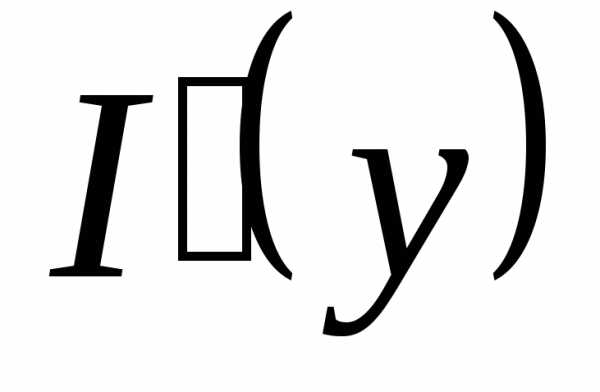 непрерывна на
непрерывна на 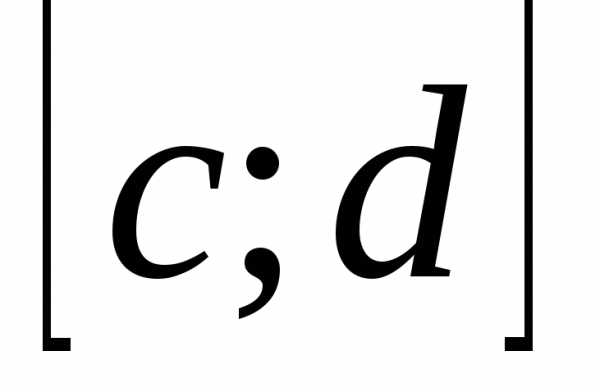 .
.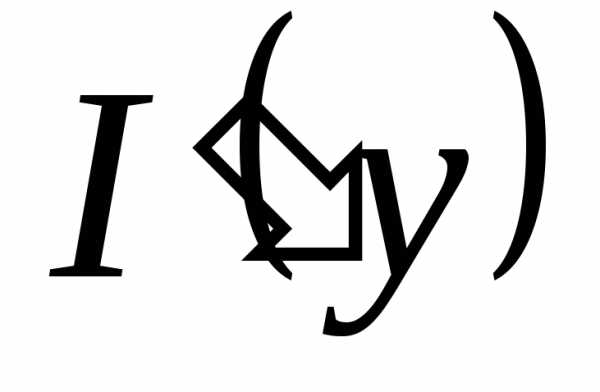 существует при
каждом
существует при
каждом 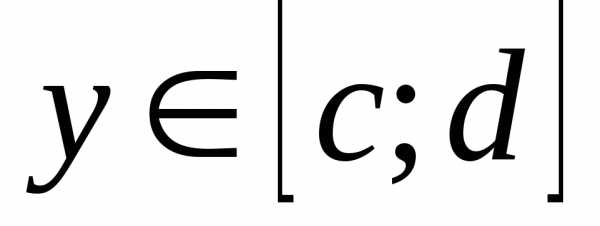 ;
;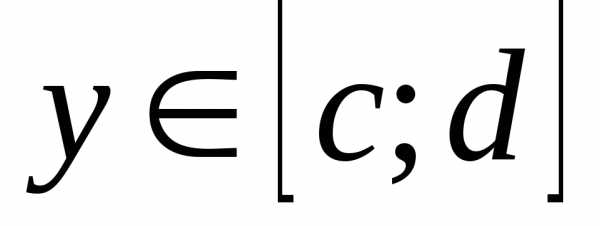 ;
;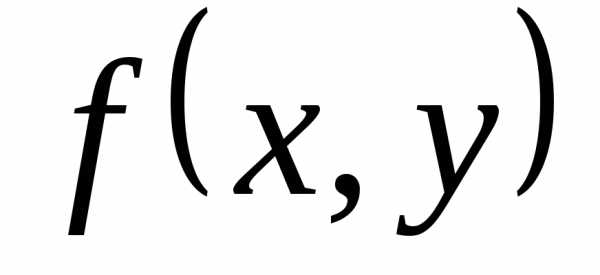 непрерывна в области
непрерывна в области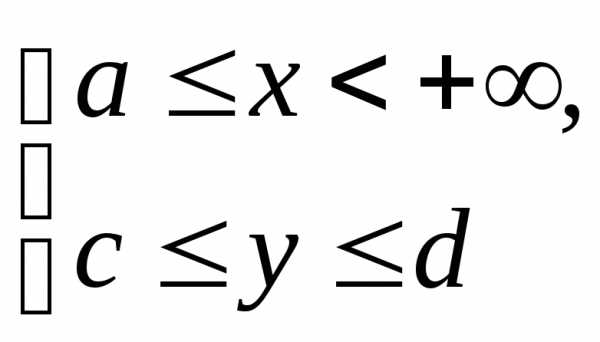
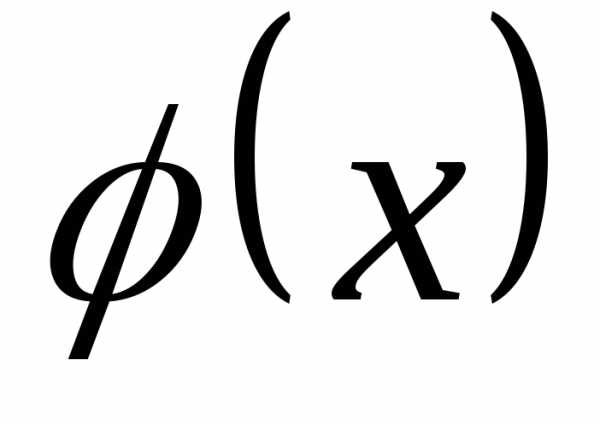 определена и непрерывна на
определена и непрерывна на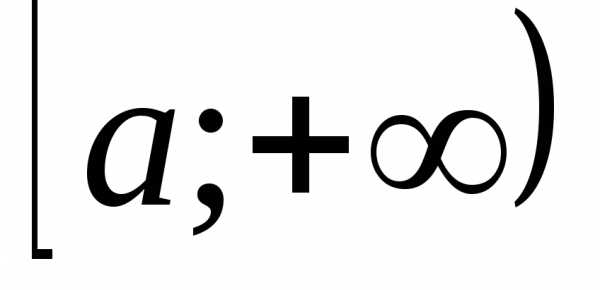 ;
;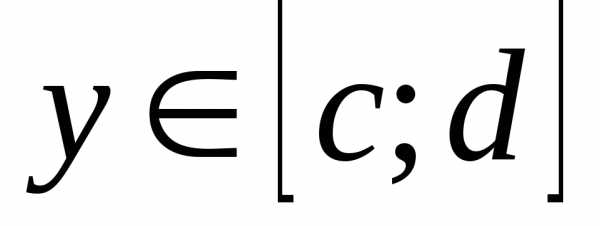 и
.
и
.