Решение некоторых задач по теории множеств
Разделы: Математика
На математическом кружке вместе с учащимися рассматривался ряд задач, благодаря наглядности которых, процесс решения становится понятным и интересным. На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.
Введем определение множества, а так же некоторые обозначения.
Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.
Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.
Можно сделать такую запись определения множества:
, где
“” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.
Два множества будем называть равными, если они состоят из одних и тех же элементов
Например:
Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если , то , где “С” знак подмножества или включения.
Графически это выглядит так (рис.1):
(рис.1)
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.
Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).
Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.
Это определение можно записать с помощью обозначений:
А υ В, где
где “ υ ” – знак объединения,
“ / ” – заменяет слова ”таких что“
(рис.2)
Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:
А ∩ В = С, где
“∩“ – знак пересечения. (рис.3)
(рис.3)
Обозначим буквой Е основное или универсальное множество, где A С Е (“”- любо число), т.е. А Е = Е; АЕ =А
Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается ĀЕ или Ā (рис.4)
Е
(рис.4)
Примерами для понимания этих понятий являются свойства:
_
А Ā=Е Ø = Е Е Ā=Ā
_
А ∩ Ā= Ø Ē = Ø (Ā)=А
Свойства дополнения имеют свойства двойственности:
________ _ _
АВ = А∩В
________ _ _
АВ = АUВ
Введем еще одно понятие – это мощность множества.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
m (A) + m (Ā) = m (E)
А = В => m(A) = m(B)
Для любых конечных множеств справедливы так же утверждения:
m (AB) =m (A) + m (В) – m (А∩В)
m (A∩B) = m (A) + m (В) – m (АВ)
m (ABC) = m (A) + m (В) + m (С)– m (А∩В) — m (А∩С) – m (В∩С) – m (А∩В∩С).
А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.
Задача №1
В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.
По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек. Ни одной задачи не решили 3 человека.
- Сколько учащихся решили все задачи?
- Сколько учащихся решили только две задачи?
- Сколько учащихся решили только одну задачу?
Задача № 2
Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.
Сколько студентов успешно решили только одну контрольную работу?
Задача № 3
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.
Сколько учеников пользуются только одним видом транспорта?
Решение задачи № 1
Запишем коротко условие и покажем решение:
- m (Е) = 40
- m (А) = 20
- m (В) = 18
- m (С) = 18
- m (А∩В) = 7
- m (А∩С) = 8
- m (В∩С) = 9
___________
m (АВС) = 3 => m (АВС) = 40 – 3 = 37
Обозначим разбиение универсального множества Е множествами А, В, С (рис.5).
(рис.5)
К1 – множество учеников, решивших только одну задачу по алгебре;
К2 – множество учеников, решивших только две задачи по алгебре и геометрии;
К3 – множество учеников, решивших только задачу по геометрии;
К4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;
К5 – множество всех учеников, решивших все три задачи;
К6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;
К7 – множество всех учеников, решивших только задачу по тригонометрии;
К8 – множество всех учеников, не решивших ни одной задачи.
Используя свойство мощности множеств и рисунок можно выполнить вычисления:
- m (К5) = m (А∩В∩С)= m (АВС) — m (А) — m (В) — m (С) + m (А∩В) + m (А∩С) + m (В∩С)
- m (К5) = 37-20-18-18+7+8+9=5
- m (К2) = m (А∩В) — m (К5) = 7-5=2
- m (К4) = m (А∩С) — m (К5) = 8-5=3
- m (К6) = m (В∩С) — m (К5) = 9-5=4
- m (К1) = m (А) — m (К2) — m (К4) — m (К5) = 20-2-3-5=10
- m (К3) = m (В) — m (К2) — m (К6) — m (К5) = 18-2-4-5=7
- m (К7) = m (С) — m (К4) — m (К6) — m (К5) = 18-3-4-5 =6
- m (К2) + m (К4) + m (К6) = 2+3+4=9 – число учеников решивших только две задачи;
- m (К1) + m (К3) + m (К7) = 10+7+6=23 – число учеников решивших только одну задачу.
Ответ:
5 учеников решили три задачи;
9 учеников решили только по две задачи;
23 ученика решили только по одной задаче.
С помощью этого метода можно записать решения второй и третьей задачи так:
Решение задачи № 2
- m (АВ) = 33
- m (АС) = 31
- m (ВС) = 32
- m (К2) + m (К4) + m (К6) + m (К5) = 20
Найти m (К1) + m (К3) + m (К7)
- m (АUВ) = m (К1) + m (К2) + m (К3) + m (К4) + m (К5) + m (К6) = m (К1) + m (К3) + 20 = 33 =>
- m (К1) + m (К3) = 33 – 20 = 13
- m (АUС) = m (К1) + m (К4) + m (К2) + m (К5) + m (К6) + m (К7) = m (К1) + m (К7) + 20 = 31 =>
- m (К1) + m (К7) = 31 – 20 = 11
- m (К3) + m (К7) = 32 – 20 = 12
- 2m (К1) + m (К3) + m (К7) = 13+11=24
- 2m (К1) + 12 = 24
- m (К3)= 13-6=7
- m (К7)=12-7=5
- m (К1) + m (К3) + m (К7) = 6+7+5=18
Ответ:
Только одну контрольную работу решили 18 учеников.
Решение задачи № 3
- m (Е) = 35
- m (А∩В∩С)= m (К5) = 6
- m (А∩В)= 15
- m (А∩С)= 13
- m (В∩С)= 9
Найти m (К1) + m (К3) + m (К7)
- m (К2) = m (А∩В) — m (К5) = 15-6=9
- m (К4) = m (А∩С) — m (К5) = 13-6=7
- m (К6) = m (В∩С) — m (К5) = 9-6=3
- m (К1) + m (К3) + m (К7) = m (Е) — m (К4) — m (К2) — m (К6) — m (К5) = 35-7-9-3-6=10
Ответ:
Только одним видом транспорта пользуется 10 учеников.
Литература: А.Х. Шахмейстер «Множества. Функции. Последовательности»
9.03.2010
xn--i1abbnckbmcl9fb.xn--p1ai
Множества — Практика — Примеры решения типовых задач
1. Записать множество Е, если , причем А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Решение.
есть не что иное, как объединение множеств А и В, т.е. множество Е будет состоять из элементов, принадлежащих как множеству А, так и множеству В: Е={2, 3, 4, 6, 8, 9, 10, 12}.
2. Записать множество , если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Требуется выполнить операцию пересечения т.е. множество Е будет состоять только из элементов, одновременно входящих как в множество А, так и в множество В: Е={6, 12}.
3. Записать множество , если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Требуется выполнить операцию разности т.е. множество Е будет состоять из всех элементов множества А, не принадлежащих В: Е={2, 4, 8, 10}.
4. Записать множество , если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Из предыдущего примера имеем . Для получения окончательного ответа требуется выполнить операцию дополнения т.е. множество Е будет состоять из элементов множества В: Е={3, 6, 9, 12}.
5. Проиллюстрировать с помощью кругов Эйлера следующую формулу:
Выполняя действие в скобках получим:
После этого получаем А\Е т.е. необходимо выделить участок множества А, не принадлежащий множеству Е. Ответ примет форму:
6. Проиллюстрировать с помощью Диаграмм Венна верность тождества:
.
Проиллюстрируем левую часть тождества, обозначив сначала объединение множеств В и С,
затем пересечение множеств А и . Окончательный вид левой части:
Теперь проиллюстрируем правую часть:
окончательный вид правой части:
Как видим диаграммы совпадают, следовательно тождество верно.
7. По диаграмме Венна записать формулу:
Запишем сначала ,
затем , получим:
8. Доказать
Решение.
,
по закону да Моргана и закону дистрибутивности
dl.nure.ua
Элементы теории множеств
Элементы теории множеств
Множество – основное математическое понятие. В обычной жизни его смысл заложен в словах: «совокупность», «класс», «стая», «табун», «стадо» и т.п. Теория множеств как математическая дисциплина создана немецким математиком Г. Кантором, которая получила признание в качестве самостоятельного раздела математики к 1890 году, когда были получены ее приложения в анализе и геометрии. Главная заслуга Георга Кантора заключается в установлении того факта, что понятие бесконечность является не абстракцией, придуманной философами, а реальностью; бесконечные совокупности предметов существуют наравне с конечными.
Множество относится к математическим объектам, для которых нет строго определения. Мы можем лишь в какой-то мере дать описание основных его свойств.
Кантор описывает множество следующим образом:
Определение. | Множество Sесть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. |
Понятие множества. Способы задания множества
Мы под множествомбудем понимать следующее:
Определение. | Множество – набор (совокупность) определенных, различимых между собой объектов, рассматриваемых как единое целое, и обладающий некоторым общим свойством. . Объекты, составляющие данное множество, называют его элементами. . |
Для того, чтобы указать, что х–
элемент множестваА, записывают и читают «хпринадлежитА». Чтобы
указать, чтохне является элементом
множестваА, записывают
и читают «хпринадлежитА». Чтобы
указать, чтохне является элементом
множестваА, записывают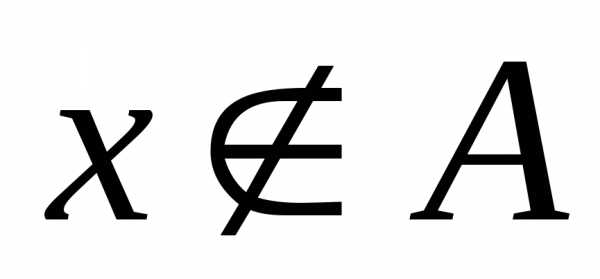 и читают «хне принадлежит множествуА».
и читают «хне принадлежит множествуА».
Для ряда числовых множеств в математике приняты стандартные обозначения:
Обозначения числовых множеств:
|
Существует два способа задания множества:
Рисунок 1. Способы задания множеств
Множества можно разделить на конечные и бесконечные.
Определение. | Конечныммножеством называется множество, состоящее из конечного числа элементов. Множество называется бесконечным, если оно состоит из бесконечного числа элементов |
Пример 1.
Конечные множества:множество букв алфавита, множество студентов 2 курса специальности «Юриспруденция» и т.д.
Бесконечные множества:множество натуральных чисел, множество точек прямой и т.д.
К конечным множествам относится и множество, не содержащее элементов вообще. Такое множество называют пустыми обозначают Ø.
Пример 2.
Ø = , поскольку среди действительных чисел нет решения данного уравнения.
Определение. | Если каждый элемент множества Вявляется также и элементом множестваА, то говорят, что множествоВназываетсяподмножествоммножестваА. (Ввключено вА). |
Пример 3.
Множество 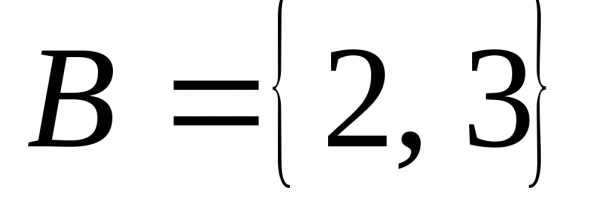 ,,
тогда,
т.е.
,,
тогда,
т.е. .
.
Определение. | Множества АиВназываютсяравными(илисовпадающими),
если они состоят из одних и тех же
элементов, т.е.
|
Если множества не равны, то пишут  .
.
Пример 4.
Множества
и,
где и
и удовлетворяют
уравнению,
т.е.
удовлетворяют
уравнению,
т.е. ,
значит
,
значит .
.
Определение. | Множество всех подмножеств множества Аназываетсямножеством-степеньюмножестваА.
|
Пример 5.
Пусть
,
тогда {Ø},
т.е. если множество состоит из двух
элементов, то множество-степень состоит
из четырех подмножеств.
{Ø},
т.е. если множество состоит из двух
элементов, то множество-степень состоит
из четырех подмножеств.
Пусть
,
тогда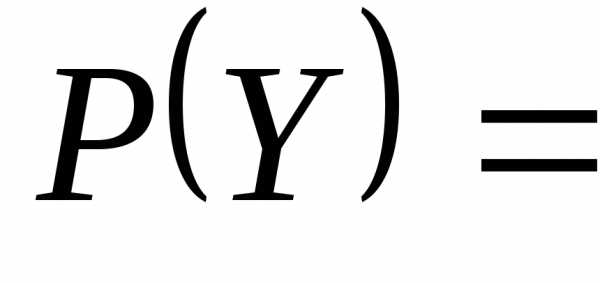 {{4},
{2,3}, {3,4}, {2,4}, Ø}, т.е. если множество состоит
из трех элементов, то множество-степень
состоит из восьми подмножеств.
{{4},
{2,3}, {3,4}, {2,4}, Ø}, т.е. если множество состоит
из трех элементов, то множество-степень
состоит из восьми подмножеств.
Таким образом, если конечное множество Асостоит изnэлементов, то число всех его подмножеств
равно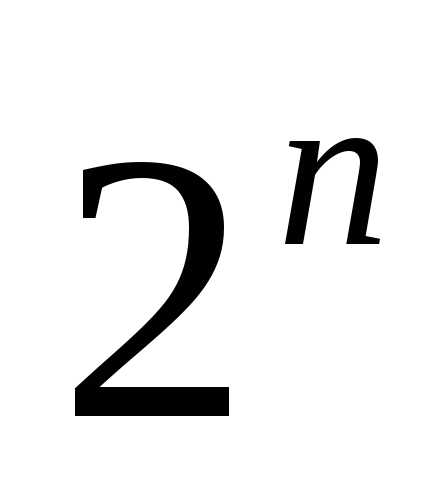 .
.
Определение. | Множество Uназываетсяуниверсальнымдля системы
множествА,B,C,
…, если каждое множество системы
является подмножествомU,
т.е.
|
studfiles.net
|
www.reshim.su
Примеры операций над множествамиПример 1. Даны множества $A=\{3,5,7,8,9\}$ и $B=\{2,3,7,8, 10\}$ Найти: $ A ∩ B $, $ A ∪ B $ , $ A \setminus B $, $ A ∆ B $ Решение.
Пример 2. Даны множества $A=\{\{a,d\},\{a,b,c\},\{a\},a,b\}$ и $B=\{\{a,b,c,d\},\{a,b,c\},\{a,b\},a\}$ Найти: $ A ∩ B $, $ A ∪ B $ , $ A \setminus B $, $ A ∆ B $ Решение.
Калькулятор вычислений над множествами.Примечание:
| ||
www.reshim.su
Раздел 1: Элементы теории множеств
Каждый с самого рождения бессознательно пользуется теорией множеств, так же как Мольеров Журден из «Мещанина во дворянстве» разговаривает прозой, сам того не ведая.
М. Стоун
1.1 Основные понятия теории множеств
В конце XIX века в математической науке возникла необходимость уточнить смысл таких ведущих понятий, как функция, непрерывность и т. д. Для этого нужно было строго определить, что такое натуральное число. Поиски ответа на эти сложные вопросы способствовали развитию новых математических идей, поэтому в конце XIX начале XX столетий происходил пересмотр старых представлений буквально во всех областях математических знаний. В результате в конце XIX века возникла новая область математики – теория множеств, одним из создателей которой был немецкий математик Георг Кантор (1845 – 1918). За небольшой срок теория множеств стала фундаментом всей математики.
Понятие множества является ключевым в математике, без которого невозможно изложение ни одного из ее разделов. Подсознательно первые представления о множестве у человека начинают формироваться с рождения, когда он погружается в многообразный мир окружающих его объектов и явлений. С первых же шагов мы не просто пополняем список знакомых нам объектов и явлений, а начинаем дифференцировать и классифицировать (горячие и холодные, сладкие и горькие, тяжелые и легкие и т. п.), объединяя тем самым объекты в некоторые совокупности.
В математике понятие множество используется для описания предметов или объектов. При этом предполагается, что предметы (объекты) данной совокупности можно отличить друг от друга и от предметов, не входящих в эту совокупность.
Создатель теории множеств Г. Кантор определил множество как «объединение в одно целое объектов, хорошо различимых нашей интуицией или мыслью», а так же «множество есть многое мыслимое нами как единое». Эти слова не могут рассматриваться как математически строгое определение множества, такого определения не существует. Понятие множества относится к исходным (не определяемым), на основании которых строятся остальные понятия математики.
Множество – это совокупность каких-либо объектов. Так, можно говорить о множестве всех книг данной библиотеки, множестве всех вершин данного многоугольника, множестве всех натуральных чисел, множестве всех точек данной прямой и т. д. Объекты, входящие в данное множество называются элементами множества. Книги данной библиотеки, вершины данного многоугольника, натуральные числа, точки данной прямой являются элементами соответствующих множеств.
Множества обычно обозначаются большими буквами A, B, X, а их элементы – малыми буквами а, b, x.
Множество называется конечным, если количество его элементов можно выразить целым неотрицательным числом (причем неважно, известно это число или нет, главное, оно существует), в противном случае множество называется бесконечным.
Пример 1: Множество книг в библиотеке, множество студентов в группе являются конечными. Множество натуральных чисел, множество точек прямой являются бесконечными.
Количество элементов множества обозначается |A|.
Пример 2: Пусть В – множество правильных многоугольников. Тогда В = {тетраэдр, куб, октаэдр, додекаэдр, икосаэдр}. |B| = 5.
Запись x Х,
означает что объект х есть элемент
множества Х,
читается «х принадлежит
множеству Х»,
«х входит
в множество Х». Если х не принадлежит
множеству Х,
то пишут х
Х,
означает что объект х есть элемент
множества Х,
читается «х принадлежит
множеству Х»,
«х входит
в множество Х». Если х не принадлежит
множеству Х,
то пишут х  Х.
Х.
Например,
если через N обозначим
множество натуральных чисел, то 3  N, 20
N, 20  N, 0
N, 0  N,
N,  N.
N.
Если
все элементы множества А принадлежат какому-то множеству В,
то говорят, что множество А является подмножеством множества В. Записывают А  В (множество А содержится
во множестве В). Любое
множество является подмножеством самого
себя, т. е. справедливо утверждение А
В (множество А содержится
во множестве В). Любое
множество является подмножеством самого
себя, т. е. справедливо утверждение А  А.
А.
Если множество не содержит ни одного элемента, то его называют пустым и обозначают символом Ø. Пустое множество является подмножеством любого множества.
Подмножества, которые содержат не все элементы множества В, называют собственными подмножествами множества В.
Пример 3: Дано множество М = {a; c; m}. Найти все его подмножества.
Решение:
M1 = {a}, M2 = {c}, M3 = {m}, M4 = {a; c}, M5 = {a; m}, M6 = {c; m}, M7 = {a; c; m}, M8 = Ø.
Множества M7 и M8 называются несобственными подмножествами множества М.
Множества А и В называют равными (А = В), если. они
состоят из одних и тех же элементов, т.е. В  Аи А
Аи А  В.
В.
Например, множества А = {3, 5, 7, 9} и В = {7, 3, 9, 5} равны, т. к. состоят из одинаковых элементов.
Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются:
Ν={1; 2; 3; …; n; …} – множество натуральных чисел – множество чисел, использующихся при счете предметов;
Ζ0={0; 1; 2; …; n; …} – множество целых неотрицательных чисел – множество натуральных чисел с нулем;
Ζ={0; ±1; ±2; …; ±n; …} – множество целых чисел – множество целых неотрицательных чисели им противоположных;
Q={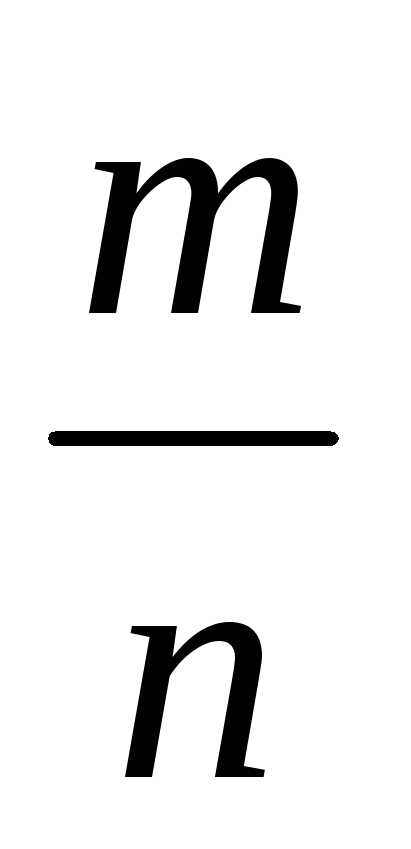 :m
:m  Z, n
Z, n  N}
– множество рациональных чисел –
множество чисел, которые можно представить
в виде обыкновенной дроби – множество
конечных и бесконечных периодических
десятичных дробей;
N}
– множество рациональных чисел –
множество чисел, которые можно представить
в виде обыкновенной дроби – множество
конечных и бесконечных периодических
десятичных дробей;
R – множество действительных чисел – объединение множеств рациональных и иррациональных чисел.
Между этими множествами существует соотношение: .
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, ½=0,5 (=0,5000…), ⅓=0,333… – рациональные числа.
Действительные
числа, не являющиеся рациональными,
называются иррациональными. Иррациональное
число выражается бесконечной
непериодической дробью. Например, 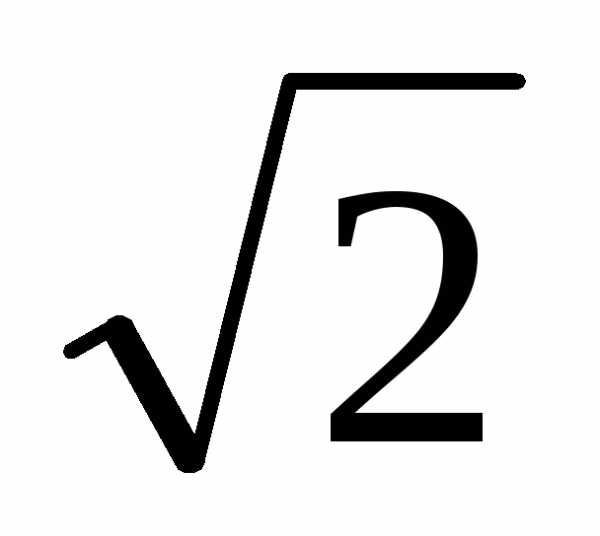 = 1,4142356…, π = 3,1415926… – иррациональные
числа.
= 1,4142356…, π = 3,1415926… – иррациональные
числа.
studfiles.net
Множества Элементы теории множеств. Операции над множествами.
Определение 1.Множеством называется совокупность некоторых объектов, объединенных в одно целое по какому ‒ либо признаку.
Объекты, из которых состоит множество, называются его элементами.
Обозначаются заглавными буквами латинского алфавита: A, B, …, X, Y, …, а их элементы обозначаются соответствующими прописными буквами: a, b, …, x, y.
Определение 1.1.Множество, не содержащее ни одного элемента, называется пустым и обозначается символом Ø.
Множество можно задать перечислением и описанием.
Пример:; .
Определение 1.2.Множеством A называется подмножеством B, если каждый элемент множества A является элементом множества B. Символически это обозначают так: AB (A содержится в B).
Определение 1.3.Два множества A и B называются равными, если они состоят из одних и тех же элементов: (A =B).
Операции над множествами.
Определение 1.4.Объединением или суммой множеств A и B называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств.
Объединение множеств обозначают AB(или A +B). Кратко можно записать AB = .
AB= A +B
Если BA, то A +B=A
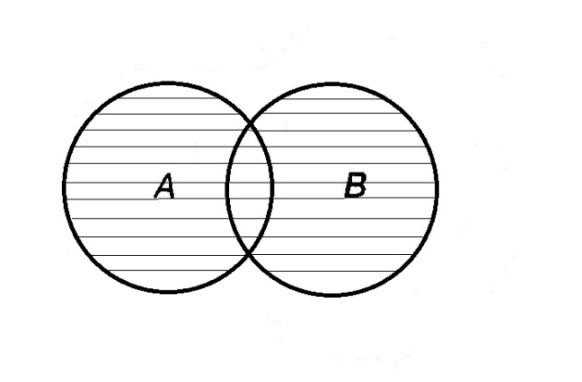

Определение 1.5. Пересечением или произведением множеств A и B называется множество, состоящее из элементов, каждый из которых принадлежит множеству A и множеству B одновременно. Пересечение множеств обозначают AB (или A·B). Кратко можно записать:
AB =.
AB =A ·B
Если BA, то A · B= B


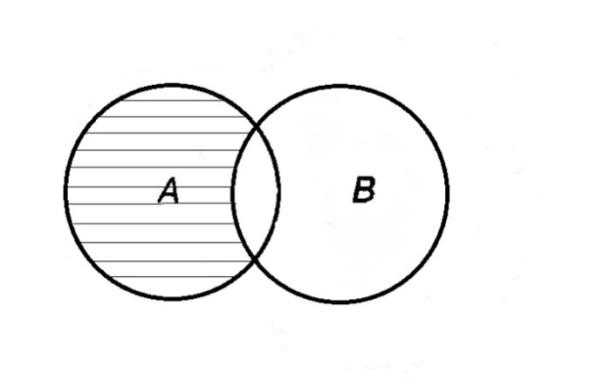
Определение 1.6. Разностью множеств A и B называется множество, каждый элемент которого является элементом множества A и не является элементом множества B. Разность множеств обозначают A\B. По определению A\B = .
A\B =A–B
Множества, элементами которых являются числа, называются числовыми.
Примерами числовых множеств являются:
N = — множество натуральных чисел.
Z= — множество целых чисел.
Q= — множество рациональных чисел.
R‒ множество действительных чисел.
Множество Rсодержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, ;… ‒ рациональные числа.
Иррациональное число выражается бесконечной непериодической десятичной дробью. Так, = 1,41421356…; = 3,14159265…. – иррациональное число.
K– множество комплексных чисел (вида Z=a+bi)
RK
Определение 1.7.Ɛ ‒ окрестностью точки x0 называется симметричный интервал (x0 – Ɛ; x0 + Ɛ), содержащий точку x0.
В частности, если интервал (x0 –Ɛ; x0 +Ɛ), то выполнятся неравенство x0 –Ɛ<x<x0 +Ɛ, или, что то же, │x– x0 │<Ɛ. Выполнение последнего означает попадание точки xв Ɛ – окрестность точки x0.
Пример 1:
= 2, Ɛ = 0,1.
(2 – 0,1; 2 + 0,1) или (1,9; 2,1) – Ɛ– окрестность.
│x– 2│< 0,1
–0,1<x – 2<0,1
2 –0,1<x< 2 + 0,1
1,9<x< 2,1
Пример 2:
A– множество делителей 24;
B– множество делителей 18.
A=.
B=.
AB= A +B =
AB =A ·B =
A /B =A –B =
Функция Понятие функции. Основные свойства функции.
Определение 1. Пусть даны два непустых множестваХ и Y.Соответствие f, при котором каждому элементу xХсоответствует один единственный элемент уY, называется функцией и записывается у = f(x),
xХили f:x→ у (x → у).
x— аргумент функции; у — значение функции.
Пример:
y = 2 x – 1
Множество Х называется областью определения функцииfи обозначается D(f). Множество всех уY называется множеством значений функции f и обозначается E(f).
Если элементами множеств Х и Yявляются действительные числа, то функцию f называют числовой функцией.
studfiles.net


 и
и .
.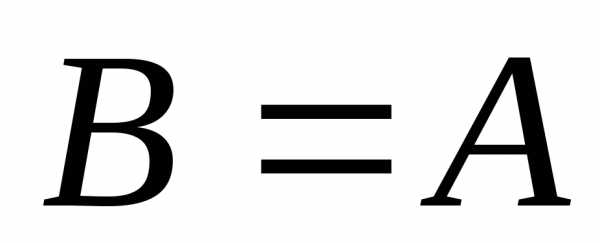
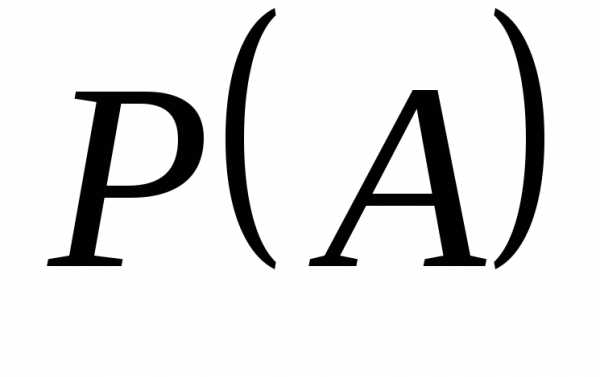
 ,
,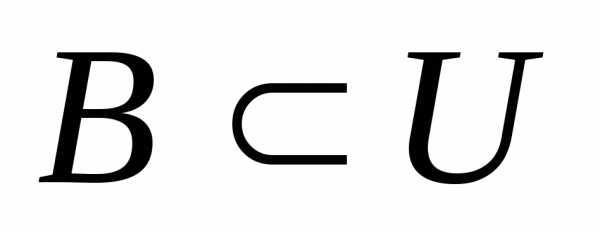 ,
, ,
…. .
,
…. .