Формула понижения степени для косинуса – , , .

Формулы понижения степени тригонометрических функций

Формулы понижения степени являются одним из видов основных тригонометрических формул. Они выражают степени (2, 3, …) тригонометрических функций синус, косинус, тангенс, котангенс через синус и косинус первой степени, но кратного угла (`\alpha, \ 3\alpha, \ …` или `2\alpha, \ 4\alpha, \ …`).

Содержание статьи:

Список всех тригонометрических формул понижения степени

Запишем данные тождества для тригонометрических функций от 2-й по 4-ю степень угла `\alpha`, а также для угла `\frac \alpha 2` и для произведения синус на косинус. Для удобства разделим их на группы.

Для квадрата

Формулы этой группы, особенно две первые, наиболее нужны. Они применяются при решении тригонометрических уравнений, интегралов и т. д.

`sin^2 \alpha=\frac{1-cos \ 2\alpha}2`
`cos^2 \alpha=\frac{1+cos \ 2\alpha}2`

`tg^2 \alpha=\frac{1-cos \ 2\alpha}{1+cos \ 2\alpha}`

`ctg^2 \alpha=\frac{1+cos \ 2\alpha}{1-cos \ 2\alpha}`

Для куба

Тождества этой группы и следующих встречаются гораздо реже, но это не повод их не знать.

`sin^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}4`
`cos^3 \alpha=\frac{3cos \ \alpha+cos \ 3\alpha}4`

`tg^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}{3cos \ \alpha+cos \ 3\alpha}`

`ctg^3 \alpha=\frac{3sin \ \alpha+sin \ 3\alpha}{3cos \ \alpha-cos \ 3\alpha}`

Для 4-й степени

`sin^4 \alpha=\frac{3-4cos \ 2\alpha+cos \ 4\alpha}8`
`cos^4 \alpha=\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`

Для функций половинного угла

Это формулы половинного угла. Но когда они записаны именно в таком виде, то их можно отнести и к тодествам понижения степени.

` sin^2 \frac \alpha 2=\frac{1-cos \alpha}2`

` cos^2 \frac \alpha 2=\frac{1+cos \alpha}2`

`tg^2 \frac \alpha 2=\frac{1-cos \alpha}{1+cos \alpha}`

`ctg^2 \frac \alpha 2=\frac{1+cos \alpha}{1-cos \alpha}`

Для произведения синус на косинус

`sin^2 \alpha \cdot cos^2 \alpha=\frac{1-cos \ 4\alpha}8`
`sin^3 \alpha \cdot cos^3 \alpha=\frac{3sin \ 2\alpha-sin \ 6\alpha}32`

`sin^4 \alpha \cdot cos^4 \alpha=\frac{3-4cos \ 4\alpha+cos \ 8\alpha}128`

`sin^5 \alpha \cdot cos^5 \alpha=\frac{10sin \ 2\alpha-5sin \ 6\alpha+sin \ 10\alpha}512`

Доказательство

Теперь перейдем непосредственно к выводу формул понижения степени тригонометрических функций.

Чтобы доказать их для квадрата, нам понадобятся фождества двойного угла `cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1`.

Формулу понижения степени синуса в квадрате получим, разрешив первое равенство относительно ` sin^2 \alpha`: `sin^2 \alpha=\frac{1-cos \ 2\alpha}2`.

Аналогично и с косинусом в квадрате, получим тождество, разрешив второе равенство относительно ` cos^2 \alpha`: `cos^2 \alpha=\frac{1+cos \ 2\alpha}2`.

Формула понижения степени тангенса и котангенса автоматически выводится из определений этих функций. Поскольку `tg  \alpha=\frac {sin \alpha}{cos \alpha}`, то `tg^2 \alpha=\frac {sin^2 \alpha}{cos^2 \alpha}=` `\frac {\frac{1-cos \ 2\alpha}2}{\frac{1+cos \ 2\alpha}2}=\frac{1-cos \ 2\alpha}{1+cos \ 2\alpha}`. Аналогично получим `ctg^2 \alpha=\frac {cos^2 \alpha}{sin^2 \alpha}=` `\frac {\frac{1+cos \ 2\alpha}2}{\frac{1-cos \ 2\alpha}2}=\frac{1+cos \ 2\alpha}{1-cos \ 2\alpha}`.

Для лучшего усвоения теоретического материала рекомендуем посмотреть видео, где подробно описывается процесс доказательстве первых двух формул:

Если формулы тройного угла `sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha` и
`cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha` разрешить относительно `sin \ 3\alpha` и `cos \ 3\alpha`, то получим формулы понижения степени для синуса и косинуса  в кубе: `sin^3 \alpha=\frac{3sin \ \alpha-sin \ 3\alpha}4` и `cos^3 \alpha=\frac{3cos \ \alpha+cos \ 3\alpha}4`.

Доказать данной равности для синуса и косинуса можно, воспользовавшись два раза формулами понижения квадратов:

`sin^4 \alpha=(sin^2 \alpha)^2=(\frac{1-cos \ 2\alpha}2)^2=` `\frac{1-2cos \ 2\alpha+cos^2 2\alpha}4=\frac{1-2cos \ 2\alpha+\frac{1+cos \ 4\alpha}2}4=` `\frac{3-4cos \ 2\alpha+cos \ 4\alpha}8`;

`cos^4 \alpha=(cos^2 \alpha)^2=(\frac{1+cos \ 2\alpha}2)^2=` `\frac{1+2cos \ 2\alpha+cos^2 2\alpha}4=\frac{1+2cos \ 2\alpha+\frac{1+cos \ 4\alpha}2}4=` `\frac{3+4cos \ 2\alpha+cos \ 4\alpha}8`.

Общий вид формул понижения степени

Для четных показателей степени (n=1, 2, 3,…):

`sin^n \alpha=\frac {C_\frac n 2^n}{2^n}+\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac n 2 -1} (-1)^{\frac n 2 -k} \cdot C_k^n \cdot cos((n-2k) \alpha)` и `cos^n \alpha=\frac {C_\frac n 2^n}{2^n}+\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac n 2 -1} C_k^n \cdot cos((n-2k) \alpha)`.

Для нечетных показателей степени (n=3, 5, 7,…):

`sin^n \alpha=\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac {n-1}2} (-1)^{\frac {n-1} 2 -k} \cdot C_k^n \cdot sin((n-2k) \alpha)` и `cos^n \alpha=\frac1{2^{n-1}} \cdot \sum_{k=0}^{\frac {n-1}2} C_k^n \cdot cos((n-2k) \alpha)`.

Примеры решения задач с применением формул понижения степени

Пример 1. Воспользуйтесь формулой понижения степени для `cos^2 4\alpha`.

Решение. Применив формулу `cos^2 \alpha=\frac{1+cos \ 2\alpha}2`, получим `cos^2 4\alpha=\frac{1+cos 2\cdot\ 4\alpha}2=\frac{1+cos 8\alpha}2`.

Ответ. `cos^2 4\alpha=\frac{1+cos 8\alpha}2`.

Пример 2. Используя выше указанные тождества, вычислить `sin^2 \frac \pi 8`.

Решение. Согласно формуле `sin^2 \alpha=\frac{1-cos \ 2\alpha}2`, понизим степень синуса. Получим `sin^2 \frac \pi 8=\frac{1-cos \ 2\frac \pi 8}2=\frac{1-cos \frac \pi 4}2`. Поскольку `cos \frac \pi 4=\frac {\sqrt 2}2`, то `sin^2 \frac \pi 8=\frac{1-cos \frac \pi 4}2=\frac{1-\frac {\sqrt 2}2}2=\frac{\frac {2-\sqrt 2}2}2=\frac {2-\sqrt 2}4`.

Ответ. `sin^2 \frac \pi 8=\frac {2-\sqrt 2}4`.

Отметим, что формулы понижения степени в тригонометрии чаще всего используются при решении уравнений и преобразовании выражений.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

matemonline.com

Формулы понижения степени. Видеоурок. Алгебра 10 Класс

Тема: Преобразование тригонометрических выражений

Урок: Формулы понижения степени

На уроке выводятся формулы понижения степени для синуса и косинуса из формул двойного аргумента, также выводятся формулы понижения степени для  тангенса и котангенса с использованием формул понижения степени для синуса и косинуса. Решается несколько задач с использованием данных формул.

Дано:

Доказать:.

Доказательство:

1) 

2) 

Итак, степень понижается за счет удвоения аргумента:

Получается,

1. Доказать:

Доказательство:

Анализ: ОДЗ не изменяется

2. Доказать:

Доказательство:

Анализ: кроме  добавляется , что сужает ОДЗ.

3. Дано:

Найти:

Анализ условия: Угол задан однозначно, см. рис.1.

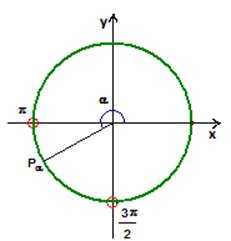
Рис. 1.

Указание: все функции половинного аргумента можно вычислять через косинус полного аргумента.

Решение:

1) 

, то , т.е. угол второй четверти, где синус величина положительная.

Ответ: .

2)

Выше показали, что  находится во второй четверти, где его косинус величина отрицательная.

Ответ:.

Проверка:

3) 

Ответ:

4) 

Ответ: .

4. Дано:  

Найти: 

Решение:

Ответ:

На уроке рассматривались формулы понижения степени и их использование при решении задач.

На следующем уроке будут рассмотрены формулы преобразования суммы тригонометрических функций в произведение.

 

Список рекомендованной литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.

8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983

 

Дополнительные веб-ресурсы

1. Интернет-портал Mathematics.ru (Источник). 

2. Портал Естественных Наук (Источник). 

3. Интернет-портал exponenta.ru (Источник). 

 

Сделай дома

№№ 21.20(а, б), 21.22(а), 21.23 (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)

interneturok.ru

Десять букв: Формулы понижения степени

Хотя в блоге можно найти и удивительные свойста числа 2013, и математические фокусы, и магические квадраты, больше всего посетителей привлекает сюда статья о правиле выноса из-под корня.

В комментариях к ней читатели задают вопросы и по другим разделам математики. Вот, например, обсуждение формулы понижения степени достойно отдельного поста.

Итак, имеем форулу косинуса двойного угла,
cos2a = cos²a — sin²a

Прибавим к обеим частям единицу
cos2a +1 = cos²a — sin²a + cos²a + sin²a
cos2a +1 = 2cos²a

Поэтому:

Так что вместо второй степени косинуса можно использовать косинус первой степени, но удвоенного угла. Аналогично квадрат синуса можно также заменять первой степенью косинуса (просто вместо прибавления единицы на первом шаге преобразования, её надо отнять):

Возникает справедливый вопрос: а можно ли понизить третью степень косинуса или синуса? Рассуждая по аналогии, попробуем вывести нужную формулу из формул тройного угла.

cos3a = cos(2a + a) = cos2a cosa — sin2a sina = (cos²a — sin²a) cosa — 2sina

cosa sina = cos³a — 3sin²a cosa = cos³a — 3(1- cos²a) cosa = 4cos³a — 3cosa

Значит, куб косинуса можно представить как:

Аналогично для куба синуса:

Для решения тригонометрических уравнений то, что после понижения степени мы получили функции от разных переменных, несколько неудобно. Но вот при интегрировании тригонометрических функций этот факт нискольrо не мешает.

Например:

Кстати, при взятиях интегралов и не только возникает нужда преобразовывать произведение тригонометрических функций в сумму. Об этом и других тригонометрических формулах есть статья-справочник в разделе «Математика в школе» блога «Эвольвента»

desyatbukv.blogspot.com

Тригонометрические формулы понижения степени — энциклопедический справочник и словарь для студента от А до Я

ОПРЕДЕЛЕНИЕ

Формулы понижения степени – это тригонометрические формулы позволяющие перейти от степеней тригонометрических функций к функциям в первой степени, но от кратного аргумента.

Формулы понижения степени для квадрата

Чаще всего на практике используются формулы понижения степени для квадрата:

Формулы (1) напрямую следуют из формул косинуса двойного угла:

Формулы понижения степени для куба косинуса или синуса

Вывести эти формулы можно двумя способами.

Первый способ. Формулы (2) напрямую следуют из тригонометрических функций тройного угла:

Второй способ. Формулы понижения степени (2) можно вывести, используя формулы (1) и формулы произведения тригонометрических функций. Рассмотрим третью степень синуса

Применим одну из формул (1) далее применим формулу произведения синусов:

Аналогично, далее применим формулу произведения косинусов:

Формулы понижения степени для четвертой степени косинуса или синуса

Эти формулы доказываются применением к ним дважды формул (1):

Примеры решения задач

ПРИМЕР 1

Задание

Понизить степень следующих выражений 1) 2)

Решение

1) Воспользуемся формулой понижения степени для квадрата косинуса , получим:

2) Применим формулы понижения степени для синуса

Ответ

ПРИМЕР 2

Задание

Вычислить, используя формулы понижения степени

1)

2)

Решение

1) Понизим степень синуса, используя формулу , получим Учитывая, что , окончательно имеем:

2) Применим к исходному выражению формулу понижения , получим:

Так как , то окончательно

Ответ

ПРИМЕР 3

Задание

Доказать тождество

Решение

По формуле понижения степени

Подставим полученное выражение в исходное тождество

Что и требовалось доказать.

sciterm.ru

Понижение степени

Определение 1

Тригонометрические формулы понижения степени — это формулы, используемые для того чтобы осуществлять перевод тригонометрического выражения, содержащего степень, в тождественное ему, содержащее меньшую степень.

Формулы понижения степени косинуса и синуса выводятся из формул двойного аргумента, выведем их для практики. Сделаем это сначала для синуса:

$\sin2x= \sin(x+x)$

К данному выражению можно применить формулу синуса суммы вида

$\sin(x+y) = \sin x \cos y + \cos x \cdot \sin y$, имеем:

$\sin2x = 2\sin x \cdot \cos x$ — данная формула называется формулой двойного аргумента для синуса.

Выразим также формулу двойного аргумента для косинуса:

$\cos2x= \cos(x+x)$

Применим к полученному выражению формулу косинуса суммы, она выглядит так — $\cos(x+y)= \cos x \cdot \cos y-\sin x \cdot \sin y$:

$\cos2x=\cos^2x-\sin^2x\left(1\right)$ — формула двойного аргумента для косинуса.

Теперь для того чтобы перейти к понижению степени, применим формулу двойного аргумента к выражению $\cos x$, получим:

$\cos x= \cos^2(\frac{x}{2})-\sin^2(\frac{x}{2})\left(2\right)$

Воспользуемся основным тригонометрическим тождеством и выразим через него квадрат косинуса половинного угла:

$\cos(\frac{x}{2})=1-\sin(\frac{x}{2})\left(3\right)$

Подставим выражение $(3)$ в $(2)$ вместо квадрата косинуса половинного аргумента:

$\cos x= 1 – \sin^2(\frac{x}{2})- \sin^2(\frac{x}{2})$

$\cos x= 1 – 2\sin^2(\frac{x}{2})$

Выразим квадрат синуса:

$\sin^2(\frac{x}{2})=\frac{1-\cos x}{2}\left(4\right)$

Полученная формула называется формулой понижения степени синуса.

Сделаем тоже самое для косинуса, для этого выразим из тригонометрического тождества квадрат синуса половинного аргумента $\sin^2(\frac{x}{2})=1-\cos^2(\frac{x}{2})$ и затем подставим в выражение $(2)$, имеем:

$\cos x=\cos^2(\frac{x}{2})-1+\cos^2(\frac{x}{2})$

$\cos x=2\cos^2(\frac{x}{2})-1$

Теперь выразим квадрат косинуса половинного аргумента:

$\cos^2(\frac{x}{2})=\frac{\cos x+1}{2}\left(5\right)$

Данная формула носит название формулы понижения степени косинуса.

Формулы $(4)$ и $(5)$ также иногда называют формулами половинного аргумента. Используя их, можно вывести формулы понижения степени для квадратов тангенса и котангенса половинного аргумента:

$tg^2(\frac{x}{2})=\frac{\sin^2(\frac{x}{2})}{\cos^2(\frac{x}{2})}=\frac{1-\cos x}{1+\cos x}$;

$ctg^2\frac{x}{2}=\frac{\cos^2(\frac{x}{2}0}{\sin^2(\frac{x}{2})}=\frac{1+\cos x}{1-\cos x}$.

Замечание 1

В случае тангенса и котангенса стоит помнить о том, что данные записи имеют смысл лишь в том случае, если в знаменателе не получается нуль.

Пример 1

Докажите, что выражение верное:

$\sin^2(\frac{π}{4}+x)=\frac{1+\sin2x}{2}$

Применим к левой части равенства формулу понижения степени для синуса:

$\sin^2(\frac{π}{4}+x)=\frac{1-\cos(2 \cdot (\frac{π}{4}+x))}{2}$

Используем формулу разложения косинуса суммы к куску $\cos(2 \cdot (\frac{π}{4}+x)$:

$\cos(2 \cdot (\frac{π}{4}+x)=\cos (\frac{π}{2}+ 2x)=\cos\frac{π}{2} \cdot \cos2x — \sin\frac{π}{2} \cdot \sin2x =0-1 \cdot \sin2x= — \sin2x$

Используем полученное и подставим в наше равенство:

$\sin^2(\frac{π}{4}+x)=\frac{1+sin2x}{2}$

Равенство выполняется, что и требовалось доказать.

spravochnick.ru

10 класс. Алгебра. Преобразование тригонометрических выражений. Формулы двойного аргумента и понижения степени. — Формулы понижения степени.

Комментарии преподавателя

Фор­му­лы по­ни­же­ния сте­пе­ни

На уроке вы­во­дят­ся фор­му­лы по­ни­же­ния сте­пе­ни для си­ну­са и ко­си­ну­са из фор­мул двой­но­го ар­гу­мен­та, также вы­во­дят­ся фор­му­лы по­ни­же­ния сте­пе­ни для  тан­ген­са и ко­тан­ген­са с ис­поль­зо­ва­ни­ем фор­мул по­ни­же­ния сте­пе­ни для си­ну­са и ко­си­ну­са. Ре­ша­ет­ся несколь­ко задач с ис­поль­зо­ва­ни­ем дан­ных фор­мул.

Дано:

До­ка­зать:.

До­ка­за­тель­ство:

1) 

2) 

Итак, сте­пень по­ни­жа­ет­ся за счет удво­е­ния ар­гу­мен­та:

По­лу­ча­ет­ся, 

1. До­ка­зать:

До­ка­за­тель­ство:

Ана­лиз: ОДЗ не из­ме­ня­ет­ся 

2. До­ка­зать:

До­ка­за­тель­ство:

Ана­лиз: кроме  до­бав­ля­ет­ся , что сужа­ет ОДЗ.

www.kursoteka.ru

Формулы понижения степени (профильный) — методическая рекомендация. Алгебра, 10 класс.

1.	Формулы тригонометрии	1 вид — рецептивный	лёгкое	1 Б.	Даны различные тригонометрические формулы. Выбрать формулы понижения степени.
2.	Применение формулы понижения степени (синус)	1 вид — рецептивный	лёгкое	1 Б.	Для выполнения данного задания необходимо применить формулу понижения степени.
3.	Формула понижения степени (косинус)	1 вид — рецептивный	лёгкое	1 Б.	Необходимо воспользоваться формулой понижения степени (косинус).
4.	Косинус	2 вид — интерпретация	лёгкое	1 Б.	Для решения данного задания необходимо воспользоваться формулой понижения степени (косинус).
5.	Синус	2 вид — интерпретация	среднее	1 Б.	Упражнение выполняется, используя формулу понижения степени (синус).
6.	Тангенс	2 вид — интерпретация	среднее	1 Б.	Применение формулы понижения степени (тангенс).
7.	Использование тригонометрических формул	3 вид — анализ	сложное	1 Б.	Для решения данного задания необходимо воспользоваться основной тригонометрической формулой и формулой понижения степени.
8.	Использование формул понижения степени	3 вид — анализ	сложное	1 Б.	Для решения данного задания необходимо воспользоваться двумя формулами понижения степени.
9.	Вычисление значения выражения	3 вид — анализ	сложное	1 Б.	Вычисление значение выражения с использованием формулы понижения степени.

www.yaklass.ru

No related posts.